Chapter 01.06
Propagation of Errors
If a calculation is made with numbers that are not exact, then the calculation itself will have
an error. How do the errors in each individual number propagate through the calculations.
Let’s look at the concept via some examples.
Example 1
Find the bounds for the propagation error in adding two numbers. For example if one is
calculating
Y
X
+
where
05
.
0
5
.
1
±
=
X
,
04
.
0
4
.
3
±
=
Y
.
Solution
By looking at the numbers, the maximum possible value of X and Y are
55
.
1
=
X
and
44
.
3
=
Y
Hence
99
.
4
44
.
3
55
.
1
=
+
=
+ Y
X
is the maximum value of
Y
X
+
.
The minimum possible value of X and Y are
45
.
1
=
X
and
.
36
.
3
=
Y
Hence
36
.
3
45
.
1
+
=
+ Y
X
81
.
4
=
is the minimum value of
Y
X
+
.
Hence
.
99
.
4
81
.
4
≤
+
≤
Y
X
One can find similar intervals of the bound for the other arithmetic operations of
. What if the evaluations we are making are function evaluations
instead? How do we find the value of the propagation error in such cases.
Y
X
Y
X
Y
X
/
and
,
*
,
−
If
f
is a function of several variables
, then the maximum
possible value of the error in is
n
n
X
X
X
X
X
,
,.......,
,
,
1
3
2
1
−
f
n
n
n
n
X
X
f
X
X
f
X
X
f
X
X
f
f
Δ
∂
∂
+
Δ
∂
∂
+
+
Δ
∂
∂
+
Δ
∂
∂
≈
Δ
−
−
1
1
2
2
1
1
.......
01.06.1
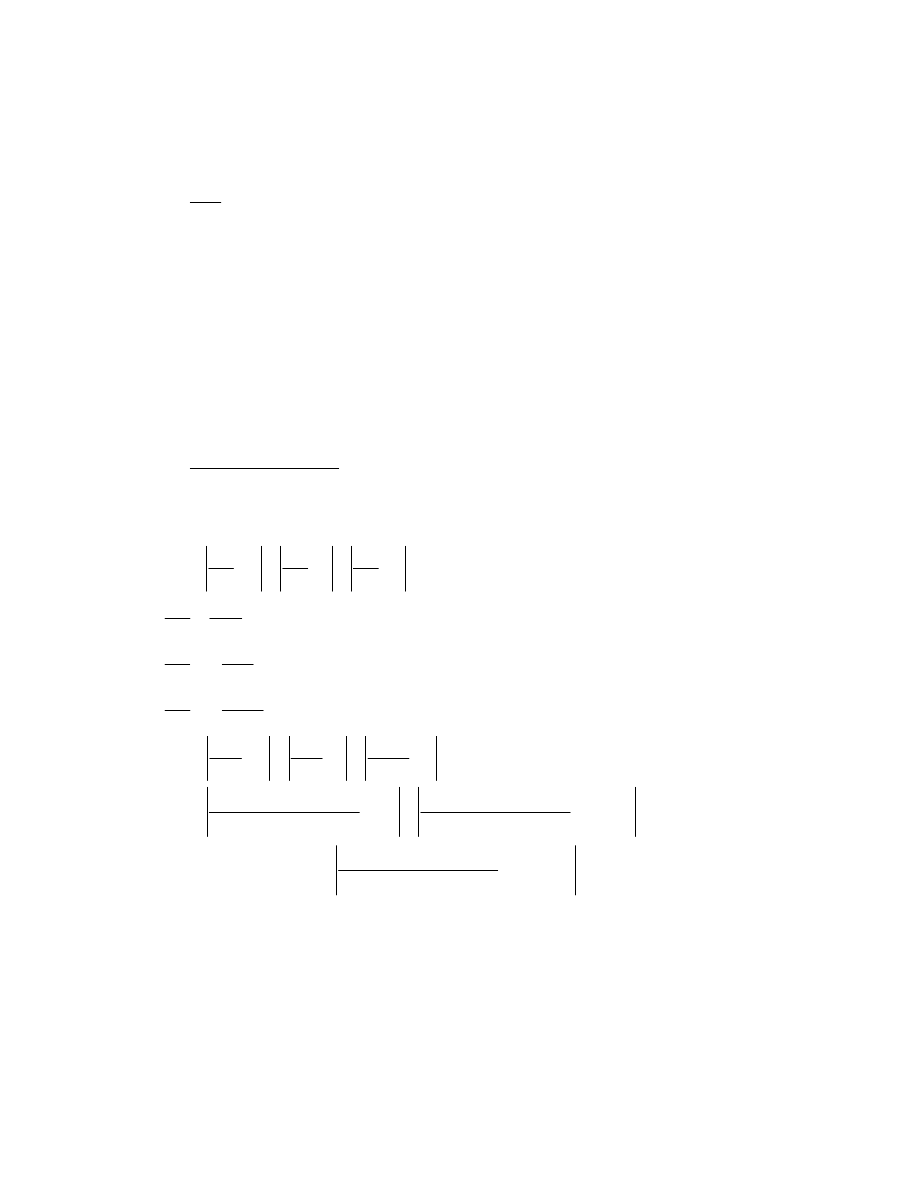
01.06.2
Chapter 01.06
Example 2
The strain in an axial member of a square cross-section is given by
E
h
F
2
∈=
where
F
=axial force in the member, N
h = length or width of the cross-section, m
E
=Young’s modulus, Pa
Given
N
9
.
0
72
±
=
F
mm
1
.
0
4
±
=
h
GPa
5
.
1
70
±
=
E
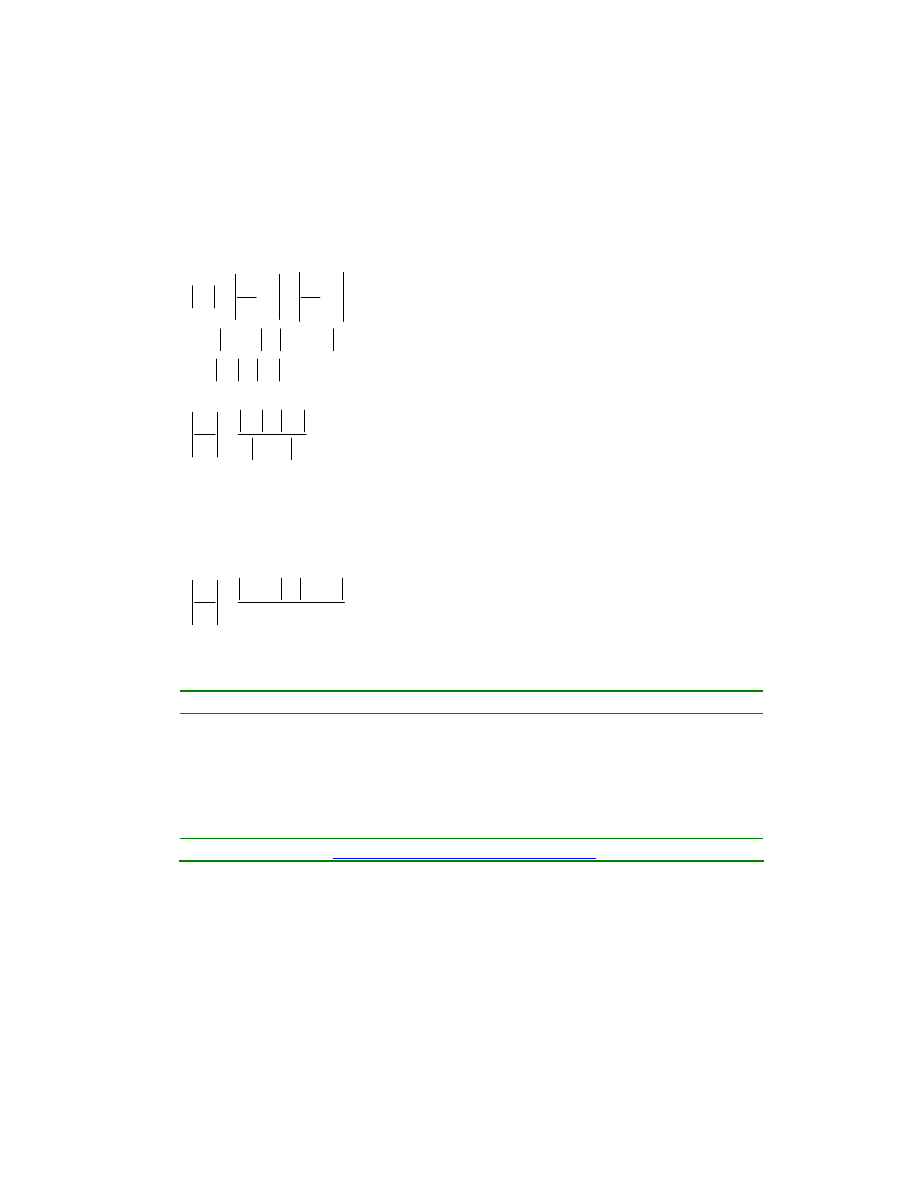
Find the maximum possible error in the measured strain.
Solution
)
10
70
(
)
10
4
(
72
9
2
3
×
×
∈=
−
6
10
286
.
64
−
×
=
μ
286
.
64
=
E
E
h
h
F
F
Δ
∂
∈
∂
+
Δ
∂
∈
∂
+
Δ
∂
∈
∂
∈=
Δ
E
h
F
2
1
=
∂
∈
∂
E
h
F
h
3
2
−
=
∂
∈
∂
2
2
E
h
F
E
−
=
∂
∈
∂
E
E
h
F
h
E
h
F
F
E
h
E
Δ
+
Δ
+
Δ
=
Δ
2
2
3
2
2
1
9
2
9
2
3
9
3
3
9
2
3
10
5
.
1
)
10
70
(
)
10
4
(
72
0001
.
0
)
10
70
(
)
10
4
(
72
2
9
.
0
)
10
70
(
)
10
4
(
1
×
×
×
×
+
×
×
×
×
+
×
×
×
=
−
−
−
6
6
7
10
3776
.
1
10
2143
.
3
10
0357
.
8
−
−
−
×
+
×
+
×
=
6
10
3955
.
5
−
×
=
μ
3955
.
5
=
Hence
)
3955
.
5
286
.
64
(
μ
μ
±
∈=
implying that the axial strain,
∈
is between
μ
8905
.
58
and
μ
6815
.
69
Propagation of Errors
01.06.3
Example 3
Subtraction of numbers that are nearly equal can create unwanted inaccuracies. Using the
formula for error propagation, show that this is true.
Solution
Let
y
x
z
−
=
Then
y
y
z
x
x
z
z
Δ
∂
∂
+
Δ
∂
∂
=
Δ
y
x
Δ
−
+
Δ
=
)
1
(
)
1
(
y
x
Δ
+
Δ
=
So the absolute relative change is
y
x
y
x
z
z
−
Δ
+
Δ
=
Δ
As
x
and become close to each other, the denominator becomes small and hence create
large relative errors.
y
For example if
001
.
0
2
±
=
x
001
.
0
003
.
2
±
=
y
|
003
.
2
2
|
001
.
0
001
.
0
−
+
=
Δ
z
z
= 0.6667
= 66.67%
INTRODUCTION TO NUMERICAL METHODS
Topic
Propagation of Errors
Summary
Textbook notes on how errors propagate in arithmetic and
function evaluations
Major
All Majors of Engineering
Authors
Autar Kaw
Last Revised
December 7, 2008
Web Site
http://numericalmethods.eng.usf.edu