8.4.2 Graniczne naprężenie przyczepności

(1)P Aby uniemożliwić zniszczenie na skutek utraty przyczepności, należy zapewnić wystarczającą
przyczepność graniczną.

(2)

Wartość obliczeniową granicznego naprężenia przyczepności f

bd

dla prętów żebrowanych

można wyznaczyć ze wzoru

f

bd

= 2,25

η

1

η

2

f

ctd

(8.2)

w którym:

f

ctd

jest wartością obliczeniową wytrzymałości betonu na rozciąganie według 3.1.6(2)P; ze
względu na zwiększoną kruchość betonu o wyższej wytrzymałości nie należy stosować
wartości f

ctk,0,05

większych niż przypisane betonowi C60/75, o ile nie można wykazać, że

średnie siły przyczepności przekraczają tę granicę,

η

1

jest współczynnikiem zależnym od jakości warunków przyczepności i pozycji pręta w
czasie betonowania (patrz Rysunek 8.2):

η

1

= 1,0 gdy warunki są „dobre”,

η

1

= 0,7 we wszystkich innych przypadkach i zawsze dla prętów w elementach konstrukcji

wykonywanych w formach ślizgowych, o ile nie można wykazać, że istnieją „dobre”
warunki przyczepności,

η

2

zależy od średnicy pręta:

η

2

= 1,0 dla

φ

≤ 32 mm,

η

2

= (132 -

φ

)/100 dla

φ

> 32 mm.

a) 45

o

≤

≤

≤

≤

α

α

α

α

≤

≤

≤

≤ 90

o

c) h > 250 mm

A - kierunek betonowania

b) h

≤

≤

≤

≤ 250 mm

d) h > 600 mm

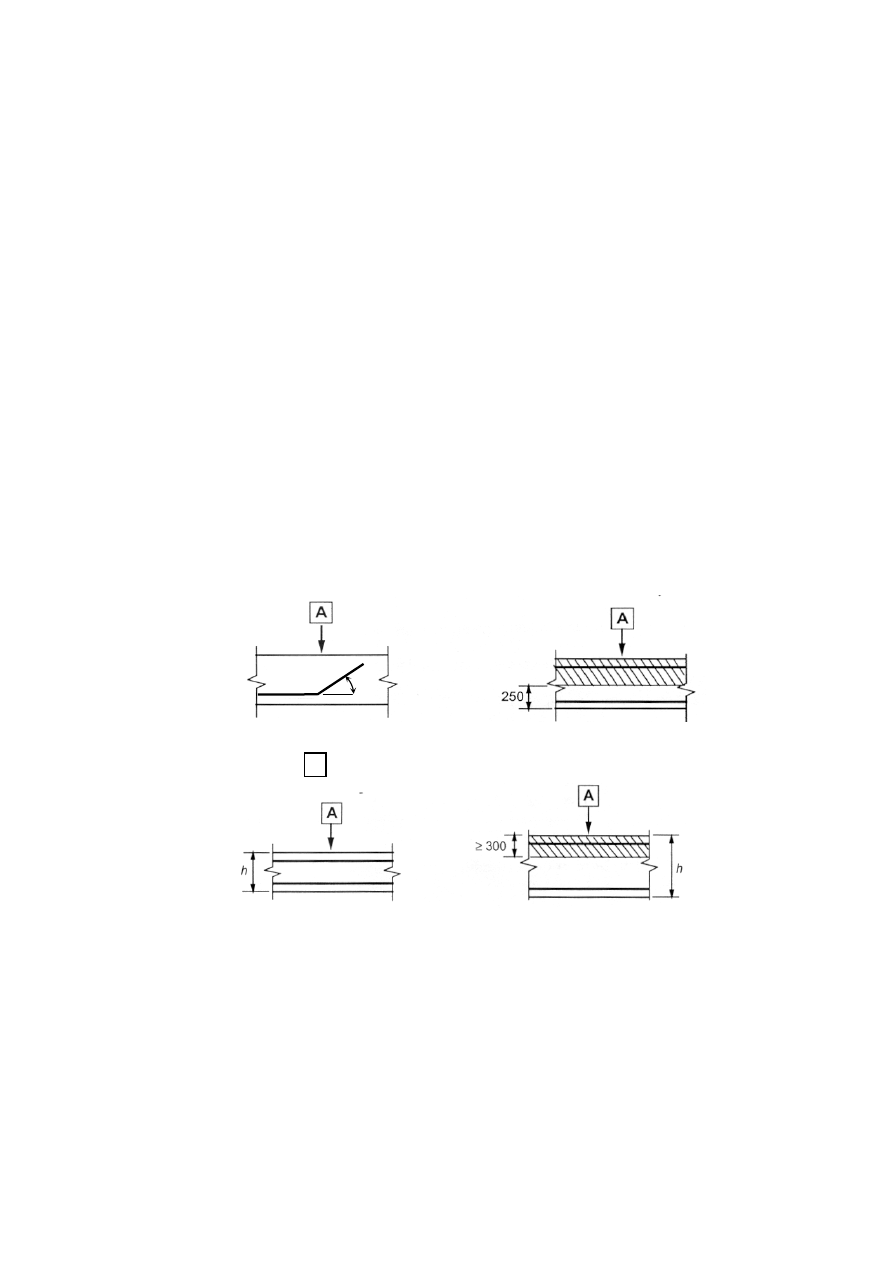
Rysunek 8.2: Warunki przyczepności

a) i b) „dobre” warunki
przyczepności wszystkich prętów

c i d) strefa niezakreskowana –
„dobre” warunki przyczepności,
strefa zakreskowana – „słabe”
warunki przyczepności

α

8.4.3 Podstawowa długość zakotwienia

(1)P Obliczając wymaganą długość zakotwienia, należy wziąć pod uwagę rodzaj stali i te właściwości
prętów, które mają wpływ na przyczepność .

(2)

Podstawową, wymaganą długość zakotwienia l

b,rqd

, potrzebną do osiągnięcia w prostym pręcie

siły A

s

σ

sd

, oblicza się - zakładając, że naprężenie przyczepności jest stałe i równe f

bd

- ze wzoru

bd

sd

rqd

b

f

l

σ

φ

4

,

=

(8.3)

w którym

σ

sd

jest naprężeniem obliczeniowym w miejscu, od którego odmierza się długość

zakotwienia. Wartości f

bd

podano w 8.4.2.

(3)

Podstawową długość zakotwienia prętów zagiętych l

b

i długość obliczeniową l

bd

mierzy się

wzdłuż osi pręta (patrz Rysunek 8.1a).

(4)

Jeżeli do utworzenia spajanej struktury stosuje się pary drutów lub prętów, to średnicę

φ

w

wyrażeniu (8.3) zastępuje się średnicą zastępczą

2

φ

φ

=

n

.

8.4.4 Obliczeniowa długość zakotwienia

(1)

Obliczeniową długość zakotwienia l

bd

wyznacza się ze wzoru

l

bd

=

α

1

α

2

α

3

α

4

α

5

l

b,rqd

, lecz nie mniej l

b,min

,

(8.4)

w którym:

α

1

,

α

2

,

α

3

,

α

4

i

α

5

są współczynnikami określonymi w Tablicy 8.2:

α

1

- jest współczynnikiem zależnym od kształtu prętów, przy założeniu, że otulenie jest

odpowiednie (Rysunek 8.1),

α

2

- jest współczynnikiem zależnym od najmniejszego otulenia betonem (Rysunek 8.3),

α

3

- jest współczynnikiem zależnym od wpływu skrępowania betonu przez zbrojenie

poprzeczne,

α

4

-

stosuje się w celu uwzględnienia wpływu jednego lub większej liczby prętów
poprzecznych (

φ

t

> 0,6

φ

) przyspojonych na obliczeniowej długości zakotwienia (patrz

także 8.6),

α

5

- stosuje się w celu uwzględnienia wpływu nacisku poprzecznego do płaszczyzny

rozłupywania wzdłuż obliczeniowej długości zakotwienia.

Iloczyn

α

2

α

3

α

5

powinien spełniać nierówność

α

2

α

3

α

5

≥ 0,7

(8.5)

l

b,rqd

- oblicza się ze wzoru (8.3),

l

b,min

- jest minimalną długością zakotwienia (gdy inne przepisy nie implikują długości

większej):

- przy kotwieniu prętów rozciąganych l

b,min

= max{0,3l

b,rqd

;10

φ

; 100 mm},

(8.6)

- przy kotwieniu prętów ściskanych l

b,min

= max{0,6l

b,rqd

; 10

φ

; 100 mm}.

(8.7)

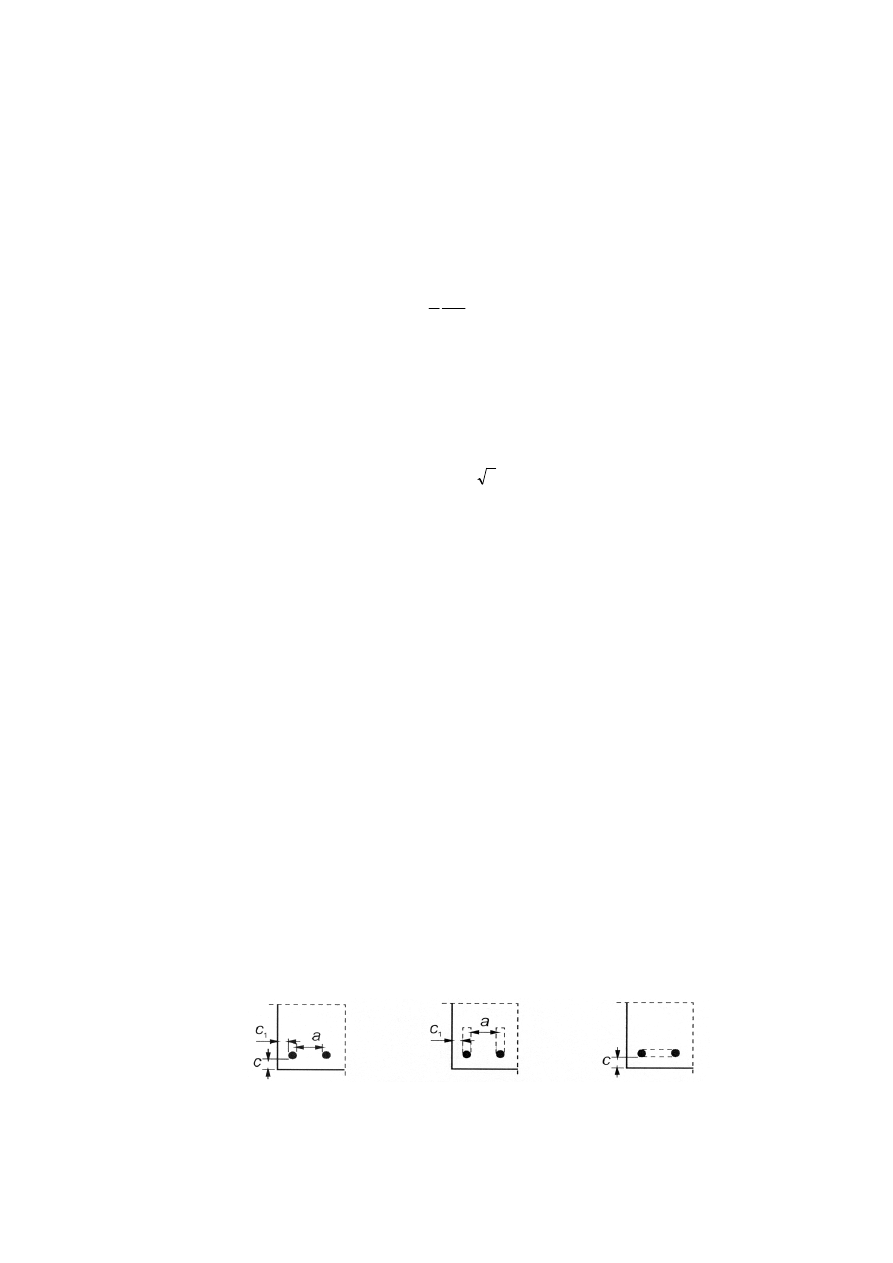
(a) Pręty proste

b) Pręty zagięte lub pręty c) Pręty z pętlami

c

d

= min{0,5a; c

1

, c} z hakami c

d

= min{0,5a; c

1

}

c

d

= c

Rysunek 8.3: Wartości c

d

w belkach i płytach

(2)

Jako uproszczenie 8.4.4(1), przy kotwieniu prętów rozciąganych o kształtach przedstawionych

na Rysunku 8.1, można stosować równoważną długość zakotwienia l

b,eq

określoną na tym rysunku,

równą:

α

1

l

b,rqd

- dla kształtów pokazanych na Rysunkach 8.1b do 8.1d (wartości

α

1

według Tablicy

8.2),

α

4

l

b,rqd

- dla kształtu według Rysunku 8.1e (wartości

α

4

według Tablicy 8.2),

α

1

i

α

4

- zdefiniowano w (1),

l

bd

- oblicza się ze wzoru (8.3).

Tablica 8.2: Wartości współczynników

α

α

α

α

1

,

α

α

α

α

2

,

α

α

α

α

3

,

α

α

α

α

4

i

α

α

α

α

5

Czynnik wpływający na
wartości współczynników

Rodzaj zakotwienia

Pręt zbrojenia

rozciągany

ściskany

Kształt prętów

Proste

α

1

= 1,0

α

1

= 1,0

Inny niż proste
(Rysunek 8.1 (b), (c) i (d))

α

1

= 0,7 jeżeli c

d

> 3

φ

,

w innych przypadkach

α

1

=

1,0
(wartości c

d

- patrz Rysunek

8.3)

α

1

= 1,0

Otulenie betonem

Proste

φ

φ

α

−

−

=

d

c

15

,

0

1

2

, lecz

nie mniej niż 0,7

i nie więcej niż 1,0

α

2

= 1,0

Inne niż proste
(Rysunek 8.1 (b), (c) i (d))

φ

φ

α

3

15

,

0

1

2

−

−

=

d

c

, lecz

nie mniej niż 0,7

i nie więcej niż 1,0

(wartości c

d

- patrz Rysunek

8.3)

α

2

= 1,0

Ograniczenie odkształceń
przez zbrojenie
poprzeczne nie
przyspojone do zbrojenia
głównego

Wszystkie rodzaje

α

3

= 1 - K

λ

, lecz

nie mniej niż 0,7

i nie więcej niż 1,0

α

3

= 1,0

Ograniczenie odkształceń
przez przyspojone
zbrojenie poprzeczne

*

Wszystkie rodzaje,
usytuowanie i wymiary jak
na Rysunku 8.1 (e)

α

4

= 0,7

α

4

= 0,7

Ograniczenie odkształceń
przez nacisk poprzeczny

Wszystkie rodzaje

α

5

= 1 – 0,04p, lecz

nie mniej niż 0,7

i nie więcej niż 1,0

-

Oznaczenia:

s

st

st

A

A

A

∑

∑

−

=

min

,

λ

∑A

st

pole przekroju zbrojenia poprzecznego wzdłuż obliczeniowej długości

zakotwienia l

bd

,

∑A

st,min

pole przekroju minimalnego zbrojenia poprzecznego równe 0,25A

s

dla

belek i zero dla płyt,

A

s

pole przekroju pojedynczego kotwionego pręta (dotyczy pręta o

największej średnicy),

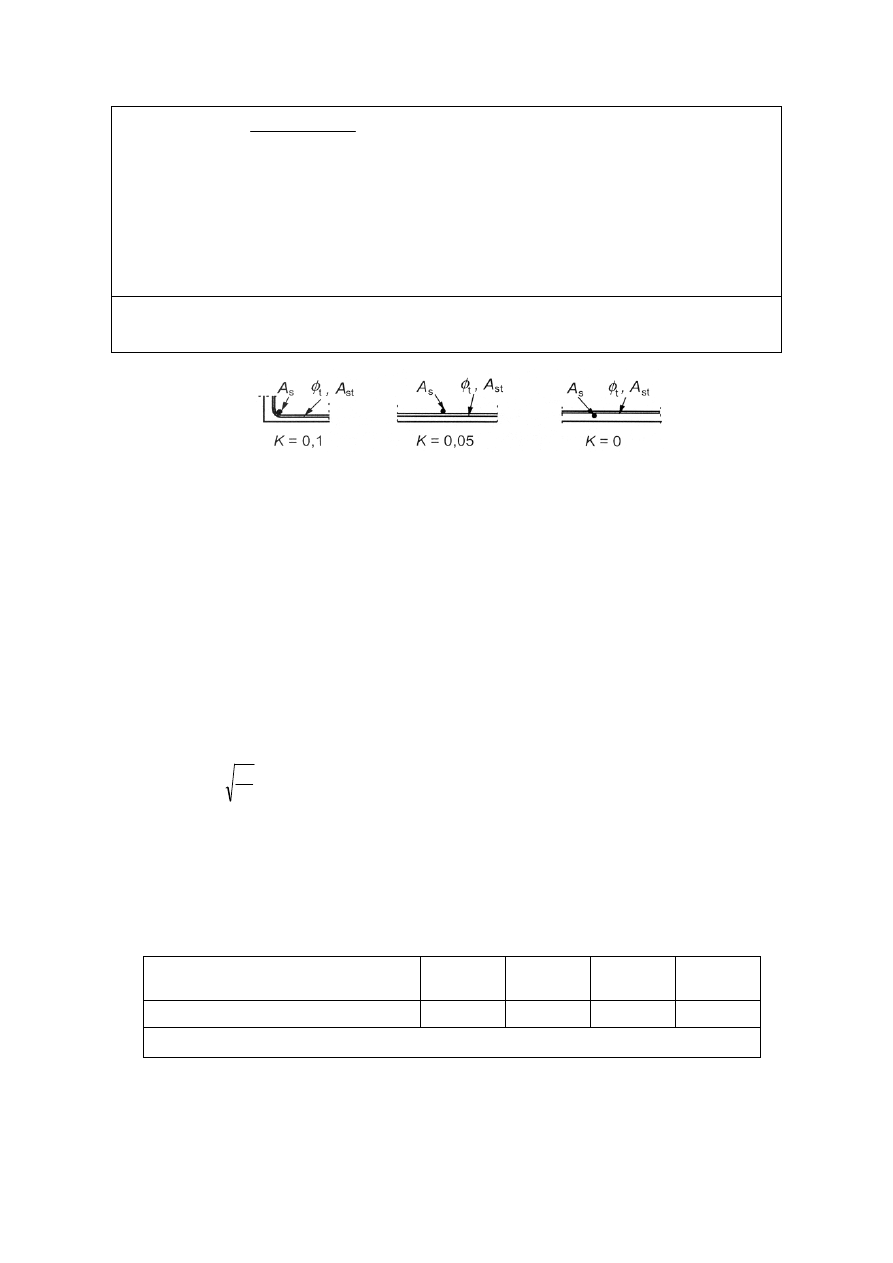
K

wartości podano na Rysunku 8.4,

p

nacisk poprzeczny [MPa] wzdłuż l

bd

w stanie granicznym nośności.

*

Patrz także 8.6: Przy podporach bezpośrednich można przyjąć l

bd

mniejsze niż l

b,min

pod warunkiem, że na

odcinku podpory znajduje się co najmniej jeden przyspojony pręt. Powinien być on umieszczony w
odległości co najmniej 15 mm od krawędzi podpory.

Rysunek 8.4: Wartości K w belkach i płytach

8.7.3 Długość zakładu

(1)

Obliczeniowa długość zakładu wynosi

,

=

,

6

5

3

2

1

0

rqd

b

l

α

α

α

α

α

l

lecz nie mniej niż l

0,min

(8.10)

W powyższym wzorze:

l

b,rqd

oblicza się ze wzoru (8.3),

l

0,min

= max{0,3

α

6

l

b,rqd

; 15

φ

; 200 mm},

(8.11)

wartości

α

1

,

α

2,

,

α

3

i

α

5

można wziąć z Tablicy 8.2; jednakże obliczając

α

3

na miejsce

∑A

st,min

należy podstawić (A

s,single

σ

sd

/f

yd

) (A

s,single

oznacza tu pole przekroju jednego pręta

łączonego na zakład),

25

1

6

ρ

α

=

, lecz nie więcej niż 1,5 i nie mniej niż 1,0,

ρ

1

oznacza udział (w całym polu przekroju zbrojenia) zbrojenia połączonego na zakłady,

które mieszczą się w obszarze rozciągającym się w dwie strony na odległość 0,65l

0

od

środka rozpatrywanej długości zakładu (patrz Rysunek 8.8); wartości

α

6

podano w

Tablicy 8.3.

Tablica 8.3: Wartości współczynnika

α

α

α

α

6

Udział prętów połączonych na zakład
w całym polu przekroju zbrojenia

< 25 %

33 %

50 %

>50 %

α

6

1

1,15

1,4

1,5

Uwaga: Wartości pośrednie można określać przez interpolację.

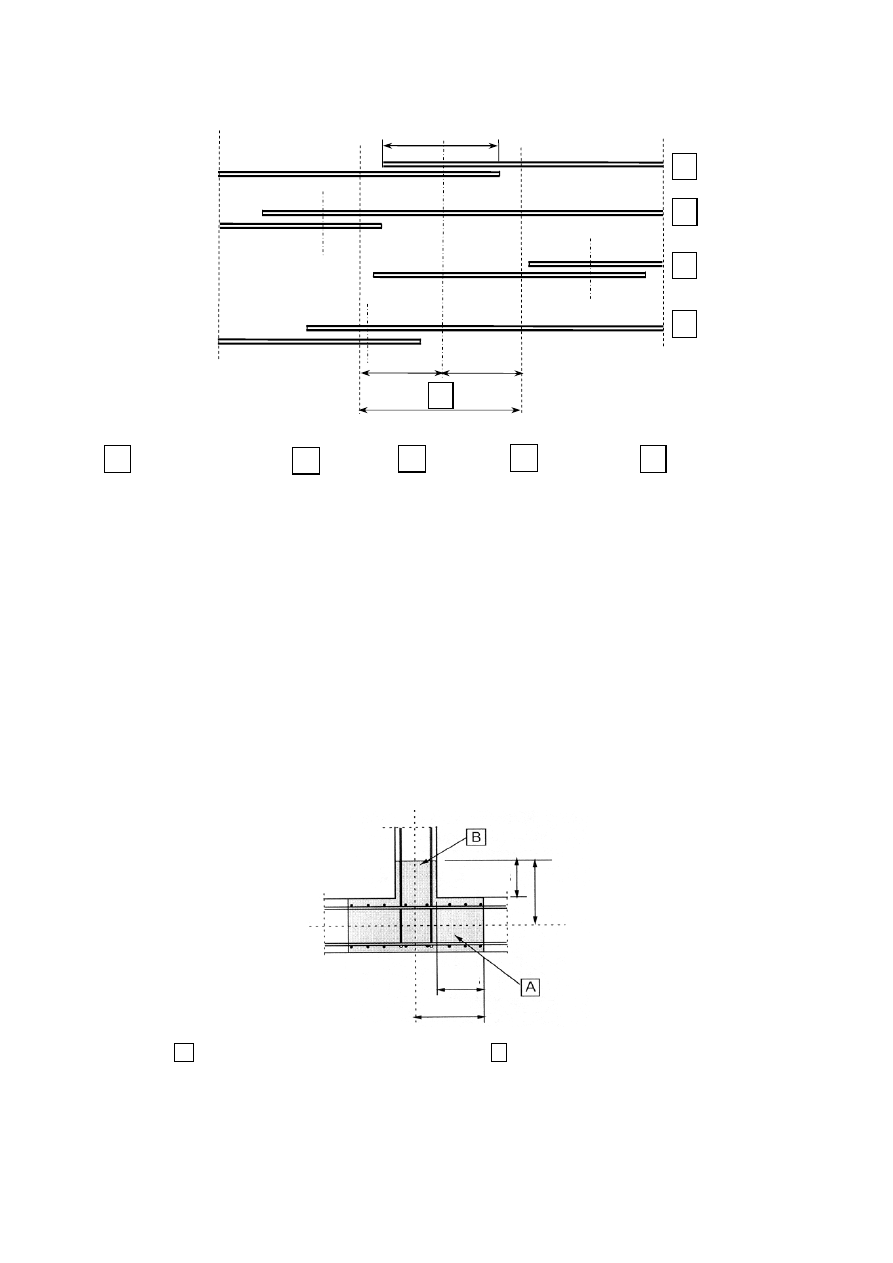
- rozważany przekrój

- pręt I

- pręt II - pręt III

- pręt IV

Przykład: pręty II i III znajdują się na zewnątrz rozważanego przekroju: ρ

1

= 50% i

α

6

= 1,4.

Rysunek 8.8: Udział prętów łączonych na zakład w środkowej części połączenia
w całym połączeniu na zakład

9.2.5 Podparcia pośrednie

(1)

Jeżeli belka jest oparta na belce, a nie na ścianie lub słupie, to należy zaprojektować i umieścić

w konstrukcji zbrojenie przenoszące wzajemne reakcje. Zbrojenie to jest dodatkiem do zbrojenia
potrzebnego z innych powodów. Regułę tę stosuje się także do płyt, które nie są oparte na górze
belki.

(2)

Zbrojenie przenoszące reakcje między dwiema belkami powinno składać się ze strzemion

otaczających zbrojenie główne elementu podpierającego. Niektóre z tych strzemion można
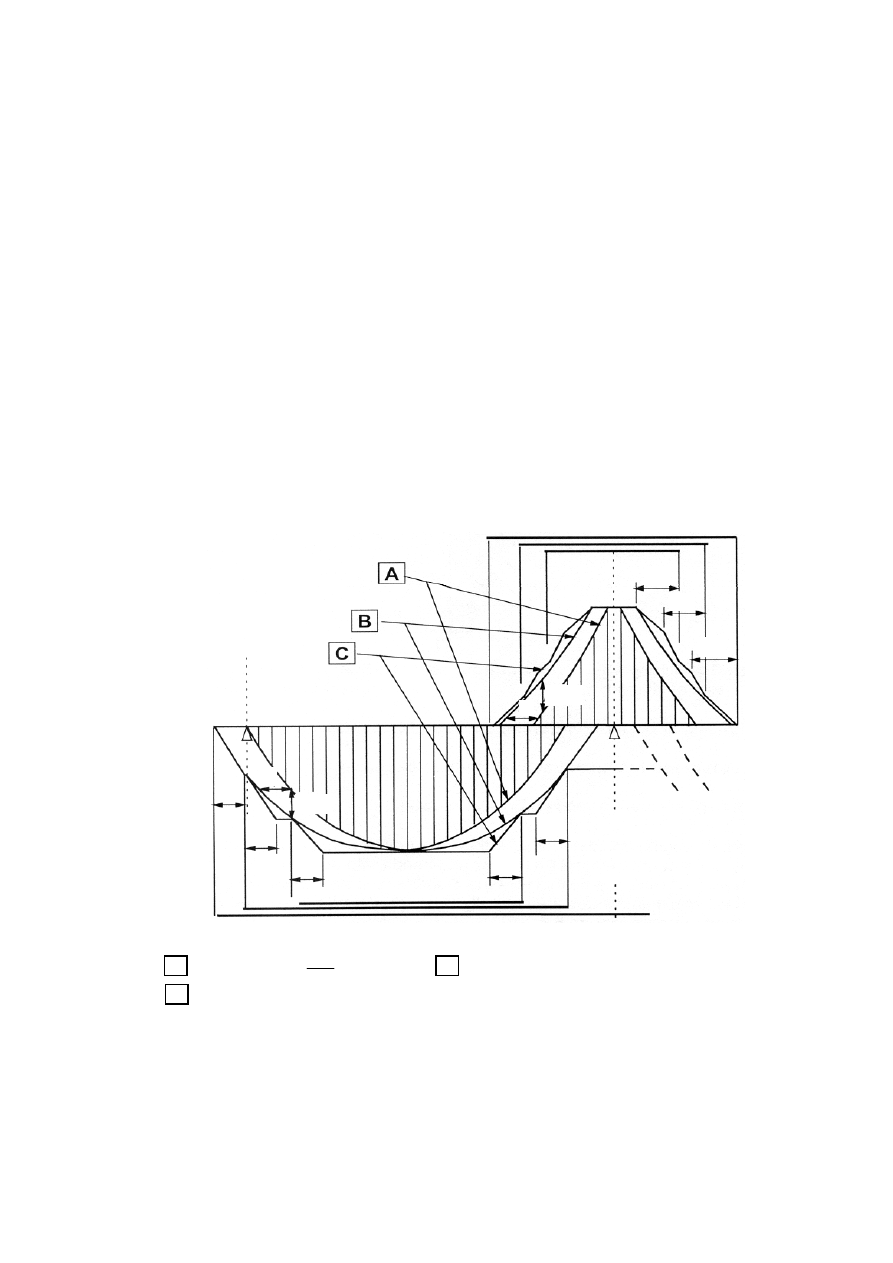
rozmieszczać poza częścią wspólną betonu dwóch łączonych belek (Rysunek 9.7).

Rysunek 9.7: Rozmieszczanie zbrojenia podporowego w strefie przecięcia dwóch belek
(widok w planie)

l

0

A

0,65 l

0

0,65 l

0

B

C

D

E

A

B

C

D

E

≤ h

1

/2

≤ h

2

/3

≤ h

2

/2

≤ h

1

/3

A - belka podpierająca o wysokości h

1

B - belka podparta o wysokości h

2

(h

1

≥ h

2

)

9.2.1.3 Kończenie rozciąganego zbrojenia podłużnego

(1)

W każdym przekroju należy umieścić zbrojenie wystarczające do przeniesienia ekstremalnych

sił rozciągających, które mogą działać w tym przekroju; wyznaczając te siły, uwzględnia się wpływ
ukośnych rys w środnikach i półkach.

(2)

W elementach wymagających zbrojenia na ścinanie dodatkową siłę rozciągającą

∆F

td

należy

obliczyć według 6.2.3(7). W elementach, które nie wymagają zbrojenia na ścinanie, wpływ

∆F

td

można

estymować, rozsuwając wykres momentów o odległość a

l

= d zgodnie z 6.2.2(5). Taką „regułę

przesuwania” można również stosować jako inny niż w 6.2.3(7) sposób uwzględniania wpływu

∆F

td

w

elementach, które wymagają zbrojenia na ścinanie, przyjmując

(

)

α

θ

cot

cot

5

,

0

−

=

z

a

l

(symbole określono w 6.2.3).

(9.2)

Dodatkowa siła rozciągająca jest zilustrowana na Rysunku 9.2.

(3)

Można założyć, że na odcinkach, na których następuje zakotwienie prętów, siła w zbrojeniu

zmienia się liniowo (patrz Rysunek 9.2). Jako bezpieczne uproszczenie udział tych odcinków w
nośności zbrojenia można pominąć.

(4)

Długość zakotwienia prętów odgiętych, które przyczyniają się do wzrostu nośności na ścinanie,

powinna być nie mniejsza niż 1,3l

bd

w strefie rozciąganej i 0,7l

bd

w strefie ściskanej. Długość tę

odmierza się od punktu przecięcia osi pręta odgiętego i zbrojenia podłużnego.

Rysunek 9.2: Rozmieszczanie zbrojenia podłużnego z uwzględnieniem wpływu rys ukośnych

i narastania nośności zbrojenia na długości zakotwienia

l

bd

l

bd

l

bd

l

bd

l

bd

l

bd

l

bd

l

bd

∆F

td

a

l

∆F

td

a

l

A – obwiednia siły

Ed

Ed

N

z

M

+

, B – siła rozciągająca w zbrojeniu F

s

,

C - nośność zbrojenia na rozciąganie F

Rs