Technika cieplna

w

inzynierii bezpieczenstwa

PROJEKT

Wymiennik ciepla do

podgrzewania wody.

Maciej Rabiej

Grupa 12B2

TEMAT:

Zaprojektować wymiennik ciepła do podgrzewania wody od temperatury 45 [

0

C] do 95

[

0

C]. Natężenie przepływu wody: 24 [kg/s], prędkość wody w rurkach: 0,8 [m/s],

czynnikiem grzewczym jest para nasycona o ciśnieniu 0,7 [MPa] (wymiennik

przeciwprądowy). Materiał rurek wymiennika K18. Średnica zewnętrzna rurek : 25

mm. Grubość ścianki rurek 2,9 mm.

Dane do projektu:

-

natężenie przepływu wody: 24 [kg/s]

-

prędkość wody w rurkach: 0,8 [m/s]

-

czynnik grzewczy, para nasycona o ciśnieniu: pA = 0,7 [MPa]

- tB2 = 45 [0 C] = 318,15 [K]

- tB1 = 95 [0 C] = 368,15 [K]

-

materiał rurek wymiennika K18

-Cpb –

ciepło właściwe wody dla średniej temperatury wody

- Cpb’ –

ciepło właściwe wody dla średniej temperatury pływów

-dz -

średnica zewnętrzna rurek: 25 [mm] ; r2 = 12,5 [mm]

grubość ścianki rurek: 2,9 [mm]

-dw -

średnica wewnętrzna rurek : 25 - 2*2,9 = 19,2 [mm] ; r1= 9,6 [mm]

Pozostałe wielkości:
C

p b

-

ciepło właściwe wody dla średniej temperatury wody = 4170 [J /

kg* K]

C

p b

' -

ciepło właściwe wody dla śr. temperatury płynów = 4240 [J/ kg*K]

ν - lepkość kinematyczna wody dla średniej temp. wody = 0,556 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[

𝒎𝒎

𝟐𝟐

/

𝒔𝒔]

ν' - lepkość kinematyczna wody dla śr. temp. płynów 0,257 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[

𝒎𝒎

𝟐𝟐

/𝒔𝒔]

ν

k

-

lepkość kinematyczna kondensatu = 0,186 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[

𝒎𝒎

𝟐𝟐

/𝒔𝒔]

ρ - gęstość wody dla średniej temperatury wody = 988,1[kg/𝒎𝒎

𝟑𝟑

]

ρ' - gęstość wody dla średniej temperatury płynów = 944,95[kg/𝒎𝒎

𝟑𝟑

]

ρ

k

-

gęstość kondensatu = 902,4[kg/𝒎𝒎

𝟑𝟑

]

ɳ - lepkość dynamiczna wody dla średniej temperatury wody 549,38 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[kg/ms]

ɳ' - lepkość dynamiczna wody dla średniej temp. płynów = 242,85 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[kg/ms]

ɳ

k

-

lepkość dynamiczna kondensatu wody przy ciś. nasycenia = 167,84 *

𝟏𝟏𝟏𝟏

−𝟔𝟔

[kg/ms]

λ

r

-

współczynnik przewodzenia materiału rurki = 49,07 [W/mK]

λ - współczynnik przewodzenia dla śr. temp. wody= 648 * 𝟏𝟏𝟏𝟏

−𝟑𝟑

[W/mK]

λ' - współczynnik przewodzenia dla śr. temp. płynów= 681,016 * 𝟏𝟏𝟏𝟏

−𝟑𝟑

[W/mK]

λ

k

-

współczynnik przewodzenia kondensatu = 685,76 * 𝟏𝟏𝟏𝟏

−𝟑𝟑

[W/mK]

𝟏𝟏

𝛂𝛂

𝟏𝟏

− 𝐨𝐨𝐨𝐨ó𝐫𝐫 𝐜𝐜𝐜𝐜𝐜𝐜𝐨𝐨𝐜𝐜𝐜𝐜𝐜𝐜 𝐨𝐨𝐨𝐨𝐨𝐨𝐨𝐨𝐨𝐨 𝐨𝐨𝐜𝐜𝐨𝐨 𝐰𝐰𝐨𝐨𝐨𝐨𝐜𝐜 = 𝟏𝟏, 𝟏𝟏𝟏𝟏𝟏𝟏𝟐𝟐𝟎𝟎 [

𝐦𝐦

𝟐𝟐

𝐊𝐊

𝐖𝐖

]

Bilans cieplny:

Przyjmujemy, że skraplanie pary zachodzi według przemiany izobarycznej i nie występuje

przechłodzenie skroplin.

.
Q = m

A

c

pA

Δt

A

= m

B

c

pB

Δt

B

.
Q = m

A

r

A

= m

B

c

pB

Δt

B

.
Q = m

A

r

A

= m

B

r

B

gdzie: r

A

–

ciepło właściwe skraplania pary

Temperaturę pary grzejnej określamy przy danym ciśnieniu (temperatura nasycenia) i
odczytujemy dla zadanego p

A

. Otrzymujemy wartość t

A1

= t

A2

oraz

ciepło właściwe

skraplania pary przy zadanym ciśnieniu pary nasyconej r

A

(entalpia parowania).

Dla p

A

= 0,7 [MPa] = 7,0 [bar]

t

A1

= t

A2

= 164,96 [

0

C] = 438,11 [K]

r

A

= 2067 [kJ/kg]

Obliczamy:

Δt

A

= t

A2

- t

A1

-

różnica temperatur pary na wlocie i na wylocie

Δt

A

u nas wynosi 0.

Stąd :

c

Pbk =

4,36 [kJ / kg K]

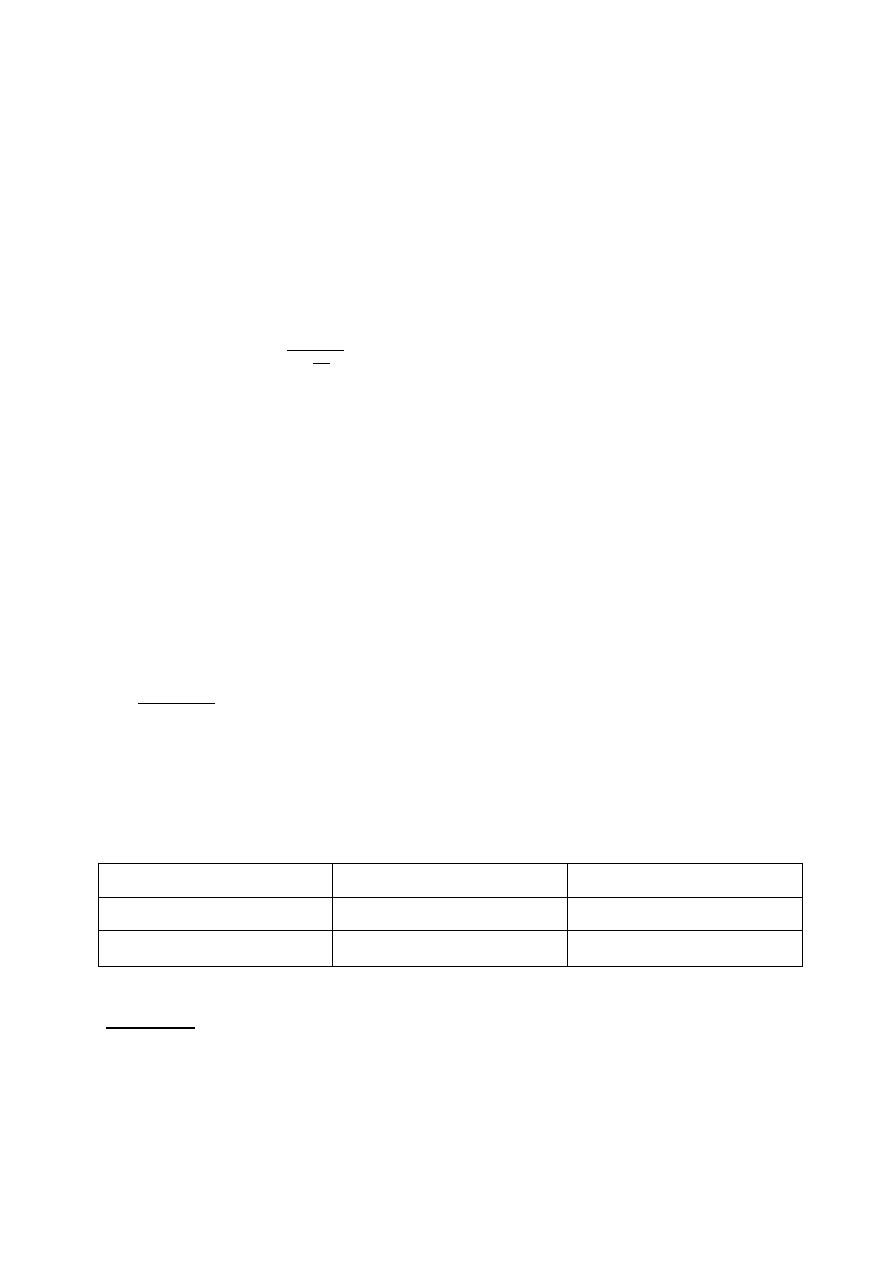
Δt

B

= t

B2

– t

B1

-

różnica temperatur wody na wlocie i na wylocie

Δt

B

= 368,15 [K] – 318,15 [K] = 50 [K]

Δt

1

= t

A1

– t

B2

-

różnica temperatur początkowych pary i wody

Δt

1

= 438,11 [K] –318,15 [K] = 119,96 [K]

Δt

2

= t

A2

– t

B1

-

różnica temperatur końcowych pary i wody

Δt

2

= 438,11 [K] –368,15 [K] = 69,96 [K]

Stosujemy wzór:

Δt

śr

=

𝚫𝚫𝚫𝚫𝟏𝟏 −𝚫𝚫𝚫𝚫𝟐𝟐

ln

𝚫𝚫𝚫𝚫𝟏𝟏

𝚫𝚫𝚫𝚫𝟐𝟐

Δt

śr

= (119,96 - 69,96) / 0,54 = 92,7 [K]

Obliczamy średnią temperaturę pary

Δt

śrA

= (t

A1

+ t

A2

) / 2 = t

A1

= t

A2

Δt

śrA

= (438,11 [K] + 438,11 [K] ) / 2 = 438,11 [K] = 164,96 [

o

C]

Δt

śrB

=

∆t

śrA

-

∆t

śr

Δt

śrB

= 438,11 [K] – 92,7 [K] = 345,41 [K] =72,26 [

o

C]

(‘)

𝚫𝚫𝚫𝚫ś𝐫𝐫𝐫𝐫 +𝚫𝚫𝚫𝚫ś𝐫𝐫𝐫𝐫

𝟐𝟐

= 391,81 [K] = 118,66 [

o

C]

Wtedy : c

Pb’ =

4,24 [kJ / kg K]

Przyjmujemy : c

pB

= 4,17 [kJ / kg K]

Oraz :

𝝂𝝂 = 0,556 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[

𝒎𝒎

𝟐𝟐

/𝒔𝒔]

𝝆𝝆 = 988,1[kg/𝒎𝒎

𝟑𝟑

]

𝜼𝜼 =549,38 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[kg/ms]

𝝂𝝂

𝒌𝒌

=0,186 *

𝟏𝟏𝟏𝟏

−𝟔𝟔

[

𝒎𝒎

𝟐𝟐

/𝒔𝒔]

𝝆𝝆

𝒌𝒌

=902,4[kg/

𝒎𝒎

𝟑𝟑

]

𝜼𝜼

𝒌𝒌

=167,84 *

𝟏𝟏𝟏𝟏

−𝟔𝟔

[kg/ms]

𝝂𝝂’ = 0,257 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[

𝒎𝒎

𝟐𝟐

/𝒔𝒔]

𝝆𝝆’=944,95[kg/𝒎𝒎

𝟑𝟑

]

𝜼𝜼’=242,85 * 𝟏𝟏𝟏𝟏

−𝟔𝟔

[kg/ms]

Obliczamy:
.
Q = m

B*

c

pB*

Δt

B

.
Q = 24 [kg/s] * 4,19 [kJ / kg K] * 50 [K] = 5028000 [J/s]

Obliczenie powierzchni wymiany ciep

ła:

.

Q = k F Δt

śr

gdzie: F – powierzchnia wymiany

Czyli:

F =

Q

(k Δtśr)

F = 5028000 [J/s] / (1200 [W / m

2

K] * 92,6 [K] ) = 45,25 [m

2

]

Dobór wst

ępny wymiennika:

Dla obliczonej powierzchni F dobieramy wstępnie wymiennik ciepła. Należy wybrać

materiał, z którego zostanie wykonany ë.

L –

długość rur

n –

liczba rur (zaokrąglić w górę)

.

m

B

=

π dw 2

4

ρwn

więc:
.

n =

4 mB

π dw 2 ρw

Prędkość wody w rurkach : 0,8 [m/s]

ρ = 988,1 [kg/m

3

]

d

z

= 25 mm = 0,025 [m]

s = 2,9 mm = 0,0029 [m]
d

w

= d

z

- 2s= 0,0192 [m]

n =

4 mB

π dw 2 ρw

n = 4 * 24/ 3,14 * ( 0,0192)

2

* 988,1 * 0,8 = 104,91

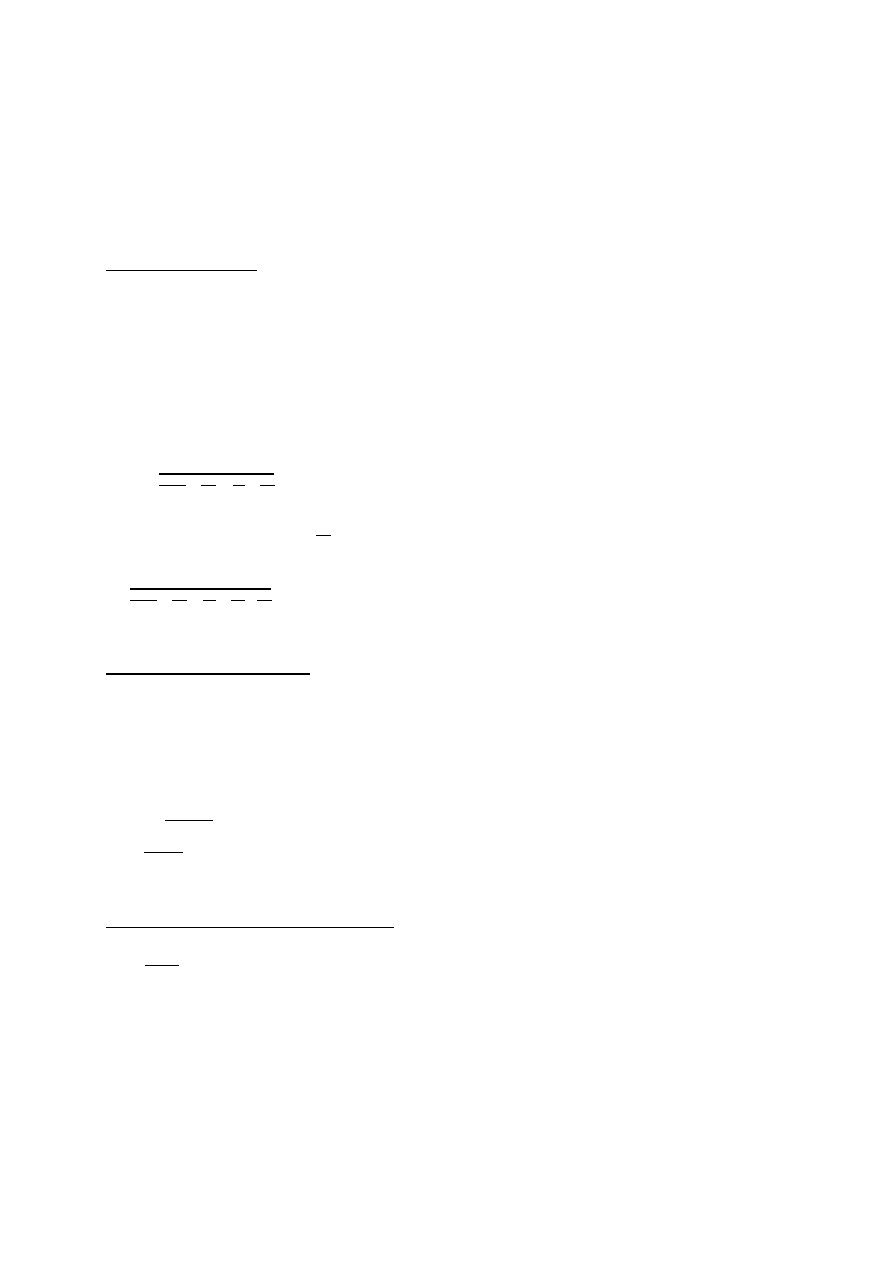
Obliczona powierzchnia wymiany:
F = n

π d

z

L

więc:
L = F / n

π d

z

L = 45,25 / 104,91* 3,14 * 0,025 = 5,494 [m]

Obliczamy liczbę k.

Aby obliczyć prawidłową wartość powierzchni należy określić k.

Zadanie zostało rozwiązane dla przyjętej wartości k i należy sprawdzić poprawność doboru

tego współczynnika.

Wiemy że Q=nkFΔt

śr

Współczynnik k zależy od wyboru powierzchni. Przyjmijmy że liczymy współczynnik dla

powierzchni zewnętrznej.
To k=

1

𝑟𝑟2

𝑟𝑟1𝛼𝛼1

+

𝑟𝑟2

𝜆𝜆𝑟𝑟

ln

𝑟𝑟2

𝑟𝑟1

+

1

𝛼𝛼2

dodaje się dodatkowy opór (

1

𝛼𝛼

0

= 0,00025 [mK/W] )

k=

1

𝑟𝑟2

𝑟𝑟1𝛼𝛼1

+

𝑟𝑟2

𝜆𝜆𝑟𝑟

ln

𝑟𝑟2

𝑟𝑟1

+

1

𝛼𝛼2

+

1

𝛼𝛼0

Obliczamy liczbę Prandtla

𝝀𝝀

𝒓𝒓

= 49,07 [W/mK]

𝝀𝝀 = 648 * 𝟏𝟏𝟏𝟏

−𝟑𝟑

[W/mK]

𝝀𝝀

𝒌𝒌

= 685,76 * 𝟏𝟏𝟏𝟏

−𝟑𝟑

[W/mK]

𝝀𝝀

′

= 681,016 * 𝟏𝟏𝟏𝟏

−𝟑𝟑

[W/mK]

Prsc’ =

𝜼𝜼’+𝐜𝐜𝐏𝐏𝐏𝐏’

λ

′

= 242,85 *

𝟏𝟏𝟏𝟏

−𝟔𝟔

+ 4,24 [kJ / kg K] / 681,016 *

𝟏𝟏𝟏𝟏

−𝟑𝟑

[W/mK] = 1,512

Pr =

𝜼𝜼+𝐜𝐜𝐏𝐏𝐏𝐏

λ

= 549,38 *

𝟏𝟏𝟏𝟏

−𝟔𝟔

[kg/ms] + 4,17 [kJ / kg K] / 648 *

𝟏𝟏𝟏𝟏

−𝟑𝟑

[W/mK] = 3,533

Obliczamy wartość liczby Reynoldsa:

Re =

𝑤𝑤 𝐷𝐷𝑤𝑤

𝑣𝑣

Re= 0,8 [m/s] * 0,0192 [m] / 0,556 *

𝟏𝟏𝟏𝟏

−𝟔𝟔

[

𝒎𝒎

𝟐𝟐

/𝒔𝒔] = 27625,89

Obliczamy Liczbę Nusselta.

Nu = 0,021 Re

0,8

Pr

0,43

((Pr / Pr

śc

)

0,25

)

Nu = 0,021 *

(𝟐𝟐𝟐𝟐𝟔𝟔𝟐𝟐𝟎𝟎, 𝟖𝟖𝟖𝟖)

𝟏𝟏,𝟖𝟖

*

(𝟑𝟑, 𝟎𝟎𝟑𝟑𝟑𝟑)

𝟏𝟏,𝟒𝟒𝟑𝟑

*

((

𝟑𝟑,𝟎𝟎𝟑𝟑𝟑𝟑
𝟏𝟏,𝟎𝟎𝟏𝟏𝟐𝟐

)

𝟏𝟏,𝟐𝟐𝟎𝟎

) = 1596,328

Obliczamy współczynnik wnikania ciepła od strony wody.

α

1

obliczamy ze wzoru na liczbę Nusselta:

Nu =

α

1

d

w

/

λ

więc:

α

1

= Nu

λ / d

w

-

dla wartości współczynników dobranych z tabel dla średniej temperatury

wody

𝛼𝛼

1

=

Nu λ

dw

𝛼𝛼

1

=

1596,328 ∗ 648 ∗ 10

−3

0,0192

= 53876,07

Obliczamy współczynnik wnikania ciepła od strony pary.

𝑚𝑚

𝐴𝐴

=

̇

𝑄𝑄

𝑟𝑟

𝐴𝐴

=

5028 𝑘𝑘𝑘𝑘

𝑠𝑠

2067 𝑘𝑘𝑘𝑘

𝑘𝑘𝑘𝑘

= 2,4325

𝑘𝑘𝑘𝑘

𝑠𝑠

g=9,81 m/s

2

𝛼𝛼

2

= 0,7

4

3

∗ [

𝜆𝜆

𝑘𝑘

3

∗𝜌𝜌

𝑘𝑘

2

∗𝐿𝐿∗𝜋𝜋∗𝑘𝑘∗𝑛𝑛

ɳ

𝑘𝑘

∗𝑚𝑚

𝐴𝐴

̇

]

1

3

= 13996,55

𝑊𝑊

𝑚𝑚

2

∗𝐾𝐾

Mając α

1

i α

2

mamy też k :

𝑘𝑘 =

1

𝑟𝑟

2

𝑟𝑟

1

∗ 𝛼𝛼

1

+ 𝑟𝑟

2

𝜆𝜆

𝑟𝑟

ln 𝑟𝑟

2

𝑟𝑟

1

+ 1

𝛼𝛼

2

+ 1

𝛼𝛼

0

=

1

0,0125𝑚𝑚

0,0096𝑚𝑚 ∗ 53876,07 𝑊𝑊

𝑚𝑚

2

∗ 𝐾𝐾

+ 0,0125𝑚𝑚

49,07 𝑊𝑊

𝑚𝑚 ∗ 𝐾𝐾

ln �0,0125𝑚𝑚

0,0096𝑚𝑚� +

1

13996,55 𝑊𝑊

𝑚𝑚

2

∗ 𝐾𝐾

+ 0,00025 𝑚𝑚

2

∗ 𝐾𝐾

𝑊𝑊

=

2422,150[

𝑊𝑊

𝑚𝑚

2

∗𝐾𝐾

]

Otrzymaliśmy nową wartość k.

Obliczamy

błąd.

∆ =

|𝑘𝑘

𝑛𝑛𝑛𝑛𝑤𝑤𝑛𝑛

− 𝑘𝑘 |

𝑘𝑘

𝑛𝑛𝑛𝑛𝑤𝑤𝑛𝑛

∗ 100% =

| 2422,150 − 1200 |

2422,150

∗ 100% = 50,46%

Wykonujemy dodatkowe obliczenia k dla nowych wartości F i L (dla nowej, obliczonej

wartości k

nowe

) do czasu, gdy błąd nie będzie większy od 5% .

Znajdujemy nową wartość powierzchni :

𝐹𝐹 =

5028000𝑊𝑊

2422,150 ∗ 92,6 = 22,417 𝑚𝑚

2

Znajdujemy nową wartość L :

𝐿𝐿 =

22,417 𝑚𝑚

2

104,91 ∗ 𝜋𝜋 ∗ 0,025𝑚𝑚 = 5,820 𝑚𝑚

Nową wartość α

2

:

𝛼𝛼

2

= 0,7

4

3

∗ [

𝜆𝜆

𝑘𝑘

3

∗ 𝜌𝜌

𝑘𝑘

2

∗ 𝐿𝐿 ∗ 𝜋𝜋 ∗ 𝑘𝑘 ∗ 𝑛𝑛

ɳ

𝑘𝑘

∗ 𝑚𝑚

𝐴𝐴

̇

]

1

3

= 14268,08

𝑊𝑊

𝑚𝑚

2

∗ 𝐾𝐾

Nowa wartość k:

𝑘𝑘 =

1

𝑟𝑟

2

𝑟𝑟

1

∗ 𝛼𝛼

1

+ 𝑟𝑟

2

𝜆𝜆

𝑟𝑟

ln 𝑟𝑟

2

𝑟𝑟

1

+ 1

𝛼𝛼

2

+ 1

𝛼𝛼

0

=

1

0,0125𝑚𝑚

0,0096𝑚𝑚 ∗ 53876,07 𝑊𝑊

𝑚𝑚

2

∗ 𝐾𝐾

+ 0,0125𝑚𝑚

49,07 𝑊𝑊

𝑚𝑚 ∗ 𝐾𝐾

ln �0,0125𝑚𝑚

0,0096𝑚𝑚� +

1

14268,08 𝑊𝑊

𝑚𝑚

2

∗ 𝐾𝐾

+ 0,00025 𝑚𝑚

2

∗ 𝐾𝐾

𝑊𝑊

=

2430,153[

𝑊𝑊

𝑚𝑚

2

∗𝐾𝐾

]

Błąd :

∆ =

|𝑘𝑘

𝑛𝑛𝑛𝑛𝑤𝑤𝑛𝑛

− 𝑘𝑘 |

𝑘𝑘

𝑛𝑛𝑛𝑛𝑤𝑤𝑛𝑛

∗ 100% =

| 2430,153 − 2422,150|

2430,153

∗ 100% = 0,33% < 5%

Dla tak obliczonej powierzchni F dodajemy 10% powierzchni jako rezerwę

( dodatkowo ilość rurek n+10%n )

F+10%F = 24,659 m

2

n+10%n = 115,401

Znając liczbę rur znajdujemy średnicę wewnętrzną płaszcza.

𝐹𝐹 = 𝜋𝜋𝑅𝑅

2

−> 𝑅𝑅 = �

𝐹𝐹
𝜋𝜋 = 2,671𝑚𝑚

Oraz dane potrzebne do rysunku graficznego przekroju wymiennika ciepła

t=(1,5÷1,25)d

z

t= (37,5mm÷31,25mm)