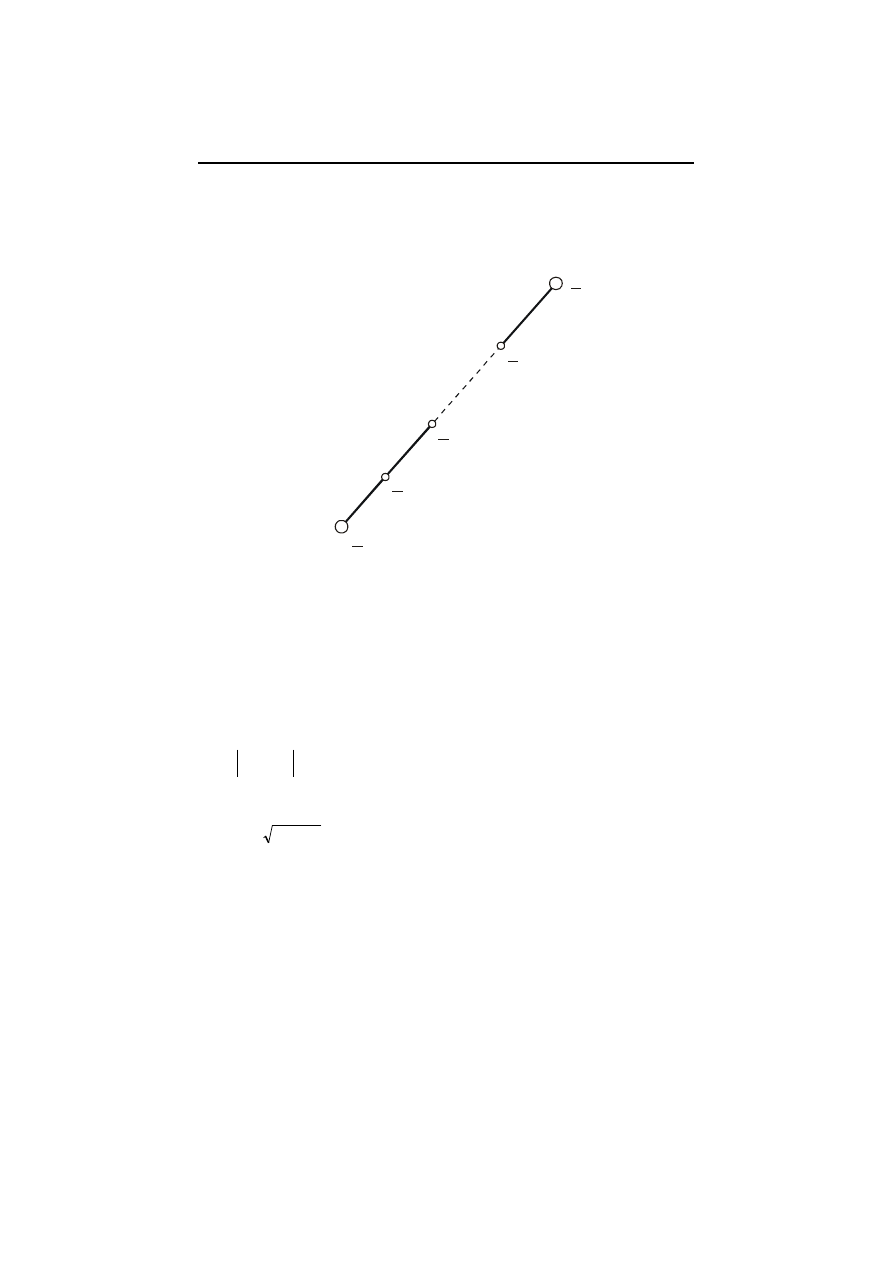
Obliczenie współrzędnych punktów posiłkowych

Punkty posiłkowe n

÷

1 występują na prostej wyznaczonej przez dwa punkty A i B o

znanych współrzędnych.

B

A

n

2

1

REALIZACJA

Obliczamy odchyłkę pomiędzy długością odcinka AB określoną z pomiaru l

AB

i długością

określoną ze współrzędnych

AB

lˆ

. Odchyłka ta powinna spełniać kryterium podane w Instrukcji

G-4

l

AB

AB

f

lˆ

l

≤

−

gdzie

2

2

l

c

l

u

f

+

=

u – współczynnik błędów przypadkowych,

l – długość odcinka,

c – błędy położenia punktów o znanych współrzędnych.

Współrzędne i-tego punktu posiłkowego liczymy wzorami

r

l

Y

Y

Y

Y

1

i

1

i

1

i

1

i

i

⋅

∆

+

=

∆

+

=

−

−

−

−

q

l

X

X

X

X

1

i

1

i

1

i

1

i

i

⋅

∆

+

=

∆

+

=

−

−

−

−

gdzie

1

i

i

1

i

l

l

l

−

−

−

=

∆

AB

AB

l

Y

r

∆

=

AB

AB

l

X

q

∆

=

Po obliczeniu przyrostów

∆

Y i

∆

X sumujemy ich wartości i porównujemy z różnicą

współrzędnych Y

B

– Y

A

i X

B

– X

A

punktów osnowy. Może wystąpić odchyłka f

y

i f

x

spowodowana niedokładnością obliczeń, odchyłkę tę w formie poprawek rozrzucamy na

poszczególne przyrosty z przeciwnym znakiem.

Kontrolę obliczeń wykonujemy wzorami

∑

=

∆

AB

l

l

r

l

Y

Y

n

n

B

⋅

∆

+

=

q

l

X

X

n

n

B

⋅

∆

+

=

Przykład

A

B

1

2

3

4

y = 1126,97

A

x = 2737,13

A

y = 1303,45

B

x = 2848,87

B

0

.

0

0

5

4

.

8

7

9

2

.

3

1

1

2

8

.

6

3

1

7

6

.

4

9

2

0

8

.

8

3

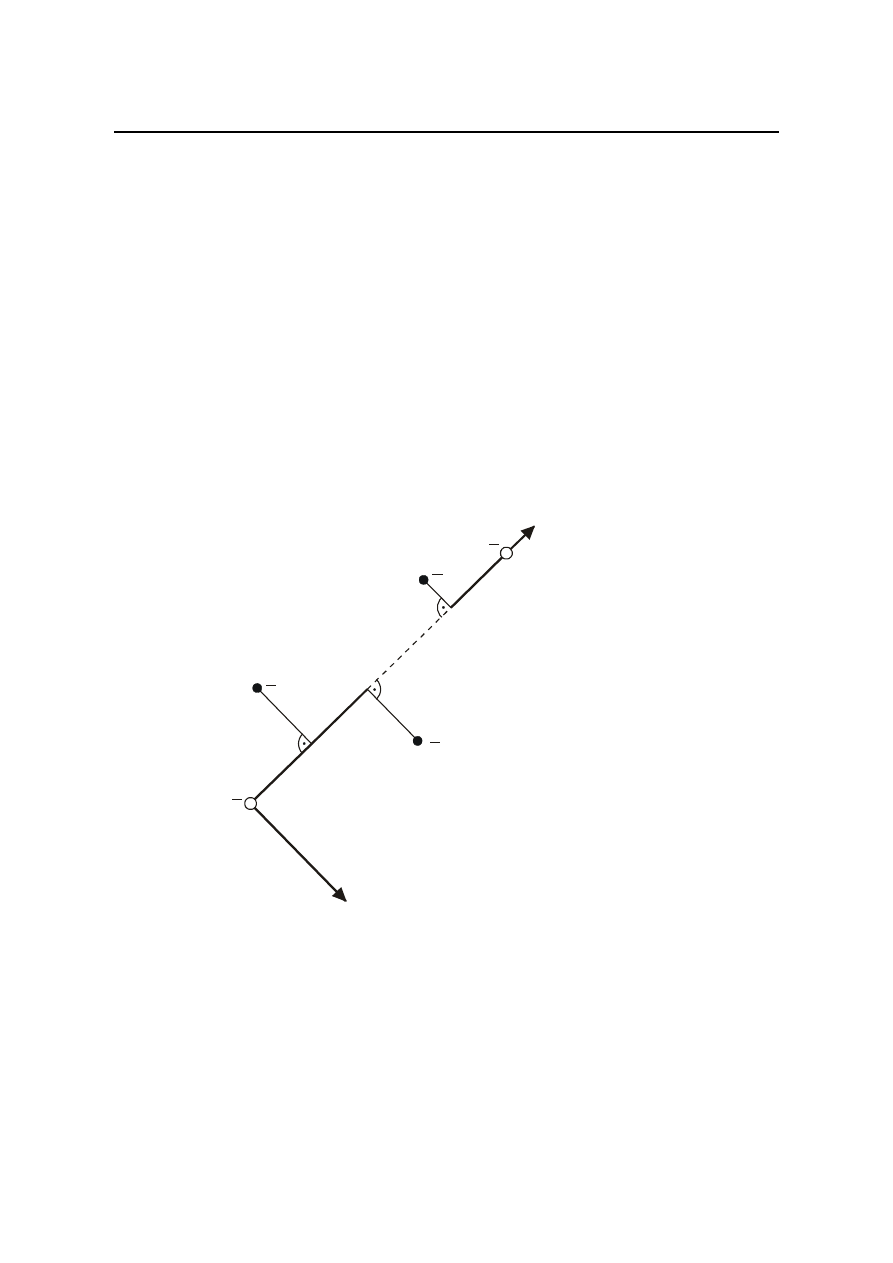
Obliczenie współrzędnych punktów na domiarach prostokątnych

Metoda rzędnych i odciętych albo inaczej domiarów prostokątnych jest jedną z

podstawowych metod zdjęcia szczegółów sytuacyjnych.

Współrzędne punktów na domiarach liczymy wzorami

q

h

r

l

Y

Y

i

i

A

i

⋅

+

⋅

+

=

r

h

q

l

X

X

i

i

A

i

⋅

−

⋅

+

=

gdzie: r, q – współczynniki określone w/w wzorami

h – rzędne,

l – odcięte.

Wzory te są słuszne dla dowolnego azymutu linii AB i lokalnego układu współrzędnych.

Układ ten wyznaczają: początek układu umieszczony w punkcie A, oś +l pokrywająca się z

prostą AB i oś +h prostopadła do osi l – skierowana na prawo

B

n

2

1

A

+ h

B

+ l

Wzory na obliczenie współrzędnych nie dają jednak możliwości kontroli obliczeń i

dlatego w praktyce powinny być stosowane wzory w następującej postaci

1

i

1

i

1

i

1

i

1

i

i

Y

Y

q

h

r

l

Y

Y

−

−

−

−

−

∆

+

=

⋅

∆

+

⋅

∆

+

=

1

i

1

i

1

i

1

i

1

i

i

X

X

r

h

q

l

X

X

−

−

−

−

−

∆

+

=

⋅

∆

−

⋅

∆

+

=

gdzie

1

i

i

1

i

l

l

l

−

−

−

=

∆

1

i

i

1

i

h

h

h

−

−

−

=

∆

q

h

r

l

Y

1

i

1

i

1

i

⋅

∆

+

⋅

∆

=

∆

−

−

−

r

h

q

l

X

1

i

1

i

1

i

⋅

∆

−

⋅

∆

=

∆

−

−

−

Kontrolę obliczeń wykonujemy także wzorami

∑

=

∆

AB

l

l

∑

=

∆

0

h

q

h

r

l

Y

Y

n

n

n

B

⋅

∆

+

⋅

∆

+

=

r

h

q

l

X

X

n

n

n

B

⋅

∆

−

⋅

∆

+

=

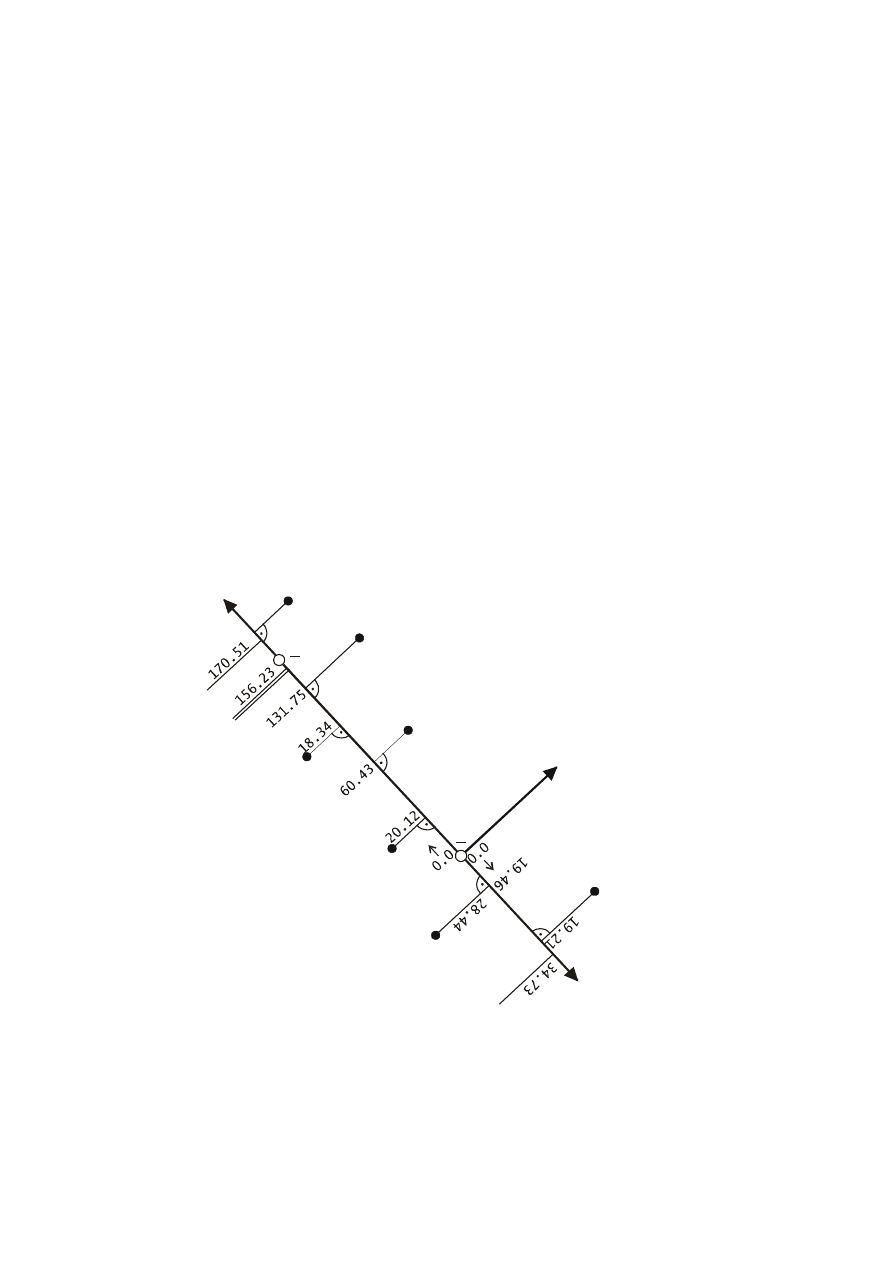
Przykłady

Obliczyć współrzędne punktów na domiarach prostokątnych dla danych podanych na

rysunku

7

17

.3

4

+ l

+h

2

1

3

4

5

6

A

B

20

.9

7

93

.7

9

24

.7

3

25

.5

1

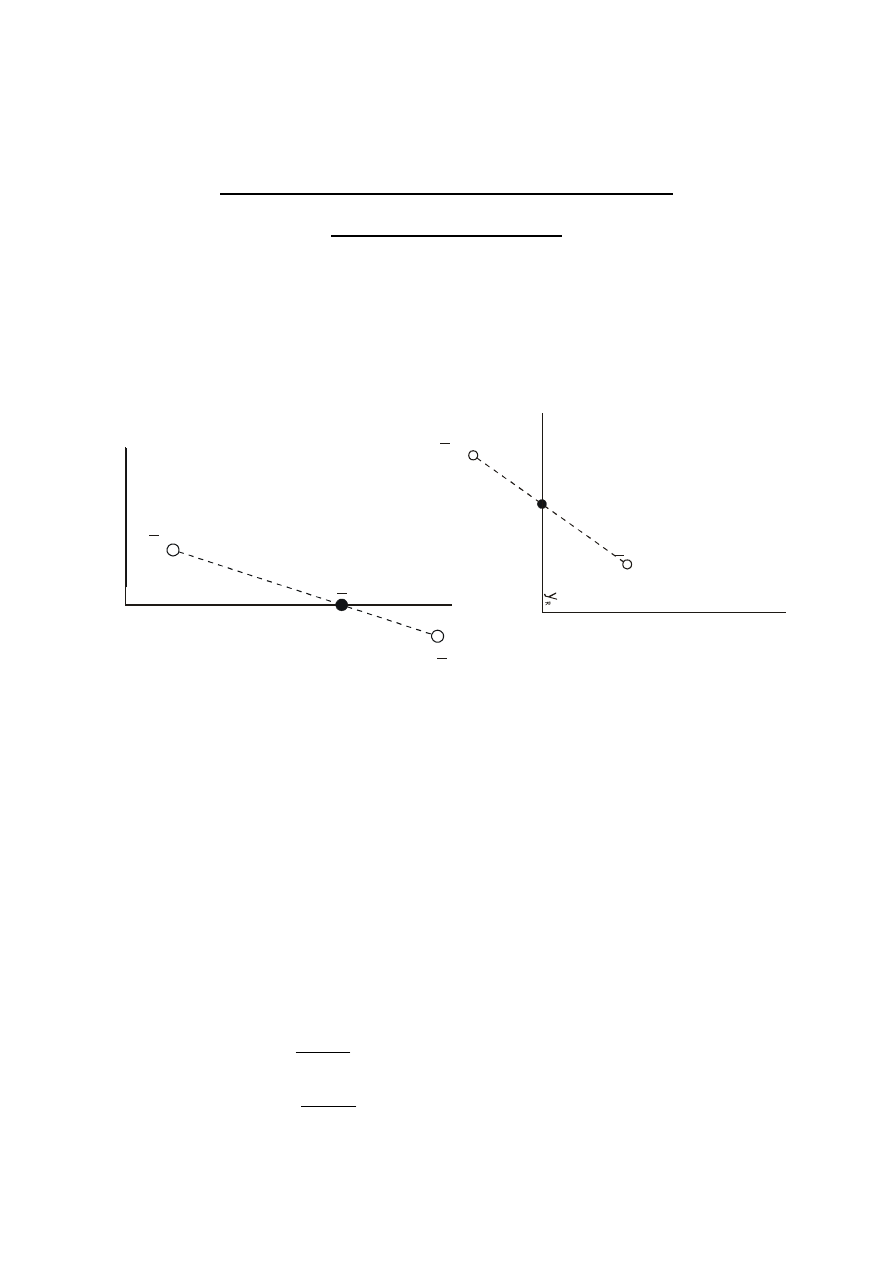
Obliczenie współrzędnych przecięcia prostej

z ramkami sekcyjnymi

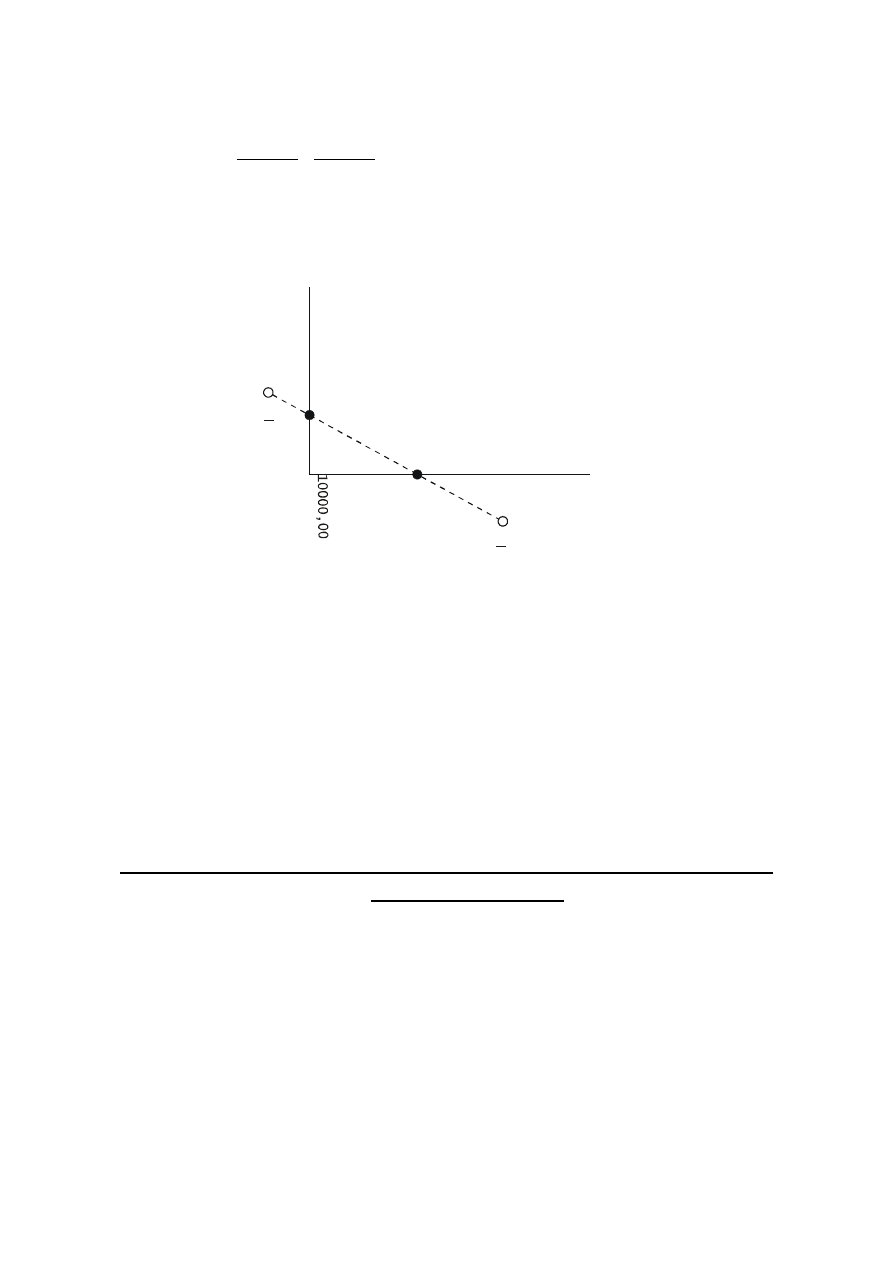
Jeżeli osnowa obejmuje kilka sekcji map to niektóre boki osnowy przecinają ramki

sekcyjne arkuszy map. Dla potrzeb kartowania, a także i obliczenia powierzchni niezbędna

jest znajomość współrzędnych tych punktów. Bok osnowy może przecinać jedną albo i dwie

ramki.

A (y

A,

x )

A

B (y

B,

x )

B

R

,

x

R

A (y

A,

x )

A

B (y

B,

x )

B

a)

b)

R

REALIZACJA

Jeśli bok osnowy przecina ramkę o współrzędnej X

R

w punkcie R (rys. a) to współrzędną

Y

R

obliczamy wzorem

(

) ( )

AB

tg

X

X

Y

Y

A

R

A

R

−

+

=

natomiast gdy bok osnowy przecina w punkcie R ramkę o współrzędnej Y

R

(rys. b), to

współrzędną X

R

liczymy wzorem

(

) ( )

AB

ctg

Y

Y

X

X

A

R

A

R

−

+

=

gdzie

A

B

A

B

X

X

Y

Y

)

AB

(

tg

−

−

=

A

B

A

B

Y

Y

X

X

)

AB

(

ctg

−

−

=

Obliczenia skontrolujemy wzorem

B

R

B

R

R

A

R

A

X

X

Y

Y

X

X

Y

Y

−

−

=

−

−

Przykłay

Obliczyć współrzędne przecięcia boku poligonowego 8 – 6 z ramkami sekcyjnymi na

podstawie danych wypisanych na rysunku

y = 9824,36

8

x = 5098,97

8

y = 10328,73

6

x = 4924,38

6

8

6

5000,00

R

1

R

2

Obliczenie współrzędnych prostokątnych punktu wyznaczonego

metodą biegunową

Metodą biegunową mogą być wyznaczane punkty pomierzonej osnowy sytuacyjnej lub

wysokościowej. Najczęściej jednak metoda ta jest stosowana do zdejmowania szczegółów

sytuacyjnych.

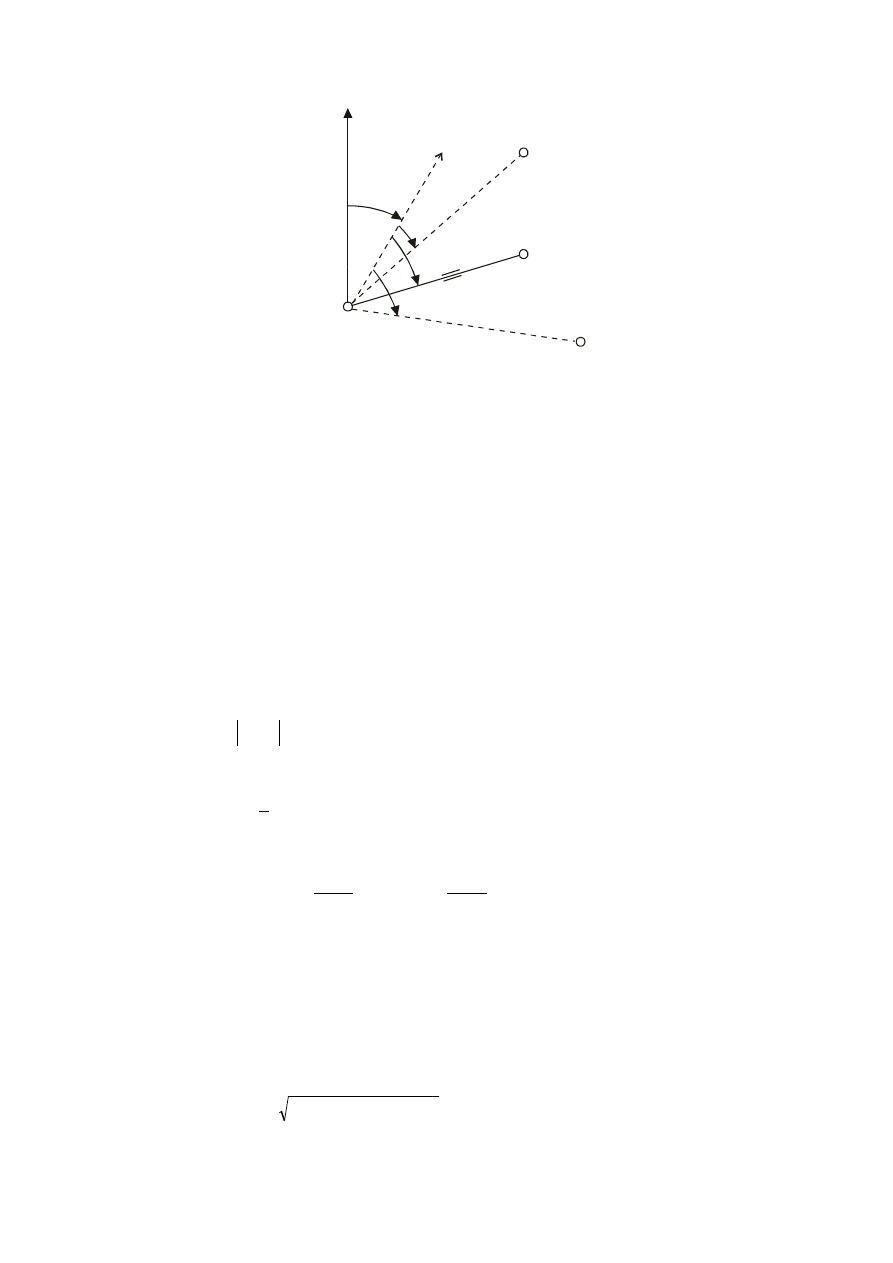
Zaleca się aby pomiary metodą biegunową dowiązywać do 2 punktów osnowy.

P

L

S

1

0

0

k

d

γ

1

L

k

1

k

P

+X

S, L, P – punkty osnowy,

1 – punkt wyznaczony biegunowo,

γ

- kąt orientacji kreski 0

0

podziału limbusa,

k

L

, k

P

– kierunki nawiązujące,

k

1

, d

1

– kierunek i odległość na wyznaczony punkt.

REALIZACJA

L

SL

''

P

SP

'

k

A

;

k

A

−

=

γ

−

=

γ

jeśli

γ

≤

γ

−

γ

f

''

'

to

(

)

''

'

2

1

γ

+

γ

=

γ

Azymuty:

SL

SL

SL

SP

SP

SP

X

Y

tg

arc

A

;

X

Y

tg

arc

A

∆

∆

=

∆

∆

=

1

1

S

k

A

+

γ

=

Współrzędne prostokątne wyznaczanego punktu:

1

S

1

S

1

A

sin

d

Y

Y

+

=

1

S

1

S

1

A

cos

d

X

X

+

=

Kontrola:

(

) (

)

2

S

1

2

S

1

.

obl

Y

Y

X

X

d

−

+

−

=

obl

.

pom

d

d

=

W przypadku nawiązania pomiaru tylko do jednego kierunku np. SL azymut kierunku S1

liczymy wzorem:

1

SL

1

S

k

A

A

+

=

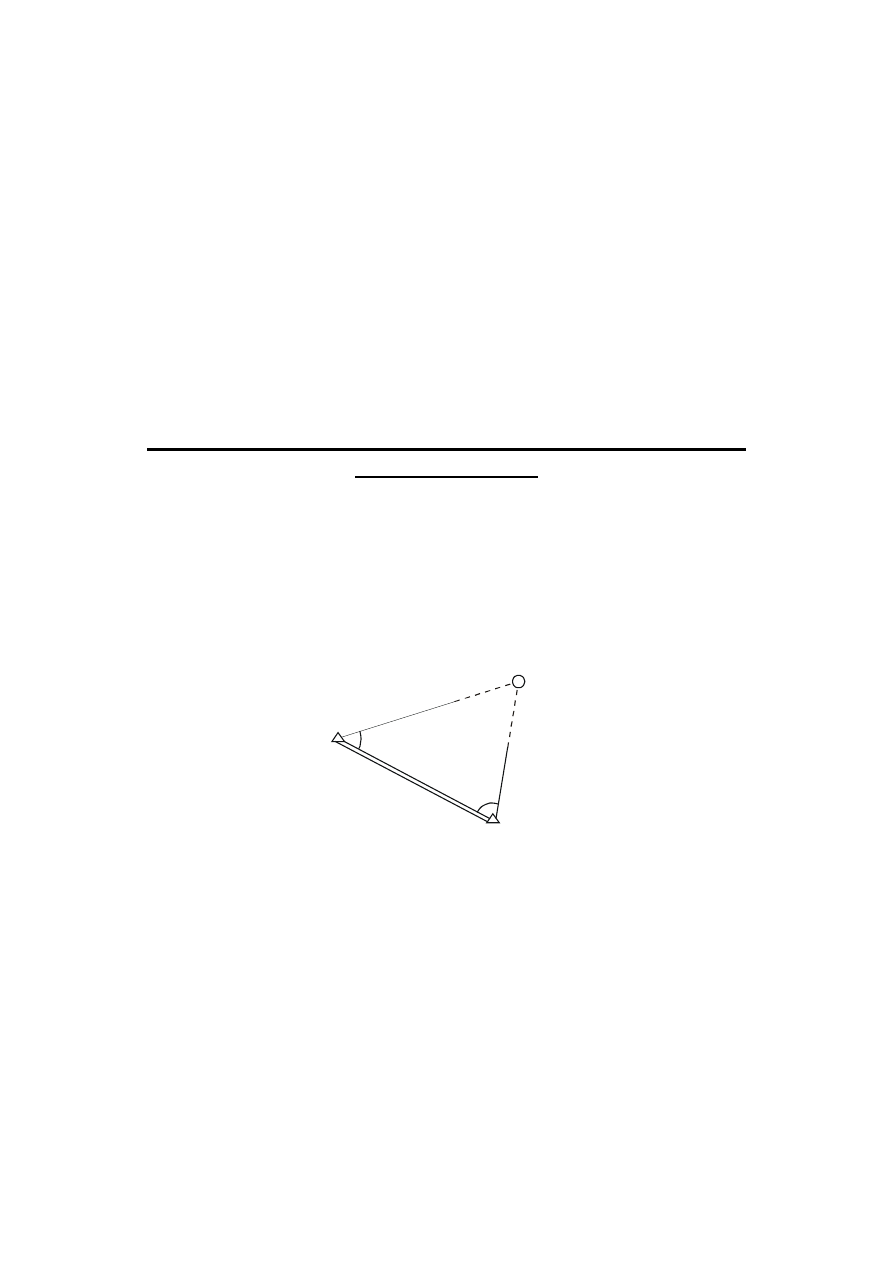
Obliczenie współrzędnych punktu wyznaczonego wcięciem

kątowym w przód

Klasyczna forma wcięcia kątowego w przód polega na pomiarze kątów wcinających

α

i

β

zawartych pomiędzy ramieniem określonym przez 2 punkty osnowy A i B i ramieniem

skierowanym z punktów A i B na punkt wyznaczany C.

B

C

A

α

β

Współrzędne punktu C określimy realizując wzory:

AC

A

C

Y

Y

Y

∆

+

=

AC

A

C

X

X

X

∆

+

=

i dla kontroli

BC

B

C

Y

Y

Y

∆

+

=

BC

B

C

X

X

X

∆

+

=

gdzie

(AC)

sin

AC

Y

AC

=

∆

(AC)

cos

AC

X

AC

=

∆

oraz

(BC)

sin

BC

Y

BC

=

∆

(BC)

cos

BC

X

BC

=

∆

(

)

β

+

α

β

=

sin

sin

AB

AC

(

)

β

+

α

α

=

sin

sin

AB

BC

2

AB

2

AB

Y

X

AB

∆

+

∆

=

Azymuty kierunków wcinających:

( ) ( )

α

+

=

AB

AC

( ) ( )

β

−

=

BA

BC

( ) ( )

0

180

AB

BA

±

=

( )

AB

AB

X

Y

tg

arc

AB

∆

∆

=

Dwukrotnie obliczone współrzędne punktu C mogą się różnić w granicach dokładności

rachunku.

Dodatkowym sprawdzeniem poprawności obliczeń będzie określenie kąta

γ

ze

współrzędnych punktów ABC i porównanie z kątem obliczonym wzorem

(

)

β

+

α

−

=

γ

180

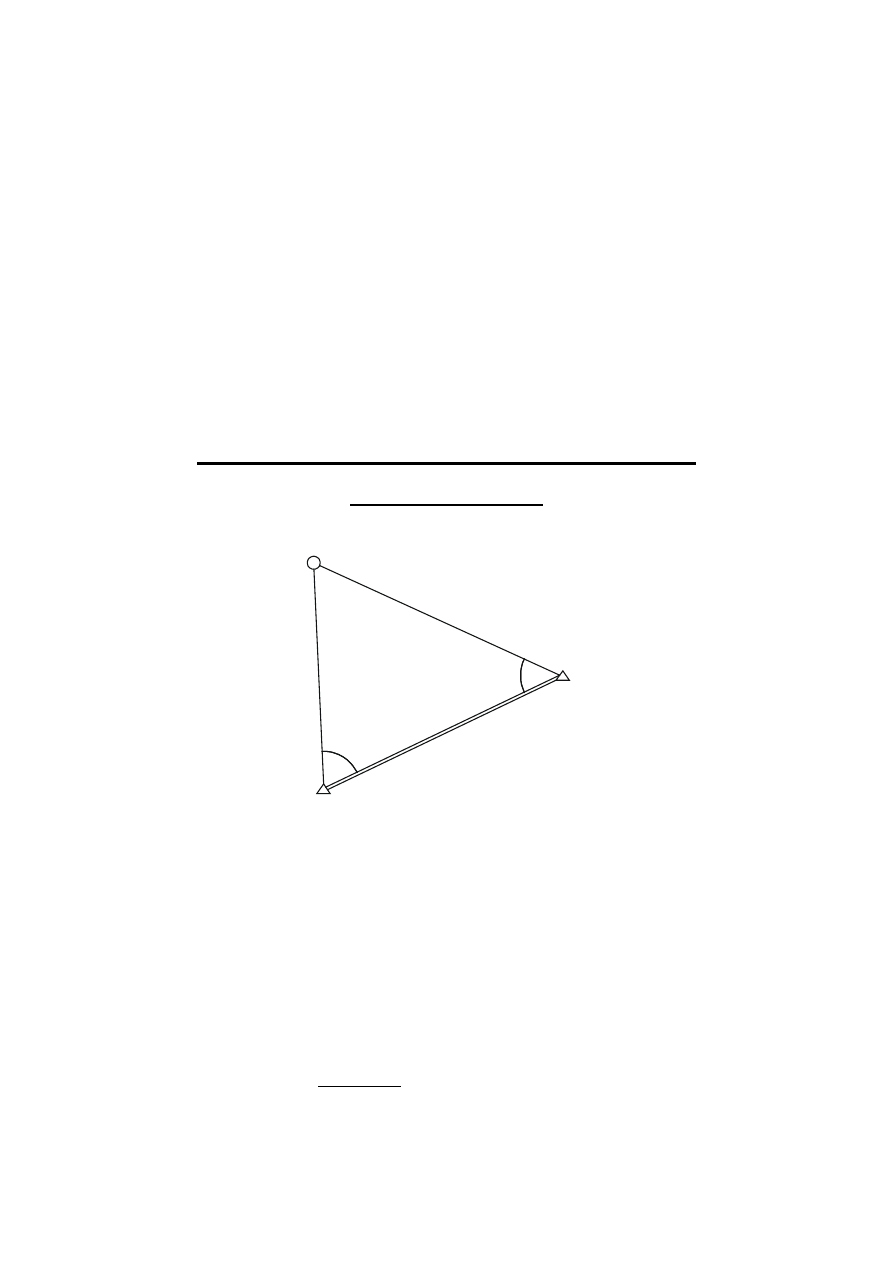
Obliczenie współrzędnych punktu wyznaczonego

wcięciem liniowym

C

A

b

a

B

l

α

β

Na podstawie elementów liniowych trójkąta obliczymy kąty

α

i

β

które wykorzystamy

następnie do wyznaczenia współrzędnych punktu C na podstawie wzorów odnoszących się do

wcięcia kątowego w przód.

Kąty

α

i

β

wyznaczymy z wzorów Carnota

α

−

+

=

cos

lb

2

b

l

a

2

2

2

β

−

+

=

cos

la

2

a

l

b

2

2

2

skąd

lb

2

a

b

l

cos

arc

2

2

2

−

+

=

α

la

2

b

a

l

cos

arc

2

2

2

−

+

=

β

Dalej do obliczenia współrzędnych punktu C stosujemy wzory odnoszące się do wcięcia

kątowego w przód. Kontrolę obliczenia współrzędnych punktu C możemy wykonać wzorem