2015-01-13
1
Z
ADANIA
WYBORU
PORTFELA
PAPIERÓW
WARTOŚCIOWYCH
Witold Jurek
S
TOPA
ZWROTU
Stopa zwrotu z papieru wartościowego (akcji),
składanie okresowe:
𝑟
𝑡
=
𝑝
𝑡
− 𝑝
𝑡−1
+ 𝑑
𝑡
𝑝
𝑡−1
Stopa zwrotu z papiery wartościowego (akcji),
składanie ciągłe
𝑟
𝑡
= ln 𝑝
𝑡
− ln 𝑝
𝑡−1
2
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
R
OZWINIĘCIE
FUNKCJI
𝑒
𝑥
W
SZEREG
T
AYLORA
Rozwinięcie funkcji
𝑓 𝑥 w szereg Taylora
𝑓 𝑥 = 𝑓 𝑥
0
+ 𝑓
′
𝑥
0
𝑥 − 𝑥
0
+ 𝑓
′′
𝑥
0
(𝑥 − 𝑥
0
)
2
+ ⋯
Rozwinięcie funkcji
𝑒
𝑥
w punkcie
𝑥
0
= 0
𝑒
𝑥
= 1 + 𝑥 + 𝑥
2
+ ⋯
Jeżeli x jest małe, to:
𝑒
𝑥
≈ 1 + 𝑥
3
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
2
Z
ALEŻNOŚCI
POMIĘDZY
STOPAMI
SKŁADANYMI
OKRESOWO
I
CIĄGLE
Jeżeli
𝐷
𝑡
= 0, to
𝑟
𝑡
=
𝑝
𝑡
𝑝
𝑡−1
− 1
Ponieważ
1 + 𝑟
𝑡
≈ 𝑒
𝑟
𝑡
dlatego
𝑟
𝑡
= ln 𝑝
𝑡
− ln 𝑝
𝑡−1
Uwaga
Stopy składane ciągle są m.in. addytywne
4
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
S
TOPY
ZWROTU
JAKO
ZMIENNE
LOSOWE
Ponieważ stopy zwrotu w momencie podejmowania decyzji
na ogół nie są znane, traktowane są jak zmienne losowe
Stopy
𝑟
𝑡
są traktowane jako wartości zmiennej losowej
𝑅
𝑡
5
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Z
MIENNE
LOSOWE
I
MOMENTY
ROZKŁADU
Wartość oczekiwana (średnia) zmiennej losowej,
𝐸(𝑅)
Własności: 𝐸 𝑐𝑅 = 𝑐𝐸(𝑅)
𝐸 𝑐 = 𝑐
Wariancja zmiennej losowej: 𝐷
2
𝑅 = 𝐸[𝑅 − 𝐸(𝑅)]
2
Własności: 𝐷
2
𝑐𝑅 = 𝑐
2
𝐷
2
𝑅
𝐷
2
𝑐 = 0
Odchylenie standardowe: 𝐷 𝑅 = 𝐸[𝑅 − 𝐸(𝑅)]
2
Własności: 𝐷 𝑐𝑅 = 𝑐𝐷 𝑅
𝐷 𝑐 = 0
6
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
3
Z
MIENNE
LOSOWE
I
MOMENTY
ROZKŁADU
Skośność:
𝑀
3
=
𝐸[𝑅 − 𝐸(𝑅)]
3
𝐷
3
(𝑅)
Jeżeli rozkład jest symetryczny to
𝑀
3
= 0
Spłaszczenie:
𝑀
4
=
𝐸[𝑅 − 𝐸(𝑅)]
4
𝐷
4
(𝑅)
− 3
Jeżeli rozkład „przypomina” rozkład normalny, to
𝑀
4
= 0
7
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
1
M
OMENTY
ROZKŁADU
STOPY
ZWROTU
Stopy Częstość Średnia Wariancja Skośność Spłaszczenie
6
0,05
0,30
0,578
-1,9652
6,6817
7
0,10
0,70
0,576
-1,3824
3,3178
8
0,20
1,60
0,392
-0,5488
0,7683
9
0,25
2,25
0,040
-0,0160
0,0064
10
0,15
1,50
0,054
0,0324
0,0194
11
0,10
1,10
0,256
0,4096
0,6554
12
0,05
0,60
0,338
0,8788
2,2849
13
0,05
0,65
0,648
2,3328
8,3981
14
0,05
0,70
1,058
4,8668
22,3873
1,00
9,40
3,940
4,6080
44,5192
8
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
1
M
OMENTY
ROZKŁADU
STOPY
ZWROTU
Średnia:
9,40
Odchylenie standardowe:
3,94 = 1,9849
Skośność:
4,608
1,9849
3
= 0,5892
Spłaszczenie:
44,5192
1,9849
4
− 3 = −0,1322
9
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
4
P
RZYKŁAD
2
M
OMENTY
ROZKŁADU
STOPY
ZWROTU
Stopy Częstość Średnia Wariancja Skośność Spłaszczenie
7
0,10
0,70
0,90
-2,70
8,10
8
0,15
1,20
0,60
-1,20
2,40
9
0,20
1,80
0,20
-0,20
0,20
10
0,10
1,00
0,00
0,00
0,00
11
0,20
2,20
0,20
0,20
0,20
12
0,15
1,80
0,60
1,20
2,40
13
0,10
1,30
0,90
2,70
8,10
1,00
10,00
3,40
0,00
21,40
10
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
2
M
OMENTY
ROZKŁADU
STOPY
ZWROTU
Średnia:
10,00
Odchylenie standardowe:
3,40 = 1,8439
Skośność:
0,00
1,8439
3
= 0,0000
Spłaszczenie:
21,4000
1,8439
4
− 3 = −0,1488
11
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
S
EMIPARAMETRY
ROZKŁADU
Semiwariancja (ujemna):
𝑆𝐷
2
𝑅 = 𝐸{[𝑅 − 𝐸(𝑅)]
−
}
2
Semiodchylenie standardowe
𝑆𝐷 𝑅 = 𝐸{[𝑅 − 𝐸(𝑅)]
−
}
2
przy czym
[𝑅 − 𝐸 𝑅 ]
−
=
𝑅 − 𝐸(𝑅) 𝑗𝑒ż𝑒𝑙𝑖 𝑅 < 𝐸(𝑅)
0
𝑗𝑒ż𝑒𝑙𝑖 𝑅 ≥ 𝐸(𝑅)
12
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
5
P
RZYKŁAD
3
S
EMIPARAMETRY
ROZKŁADU
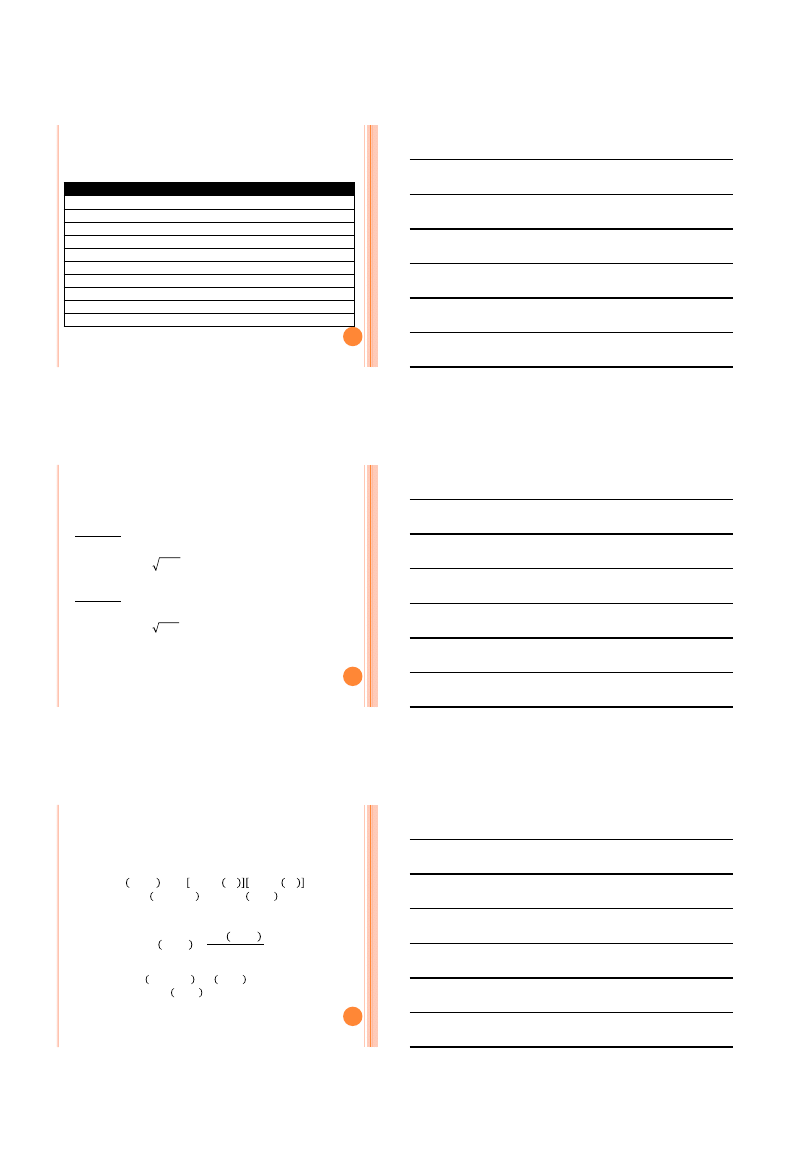
Stopy Częstość SWariancja
Stopy Częstość
SWariancja
6
0,05
0,30
7
0,10
0,70
7
0,10
0,90
8
0,20
1,60
8
0,15
0,60
9
0,25
2,25
9
0,20
0,20
10
0,15
0,00
10
0,10
0,00
11
0,10
0,00
11
0,20
0,00
12
0,05
0,00
12
0,15
0,00
13
0,05
0,00
13
0,10
0,00
14
0,05
0,00
1,00
4,85
1,00
1,70
13
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
3
S
EMIPARAMETRY
ROZKŁADU
Przykład 1
Semiwarinacja: 4,85
Semiodchylenie:
4,85 = 2,2027
Przykład 2
Semiwarinacja: 1,70
Semiodchylenie:
1,70 = 1,3038
14
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
M
IARY
POWIĄZANIA
ZMIENNYCH
LOSOWYCH
Kowariancja
𝑐𝑜𝑣 𝑅
1
, 𝑅
2
= 𝐸{ 𝑅
1
− 𝐸 𝑅
1
𝑅
2
− 𝐸 𝑅
2
}
Własności:
𝑐𝑜𝑣 𝑐
1
𝑅
1
, 𝑐
2
𝑅
2
= 𝑐
1
𝑐
2
𝑐𝑜𝑣 𝑅
1
, 𝑅
2
Współczynnik korelacji
𝜌 𝑅
1
, 𝑅
2
=
𝑐𝑜𝑣 𝑅
1
, 𝑅
2
𝐷(𝑅
1
)𝐷(𝑅
2
)
Własności:
𝜌 𝑐
1
𝑅
1
, 𝑐
2
𝑅
2
= 𝜌 𝑅
1
, 𝑅
2
−1 ≤ 𝜌 𝑅
1
, 𝑅
2
≤ 1
15
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
6
P
RZYKŁAD
4
W
SPÓŁCZYNNIK
KORELACJI
Dwie zmienne o stopach podanych w tabeli
16
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
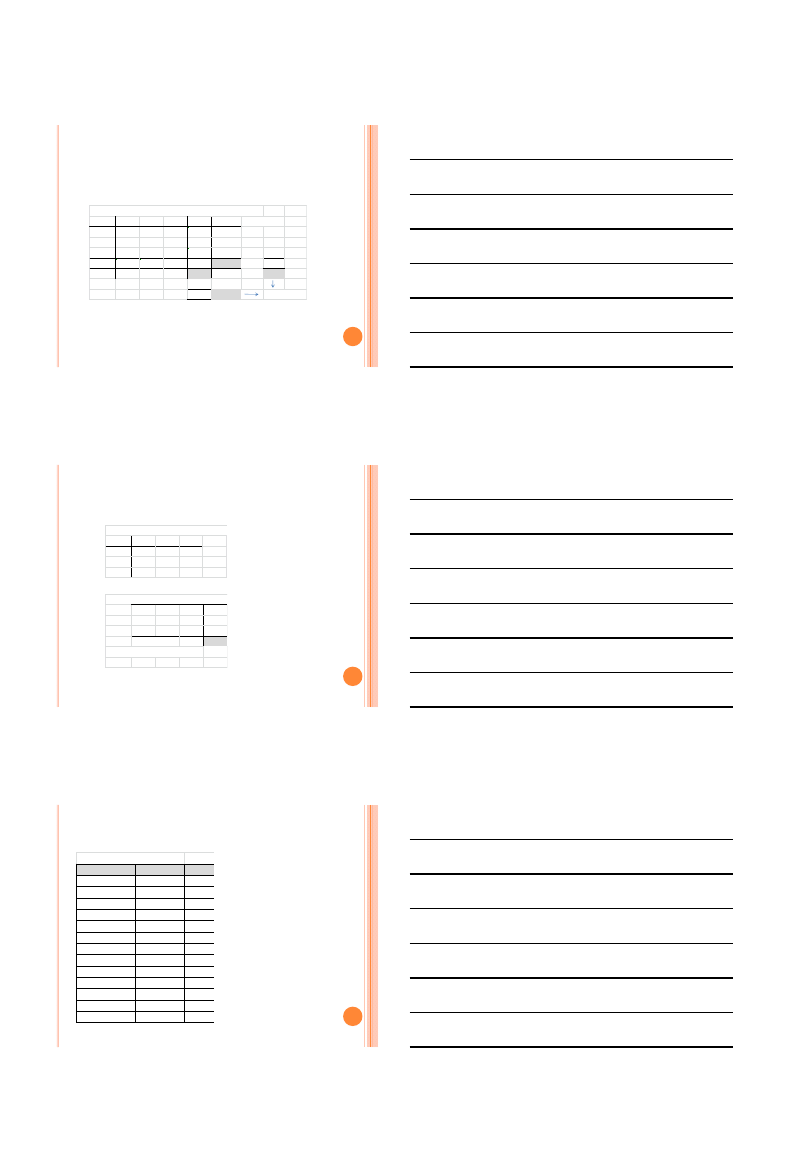
Prawdopodobieństwa. Średnie. Odchylenia std.
Stopy
7
8
9
Średnia Kwadr
3
0,2
0,0
0,0
0,2
0,6
1,21
0,24
4
0,1
0,3
0,1
0,5
2,0
0,01
0,01
5
0,1
0,2
0,0
0,3
1,5
0,81
0,24
0,4
0,5
0,1
1,0
4,1
0,490
Średnia
2,8
4,0
0,9
7,7
0,700
Kwadr
0,49
0,09
1,69
0,196 0,045 0,169 0,410
0,640
Odchylenia
P
RZYKŁAD
4
W
SPÓŁCZYNNIK
KORELACJI
17
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Odchylenia od średnich i ich iloczyny
-0,7
0,3
1,3
-1,1
0,77 -0,33 -1,43
-0,1
0,07 -0,03 -0,13
0,9 -0,63
0,27
1,17
Odchylenia od średnich * prawdopob.
0,154 0,000 0,000 0,154
0,007 -0,009 -0,013 -0,015
-0,063 0,054 0,000 -0,009
Kowariancja
0,130
Wspólczynnik korelacji =
0,290
P
RZYKŁAD
5
W
SPÓŁCZYNNIK
KORELACJI
. N
OTOWANIA
Z
ad
an
ie
w
yb
or
u
p
or
tfel
a
18
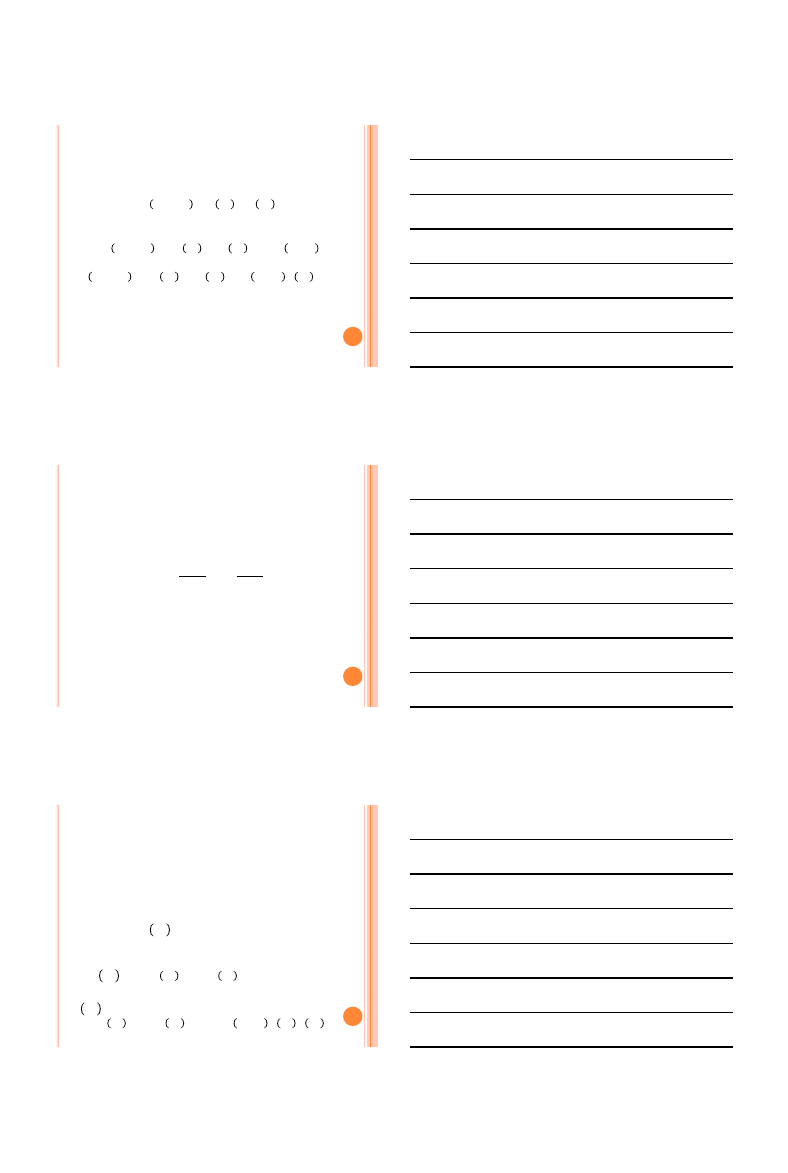
Notowania zamknięcia
Data
WIG
Bytom
8 Jan 2015 52391,00
1,44
7 Jan 2015 51350,42
1,50
5 Jan 2015 50516,71
1,56
2 Jan 2015 51378,00
1,34
30 Dec 2014 51416,08
1,23
29 Dec 2014 51159,06
1,25
23 Dec 2014 51511,68
1,26
22 Dec 2014 51487,54
1,26
19 Dec 2014 51297,12
1,26
18 Dec 2014 51739,04
1,25
17 Dec 2014 50932,48
1,29
16 Dec 2014 50683,91
1,25
15 Dec 2014 51621,14
1,20
Współczynnik korelacji =
-0,1284
2015-01-13
7
S
UMA
ZMIENNYCH
LOSOWYCH
I
JEJ
MOMENTY
Wartość oczekiwana sumy zmiennych losowych
𝐸 𝑅
1
+ 𝑅
2
= 𝐸 𝑅
1
+ 𝐸 𝑅
2
Wariancja sumy zmiennych losowych
𝐷
2
𝑅
1
+ 𝑅
2
= 𝐷
2
𝑅
1
+ 𝐷
2
𝑅
2
+ 2𝑐𝑜𝑣 𝑅
1
, 𝑅
2
albo
𝐷
2
𝑅
1
+ 𝑅
2
= 𝐷
2
𝑅
1
+ 𝐷
2
𝑅
2
+ 2𝜌 𝑅
1
, 𝑅
2
𝐷 𝑅
1
𝐷(𝑅
2
)
19
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
ORTFEL
ZŁOŻONY
Z
DWÓCH
PAPIERÓW
WARTOŚCIOWYCH
Kapitał w zainwestowany w dwa papiery wartościowe
𝑤
1
+ 𝑤
2
= 𝑤 > 0
Proporcje inwestycji
𝑋
1
=
𝑤
1
𝑤
1
+𝑤
2
;
𝑋
2
=
𝑤
2
𝑤
1
+𝑤
2
Oczywiście
𝑋
1
+ 𝑋
2
= 1
Uwaga
Jeżeli wykluczona jest tzw. krótka sprzedaż,
to zmienne 𝑋
1
, 𝑋
2
są nieujemne
20
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
S
TOPA
ZWROTU
Z
PORTFELA
DWÓCH
PAPIERÓW
WARTOŚCIOWYCH
Stopa zwrotu
𝑅
𝑝
= 𝑋
1
𝑅
1
+ 𝑋
2
𝑅
2
Oczekiwana stopa zwrotu
𝐸 𝑅
𝑝
= 𝑋
1
𝐸(𝑅
1
) + 𝑋
2
𝐸(𝑅
2
)
Wariancja stopy zwrotu
𝐷
2
𝑅
𝑝
= 𝑋
1
2
𝐷
2
𝑅
1
+ 𝑋
2
2
𝐷
2
𝑅
2
+ 2𝑋
1
𝑋
2
𝑐𝑜𝑣(𝑅
1
, 𝑅
2
)
albo
𝐷
2
𝑅
𝑝
=
= 𝑋
1
2
𝐷
2
𝑅
1
+ 𝑋
2
2
𝐷
2
𝑅
2
+ 2𝑋
1
𝑋
2
𝜌 𝑅
1
, 𝑅
2
𝐷 𝑅
1
D
𝑅
2
21
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
8
P
OWIĄZANIE
STÓP
ZWROTU
Uwaga
(1) oczekiwana stopa zwrotu z portfela nie zależy od kowariancji
(współczynnika korelacji), tj. od powiązania stóp zwrotu
(2) ryzyko mierzone wariancją (odchyleniem standardowym) zależy
od kowariancji (współczynnika korelacji), tj. od powiązania stóp
zwrotu
Warto zauważyć, że
(1) stopy zwrotu spółek tej samej branży są na ogół silnie
skorelowane dodatnio
(2) stopy zwrotu spółek pozostających w „ciągu technologicznym”
są na ogół silnie skorelowane ujemnie
22
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
S
TOPA
ZWROTU
I
RYZYKO
.
W
SPÓŁCZYNNIK
KORELACJI
RÓWNY
1
Oczekiwana stopa zwrotu
𝐸 𝑅
𝑝
= 𝑋
1
𝐸(𝑅
1
) + 𝑋
2
𝐸(𝑅
2
)
Wariancja stopy zwrotu
𝐷
2
𝑅
𝑝
= 𝑋
1
2
𝐷
2
𝑅
1
+ 𝑋
2
2
𝐷
2
𝑅
2
+ 2𝑋
1
𝑋
2
𝐷 𝑅
1
D
𝑅
2
Odchylenie standardowe
𝐷 𝑅
𝑝
= 𝑋
1
𝐷 𝑅
1
+ 𝑋
2
𝐷 𝑅
2
Uwaga
Odchylenie standardowe stopy zwrotu wyraża się taka samą
funkcją, co oczekiwana stopa zwrotu
23
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
S
TOPA
ZWROTU
I
RYZYKO
.
W
SPÓŁCZYNNIK
KORELACJI
RÓWNY
-1
Oczekiwana stopa zwrotu
𝐸 𝑅
𝑝
= 𝑋
1
𝐸(𝑅
1
) + 𝑋
2
𝐸(𝑅
2
)
Wariancja stopy zwrotu
𝐷
2
𝑅
𝑝
= 𝑋
1
2
𝐷
2
𝑅
1
+ 𝑋
2
2
𝐷
2
𝑅
2
− 2𝑋
1
𝑋
2
𝐷 𝑅
1
D
𝑅
2
Odchylenie standardowe
𝐷 𝑅
𝑝
= 𝑋
1
𝐷 𝑅
1
− 𝑋
2
𝐷 𝑅
2
Uwaga
(1) Odchylenie standardowe stopy zwrotu wyraża się taka samą
funkcją, co oczekiwana stopa zwrotu
(2) Możliwe jest znalezienie portfela papierów wartościowych o
zerowym ryzyku
24
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
9
P
RZYKŁAD
P
ORTFEL
ZŁOŻONY
Z
DWÓCH
PAPIERÓW
W
ARTOŚCIOWYCH
R
ÓŻNE
SKORELOWANIE
STÓP
ZWROTU
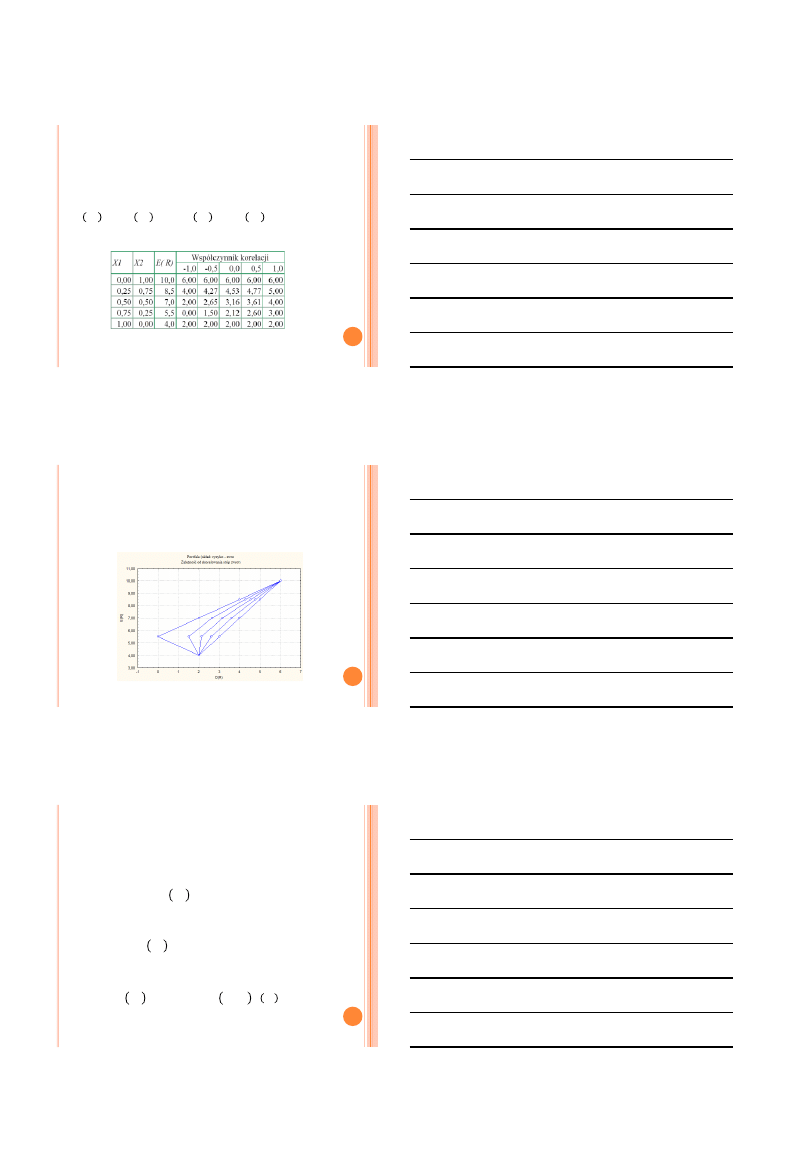
Papiery wchodzące w skład portfela charakteryzują się
następującymi parametrami
𝐸 𝑅
1
= 4, 𝐸 𝑅
2
= 10, 𝐷 𝑅
1
= 2, 𝐷 𝑅
2
= 6
Odchylenie standardowe zależne od skorelowania stóp
25
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
P
ORTFEL
ZŁOŻONY
Z
DWÓCH
PAPIERÓW
W
ARTOŚCIOWYCH
R
ÓŻNE
SKORELOWANIE
STÓP
ZWROTU
26
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Układ: zwrot – ryzyko dla portfeli, jakie można utworzyć z
dwóch analizowanych papierów wartościowych
P
ORTFEL
ZŁOŻONY
Z
WIELU
PAPIERÓW
WARTOŚCIOWYCH
Oczekiwana stopa zwrotu
𝐸 𝑅
𝑝
= 𝑋
𝑖
𝐸(𝑅
𝑖
)
𝑛
𝑖=1
Wariancja stopy zwrotu
𝐷
2
𝑅
𝑝
= 𝑋
𝑖
𝑋
𝑗
𝑐𝑜𝑣(𝑅
𝑖
, 𝑅
𝑗
)
𝑛
𝑗=1
𝑛
𝑖=1
𝐷
2
𝑅
𝑝
= 𝑋
𝑖
𝑋
𝑗
𝜌 𝑅
𝑖
, 𝑅
𝑗
𝐷 𝑅
𝑖
𝐷(𝑅
𝑗
)
𝑛
𝑗=1
𝑛
𝑖=1
27
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la

2015-01-13
10
P
RZYKŁAD
P
ORTFEL
ZŁOŻONY
Z
3
PAPIERÓW
WARTOŚCIOWYCH
Wyznaczyć charakterystyki portfela złożonego z 3 papierów
wartościowych o charakterystykach podanych w tabeli
𝐸 𝑅
𝑝
= 8 × 0,5 + 20 × 0,3 + 15 × 0,2 = 13
28
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
K
ORELACJA
I
KOWARIANCJA
Macierz współczynników korelacji
Macierz kowariancji
29
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
W
ARIANCJA
STOPY
ZWROTU
Wariancja
Suma elementów macierzy wynosi 60,35
Tak więc
𝐷
2
𝑅
𝑝
= 60,35 𝐷 𝑅
𝑝
= 7,67
30
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
11
Z
ADANIE
MAKSYMALIZACJI
ZWROTU
Z
PORTFELA
(
PRZY
DANYM
POZIOMIE
RYZYKA
)
𝐸 𝑅
𝑝
= 𝑋
𝑖
𝐸(𝑅
𝑖
)
𝑛
𝑖=1
→ 𝑚𝑎𝑥
𝐷
2
𝑅
𝑝
= 𝑋
𝑖
𝑋
𝑗
𝜌 𝑅
𝑖
, 𝑅
𝑗
𝐷 𝑅
𝑖
𝐷(𝑅
𝑗
)
𝑛
𝑗=1
𝑛
𝑖=1
= 𝑉
0
𝑋
𝑖
= 1
𝑛
𝑖=1
Jeżeli wykluczona jest krótka sprzedaż, to
𝑋
1
≥ 0.
31
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Z
ADANIE
MINIMALIZACJI
RYZYKA
PORTFELA
(
PRZY
DANYM
ZWROCIE
)
𝐷
2
𝑅
𝑝
= 𝑋
𝑖
𝑋
𝑗
𝜌 𝑅
𝑖
, 𝑅
𝑗
𝐷 𝑅
𝑖
𝐷(𝑅
𝑗
) → 𝑚𝑖𝑛
𝑛
𝑗=1
𝑛
𝑖=1
𝐸 𝑅
𝑝
= 𝑋
𝑖
𝐸(𝑅
𝑖
)
𝑛
𝑖=1
= 𝑟
0
𝑋
𝑖
= 1
𝑛
𝑖=1
Jeżeli wykluczona jest krótka sprzedaż, to
𝑋
1
≥ 0.
32
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Z
ADANIE
M
ARKOWITZA
WYBORU
PORTFELA
𝐸 𝑅
𝑝
− 𝜆𝐷
2
𝑅
𝑝
→ 𝑚𝑎𝑥
𝐸 𝑅
𝑝
= 𝑋
𝑖
𝐸(𝑅
𝑖
)
𝑛
𝑖=1
𝐷
2
𝑅
𝑝
= 𝑋
𝑖
𝑋
𝑗
𝜌 𝑅
𝑖
, 𝑅
𝑗
𝐷 𝑅
𝑖
𝐷(𝑅
𝑗
)
𝑛
𝑗=1
𝑛
𝑖=1
𝑋
𝑖
= 1
𝑛
𝑖=1
Jeżeli wykluczona jest krótka sprzedaż, to
𝑋
1
≥ 0.
33
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
2015-01-13
12
Z
ADANIE
M
ARKOWITZA
(
FUNKCJA
UŻYTECZNOŚCI
,
KRZYWA
OBOJĘTNOŚCI
)
Zadanie Markowitza konstruuje się z wykorzystaniem
wartości oczekiwanej kwadratowej funkcji użyteczności,
którą dla zadania wyboru portfela można zapisać w postaci
𝑈 𝑅
𝑝
= 𝑎 + 𝑏𝑅
𝑝
− 𝑐(𝑅
𝑝
− 𝐸 𝑅
𝑝
)
2
𝑎, 𝑏, 𝑐 ≥ 0
Krzywa obojętności
𝐸 𝑈 𝑅
𝑝
= 𝑐𝑜𝑛𝑠𝑡
skąd wynika, że
𝐸 𝑅
𝑝
= 𝛿
1
+ 𝛿
2
𝐷
2
(𝑅
𝑝
)
34
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
1
PORTFELA
ZŁOŻONEGO
Z
3
PAPIERÓW
WARTOŚCIOWYCH
Na podstawie danych o 3 papierach wartościowych
Skonstruować portfel papierów wartościowych
maksymalizujący zwrot przy, mierzonym wariancją, ryzyku
nie przekraczającym 60 %
2
35
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Numer
papieru
Oczekiwany
zwrot
Odchylenie
standardowe
1
8
5
0,5 0,6
2
20
15
0,7
3
15
10
Skorelowanie
P
RZYKŁAD
1
PORTFELA
ZŁOŻONEGO
Z
3
PAPIERÓW
WARTOŚCIOWYCH
36
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
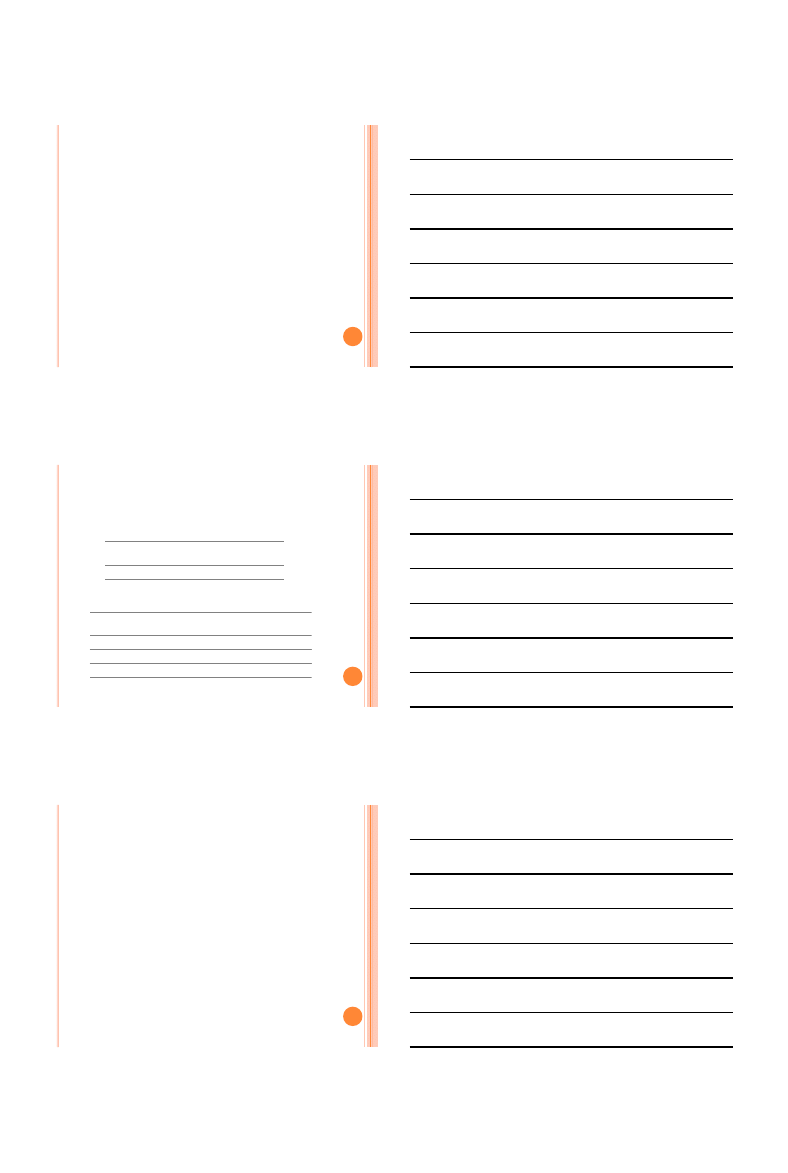
Komórka celu (Maks)
Komórka Nazwa
Wartość
początkowa
Wartość
końcowa
$G$6
Zwrot Średni
0
13,4896
Komórki zmiennych
Komórka Nazwa
Wartość
początkowa
Wartość
końcowa
Całkowite
$C$5
X1
0
0,37797
Ciągłe
$D$5
X2
0
0,22708
Ciągłe
$E$5
X3
0
0,39495
Ciągłe
2015-01-13
13
P
RZYKŁAD
2
PORTFELA
ZŁOŻONEGO
Z
3
PAPIERÓW
WARTOŚCIOWYCH
Na podstawie tych samych danych o 3 papierach
wartościowych skonstruować portfel minimalizujący,
mierzone wariancją, ryzyko przy zwrocie równym co
najmniej 10%
37
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
P
RZYKŁAD
2
PORTFELA
ZŁOŻONEGO
Z
3
PAPIERÓW
WARTOŚCIOWYCH
38
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Komórka celu (Min)
Komórka Nazwa
Wartość
początkowa
Wartość
końcowa
$G$28
0
32,5
Komórki zmiennych
Komórka Nazwa
Wartość
początkowa
Wartość
końcowa
Całkowite
$C$5
X1
0
0,76
Ciągłe
$D$5
X2
0
0,07
Ciągłe
$E$5
X3
0
0,17
Ciągłe
P
RZYKŁAD
3
PORTFELA
ZŁOŻONEGO
Z
3
PAPIERÓW
WARTOŚCIOWYCH
39
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Zadanie Markowitza
Na podstawie tych samych danych o 3 papierach
wartościowych skonstruować portfel będący rozwiązaniem
zadania Markowitza.
Przyjąć, że
𝜆 = 7
2015-01-13
14
P
RZYKŁAD
3
PORTFELA
ZŁOŻONEGO
Z
3
PAPIERÓW
WARTOŚCIOWYCH
40
Z
a
d
a
n
ie
w
y
b
o
ru
p
o
rt
fe
la
Komórka celu (Maks)
Komórka Nazwa
Wartość
początkowa
Wartość
końcowa
$L$7
FC
0
-167
Komórki zmiennych
Komórka Nazwa
Wartość
początkowa
Wartość
końcowa
Całko
wite
$C$5
X1
0,5
1
Ciągłe
$D$5
X2
0,3
0
Ciągłe
$E$5
X3
0,2
0
Ciągłe
Wyszukiwarka
Podobne podstrony:
Portfel papierow wartosciowych(1)
Papiery wartościowe jako składniki portfeli inwestycyjnych
gpw i gielda papierow wartosciowych w praktyce
Catalyst Przewodnik dla inwestorów, Giełda Papierów Wartościowych, Warszawa 2009
daytrading amerykanski rynek papierow wartosciowych (nasdaq i nyse, inwestowanie) UVG7DGTIDBHUTFXK5
FP ocena rentowności papierów wartościowych
Test podstawowy dla mnie papiery wartościowe
4 Rynek pierwotny papierow wartosciowych
rynek papierów wartościowych-, NAUKA, [Rynek Kapitałowy]
papiery wartościowe
Papiery wartościowe
GIEŁDA PAPIERÓW WARTOŚCIOWYCH, semestr 3, Rynki finansowe, wykłady
więcej podobnych podstron