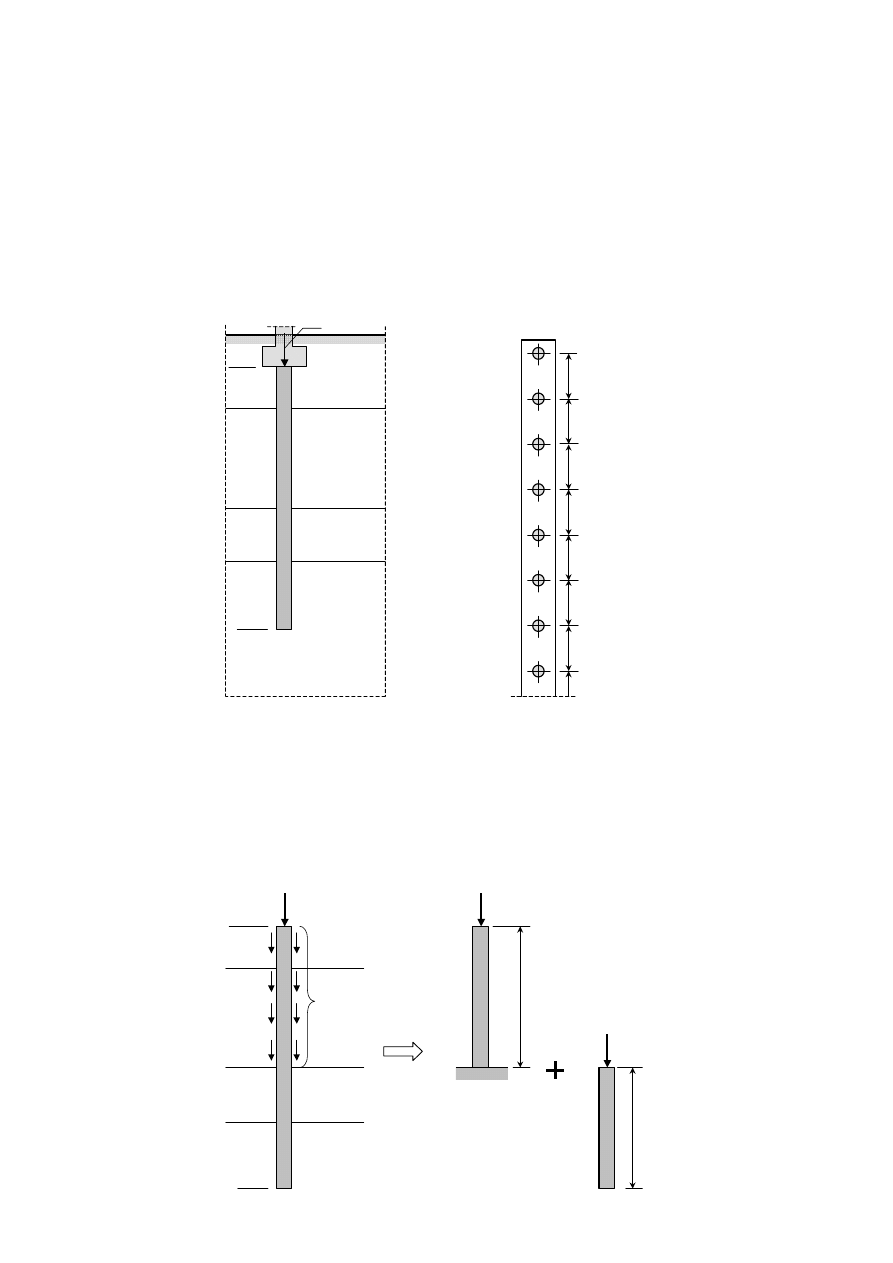
Przykład obliczenia osiadań pali pojedynczych i w grupie, wg PN-83/B-02482
1. Dane wyjściowe
Przyjęto pale wiercone
φ500 mm, rozmieszczone w jednym rzędzie w rozstawie co r = 2.0 m.
Obciążenia pali:
- siła zewnętrzna charakterystyczna: Q
n
= 1000 kN,
- tarcie negatywne: T
n
= 120 kN
Beton pala: B25
→ E
t
= 30000 MPa
2. Osiadanie pala pojedynczego
Ze względu na uwarstwione podłoże gruntowe oraz tarcie negatywne pal podzielono na dwa pale
składowe (rys. poniżej):
- pal (1) – pal na podłożu nieściśliwym pod podstawą (tak jak na skale)
- pal (2) – pal w podłożu uwarstwionym z warstwą mniej ściśliwą pod podstawą
Osiadanie całkowite pala będzie sumą osiadań pali (1) i (2).
0.0
-1.5
-3.5
-7.5
-10.0
-12.5
Gp, gen. C
I
L
= 0.35
E
0
= 12 MPa
T/Nm
E
0
= 1.0 MPa
Pg, gen. C
I
L
= 0.20
E
0
= 20 MPa
Ps,
I
D
= 0.70
E
0
= 110 MPa
Q
n
2.0
2.0
2.0
2.0
2.0
2.0
2.0
1
2
3
4
5
6
7
8
Przekrój pionowy z profilem geotechnicznym
Plan fundamentu palowego
-1.5
-3.5
-7.5
-10.0
-12.5
Gp
T/Nm
Pg
Ps
Q
n
T
n
Q
n
Q
n
+ T
n
h
1
= 6.0 m
h
2
= 5.0 m
pal (1)
pal (2)
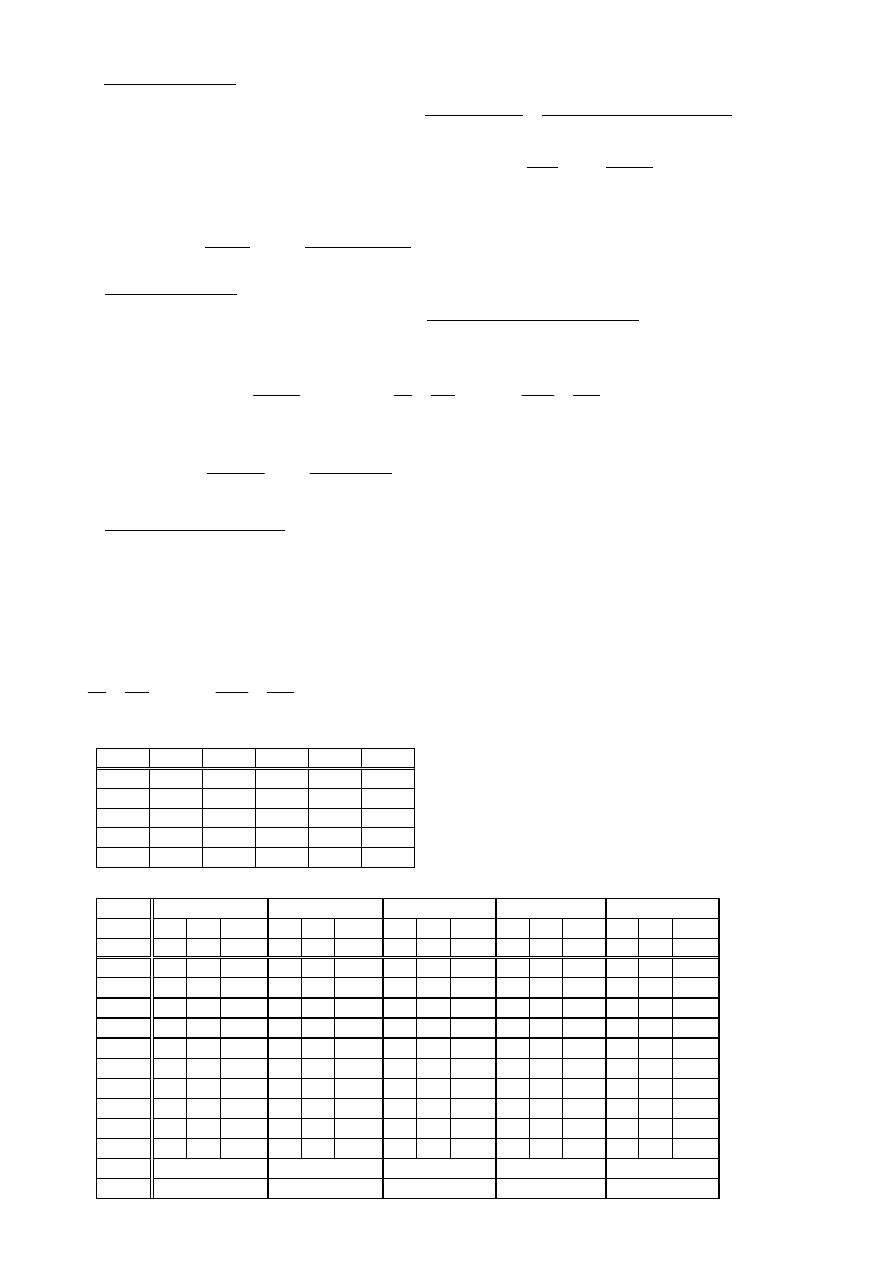
a) Osiadanie pala (1)
Uśredniony moduł gruntu wzdłuż pala:
3
4
0
6
0
4
0
1
0
1
0
2
0
12
9
0
0
1
0
.
.
.
.
.
.
.
.
h
h
E
S
E
i
i
i
si
s
=
⋅
⋅
+
⋅
⋅
=
⋅
⋅
=
∑
∑
MPa
Pal o pełnym kształcie
→
0
1.
R
A
=
, współczynnik
7000
0
1
3
4
30000
1
0
1
≈
⋅
=
⋅
=
.
.
R
E
E
K
A
s
t
A
Przekrój pala:
196
0
5
0
25
0
2
.
.
.
A
t
=
⋅
=
π
m
2
,
0
12
5
0
0
6
1
.
.
/
.
D
/
h
=
=
→
99
0.
M
R
=
przyjęto
0
1.
M
R
=
Osiadanie:
3
7
1
1
10
02
1
196
0
10
0
3
0
6
1000
−
⋅
=
⋅
⋅
⋅
=
⋅
⋅
⋅
=
.
.
.
.
M
A
E
h
Q
s
R
t
t
n
m = 1.02 mm
b) Osiadanie pala (2)
Uśredniony moduł gruntu wzdłuż pala:
0
53
0
5
5
2
0
110
8
0
5
2
0
20
9
0
2
0
.
.
.
.
.
.
.
.
E
s
=
⋅
⋅
+
⋅
⋅
=
MPa
Moduł gruntu pod podstawą pala:
110
110
0
1
0
=
⋅
=
⋅
=
.
E
S
E
p
b
MPa
Współczynniki:
566
0
.
1
0
.
53
30000
2
=
⋅
=
A
K
,
0
10
5
0
0
5
2
.
.
.
D
h
=
=
,
08
2
53
110
2
0
.
E
E
s
b
=
=
→
5
1
0
.
I
k
=
, 75
0.
R
b
=
13
1
75
0
5
1
0
.
.
.
R
I
I
b
k
w
=
⋅
=
⋅
=
Osiadanie:
3
3
2
0
2
2
10
78
4
13
1
10
53
0
5
120
1000
−
⋅
=
⋅
⋅
⋅
+
=
⋅
⋅
+
=
.
.
.
I
E
h
T
Q
s
w
s
n
n
m = 4.78 mm
b) Osiadanie całkowite pala
s
= s
1
+ s
2
= 1.02 + 4.78 = 5.80 mm
3. Osiadanie pali w grupie
Osiadanie pala „i” w grupie pali o liczbie „k” pali określa wzór:
∑
=
+
⋅
=
k
j
i
ij
j
gi
s
)
s
(
s
1
1
0
2
α
Współczynnik
)
(
F
Eij
Fij
E
Fij
ij
0
0
0
0
α
α
α
α
−
−
=
,
0
Fij
α
,
0
Eij
α
- odp. wg rys. 14 i 16 (PN),
0
ii
α
= 1.0
0
10
5
0
0
5
2
.
.
.
D
h
=
=
,
08
2
53
110
2
0
.
E
E
s
b
=
=
→
22
0
.
F
E
≈
wg. rys. 17 (PN)
Tablica 1. Wyznaczenie współczynników
α
0
ij
r
ij
[m]
2.0
4.0
6.0
8.0
10.0
r
ij
/D
4.0
8.0
12.0
16.0
20.0
D/r
ij
0.25
0.13
0.08
0.06
0.05
α
0
Fij
0.38
0.21
0.15
0.09
0.08
α
0
Eij
0.02
0.01
0
0
0
α
0
ij
0.30
0.17
0.12
0.07
0.06
W obliczeniach przyjęto, że wzajemne oddzia-
ływanie pali na siebie sięga na 4 pale we
wszystkich kierunkach.
Osiadania policzono dla 5 skrajnych pali
fundamentu.
Tablica 2. Obliczenia osiadań pali w grupie
Pal "i"
1
2
3
4
5
r
ij
α
0
ij
α
0
ij
⋅s
2j
r
ij
α
0
ij
α
0
ij
⋅s
2j
r
ij
α
0
ij
α
0
ij
⋅s
2j
r
ij
α
0
ij
α
0
ij
⋅s
2j
r
ij
α
0
ij
α
0
ij
⋅s
2j
Pal "j"
[mm]
[mm]
[mm]
[mm]
[mm]
1
0.0
1.00
4.78
2.0
0.30
1.43
4.0
0.17
0.81
6.0
0.12
0.57
8.0
0.07
0.33
2
2.0
0.30
1.43
0.0
1.00
4.78
2.0
0.30
1.43
4.0
0.17
0.81
6.0
0.12
0.57
3
4.0
0.17
0.81
2.0
0.30
1.43
0.0
1.00
4.78
2.0
0.30
1.43
4.0
0.17
0.81
4
6.0
0.12
0.57
4.0
0.17
0.81
2.0
0.30
1.43
0.0
1.00
4.78
2.0
0.30
1.43
5
8.0
0.07
0.33
6.0
0.12
0.57
4.0
0.17
0.81
2.0
0.30
1.43
0.0
1.00
4.78
6
10.0
0.06
0.29
8.0
0.07
0.33
6.0
0.12
0.57
4.0
0.17
0.81
2.0
0.30
1.43
7
12.0
-
-
10.0 0.06
0.29
8.0
0.07
0.33
6.0
0.12
0.57
4.0
0.17
0.81
8
14.0
-
-
12.0
-
-
10.0
0.06
0.29
8.0
0.07
0.33
6.0
0.12
0.57
9
16.0
-
-
14.0
-
-
12.0
-
-
10.0 0.06
0.29
8.0
0.07
0.33
10
20.0
-
-
16.0
-
-
14.0
-
-
12.0
-
-
10.0 0.06
0.29
s
1i
[mm]
1.02
1.02
1.02
1.02
1.02
s
gi
[mm]
9.24
10.68
11.49
12.06
12.40
Wyszukiwarka
Podobne podstrony:
Osiadanie pali przykl
Iteracyjne wyznaczenie długości pala pracującego w grupie pali, przykład
Obliczenie nośności i osiadań pali na podstwie sondowań statycznych CPT
Nośność pali przykład
Kościk Analiza osiadań pali pojedynczych wykonywanych techno logiami iniekcyjnymi w świetle próbnych
Obliczenie nośności i osiadań pali na podstwie sondowań statycznych CPT
osiadanie pali
Nosnosc pali przyklad
Fundament bezpośredni - przyklad obliczenia I i II SG c. d., tabela osiadań
Alagaddapama Sutta przykład z wężem, Kanon pali -TEKST (różne zbiory)
Kakacupama Sutta MN.21 przykłąd z piłą, Kanon pali -TEKST (różne zbiory)
Przyklady zajec Pali się, Policjant
Asembler ARM przyklady II
Sily przyklady
Przykłady roli biologicznej białek
style poznawcze jako przykład preferencji poznawczych
więcej podobnych podstron