13
Określanie sil węzłowych od obciążenia elementu
(wyrazów wolnych)
a) uwzględnienie sił masowych:
– przyjmijmy, że jedynymi siłami masowymi jest ciężar własny konstrukcji
γ. Wówczas
wektor obciążeń od sił masowych dla elementu „e” (rys.7.) ma postać:
{ }
{
}
{
}
T
T
y
x
M
f
γ
ρ
ρ
0
=
=
,
a wektor sił węzłowych spowodowanych tym obciążeniem przyjmie postać:
{ } {
}
[ ]
{ }
(
)
dV
N
V
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
⋅
⋅
=
=
=
∫
M
T
T
M
r
y
M
r
x
M
k
y
M
k
x
M
j
y
M
j
x
M
i
y
M
i
x
M
f
F
F
F
F
F
F
F
F
F
Po podstawieniu postaci funkcji kształtu i wektora obciążeń oraz wykonaniu całkowania
otrzymamy:
{ }
⎪
⎪
⎪
⎪
⎪
⎪
⎭
⎪⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎪
⎪
⎪
⎨
⎧
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
⋅
⋅
⋅
⋅
=
⋅
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎭
⎬
⎫
⎩
⎨
⎧
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
=
∫ ∫
∫ ∫ ∫
− −
− − −
t
b
a
t
b
a
t
b
a
t
b
a
dxdy
n
n
n
n
t
dtdxdy
n
n
n
n
n
n
n
n
F
F
F
F
F
F
F
F
F
a
a
b
b
r
k
j
i
t
t
a
a
b
b
r
r
k
k
j
j
i
i
M
r
y
M
r
x
M
k
y
M
k
x
M
j
y
M
j
x
M
i
y
M
i
x
M
γ
γ
γ
γ
γ
γ
γ
γ
γ
4
1
0
4
1
0
4
1
0
4
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2
2
2
2
2
2
2
2
2
2
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
14
b) uwzględnienie sił powierzchniowych:
Przyjmijmy, że powierzchnia boczna elementu „e” (rys7) na odcinku j-r jest obciążona
równomiernie rozłożonym obciążeniem powierzchniowym o intensywności q
x
[kN/m
2
]
skierowanym zgodnie z osią „x” lokalnego układu współrzędnych.
Wówczas wektor obciążeń powierzchniowych przyjmie postać:
,
{ } {
}
⎭
⎬
⎫
⎩
⎨
⎧
=
=
−
−
0
x
T
r
j
y
r
j
x
S
q
p
p
f
a wektor sił węzłowych w elemencie spowodowanych tym obciążeniem przyjmie postać:
{ } {
}
[ ]
{ }
(
)
dS
f
N
F
F
F
F
F
F
F
F
F
S
S
T
T
S
r
y
S
r
x
S
k
y
S
k
x
S
j
y
S
j
x
S
i
y
S
i
x
S
⋅
⋅
=
=
∫
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
Po podstawieniu funkcji kształtu oraz wektora obciążeń i wykonaniu całkowania otrzymamy:
{ }
⎪
⎪
⎪
⎪
⎪
⎪
⎭
⎪⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎪
⎪
⎪
⎨
⎧
⋅
+
⋅
⋅
−
⋅
⋅
+
⋅
⋅
−
⋅
⋅
=
⋅
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎭
⎬
⎫
⎩
⎨
⎧
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
=
∫ ∫
− −
0
)
2
1
(
0
)
2
1
(
0
)
2
1
(
0
)
2
1
(
4
0
0
0
0
0
0
0
0
0
2
2
2
2
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
a
x
b
a
x
b
a
x
b
a
x
b
t
q
dtdy
q
n
n
n
n
n
n
n
n
F
F
F
F
F
F
F
F
F
x
t
t
b
b
x
r
r
k
k
j
j
i
i
S
r
y
S
r
x
S
k
y
S
k
x
S
j
y
S
j
x
S
i
y
S
i
x
S
Uwzględniając przy tym, że dla boku elementu j-r wartość x=+a/2 ostatecznie wektor sił
węzłowych spowodowanych obciążeniem powierzchniowym przyjmie postać:
{ }
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
⋅
⋅
⋅
⋅
=
⎪
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎪
⎬
⎫
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
=
0
2
0
0
0
2
0
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
x
x
S
r
y
S
r
x
S
k
y
S
k
x
S
j
y
S
j
x
S
i
y
S
i
x
S
q
b
t
q
b
t
F
F
F
F
F
F
F
F
F
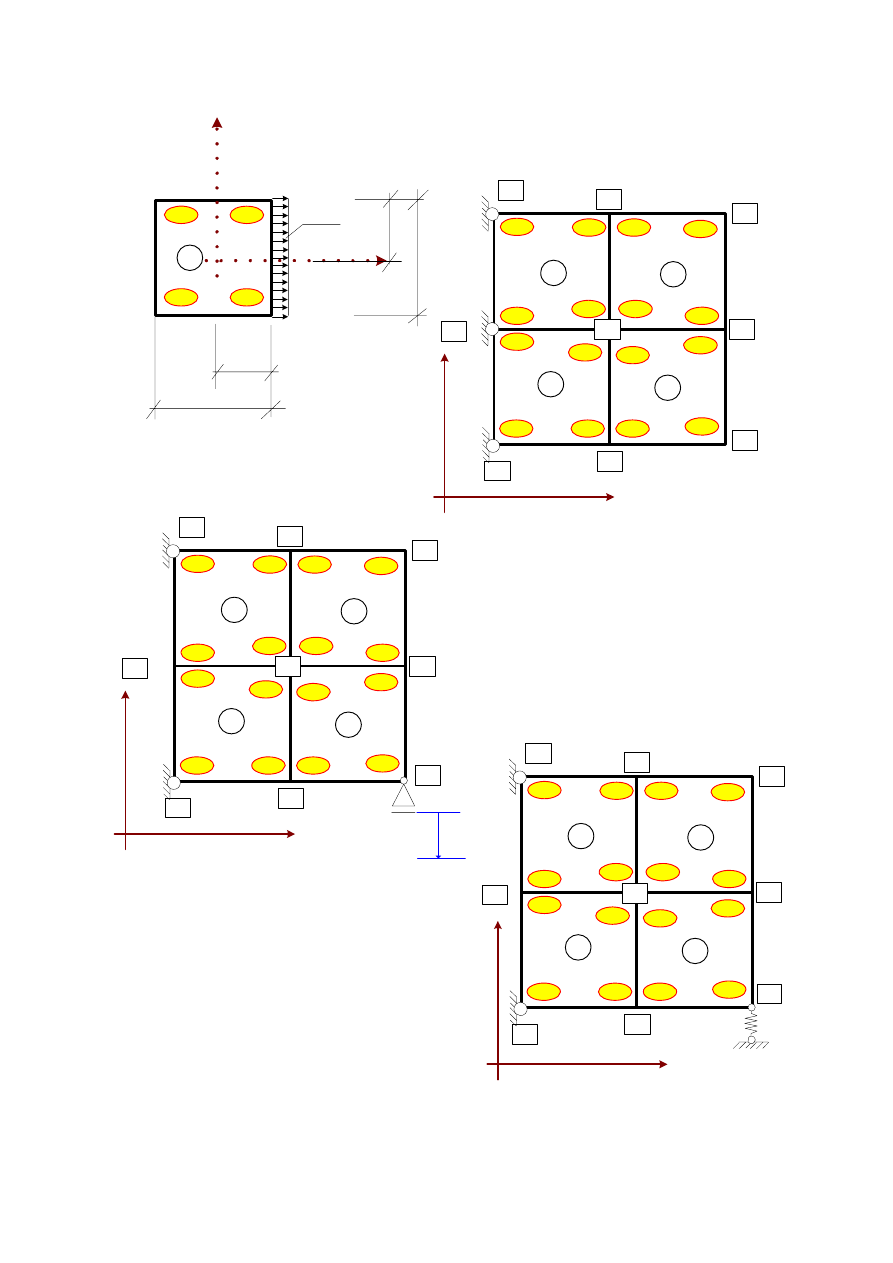
15
obciążenie elementu
i
j
r
k
x
y
podział tarczy i numeracja
elementów i węzłów w układzie
globalnym
3
y
a
a/2
e
q [kN/m
2
b
b/2
x
-
4
2
3
4
1
8
9
5
6
7
1
2
r
k
j
i
r
k
j
i
r
k
j
i
r
k
j
i
-
Rys.4.
Rys.7
podział tarczy i numeracja
elementów i węzłów w układzie
globalnym
3
x
-
2
3
4
1
4
3
8
9
5
6
7
1
2
r
k
j
i
r
k
j
i
r
k
j
i
r
k
j
i
Rys.5.
k
podział tarczy i numeracja
elementów i węzłów w układzie
globalnym
y
-
x
-
4
2
3
4
1
8
9
5
6
7
1
2
r
k
j
i
r
k
j
i
r
k
j
i
r
k
j
i
y
-
δ
Rys.6.