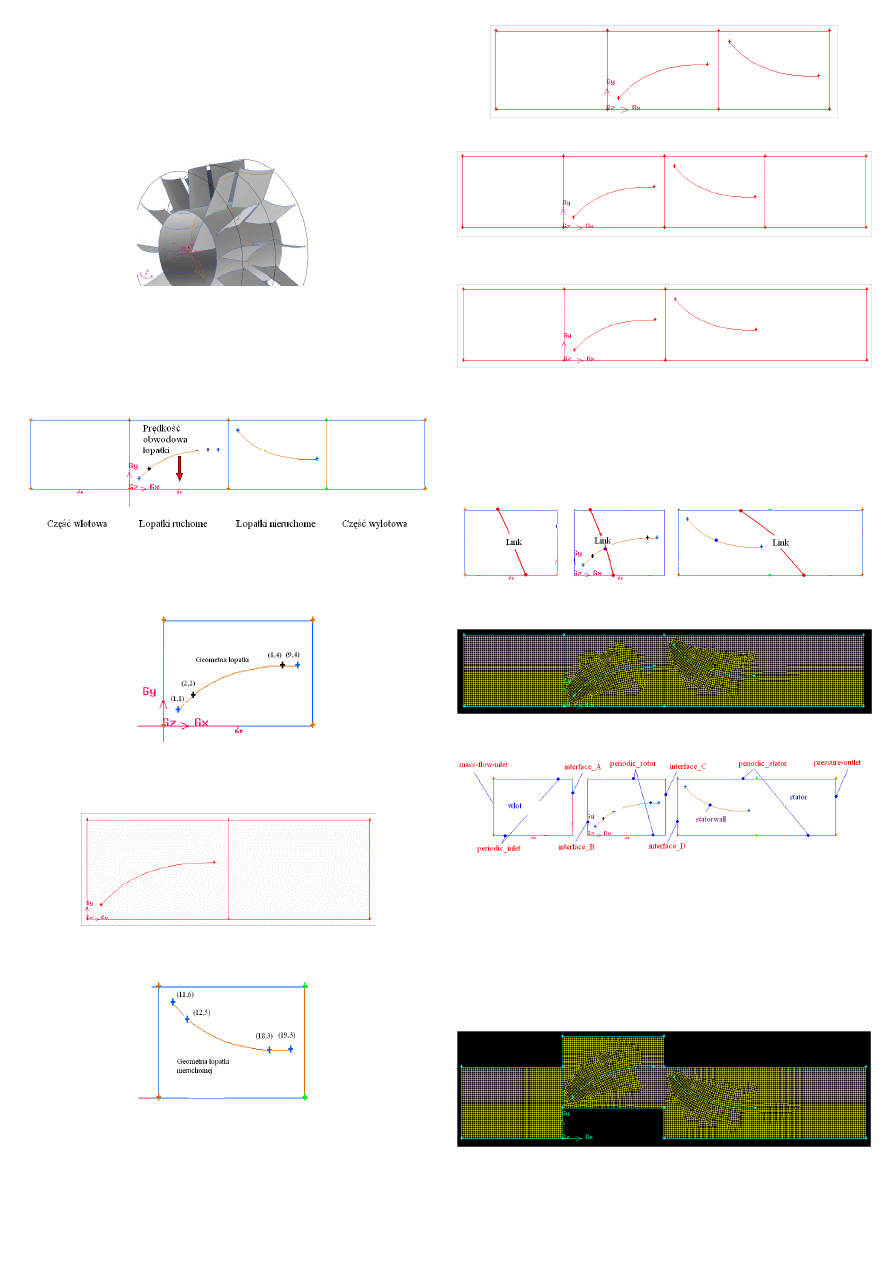
Modelowanie przepływu w stopniu sprężarki

osiowej (GAMBIT)

Typowy stopień sprężarki osiowej składa się z części wlotowej,
ruchomych łopatek, łopatek stałych i części wylotowej. Układ
taki jest oczywiście układem trój-wymiarowym.

Dokonujemy uproszczenia: analizujemy przepływ dla jednej
pary łopatek na pewnym promieniu. Przepływ trójwymiarowy
zastępujemy przepływem dwu-wymiarowym.
Obliczenia

przeprowadzimy

dla

segmentu

wirnika

obejmującego jedną łopatkę ruchomą i jedną nieruchomą na
powierzchni cylindrycznej którą łopatki przecinają.
Nasz stopień sprężarki składa się zatem z 4 elementów

Tworzenie geometrii – GAMBIT

1.Tworzymy segment palisady rotora o wymiarach 10 x 7
2.Tworzymy 4 punkty charakterystyczne dla łopatki rotora
(ruchomej) oraz jej krawędź (NURBS)

3. Usuwamy niepotrzebne 2 punkty a następnie splitujemy
segment palisady przy pomocy łopatki rotora

4.

Tworzymy segment palisady statora o wymiarach10 x 7 i

przesuwamy go o 10 jednostek w prawo

5. Tworzymy 4 punkty charakterystyczne dla łopatki statora
(nieruchomej) oraz jej krawędź (NURBS)

6. Usuwamy niepotrzebne 2 punkty a następnie splitujemy
segment palisady przy pomocy łopatki statora i nadajemy mu
nazwę „stator”

7. Tworzymy segment o wymiarach 10 x 7, przesuwamy o 10
jednostek w lewo i nadajemy mu nazwę „cz-wlotowa”

8. Tworzymy segment o wymiarach 10 x 7, przesuwamy o 20
jednostek w prawo

9. Łączymy segment „stator” z segmentem ostatnim (Face > Unit
Faces z opcja Real) nadając nazwę całości „stator-wylot”

10. Przed wykonaniem siatki linkujemy odpowiednie pary
krawędzi jak na rysunku (Mesh > Edge > Link Edge Meshes z
opcją Periodic).
Uwaga: śeby linkowanie krawędzi było poprawne, obie
krawędzie muszą mieć ten sam zwrot! Jeśli tak nie jest, możemy
zmienić zwrot jednej z nich naciskając Shift i środkowy klawisz
myszki.

11. Siatkowanie – Tworzymy siatki czworościenne (Mesh Faces
> Quad, Pave) o wymiarze 0.2

12. Nadajemy warunki brzegowe

Na wlocie nadajemy warunek brzegowy Mass_Flow_Inlet.
Warunek Pressure-Outlet na wylocie potrzebny jest nam dla
ustalenia poziomu ciśnienia panującego na wylocie. Zadając
ciśnienie na wylocie można obliczyć ciśnienia w pozostałym
obszarze (także na wlocie).
Krawędziom pomiędzy cz. wlotową a rotorem oraz rotorem a
segmentem „stator-wylot) nadajemy warunek brzegowy typu
Interface z opcją Periodic (inter-a, inter-b, inter-c, inter-d). Dla
ułatwienia można na chwilę segment „rotor” przesunąć w górę
lub w dół.

14. Po nadaniu nazw wlot, rotor i stator, wylot zapamiętujemy
wykonaną pracę a następnie eksportujemy siatkę dwu-
wymiarową.

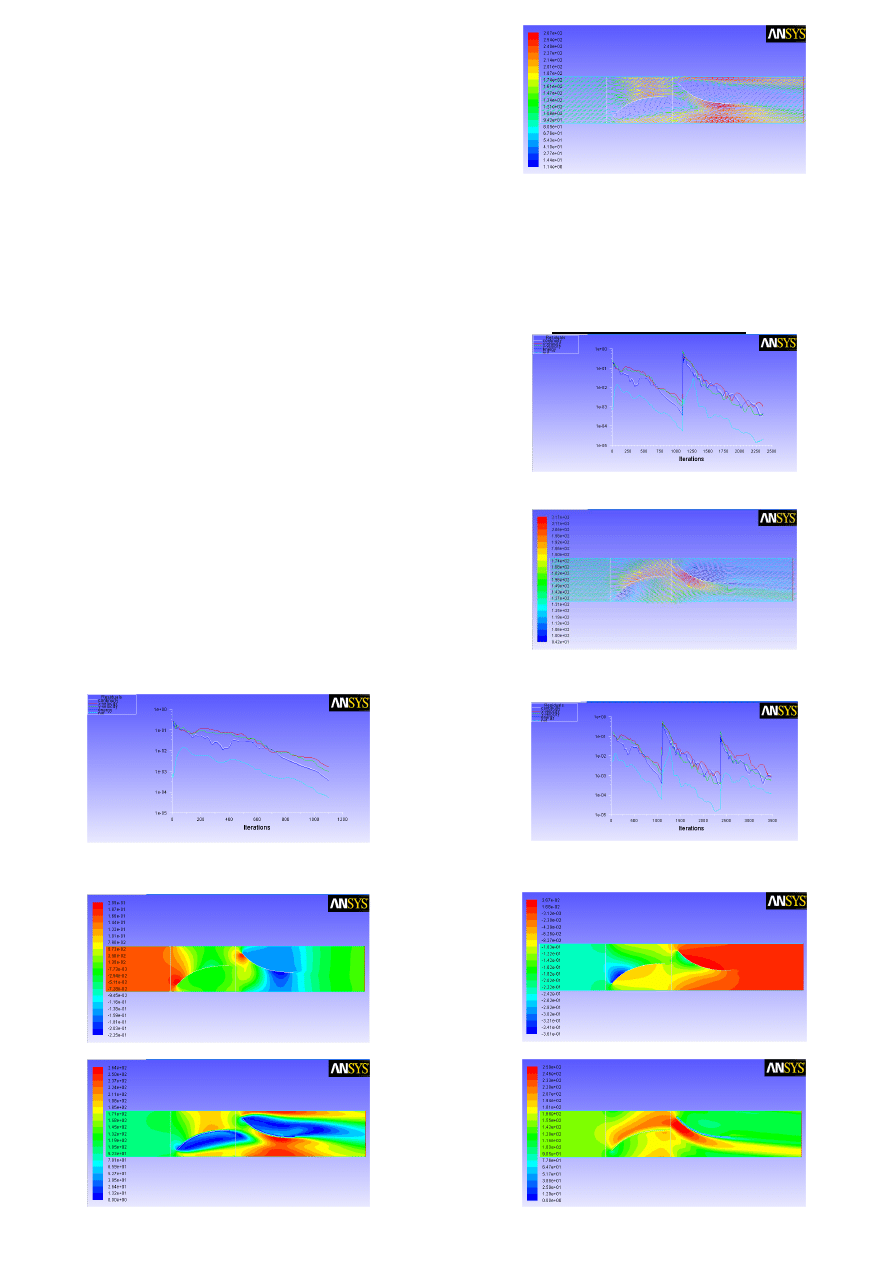
Obliczenia – FLUENT

Ustawienia ogólne:

•

2d, Serial

•

Wczytanie i sprawdzenie siatki

•

Skalowanie siatki (wymiary w cm)

•

Ustawienie solvera: Density Based, Absolute, Steady, Planar

•

Jednostki ciśnienia: bar (10

5

Pa)

•

Models: model turbulencji Spalarta Allmarasa

•

Włączone równanie energii

•

Materiał :powietrze, ideal-gas

•

Operating Conditions: 1 bar

•

Solution controls: Courant Number = 5

Warunki brzegowe:

•

wlot: mass-flow-inlet, Reference Frame-Absolute, Mass-Flow
Specification Method – Mass Flow Rate, Mass Flow Rate
(kg/s) = 10, Total Temperature = 300 K

(Przyjęta wartość Mass-Flow Rate wynika z następującego
rozumowania:
• prędkość samolotu =450 km/h = 125 m/s
• szerokość segmentu wlotowego = 0.07 m (średnica podziałowa)
• wysokość segmentu wlotowego = 1 m
• gęstość powietrza = 1.19 kg/ m3
•wydatek masowy (mass-flow-rate = 1.19 x 125 x 0.07 = 10.4
kg/s)

•

wylot: Gauge Pressure = 0 bar, Backflow Total Temperature
= 300 K

Ustalenie interfejsów (Mesh Interfaces):

•

interface_A z interface_B oraz interface_C z interface_D

•

Interface Options: Periodic Repeats

I. Obliczenia rozpoczynamy od przypadku, gdy rotor
jest nieruchomy

•

inicjalizacja z wlotu

•

iterujemy (zbieżność procesu po ok. 1250 iteracjach)

Wyniki obliczeń:
pole ciśnień,

pole prędkości,

wektory prędkości

II. Obliczenia dla pozornie ruchomego wirnika

=> Cell Zone Conditions

•

Rotor: w zakładce Motion Type ustawiamy opcję Moving
Reference Frame i wartość prędkości ruchu łopatki
(Translational Velocity Speed) Y = -120 m/s

•

iterujemy – już bez ponownej inicjalizacji!

Wyniki obliczeń

-

wektory prędkości

•

ustawiamy nową wartość Translational Velocity Speed = -150
m/s i iterujemy dalej (rozwiązanie powinno zbiegać się po ok.
1000 iteracjach)

Wyniki obliczeń:
pole ciśnień,

pole prędkości,

wektory prędkości,

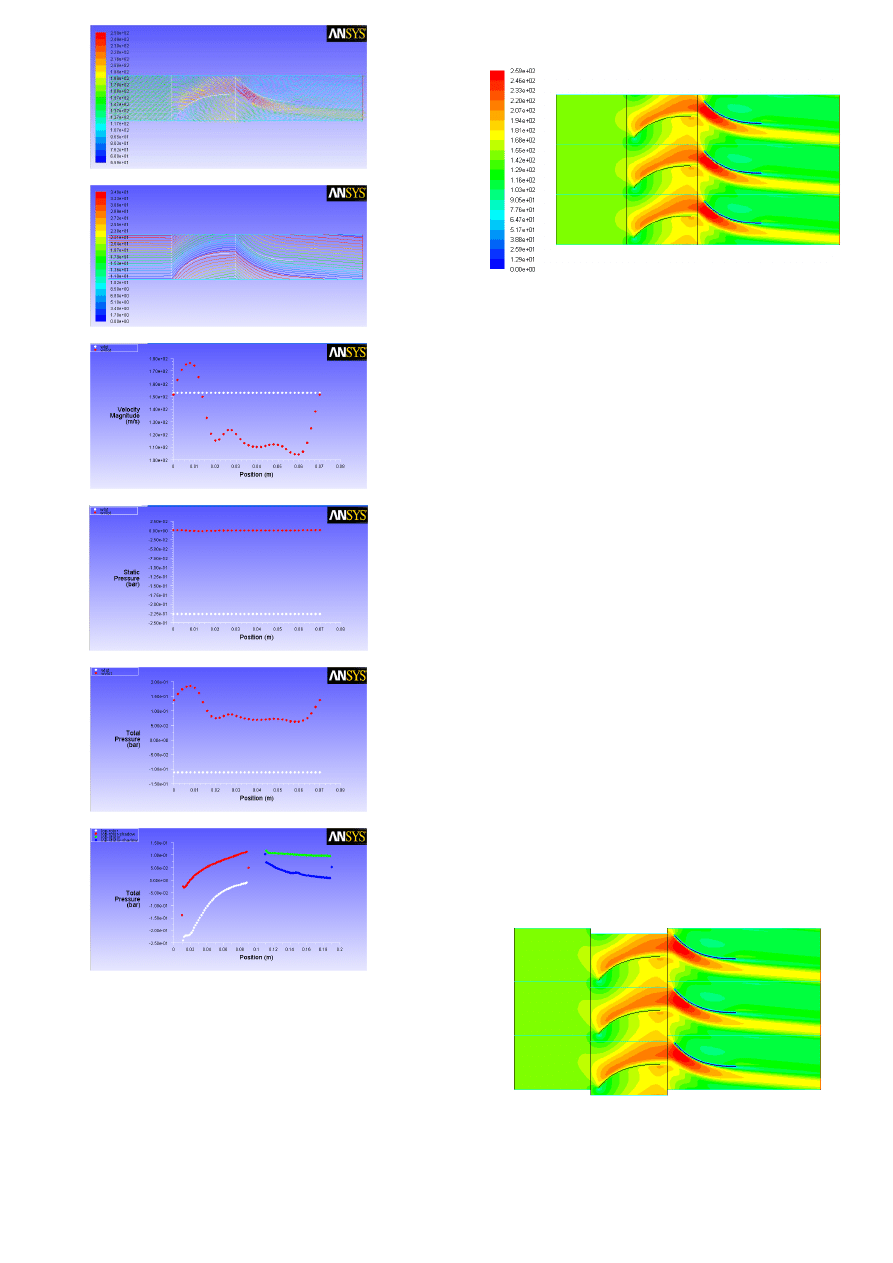
linie prądu

prędkości na wlocie i wylocie,

ciśnienia na wlocie i wylocie (stopień sprężania),

ciśnienia całkowite na wlocie i wylocie,

rozkłady ciśnienia na powierzchni łopatek (rotora i statora).

III. Modelowanie przepływu nieustalonego

Łopatki statora są nieruchome, łopatki rotora poruszają się z
zadaną prędkością (Moving Mesh)

1. Zmieniamy typ solwera z Steady na Transient (= Unsteady)
2. Rotor: w zakładce Motion Type zamiast opcji Moving

Reference Frame ustawiamy opcję Moving Mesh. Wartość
prędkości ruchu łopatki (Translational Velocity Speed) Y = -
150 m/s pozostawiamy bez zmiany.

3. Pozostałe ustawienia bez zmian
4. Zmieniamy sposób wyświetlania z 1 na 3 segmenty (Display >

Views > Periodic Repeats Define). Ustawiamy w oknie

translation wartość Y=0.07 m, względnie -0.07 oraz Number
of Repeats = 3 i naciskamy Set.

5. Przygotowanie animacji

Calculation Activities > Solution Animations > Create/Edit
Animation Sequences = 2 (np. cisnienie i predkosc)

Dalej ustawiamy wyświetlanie map konturowych ciśnienia i
prędkości

6. Ustalenie kroku czasowego
Najmniejszy wymiar liniowy

∆∆∆∆

x w Gambicie wynosi 0.2, czyli we

Fluencie (po przeskalowaniu)

∆∆∆∆

x = 0.002 m = 2 mm

Krok czasowy wyraża się wzorem

∆∆∆∆

t =

∆∆∆∆

x / (V

max

+ a)

Maksymalną wartość prędkości odczytujemy z mapy
konturowej jako V

max

= 260 m/s , prędkość dźwięku

przyjmiemy jako a = 340 m/s. Stąd

∆∆∆∆

t =

∆∆∆∆

x / (V + a) = 2 x 10

-3

/ 600 = 3 x 10

-6

s

(Dla przyspieszenia obliczeń możemy nawet przyjąć większy
krok czasowy większy np.

∆∆∆∆

t = 5 x 10

-6

s.)

Dla prędkości przesuwu (unoszenia) rotora równej ok. 150 m/s i
odległości między łopatkami rotora równej 0.07 m (wartość po
przeskalowaniu) otrzymamy czas odpowiadający przejściu tej
odległości jako
T = 0.07 / 150 = 4.7 x 10

-4

s

Uwzględniając przyjęty krok czasowy otrzymamy ilość kroków
odpowiadającą jednemu przejściu jako
TS = T /

∆∆∆∆

t = 4.7 x 10

-4

/ 3 x 10

-6

s = 157

śeby zobrazować jeden pełny cykl ruchu łopatek musimy zrobić
157 kroków czasowych i tyle samo zdjęć do animacji.

7. W zakładce Run Calculation ustawiamy:

Time Step Size (s) = 5e-6 oraz Numer of Time Steps = 10 (na
początek)

Wykonujemy iteracje (Calculate)

8. Sprawdzamy wynik (czy rotor się przesuwa oraz czy

nagrywają się filmy)

9. Wykonujemy pozostałe iteracje

10. Sprawdzamy wyniki oglądając animacje (filmy).