jest również udział wspinania dyslokacji
wokół wydzieleń (rys. 3.60). Zmniejszenie
umocnienia stopu następuje w tych warun-
kach w wyniku przyspieszonego zdrowienia
dynamicznego osnowy.

Twarde i trudno odkształcalne fazy

wtórne decydują o wzroście gęstości dysloka-
cji i umocnieniu stopu, gdy rzeczywiste
odkształcenie plastyczne zwiększa się
do

ε

= 1. Dalsze zwiększenie odkształcenia

ε

powoduje odkształcanie i kruszenie się
cząstek tych faz, w wyniku czego zmniejsza
się umocnienie stopu. Pokruszone cząstki faz
najczęściej są usytuowane na granicach
podziarn lub w ściankach komórek dysloka-
cyjnych. Dalsze zwiększenie odkształcenia

ε

wpływa na zmniejszenie umocnienia stopów
w wyniku tworzenia i rozwoju pasm ścinania.

3. Struktura i umocnienie metali i stopów

174

Rysunek 3.58

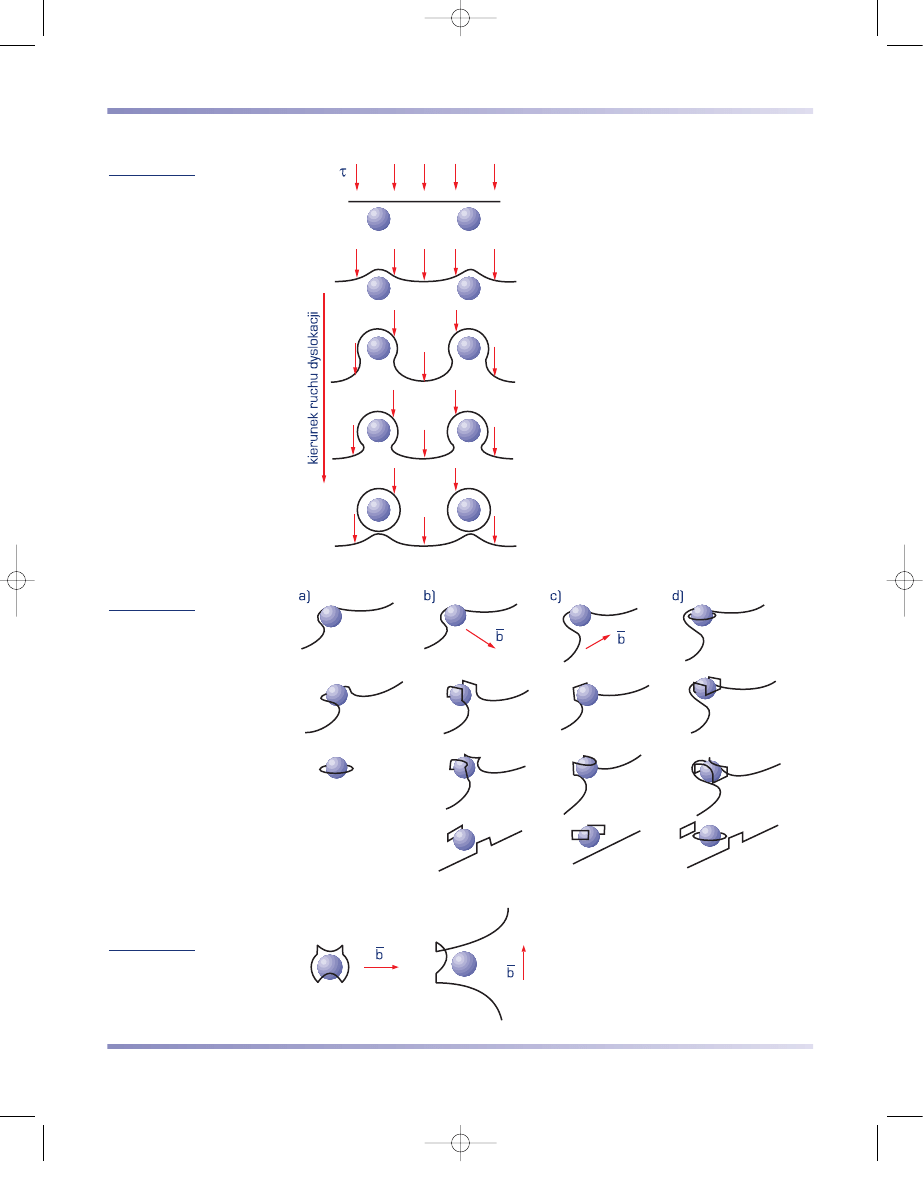
Schemat omijania wydzieleń
przez dyslokację pozostawia-
jącą wokół nich zamknięte
pętle (według E. Orowana)

Rysunek 3.59

Schemat mechanizmów
omijania wydzieleń
przez dyslokację
a) według mechanizmu
Orowana,
b, c) za pośrednictwem
poślizgu poprzecznego,
d) przy jednoczesnym
działaniu mechanizmu
Orowana i poślizgu
poprzecznego
(według A.S. Argona)

Rysunek 3.60

Schemat wspinania dys-
lokacji wokół wydzieleń
(według A.S. Argona)

3 roz 6-11-02 22:49 Page 174

3.1. Krystaliczna struktura metali

175

175

Struktura 1) cienkiej folii ze stali typu
15MnNb5 (P355NL1); ferryt z węglikami
globularnymi, pow. 14000x; 2) stali typu
15MnNb5 (P355NL1); ferryt i perlit
w układzie pasmowym, pow. 500x; 3)
cienkiej folii ze stali typu 15MnNb5
(P355NL1); obszary perlitu w otoczeniu
ferrytu, pow. 11000x; 4) stali typu 70Cr4;
perlit, pow. 3000x, mikroskop skaningowy;
5) cienkiej folii ze stali 38MnSi6; perlit,
pow. 12000x; 6) cienkiej folii ze stali
100Cr6; perlit po walcowaniu z chłodzeniem
w powietrzu, pow. 11000x; 7) cienkiej folii ze
stali 100Cr6; sfragmentowany perlit po
wyżarzaniu sferoidyzującym udarowym,
pow. 32000x; 8) cienkiej folii ze stali
100Cr6; sferoidyt po wyżarzaniu sferoidyzu-
jącym udarowym, pow. 20000x

1

2

3

4

5

6

7

8

Ferryt i perlit

3 roz 6-11-02 22:49 Page 175

3. Struktura i umocnienie metali i stopów

176

176

Struktura 1) węglików pierwotnych typu M

6

C w zahartowanej stali

szybkotnącej typu HS11-0-2+Si+Nb nadtopionej w czasie austenity-
zowania w 1300°C przez 100 s, pow. 2500x; 2) rozdrobnionych
węglików pierwotnych i wtórnych typu MC, M

6

C i M

23

C

6

równomiernie rozmieszczonych w osnowie ferrytu stopowego
w stali szybkotnącej typu HS9-2-2+Si+Nb w stanie wyżarzonym sfe-
roidyzująco, pow. 4000x, mikroskop skaningowy; 3) węglików typu
M

23

C

6

w osnowie ferrytu stopowego w cienkiej folii ze stali typu

HS12-0-2C wyżarzonej sferoidyzująco, pow. 26000x, 4) węglików
typu M

6

C i MC, częściowo rozpuszczonych w czasie austenity-

zowania w 1240°C przez 100 s, na granicach ziarn austenitu pier-
wotnego zahartowanej stali szybkotnącej typu HS11-2-2+Si, pow.
2500x, mikroskop skaningowy; 5) węglika pierwotnego typu M

6

C

nierozpuszczonego w trakcie austenityzowania w osnowie marten-
zytu odpuszczonego w cienkiej folii ze stali typu HS11-0-2+Si+Nb
zahartowanej z 1240°C i odpuszczonej w 570°C, pow. 21000x; 6)
przedeutektoidalnych wydzieleń węglików typu M

4

C

3

w cienkiej

folii ze stali typu HS11-0-2-5+Si zahartowanej z 1240°C, pow.
43000x; 7) dyspersyjnych wydzieleń węglików typu M

4

C

3

decydują-

cych o efekcie twardości wtórnej, w osnowie martenzytu odpusz-
czonego w cienkiej folii ze stali typu HS12-0-2C zahartowanej
z 1190°C i odpuszczonej w 600°C, pow. 36000x; 8) dyspersyjnych
wydzieleń węglików typu M

4

C

3

decydujących o efekcie twardości

wtórnej, w osnowie martenzytu odpuszczonego w cienkiej folii ze
stali typu HS6-5-2 zahartowanej z 1180°C i odpuszczonej w 570°C,
pow. 350000x, obraz w polu ciemnym z refleksu (111) M

4

C

3

1

2

3

4

5

6

7

8

Węgliki w stalach szybkotnących

3 roz 6-11-02 22:49 Page 176

3.4. Układy
równowagi fazowej

3.4.1. Równowaga termodynamiczna układu

i energia swobodna

STAN RÓWNOWAGI TERMODYNAMICZNEJ

Stopy metali wykazują trwałość budowy fazowej w stanie równowagi termody-

namicznej, która zostaje osiągnięta, gdy energia swobodna układu uzyska mini-
mum lub gdy potencjały chemiczne składników we wszystkich fazach układu staną
się sobie równe i ustaje ich przepływ przez granice fazowe.

ENERGIA SWOBODNA HELMHOLTZA

W przypadku równowagi w dowolnym układzie, w którym temperatura i obję-

tość są ustalone, funkcja energii swobodnej Helmholtza F, zwana także potencja-
łem termodynamicznym, osiąga swoje minimum:

F = E – TS,

(3.20)

gdzie:

E – energia wewnętrzna,
T – temperatura bezwzględna,
S – entropia.

ENERGIA WEWNĘTRZNA

Energia wewnętrzna E układu jest sumą energii potencjalnej, tj. energii wza-

jemnego oddziaływania, i energii kinetycznej wszystkich atomów układu. W krysz-
tałach znaczna część energii wewnętrznej wiąże się z drganiami atomów w sieci.
Amplituda drgań wzrasta wraz z podwyższeniem temperatury, powodując wzrost
energii wewnętrznej

∆

E:

∆

E =

∆

Q +

∆

L,

(3.21)

gdzie:

∆

Q – przyrost ciepła,

∆

L – przyrost pracy.

ENTROPIA

Entropia S jest funkcją stanu i zależy od aktualnego stanu układu, a nie od

drogi, jaką go osiągnięto. Entropia i energia wewnętrzna, jako własności pojem-
nościowe, są proporcjonalne do ilości materiału. Entropia określa równowagę

177

3 roz 6-11-02 22:49 Page 177

układu (gdy jej przyrost

∆

S = 0) oraz kierunek przemiany:

(3.22)

ENERGIA SWOBODNA GIBBSA

Gdy układ znajduje się w stałej temperaturze i działa na niego stałe ciśnienie,

po ustaleniu się równowagi energia swobodna Gibbsa G jest minimalna:

G = E + pV

−

TS,

(3.23)

gdzie:

p – ciśnienie,
V – objętość.

Procesy metalurgiczne zachodzące przy stałym ciśnieniu wymagają rozpatry-

wania energii swobodnej Gibbsa G. Nieznaczne zmiany objętości umożliwiają
pominięcie czynnika pV i rozpatrywanie energii swobodnej Helmholtza F.

ENTALPIA

Funkcję stanu, przy stałym ciśnieniu opisuje entalpia H:

H = E + pV.

(3.24)

ENERGIA SWOBODNA FAZ STOPU

Analiza energii swobodnej różnych faz układu stwarza możliwość określenia

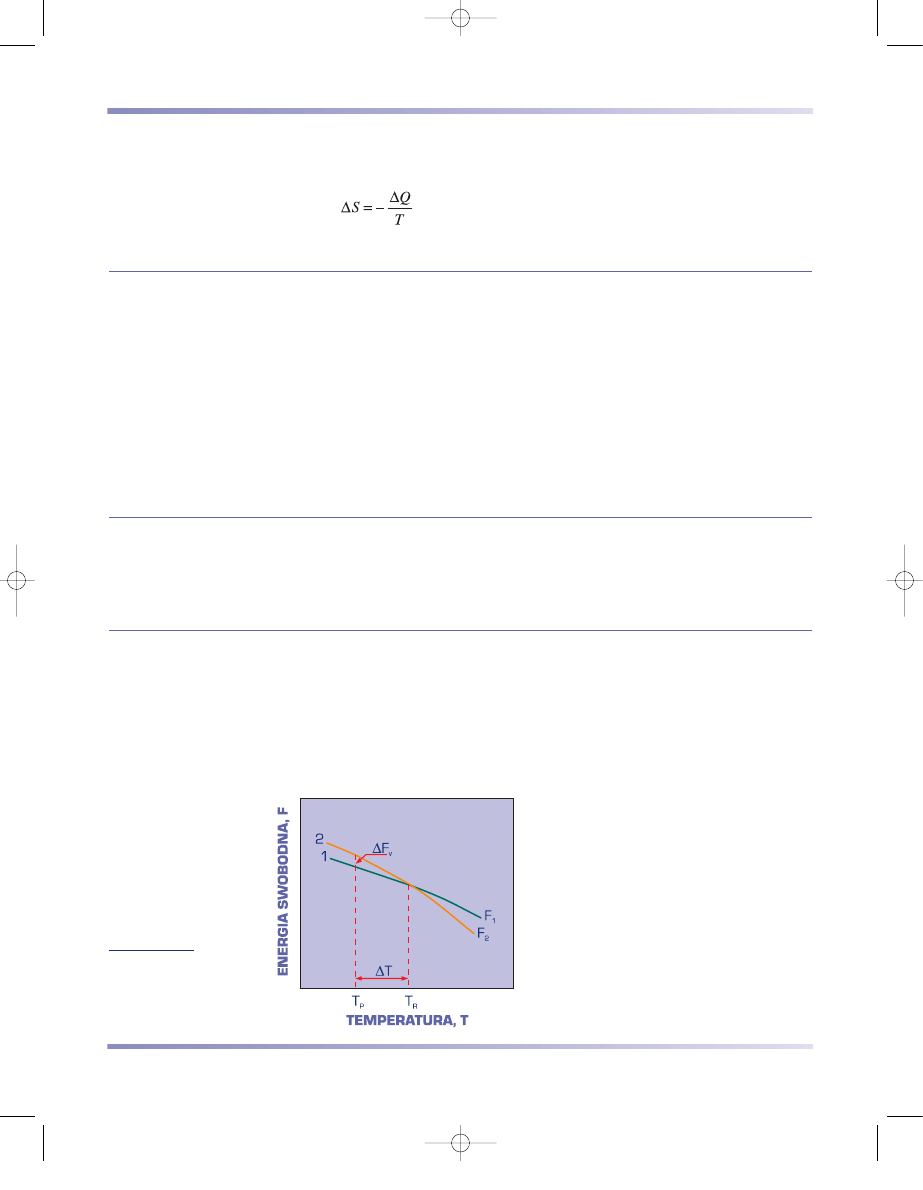
struktury stopu. Każdorazowo trwała jest faza o mniejszej energii swobodnej (rys.
3.61). W temperaturze niższej od temperatury równowagi T

R

, gdy F

1

< F

2

, trwała

jest więc faza 1. Odwrotnie jest w temperaturze wyższej od T

R

.

Na rysunku 3.62a przedstawiono zależność energii swobodnej roztworu stałe-

go od stężenia składników. Krzywa ma kształt litery U. Fazy międzymetaliczne
(rys. 3.62b i c) wykazują podobny charakter zmian energii swobodnej w funkcji
stężenia składników. Ponieważ fazy te występują w wąskim zakresie stężeń, na krzy-

wych opisujących ich energię swobodną wy-
stępuje ostre minimum (rys. 3.62b). Zakres
występowania danej fazy zależy przy tym od
względnego położenia krzywych energii swo-
bodnej sąsiednich faz (rys. 3.62b i c).
W przypadku mieszaniny faz

α

+

β

funkcja

energii swobodnej roztworu stałego od stę-
żenia składników F = f(c) wykazuje dwa mi-
nima (rys. 3.62d). W zakresie stężeń między
c

α

a c

β

minimalna jest energia swobodna

mieszaniny, określona przez styczną łączącą
punkty o najniższej energii swobodnej na
krzywej F

=

f (c).

3. Struktura i umocnienie metali i stopów

178

Rysunek 3.61

Schemat zmian energii
swobodnej dwóch faz
w funkcji temperatury

.

3 roz 6-11-02 22:49 Page 178

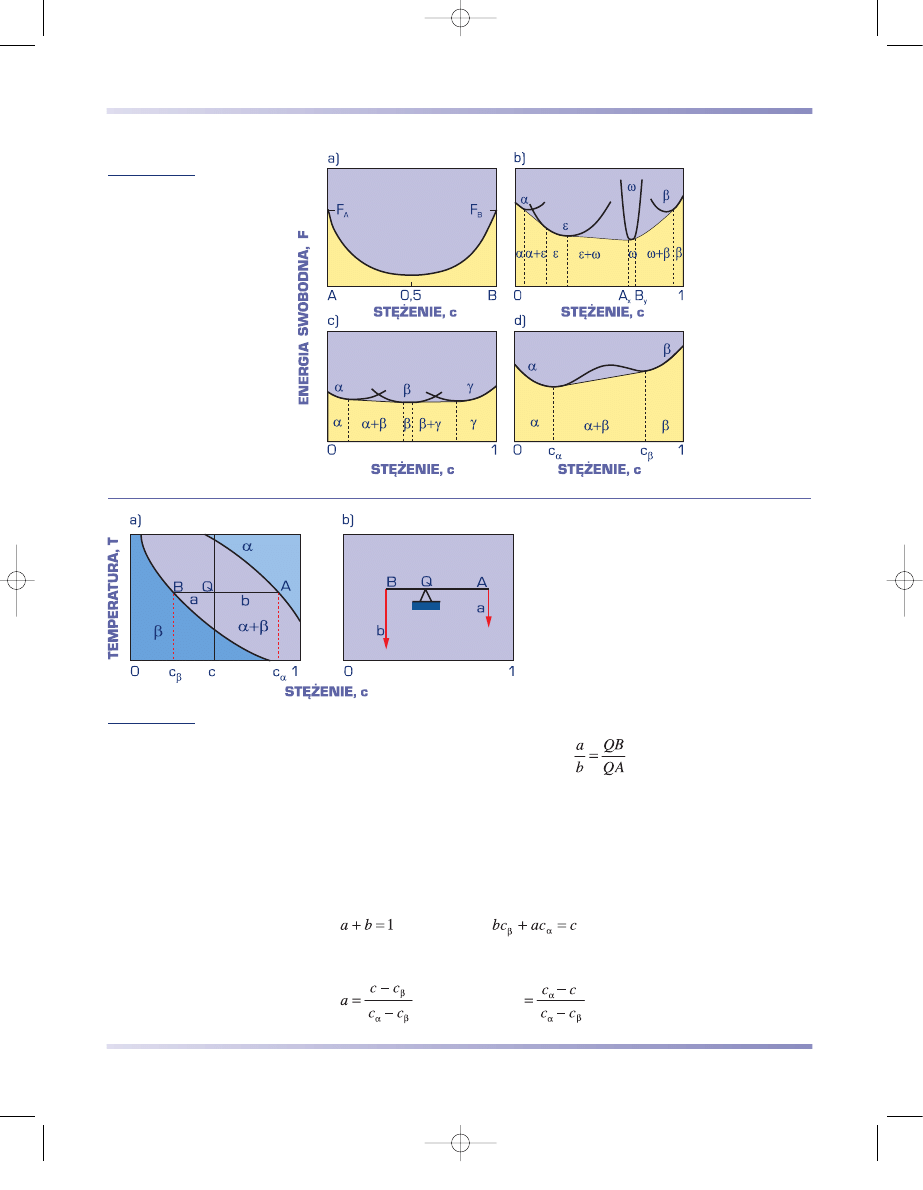
REGUŁA DŹWIGNI

Stosunek udziału obu faz mieszaniny

α

+

β

, przy danym stężeniu składników

c i stężeniu składników w poszczególnych
fazach odpowiednio c

α

i c

β

, dla każdej tempe-

ratury T z zakresu dwufazowego od T

1

do T

2

określa reguła dźwigni, zwana też regułą
odcinków. Zgodnie z tą regułą w punkcie Q
obszaru równowagi faz

α

i

β

(rys. 3.63a) sto-

sunek udziału a fazy

α

do udziału b fazy

β

zależy od warunków równowagi wynikają-
cych z położenia punktu Q, i równa się sto-
sunkowi odcinków QB do QA (rys. 3.63b):

(3.25)

Stosunek udziałów masowych faz pozostających w równowadze jest równy od-

wrotności stosunku odchyleń składów tych faz od średniego nominalnego składu
stopu. Schematycznie i poglądowo regułę tę można przedstawić za pomocą dźwig-
ni dwustronnej pozostającej w równowadze, podpartej w punkcie Q (rys. 3.63b).
Długości ramion dźwigni są proporcjonalne do długości odcinków QA i QB,
obciążenia zaś do udziałów faz – odpowiednio b i a. Ponieważ:

(3.26)

zatem udział poszczególnych faz wynosi:

(3.26a)

3.4. Układy równowagi fazowej

179

Rysunek 3.62

Schemat zależności energii
swobodnej od stężenia;
a) roztworu stałego,
b) i c) układów z fazami
międzymetalicznymi,
d) mieszaniny faz

.

,

,

,

.

b

Rysunek 3.63

Schematyczne przedstawienie reguły dźwigni;
a) fragment wykresu równowagi, b) reguła dźwigni

3 roz 6-11-02 22:49 Page 179

REGUŁA FAZ

Równowagę faz opisuje reguła faz W. Gibbsa. Zgodnie z tą regułą suma maksy-

malnej liczby faz f, które mogą współistnieć w układzie w stanie równowagi, oraz
liczby stopni swobody z jest równa liczbie niezależnych składników układu
s powiększonej o 2:

f + z = s +2.

(3.27)

Stopniami swobody z są parametry określające stan termodynamiczny układu,

takie jak temperatura, ciśnienie i stężenie składników, które niezależnie mogą ule-
gać zmianom. Liczbę składników s można przyjąć jako równą liczbie pierwiastków.
W odniesieniu do stopów dwuskładnikowych, gdy ciśnienie – jak we wszystkich
układach metalurgicznych – jest stałe, a zmianom ulegają tylko temperatura
i stężenie, reguła faz przybiera postać:

f + z = 3.

(3.28)

Na podstawie powyższej postaci reguły faz dla układów dwuskładnikowych

można sformułować cztery wnioski:

równowaga czterech i więcej faz w układach dwuskładnikowych jest
niemożliwa;
równowaga trzech faz w układach dwuskładnikowych jest możliwa tylko w jed-
nej stałej temperaturze przy określonym stężeniu składników w fazach i odpo-
wiada przemianom typu eutektycznego lub perytektycznego (rys. 3.55); licz-
ba stopni swobody układu jest w tym przypadku równa zeru;
dwie fazy pozostają w równowadze, gdy układ ma jeden stopień swobody;
zmiany stanu układu nie występują, gdy jest zmieniane albo stężenie
składników w fazach, albo temperatura;
gdy istnieje tylko jedna faza, układ ma dwa stopnie swobody, a więc bez naru-
szenia stanu równowagi zmianom mogą ulegać niezależnie temperatura
i stężenie.

3.4.2. Wykresy równowagi fazowej

i metody ich wyznaczania

METODY OPRACOWYWANIA WYKRESÓW

Układy równowagi fazowej przedstawia się w postaci wykresów równowagi.

Wykresy te są opracowywane doświadczalnie, różnymi metodami. Przemiany
fazowe polegające na zmianie stanu skupienia z ciekłego na stały lub odwrotnie są
badane metodą analizy termicznej. Przemiany w stanie stałym mogą być badane
różnymi metodami – w tym metalograficznymi, dylatometryczną, elektryczną,
magnetyczną albo radiograficzną. Badania te są wykonywane w czasie nagrzewa-
nia lub chłodzenia z możliwie najmniejszą szybkością zmian temperatury,
w warunkach najbardziej zbliżonych do stanu równowagi termodynamicznej.

3. Struktura i umocnienie metali i stopów

180

3 roz 6-11-02 22:49 Page 180

ANALIZA TERMICZNA

Metoda analizy termicznej polega na rejestrowaniu zmian temperatury stopu

w funkcji czasu chłodzenia ze stanu ciekłego do temperatury pokojowej lub nawet
niższej (gdy zastosowano wymrażanie). Zmiany temperatury w funkcji czasu
można również rejestrować podczas nagrzewania.

W zależności od rodzaju przemian na krzywych zmiany temperatury w funkcji

czasu obserwuje się charakterystyczne załamania lub przystanki izotermiczne,
powodowane wydzielaniem utajonego ciepła krzepnięcia lub pochłanianiem ciepła
topnienia. Czyste metale, fazy międzymetaliczne, a także mieszaniny eutektyczne
i perytektyczne krzepną w stałej temperaturze. Natomiast roztwory stałe krzepną
w pewnym zakresie temperatury.

ANALIZA TERMICZNA RÓŻNICOWA

Do badań efektów cieplnych podczas nagrzewania lub chłodzenia stopów są

stosowane nowoczesne termoanalizatory, umożliwiające analizę termiczną
różnicową DTA. Jednocześnie i w identycznych warunkach są nagrzewane lub
chłodzone próbka badanego stopu i próbka wzorcowa, nie wykazująca w badanym
zakresie temperatury żadnych przemian fazowych. Próbki znajdują się w takich
samych tyglach, np. alundowych. Gdy w badanej próbce zachodzi przemiana
związana z wydzielaniem lub pochłanianiem ciepła, występuje różnica temperatu-
ry między próbką badaną a próbką wzorcową.

Na krzywej DTA różnicy temperatury próbek badanej i wzorcowej, zarejestro-

wanej w funkcji czasu badania, występują charakterystyczne piki, odpowiadające
przemianom fazowym. Jednocześnie z krzywą DTA – w funkcji czasu – są rejestro-
wane zmiany temperatury próbki wzorcowej. Umożliwia to określenie temperatu-
ry poszczególnych przemian fazowych, zarejestrowanych na krzywej DTA.

OPRACOWYWANIE WYKRESÓW RÓWNOWAGI

W celu uzyskania pełnego wykresu równowagi fazowej należy zarejestrować

odpowiednio dużo krzywych chłodzenia lub nagrzewania dla stopów danego ukła-
du, różniących się stężeniem poszczególnych pierwiastków. Punkty odpowiadające
temperaturze charakterystycznej początku i końca przemiany odczytane z każdej
krzywej chłodzenia nanosi się na układ współrzędnych: temperatura – stężenie
składników. W wyniku połączenia tych punktów uzyskuje się wykres równowagi.

Wykres układu dwuskładnikowego można przedstawić w prostokątnym

układzie współrzędnych.

W technice wiele użytecznych stopów ma nie tylko 2 składniki, lecz 3 i więcej.

Zasady stosowane do opisu równowagi w układach dwuskładnikowych obowiązują
również w odniesieniu do układów wieloskładnikowych. Należy się jednak liczyć
z następującymi trudnościami:

przy gromadzeniu danych dla kompletnego układu n–składnikowego wzrastają
trudności, jeżeli n zwiększa się,
przedstawienie układów n–składnikowych wymaga przestrzeni n–wymiarowej,
co stanowi dodatkową trudność, jeżeli n > 3.

Z podanych powodów zbadano niewiele układów trójskładnikowych, a niemal

zupełnie nie opracowano układów o większej liczbie składników.

3.4. Układy równowagi fazowej

181

3 roz 6-11-02 22:49 Page 181

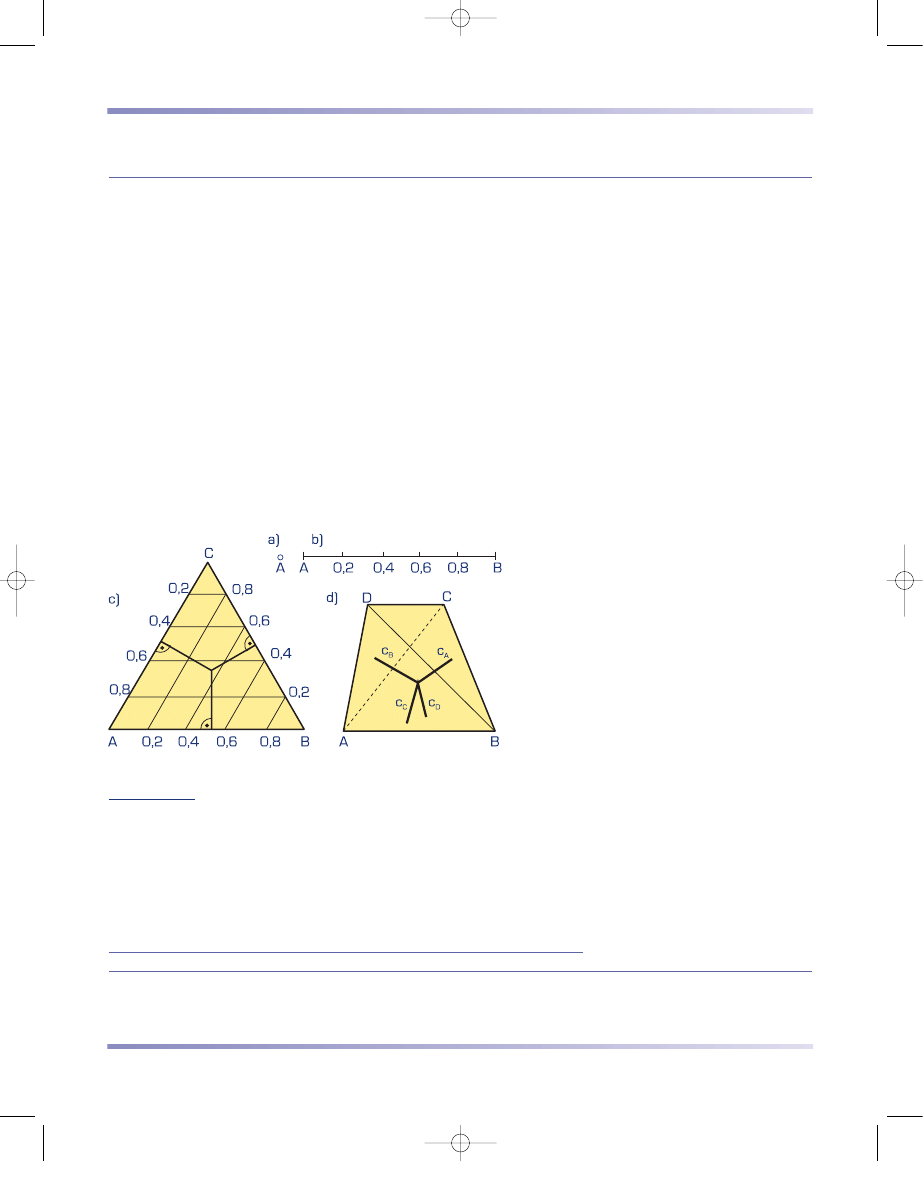
POJĘCIE SIMPLEKSU

Praktycznie analiza układu wieloskładnikowego sprowadza się często do rozwa-

żania zmian składu chemicznego stopów, gdyż zakłada się, że temperatura i ciśnie-
nie są stałe. Do przedstawienia składów w układach równowagi o różnej liczbie
składników wykorzystuje się topologiczne pojęcie simpleksu, co schematycznie
zilustrowano na rysunku 3.64. Simpleks bezwymiarowy s

0

jest punktem, który

reprezentuje określony składnik (rys. 3.64a). Simpleks jednowymiarowy s

1

jest

odcinkiem, odpowiadającym podstawie wykresu dwuskładnikowego (rys. 3.64b).
Dwa punkty końcowe tego odcinka odpowiadające poszczególnym składnikom
stopowym A i B nie stanowią części simpleksu s

1

, gdyż są simpleksami bezwymia-

rowymi s

0

. Dwuwymiarowy simpleks s

2

jest powierzchnią trójkąta równobocznego

zwanego także trójkątem stężeń Gibbsa (rys. 3.64c) i umożliwia przedstawienie
wszystkich możliwych składów układu trójskładnikowego. Trójwymiarowy sim-
pleks s

3

jest objętością czworościanu foremnego i reprezentuje wszystkie możliwe

składy, w układzie czteroskładnikowym (rys. 3.64d). Wykorzystanie simpleksu
czterowymiarowego s

4

umożliwia przedstawienie układu 5–składnikowego

składników A, B, C, D i E. W całości wykresu czterowymiarowego nie można
wykonać, można natomiast przedstawić przekroje trójwymiarowe po przyjęciu
stałej wartości jednej ze zmiennych, np. stężenia składnika E. Matematycznie jest

to równoznaczne z przecięciem hiper-
objętości s

4

wzdłuż stałej wartości składnika

E i z uzyskaniem hiperpowierzchni s

3

, odpo-

wiadającej geometrycznie simpleksowi
trójwymiarowemu s

3

, wystarczającemu do

przedstawienia układu czteroskładnikowego.
Odpowiednie przecięcie trójwymiarowego
wykresu s

3

układu czteroskładnikowego

prowadzi do uzyskania wykresu dwuwymia-
rowego s

2

. Simpleksy wyższego rzędu s

n–1

umożliwiają przedstawienie składów fazo-
wych układów n–składnikowych.

3.4.3. Dwuskładnikowe układy równowagi fazowej

DWUSKŁADNIKOWY UKŁAD RÓWNOWAGI FAZOWEJ

O ZUPEŁNEJ ROZPUSZCZALNOŚCI SKŁADNIKÓW W STANIE STAŁYM

Układy dwuskładnikowe o zupełnej rozpuszczalności składników w stanie

stałym (rys. 3.65a) są tworzone przez izomorficzne składniki A i B rozpuszczające
się wzajemnie przy dowolnych stosunkach ilościowych – zarówno w stanie

3. Struktura i umocnienie metali i stopów

182

Rysunek 3.64

Wykorzystanie simpleksu do przedstawienia składu stopów
a) w układzie jednoskładnikowym – s

0

, b) w układzie dwuskładnikowym – s

1

,

c) w układzie trójskładnikowym – s

2

, d) w układzie czteroskładnikowym – s

3

(według A.G. Guya)

3 roz 6-11-02 22:49 Page 182

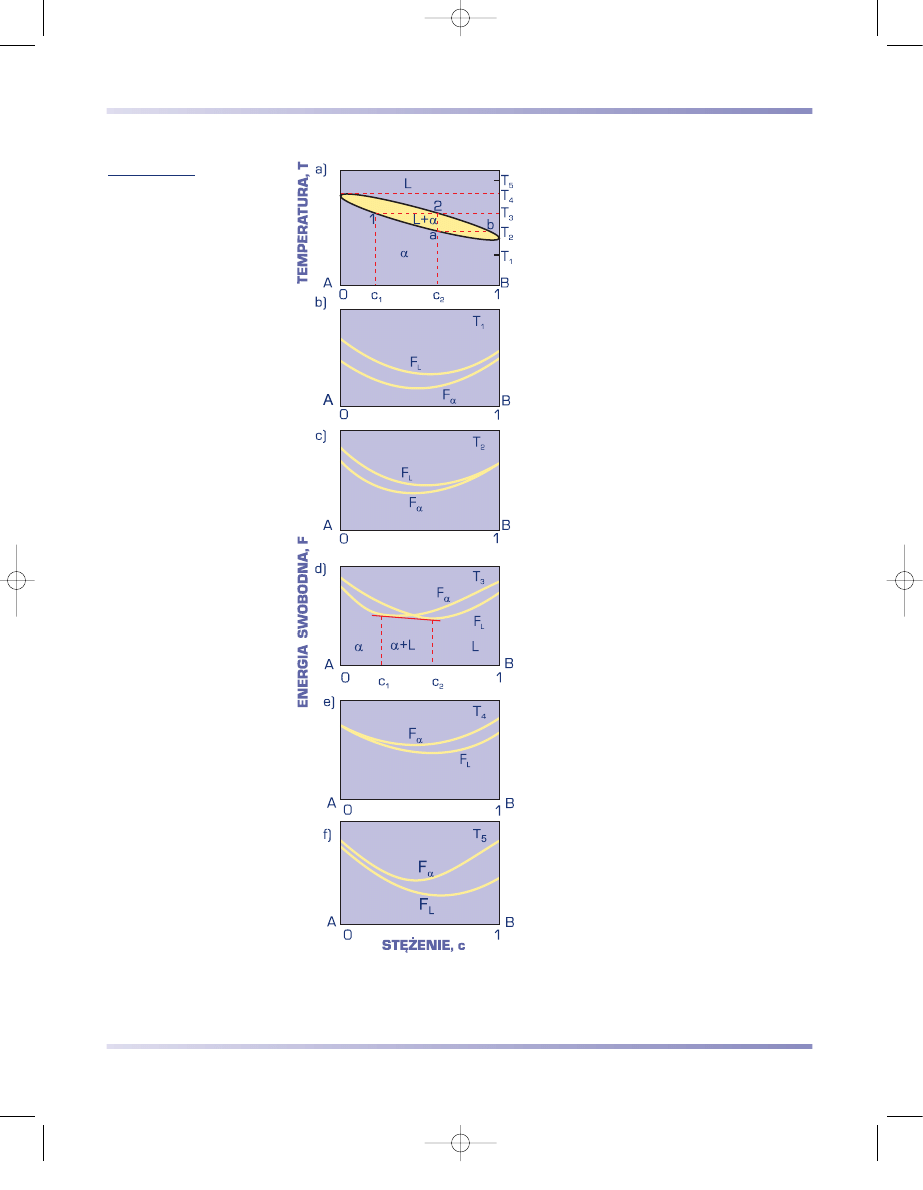
ciekłym, jak i stałym. Na rysunkach 3.65b

÷

f

podano również przebieg krzywych energii
swobodnej roztworów stałego i ciekłego
w różnej temperaturze T

1

÷T

5

.

Proces krzepnięcia roztworu stałego

przebiega podobnie dla wszystkich stopów
układu. Krzepnięcie stopu o stężeniu c

2

rozpoczyna się w temperaturze T

3

przecięcia

się linii składu stopu c

2

z linią likwidusu (rys.

3.65a). Likwidusem jest nazywana linia
przedstawiająca na wykresie równowagi
wartości temperatury, powyżej których stopy
w całym zakresie stężeń są ciekłe. W tempe-
raturze T

3

z cieczy wydzielają się pierwsze

zarodki roztworu stałego

α

o stężeniu c

1

odpowiadającym punktowi 1. W miarę dal-
szego obniżania temperatury skład krzep-
nącego stopu zmienia się wzdłuż solidusu od
punktu 1 do

α

, cieczy zaś wzdłuż likwidusu

od 2 do b. Solidusem jest nazywana linia na
wykresie równowagi oznaczająca wartości
temperatury, poniżej których stopy w całym
zakresie stężeń występują w stanie stałym.
Ilościowe udziały faz stałej i ciekłej w prze-
dziale krzepnięcia między likwidusem a soli-
dusem określa prawo dźwigni.

Po zakończeniu krzepnięcia (punkt a)

wszystkie ziarna roztworu stałego powinny
osiągnąć skład c

2

, co następuje w wyniku dy-

fuzji między fazą stałą i ciekłą, zachodzącej
podczas krzepnięcia. W rzeczywistości
wyrównanie składu chemicznego wszystkich
ziarn w wyniku dyfuzji przebiega znacznie
wolniej niż krzepnięcie. Temperatura zakoń-
czenia krzepnięcia jest również niższa od
odpowiadającej punktowi a, a skład osta-
tnich krzepnących kropel cieczy – bogatszy
w składnik B bardziej, niż wynika to z poło-
żenia punktu b w stanie równowagi. Stopy
krzepnące w warunkach technicznych
charakteryzują się więc znaczną segregacją
(niejednorodnością) składu chemicznego
w obrębie ziarn.

3.4. Układy równowagi fazowej

183

Rysunek 3.65

Wykresy
a) równowagi faz
podwójnego układu
z nieograniczoną
rozpuszczalnością
składników w sta-
nie stałym,
b)

÷

f) energii swo-

bodnej faz w różnej
temperaturze

3 roz 6-11-02 22:49 Page 183

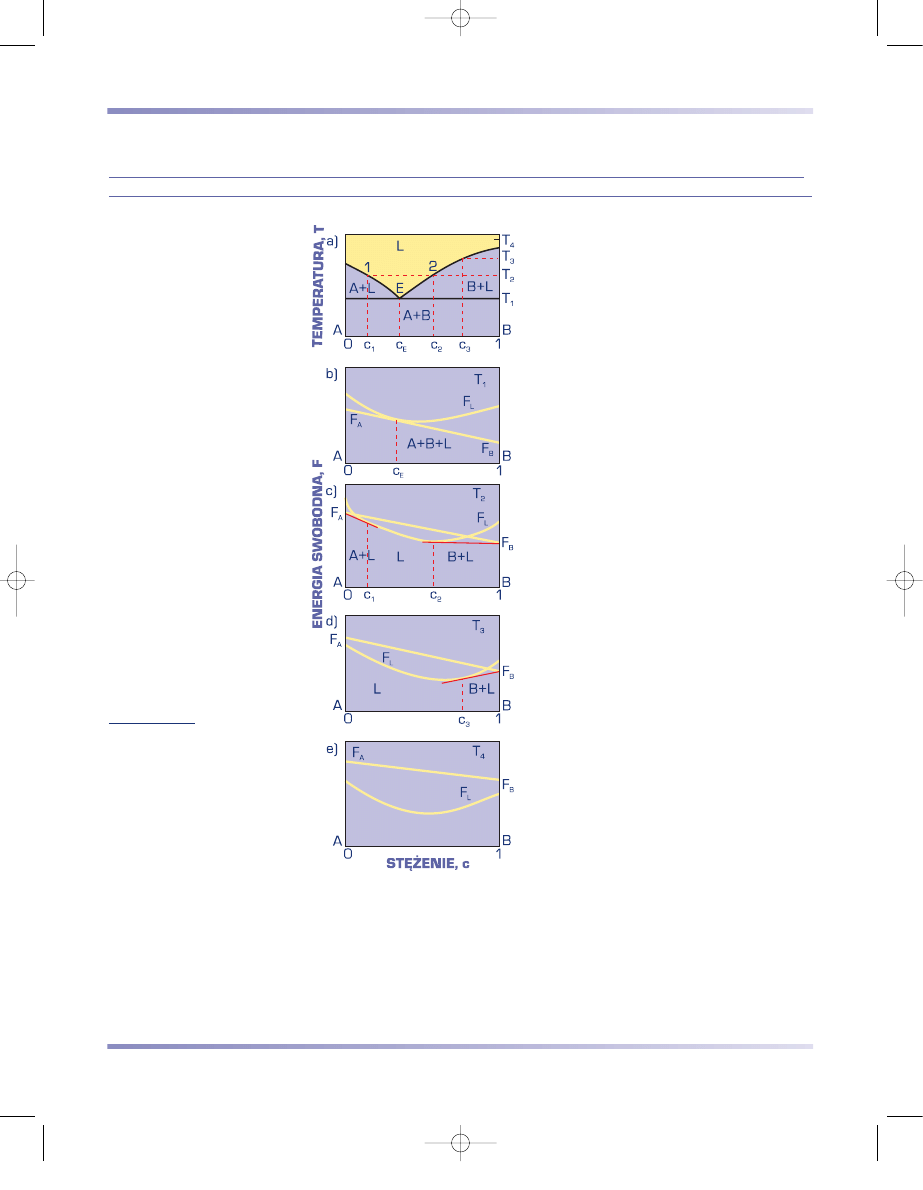
DWUSKŁADNIKOWY UKŁAD RÓWNOWAGI FAZOWEJ O CAŁKOWITYM BRAKU

ROZPUSZCZALNOŚCI SKŁADNIKÓW W STANIE STAŁYM Z EUTEKTYKĄ

Cechą charakterystyczną dwuskładniko-

wego układu równowagi o całkowitym braku
rozpuszczalności składników w stanie stałym
z eutektyką jest występowanie mieszaniny
czystych składników A + B o energii swo-
bodnej, której obrazem jest prosta łącząca
energie swobodne czystych składników (rys.
3.66). W temperaturze T

1

, zwanej tempera-

turą eutektyczną (i oznaczanej T

E

), naj-

mniejszą energią swobodną w całym zakresie
stężeń charakteryzuje się mieszanina fazy
ciekłej L i składników A + B. W tempera-
turze niższej od T

1

najmniejsza jest energia

swobodna mieszaniny eutektycznej A + B.

Proces krzepnięcia roztworu ciekłego

o stężeniu c

E

, zwanym składem eutekty-

cznym, następuje przez wydzielanie krysz-
tałów obu składników A i B z jednorodnej
cieczy L

E

(rys. 3.66a). Proces ten przebiega

w stałej temperaturze eutektycznej T

E

aż do

chwili, gdy cała ciecz ulegnie zakrzepnięciu.
Przemianę eutektyczną można zapisać
w następujący sposób:

L

E

→

A + B .

(3.29)

Podczas krzepnięcia stopów podeutekty-

cznych – o stężeniu c < c

E

– z jednorodnej

cieczy wydzielają się początkowo kryształy
metalu A, a skład cieczy zmienia się wzdłuż
linii likwidusu od punktu 1 do E (rys. 3.66a).
Dopiero wówczas reszta cieczy krzepnie
w stałej temperaturze eutektycznej T

E

, jako

mieszanina kryształów metali A i B. Struk-
turę takiego stopu stanowi mieszanina pier-
wotnie wydzielonych dużych kryształów
metalu A i drobnoziarnista mieszanina
eutektyczna metali A i B.

Stopy nadeutektyczne – o stężeniu c > c

E

– krzepną podobnie jak stopy

podeutektyczne, z tym że początkowo wydzielają się kryształy metalu B.

Układy równowagi metali o całkowitym braku rozpuszczalności składników

praktycznie nie występują, jednak wykorzystuje się je do analizy stopów metali
o bardzo małej wzajemnej rozpuszczalności składników w stanie stałym.

3. Struktura i umocnienie metali i stopów

184

Rysunek 3.66

Wykresy
a) równowagi faz podwójnego
układu o zupełnym braku
rozpuszczalności składników
w stanie stałym z eutektyką,
b)

÷

e) energii swobodnej faz

w różnej temperaturze

3 roz 6-11-02 22:49 Page 184

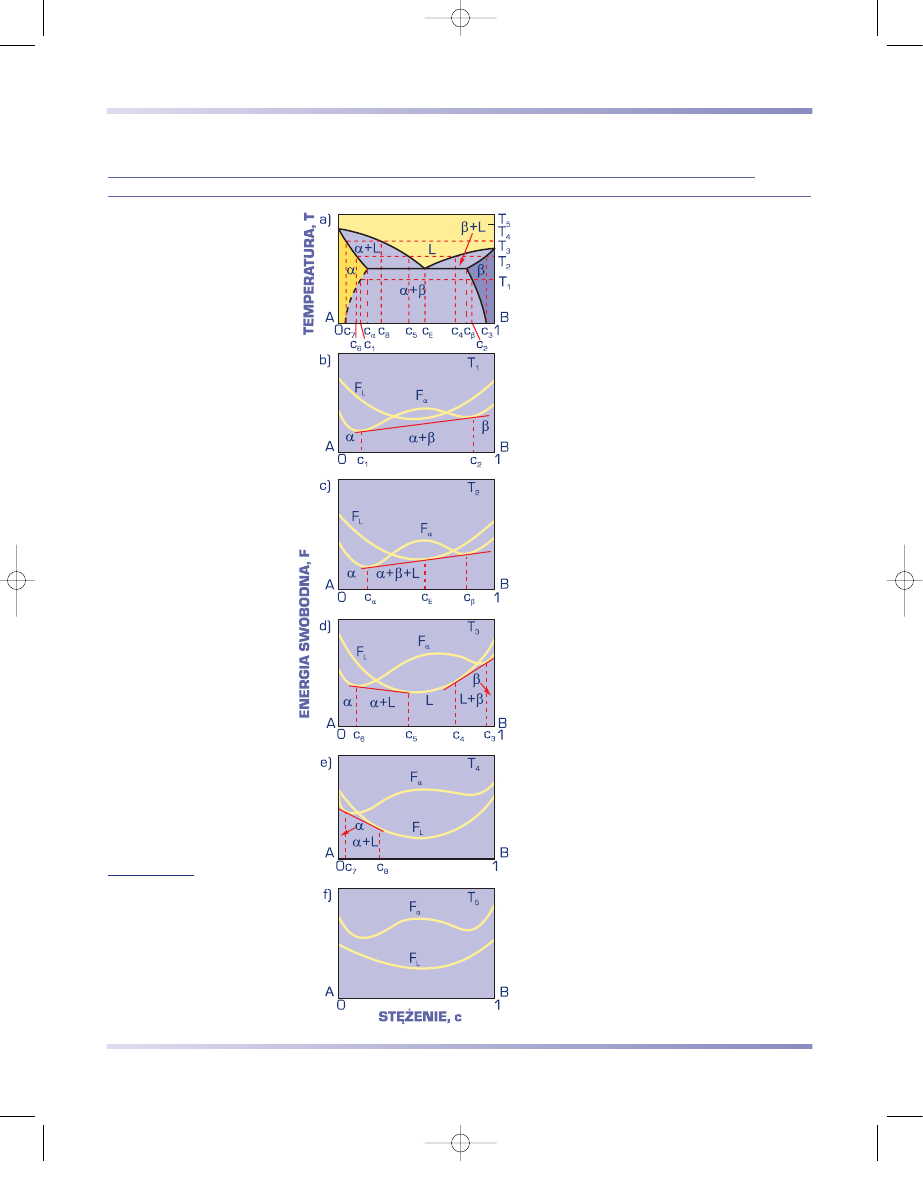
DWUSKŁADNIKOWY UKŁAD RÓWNOWAGI FAZOWEJ O OGRANICZONEJ

ROZPUSZCZALNOŚCI SKŁADNIKÓW W STANIE STAŁYM Z EUTEKTYKĄ

Dwuskładnikowe układy równowagi fazo-

wej o ograniczonej rozpuszczalności składni-
ków w stanie stałym z eutektyką są tworzone
przez pierwiastki o jednakowych lub różnych
sieciach krystalograficznych i różniące się
promieniami atomowymi więcej niż o 15%.
Gdy sieci krystalograficzne składników są
różne, różnią się również sieci każdego
z roztworów stałych, a energia swobodna
każdego z nich jest opisywana oddzielną
krzywą w kształcie litery U (rys. 3.67). Gdy
sieci przestrzenne każdego ze składników są
jednakowe, energia swobodna roztworu sta-
łego jest opisywana jedną krzywą z dwoma
minimami (rys. 3.67).

Opisywany układ stanowi jak gdyby połą-

czenie obu wykresów opisanych poprzednio.
Stopy o stężeniu c < c

α

oraz c > c

β

krzepną

jak roztwory stałe ciągłe. Strukturę stopów
o takim składzie stanowią odpowiednio jed-
norodne ziarna roztworu stałego

α

lub

β

.

Środkowa część wykresu, obejmująca stopy
o stężeniu c

α

< c < c

β

, jest analogiczna jak na

wykresie o całkowitym braku rozpuszczal-
ności w stanie stałym z eutektyką – z tą
różnicą, że podczas krzepnięcia początkowo
wydzielają się kryształy roztworów stałych –
odpowiednio

α

(c

α

) lub

β

(c

β

). Eutektyka jest

w tym przypadku mieszaniną nasyconych
roztworów stałych

α

i

β

, a przemianę można

zapisać następująco:

L

E

→ α

(c

α

) +

β

(c

β

) .

(3.30)

Poniżej temperatury eutektycznej linie ogra-
niczające pola roztworów stałych

α

i

β

wska-

zują na zmniejszanie się rozpuszczalności
składnika B w fazie

α

i składnika A w fazie

β

(rys. 3.67a). Powoduje to wydzielanie się

faz wtórnych z tych roztworów podczas
obniżania temperatury (porównaj opis do
rys. 3.69a).

3.4. Układy równowagi fazowej

185

Rysunek 3.67

Wykresy
a) równowagi faz podwójnego
układu o ograniczonej
rozpuszczalności składników
w stanie stałym z eutektyką,
b)÷ f) energii swobodnej
faz w różnej temperaturze

3 roz 6-11-02 22:49 Page 185

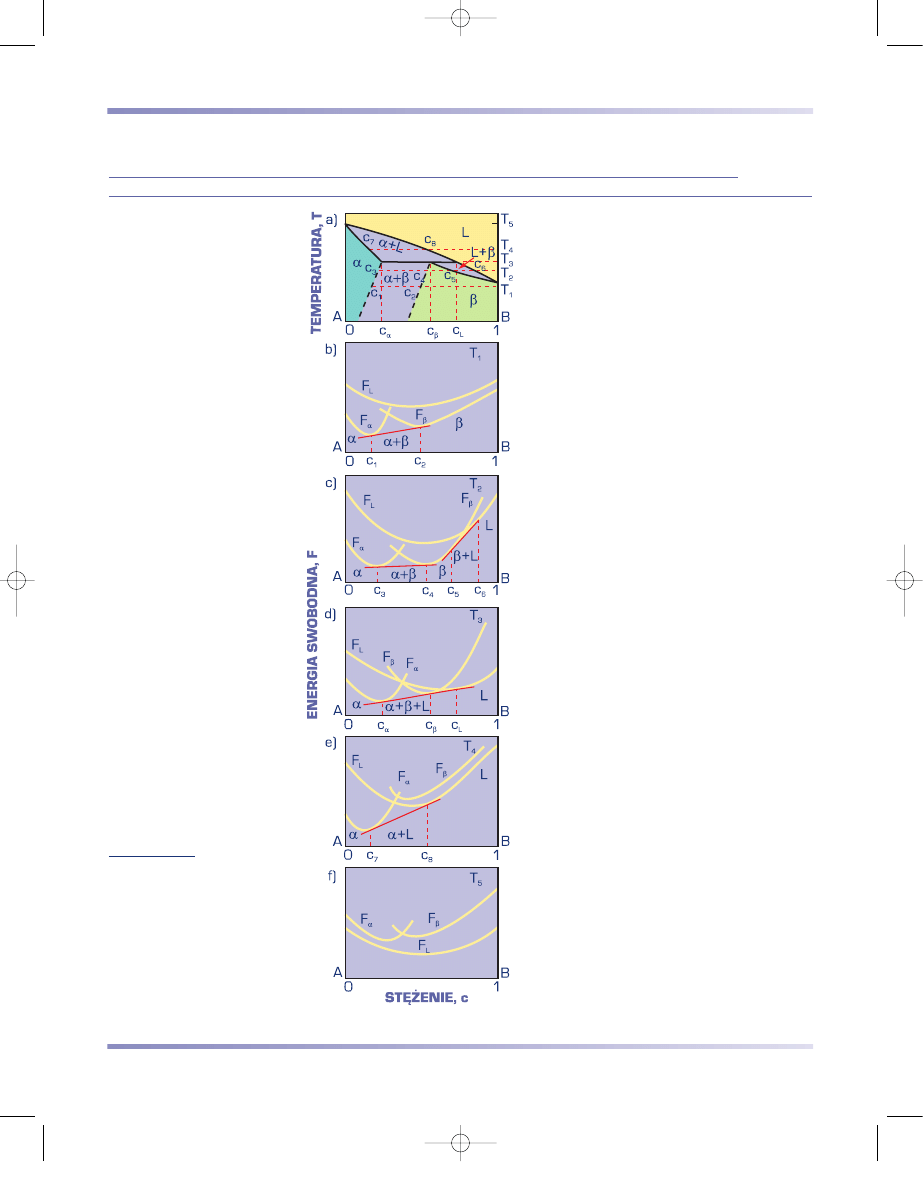
DWUSKŁADNIKOWY UKŁAD RÓWNOWAGI FAZOWEJ O OGRANICZONEJ

ROZPUSZCZALNOŚCI SKŁADNIKÓW W STANIE STAŁYM Z PERYTEKTYKĄ

Dwuskładnikowe układy równowagi fazo-

wej o ograniczonej rozpuszczalności składni-
ków w stanie stałym z perytektyką, podobnie
jak układy z eutektyką, są tworzone przez
pierwiastki różniące się więcej niż o 15%
promieniami atomowymi, o jednakowych
lub różnych sieciach krystalograficznych.
Składniki tworzące układy z perytektyką
znacznie różnią się jednak wartością tempe-
ratury krzepnięcia.

Na rysunku 3.68 przedstawiono układ

równowagi o ograniczonej rozpuszczalności
z perytektyką oraz zależność krzywych
energii swobodnej roztworów stałych

α

i

β

,

mieszanin cieczy i roztworu

α

, cieczy i roz-

tworów

α

i

β

oraz roztworów

α

i

β

, w różnej

temperaturze.

Stopy o stężeniu c < c

α

oraz c > c

L

(rys.

3.68a) krzepną jako roztwory stałe, oznaczo-
ne odpowiednio –

α

lub

β

. Podczas chło-

dzenia stopów o stężeniu np. c

8

z zakresu

c

α

< c < c

β

z cieczy o składzie zmieniającym

się od c

8

do c

L

początkowo wydzielają się

kryształy roztworu

α

o składzie zmieniają-

cym się od c

7

do c

α

. W temperaturze perytek-

tycznej stop jest złożony z mieszaniny cieczy
o składzie c

L

i kryształów roztworu stałego

o stężeniu c

α

. W tej stałej temperaturze prze-

biega przemiana perytektyczna. Ciecz o stę-
żeniu c

L

reaguje z wydzielonymi wcześniej

kryształami roztworu stałego

α

o stężeniu c

α

,

w wyniku czego powstają kryształy roztworu
stałego

β

o stężeniu c

β

. Można to zapisać

następująco:

α

(c

α

) + L(c

L

)

→ β

(c

β

) .

(3.31)

Przemiana perytektyczna przebiega aż

do wyczerpania się cieczy. Poniżej solidusu
strukturę stopu o składzie c

8

stanowi miesza-

nina kryształów roztworu stałego

α

(wydzie-

lonych w temperaturze powyżej perytekty-
cznej) i roztworu

β

(utworzonych w wyniku

reakcji perytektycznej).

3. Struktura i umocnienie metali i stopów

186

Rysunek 3.68

Wykresy
a) równowagi faz podwójnego
układu o ograniczonej
rozpuszczalności składników
w stanie stałym z perytektyką,
b)

÷

f) energii swobodnej faz

w różnej temperaturze

3 roz 6-11-02 22:49 Page 186

W stopie o składzie c

β

przemiana perytektyczna przebiega aż do zupełnego

wyczerpania się cieczy i kryształów roztworu stałego

α

, a stop w stanie stałym ma

strukturę jednofazową roztworu stałego

β

.

Początek krzepnięcia stopów o stężeniu c

β

< c < c

L

jest podobny i polega na

wydzielaniu się z cieczy kryształów roztworu stałego

α

. W temperaturze perytekty-

cznej strukturę stopu stanowi mieszanina kryształów roztworu stałego

α

oraz

cieczy w ilości większej niż niezbędna do utworzenia roztworu stałego

β

. W wyni-

ku przemiany perytektycznej przebiegającej aż do całkowitego wyczerpania się
roztworu stałego

α

powstają kryształy roztworu stałego

β

. W stopie o składzie c

5

(rys. 3.68) podczas dalszego chłodzenia w temperaturze niższej od perytektycznej
skład pozostałej cieczy zmienia się od c

L

do c

6

, a kryształy roztworu stałego

β

mają

skład zmieniający się od c

β

do c

5

. Po zakrzepnięciu stop ma strukturę roztworu

stałego

β

.

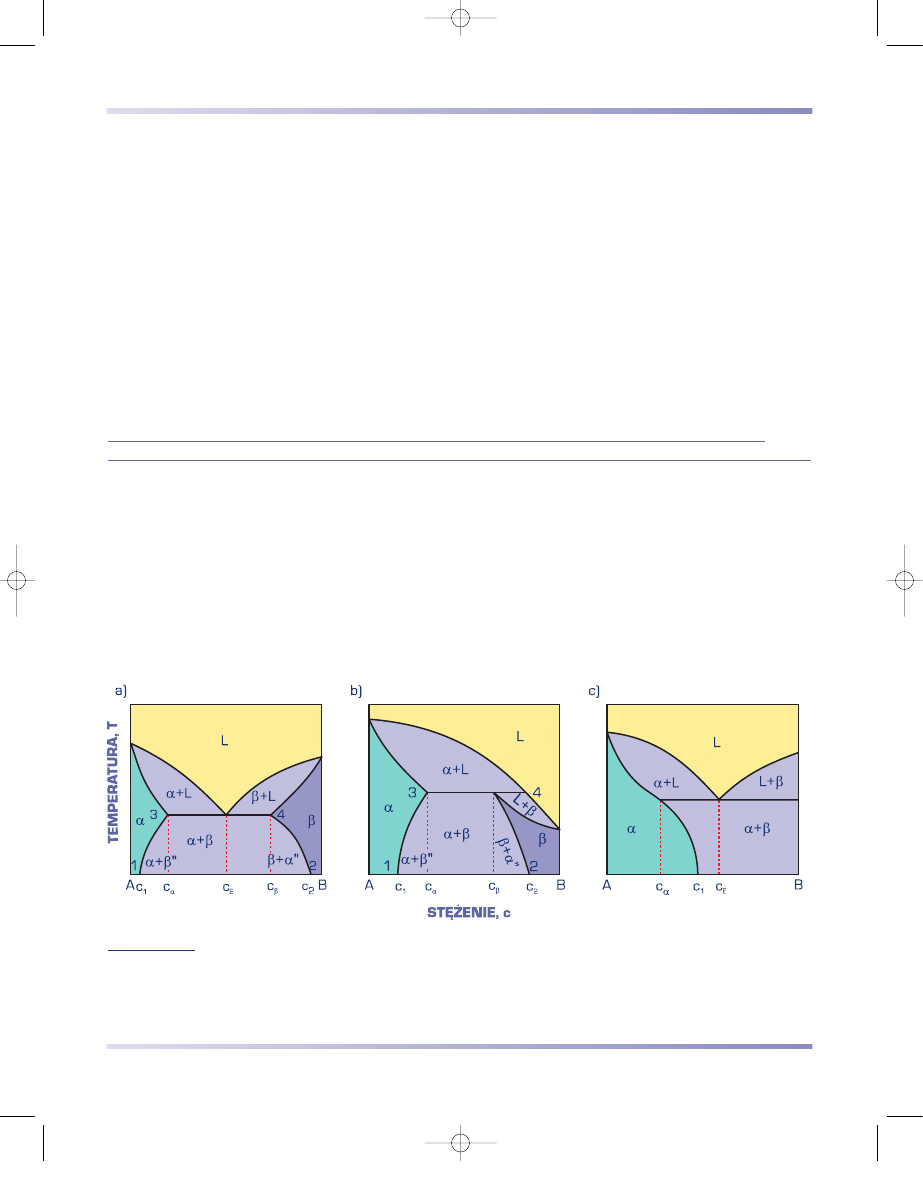
DWUSKŁADNIKOWE UKŁADY RÓWNOWAGI FAZOWEJ O OGRANICZONEJ

ZMIENNEJ ROZPUSZCZALNOŚCI SKŁADNIKÓW W STANIE STAŁYM

Układy z eutektyką i perytektyką (rys. 3.69) najczęściej charakteryzują się

graniczną wzajemną rozpuszczalnością składników, zmienną wraz z obniżaniem
temperatury.

Podczas chłodzenia stopów o składzie c

1

< c < c

α

poniżej temperatury eutek-

tycznej zmniejsza się rozpuszczalność składnika B w metalu A (rys. 3.69a). Z nasy-
conych kryształów roztworu

α

wydzielają się wtedy bogate w składnik B kryształy

roztworu stałego

β

o składzie zmieniającym się wzdłuż linii 4–2. Takie wydzielenia

powstające z kryształów roztworu stałego są nazywane fazami wtórnymi i ozna-
czane

β′′

. Analogicznie przebiega również wydzielanie wtórnych faz

α′′

.

Podobnie zmienna rozpuszczalność składników w roztworach stałych

występuje również w układach z perytektyką (rys. 3.69b).

3.4. Układy równowagi fazowej

187

Rysunek 3.69

Schematy układów równowagi o ograniczonej zmiennej rozpuszczalności składników w stanie stałym
(opis w tekście)

3 roz 6-11-02 22:49 Page 187

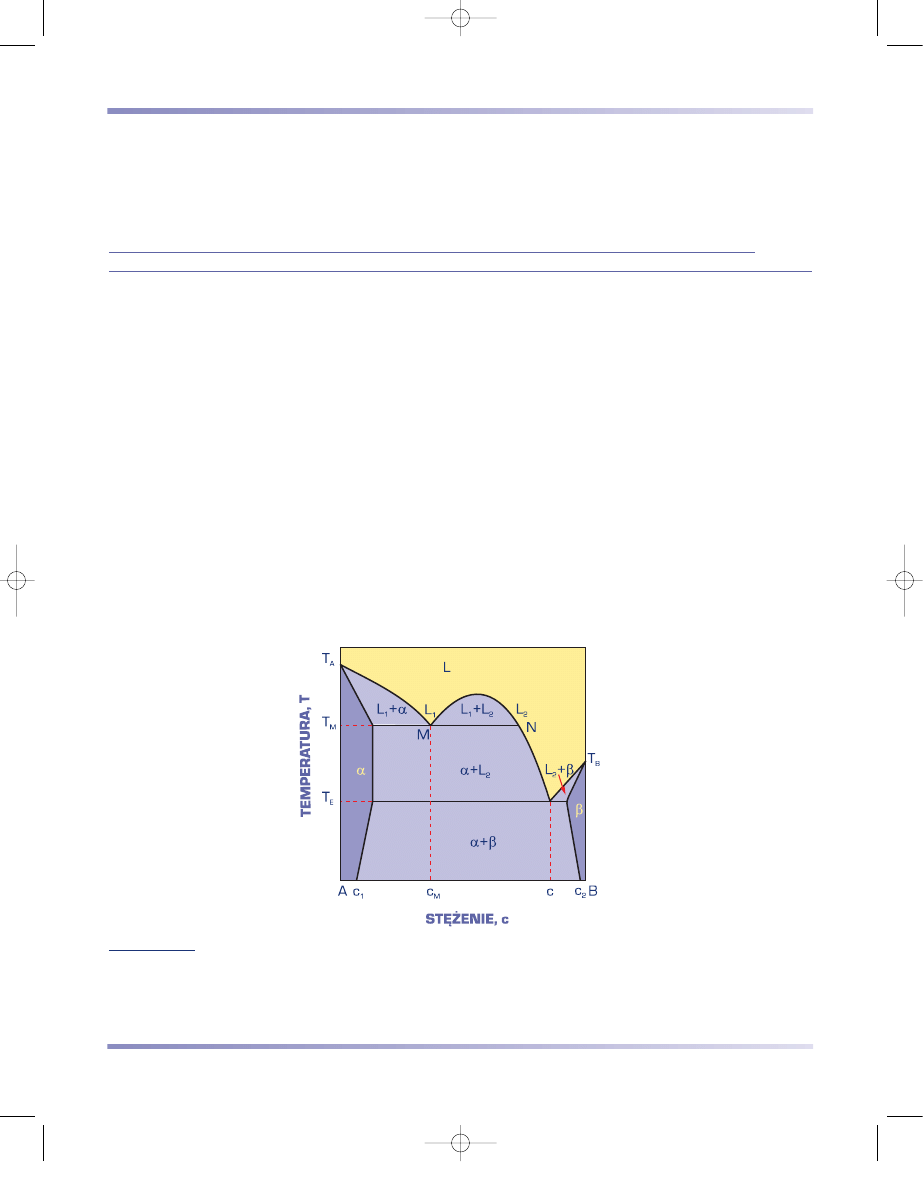
W dwuskładnikowych układach równowagi rzadko występuje zwiększenie roz-

puszczalności składników w stanie stałym wraz z obniżaniem temperatury (rys.
3.69c).

DWUSKŁADNIKOWY UKŁAD RÓWNOWAGI FAZOWEJ O OGRANICZONEJ

ROZPUSZCZALNOŚCI SKŁADNIKÓW W STANIE CIEKŁYM Z MONOTEKTYKĄ

Dwuskładnikowy układ równowagi fazowej z monotektyką tworzą składniki

rozpuszczające się częściowo w stanie ciekłym i nierozpuszczające się wzajemnie
w stanie stałym lub wykazujące małą rozpuszczalność w stanie stałym. Obniżenie
temperatury roztworu ciekłego L o składzie chemicznym zawartym między punk-
tem monotektycznym M a punktem N do linii granicznej powoduje utworzenie
mieszaniny dwóch roztworów ciekłych L

1

i L

2

, bogatych odpowiednio w metale A

i B (rys. 3.70). Mieszanina roztworów ciekłych L

1

i L

2

jest trwała do temperatury

przemiany monotektycznej T

M

. W wyniku przemiany monotektycznej, która ma

charakter przemiany eutektycznej:

L

1

→ α

+ L

2

,

(3.32)

roztwór ciekły L

1

ulega przemianie w fazę stałą

α

oraz roztwór ciekły L

2

bogaty

w składnik B. Dalsze obniżanie temperatury powoduje wydzielanie się roztworu
stałego

α

i związane z tym zwiększenie stężenia składnika B w cieczy, aż do składu

c

E

. W temperaturze T

E

następuje przemiana eutektyczna cieczy L

2

w mieszaninę

faz

α + β

(rys. 3.70). Krystalizacja stopów o stężeniu składnika B większym niż

w punkcie N, przebiega podobnie jak w układzie o ograniczonej rozpuszczalności
składników w stanie stałym z eutektyką (porównaj rys. 3.67 i 3.69a).

3. Struktura i umocnienie metali i stopów

188

E

Rysunek 3.70

Wykres równowagi fazowej dwuskładnikowego układu z monotektyką

3 roz 6-11-02 22:49 Page 188

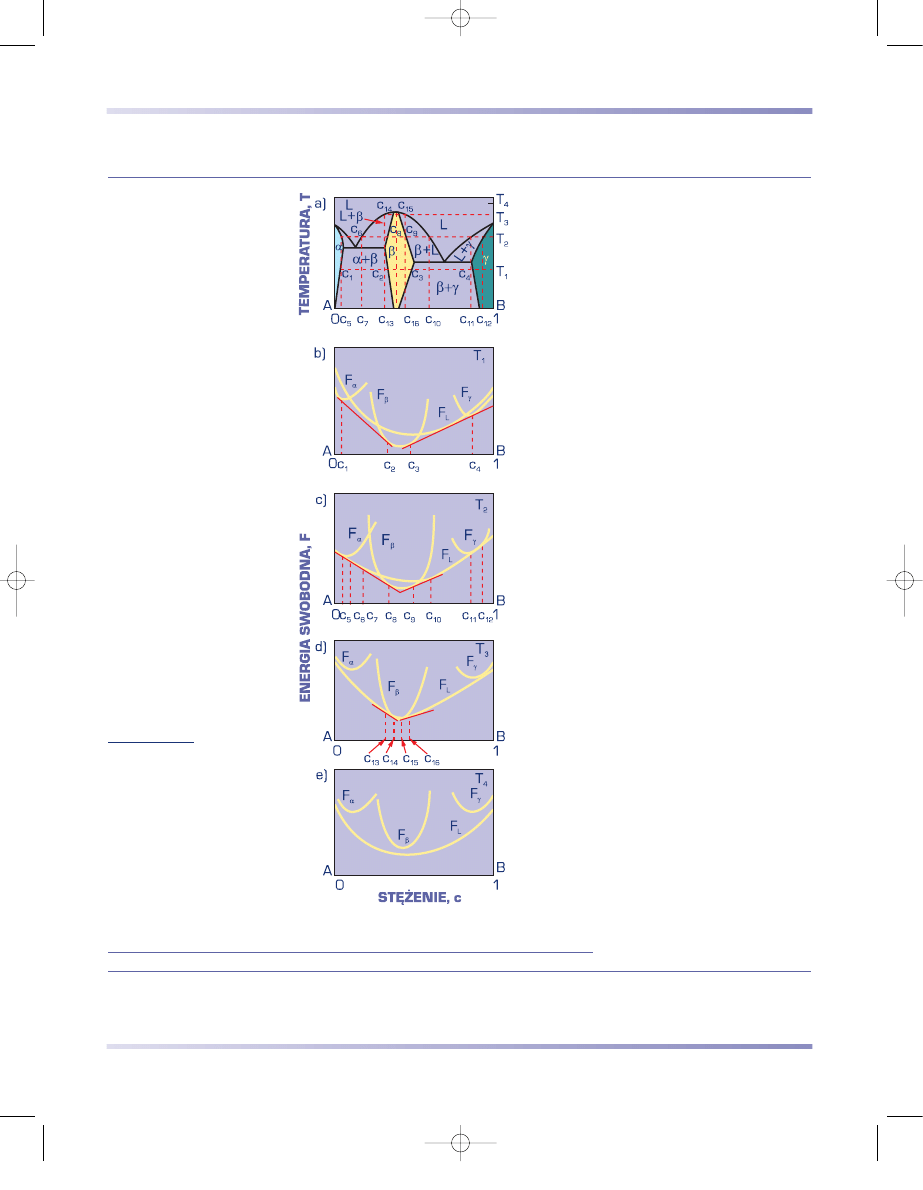
DWUSKŁADNIKOWY UKŁAD RÓWNOWAGI Z FAZAMI MIĘDZYMETALICZNYMI

Dwuskładnikowe układy równowagi z fa-

zami międzymetalicznymi występują bardzo
często. Na rysunku 3.71 przedstawiono przy-
kład układu dwuskładnikowego z fazą mię-
dzymetaliczną, będącą roztworem wtórnym,
oraz z dwiema eutektykami. Na rysunku tym
podano również krzywe energii swobodnej
roztworów stałych

α

i

γ

oraz fazy międzyme-

talicznej

β

, a także ich mieszanin w różnej

temperaturze.

Układy dwuskładnikowe mogą zawierać

nie tylko jedną, ale kilka różnych faz mię-
dzymetalicznych, np. w stopach Cu–Zn
i Cu–Sn (porównaj rys. 7.13 i 7.15 w rozdz.
7.2). Fazy te nie zawsze krystalizują bezpo-
średnio z cieczy, lecz np. powstają w wyniku
reakcji perytektycznej. Powoduje to, że nie-
które układy równowagi są bardzo złożone.
Nawet najbardziej skomplikowany układ
równowagi można jednak podzielić na
proste fragmenty, w których przemiany
fazowe zachodzą tak, jak w opisanych
poprzednio elementarnych przypadkach.

Utworzone podczas krystalizacji fazy

międzymetaliczne nie zawsze są trwałe aż do
temperatury pokojowej, lecz mogą ulegać
przemianom fazowym w stanie stałym pod-
czas obniżania temperatury stopu. Niektóre
z faz międzymetalicznych ulegają uporząd-
kowaniu w nadstrukturę (np. faza

β

w

β

’

w układzie Cu–Zn, porównaj rys. 7.13), inne
zaś ulegają rozpadowi eutektoidalnemu na
dwie różne fazy.

DWUSKŁADNIKOWE UKŁADY RÓWNOWAGI FAZOWEJ

Z PRZEMIANAMI W STANIE STAŁYM

Dotychczas omówione układy równowagi fazowej dotyczą metali niewykazują-

cych odmian alotropowych. Z wyjątkiem zmiennej rozpuszczalności w stanie
stałym w układach tych występują przemiany związane z krzepnięciem pierwotnym.

3.4. Układy równowagi fazowej

189

Rysunek 3.71

Wykresy
a) równowagi faz podwójnego
układu ze związkiem między-
metalicznym i z dwiema
eutektykami,
b)

÷

e) energii swobodnej

faz w różnej temperaturze

3 roz 6-11-02 22:49 Page 189

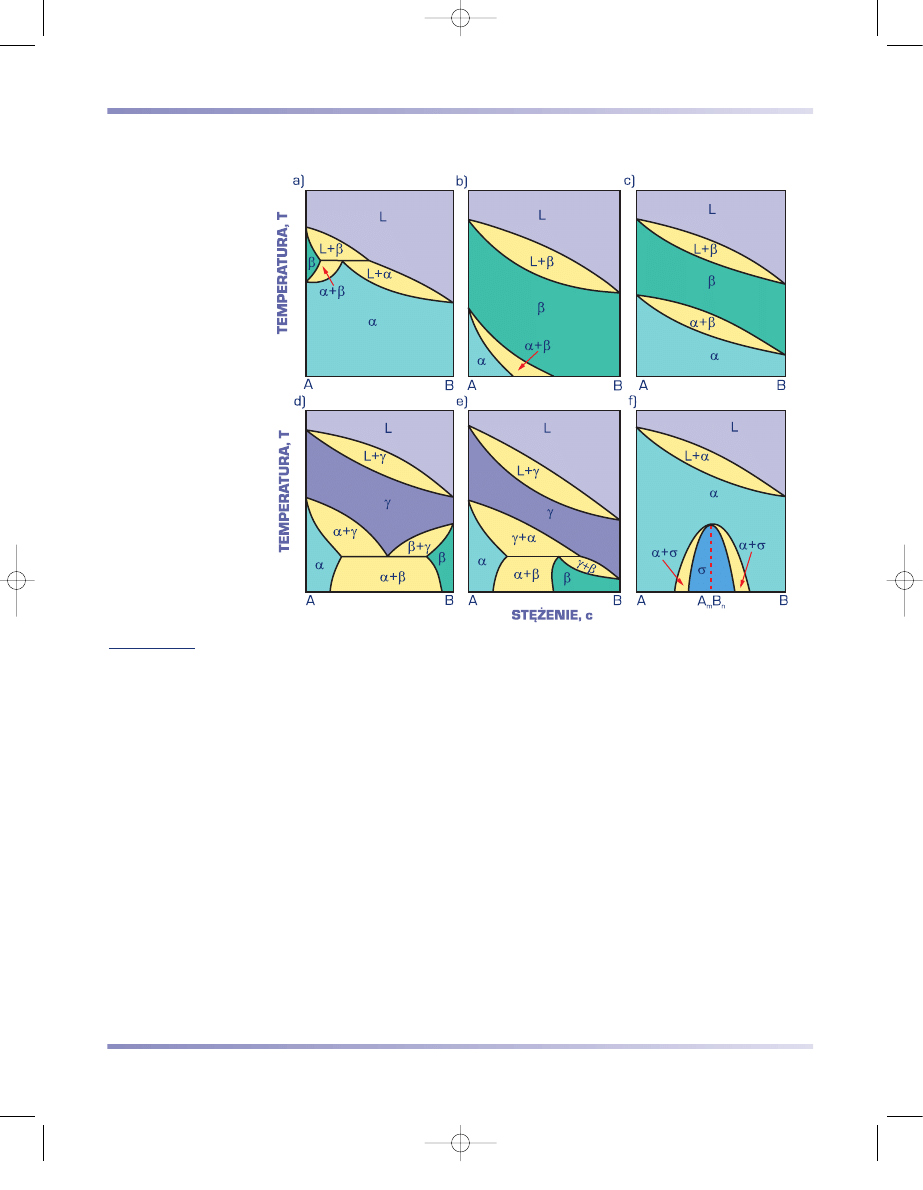
Jeżeli którykolwiek ze składników wykazuje odmiany alotropowe, to również w
stanie stałym przebiegają przemiany fazowe.

Na rysunku 3.72a przedstawiono układ z perytektyką, w którym składnik A ma

dwie odmiany alotropowe A

α

i A

β

, na rys. 3.72b – układ z roztworem stałym

granicznym składnika B w odmianie alotropowej A

α

. Jeżeli obydwa składniki

wykazują po dwie odmiany alotropowe, mogą tworzyć nieograniczone roztwory
stałe (rys. 3.72c), a przy ograniczonej rozpuszczalności – układ z eutektoidem (rys.
3.72d) lub perytektoidem (rys. 3.72e). Przemiany eutektoidalna i perytektoidalna
przebiegają analogicznie jak odpowiednio przemiana eutektyczna lub perytektycz-
na, z tym że w równowadze w czasie reakcji pozostaje nie roztwór ciekły L, lecz
roztwór stały, oznaczony na rysunkach 3.72d,e jako

γ

.

W stanie stałym mogą powstawać również fazy międzymetaliczne. Układ

dwuskładnikowy z fazą międzymetaliczną wydzielającą się w stanie stałym przed-
stawia rysunek 3.72f.

3. Struktura i umocnienie metali i stopów

190

Rysunek 3.72

Schematy układów równowagi z przemianami fazowymi w stanie stałym

3 roz 6-11-02 22:49 Page 190

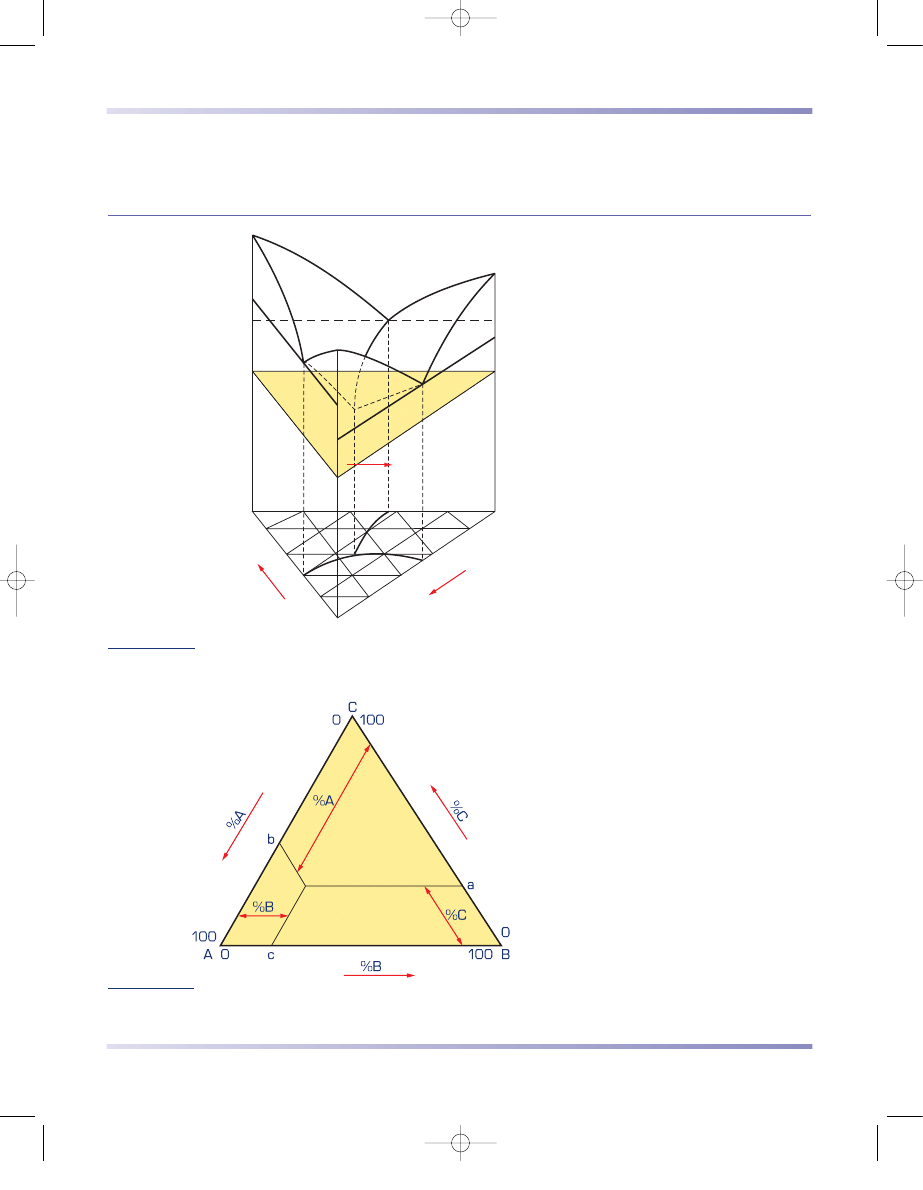
3.4.4. Wieloskładnikowe układy równowagi fazowej

TRÓJSKŁADNIKOWE UKŁADY RÓWNOWAGI FAZOWEJ

Trójskładnikowy układ równowagi można

przedstawić w przestrzennym układzie
współrzędnych (rys. 3.73). Podstawę wykre-
su stanowi trójkąt stężeń Gibbsa składników
A, B, C (rys. 3.74). Na osiach pionowych
jest oznaczona temperatura.

Wykresy przestrzenne nie są jednak

przejrzyste i dlatego stosuje się płaskie
wykresy układów trójskładnikowych. Tworzy
się je przez zrzutowanie izoterm wykresu
przestrzennego na trójkąt stężeń w podsta-
wie wykresu. Izotermy, tj. linie stałej tempe-
ratury, są utworzone jako ślady przecięcia
powierzchni wykresu przestrzennego przez
płaszczyzny odpowiadające stałym warto-
ściom temperatury, zmienianym np. co 50°.
Zwykle dla przejrzystości takiego wykresu są
podawane tylko izotermy likwidusu, krzywe
i punkty eutektyk oraz perytektyk. Rzadziej
są zaznaczane jednocześnie izotermy likwi-
dusu i solidusu.

Płaski wykres układu trójskładnikowego

uzupełnia się zwykle kładami wykresów
składowych układów dwuskładnikowych
(rys. 3.75).

Oprócz wykresów płaskich często stosuje

się również izotermiczne i stężeniowe
przekroje wykresów przestrzennych. Prze-
kroje izotermiczne (rys. 3.76) są otrzymy-
wane przez przecięcie wykresu przestrzenne-
go płaszczyzną odpowiadającą danej tempe-
raturze. W wyniku utworzenia przekroju
izotermicznego uzyskuje się zależność
przemian w stałej temperaturze od składu
stopu trójskładnikowego (rys. 3.76). Przekrój
stężeniowy powstaje przez przecięcie wykre-
su przestrzennego płaszczyzną prostopadłą
do trójkąta stężeń podstawy wykresu (rys.
3.77). Przekroje mogą być uzyskane przy
stałym stężeniu jednego ze składników (pro-
sta MN na rys. 3.77a,b) lub przy zmiennym
stężeniu każdego ze składników (prosta AD
na rys. 3.77).

3.4. Układy równowagi fazowej

191

Rysunek 3.74

Trójkąt stężeń Gibbsa (według S. Prowansa)

e

3

e

3

L

L

e

3

e

3

''

e

2

e

2

e

1

e

1

e

2

e

2

''

e

1

e

1

''

T

A

T

A

T

C

T

C

T

B

T

B

20

20

20

20

20

20

40

40

40

40

40

40

60

60

60

60

60

60

80

80

80

80

80

80

E'

E'

E

E

C

C

A

A

A%

A%

B%

B%

C%

C%

B

B

Rysunek 3.73

Przestrzenny wykres równowagi układu trójskładnikowego
(według S. Prowansa)

3 roz 6-11-02 22:49 Page 191

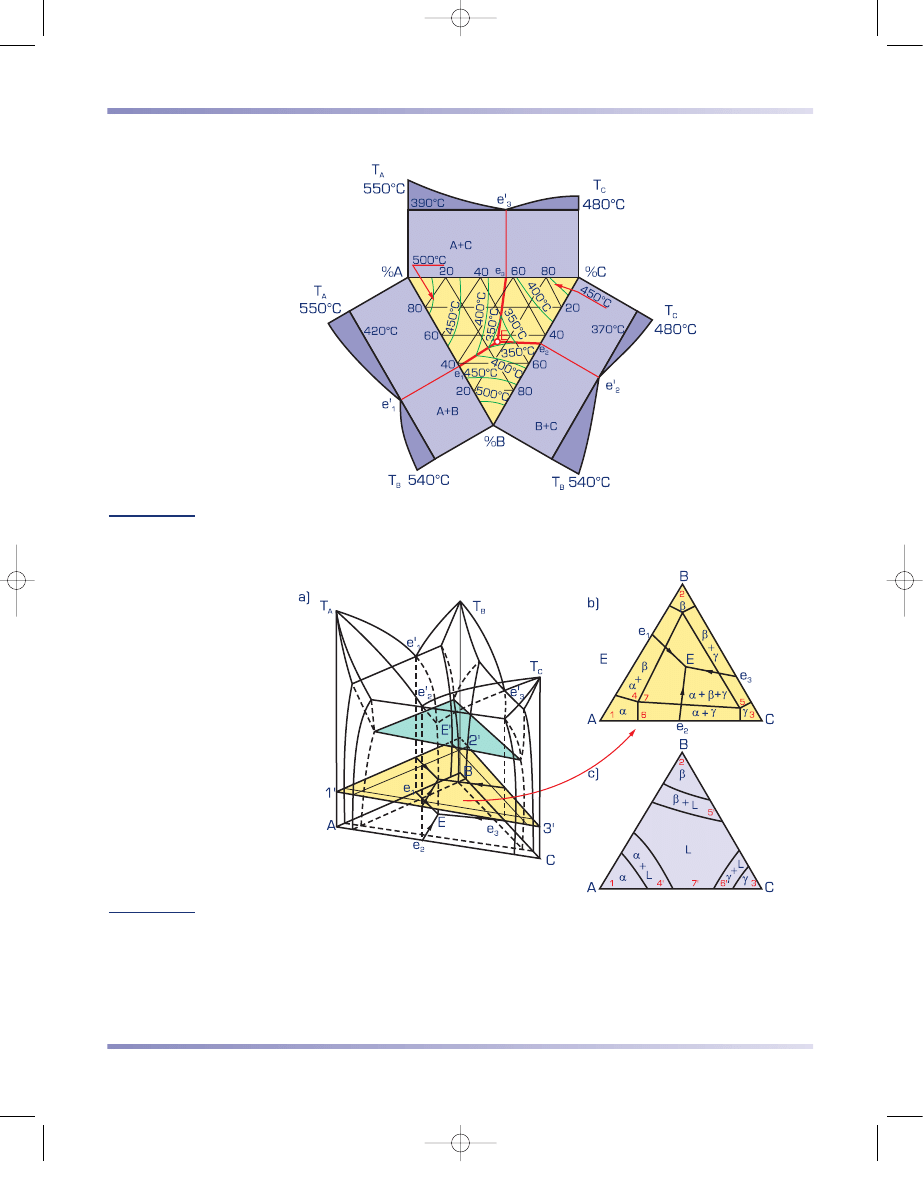
3. Struktura i umocnienie metali i stopów

192

Rysunek 3.75

Płaski wykres równowagi układu trójskładnikowego z rysunku 3.73 z kładami wykresów układów
dwuskładnikowych (według S. Prowansa)

Rysunek 3.76

Przekrój izotermiczny
a) schemat tworzenia na przestrzennym wykresie równowagi układu trójskładnikowego,
b) przekrój izotermiczny w temperaturze pokojowej,
c) przekrój izotermiczny w temperaturze między solidusem a likwidusem (według S. Prowansa)

3 roz 6-11-02 22:49 Page 192

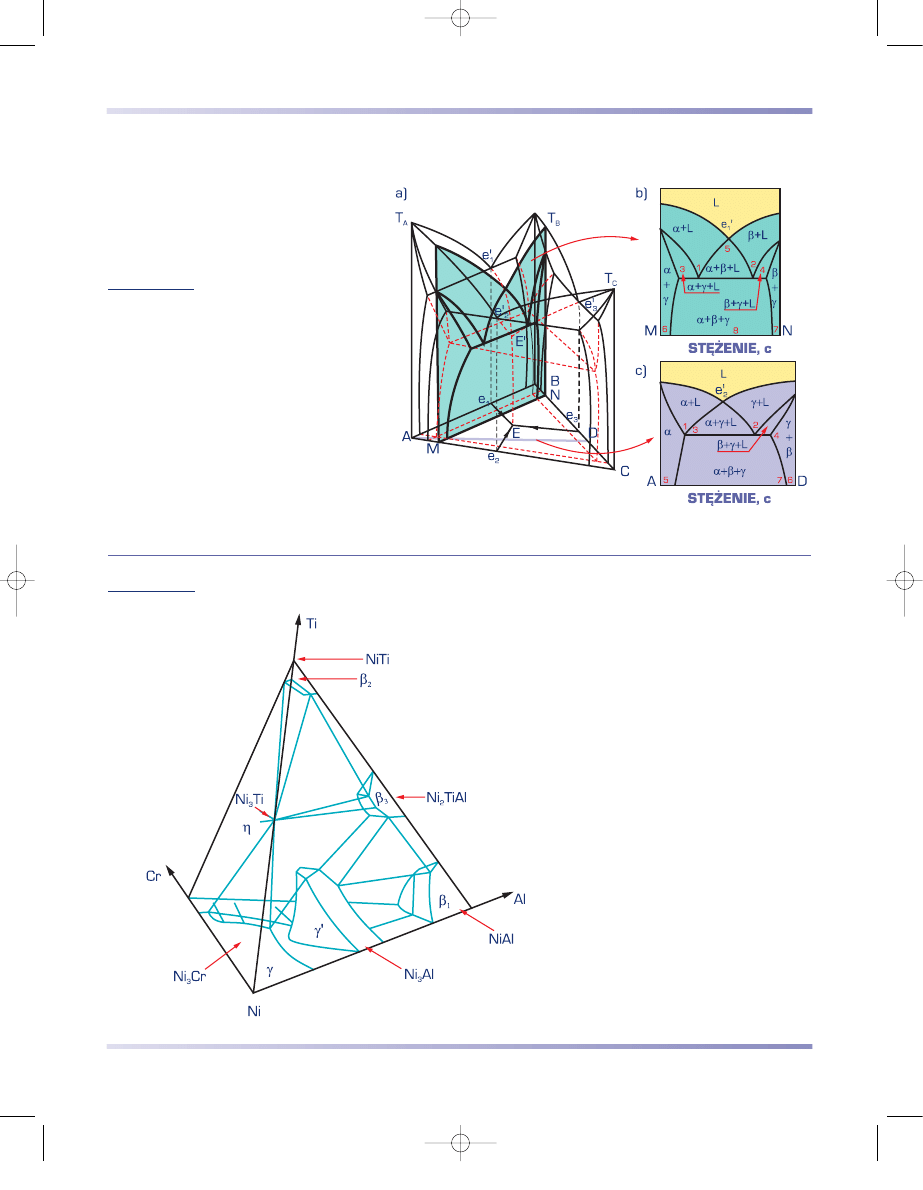
CZTEROSKŁADNIKOWE UKŁADY RÓWNOWAGI FAZOWEJ

W przypadku stopów czteroskładni-

kowych skład stopów można przedstawić za
pomocą czworościanu stężeń, przykładowo
przedstawionego na rysuku 3.78 dla stopów
żarowytrzymałych Ni–Cr–Ti–Al w tempera-
turze 750°C. Na rysunku 3.79 przykładowo
przedstawiono model likwidusu stopów
Al–Fe–Si–Mg bogatych w Al. Na prawej, tyl-
nej i górnej powierzchni modelu są przed-
stawione układy trójskładnikowe stopów
przy określonym stężeniu odpowiednio Si,
Fe i Mg. Na lewej, czołowej i dolnej powierz-
chni modelu przedstawione są linie likwi-
dusu układów trójskładnikowych odpowied-
nio stopów Al–Mg–Fe, Al–Mg–Si oraz
Al–Si–Fe. W przytoczonym układzie wystę-
puje siedem obszarów krystalizacji pierwot-
nej różnych faz. Linie przecięcia tych
powierzchni odpowiadają jednoczesnej krys-
talizacji dwóch faz, natomiast punkty prze-
cięć tych linii odpowiadają jednoczesnej
krystalizacji trzech lub czterech faz.

Podobnie można przedstawić model po-

wierzchni solidus lub model przekroju izoter-
micznego w wybranej temperaturze.

3.4. Układy równowagi fazowej

193

Rysunek 3.78

Czteroskładnikowy układ
równowagi fazowej stopów
Ni–Cr–Al–Ti w tempera-
turze 750°C
(według W. Betteridge’a
i J. Heslopa)

Rysunek 3.77

Przekrój stężeniowy
a) schemat tworzenia na
przestrzennym wykresie
równowagi układu
trójskładnikowego,
b) przekrój stężeniowy przy
stałym stężeniu metalu C,
c) przekrój stężeniowy wzdłuż
linii AD z rysunku 3.77a
(według S. Prowansa)

3 roz 6-11-02 22:49 Page 193