Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
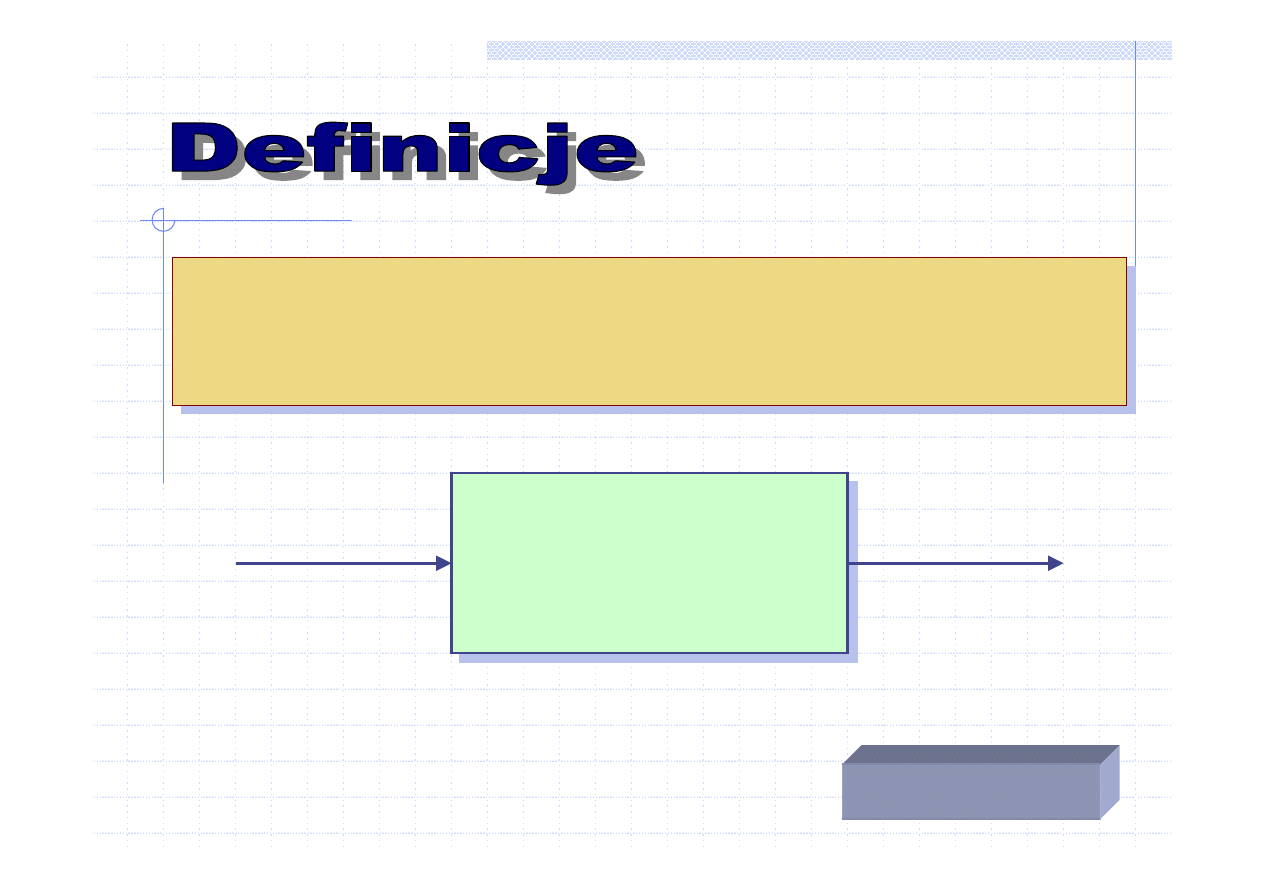
Algorytmem
nazywamy sko
ń
czony ci
ą
g czynno
ś
ci,
przekształcaj
ą
cy zbiór danych wej
ś
ciowych (danych)
na zbiór danych wyj
ś
ciowych (wyników).
Algorytmem
Algorytmem
nazywamy sko
ń
czony ci
ą
g czynno
ś
ci,
nazywamy sko
ń
czony ci
ą
g czynno
ś
ci,
przekształcaj
ą
cy zbiór danych wej
ś
ciowych (danych)
przekształcaj
ą
cy zbiór danych wej
ś
ciowych (danych)
na zbiór danych wyj
ś
ciowych (wyników).
na zbiór danych wyj
ś
ciowych (wyników).
DANE
DANE
WYNIKI
WYNIKI
Algorytm
Algorytm
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Algorytmy,
które wykonuj
ą
działania matematyczne
na danych liczbowych, nazywamy algorytmami
numerycznymi.
Algorytmy,
Algorytmy,
które wykonuj
ą
działania matematyczne
które wykonuj
ą
działania matematyczne
na danych liczbowych, nazywamy
na danych liczbowych, nazywamy
algorytmami
algorytmami
numerycznymi.
numerycznymi.
Algorytmika,
to dział informatyki zajmuj
ą
cy si
ę
ró
ż
nymi
aspektami
tworzenia
i
analizowania
algorytmów
Algorytmika
Algorytmika
,
,
to dział informatyki zajmuj
ą
cy si
ę
to dział informatyki zajmuj
ą
cy si
ę
ró
ż
nymi
aspektami
tworzenia
i
analizowania
ró
ż
nymi
aspektami
tworzenia
i
analizowania
algorytmów
algorytmów
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Program komputerowy
to logicznie uporz
ą
dkowany
ci
ą
g instrukcji j
ę
zyka programowania realizuj
ą
cy
algorytm.
Program komputerowy
Program komputerowy
to logicznie uporz
ą
dkowany
to logicznie uporz
ą
dkowany
ci
ą
g instrukcji j
ę
zyka programowania realizuj
ą
cy
ci
ą
g instrukcji j
ę
zyka programowania realizuj
ą
cy
algorytm.
algorytm.
Specyfikacja zadania
to szczegółowy opis zadania,
w którym wymienia si
ę
dane wej
ś
ciowe i wyniki oraz
warunki jakie musz
ą
spełnia
ć
. Specyfikacja okre
ś
la
zatem zwi
ą
zek pomi
ę
dzy danymi a wynikami.
Specyfikacja zadania
Specyfikacja zadania
to szczegółowy opis zadania,
to szczegółowy opis zadania,
w którym wymienia si
ę
dane wej
ś
ciowe i wyniki oraz
w którym wymienia si
ę
dane wej
ś
ciowe i wyniki oraz
warunki jakie musz
ą
spełnia
ć
. Specyfikacja okre
ś
la
warunki jakie musz
ą
spełnia
ć
. Specyfikacja okre
ś
la
zatem zwi
ą
zek pomi
ę
dzy danymi a wynikami.
zatem zwi
ą
zek pomi
ę
dzy danymi a wynikami.
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
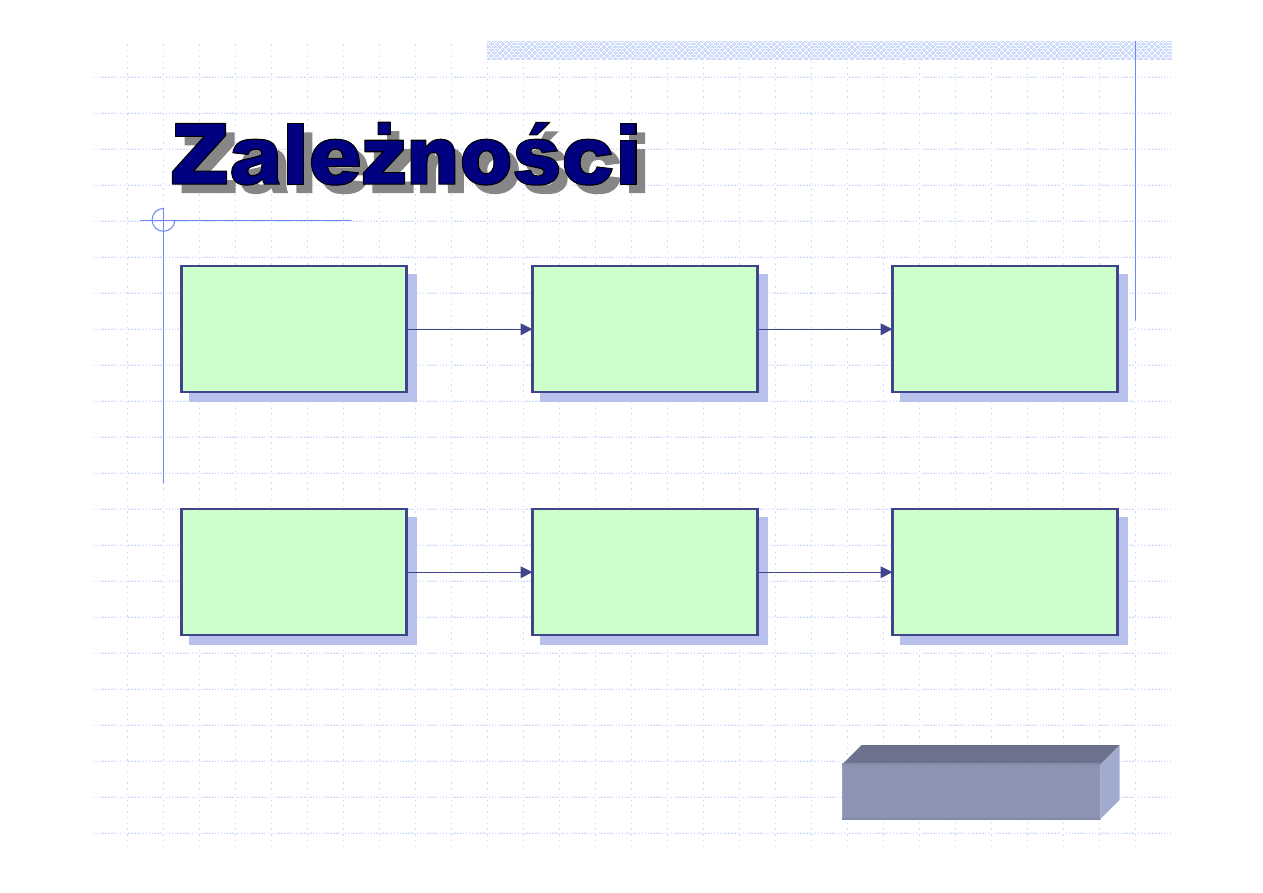
Problem
Problem
Algorytm
Algorytm
Program
Program
Program
Program
komputerowy
komputerowy
Komputer
Komputer
Algorytm
Algorytm
zapis
wykonuje
realizuje
wybór
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Problem:
oblicz
ś
redni
ą
arytmetyczn
ą
trzech
dowolnych liczb rzeczywistych.
Problem:
Problem:
oblicz
ś
redni
ą
arytmetyczn
ą
trzech
oblicz
ś
redni
ą
arytmetyczn
ą
trzech
dowolnych liczb rzeczywistych.
dowolnych liczb rzeczywistych.
Dane:
trzy dowolne liczby rzeczywiste A, B, C
Dane:
Dane:
trzy dowolne liczby rzeczywiste
trzy dowolne liczby rzeczywiste
A
A
,
,
B
B
,
,
C
C
Wynik:
warto
ść
ś
redniej arytmetycznej liczb A, B, C,
równ
ą
SR
Wynik:
Wynik:
warto
ść
ś
redniej arytmetycznej liczb
warto
ść
ś
redniej arytmetycznej liczb
A
A
,
,
B
B
,
,
C
C
,
,
równ
ą
równ
ą
SR
SR
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
1. Zacznij algorytm
2. Wprowadź wartość trzech liczb A, B, C
3. Oblicz wartość wyrażenia: SUMA:=A+B+C
4. Oblicz wartość wyrażenia SR:=SUMA/3
5. Wyprowadź wynik: SR
6. Zakończ algorytm
1.
1.
Zacznij algorytm
Zacznij algorytm
2.
2.
Wprowadź wartość trzech liczb A, B, C
Wprowadź wartość trzech liczb A, B, C
3.
3.
Oblicz wartość wyrażenia: SUMA:=A+B+C
Oblicz wartość wyrażenia: SUMA:=A+B+C
4.
4.
Oblicz wartość wyrażenia SR:=SUMA/3
Oblicz wartość wyrażenia SR:=SUMA/3
5.
5.
Wyprowadź wynik: SR
Wyprowadź wynik: SR
6.
6.
Zakończ algorytm
Zakończ algorytm
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Problem:
oblicz warto
ść
bezwzgl
ę
dn
ą
dowolnej
liczby rzeczywistej.
Problem:
Problem:
oblicz warto
ść
bezwzgl
ę
dn
ą
dowolnej
oblicz warto
ść
bezwzgl
ę
dn
ą
dowolnej
liczby rzeczywistej.
liczby rzeczywistej.
Dane:
dowolna liczba rzeczywista A
Dane:
Dane:
dowolna liczba rzeczywista
dowolna liczba rzeczywista
A
A
Wynik:
warto
ść
bezwzgl
ę
dna liczby A równa W
Wynik:
Wynik:
warto
ść
bezwzgl
ę
dna liczby
warto
ść
bezwzgl
ę
dna liczby
A
A
równa
równa
W
W
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
1. Zacznij algorytm
2. Wprowadź wartość liczbę A
3. Jeżeli A>=0, to W:=A. W przeciwnym
wypadku W:=-A
4. Wyprowadź wynik: W
5. Zakończ algorytm
1.
1.
Zacznij algorytm
Zacznij algorytm
2.
2.
Wprowadź wartość liczbę A
Wprowadź wartość liczbę A
3.
3.
Jeżeli A>=0, to W:=A. W przeciwnym
Jeżeli A>=0, to W:=A. W przeciwnym
wypadku W:=
wypadku W:=
-
-
A
A
4.
4.
Wyprowadź wynik: W
Wyprowadź wynik: W
5.
5.
Zakończ algorytm
Zakończ algorytm
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
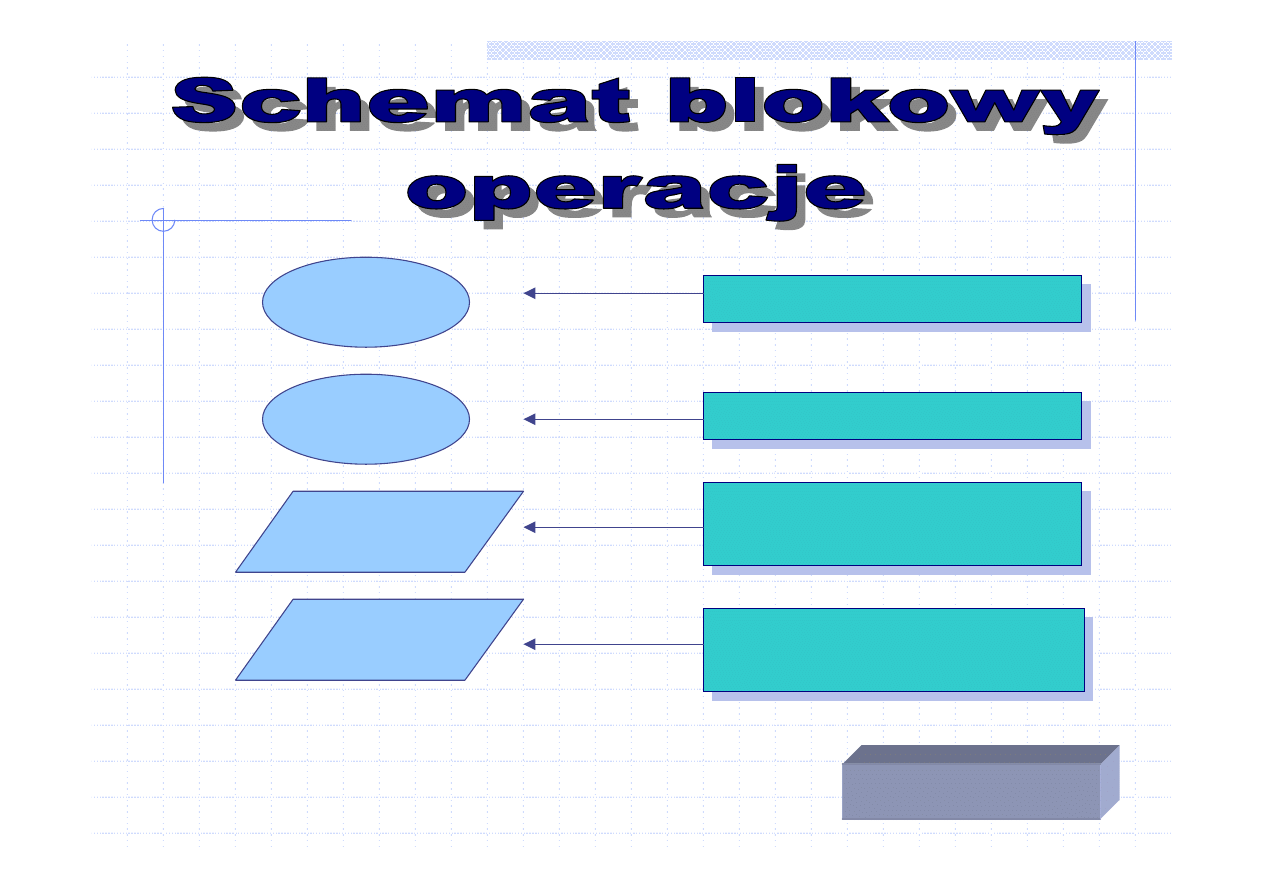
STOP
STOP
START
START
Wprowadź (A, B)
Wprowadź (A, B)
Wyprowadź (W)
Wyprowadź (W)
Początek algorytmu
Początek algorytmu
Początek algorytmu
Koniec algorytmu
Koniec algorytmu
Koniec algorytmu
Wprowadzanie danych
Blok wejścia
Wprowadzanie danych
Wprowadzanie danych
Blok wejścia
Blok wejścia
Wyprowadzanie danych
Blok wyjścia
Wyprowadzanie danych
Wyprowadzanie danych
Blok wyjścia
Blok wyjścia
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
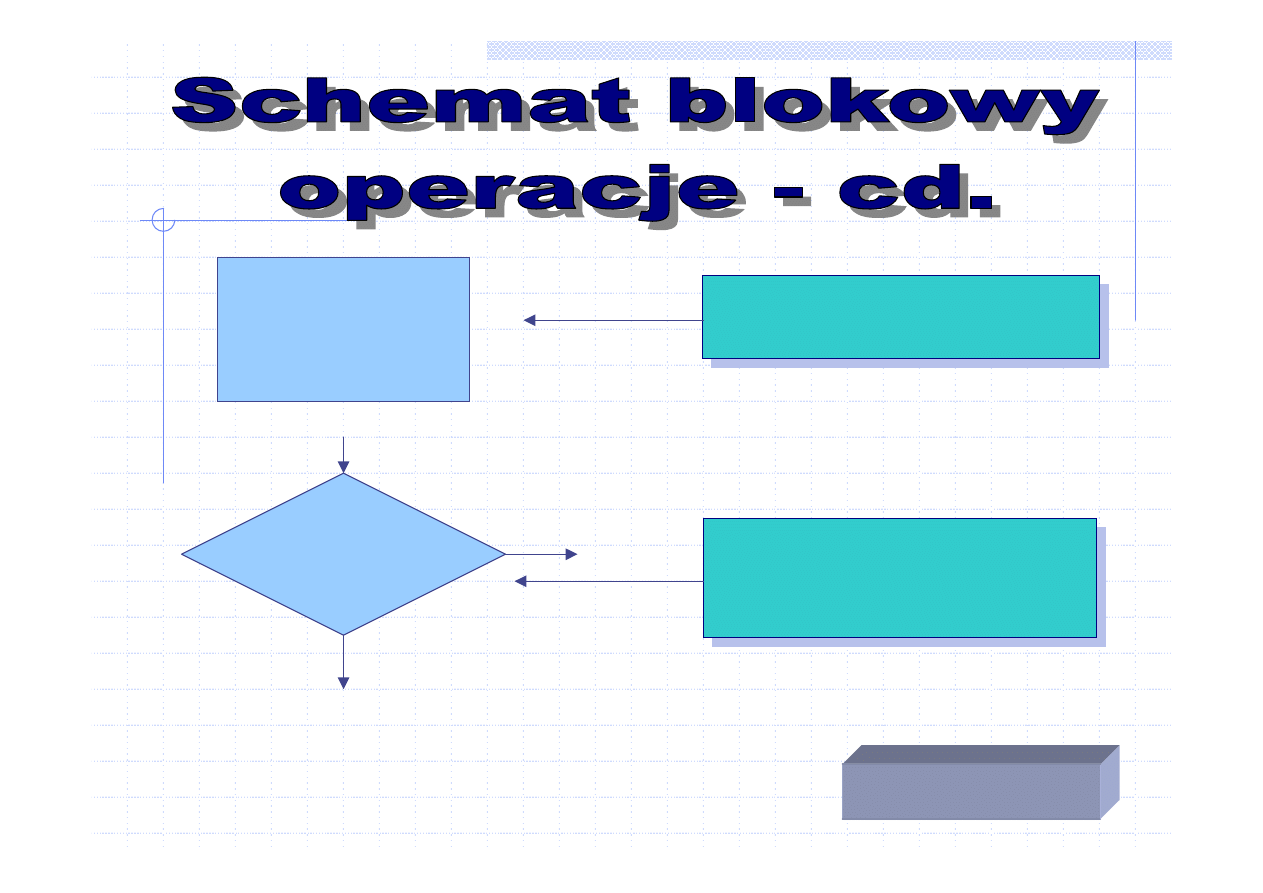
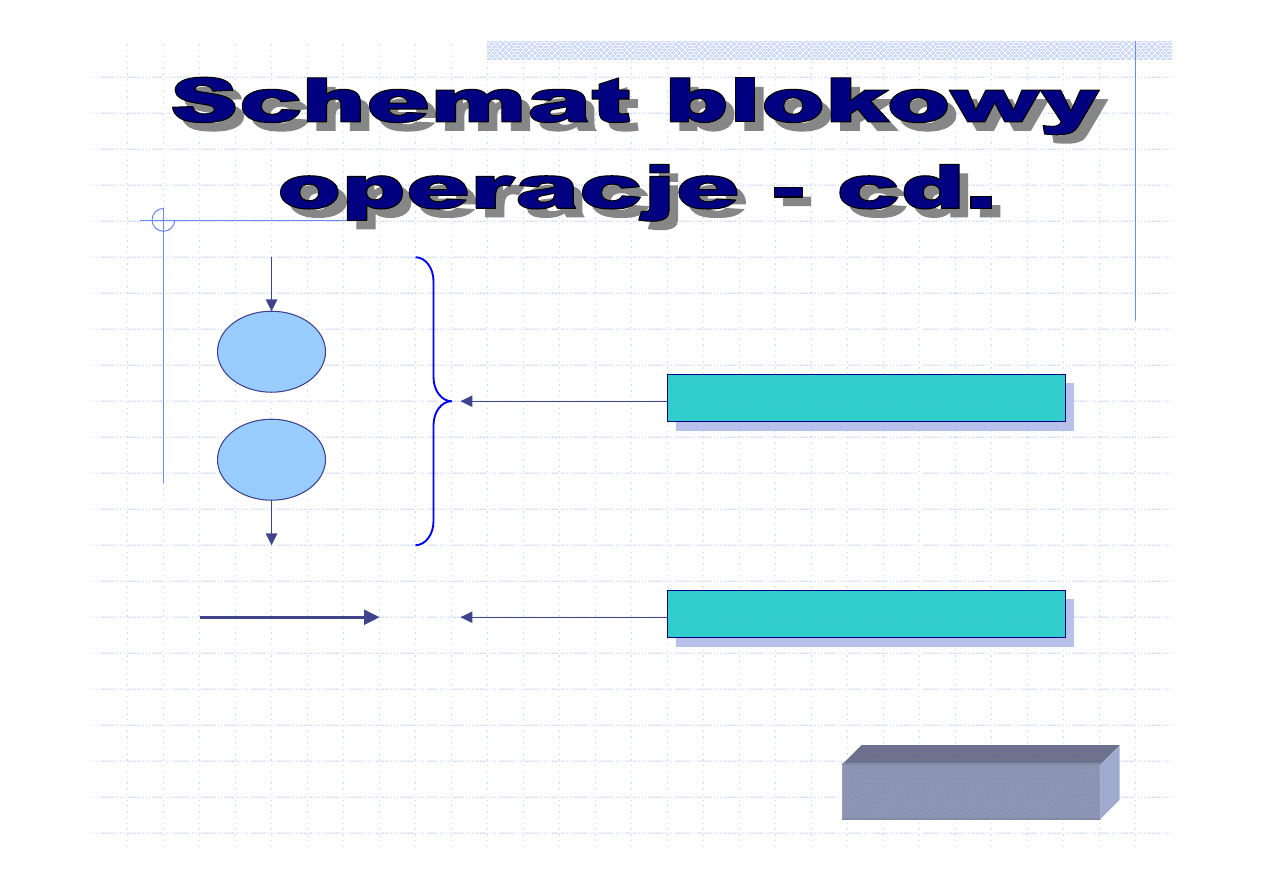
S:=A+B
S:=A+B
W:=C/A
W:=C/A
Czy
Czy
A=0?
A=0?
TAK
TAK
NIE
NIE
Sprawdzanie warunków
Blok warunkowy
albo decyzyjny
Sprawdzanie warunków
Sprawdzanie warunków
Blok warunkowy
Blok warunkowy
albo decyzyjny
albo decyzyjny
Wykonywanie obliczeń
Blok operacyjny
Wykonywanie obliczeń
Wykonywanie obliczeń
Blok operacyjny
Blok operacyjny
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
1
1
1
1
Łącznik
Łącznik
Łącznik
Połączenie
Połączenie
Połączenie
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
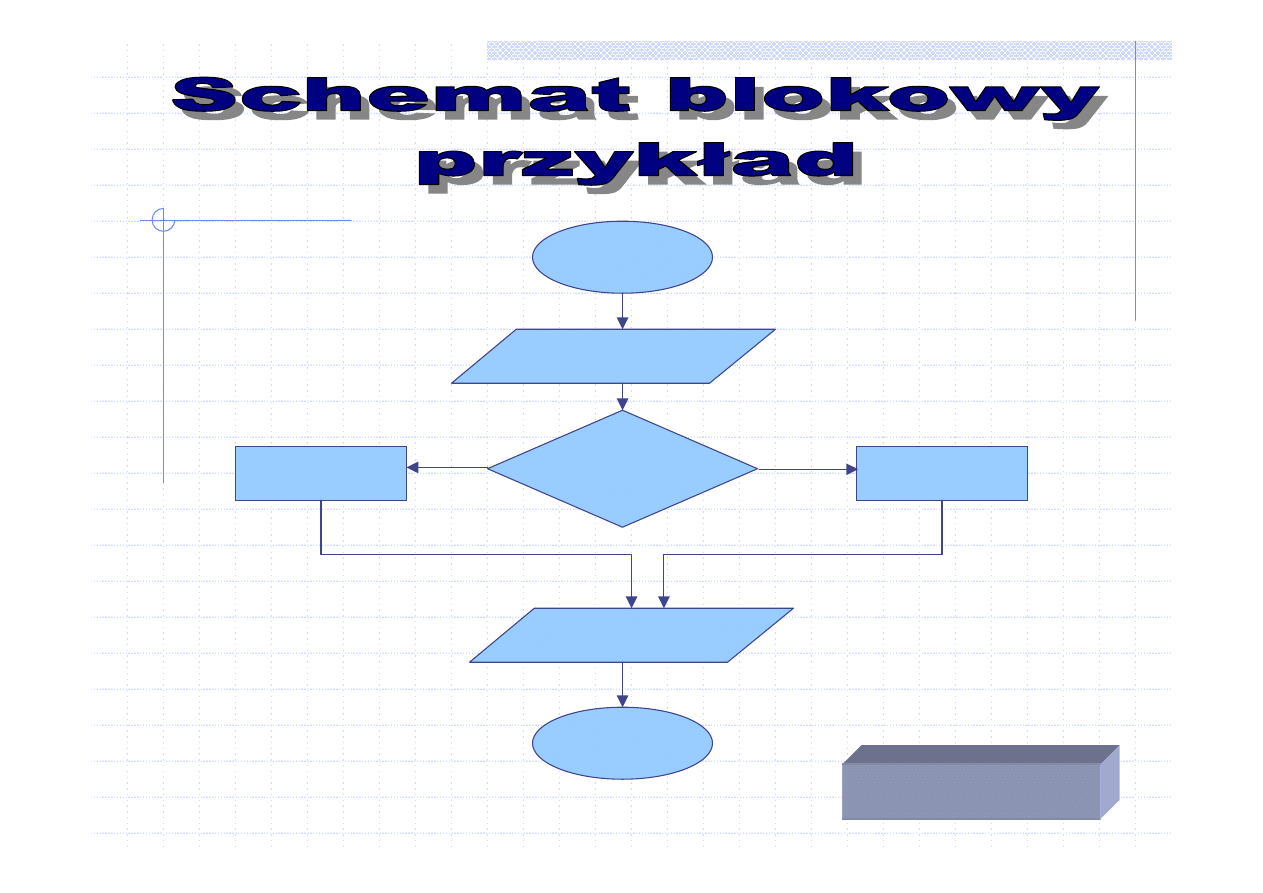
Średnia
Średnia
arytmetyczna trzech
arytmetyczna trzech
dowolnych liczb
dowolnych liczb
rzeczywistych
rzeczywistych
STOP
STOP
START
START
Wprowadź (A, B, C)
Wprowadź (A, B, C)
Wyprowadź (SR)
Wyprowadź (SR)
SUMA:=A+B+C
SUMA:=A+B+C
SR:=SUMA/3
SR:=SUMA/3
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Wartość bezwzględna
Wartość bezwzględna
dowolnej liczby
dowolnej liczby
rzeczywistej.
rzeczywistej.
Algorytm z warunkiem.
Algorytm z warunkiem.
STOP
STOP
START
START
Wprowadź (A)
Wprowadź (A)
Wyprowadź (W)
Wyprowadź (W)
W:=A
W:=A
Czy
Czy
A>0?
A>0?
NIE
NIE
W:=
W:=
-
-
A
A
TAK
TAK
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Notacja zwana „DRZEWEM ALGORYTMU”
nadaje się do prostego przedstawiania
algorytmów porządkowania.
DRZEWO ALGORYTMU składa się z:
• korzenia
• wierzchołków pośrednich (węzłów)
• wierzchołków końcowych (liści)
Notacja zwana
Notacja zwana
„DRZEWEM ALGORYTMU”
„DRZEWEM ALGORYTMU”
nadaje się do prostego przedstawiania
nadaje się do prostego przedstawiania
algorytmów porządkowania.
algorytmów porządkowania.
DRZEWO ALGORYTMU
DRZEWO ALGORYTMU
składa się z:
składa się z:
•
•
korzenia
korzenia
•
•
wierzchołków pośrednich (węzłów)
wierzchołków pośrednich (węzłów)
•
•
wierzchołków końcowych (liści)
wierzchołków końcowych (liści)
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Porządkowanie
Porządkowanie
trzech dowolnych
trzech dowolnych
liczb A, B, C.
liczb A, B, C.
A<=B
A<=B
C<=B
C<=B
C<=A
C<=A
B<=C
B<=C
C<=A
C<=A
(C, A, B)
(C, A, B)
(C, B, A)
(C, B, A)
(A, B, C)
(A, B, C)
(A, C, B)
(A, C, B)
(B, C, A)
(B, C, A)
(B, A, C)
(B, A, C)
TAK
TAK
NIE
NIE
TAK
TAK
TAK
TAK
TAK
TAK
TAK
TAK
NIE
NIE
NIE
NIE
NIE
NIE
NIE
NIE
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
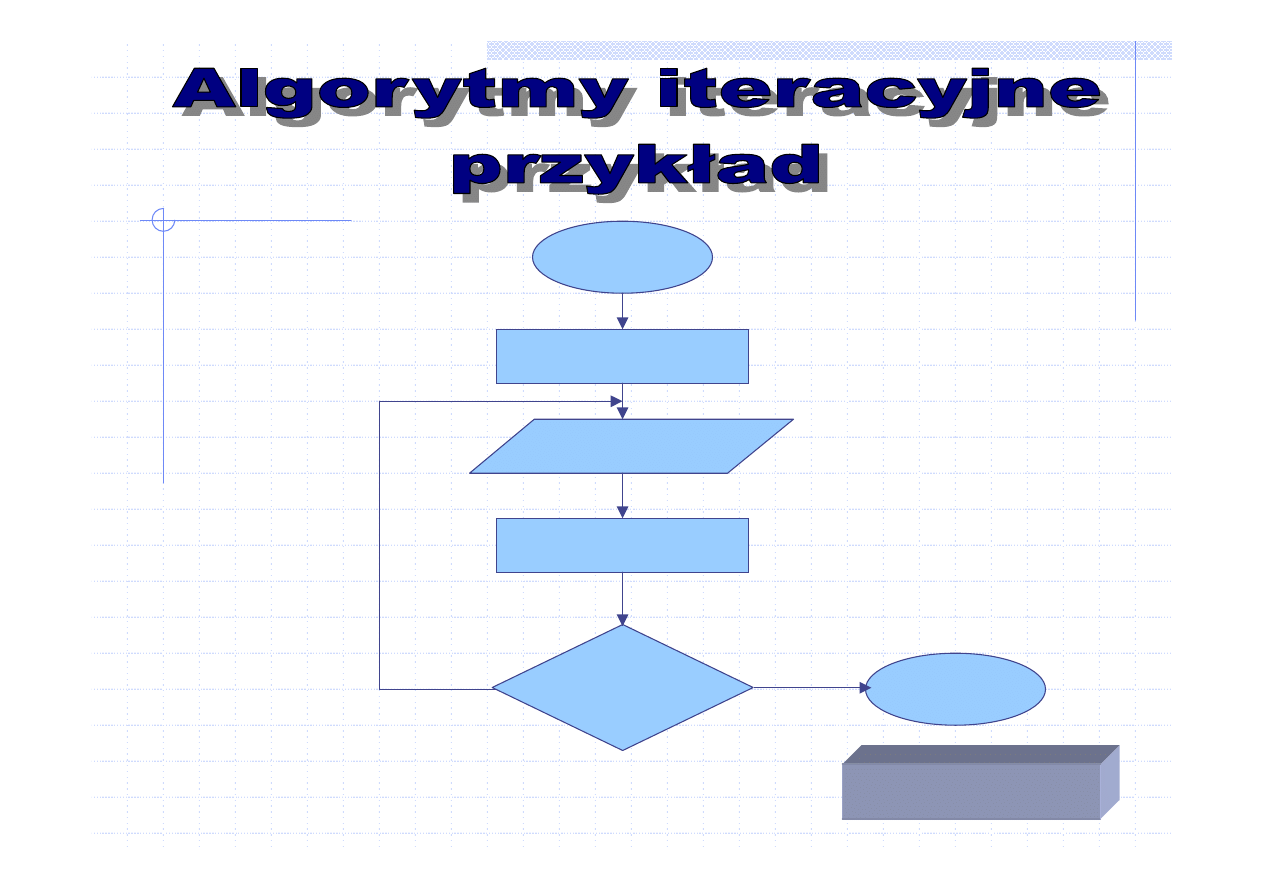
ITERACJĄ nazywamy instrukcję powtarzania
ciągu instrukcji. Liczba powtórzeń może być
ustalona bądź zależeć od spełnienia
określonego warunku sprawdzanego w każdej
iteracji.
Iterację często nazywamy PĘTLĄ.
ITERACJĄ
ITERACJĄ
nazywamy instrukcję powtarzania
nazywamy instrukcję powtarzania
ciągu instrukcji. Liczba powtórzeń może być
ciągu instrukcji. Liczba powtórzeń może być
ustalona bądź zależeć od spełnienia
ustalona bądź zależeć od spełnienia
określonego warunku sprawdzanego w każdej
określonego warunku sprawdzanego w każdej
iteracji.
iteracji.
Iterację często nazywamy
Iterację często nazywamy
PĘTLĄ.
PĘTLĄ.
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Wyświetlanie
Wyświetlanie
kolejnych liczb
kolejnych liczb
od 0 do 14
od 0 do 14
STOP
STOP
START
START
K:=0
K:=0
Wyprowadź (K)
Wyprowadź (K)
K:=K+1
K:=K+1
K < 15
K < 15
TAK
TAK
NIE
NIE
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Algorytm
ten stosuje si
ę
do wyszukiwania
najwi
ę
kszego (najmniejszego) elementu w zbiorze.
Algorytm
Algorytm
ten stosuje si
ę
do wyszukiwania
ten stosuje si
ę
do wyszukiwania
najwi
ę
kszego (najmniejszego) elementu w zbiorze.
najwi
ę
kszego (najmniejszego) elementu w zbiorze.
Dane:
dziesi
ęć
nieuporz
ą
dkowanych dowolnych liczb
Dane:
Dane:
dziesi
ęć
nieuporz
ą
dkowanych dowolnych liczb
dziesi
ęć
nieuporz
ą
dkowanych dowolnych liczb
Wynik:
najwi
ę
ksza i najmniejsza liczba
Wynik:
Wynik:
najwi
ę
ksza i najmniejsza liczba
najwi
ę
ksza i najmniejsza liczba
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
1. Zacznij algorytm
2. Przyjmij za MAX (MIN) pierwszą liczbę
3. Dla kolejnych liczb jeśli MAX jest mniejszy od
kolejnej liczby X (MAX<X) wykonaj MAX:=X
(jeśli MIN jest większy od kolejnej liczby X
(MIN>X) wykonaj MIN:=X)
4. Wyprowadź wynik: MAX (MIN)
5. Zakończ algorytm
1.
1.
Zacznij algorytm
Zacznij algorytm
2.
2.
Przyjmij za MAX (
Przyjmij za MAX (
MIN
MIN
) pierwszą liczbę
) pierwszą liczbę
3.
3.
Dla kolejnych liczb jeśli MAX jest mniejszy od
Dla kolejnych liczb jeśli MAX jest mniejszy od
kolejnej liczby X (MAX<X) wykonaj MAX:=X
kolejnej liczby X (MAX<X) wykonaj MAX:=X
(
(
jeśli MIN jest większy od kolejnej liczby X
jeśli MIN jest większy od kolejnej liczby X
(MIN>X) wykonaj MIN:=X
(MIN>X) wykonaj MIN:=X
)
)
4.
4.
Wyprowadź wynik: MAX (
Wyprowadź wynik: MAX (
MIN
MIN
)
)
5.
5.
Zakończ algorytm
Zakończ algorytm
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Zasada ta ma nast
ę
puj
ą
cy cel:
Problem algorytmiczny dzielimy na mniejsze cz
ęś
ci,
których rozwi
ą
zanie daje rozwi
ą
zanie problemu
głównego. Najcz
ęś
ciej w ten sposób mo
ż
na
efektywniej rozwi
ą
za
ć
problem główny.
Zasada ta ma nast
ę
puj
ą
cy cel:
Zasada ta ma nast
ę
puj
ą
cy cel:
Problem algorytmiczny dzielimy na mniejsze cz
ęś
ci,
Problem algorytmiczny dzielimy na mniejsze cz
ęś
ci,
których rozwi
ą
zanie daje rozwi
ą
zanie problemu
których rozwi
ą
zanie daje rozwi
ą
zanie problemu
głównego. Najcz
ęś
ciej w ten sposób mo
ż
na
głównego. Najcz
ęś
ciej w ten sposób mo
ż
na
efektywniej rozwi
ą
za
ć
problem główny.
efektywniej rozwi
ą
za
ć
problem główny.
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Algorytm
ten stosuje si
ę
do jednoczesnego
wyszukiwania
najwi
ę
kszego
i
najmniejszego
elementu w zbiorze.
Algorytm
Algorytm
ten stosuje si
ę
do jednoczesnego
ten stosuje si
ę
do jednoczesnego
wyszukiwania
najwi
ę
kszego
i
najmniejszego
wyszukiwania
najwi
ę
kszego
i
najmniejszego
elementu w zbiorze.
elementu w zbiorze.
Dane:
dziesi
ęć
nieuporz
ą
dkowanych dowolnych liczb
Dane:
Dane:
dziesi
ęć
nieuporz
ą
dkowanych dowolnych liczb
dziesi
ęć
nieuporz
ą
dkowanych dowolnych liczb
Wynik:
najwi
ę
ksza i najmniejsza liczba
Wynik:
Wynik:
najwi
ę
ksza i najmniejsza liczba
najwi
ę
ksza i najmniejsza liczba
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
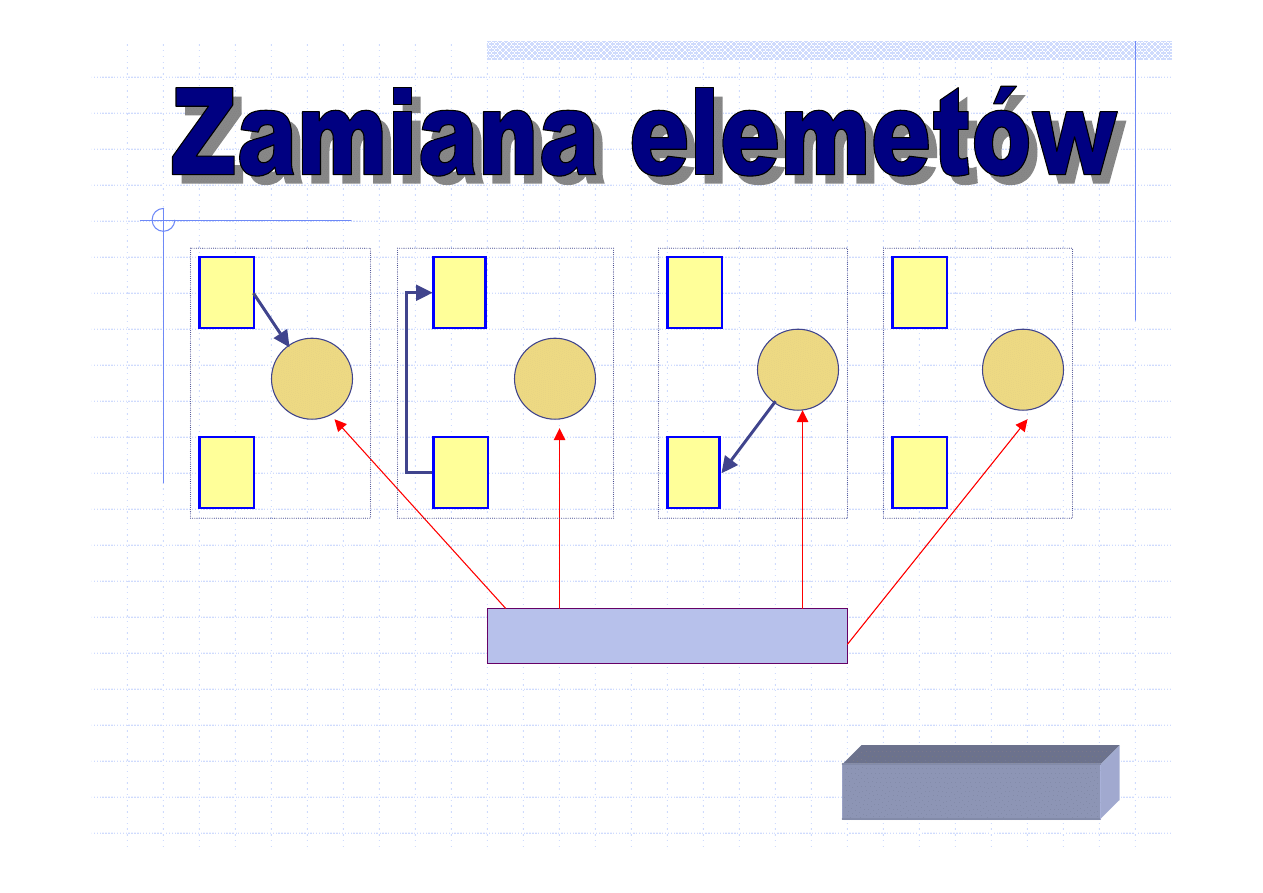
W celu wyszukania najmniejszej i najwi
ę
kszej
liczby
mo
ż
na
oczywi
ś
cie
wykona
ć
najpierw
algorytm MAX a potem algorytm MIN. Takie
post
ę
powanie jest jednak mało ekonomiczne bo
wymaga przejrzenia całego zbioru liczb dwukrotnie.
Wst
ę
pnie podzielimy zbiór liczba na dwa podzbiory
wykonuj
ą
c porównania s
ą
siednich liczb (kolejny
slajd)
W celu wyszukania najmniejszej i najwi
ę
kszej
W celu wyszukania najmniejszej i najwi
ę
kszej
liczby
mo
ż
na
oczywi
ś
cie
wykona
ć
najpierw
liczby
mo
ż
na
oczywi
ś
cie
wykona
ć
najpierw
algorytm MAX a potem algorytm MIN. Takie
algorytm MAX a potem algorytm MIN. Takie
post
ę
powanie jest jednak mało ekonomiczne bo
post
ę
powanie jest jednak mało ekonomiczne bo
wymaga przejrzenia całego zbioru liczb dwukrotnie.
wymaga przejrzenia całego zbioru liczb dwukrotnie.
Wst
ę
pnie podzielimy zbiór liczba na dwa podzbiory
Wst
ę
pnie podzielimy zbiór liczba na dwa podzbiory
wykonuj
ą
c porównania s
ą
siednich liczb (kolejny
wykonuj
ą
c porównania s
ą
siednich liczb (kolejny
slajd)
slajd)
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Zbiór liczb:
2, 5, 3, 7, 9, 1, 4, 8, 0, 6
Zbiór liczb:
Zbiór liczb:
2, 5, 3, 7, 9, 1, 4, 8, 0, 6
2, 5, 3, 7, 9, 1, 4, 8, 0, 6
2<5
2<5
3<7
3<7
9>1
9>1
4<8
4<8
0<6
0<6
Kandydaci na MAX
Kandydaci na MAX
-
-
Kandydaci na MIN
Kandydaci na MIN
-
-
2
2
3
3
1
1
4
4
0
0
5
5
7
7
9
9
8
8
6
6
Pierwszy zbiór przetwarzamy algorytmem MAX a drugi
algorytmem MIN otrzymuj
ą
c szukane warto
ś
ci.
Pierwszy zbiór przetwarzamy algorytmem MAX a drugi
Pierwszy zbiór przetwarzamy algorytmem MAX a drugi
algorytmem MIN otrzymuj
ą
c szukane warto
ś
ci.
algorytmem MIN otrzymuj
ą
c szukane warto
ś
ci.
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
Porz
ą
dkowanie przez wybór (selection sort)
Algorytm ten wykorzystuje poznany wcze
ś
niej
algorytm
MIN.
Wyszukiwany
jest
najmniejszy
element, a nast
ę
pnie zamieniany jest miejscami z
ostatnim elementem przeszukiwanego podci
ą
gu
warto
ś
ci. Kolejne wyszukiwanie prowadzone jest
bez elementów, które zostały ju
ż
uporz
ą
dkowane.
Porz
ą
dkowanie przez wybór (
Porz
ą
dkowanie przez wybór (
selection
selection
sort)
sort)
Algorytm ten wykorzystuje poznany wcze
ś
niej
Algorytm ten wykorzystuje poznany wcze
ś
niej
algorytm
MIN.
Wyszukiwany
jest
najmniejszy
algorytm
MIN.
Wyszukiwany
jest
najmniejszy
element, a nast
ę
pnie zamieniany jest miejscami z
element, a nast
ę
pnie zamieniany jest miejscami z
ostatnim elementem przeszukiwanego podci
ą
gu
ostatnim elementem przeszukiwanego podci
ą
gu
warto
ś
ci. Kolejne wyszukiwanie prowadzone jest
warto
ś
ci. Kolejne wyszukiwanie prowadzone jest
bez elementów, które zostały ju
ż
uporz
ą
dkowane.
bez elementów, które zostały ju
ż
uporz
ą
dkowane.
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
1
1
1
1
1
1
1
1
1
1
1
1
---
---
1
1
2
2
2
2
2
2
2
2
2
2
---
---
2
2
2
2
2
2
2
2
2
2
2
2
---
---
4
4
4
4
2
2
3
3
3
3
3
3
---
---
4
4
2
2
2
2
3
3
4
4
4
4
---
---
7
7
7
7
7
7
7
7
4
4
4
4
---
---
4
4
4
4
2
2
2
2
1
1
4
4
---
---
6
6
6
6
6
6
6
6
6
6
5
5
6
6
7
7
7
7
7
7
3
3
3
3
3
3
3
3
7
7
6
6
4
4
4
4
4
4
4
4
4
4
4
4
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.
2
2
7
7
7
7
7
7
2
2
7
7
2
2
2
2
Komórka pomocnicza
Algorytmy
Algorytmy
–
–
A.
A.
Jędryczkowski
Jędryczkowski
Copyright
Copyright
–
–
2005 r.
2005 r.