Graf (lub

siec)

sklada

si~ ze zbioru

punkt6w

zwanych

wierzcholkami,

pol~czonych

parami

przez

zbi6r

linii

zwanych

galeziami

(takze

zwanych

kraw~dziami

lub wi~zaniami).

Na

przyklad

rysunek

1.1 przedstawia

graf z 6 wierzcholkami

i 8

gal~ziami.

M6wimy,

ze j akas gal~i

pol~czona

z wierzcholkiem

jest

incydentna

z tym wierzcholkiem.

Pytla jest

gal~zi~,

kt6ra

l~czy

dany wierzcholek

ze samym

sob~.

Graf bez p~tli jest

zwany

prostym.

Wierzcholek,

kt6ry

nie ma gal~zi

incydentnych

z nim jest

zwany

izolowanym.

Graf jest

zwany

pohczonym

(lub w pelni

zdefiniowanym),

jesli

nie ma

wierzcholk6w

izolowanych.

We wszystkich

trzech

pro blemach

wspomnianych

wczesniej

zakladamy,

ze zwi~zane

z nimi

grafy

s~

proste

i POfqCZone.

Lancuch

pomi~dzy

dwoma

wierzcholkami

jest

sekwencj~

gal~zi,

l~cz~cych

te dwa wierzcholki.

Na przyklad

sekwencja

gal~zi

(1, 2),

(2, 5), i (5, 3) tworzy

lancuch

l~cz~cy

wierzcholki

1 i 3.

Sciezka

jest

skierowanym

lancuchem.

Na przyklad

w powyzszym

lancuchu

jesli

wyszczeg61nimy

kierunek

podr6zy

od wierzcholka

1

do 3 (jak odwrotnosc

3 do 1), lancuch

jest

sciezk~.

'

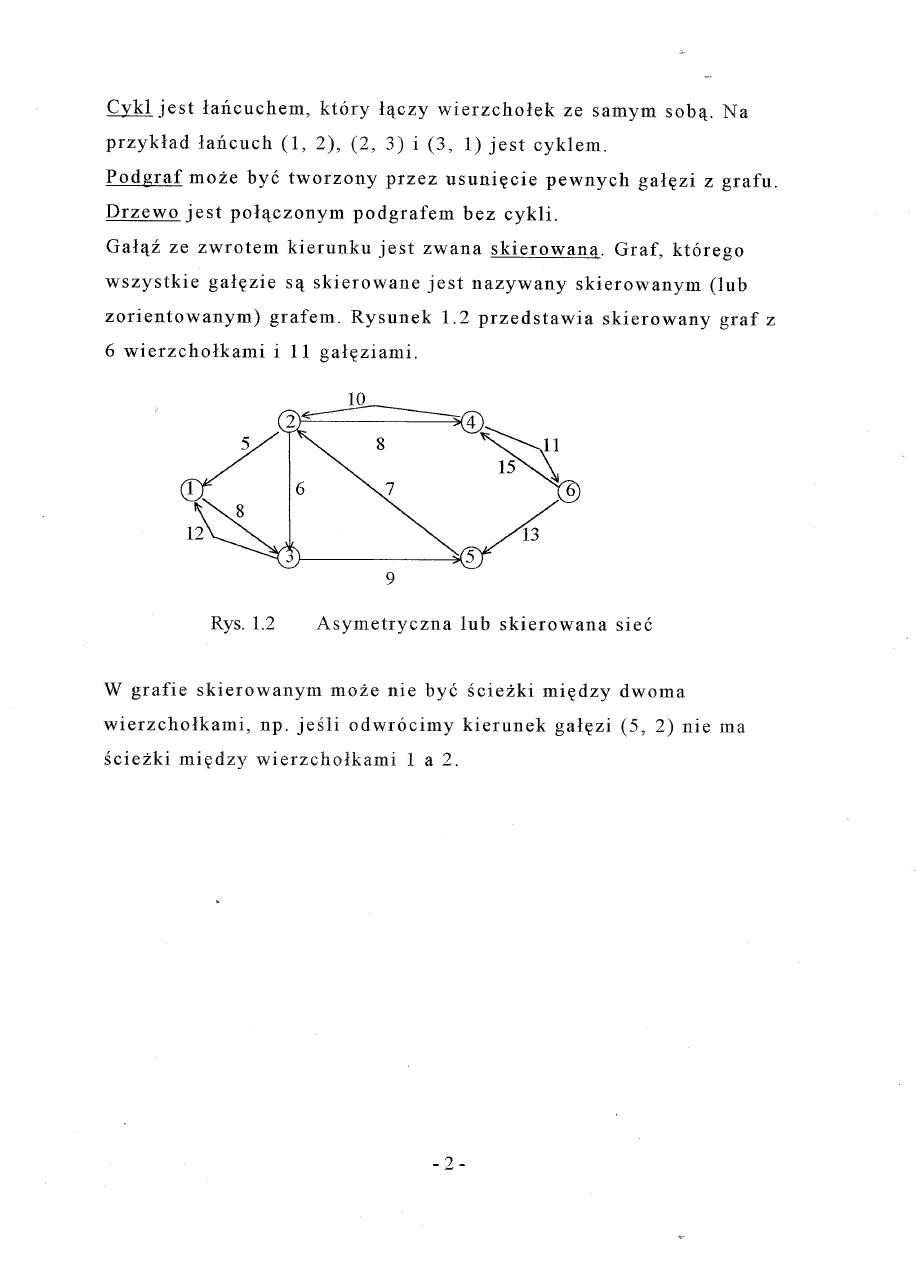
Cykl jest

lancuchem,

kt6ry

l~czy wierzcholek

ze samym

sob~. Na

przyklad

lancuch

(1,2),

(2, 3) i (3, 1) jest

cyklem.

Podgraf

moze

bye tworzony

przez

usuni~cie

pewnych

gal~zi

z grafu.

Drzewo

jest

pol~czonym

podgrafem

bez cykli.

Gal~i

ze zwrotem

kierunku

jest

zwana

skierowana.

Graf,

kt6rego

wszystkie

gal~zie

s~ skierowane

jest

nazywany

skierowanym

(lub

zorientowanym)

grafem.

Rysunek

1.2 przedstawia

skierowany

graf z

6 wierzcholkami

i 11 gal~ziami.

W grafie

skierowanym

moze nie bye sciezki

mi~dzy

dwoma

wierzcholkami,

np. jesli

odwr6cimy

kierunek

gal~zi

(5, 2) nie ma

sciezki

mi~dzy

wierzcholkami

1 a 2.

PROBLEM

NAJKROTSZEJ

SCIEZKI.

Problem

najkr6tszej

seiezki

lub najkr6tszej

trasy

jest

zwi~zany

ze

znajdowaniem

najkr6tszej

trasy

z jednego

polozenia

(wierzeholka)

do inllego

polozenia

(wierzeholka)

w pol~ezonej

sieei.

Pierwsze

polozenie

moze bye poez~tkiem

sieei,

a inne polozenie

moze bye

eelem

lub koneem

sieei.

Inaezej

m6wi~e

zalezy

nam na znalezieniu

najkr6tszej

odleglosei

pomi~dzy

punktem

nadania

i punktem

odbioru

w Sleel.

Problem

najkr6tszej

seiezki

moze bye rozwazany

w kategoriaeh

odleglosei,

ezasu,

kosztu,

itp.

Algorytm

najkr6tszej

seiezki

zapewnia

najkr6tsz~

drog~

przejazdu

z punktu

nadania

do kazdego

wierzeholka

w sieei.

Znajduje

on kolejno

najkr6tsz~

seiezk~

do kazdego

wierzeholka

w

sieei,

ulozonyeh

w porz~dku

ieh najkr6tszyeh

odleglosei

od punktu

nadania.

Znaleze

najkr6tsz~

drog~ z X do Y.

Algorytm

1. Znajdujemy

wierzeholek

najblizszy

punktowi

nadania

X.

2. Znajduje'my

drugi

llajblizszy

wierzeholek

w stosunku

do X i

kolejne

najblizsze

...

3. W trakeie

realizaeji

proeedury

skreslamy

kazdtt

ga1ttz sieei,

ktora

nie znajduje

si~ na najkr6tszej

seiezee

z poprzednio

rozwazanego

wierzcholka

do nast~pnego

- najblizszego

wierzcholka,

kt6ry

wlasnie

okreslilismy.

PROBLEM

MINIMALNIE

ROZGALEZIONEGO

DRZEW A.

Problem

drzewa

rozgal~zionego

dotyczy

wybierania

gal~zi

w

pelni

zdefiniowanej

sieci,

kt6re

maj~ najkr6tsz~

calkowit~

dlugose,

podczas

gdy wyznaczaj~

tras~

l~cz~c~

kazdy

wierzcholek.

Gal~zie

musz~

bye wybierane

w taki

spos6b,

ze siee wynikowa

tworzy

drzewo

z minimaln~

calkowit~

dlugosci~

gal~zi.

Inaczej,

minimalnie

rozgal~zione

drzewo

to zbi6r

gal~zi

w sieci,

kt6re

l~cz~ wszystkie

wierzcholki

w taki

spos6b,

aby

zagwarantowae

minimaln~

dlugose

calkowit~

dla calego

zbioru.

Wartosci

numeryczne

przypisane

do gal~zi

oznaczaj~

odleglosci,

koszty

lub wartosci

czasu.

Problem

ten jest

typowym

problemem

sieci

transportowych

i

dystrybucyjnych.

Rysunek

2.1 pokazuje

siee w pelni

zdefiniowanq,

przedstawiaj~cq

10 wierzcholk6w

i 18 gal~zi,

kt6re

l~czq pary wierzcholk6w.

Wartosci

przedstawione

w s~siedztwie

gal~zi

Sq

odleglosciami

pomi~dzy

kazd'l

pol'lczon'l

par'l

wierzcholk6w.

5

Rysunek

2.2 pokazuje

drzewo

rozgal~zione,

niekoniecznie

minimalnie

rozgal~zione

drzewo

sieci

pokazanej

na rysunku

2.1.

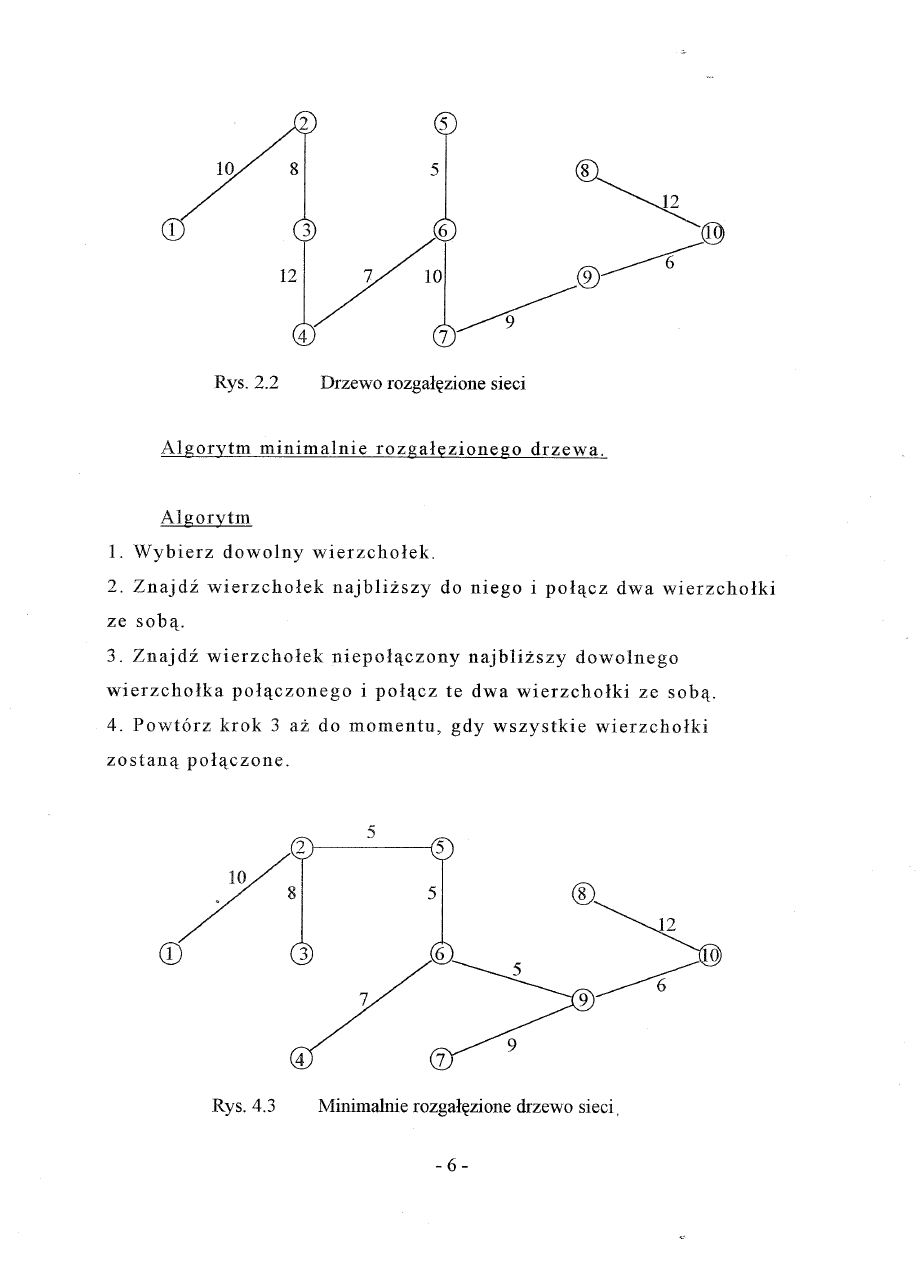
Algorytm

1. Wybierz

dowolny

wierzcholek.

2. Znajdz

wierzcholek

najblizszy

do niego

i pol,!:cz dwa wierzcholki

ze sob,!:.

3. Znajdz

wierzcholek

niepol,!:czony

najblizszy

dowolnego

wierzcholka

pol&.czonego

i pol&.cz te dwa wierzcholki

ze sob&..

4. Powt6rz

krok

3 az do momentu,

gdy wszystkie

wierzcholki

zostan&. pol&.czone.

CD

Problem

maksymalnego

przeplywu

wybiera

te sciezki

w sieci,

ktore b~d(l maksymalizowaly

przeplyw

od zrodla

(pocz(ltku)

sieci do

ujscia

(konca)

sieci.

Poszukuje

si~ max przeplywu

np. pojazdow,

ktore mog(l przejechac

przez

siec w ustalonym

czasie.

Kazda

gal(lz sieci ma ustalon(l

gorn(l granic~

przeplywu

w danym

kierunku

w ustalonym

przedziale

czasowym.

Ie granice

S(l

przepustowosciami

przeplywu

(gal~zi).

Rysunek

3.1 pokazuje

siec w pelni

zdefiniowan(l,

przedstawiaj(lc(l

6

wierzcholkow

i 9 gal~zi,

ktore l(lcz(l pary wierzcholkow.

Wartosci

przedstawione

w s(lsiedztwie

gal~zi

S(l pojemnosciami

maksymalnego

przeplywu

kazdej

gal~zi we wskazanym

kierunku.

Zanim zastosujemy

algorytm

b'tdziemy

si

y

starac

rozwi&ezac problem

metod~

przegl~du

rozwi~zania.

Aby uzyc metod't

przegl&:du

rozwi&:zania,

rozpoczynamy

od identyfikacji

wszystkich

mozliwych

sciezek

w sieci.

Mozliwe

sciezki

s&:pokazane

w tabeli

3.

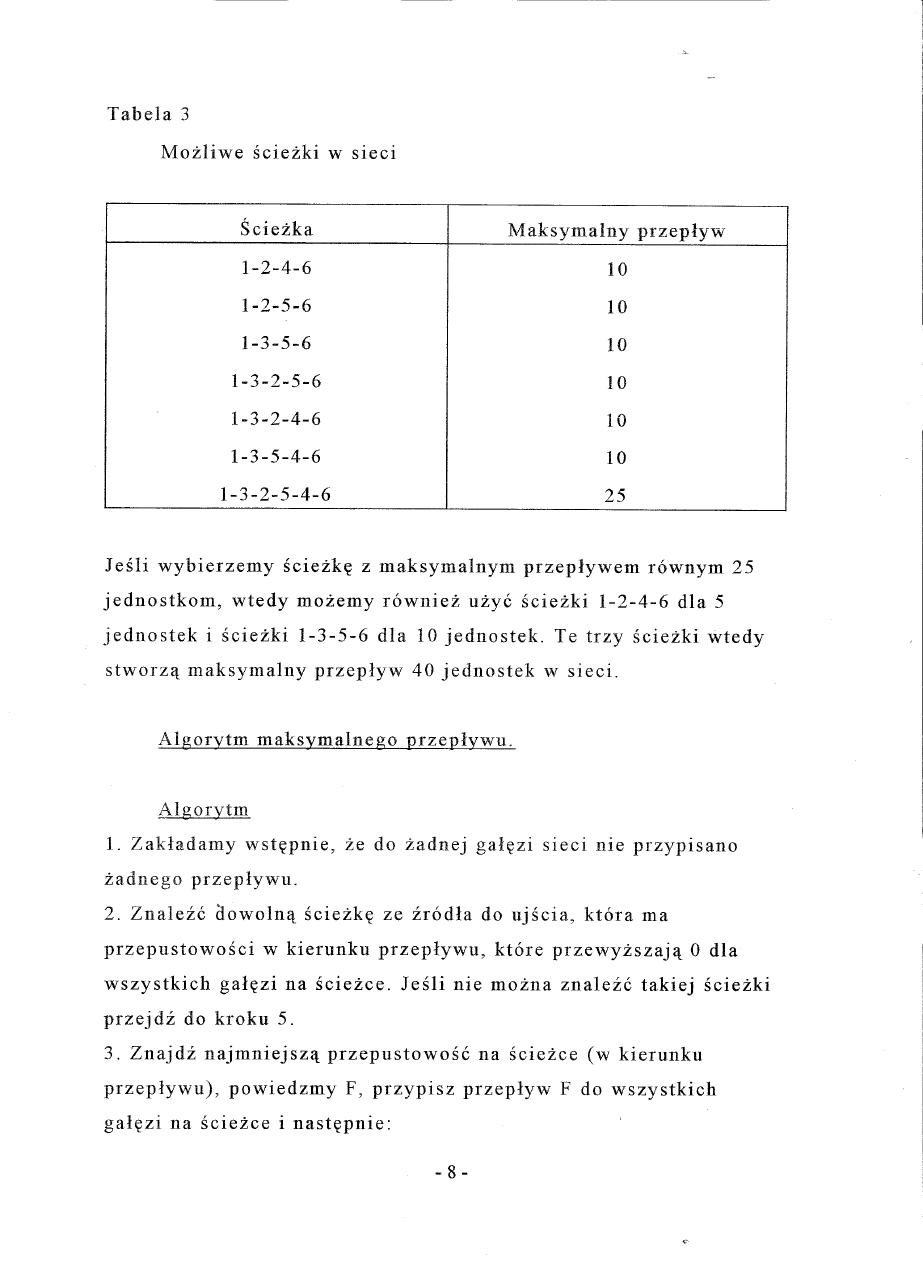
Tabela

3

Mozliwe

sciezki

w sieci

Sciezka

!\1aksymalny

przeplyw

1-2-4-6

10

1-2-5-6

10

1-3-5-6

10

1-3-2-5-6

10

1-3-2-4-6

10

1-3-5-4-6

10

1-3-2-5-4-6

25

J esli wybierzemy

sciezk~

z maksymalnym

przeplywem

rownym

25

jednostkom,

wtedy

mozemy

rowniez

uzyc

sciezki

1-2-4-6

dla 5

jednostek

i sciezki

1-3-5-6

dla

10 jednostek.

Te trzy

sciezki

wtedy

stworz<l: maksymalny

przeplyw

40 jednostek

w sieci.

Algorytm

1. Zakladamy

wstltpnie,

ze do zadnej

gal~zi

sieci

nie przypisano

zadnego

przeplywu.

2. Znalezc

aowoln<l: sciezklt

ze zrodla

do ujscia,

ktora

ma

przepustowosci

w kierunku

przeplywu,

ktore

przewyzszaj::t

0 dla

wszystkich

ga1ltzi na sciezce.

Jesli

nie mozna

znalezc

takiej

sciezki

przej dz do kroku

5.

3. Znajdz

najmniejsz<l:

przepustowosc

na sciezce

(w kierunku

przeplywu),

powiedzmy

F, przypisz

przeplyw

F do wszystkich

ga1ltzi na sciezce

i nastltpnie:

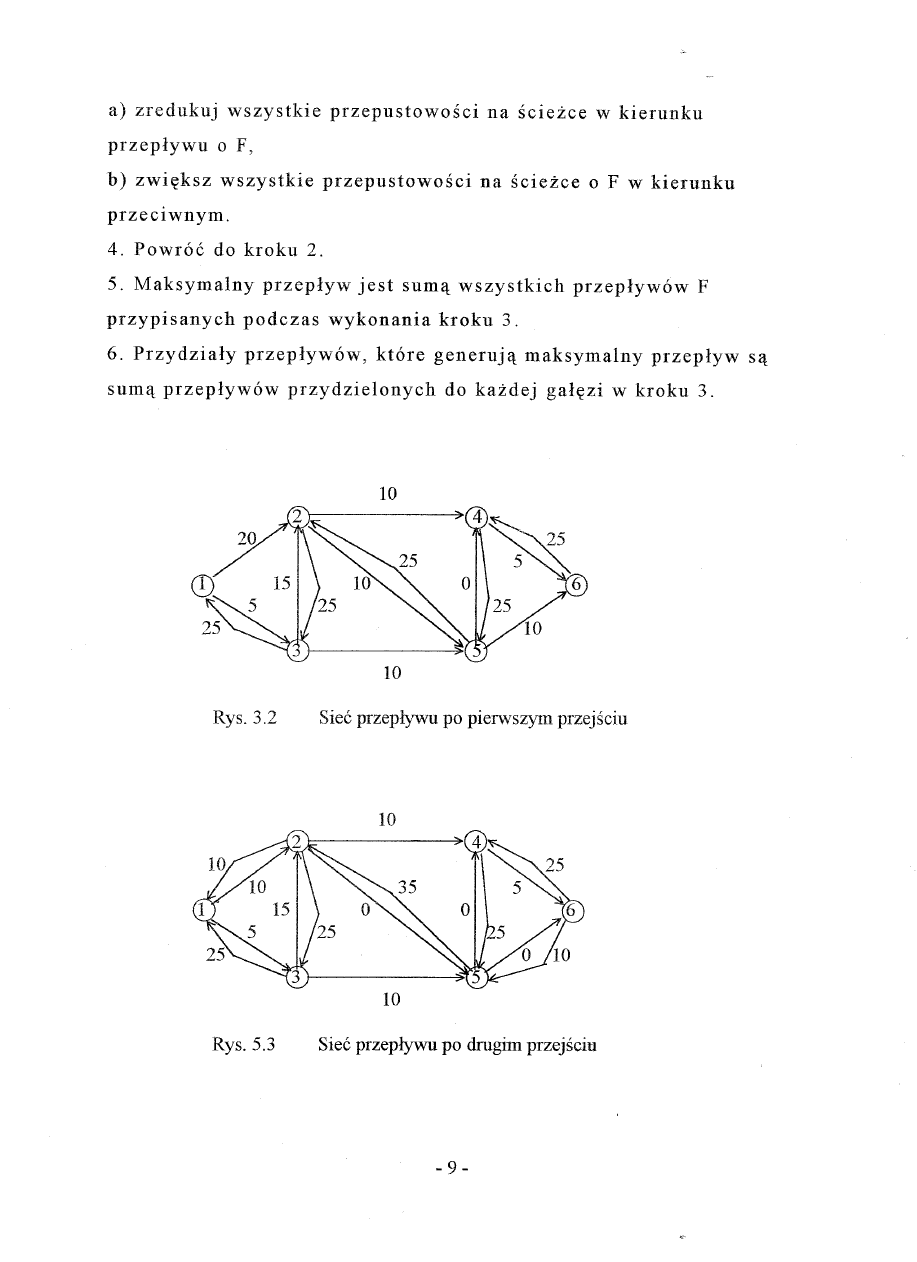
a) zredukuj

wszystkie

przepustowosci

na sciezce

w kierunku

przeplywu

0

F,

b) zwi~ksz wszystkie

przepustowosci

na sciezce

0

F w kierunku

przeclwnym.

4. Powro6 do kroku 2.

5. Maksymalny

przeplyw

jest sum:t wszystkich

przeplywow

F

przypisanych

podczas

wykonania

kroku 3.

6. Przydzialy

przeplywow,

ktore generuj:t

maksymalny

przeplyw

s:t

sum:t przeplywow

przydzielonych

do kazdej

gal~zi w kroku 3.