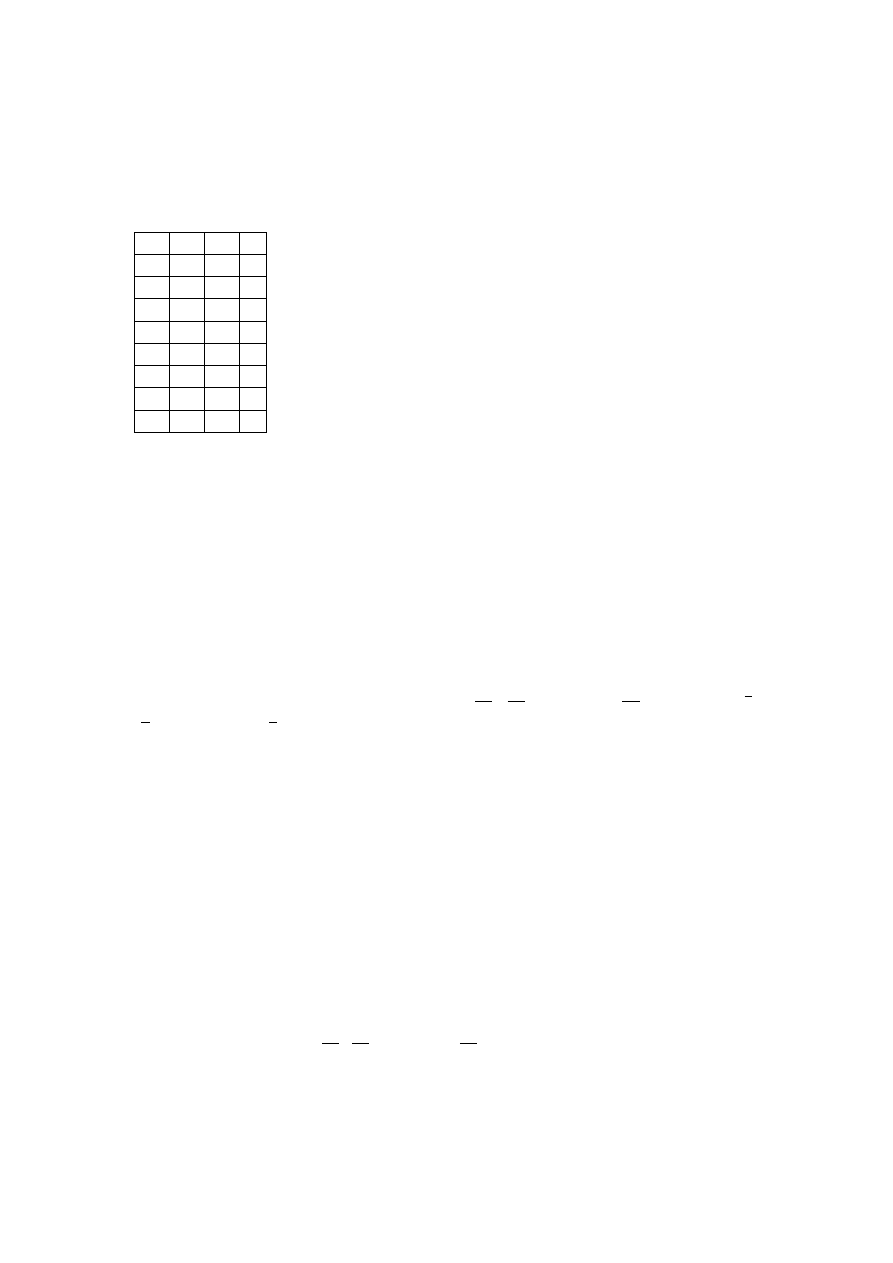
PA - Ukªady logiczne: zadania do samodzielnego rozwi¡zania

Synteza i minimalizacja funkcji logicznych

Zad1. Utworzy¢ postacie kanoniczne funkcji y = f(x

1

, x

2

, x

3

)

, zdeniowanej w podanej tablicy,

zminimalizowa¢ je metod¡ przeksztaªce« algebraicznych; przedstawi¢ tablic¦ Karnaugha

tej funkcji oraz zapisy symboliczne (liczbowe).

x

1

x

2

x

3

y

0

0

0 0

0

0

1 1

0

1

0 0

0

1

1 1

1

0

0 0

1

0

1 1

1

1

0 1

1

1

1 1

Zad2. Korzystaj¡c z tablic Karnaugha, wyznaczy¢ minimalne postacie: alternatywn¡ i ko-

niunkcyjn¡ funkcji:

• y

1

(a, b, c, d) =

P 0, 1, 3, 4, 5, 7, 10, 14, 15

,

• y

2

(x

1

, x

2

, x

3

, x

4

) =

Q 0, 3, 4, 6, 9, 10(1, 2, 8, 15)

,

• y

3

(x

1

, x

2

, x

3

, x

4

) =

Q 0, 2, 3, 4, 5, 7, 13, 14

,

• y

4

(x

1

, x

2

, x

3

, x

4

) =

Q 2, 3, 7, 12, 13, 14

,

• y

5

(a, b, c, d) =

P 0, 2, 7, 8, 10, 12, 14

.

Zad3. Zbudowa¢ tablice Karnaugha funkcji y

1

= x

1

· x

3

+ x

2

· x

3

+ x

2

· x

4

i y

2

= (b + c) ·

(a + c + d) · (b + c + d)

oraz utworzy¢ zapisy symboliczne (liczbowe) tych funkcji (np.

y

1

(x

1

, x

2

, x

3

, x

4

) =

P ......

oraz y

2

(x

1

, x

2

, x

3

, x

4

) =

Q .....

).

Projektowanie ukªadów kombinacyjnych

Zad3. Zbudowa¢ ukªady przeka¹nikowe realizuj¡ce trójargumentowe funkcje: alternatyw¦, ko-

niunkcj¦, NOR, NAND. Jako element wyj±ciowy wykorzysta¢ »arówk¦. Przedstawi¢ wa-

rianty ukªadów:

a) przeka¹niki wej±ciowe maj¡ jeden tylko zestyk n.o.

b) mo»na wykorzysta¢ przeka¹niki wej±ciowe o jednym zestyku n.o. i jednym n.z.

Zad4. wykorzystuj¡c minimaln¡ liczb¦ zestyków zbudowa¢ ukªad przeka¹nikowy realizuj¡cy

funkcj¦ y(x

1

, x

2

, x

3

, x

4

) =

Q 0, 3, 4, 6, 9, 10(1, 2, 8, 15)

.

Zad5. Zrealizowa¢ funkcj¦ y = x

1

· x

3

+ x

2

· x

3

+ x

2

· x

4

projektuj¡c ukªad

a) przeka¹nikowy

b) z elementów NOR

c) z elementów NAND

1

Zad6. Zrealizowa¢ funkcj¦ y = (b + c) · (a + c + d) · (b + c + d) projektuj¡c ukªad

a) przeka¹nikowy

b) z elementów NOR

c) z elementów NAND

2