Zadanie 1 [10 pkt]

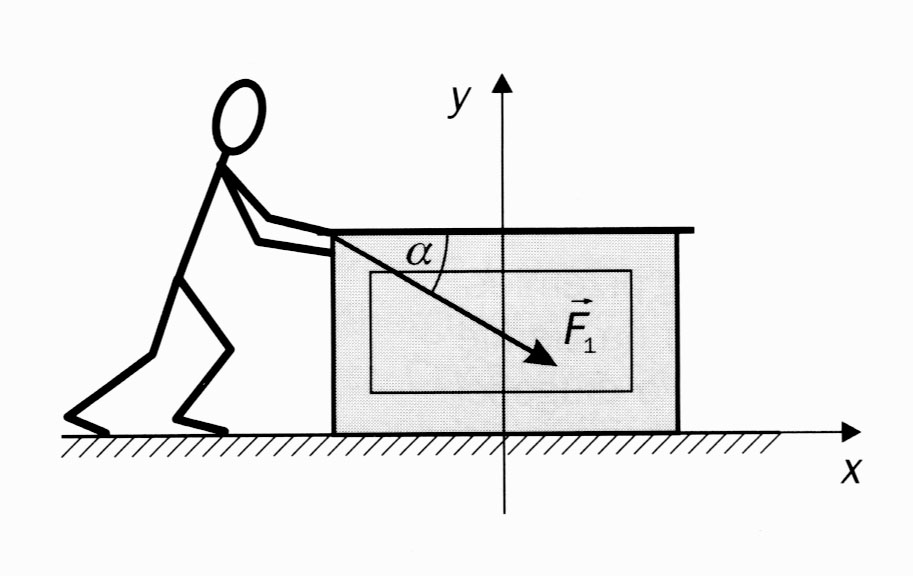
Robotnik pcha szafkę o masie m=30kg siłą skierowaną pod kątem α=30° do podłogi tak, jak pokazuje rysunek. Wartość siły F₁=150N, a współczynnik tarcia kinetycznego między szafką a podłogą f=0,2.

a) Oblicz pracę, którą wykonał robotnik, jeśli przesunął szafkę o l=2m;

b) Oblicz, jaka część tej pracy była potrzebna na zwiększenie energii kinetycznej szafki, a jaka na pokonanie siły tarcia? (Pamiętaj, że zmiana energii kinetycznej jest równa pracy siły wypadkowej).

c) Oblicz czas przesuwania szafki;

d) Oblicz moc średnią robotnika; czyjego moc była stała podczas przesuwania szafki?

e) Wyprowadź wzór na moc chwilową robotnika: P(t). Na podsta­wie otrzymanego wzoru oblicz jego moc maksymalną.

Zadanie 2. Siatka dyfrakcyjna [11 pkt]

Na wykresie przedstawiono zależność kąta odchylenia widma pierwszego rzędu, wą­skiej wiązki światła padające­go na siatkę dyfrakcyjną od długości fali.

1. Oblicz stałą siatki. (sin20°=0,342) (3pkt)

2. Oblicz kąt odchylenia widma drugiego rzędu dla światła o długości fali 0,35μm padającego na tę siatkę dyfrakcyjną. (2 pkt)

3. Określ maksymalny rząd pełnego widma światła białego, jaki można obserwować za pomocą tej siatki dyfrakcyjnej. (3pkt)

4. Oblicz energię fotonu odchylonego przez tę siatkę o kąt 30°. Wynik podaj w elektronowoltach. (3 pkt)

Zadanie 3.Zjawisko fotoelektryczne [16 pkt]

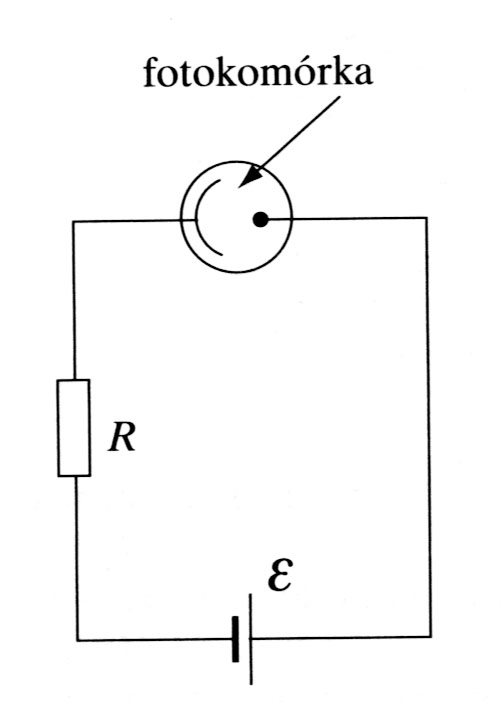
Na fotokomórkę włączoną w obwód, którego schemat jest przedstawiony na rysunku, pada wiązka światła o mocy 1mW i długości fali 350nm, uwalniając elektrony. Graniczna długość fali dla fotokatody wynosi 660nm. Przyjmij, że tylko połowa fotonów padających na fotokomórkę wywołuje zjawisko fotoelektryczne, a opornik R ma opór 5Ω.

1. Oblicz, jaka część energii fotonu o długości fali 350nm pada­jącego na powierzchnię fotokatody zostaje wykorzystana do wy­konania pracy wyjścia. (4 pkt)

2. Oblicz napięcie na oporniku R. (4 pkt)

3. Oblicz SEM źródła, wiedząc, że po odwrotnym włączeniu źródła w obwód nowa graniczna długość fali dla tej sytuacji zmalała do 500nm. (3 pkt)

4. Naszkicuj wykres zależności energii kinetycznej uwalnianych w tej fotokomórce elektronów od częstotliwości padających na nią fotonów. (5 pkt)

Zadanie 4 Zamknięty cykl p-V [13 pkt]

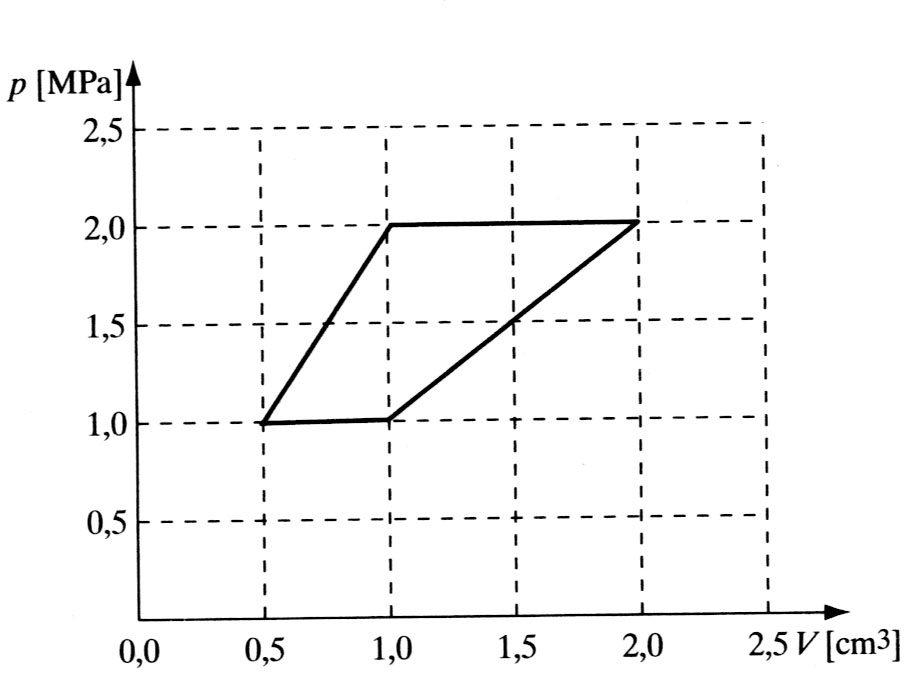
Na wykresie przedstawiono zamknięty cykl przemian termodynamicznych wykonywanych przez stałą masę helu w pewnym silniku. Wykonując obliczenia, potraktuj gaz jak gaz doskonały.

1. Oblicz sprawność tego cyklu. (4 pkt)

2. Oblicz masę helu, wiedząc, że maksy­malna temperatura, jaką gaz osiągał w tym cyklu, wynosiła 1000 K. (3 pkt)

3. Oblicz moc tego silnika, gdy wiesz, że podczas pracy wykonuje 10 cykli w ciągu jednej sekundy. Pomiń tarcie. (3 pkt)

4. Oblicz najniższą temperaturę osiąga­ną przez gaz w tym cyklu. (3 pkt)

---