Zadanie 1 
Do wyznaczenia lepkości płynu wykorzystano lepkościomierz kapilarny o długości 
L=…[m]  i  średnicy  D=…[mm].  Wiedząc,  że  objętościowy  wydatek  przepływu 
przez  kapilarę  wynosi  Q=…[m

3

/s],  a  różnica  ciśnień  na  jej  końcach  wynosi 

p

∆

=..[Pa], wyznaczyć lepkość płynu. 

Zadanie 2 
Dynamiczny współczynnik lepkości oleju µ= …[Pa·s] wyznaczono wykorzystując 
lepkościomierz  kapilarny  o  długości  L=…[m].  Jaka  jest  średnica  kapilary  jeżeli 
objętościowy  wydatek  przepływu  przez  kapilarę  wynosi  Q=…[m

3

/s],  a  różnica 

ciśnień na jej końcach wynosi 

p

∆

=...[Pa]. 

Zadanie 3 
Do  wyznaczenia  lepkości  płynu  (µ=  [Pa·s],  ρ

p

=…[kg/m

3

])  wykorzystano 

lepkościomierz  z  opadającą  kulką  (ρ

k

=…[kg/m

3

]).  Wiedząc,  że  w  czasie  …[s], 

kulka przebyła drogę równą …[m], wyznaczyć promień opadającej kulki. 
Zadanie 4 
W  łożysku  ślizgowym  o  długości  …  wiruje  wał  o  średnicy  …  z  prędkością  …. 
Mimośród względny wynosi …, a średni luz promieniowy mierzony w µm wynosi 
….  O  jakiej  lepkości  należy  zastosować  olej  aby  siła  nośna  łożyska  wynosiła 
….Poise (1Poise=1g/(cm·s)). 
Zadanie 5 
W  poziomym  odcinku  rury  o  średnicy  D=…[mm]  i  średniej  wysokości 
chropowatości ścianek rury e=…[mm] płynie woda (ρ=1000[kg/m

3

], µ=10

-3

[Pa·s]) 

z  wydatkiem  objętościowym  Q=…[m

3

/s].  Wyznaczyć  długość  rury,  jeżeli 

wiadomo, że różnica ciśnień na jej końcach wynosi ∆p=…[Pa]. 
Zadanie 6 
W  poziomym  odcinku  rury  o  średnicy  D=…[mm],  długości  L[m]  i  średniej 
wysokości  chropowatości  ścianek  rury  e=…[mm]  płynie  woda  (ρ=1000[kg/m

3

], 

µ=10

-3

[Pa·s]) z wydatkiem objętościowym Q=…[m

3

/s]. Wyznaczyć wysokość strat 

tarcia. 
Zadanie 7 
Słup  o  wysokości  …[m]  i  średnicy  ...[cm]  jest  opływany  wiatrem  wiejącym  z 
prędkością  …[km/godz].  Temperatura  powietrza  wynosi  ...[K],  ciśnienie 
atmosferyczne …[Pa] a współczynnik lepkości wynosi 1.81·10

-5

 [Pa s]. Wiedząc, 

ż

e stała gazowa dla powietrza wynosi 287[J/kg·K] wyznaczyć wartość siły oporu. 

Zadanie 8 
Kulka o średnicy …[cm] opada pionowo w wodzie (ρ=1000[kg/m

3

], µ=10

-3

[Pa·s]) 

ze  stałą  prędkością  …[m/s].  Obliczyć  gęstość  materiału  z  jakiego  kulka  jest 
wykonana (lub masę kulki). 
 

Zadanie 9 
W  kanale  otwartym  o  przekroju  trójkątnym  tworzącym  z  poziomem  kąt  α=…

O

 

wykonanym  ze  stali  pomalowanej  płynie  woda.  Obliczyć  głębokość  wody  w 
kanale  jeżeli  objętościowe  natężenie  przepływu  wynosi  …[litra/s],  a  kąt 
wierzchołkowy przekroju poprzecznego kanału …

O

. 

Zadanie 10 
Obliczyć objętościowe natężenie przepływu wody w kanale otwartym o przekroju 
prostokątnym  tworzącym  z  poziomem  kąt  α=…

O

  wykonanym  ze  stali 

pomalowanej,  jeżeli  głębokość  wody  w  kanale  wynosi  …[cm],  a  szerokość  dna 
…[cm]. 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 
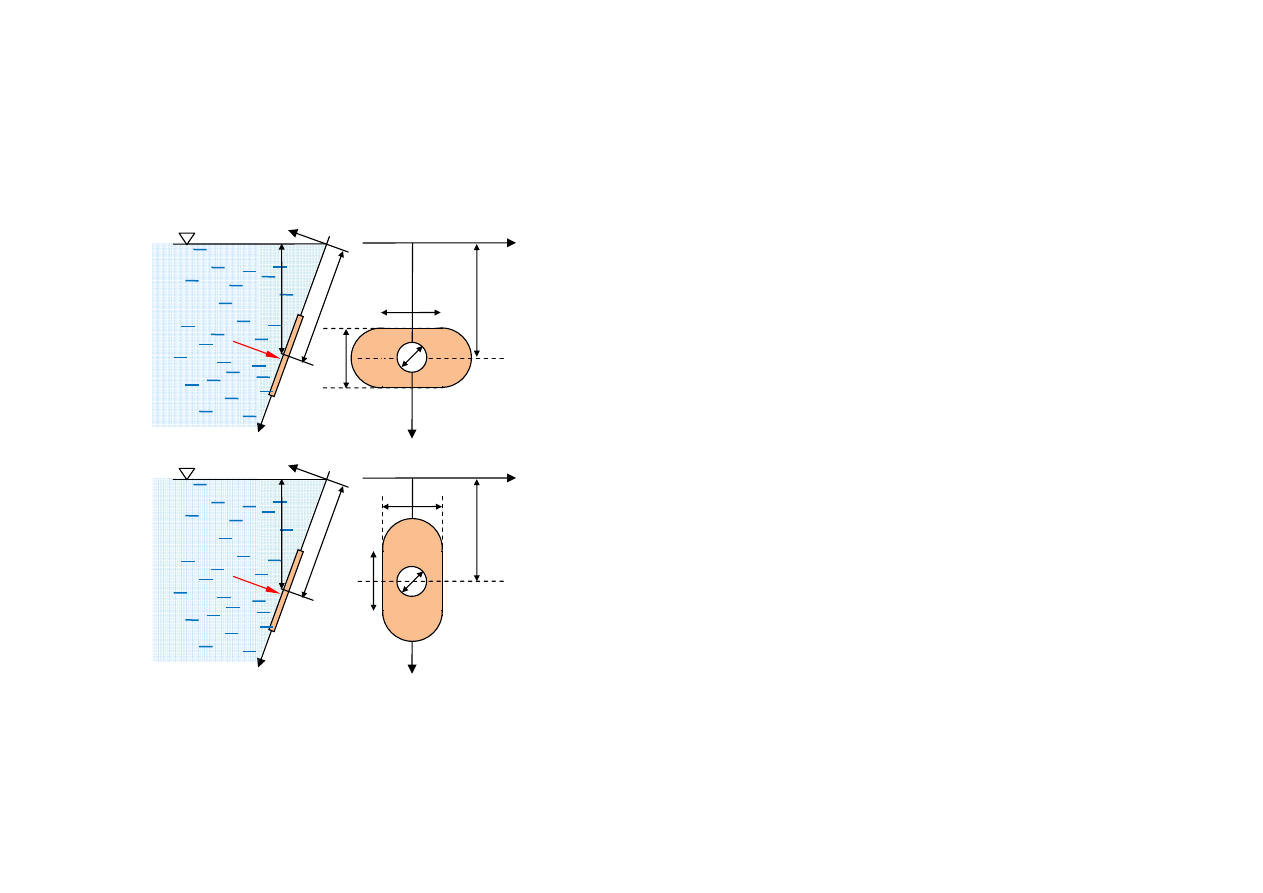
Zadanie do rozwiązania przy pomocy programów 
Zadanie 1 
Boczna ściana zbiornika tworzy z poziomem kąt β=70

O

.

 

Obliczyć siłę naporu wody 

na  zastawę  umieszczoną  na  tej  ścianie  i  przedstawioną  na  rysunku  1.  Znaleźć 
miejsce  jej  działania  jeśli  odległość  środka  geometrycznego  zastawy  od 
powierzchni swobodnej jest równa 3m. 
P= 

 

xs= 

 

ys= 

 

 

Zadanie 2 
Woda  (ρ=1000  kg/m

3

)  o  kinematycznym  współczynniku  lepkości  υ=10

-6 

m

2

/s 

przepływa  rurą  o  długości  400  m,  średnicy  25  cm  i  chropowatości  ścianek  0,45 
mm. Obliczyć wydatek przepływu jeżeli wiadomo, że różnica ciśnień na końcach 
rury wynosi ∆p=450 Pa. 
Re= 

 

v

sr

= 

 

Q= 

Zadanie 3 

Woda  (ρ=1000  kg/m

3

)  o  dynamicznym  współczynniku  lepkości  1.0·10

-3 

Pa·s 

przepływa  rurą  o  długości  350  m,  średnicy  25  cm  i  chropowatości  względnej 
ś

cianek 0.0004. Obliczyć średnią prędkość przepływu, jeżeli wiadomo, że różnica 

ciśnień na końcach rury wynosi 450 Pa. 
Re= 

 

v

sr

= 

 

Q= 

Zadanie 4 
Woda  (ρ=1000  kg/m

3

)  o  dynamicznym  współczynniku  lepkości  1.0·10

-3 

Pa·s 

przepływa  rurą  o  długości  350  m  i  chropowatości  ścianek  0.5  mm.  Obliczyć 
ś

rednicę rury, jeżeli wiadomo, że różnica ciśnień na jej końcach wynosi 450 Pa, a 

wydatek przepływu 7 l/s 
Re= 

 

D= 

 

v

sr

= 

Zadanie 5 
Woda  (ρ=1000  kg/m

3

)  o  kinematycznym  współczynniku  lepkości  1.00·10

-6 

m

2

/s 

przepływa  rurą  o  długości  400  m  i  chropowatości  ścianek  0,45  mm.  Obliczyć 
ś

rednicę  rury  jeżeli  wiadomo,  że  wysokość  strat  tarcia  wynosi  1.5  m  a  wydatek 

przepływu 30 l/s. 
Re= 

 

D= 

 

v

sr

= 

Zadanie 6 
W kanale otwartym o przekroju cylindrycznym o promieniu R=50 cm, tworzącym 
z  poziomem  kąt  α=5

O

  wykonanym  ze  stali  pomalowanej  płynie  woda  (ρ=1000 

kg/m

3

,  µ=1.0·10

-3 

Pa·s).  Obliczyć  głębokość  wody  w  kanale,  jeżeli  objętościowe 

natężenie przepływu wynosi 0,1 m

3

/s 

Y= 
Zadanie 7 
W  kanale  otwartym  o  przekroju  prostokątnym,  tworzącym  z  poziomem  kąt  α=5

O

 

wykonanym  ze  stali  pomalowanej  płynie  woda.  Obliczyć  głębokość  wody  w 
kanale oraz średnią prędkość przepływu, jeżeli objętościowe natężenie przepływu 
wynosi 0,1[m

3

/s] a szerokość dna kanału 1[m]. 

Y= 

 

v

sr

= 

Zadanie 8 
Obliczyć  masę  stalowej  kulki  (ρ

s

=7,86  g/cm

3

)  o  średnicy  d=1  cm  oraz  średnią 

prędkość jej opadania w wodze (µ=1.0·10

-3 

Pa·s) o gęstości ρ

w

=1000 kg/m

3

. 

m= 

 

v

sr

= 

Zadanie 9 
W łożysku ślizgowym o długości 4 in wiruje wał o średnicy 3 in (1 m = 39,37 in) z 
prędkością  555  obr/min.  Lepkości  oleju  wynosi    0,08  Poise  (1  Poise=  g/(cm·s)). 
Mimośród względny wynosi 0,5 a średni luz promieniowy mierzony w µm wynosi 
15,8. Obliczyć: siłę nośną łożyska, moment tarcia lepkiego oraz moc rozpraszaną 
w łożysku. 
F= 

 

M= 

 

P= 

 

3m 

x 

Woda 

z 

P 

1m 

x 

y 

xc 

xc 

d=0.5m 

d 

1m 

3m 

x 

Woda 

z 

P 

1m 

x 

y 

xc 

xc 

d 

d=0.5m 

1m