Algebra liniowa 1
I kolokwium, semestr zimowy 2007/2008
Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.
A6
1
2
3
4
Suma
Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!
Teresa Jurlewicz
ZADANIA
1. Znaleźć wszystkie liczby zespolone
spełniające układ równań
x
, y
.
( 2 + i ) x +
i y
= 4
i x
− ( 1 − i ) y = 1
2. Wyznaczyć moduł i argument główny liczby zespolonej
.
z =
( 1 + i )
42
(
3 − i )
17
3. Wyznaczyć wszystkie pierwiastki wielomianu zespolonego
.
z
4
− 2z
2
− 3z − 2
4. Rozłożyć na rzeczywiste ułamki proste funkcję wymierną
.
x
3
− x
2
+ 3
x
4
+ 3x
2
Odpowiedzi do zestawu
A6
1.
,
;
x =
11 − 2i
5
y =
4i − 7
5
2.
;
z = 16, arg z =
4π
3
3.
,
;
−1, 2,
−1 − i 3
2
−1 + i 3
2
4.
.
1
x
2
−
x − 2
x
2
+ 3
Algebra liniowa 1
I kolokwium, semestr zimowy 2007/2008
Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.
B6
1
2
3
4
Suma
Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!
Teresa Jurlewicz
ZADANIA
1. Przedstawić na płaszczyźnie zespolonej zbiór
.
{ z ∈ C : z
2
≥ 5 + Im ( 4z ) }
2. Podać w postaci trygonometrycznej wszystkie elementy zbioru
3
2i − 2 .
Sporządzić rysunek.
3. Zapisać jako iloczyn dwumianów wielomian zespolony
.
z
6
+ z
5
− 5z
4
− 5z
3
− 6z
2
− 6z
4. Funkcję wymierną
3x
2
− 5
x
4
+ 10x
2
+ 9
rozłożyć na rzeczywiste i zespolone ułamki proste.
Odpowiedzi do zestawu
B6
1. Zewnętrze wraz z brzegiem sumy dwóch kół o środkach
,
z
1
= 2i
i promieniach
;
z
2
= −2i
r
1
= r
2
= 3
2.
dla
,
,
;
2 ( cos ϕ + i sin ϕ )
ϕ ∈ {
π
4
11π
12
19π
12
}
3.
;
z ( z + 1 ) ( z + i ) ( z − i ) ( z + 6 ) ( z − 6 )
4.
,
.
4
x
2
+ 9
−
1
x
2
+ 1
2i
3 ( x + 3i )
−
2i
3 ( x − 3i )
+
i
2 ( x − i )
−
i
2 ( x + i )
Algebra liniowa 1
I kolokwium, semestr zimowy 2007/2008
Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.
C6
1
2
3
4
Suma
Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!
Teresa Jurlewicz
ZADANIA
1. Wyznaczyć liczbę zespoloną z równania
z
.
Re z − i z − 2i
( i + 1 ) Im z − i
= 1 − 3i
2. Wyznaczyć liczbę zespoloną oraz jej pierwiastki stopnia ,
z
3
jeżeli jednym z nich jest liczba
Sporządzić rysunek.
1 + 2i.
3. Rozłożyć na czynniki liniowe wielomian zespolony
.
z
4
− 2z
3
+ 2z
2
− 2z + 1
4. Rozłożyć na rzeczywiste ułamki proste funkcję wymierną
.
x
2
( x
2
− 1 )
2
Odpowiedzi do zestawu
C6
1.
;
z = 3 + 2i
2.
, pozostałe pierwiastki
z = −11 − 2i
,
;
−1 − 2 3
2
+ i
−2 +
3
2
−1 + 2 3
2
− i
2 +
3
2
3.
;
( z − 1 )
2
( z + i ) ( z − i )
4.
.
−1
2 ( x + 2 )
+
1
2 ( x + 2 )
2
+
1
x − 2
+
1
( x − 2 )
2
Algebra liniowa 1
I kolokwium, semestr zimowy 2007/2008
Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.
D6
1
2
3
4
Suma
Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!
Teresa Jurlewicz
ZADANIA
1. Naszkicować na płaszczyźnie zespolonej zbiór
.
{ z ∈ C : Re z
3
≤ 0 }
2. Znaleźć postać algebraiczną wszystkich pierwiastków równania
( z − 3 )
4
= ( 1 + i )
12
, z ∈ C .
3. Znaleźć wielomian o współczynnikach rzeczywistych najniższego
stopnia, którego pierwiastkami są liczby
z
1
= 3, z
2
= 1 − 2i
i który przy dzieleniu przez dwumian
daje resztę
.
z + 3i
5 − i
4. Funkcję wymierną
x
3
+ 4x
2
+ 1
2x
4
+ x
2
rozłożyć na rzeczywiste ułamki proste.
Odpowiedzi do zestawu
D6
1. Suma trzech obszarów kątowych:
,
,
π
6
≤ arg z ≤
π
2
5π
6
≤ arg z ≤
7π
6
oraz punktu
;
3π
2
≤ arg z ≤
11π
6
z = 0
2.
,
,
,
;
5 + 2i 1 + 2i 1 − 2i 5 − 2i
3.
;
1
6
z
3
−
5
6
z
2
+
11
6
z −
5
2
4.
.
1
x
2
+
x + 2
2x
2
+ 1
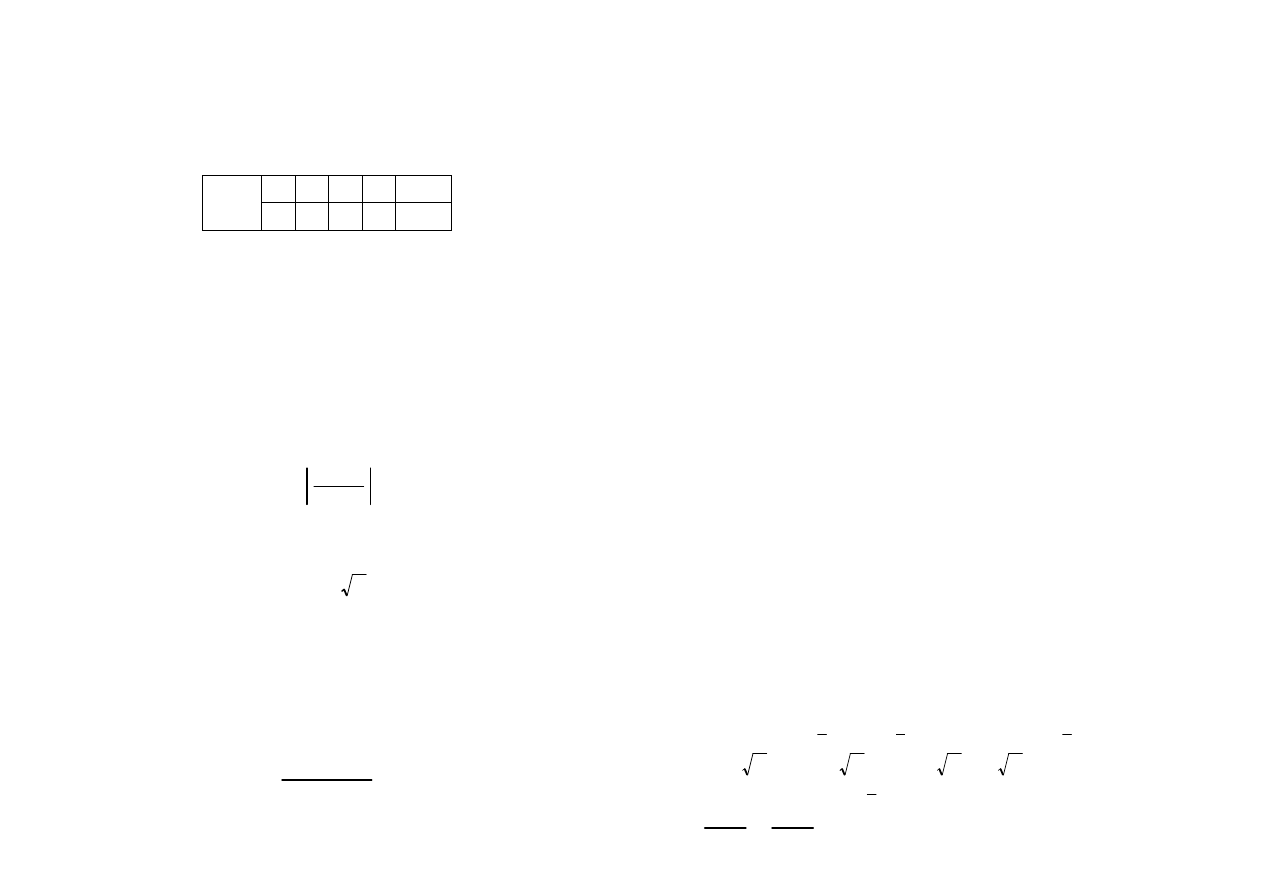
Algebra liniowa 1
I kolokwium, semestr zimowy 2007/2008
Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.
E6
1
2
3
4
Suma
Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!
Teresa Jurlewicz
ZADANIA
1. Na płaszczyźnie zespolonej przedstawić zbiór
.
{ z ∈ C :
3iz − 4
3z − 2
≥ 1 }
2. Podać w postaci algebraicznej wszystkie pierwiastki stopnia
4
z liczby zespolonej
.
w = ( 1 − i 3 )
8
3. Znaleźć wszystkie pierwiastki wielomianu
3x
4
− 2x
3
− 4x
2
+ 2x + 1
i podać ich krotności.
4. Funkcję wymierną
x
2
+ x + 4
x
4
+ 5x
2
+ 6
rozłożyć na rzeczywiste ułamki proste.
Odpowiedzi do zestawu
E6
1. Górna półpłaszczyzna z brzegiem ograniczona symetralną odcinka
o końcach
,
, bez punktu
;
z
1
=
2
3
z
2
= −
4
3
i
z
3
=
2
3
2.
,
,
,
;
2 + 2 3 i 2i − 2 3
−2 − 2 3 i 2 3 − 2i
3. Pierwiastki
, krotności odpowiednio
;
1, −1, −
1
3
2, 1, 1
4.
.
x + 2
x
2
+ 2
−
x + 1
x
2
+ 3
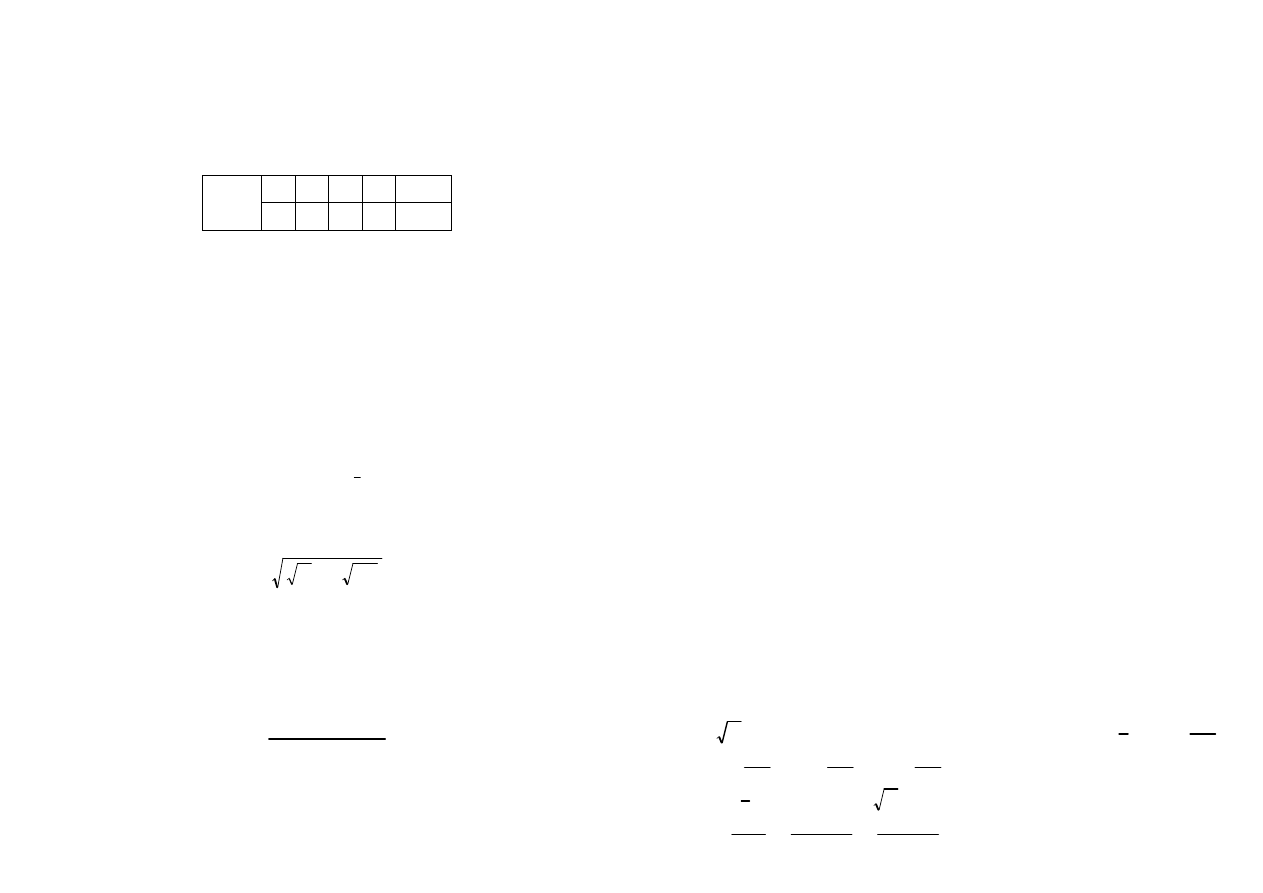
Algebra liniowa 1
I kolokwium, semestr zimowy 2007/2008
Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.
F6
1
2
3
4
Suma
Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!
Teresa Jurlewicz
ZADANIA
1. W zbiorze liczb zespolonych rozwiązać równanie
.
2 z − 1 = z
2
2. Wypisać w postaci trygonometrycznej wszystkie elementy zbioru
.
5
8 − i 24
3. Wyznaczyć wszystkie rzeczywiste pierwiastki wielomianu
.
2x
5
− 3x
4
+ x
3
− 4x
2
+ 6x − 2
4. Funkcję wymierną
x
4
+ 3x
3
− x − 4
( x + 1 )
3
zapisać w postaci sumy wielomianu i ułamków prostych.
Odpowiedzi do zestawu
F6
1.
;
z
1
= 1, z
2
= −1 + 2i, z
3
= −1 − 2i
2.
dla
,
,
{
2 (cos ϕ
k
+ i sin ϕ
k
) : k = 0, 1, 2, 3, 4 }
ϕ
0
=
π
3
ϕ
1
=
11π
15
,
,
;
ϕ
2
=
17π
15
ϕ
3
=
23π
15
ϕ
4
=
29π
15
3.
,
;
x
1
=
1
2
x
2
= 1, x
3
=
3
2
4.
.
x −
3
x + 1
+
4
( x + 1 )
2
−
5
( x + 1 )
3
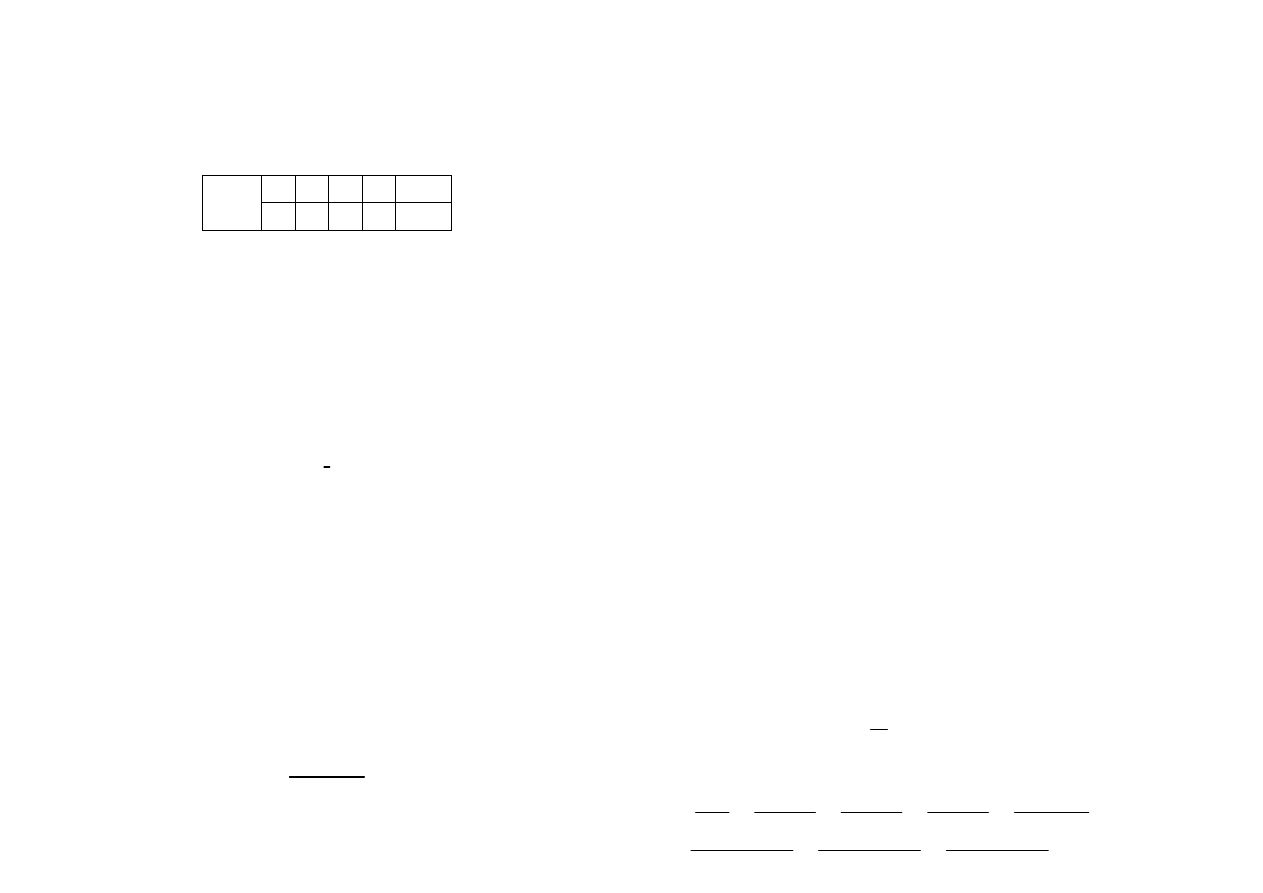
Algebra liniowa 1
I kolokwium, semestr zimowy 2007/2008
Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.
G6
1
2
3
4
Suma
Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!
Teresa Jurlewicz
ZADANIA
1. Stosując postać wykładniczą liczb zespolonych naszkicować zbiór
{ z ∈ C : z
5
= 9iz
3
}.
2. Punkty
z
1
= 1 − 3i, z
3
= −1 + 5i
są przeciwległymi wierzchołkami kwadratu. Znaleźć pozostałe
wierzchołki tego kwadratu. Sporządzić rysunek.
3. Znaleźć pierwiastki trójmianu kwadratowego
.
z
2
+ 3z + 3 + i
4. Napisać ogólną postać rozkładu funkcji wymiernej
x
4
− 5
( x
3
+ 8 )
4
na rzeczywiste ułamki proste.
Odpowiedzi do zestawu
G6
1. Punkt oraz osiem punktów okręgu o środku i promieniu
0
0
o argumentach
dla
;
r = 3
kπ
16
k = 3, 7, 11, 15, 19, 23, 27, 31
2.
,
;
z
2
= −4 z
4
= 4 + 2i
3.
,
;
z
1
= −1 − i z
2
= 2 + i
4.
A
x + 2
+
B
( x + 2 )
2
+
C
( x + 2 )
3
+
D
( x + 2 )
4
+
Ex + F
x
2
− 2x + 4
+
.
Gx + H
( x
2
− 2x + 4 )
2
+
Ix + J
( x
2
− 2x + 4 )
3
+
Kx + L
( x
2
− 2x + 4 )
4
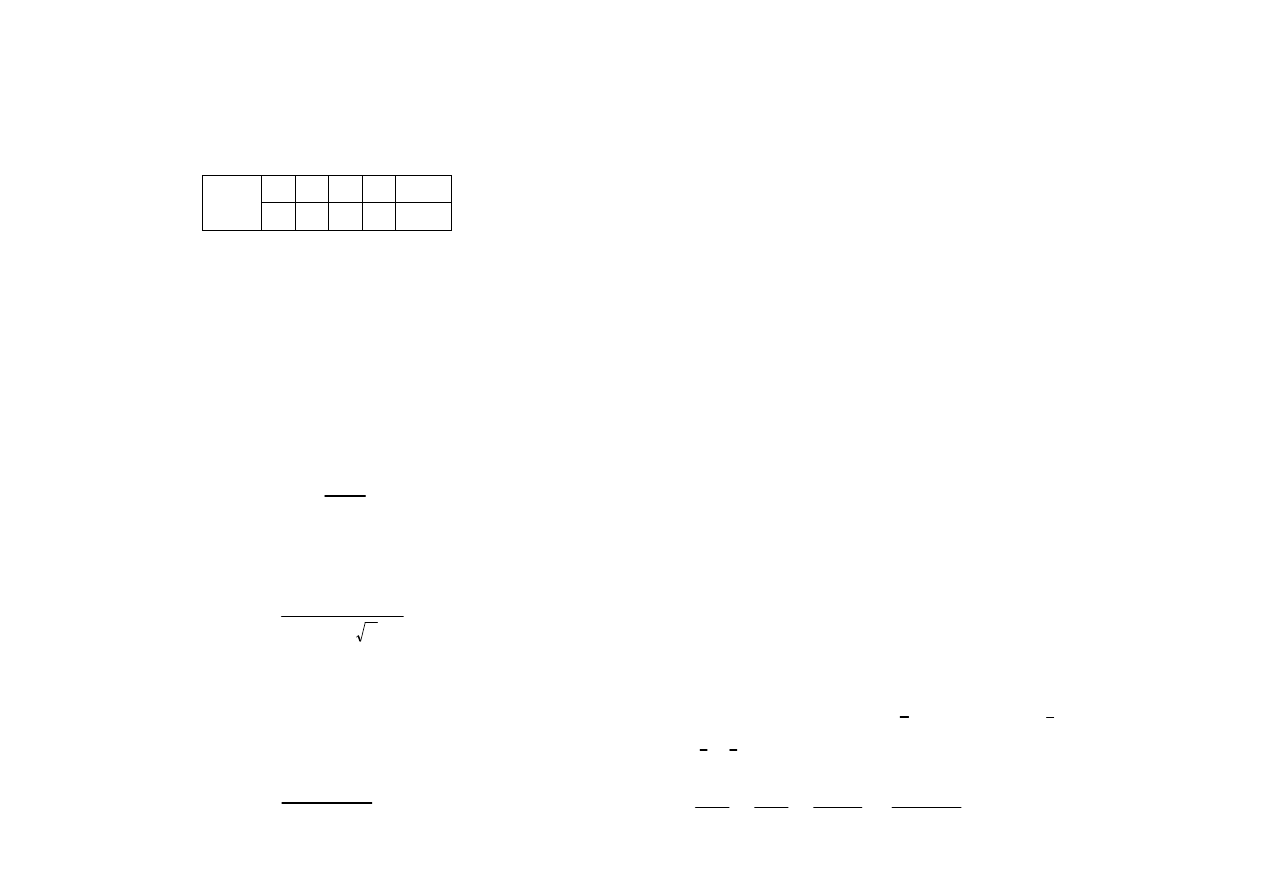
Algebra liniowa 1
I kolokwium, semestr zimowy 2007/2008
Na pierwszej stronie pracy proszę napisać nazwę kursu, z którego odbywa się kolokwium,
swoje imię i nazwisko, numer indeksu, wydział, kierunek, rok studiów, imię i nazwisko
wykładowcy (osoby prowadzącej ćwiczenia), datę oraz sporządzić poniższą tabelkę. Po-
nadto proszę ponumerować i podpisać wszystkie pozostałe kartki pracy.
H6
1
2
3
4
Suma
Treści zadań proszę nie przepisywać. Rozwiązanie zadania o numerze n należy napi-
sać na n-tej kartce pracy. Na rozwiązanie zadań przeznaczono 60 minut, za rozwiązanie
każdego zadania można otrzymać od 0 do 5 punktów. W rozwiązaniach należy dokładnie
opisywać przebieg rozumowania, tzn. formułować wykorzystywane definicje i twierdzenia,
przytaczać stosowane wzory, uzasadniać wyciągane wnioski. Ponadto proszę sporządzać
staranne rysunki z pełnym opisem. Powodzenia!
Teresa Jurlewicz
ZADANIA
1. Naszkicować zbiór wszystkich liczb zespolonych , dla których
z
liczba
w =
z − 3i
z + 4
jest czysto urojona.
2. Przedstawić w postaci algebraicznej liczbę
.
z =
( 1 − i )
5
i
11
( 1 + i 3 )
3
3. Znaleźć wszystkie pierwiastki wielomianu zespolonego
z
3
− 2z + 4 .
4. Napisać ogólną postać rozkładu funkcji wymiernej
x
2
+ 3x − 4
x
6
+ 3x
4
− 4
na rzeczywiste ułamki proste.
Odpowiedzi do zestawu
H6
1. Okrąg o środku
, promieniu
bez punktu
;
z
0
= −2 +
3
2
i
r =
5
2
z
1
= −4
2.
;
1
2
+
1
2
i
3.
;
−2, 1 − i, 1 + i
4.
, przy czym
.
A
x − 1
+
B
x + 1
+
Cx + D
x
2
+ 2
+
Ex + F
( x
2
+ 2 )
2
A = 0