Badania operacyjne

Wykład 2

Wykład 2

Programowanie liniowe

Plan wykładu



Programowanie liniowe



Metoda graficzna rozwiązywania zadań programowania
liniowego

2012-10-19

2

Programowanie liniowe



Jednym z najczęściej wykorzystywanych modeli
decyzyjnych jest model programowania liniowego.



Składa się on z trzech podstawowych części:



funkcji celu odzwierciedlającej kryterium decyzyjne



funkcji celu, odzwierciedlającej kryterium decyzyjne,



warunków ograniczających, opisujących warunki podejmowania
decyzji,



warunku nieujemności zmiennych decyzyjnych (musi to być
zastrzeżone w modelu, gdyż moglibyśmy otrzymać w rozwiązaniu
liczby ujemne, które zwykle nie mają żadnego sensu

y j

,

y

ją

g

praktycznego).

2012-10-19

3

Programowanie liniowe



Zagadnienia programowania liniowego, które posiadają
tylko dwie zmienne decyzyjne, można rozwiązać

metodą

fi

graficzną

.



Gdy problem jest bardziej złożony i występuje większa



Gdy problem jest bardziej złożony i występuje większa
liczna zmiennych decyzyjnych, to takie zagadnienie
rozwiązujemy

algorytmem simpleks

lub korzystając

z profesjonalnych pakietów komputerowych.



Jeżeli w zadaniu decyzyjnym wszystkie relacje są liniowe



Jeżeli w zadaniu decyzyjnym wszystkie relacje są liniowe
oraz wszystkie zmienne są ciągłe, to takie zadanie
nazywamy zadaniem programowania liniowego (PL).

2012-10-19

4

y

y

p g

g (

)

Programowanie liniowe



Zadanie programowania liniowego można sformułować
następująco:



gdzie:

5

2012-10-19

5

Programowanie liniowe



Alternatywnie zadanie programowania liniowego
w zapisie macierzowym można sformułować następująco:



gdzie:

2012-10-19

6

Przykład

2012-10-19

7

Programowanie liniowe



Każdy wektor zmiennych decyzyjnych
nazywamy rozwiązaniem dopuszczalnym zadania PL.



Rozwiązanie dopuszczalne, dla którego funkcja celu
osiąga maksimum (minimum) nazywamy

rozwiązaniem

osiąga maksimum (minimum), nazywamy

rozwiązaniem

optymalnym

.

8

2012-10-19

Zastosowanie modelu
programowania liniowego



Problem alokacji środków produkcji

, zwany również

problemem optymalnego rozdziału środków produkcji, jest
j d

kl

h

d i ń b d ń

j

h

jednym z klasycznych zagadnień badań operacyjnych.



W ogólnym ujęciu polega on na takim rozdziale



W ogólnym ujęciu polega on na takim rozdziale
posiadanych przez przedsiębiorstwo środków produkcji
(surowców, materiałów, robocizny, maszyn) pomiędzy
poszczególne asortymenty produkcji, aby łączny zysk
produkcji wszystkich wyrobów by możliwie jak największy.

9

2012-10-19

Zastosowanie modelu
programowania liniowego



Do rozwiązania problemu stosuje się model
programowania liniowego, uwzględniający posiadane
il ś i

ól

h ś dkó

d k ji

ilości poszczególnych środków produkcji oraz
zapotrzebowanie na te środki produkcji przy produkcji
poszczególnych wyrobów

poszczególnych wyrobów.



Rozwiązaniem problemu jest optymalny plan
asortymentowy produkcji, określający ile którego wyrobu
należy produkować dla osiągnięcia maksymalnego zysku.

10

2012-10-19

Przykład (1 / 3)



Przedsiębiorstwo produkuje cztery wyroby W

1

, W

2

, W

3

oraz W

4

. Dwa spośród wielu środków wykorzystywanych

i

d k ji

li it

Li it t

w procesie produkcji są limitowane. Limity te wynoszą
90000 jednostek na środek pierwszy oraz 120000
jednostek na środek drugi Nakłady limitowanych środków

jednostek na środek drugi. Nakłady limitowanych środków
na jednostkę produkcji podano w tabeli:

11

2012-10-19

Przykład (2 / 3)



Zysk osiągany na jednostce produkcji kształtuje się
odpowiednio: 4, 6, 3 oraz 12 zł.



Polecenie: Zbuduj model matematyczny (określ zmienne
decyzyjne, funkcję celu i ograniczenia).

12

2012-10-19

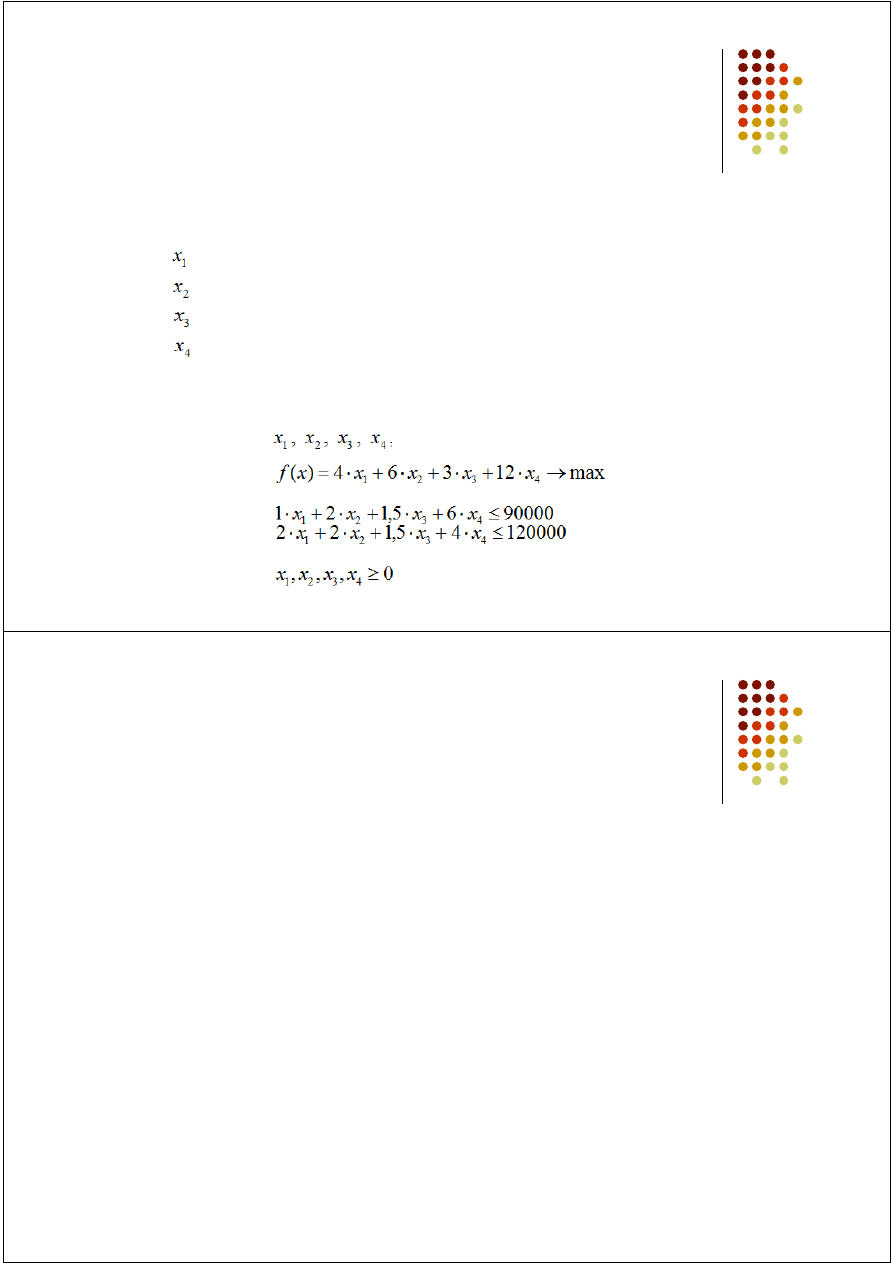
Przykład (3 / 3)



Tworząc model przyjmujemy następującą listę zmiennych
decyzyjnych:



- liczba produkowanych wyrobów W1 (szt.)



- liczba produkowanych wyrobów W2 (szt.)



liczba produkowanych wyrobów W3 (szt )



- liczba produkowanych wyrobów W3 (szt.)



- liczba produkowanych wyrobów W4 (szt.)



Ustalenie optymalnego rozmiaru produkcji poszczególnych



Ustalenie optymalnego rozmiaru produkcji poszczególnych
wyrobów sprowadza się do znalezienia takich wartości
zmiennych aby:

13

2012-10-19

Budowa modelu matematycznego



Aby zbudować model matematyczny należy podać:



jakie wielkości mają być wyznaczone (podanie zmiennych
d

j

h)

decyzyjnych),



jakie wielkości są dane (określenie parametrów),



jakie warunki ograniczające musi spełnić decyzja dopuszczalna



jakie warunki ograniczające musi spełnić decyzja dopuszczalna
(zapisanie warunków ograniczających),



cel jaki chcemy osiągnąć (określenie funkcji celu).



Decyzje zgodne z warunkami ograniczającymi to decyzje
dopuszczalne

dopuszczalne.



Decyzja najlepsze z punktu widzenia przyjętych celów to

14

decyzja optymalna.

2012-10-19

Budowa modelu matematycznego



Zadanie PL może mieć rozwiązanie dopuszczalne lub być
zadaniem sprzecznym, nie mającym rozwiązania
d

l

dopuszczalnego.



Jeżeli zadanie PL na rozwiązanie dopuszczalne to



Jeżeli zadanie PL na rozwiązanie dopuszczalne, to
zachodzi jedna z trzech możliwości:



istnieje jedno rozwiązanie optymalne,



istnieje wiele rozwiązań optymalnych,



brak rozwiązania optymalnego.



W przypadku dwóch zmiennych bardzo łatwo jest znaleźć
rozwiązanie optymalne lub pokazać, że go nie ma.

15

ą

p y

p

,

g

Stosujemy wówczas metodę graficzną.

2012-10-19

Metoda graficzna



Problem znajdowania rozwiązania zadania PL metodą
graficzną sprowadza się do:



wyznaczenia półpłaszczyzn odpowiadających poszczególnym
nierównościom,



znalezienia części wspólnej dla wszystkich półpłaszczyzn ZRD



znalezienia części wspólnej dla wszystkich półpłaszczyzn ZRD
(zbiór rozwiązań dopuszczalnych),



wyszukania w ZRD rozwiązania najlepszego dla przyjętej funkcji

l (

i

i

t

l

)

celu (rozwiązania optymalnego).



Jeżeli ZRD jest zbiorem pustym lub zbiorem

j

p

y

nieograniczonym w kierunku wzrostu wartości funkcji celu
dla zadania na maksimum bądź spadku dla zadania na

i i

t

d i

i

i

i

t

l

16

minimum, to zadanie nie ma rozwiązania optymalnego.

2012-10-19

Literatura



Ignasiak E. (red.), Badania operacyjne. Polskie
Wydawnictwo Ekonomiczne, Warszawa 1996.



Mitchell G.H. (red.), Badania operacyjne. Metody
i przykłady. Wydawnictwo Naukowo-Techniczne,
Warszawa 1977

Warszawa 1977.



Łucki Z. (red.), Matematyczne techniki zarządzania.
Przykłady i zadania Wydawnictwa AGH Kraków 1998

Przykłady i zadania. Wydawnictwa AGH, Kraków 1998.



Sawik T., Badania operacyjne dla inżynierów
zarządzania Wydawnictwa AGH Kraków 1998

zarządzania. Wydawnictwa AGH, Kraków 1998.



Wagner H.M., Badania operacyjne: zastosowania
w zarządzaniu. Państwowe Wydawnictwo Ekonomiczne,

17

ą

y

,

Warszawa 1980.

17

2012-10-19