Badania operacyjne

Wykład II

Analiza wrażliwości.

Dualizm w programowaniu

liniowym.

Analiza wrażliwości zajmuje się badaniem
wrażliwości optymalnego rozwiązania
zagadnienia PL na zmianę parametrów. Na
podstawie analizy wrażliwości możemy
odpowiedzieć na następujące pytania:

• Jaką zmianę rozwiązania optymalnego wywoła

zmiana współczynników funkcji celu?

• W jakim zakresie możemy zwiększyć

(zmniejszyć) współczynniki funkcji celu, aby

rozwiązanie optymalne nie uległo zmianie?

• Jaką zmianę rozwiązania optymalnego wywoła

zmiana wielkości wyrazów wolnych, stojących

po prawej stronie ograniczeń?

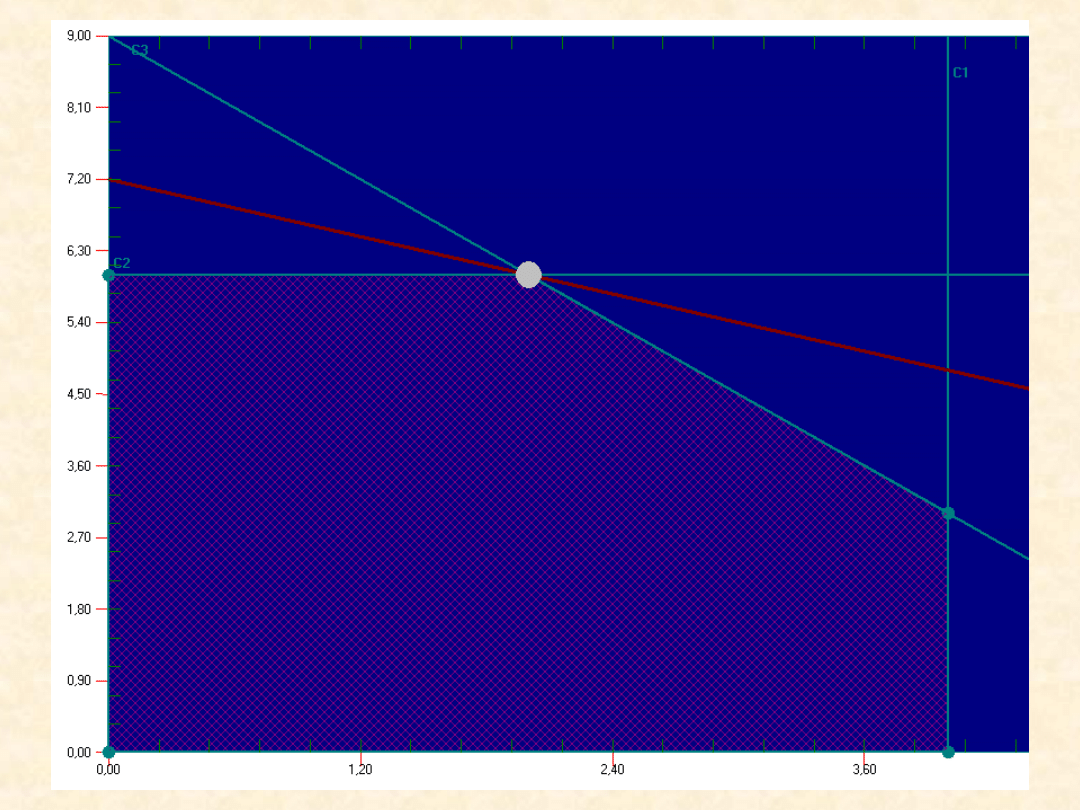
Przykład – firma „Oko świata”

Zakład

Czasochłonność

Dziennie

limity

czasowe

Wyrób 1

Wyrób 2

1
2
3

1
0
3

0
2
2

4

12
18

Zysk

jednostkowy

(w zł)

30

50

max

Wielkość

produkcji

x

1

x

2

 

Odp.: Optymalnym rozwiązaniem była produkcja dwóch
wyrobów 1

i sześciu wyrobów 2. Przy takim planie maksymalny
dzienny zysk wynosi 360 zł

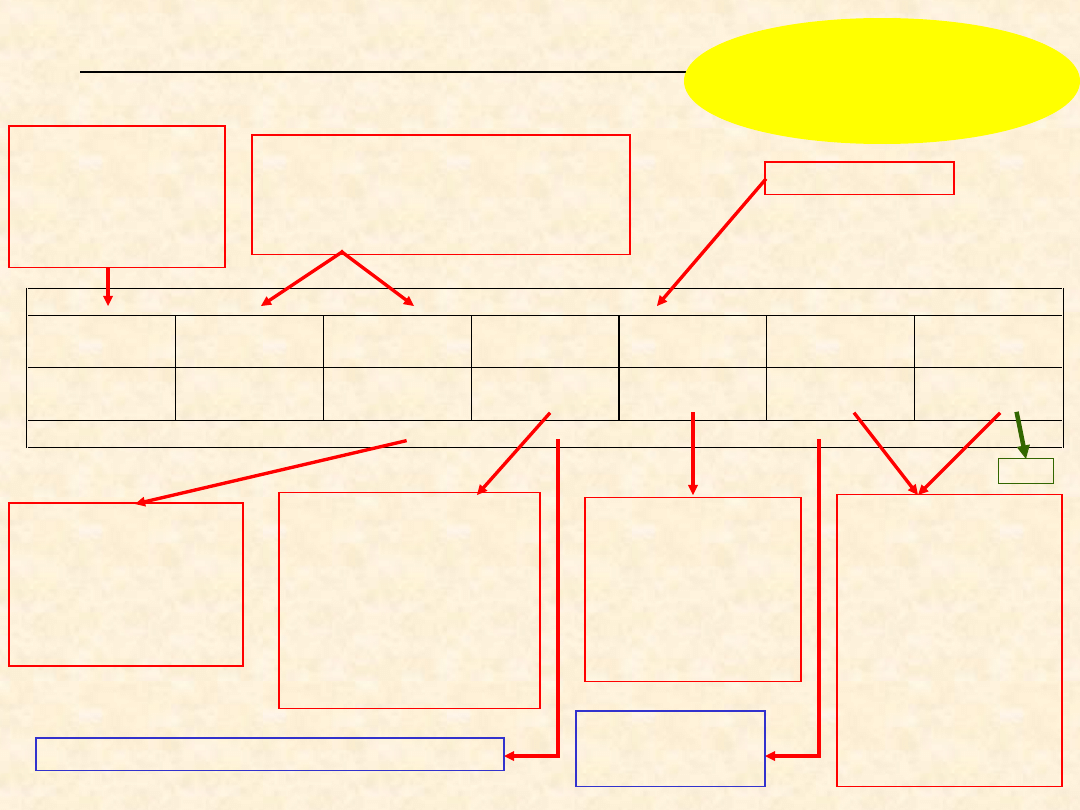
WYDRUK Z PROGRAMU QSB+

WYDRUK Z PROGRAMU QSB+

CZĘŚĆ PIERWSZA

CZĘŚĆ PIERWSZA

Summarized Report for......................

Number

Variable

Solution

Opportunity

Cost

Objective

Coefficient

Minimum

Obj. Coeff.

Maximum

Obj. Coeff.

1

2

X1

X2

+2,0

+6,0

0

0

+30,0

+50,0

0

+20,0

+75

+Infinity

Max (Min) Obj = .... Iteration = .... Elapsed CPU Second = ......

Nazwa projektu

Przy interpretacji wydruku

obowiązuje podwójny język:

• matematyczny

• ekonomiczny (menedżerski)

Numer zmiennej

decyzyjnej

 numer wyrobu
 numer składnika

mieszanki

Rozwiązanie (optymalne wartości

zmiennych decyzyjnych)

 ilości produkowanych wyrobów
 ilości użytych składników

Koszty alternatywne

(względne)

O ile trzeba zmienić
współczynnik funkcji
celu, aby wyrób (skład-
nik) wszedł do rozwią-
zania optymalnego (w
przykładzie = 0, gdyż
ilości są różne od zera)

Współczynniki

funkcji celu

(macierz C)

 zyski jednost-

kowe z wyrobów

 ceny składników

mieszanki

Optymalna wartość

funkcji celu

 maksymalny zysk

producenta

 minimalny koszt

mieszanki

Optymalne zakresy

współczynników

funkcji celu

 przedziały zysku

jednostkowego nie
powodujące zmiany
planu produkcji

 przedziały ceny

składników nie po-
wodujące zmiany
receptury miesza-
nki

Liczba iteracji wykonanych przez komputer

Czas szukania

optymalnego

rozwiązania





Podsumowując:

Jeśli zysk z jednostki wyrobu 2 pozostanie na poziomie 50

złotych (c

2

=50), to optymalny zakres dla współczynnika

c

1

(jednostkowego zysku z wyrobu 1) będzie

następujący:

Jeśli zysk z jednostki wyrobu 1 pozostanie na poziomie 30

złotych (c

1

=30), to optymalny zakres dla współczynnika

c

2

(jednostkowego zysku z wyrobu 2) będzie

następujący:

20

2



c

75

0

1



c

WPŁYW ZMIANY PRAWEJ STRONY
OGRANICZEŃ

Zmiana ograniczenia pociąga za sobą zmianę obszaru rozwiązań

dopuszczalnych oraz zmianę optymalnego rozwiązania
rozważanego problemu.

Wielkość zmiany optymalnej wartości funkcji celu

wywołana powiększeniem prawej strony ograniczenia
o jednostkę jest zwana cena dualną danego środka
produkcji.

Z każdym ograniczeniem związany jest pewien dopuszczalny zakres

wartości prawych stron ograniczeń.

Zmiana wartości prawej

strony ograniczenia o dowolną liczbę w granicach
tego zakresu wywołuje zmianę optymalnej wartości
funkcji celu o iloczyn ceny dualnej i tej liczby.

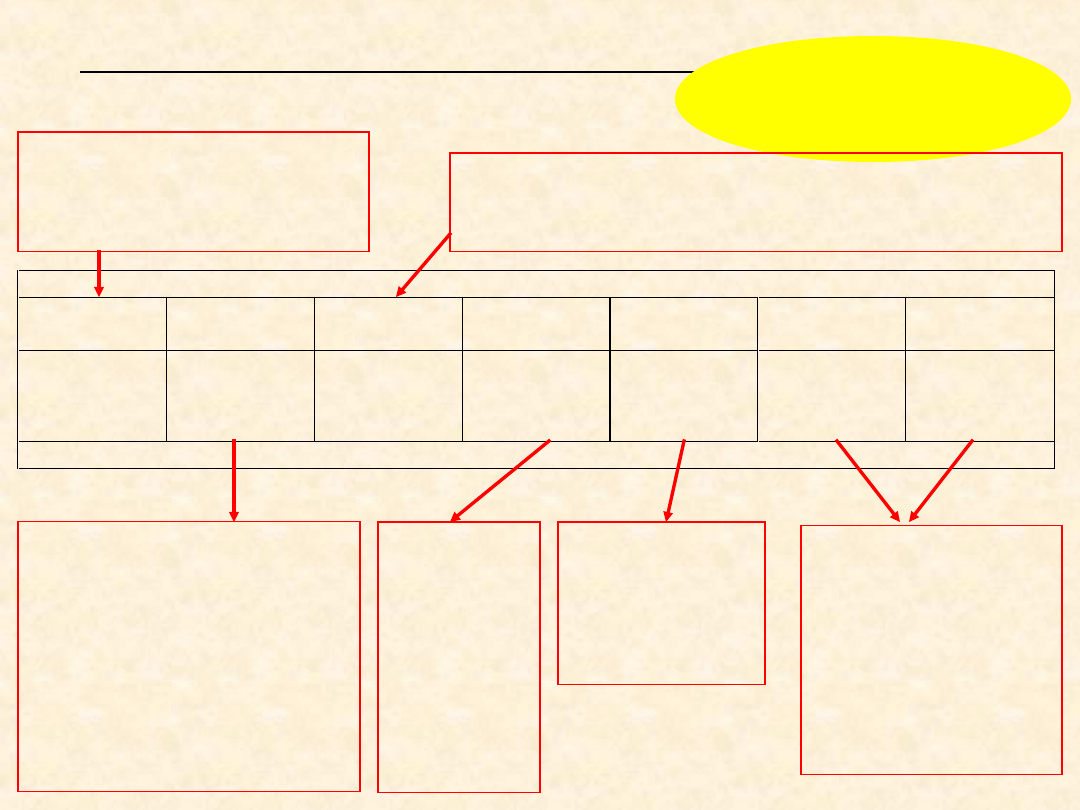
WYDRUK Z PROGRAMU QSB+

WYDRUK Z PROGRAMU QSB+

CZĘŚĆ DRUGA

CZĘŚĆ DRUGA

Przy interpretacji wydruku

obowiązuje podwójny język:

• matematyczny

• ekonomiczny (menedżerski)

S

u

m

m

a

r

i

z

e

d

R

e

p

o

r

t

f

o

r

.

.

.

.

.

.

.

C

o

n

s

t

r

a

i

n

t

S

t

a

t

u

s

R

H

S

S

h

a

d

o

w

P

r

i

c

e

S

l

a

c

k

o

r

S

u

r

p

l

u

s

M

i

n

R

H

S M

a

x

R

H

S

1

2

3

L

o

o

s

e

T

i

g

h

t

T

i

g

h

t

)

(





+

4

,

0

)

(





+

1

2

,

0

)

(





+

1

8

,

0

0

1

5

1

0

+

2

,

0

0

0

+

2

,

0

+

6

,

0

+

1

2

,

0

+

I

n

fi

n

i

t

y

+

1

8

+

2

4

M

a

x

(

M

i

n

)

O

b

j

=

.

.

.

.

.

.

I

t

e

r

a

t

i

o

n

=

.

.

.

.

.

.

E

l

a

p

s

e

d

C

P

U

S

e

c

o

n

d

=

.

.

.

.

.

.

Numer ograniczenia (warunku)

 numer środka produkcji
 numer komponentu

mieszanki

Sposób spełniania nierówności

z warunków ograniczających

(loose = nierówność silna,

tight = nierówność słaba)

 loose = środek produkcji jest

w nadmiarze; tight = środek
produkcji wyczerpany

 loose = komponent jest w

nadmiarze; tight = komponen-
tu jest dokładnie według wy-
magań normy

Ograniczenia (macierz B) z nierównością

 ilości posiadanych środków produkcji
 najmniejsze dopuszczalne ilości komponentów (normy)

Ceny dualne

 dodatkowy

zysk z dodat-
kowej jedno-
stki środka

 zmiana ko-

sztu miesza-
nki po zmnie-
jszeniu nor-
my o jednos-
tkę

Luz czyli nadmiar

 ilość niewycze-

rpanego środka
produkcji

 ilość kompone-

ntu ponad normę

Wartości zakresów

ograniczeń (macierzy

B), w których wartość

optymalna funkcji celu

zmienia się zgodnie z

cenami dualnymi

 zakresy dla ilości

środka produkcji

 zakresy dla ilości

komponentu mieszanki

Dualność zadań programowania liniowego

Z każdym zadaniem programowania liniowego sprzężone jest pewne inne

zadanie PL zwane zadaniem dualnym (dwoistym).

Tworzenie zadania dualnego

n

j

x

b

x

a

x

a

x

a

b

x

a

x

a

x

a

b

x

a

x

a

x

a

j

m

n

mn

m

m

n

n

n

n

,...

2

,

1

,

0

,

*

...

*

*

...

,

*

...

*

*

,

*

...

*

*

2

2

1

1

2

2

2

22

1

21

1

1

2

12

1

11









































m

i

y

c

y

a

y

a

y

a

c

y

a

y

a

y

a

c

y

a

y

a

y

a

i

n

m

mn

n

n

m

m

m

m

,...

2

,

1

,

0

,

*

...

*

*

...

,

*

...

*

*

,

*

...

*

*

2

2

1

1

2

2

2

22

1

12

1

1

2

21

1

11









































Wzajemnie dwoiste zadania PL mają

postać:

Pierwotne (prymalne)
zadanie PL
max Z = c

1

*x

1

+ c

2

*x

2

+ ... +

c

n

*x

n

Dualne zadanie PL
min f = b

1

*y

1

+ b

2

*y

2

+ ... +

b

m

*y

m

Właściwości zadań wzajemnie

dualnych

1. Jeśli pierwotne zadanie jest zadanie na maksimum, to wtedy

zadanie dwoiste będzie na minimum i odwrotnie, jeśli pierwotne
zadanie jest zadanie na minimum, to wtedy zadanie dwoiste
będzie na maksimum.

2. Współczynniki funkcji celu pierwotnego zadania będą

wolnymi wyrazami dla ograniczeń zadania dwoistego.

3. Wolne wyrazy ograniczeń pierwotnego zadania będą

współczynnikami funkcji celu zadania dwoistego.

4. Macierzy ograniczeń zadań pierwotnego i dwoistego to są

macierze transponowane.

5. Jeśli pierwotne zadanie jest zadanie maksymalizacji, wtedy

układ ograniczeń ma postać nierówności typu „”. Dwoiste

zadanie będzie rozwiązane na minimum, a ograniczenia
przedstawiony w postaci nierówności typu „”.

6. Ilość ograniczeń pierwotnego zadania równa się ilości

zmiennych zadania dwoistego, a ilość ograniczeń zadania
dwoistego równa się ilości zmiennych zadania pierwotnego.

7. Wszystkie zmienne w zadaniach pierwotnym i dwoistym są

nieujemne.

Właściwości dualnych zadań programowania liniowego











m

i

i

i

n

j

j

j

y

b

x

c

1

1

Twierdzenie 1. Dla dowolnych planów dopuszczalnych х= (x

1

;

x

2

; ... ; x

n

) i у = (y

1

; y

2

; ... ; у

m

) pierwotnego i dwoistego ZPL

będzie spełniona nierówność Z(x)



f(y), to znaczy

Treść ekonomiczna nierówności polega na tym, że dla
dowolnego dopuszczalnego planu produkcji х i dla
dowolnego wektora cen у surowców zsumowany zysk od
stworzonej produkcji nie przekracza zsumowanych kosztów
surowców.

Interpretacja

ekonomiczna

wartości

zmiennych dualnych:

Optymalna wartość zmiennej dualnej, tzw. cena
dualna to krańcowa produktywność jednostki
danego środka – informuje nas o tym, ile
wzrośnie (spadnie) wartość funkcji celu zadania
pierwotnego, jeśli wyraz wolny b

i

warunku

pierwotnego wzrośnie (spadnie) o jednostkę, dla
zmian b

i

w pewnych dopuszczalnych granicach.

Wartość

zmiennej

dualnej

jest,

zatem

maksymalną ceną, jaką warto zapłacić, za
dodatkową jednostką zasobu i.

Interpretacja

ekonomiczna

warunków

twierdzenia o równowadze:

Jeżeli zużycie i-tego środka produkcji jest mniejsze od
posiadanego

zasobu,

to

wycena

(krańcowa

produktywność) jednostki i-tego środka jest zerowa

Jeżeli wartość środków zużytych na wytworzenia jednostki
j-tego produktu jest większa od jego ceny, to produkcja
wyrobu jest zerowa

Jeżeli wycena i-tego środka jest dodatnia, to zużycie
środka musi być równe jego zasobowi,

Jeżeli produkcja j-tego wyrobu jest dodatnia, to wartość
środków zużytych na jednostkę j-tego produktu jest równa
jego cenie

Metoda Simplex

Metoda Simplex – algorytm sympleksowy lub metoda
sympleks(ów):

- stosowana w matematyce iteracyjna metoda
rozwiązywania zadań programowania liniowego za
pomocą optymalizacji rozwiązania

- twórcą metody Simplex jest George Bernard Dantzig
( 1947 r. )

- nazwa metody pochodzi od sympleksu

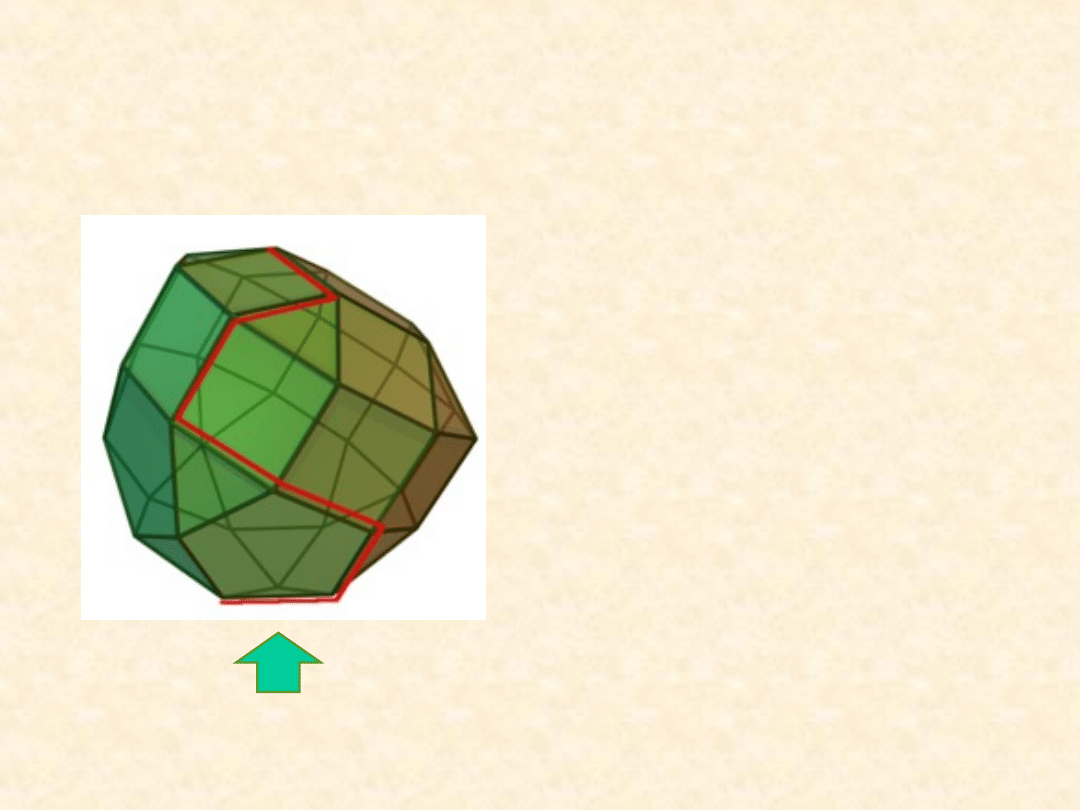
Symplex

• to najprostsza n-wymiarowa

figura wypukła określona przy
pomocy n+1 wierzchołków

• w przestrzeni jednowymiarowej

taką figurą jest prosta

• w przestrzeni dwuwymiarowej

jest to trójkąt

• w przestrzeni trójwymiarowej

jest to czworościan

Wielościan algorytmu sympleksowego w trzech
wymiarach

Metoda Simplex - polega na sekwencyjnym (krokowym) i
ściśle ukierunkowanym (efektywnym) przeglądzie tzw.
rozwiązań bazowych programu liniowego o postaci
kanonicznej (czyli takiej, w której wszystkie warunki
ograniczające mają postać równości) w następujący sposób:

1. Znajdujemy (dowolne) rozwiązanie bazowe programu

2. Sprawdzamy czy jest ono optymalne

3. Jeżeli dane rozwiązanie nie jest optymalne, znajdujemy
następne rozwiązanie

4.Postepowanie kończy się gdy aktualnego rozwiązania
bazowego nie można już poprawić, czyli jest optymalne

Rozważmy problem optymalizacji
przedstawiony w standardowej postaci :

Funkcja celu :

z(x

1

, x

2

,…, x

n

) = c

1

x

1

+ c

2

x

2

+ … + c

n

x

n

max

Ograniczenia :

a

11

x

1

+ a

12

x

2

+ … + a

1n

x

n

≤ b

1

a

21

x

1

+ a

22

x

2

+ … + a

2n

x

n

≤ b

2

. . . . . . . . . .

a

m1

x

1

+ a

m2

x

2

+ … + a

mn

x

n

≤ b

m

x

1

, x

2

,…, x

n

≥ 0

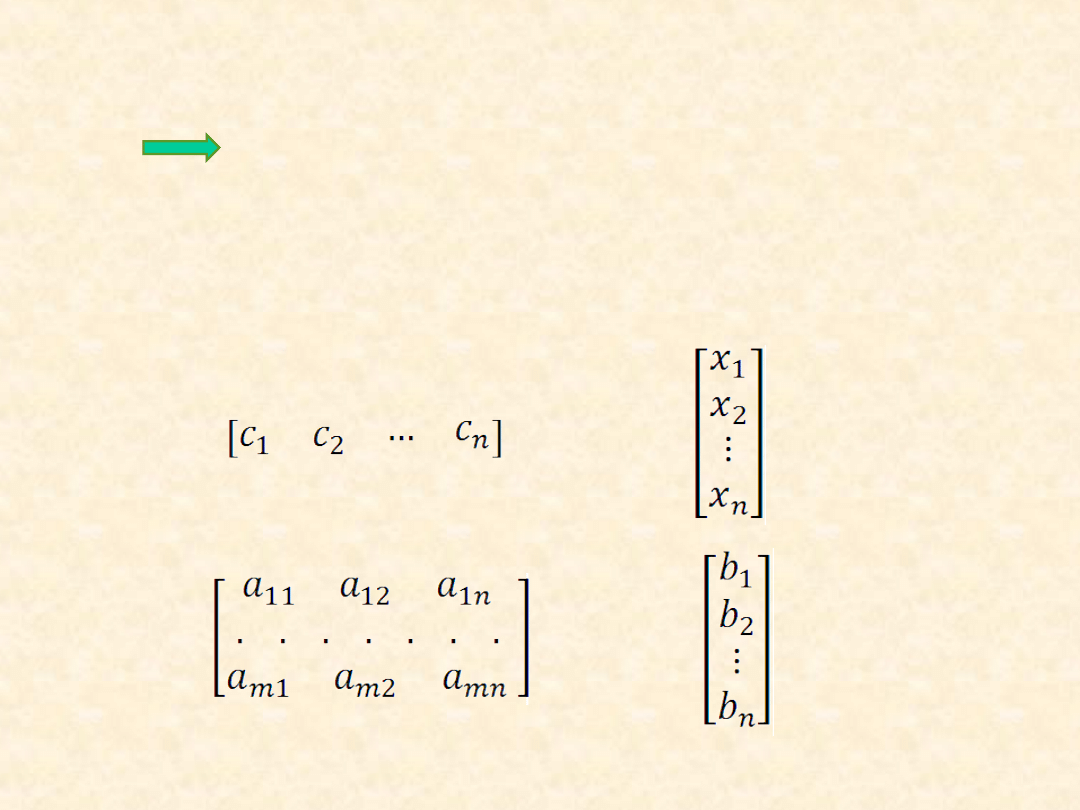
Postać macierzowa :

C X max

A X ≤ B

X ≥ 0

gdzie :

C= X =

A = B =

       

Algorytm Simplex polega na badaniu rozwiązań bazowych
programu o postaci kanonicznej, zatem przed przestąpieniem do
budowy pierwszej tablicy simpleks zamieniamy wszystkie
nierówności na równości przez wprowadzenie dodatkowych
zmiennych.

a

11

x

1

+ a

12

x

2

+ … + a

1n

x

n

+ x

n +1

=b

1

a

21

x

1

+ a

22

x

2

+ … + a

2n

x

n

+ + x

n +2

= b

2

. . . . . . . . . . . . . . .

a

m1

x

1

+ a

m2

x

2

+ … + a

mn

x

n

+ + x

n +m

= b

m

wiemy, że max(z)=min(-z) zatem nasza funkcja celu przyjmuje
postać

-c

1

x

1

- c

2

x

2

+ … - c

n

x

n

min

Przykład – problem doboru składu

mieszanki

Zakład przerabiający ropę uzyskuje 4 półfabrykaty: 400

tys. litrów półfabrykatu I, 250 tys. litrów półfabrykatu
II, 250 tys. litrów półfabrykatu III, 100 tys. litrów
półfabrykatu IV.

W rezultacie połączenia tych czterech składników w

różnych proporcjach powstają trzy asortymenty
benzyny: benzyna A – 2:3:5:2, benzyna B – 3:1:2:1,
benzyna C – 2:2:1:3.

Wartość jednego litra poszczególnych asortymentów

benzyny wynosi: A – 120 j.p., B – 100 j.p., C – 150 j.p.

Dokonać połączenia składników w taki sposób, aby

zapewnić maksymalną wartość produkcji.

Rozwiązanie

Jeśli przez x

1

, x

2

, x

3

oznaczymy wielkości produkcji

poszczególnych asortymentów benzyny, to zapis
modelu matematycznego jest następujący:

przy warunkach:

max,

150

100

120

3

2

1









x

x

x

z

0

,

,

,

100

8

3

7

1

12

2

,

250

8

1

7

2

12

5

,

250

8

2

7

1

12

3

,

400

8

2

7

3

12

2

3

2

1

3

2

1

3

2

1

3

2

1

3

2

1



























x

x

x

x

x

x

x

x

x

x

x

x

x

x

x