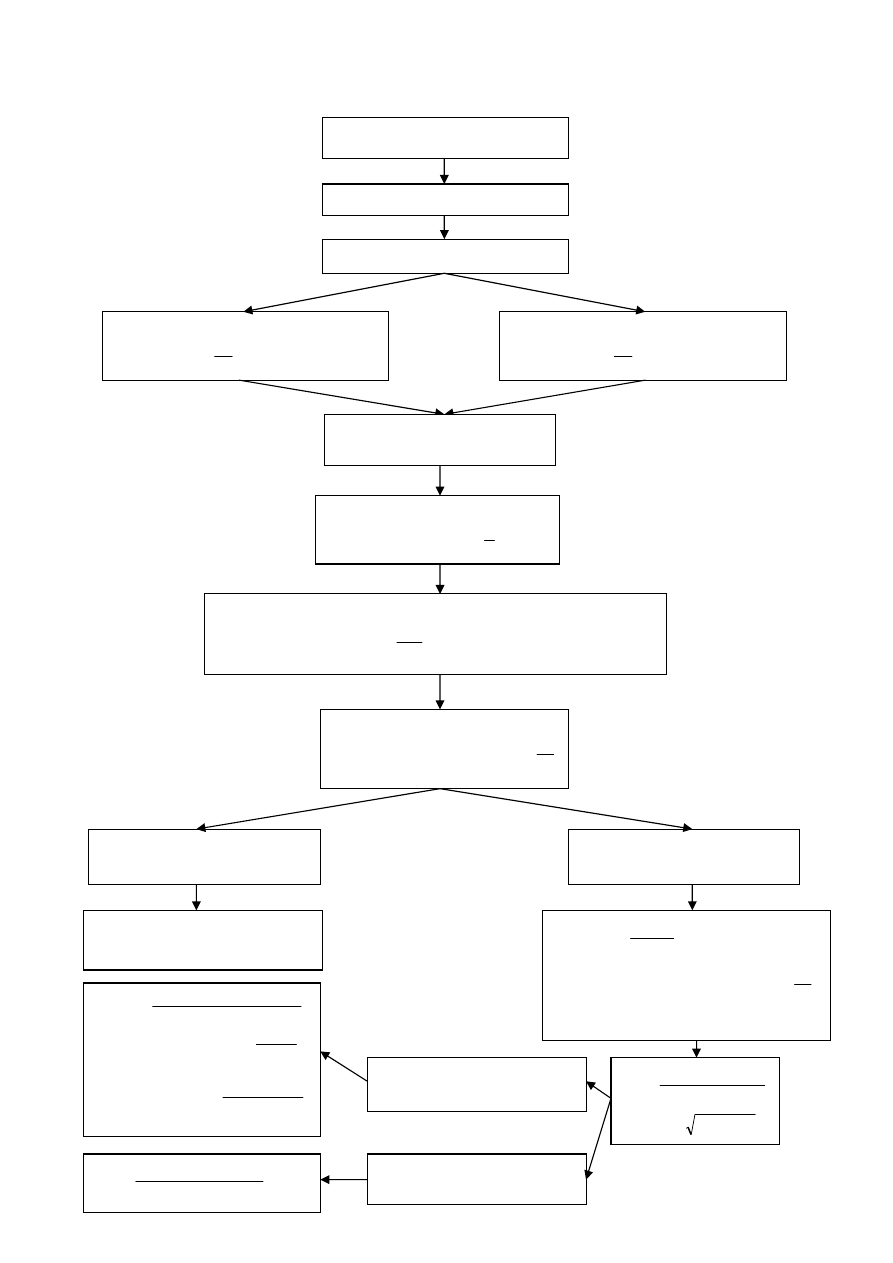
Algorytm dla zginania przekroju teowego
Określenie geometrii przekroju
Dla przekrojów symetrycznych:
b
L
b
b
w
eff
≤
+
=
5
0
(12) rys.7
Wielkość L
0
określamy z rys.8
Dla przekrojów półką z jednej strony:
b
L
b
b
w
eff
≤
+
=
10
0
(13) rys.7
Dane: b
w
h h
f
M
sd
f
cd
f
yd
α ξ
eff,Lim
Wysokość użyteczna przekroju:
2
φ
φ
−
−
−
=
s
c
h
d
Obliczamy moment płytowy:
)
2
(
*
*
*
*
f
f
eff
cd
Rdpl
h
d
h
b
f
M
−
=
α
Przekrój pozornie teowy:
Rdpl
sd
M
M
<
Przekrój rzeczywiście teowy:
Rdpl
sd
M
M
>
Projektowanie jak dla przekroju
prostokątnego z zamianą b=b
eff
Minimalne pole zbrojenia:
=
d
b
d
b
f
f
A
eff
eff
yk
ctm
s
*
*
0013
.
0
*
*
*
26
.
0
max
,min
)
(
*
*
*
*
1
w
eff
f
yd
cd
s
b
b
h
f
f
A
−
=
α
)
2
(
*
)
(
*
*
*
*
f
w
eff
f
cd
Rd
h
d
b
b
h
f
M
−
−
=
α
*
Rd
sd
Rd
M
M
M
−
=
∆
Przekrój podwójnie zbrojony
lim
,
eff
eff
ξ
ξ
>
yd
eff
w
cd
I
s
f
d
b
f
A
*
*
*
*
lim
,
lim
,
1
ξ
α
=
−
=
2
*
*
*
*
*
*
lim
,
lim
,
lim
,
d
d
d
b
f
M
eff
eff
w
cd
I
sd
ξ
ξ
α
I
sd
Rd
M
M
M
lim
,
−
∆
=
∆
(
)
2
1
2
1
*
a
d
f
M
A
A
A
yd
s
s
II
s
−
∆
=
∆
=
=
II
s
I
s
s
s
A
A
A
A
1
lim
,
1
*
1
1
+
+
=
yd
eff
w
cd
s
f
d
b
f
A
*
*
*
*
1
ξ
α
=
Przekrój pojedynczo zbrojony
lim
,
eff
eff
ξ
ξ
≤
2
*
*
*
d
b
f
M
S
w
cd
Rd
c
α
∆
=
c
eff
S
*
2
1
1
−
−
=
ξ
Zakładamy średnice zbrojenia
głównego i strzemion: Φ Φ
s