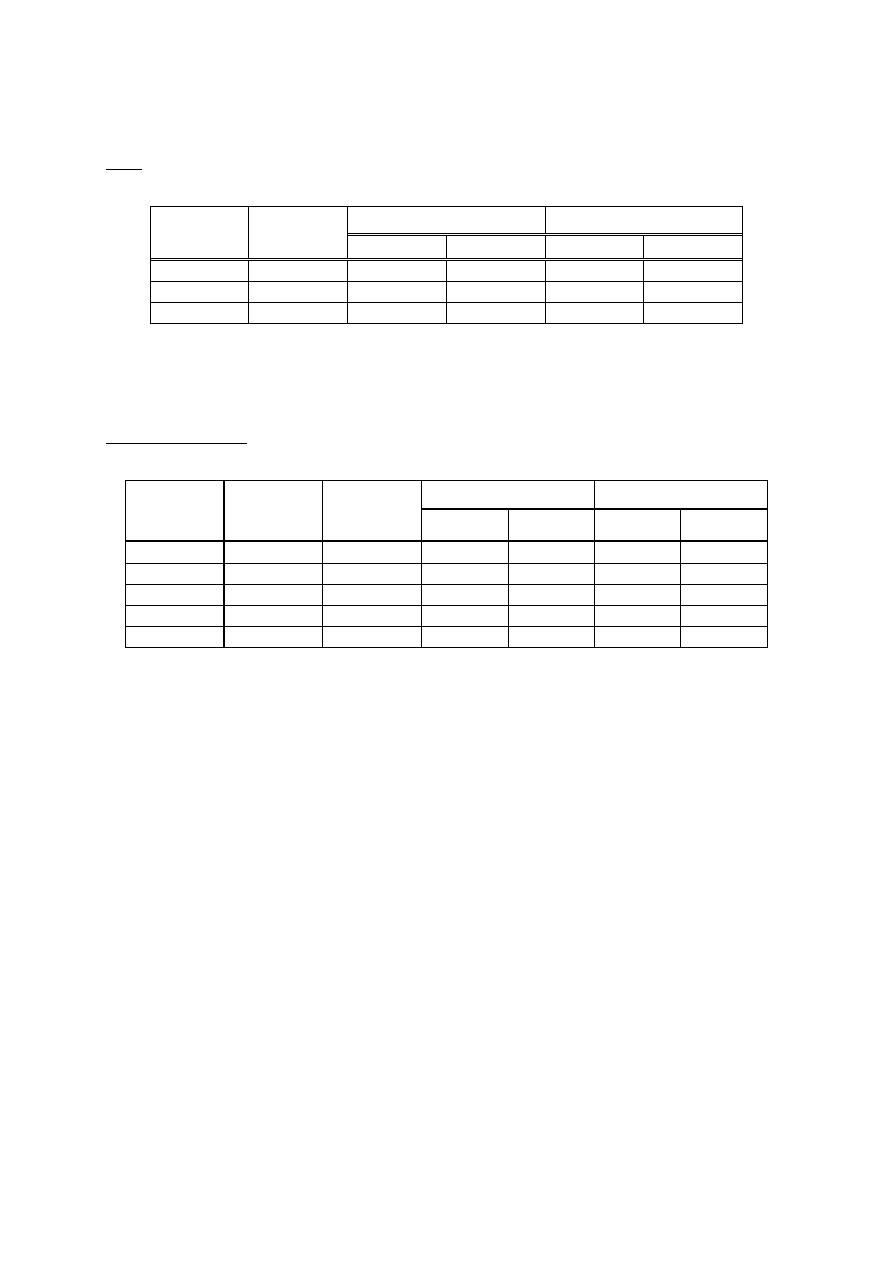
1

1

MATERIA

ŁY KONSTRUKCYJNE

1.1

Materia

ły i sploty sprężające (wg PN-B-03264:2002)

Druty

Tab. 1 Druty do spr

ężania

Wytrzyma

łość f

pk

, MPa

Si

ła zrywająca F

pk

, kN

Oznaczenie

średnica,

mm

Przekrój,

mm

2

odm. I

odm. II

odm. I

odm. II

φ 2,5

4,9

2160

1860

10,6

9,1

φ 5,0

19,6

1670

1470

32,7

28,8

φ 7,0

38,5

1470

-

56,6

-

Modu

ł sprężystości drutów E

p

= 200 GPa.

Druty stosuje si

ę jako samodzielne cięgna w konstrukcjach strunobetonowych. Z gładką po-

wierzchni

ą do średnicy max. 5 mm, z powierzchnią nagniataną – do 7 mm. W systemach kablobeto-

nowych wyparte z u

życia przez sploty 7-mio drutowe (za wyjątkiem kabli systemu BBRV)

Sploty 7-mio drutowe

Tab. 2 Sploty 7-mio drutowe

Wytrzyma

łość f

pk

, MPa

Si

ła zrywająca F

pk

, kN

Oznaczenie

Średnica,

mm

Przekrój,

mm

2

odm. I

odm. II

odm. I

odm. II

6

×2,5+1×2,8

7,8

35,6

1940

1740

69,0

62,0

6

×5+1×5,5

15,5

141,5

1470

1370

208,0

194,0

Y 1860 S7

12,5

93,0

1860

-

173,0

-

Y 1860 S7

13,0

100,0

1860

-

186,0

-

Y 1770 S7

16,0

150,0

1770

-

265,0

-

Modu

ł sprężystości splotów E

p

= 190 GPa, o ile dla partii wyrobu nie podaje si

ę innych wartości

Sploty obecnie stanowi

ą podstawowy wyrób tworzący cięgna i kable sprężające. w konstruk-

cjach strunobetonowych maja zastosowanie sploty o

średnicy do 13 mm (wyjątkowo, w dużych bel-

kach do 16 mm). W konstrukcjach kablobetonowych i bez przyczepno

ści stosuje się powszechnie

sploty o

średnicach od 12,5 do 16 mm, tworząc z nich kable jedno- lub wielosplotowe.

1.2

Beton
Do konstrukcji kablobetonowych nale

ży stosować beton klasy nie niższej niż B30, zaś strunobe-

tonowych nie ni

ższej niż B37. Wytrzymałości i inne właściwości betonów poszczególnych klas przyj-

mowa

ć zgodnie z norma [N5]

1.3

Stal zbrojeniowa
Stal zbrojeniowa w konstrukcjach spr

ężonych pełni role przeciwskurczową, pomocniczą i kon-

strukcyjn

ą Wytrzymałości i inne właściwości stali poszczególnych klas przyjmować zgodnie z norma

[N5]. W konstrukcjach wst

ępnie sprężonych nie należy stosować stali klasy A0, zaś w konstrukcjach

poddanych obci

ążeniom wielokrotnie zmiennym, także stali klasy AII z gatunku innego niż 18G2 i AIII

oraz AIIIN.

2

2

OBCI

ĄśENIA I INNE ODDZIAŁYWANIA

2.1

Obci

ążenia statyczne i dynamiczne

Warto

ści obciążeń wynikających z wytycznych projektu należy przyjmować na podstawie odpo-

wiednich norm obci

ążeniowych, lub założeń technologicznych (np. dane technologiczne suwnic)

2.2

Warunki

środowiska

Warunki

środowiska w jakim będzie znajdowała się projektowana konstrukcja, sklasyfikowane w

Tablicy 6 w [N5], maj

ą wpływ na graniczne szerokości rozwarcia rys w

lim

(Tablica 7 w [N5]) oraz na

grubo

ść otuliny.

3

PROCEDURA PROJEKTOWANIA ELEMENTU SPR

ĘśONEGO

Norma [N5] formu

łując pakiet wymagań koniecznych do spełnienia przez projektowaną konstruk-

cje okre

śla pewien obszar rozwiązań dopuszczalnych. Wybór rozwiązania optymalnego nie jest jed-

noznacznie wynikaj

ący z warunków normy. Poniżej przedstawiona ogólna procedura ułatwia popraw-

ne zaprojektowanie konstrukcji spr

ężonej w sposób logiczny i znalezienie rozwiązania optymalnego.

Ilekro

ć w niniejszym rozdziale jest mowa o Normie, rozumie się przez to normę [N5], a przywołując

wzory, tablice, rysunki i podrozdzia

ły w niej zawarte, ich numer poprzedza się literą „N”, np: (N12).

1. Ustalenie obci

ążeń i schematu statycznego. Wyznaczenie obwiedni sił wewnętrznych

• Sytuacja początkowa

Uwzgl

ędniane są obciążenia zewnętrzne, działające w chwili sprężenia (np. ciężar własny

elementu). Spr

ężenie także traktowane jest jako obciążenie zewnętrzne.

• Sytuacja montażowa

Rozpatrywana w przypadku konstrukcji zespolonych o zwi

ększanej nośności (poprzez ze-

spolenie) lub zmienianym schemacie statycznym. Uwzgl

ędnia się ciężar własny oraz zamon-

towanych elementów konstrukcyjnych wywo

łujących obciążenie oraz tzw. obciążenie zmien-

ne monta

żowe.

• Sytuacja trwała

Uwzgl

ędnia się wszystkie obciążenia stałe, technologiczne i klimatyczne.

2. Dobór materia

łów konstrukcyjnych

• Beton (na podstawie zaleceń normowych)

• Cięgna sprężające (według zaleceń i opisu p.-tu 1.1), określając dla pojedynczego cięgna

jego pole przekroju – A

1p

, no

śność charakterystyczną – F

1pk

lub, w przypadku drutów i pr

ę-

tów, wytrzyma

łość charakterystyczną - f

pk

.

3. Dobór zasadniczych wymiarów przekroju i ilo

ści zbrojenia sprężającego

Ukszta

łtowaniu podlega zwykle przekrój poprzeczny i podłużny. Dobranie odpowiedniego przekro-

ju poprzecznego belki spr

ężonej jest punktem wyjścia do dalszej analizy obliczeniowej. Przekrój

musi wi

ęc być założony przez konstruktora w oparciu o wymagania wytrzymałościowe, wykonaw-

cze i u

żytkowe, a obliczenie statyczne uzasadnia jego prawidłowość. Optymalny przekrój belki

zginanej to taki, który ma niezb

ędną powierzchnię strefy ściskanej od obciążeń zewnętrznych, mi-

nimaln

ą powierzchnię strefy rozciąganej, w której rozmieszczono cięgna sprężające, i taki przekrój

środnika łączącego obydwie strefy, jaki jest konieczny ze względów technologicznych i wytrzyma-

łościowych. Położenie cięgien sprężających, tj. zbrojenie belki - powinno zapewniać możliwie naj-
wi

ększe ramię sił wewnętrznych. Prowadzi to w konsekwencji do przekroju dwuteowego, w którym

górna pólka okre

ślona jest warunkami wytrzymałościowymi, a dolna - możliwością rozmieszczenia

ci

ęgien sprężających i nośnością elementu w stadium początkowym.

• Ustalenie wysokości przekroju

Wysoko

ści sprężonych belek stropowych i dachowych orientacyjnie można przyjmować:

h = (1/30-1/15)L

Wysoko

ść belek, które wymagają większej sztywności (np. belki podsuwnicowe), musi być

wy

ższa:

h = (1/15-1/5)L

W belkach dwuteowych, ci

ężar własny w sposób przybliżony można wyznaczać z warunku:

2

bet

k

h

)

25

,

0

2

,

0

(

g

÷

γ

=

gdzie:

γ

bet

– ci

ężar obj. betonu, kN/m

3

h – wysoko

ść belki, m

3

• Ustalenie wymaganej nośności cięgien i dobór ich liczby

Punktem wyj

ścia do obliczeń jest warunek równowagi mo-

mentów zginaj

ących w SGN w sytuacji trwałej. Zakłada się,

że ramię sił wewnętrznych (rozciąganie w cięgnach i ściska-
nie w betonie) równowa

żących moment zginający od obcią-

żeń M

Sd

wynosi:

z = (0,8

÷ 0,85)h

St

ąd, wartość sił wynosi:

z

M

F

Sd

=

Znaj

ąc siłę, jaką muszą przenieść cięgna rozciągane w SGN

w sytuacji trwa

łej, ich wymaganą liczbę - n

req

wyznacza si

ę

ze wzoru:

pd

1

req

F

F

n

=

lub

pd

1

p

req

f

A

F

n

=

gdzie:

pk

1

pd

1

F

25

,

1

9

,

0

F

=

pk

pd

f

25

,

1

9

,

0

f

=

Znaj

ąc tę liczbę i rozpatrując wymagania Normy w zakresie min. liczby cięgien sprężających

(Tablica N15) dokonuje si

ę przyjęcia liczby cięgien – n

prov

. Zazwyczaj jest:

req

prov

n

n

≥

.

W belkach strunobetonowych stosuje si

ę cięgna górne, zabezpieczające górną półkę przed

zniszczeniem wskutek dzia

łania sprężenia i ciężaru własnego w transporcie i wadliwym

sk

ładowaniu.

Potrzebn

ą ilość tego zbrojenia n

2,prov

mo

żna obliczyć z uproszczonego wzoru:

1

pd

g

,

Sd

prov

,

2

zF

M

n

=

lub

pd

1

p

g

,

Sd

prov

,

2

f

zA

M

n

=

gdzie M

Sd,g

– obliczeniowy moment zginaj

ący wywołany ciężarem własnym elementu

Przyj

ętą liczbę cięgien umieszcza się w półce górnej.

• Ustalenie wymaganej powierzchni strefy ściskanej betonu

Strefa

ściskana betonu tworząca górną półkę musi równoważyć siłę w cięgnach. Stąd jej po-

le przekroju powinno spe

łniać warunek:

cd

prov

,

pd

cc

f

F

A

α

=

gdzie:

pd

1

prov

prov

,

pd

F

n

F

=

lub

pd

1

p

prov

prov

,

pd

f

A

n

F

=

W przypadku p

łyt, szerokość elementu - b jest szerokością strefy ściskanej. Stąd, konieczna

wysoko

ść strefy ściskanej wynika z warunku:

b

A

h

cc

2

=

W przypadku belek, szeroko

ść – b

2

i wysoko

ść - h

2

zaleca si

ę przyjmować, kierując się

ograniczeniami:

w

2

b

5

b

≤

;

eff

2

b

b

≤

(b

eff

- p-kt N4.4.3.);

60

L

b

2

≥

;

2

2

b

25

,

0

h

≥

b

2

b

1

b

w

h

1

h

2

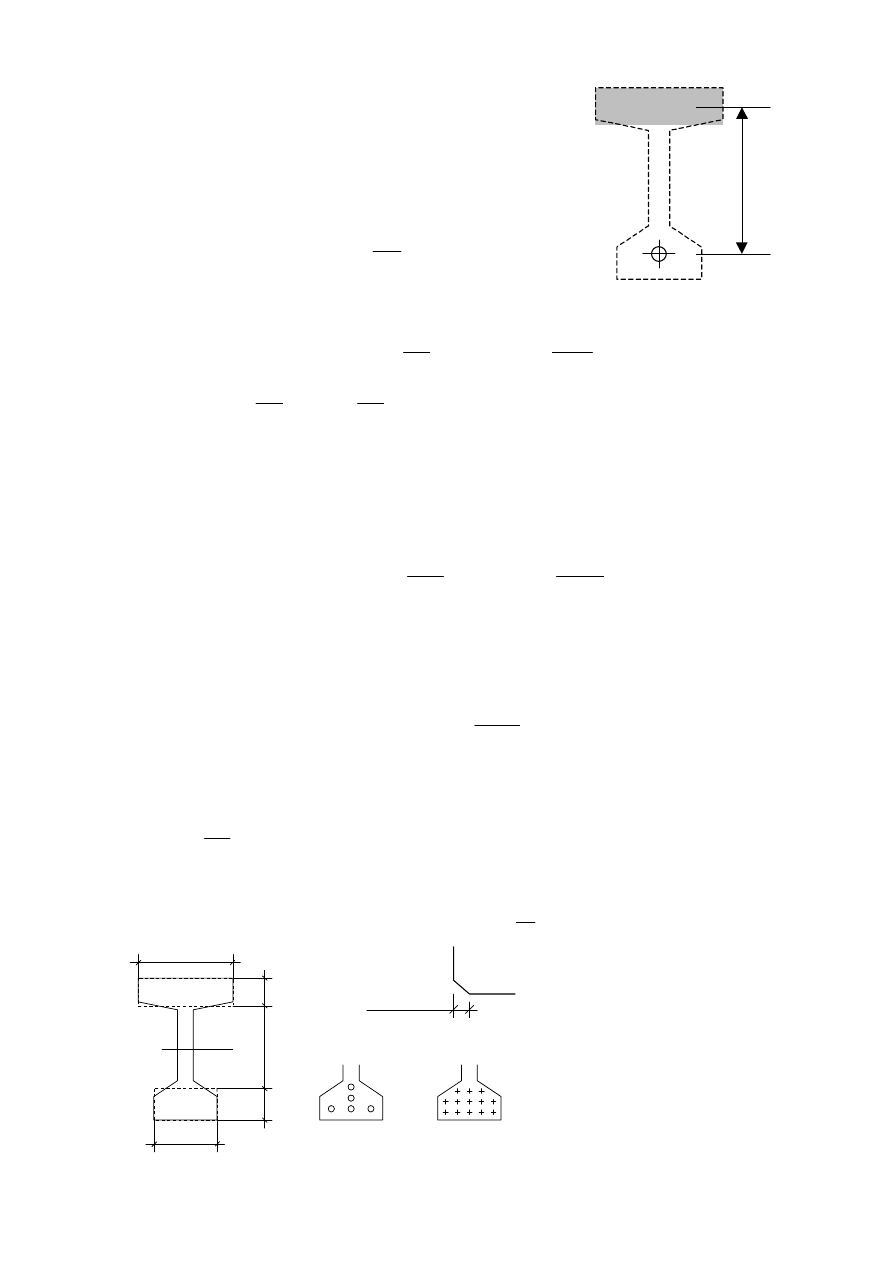
Rozmieszczenie

kabli

Rozmieszczenie

strun

1:6

Sfazowanie kraw

ędzi

pod

łużnych

ok. 10

÷15 mm

Rys. 1
Kszta

łtowanie przekroju dwuteowego

z

4

• Ustalenie wymaganej powierzchni strefy rozciąganej betonu

Pole powierzchni strefy rozci

ąganej betonu ma zapewnić właściwe rozmieszczenie i otulenie

ci

ęgien sprężających z uwzględnieniem oddziaływań środowiskowych (por p. 2.2. i 2.3.). Za-

leca si

ę aby w strunobetonie cięgna rozmieszczone były w układzie ortogonalnym, przy nie-

parzystej liczbie kolumn. W konstrukcjach kablobetonowych najbardziej korzystny jest uk

ład

┴. Środek ciężkości cięgien powinien pokrywać się ze środkiem ciężkości strefy rozciąganej
Pole przekroju strefy rozci

ąganej: A

ct

= b

1

h

1

, mo

żna oszacować ze wzoru:

w konstrukcjach strunobetonowych: A

ct

= 50A

p

w konstrukcjach kablobetonowych:

A

ct

= 40A

p.

gdzie A

p.

– pole przekroju ci

ęgien dolnych.

Szeroko

ść tej strefy powinna spełniać warunek

w

1

b

3

b

≤

• Ustalenie szerokości środnika

O szeroko

ści środnika decydują względy statyczne i technologiczne. Z przyczyn technolo-

gicznych, szeroko

ść środnika powinna spełniać warunki

h

1

,

0

b

w

≥

i

mm

80

b

w

≥

. W kon-

strukcjach kablobetonowych szeroko

ść ta musi zapewnić właściwy rozstaw i otulenie kabli

prowadzonych w

środniku.

4. Przyj

ęcie wymiarów elementu

• Przekrój poprzeczny w przęśle

Przyj

ęcie kształtu i wymiarów górnej i dolnej półki oraz środ odm. I nika określa kształt prze-

kroju w prz

ęśle. Uwzględniając wymagania technologiczne należy ukształtować skosy we-

wn

ętrznych powierzchni półek (min. 1:6) oraz ewentualne sfazowania naroży.

• Przekrój poprzeczny przy podporze

W elementach strunobetonowych d

ąży się do zachowania stałego kształtu przekroju. O ile

jest to konieczne, dokonuje si

ę poszerzenia środnika belki (do szerokości pasa dolnego) w

celu zwi

ększenia nośności na ścinanie i rysy ukośne. W elementach kablobetonowych po-

szerzenie

środnika pozwala także na właściwe rozmieszczenie zakotwień. Zasięg poszerze-

nia wynika z oblicze

ń (ścinanie, strefa zakotwień), zaś skos podłużny ma pochylenie ok. 1:3.

• Kształt podłużny elementu

Zmiana kszta

łtu elementu na jego długości – najczęściej poprzez zmianę jego wysokości –

jest racjonalnym rozwi

ązaniem w elementach poddanych zginaniu i pozwala na zmniejsze-

nie ci

ężaru własnego bez znaczącej utraty nośności i sztywności. W elementach dachowych

umo

żliwia to jednocześnie wykształcenie żądanych spadków. W elementach stropowych –

konieczno

ść zachowanie płaskiej powierzchni górnej powoduje, że zmianę wysokości ele-

mentu mo

żna uzyskać poprzez zakrzywienie pasa dolnego. Nie zawsze jest to pożądane

czy te

ż dopuszczalne. Kształt przekroju podłużnego belki sprężonej związany jest także z

rodzajem zastosowanego spr

ężenia, z jego przebiegiem oraz warunkami, w których element

ma by

ć użytkowany. Elementy strunobetonowe mają najczęściej stały przekrój na całej swej

d

ługości. Elementy kablobetonowe dają natomiast większą swobodę kształtowania przekroju

pod

łużnego.

• Położenie cięgien - trasa cięgien

Stosowanie w belkach ci

ęgien odgiętych i krzywoliniowych umożliwia kształtowanie przekro-

ju pod

łużnego zgodnie z przebiegiem sił wewnętrznych i daje następujące korzyści:

c) w

łaściwe usytuowanie cięgien w charakterystycznych przekrojach,

b) mo

żliwość zmniejszania sił poprzecznych w strefie przypodporowej,

c) uzyskanie bardziej równomiernego rozk

ładu sił pod zakotwieniami na czole belki. W kon-

strukcjach strunobetonowych stosuje si

ę cięgna proste lub odgięte. Dodatkowo, można

zró

żnicować siłę sprężającą działającą na beton poprzez pozbawianie odcinków końcowych

niektórych ci

ęgien przyczepności do betonu (tzw. „cięgna wyłączane”).

5

Dewiatory

D

ługość

zakowienia

si

ła sprężająca P

si

ła sprężająca P

moment zginaj

ący

od spr

ężenia Pe

moment zginaj

ący

od spr

ężenia Pe

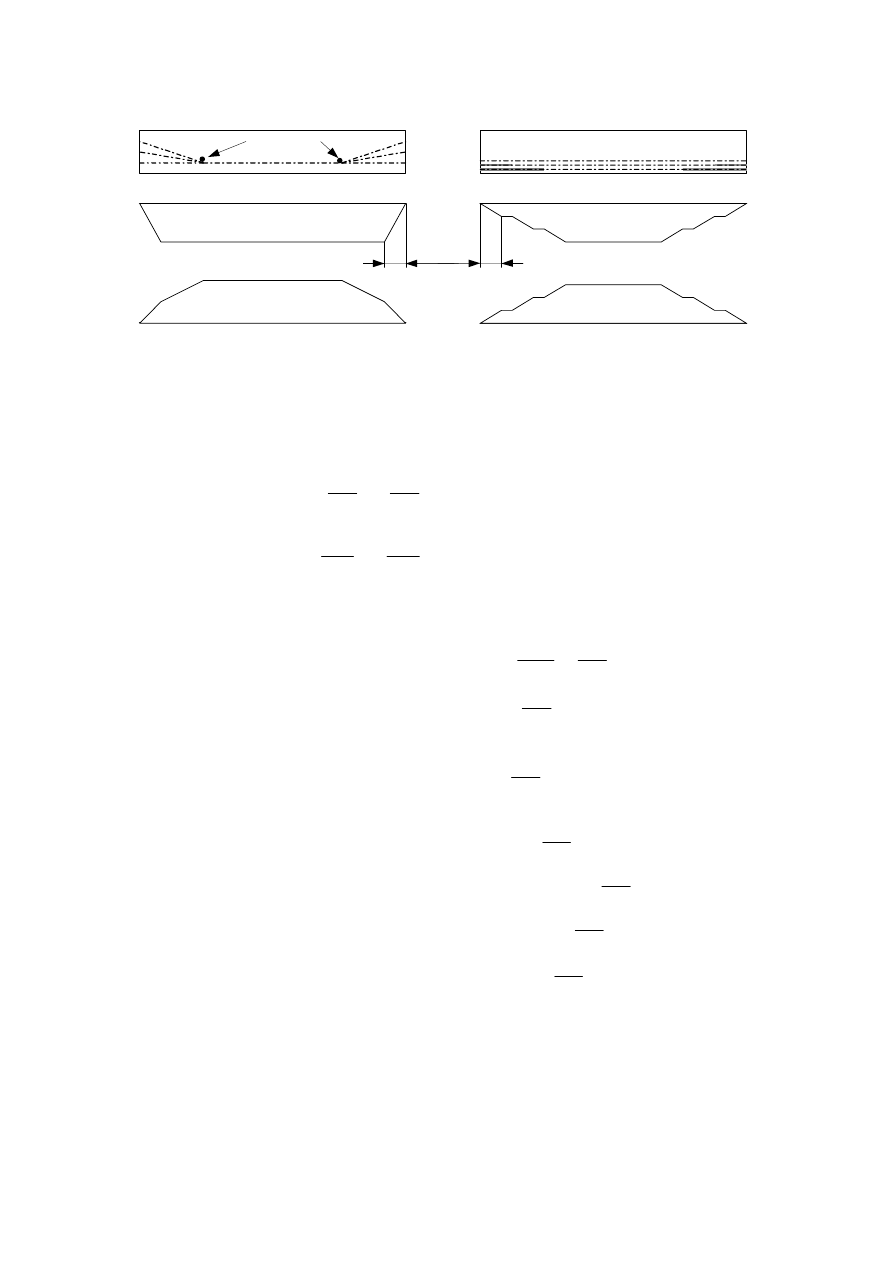
Ci

ęgna odgięte

P = const. e

≠ const.

Ci

ęgna wyłączane

P

≠ const. e = const.

Rys. 2

Si

ła sprężająca na długości elementu

W konstrukcjach kablobetonowych ukszta

łtowanie trasy kabla zgodnie z przebiegiem wykre-

su momentu zginaj

ącego jest z punktu widzenia statycznego najlepsze i ekonomicznie

oszcz

ędne (min. liczba kabli). W przypadku belek, najczęściej jest to trasa paraboliczna o

ogólnym równaniu:

0

2

2

e

x

L

e

4

x

L

e

4

)

x

(

e

+

∆

−

∆

=

, gdzie

0

max

e

e

e

−

=

∆

Trasa indywidualnego kabla:

0

i

2

2

i

i

e

x

L

e

4

x

L

e

4

)

x

(

e

+

∆

−

∆

=

;gdzie

0

,i

max

,i

i

e

e

e

−

=

∆

Wielko

ści opisujące geometrie trasy kabla mają zastosowanie przy obliczaniu wartości siły

spr

ężającej:

− kąt nachylenia trasy kabla wypadkowego do osi podłużnej elementu

w dowolnym punkcie trasy:

)

L

x

2

(

L

e

4

dx

)

x

(

de

arctan

)

x

(

2

−

∆

≅













=

φ

na czole elementu (x = 0):

L

e

4

0

∆

−

≅

φ

w po

łowie rozpiętości elementu (x = L/2):

0

2

/

L

=

φ

na ko

ńcu elementu (x = L):

L

e

4

L

∆

≅

φ

− kat odgięcia trasy kabla od czoła elementu (zakotwienia czynnego)

w dowolnym punkcie trasy:

x

L

e

8

)

x

(

)

x

(

2

0

∆

≅

φ

−

φ

=

Θ

w po

łowie rozpiętości elementu (x = L/2):

L

e

4

0

2

/

L

2

/

L

∆

≅

φ

−

φ

=

Θ

na ko

ńcu elementu (x = L):

L

e

8

0

L

L

∆

≅

φ

−

φ

=

Θ

− średni promień krzywizny trasy kabla:

e

8

L

r

2

∆

≅

6

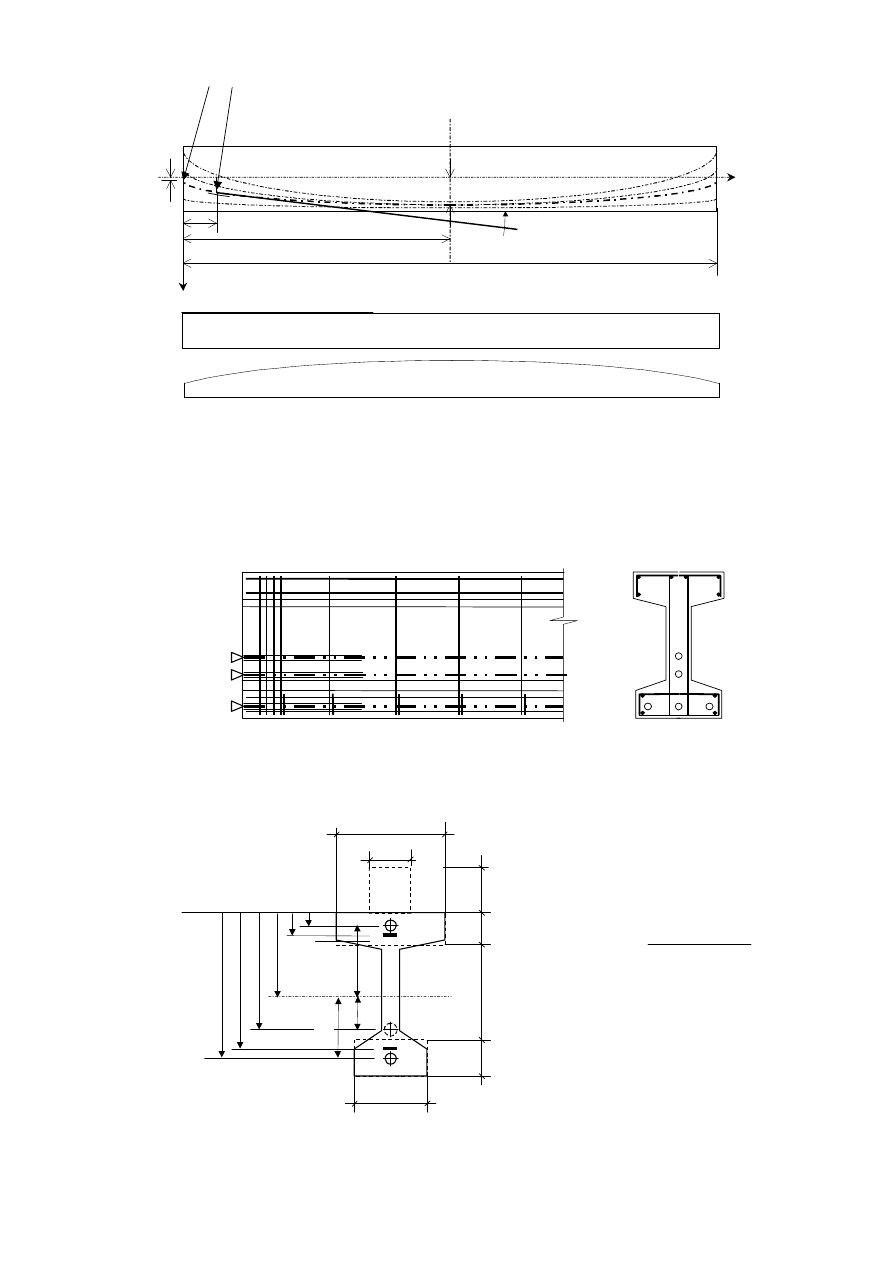
X

e(x)

r

Θ

x

L/2

φ

x

e

0

L

e

max

x

si

ła sprężająca P

moment zginaj

ący

od spr

ężenia Pe

Ci

ęgna zakrzywione

P = const. e

≠ const.

Rys. 3

Parametry parabolicznej trasy kabli

• Konstrukcja zbrojenia pomocniczego

Zbrojenie pomocnicze wykonane ze stali zbrojeniowej (z regu

ły klasy AII lub AIII) utworzone

jest jako zbrojenie poprzeczne – strzemiona – przenosz

ące siłę poprzeczną (ścinanie),

skurcz i usztywniaj

ące kable. Zbrojenie podłużne przeciwdziała skurczowi, usztywnia szkie-

let zbrojenie i wspomaga no

śność i rysoodporność – także w sytuacji początkowej.

Rys. 4

Zbrojenie poprzeczne i pod

łużne

• Charakterystyki geometryczne przekroju

b

2

b

1

b

w

h

1

h

2

z

cp

1

A

p2

, A

d2

A

s2

A

s1

z

cp

z

cp

2

d

p

1

d

s1

d

p

y

2

d

s2

d

p

2

A

p

, A

d

A

p1

, A

d1

h

w

h

n

b

n

Rys. 5

Oznaczenia wielko

ści geometrycznych przekroju

A

d

– pole

przekroju

kanałów kablowych

2

p

1

p

p

A

A

A

+

=

p

2

p

2

p

1

p

1

p

p

A

d

A

d

A

d

+

=

2

d

1

d

d

A

A

A

+

=

7

Charakterystyki geometryczne przekroju tj. pole powierzchni, po

łożenie środka cięż-

ko

ści i moment bezwładności należy obliczać dla przekroju w przęśle i na podporze (o ile

si

ę różnią), uwzględniając zbrojenie posiadające przyczepność do betonu w odpowiednich

sytuacjach obliczeniowych. Nale

ży uwzględnić odmienność sprężystości poszczególnych

materia

łów stosując współczynniki:

cm

p

p

E

E

=

α

;

cm

s

s

E

E

=

α

;

cm

n

cm

c

E

E

=

α

gdzie: E

cm

– modu

ł sprężystości betonu prefabrykatu

E

p

– modu

ł sprężystości cięgien sprężających

E

s

– modu

ł sprężystości stali zbrojenia pomocniczego

E

n

cm

– modu

ł sprężystości betonu uzupełniającego (nadbetonu)

Charakterystyki geometryczne przekroju betonu prefabrykatu
Pole przekroju betonu:

w

w

2

2

1

1

c

h

b

h

b

h

b

A

+

+

=

Mom. statyczny betonu wzgl. górnej kraw

ędzi:













+

+

+











 −

=

2

h

h

h

b

2

h

b

2

h

h

h

b

S

w

2

w

w

2

2

2

1

1

1

c

Środek ciężkości betonu (liczony wzgl. górnej krawędzi):

c

c

c

A

S

d

=

Mom. bezw

ładności betonu:

2

c

1

1

1

3

1

1

2

w

2

c

w

w

3

w

w

2

2

c

2

2

3

2

2

c

d

2

h

h

h

b

12

h

b

2

h

h

d

h

b

12

h

b

2

h

d

h

b

12

h

b

J













−

−

+

+













−

−

+

+













−

+

=

• Charakterystyki geometryczne przekrojów w sytuacji początkowej

W sytuacji pocz

ątkowej, przekrój poprzeczny tworzy betonowy prefabrykat z przekro-

jem pr

ętów pomocniczego zbrojenia podłużnego i cięgnami sprężającymi w strunobetonie.

W kablobetonie, ci

ęgna nie posiadają przyczepności do betonu więc ich się nie uwzględnia,

ponadto, trzeba uwzgl

ędnić puste przestrzenie wytworzone przez kanały kablowe.

Pole przekroju w sytuacji pocz

ątkowej:

∑







−

−

−

α

+

−

α

+

=

kablobeton

A

-

n

strunobeto

A

)

1

(

A

)

1

(

A

A

d

p

p

si

s

c

0

cs

Mom. statyczny przekroju wzgl. górnej kraw

ędzi:

∑







−

−

−

α

+

−

α

+

=

kablobeton

d

A

-

n

strunobeto

d

A

)

1

(

d

A

)

1

(

S

S

p

d

p

p

p

si

si

s

c

0

cs

Środek ciężkości przekroju (liczony wzgl. górnej krawędzi):

0

cs

0

cs

0

cs

A

S

d

=

Mom. bezw

ładności przekroju

∑









−

−

−

−

−

α

+

−

−

α

+

−

+

=

kablobeton

)

d

d

(

A

-

n

strunobeto

)

d

d

(

A

)

1

(

)

d

d

(

A

)

1

(

)

d

d

(

A

J

J

2

0

cs

p

d

2

0

cs

p

p

p

2

0

cs

si

si

s

2

0

cs

c

c

c

0

cs

mimo

śród wszystkich cięgien:

0

,

2

p

0

cp

y

d

z

−

=

• Charakterystyki geometryczne przekrojów w sytuacji montażowej (przejściowej)

Dla konstrukcji strunobetonowych nie ma ró

żnic. W kablobetonie uwzględnia się wy-

pe

łnienie kanałów kablowych iniekcją wiążącą cięgna z betonem w przekroju

Pole przekroju w sytuacji monta

żowej:

p

p

d

0

cs

cst

A

)

1

(

A

A

A

−

α

+

+

=

Mom. statyczny przekroju wzgl. górnej kraw

ędzi:

p

p

p

p

d

0

cs

cst

d

A

)

1

(

d

A

S

S

−

α

+

+

=

Środek ciężkości przekroju (liczony wzgl. górnej krawędzi):

cst

cst

cst

A

S

d

=

8

Mom. bezw

ładności przekroju

[

]

2

cst

p

p

p

d

2

cst

0

cs

0

cs

0

cs

cst

)

d

d

(

A

)

1

(

A

)

d

d

(

A

J

J

−

−

α

+

+

−

+

=

mimo

śród wszystkich cięgien:

cst

p

cpt

d

d

z

−

=

• Charakterystyki geometryczne przekrojów w sytuacji trwałej

Je

śli nie ma zespolenia, nie ma różnic w porównaniu do sytuacji przejściowej. W przy-

padku zespolenia, charakterystyki dla obu typów konstrukcji oblicza si

ę następująco:

Pole przekroju w sytuacji trwa

łej:

n

n

cn

h

b

A

=

;

cn

c

cst

cs

A

A

A

α

+

=

Mom. statyczny przekroju wzgl. górnej kraw

ędzi:

2

h

A

S

S

n

cn

c

cst

cs

α

−

=

Środek ciężkości przekroju (liczony wzgl. górnej krawędzi):

cs

cs

cs

A

S

d

=

Mom. bezw

ładności przekroju

2

cs

n

cn

c

2

cst

cs

cst

cst

cs

)

d

2

h

(

A

)

d

d

(

A

J

J

+

α

+

−

+

=

mimo

śród wszystkich cięgien:

cs

p

cp

d

d

z

−

=

5. Programowanie naci

ągu wstępnego

Programowanie naci

ągu wstępnego polega na założeniu wielkości naciągu wstępnego, obli-

czeniu strat si

ły sprężającej i sprawdzenia warunków ograniczenia naprężeń w cięgnach.

Obliczenia prowadzi

ć można dla cięgna wypadkowego, reprezentującego naciąg, pole prze-

kroju i geometri

ę trasy wszystkich cięgien. O ile wymagana jest większa dokładność obli-

cze

ń, to obliczenia prowadzi się dla poszczególnych cięgien (kabli).

• Przyjęcie siły naciągu

Spr

ężenie konstrukcji jest działaniem korzystnym (to stwierdzenie leży u podstaw rozwoju

konstrukcji spr

ężonych). Jeśli tak, to ustalone z uwagi na nośność zbrojenie sprężające war-

to podda

ć naciągowi wstępnemu o maksymalnej dopuszczalnej wartości, zapewniając jed-

nocze

śnie bezpieczeństwo konstrukcji poddanej takiemu oddziaływaniu (sytuacja początko-

wa, strefy zakotwie

ń, dopuszczalne naprężenia w cięgnach).

Norma podaje nast

ępujące ograniczenia maksymalnych naprężeń rozciągających jakim mo-

g

ą być poddane cięgna w procesie naciągu:

pk

max

,

0

f

80

,

0

≤

σ

i

k

1

,

0

p

max

,

0

f

90

,

0

≤

σ

co prowadzi do wzorów:

pk

max

,

0

F

80

,

0

P

≤

i

k

1

,

0

p

max

,

0

F

90

,

0

P

≤

gdzie

pk

1

prov

,

p

pk

F

n

F

=

lub

pk

p

pk

f

A

F

=

Zaleca si

ę przyjmować siłę naciągu:

max

,

0

0

m

P

P

=

• Obliczenie strat doraźnych

W konstrukcjach strunobetonowych do strat dora

źnych, czyli występujących przed lub w

procesie kotwienia w betonie (przekazania si

ły naciągu na beton konstrukcji) zalicza się (w

kolejno

ści występowania):

− straty spowodowane tarciem cięgien o dewiatory ∆P

µ

(x) (uwzgl

ędniane tylko w przypad-

ku stosowania ci

ęgien odgiętych. Oblicza się je ze wzoru (N142) przyjmując k = 0 i Θ ja-

ko k

ąt odchylenia trasy cięgna.

− straty spowodowane częściową relaksacją cięgien ∆P

ir

ze wzoru (N146). Dla poziomu

napr

ężeń obliczonych ze wzoru:















=













 σ

pk

0

pk

0

p

F

P

f

przyjmuje si

ę z Rys. N35 wielkość re-

laksacji, a z Tab. N16 jej wzrost w czasie od naci

ągu cięgien do przekazania siły na be-

ton (czas ten zasadniczo obejmuje ca

ły proces montażu zbrojenia, ułożenia i dojrzewa-

nia betonu do chwili jego rozformowania). Skrótowo mo

żna to zapisać:

0

ir

P

[%]"

16

.

Tab

[%]"

35

.

Rys

"

P

×

×

=

∆

9

− straty spowodowane odkształceniem sprężystym betonu ∆P

c

ze wzoru (N147), gdzie

proponuje si

ę przyjąć za siłę P

0

warto

ść tej siły pomniejszonej o poprzednie straty, tj:

P

0

= P

0

–

∆P

µ

(x)–

∆P

ir

. Do oblicze

ń należy zastosować charakterystyki geometryczne

przekrojów w sytuacji pocz

ątkowej.

Dodatkowa strata si

ły sprężającej powstaje wskutek różnicy temperatur cięgien i urządzeń

oporowych przy produkcji elementów na d

ługich torach, w czasie której następuje ogrzanie

mieszanki betonowej w celu przyspieszenia procesu dojrzewania betonu. Strata ta nie jest
uj

ęta w aktualnej normie, a jej wielkość może byś określana za [3] wzorem:

T

E

A

9

,

0

P

p

p

T

T

∆

α

=

∆

gdzie

αT– liniowy współczynnik rozszerzalności termicznej stali

∆T – różnica temperatur. Przy braku bliższych danych można przyjmować ∆T = 60

o

C

Podwy

ższona temperatura procesu dojrzewania betonu może także zwiększyć 2÷3 –krotnie

strat

ę od częściowej relaksacji stali ∆P

ir

.

Innymi stratami technologicznymi mog

ą być straty poślizgu w zakotwieniach zewnętrznych.

S

ą one jednak łatwe do określenia i zniwelowania modyfikacją procesu napinania cięgien.

W konstrukcjach kablobetonowych do strat dora

źnych zalicza się:

− straty spowodowane tarciem kabli o ścianki kanału ∆P

µ

(x). Oblicza si

ę je ze wzoru

(N142) przyjmuj

ąc sumę kątów zakrzywienia trasy kabla Θ na podstawie geometrii trasy

kabla.

− straty wywołane poślizgiem cięgien w zakotwieniu ∆P

sl

. Oblicza si

ę je ze wzoru (N143).

Jako bardziej niekorzystn

ą wartość x

0

(por. wzory (N144) i (N145)) nale

ży przyjąć war-

to

ść większą.

− straty spowodowane odkształceniem sprężystym betonu ∆P

c

ze wzoru (N148), przyjmu-

j

ąc za liczbę n liczbę etapów sprężania:

j

k

n

n

n

=

gdzie

n

k

– ogólna liczba kabli

n

j

– liczba kabli napinanych jednocze

śnie

Je

żeli kable naciąga się równocześnie straty sprężyste ∆P

c

= 0. Je

żeli indywidualnie –

strat

ę można zniwelować różnicą naciągu poszczególnych kabli(zwiększać naciąg

i-tego kabla o

∆P

ci

):

max

,

0

cp

cp

2

cp

p

p

2

ci

P

I

A

z

1

n

i

n

P















+

ρ

α

−

=

∆

gdzie

i – numer etapu spr

ężania

• Sprawdzenie naprężeń w cięgnach w sytuacji początkowej (po stratach doraźnych)

Warto

ść siły w cięgnach po wystąpieniu strat doraźnych opisują wzory:

w strunobetonie:

T

c

ir

0

0

m

P

P

P

)

x

(

P

P

P

∆

−

∆

−

∆

−

∆

−

=

µ

w kablobetonie:

c

sl

0

0

m

P

P

)

x

(

P

P

P

∆

−

∆

−

∆

−

=

µ

Norma narzuca warunki ograniczaj

ące poziom naprężeń w cięgnach po zakotwieniu:

pk

0

pm

f

75

,

0

≤

σ

i

k

1

,

0

p

0

pm

f

85

,

0

≤

σ

co prowadzi do wzorów:

pk

0

m

F

75

,

0

P

≤

i

k

1

,

0

p

0

m

F

85

,

0

P

≤

Je

śli obliczona wartość siły nie spełnia któregoś z powyższych warunków, należy zmniejszyć

warto

ść naciągu wstępnego P

0

i powtórnie obliczy

ć straty doraźne.

• Obliczenie strat opóźnionych (wzór N151 i N152)

Straty opó

źnione oblicza się zazwyczaj w najbardziej obciążonym przekroju, przyjmując czas

życia konstrukcji t = ∞.
− przewidywane odkształcenia skurczowe ε

cs

(t,t

s

) dla t =

∞ przy braku bardziej szczegóło-

wych danych technologicznych mo

żna przyjmować wg Tab. N.B.1 (przy dowolnym t

s

)

10

− współczynnik pełzania betonu φ(t,t

0

) dla t =

∞ przy braku bardziej szczegółowych danych

technologicznych mo

żna przyjmować wg Tab. NA.2. Za wiek betonu w chwili obciążenia

t

0

nale

ży przyjąć jego wiek w chwili sprężenia.

− stopień zbrojenia ρ

p.

nale

ży obliczyć dla pola powierzchni przekroju w sytuacji trwałej.

− naprężenia σ

cg

nale

ży obliczać uwzględniając zmianę charakterystyk geometrycznych

elementów zespolonych i schematu statycznego oraz odpowiedni przyrost obci

ążeń sta-

łych.

− naprężenia σ

cp0

nale

ży obliczać ze wzoru:

0

cs

2

0

cp

0

m

0

cs

0

m

0

cp

J

z

P

A

P

+

=

σ

− obliczenia straty naprężeń wywołanej relaksacją ∆σ

pr

Nale

ży obliczyć

cg

p

p

0

m

0

pg

p

A

P

σ

α

+

=

σ

=

σ

Dla t =

∞ strata ∆σ

pr

, jest równa

p

pr

[%]"

35

N

.

Rys

"

2

σ

×

×

=

σ

∆

• Sprawdzenie naprężeń w cięgnach w sytuacji trwałej (po stratach całkowitych)

Warto

ść siły w cięgnach po wystąpieniu strat całkowitych (doraźnych i opóźnionych) opisuje

wzór:

)

t

(

P

P

P

t

0

m

mt

∆

−

=

Norma narzuca warunek ograniczaj

ący poziom naprężeń w cięgnach po wszystkich stratach:

pk

pmt

f

65

,

0

≤

σ

co prowadzi do wzoru:

pk

mt

F

65

,

0

P

≤

Je

śli obliczona wartość siły nie spełnia tego warunku, należy zmniejszyć wartość naciągu

wst

ępnego P

0

i powtórnie obliczy

ć straty doraźne i opóźnione.

6. Sprawdzenie elementu w sytuacji pocz

ątkowej

• Ustalenie naprężeń dopuszczalnych w betonie

Warto

ści dopuszczalnych naprężeń ściskających podane są w punkcie N7.1.7.1. Jeśli pro-

jekt jest skoordynowany z procesem technologicznym, o poziomie napr

ężeń dopuszczalnych

decyduje rzeczywista wytrzyma

łość betonu w chwili sprężenia konstrukcji. W innych warun-

kach decyduje projektowana klasa betonu.
Dopuszczalne napr

ężenia rozciągające przyjmuje się równe f

ctk

.

• Sprawdzenie naprężeń w betonie

Oprócz si

ły sprężającej wywołującej moment zginający (ściskający dolne włókna a

rozci

ągający górne), na element sprężony w sytuacji początkowej może oddziaływać ciężar

w

łasny. Prawidłowe podparcie elementu (na końcach – rys a) i b)) wywołuje moment zgina-

j

ący o kształcie paraboli lecz przeciwnego znaku, co może zmniejszać moment od spręże-

nia. Najbardziej niekorzystne podparcie (w

środku rozpiętości) wywoła momenty wsporniko-

we, sumuj

ące się z działaniem siły sprężającej.

Napr

ężenia w przekroju betonowym wywołane sprężeniem (i ciężarem własnym) wyznacza

si

ę zgodnie z zasadami analizy liniowo sprężystej:

w

łókna dolne:

(

)

0

cs

0

cs

Sd

0

cs

pd

0

cp

J

d

h

M

A

N

−

+

=

σ

; w

łókna górne:

0

cs

0

cs

Sd

0

cs

pd

0

cp

J

d

M

A

N

−

=

σ

gdzie:

0

m

0

m

sup

sup

,

k

pd

P

1

,

1

P

r

P

N

=

×

=

=

g

0

zp

pd

Sd

M

z

N

M

m

=

Sprawdzenie napr

ężeń w betonie polega na wykazaniu, że naprężenia na krawędzi ściska-

nej nie przekraczaj

ą obliczonych wartości dopuszczalnych, a na krawędzi górnej, jeśli wy-

st

ępuje rozciąganie, to nie przekraczają f

ctk

.

• Sprawdzenie SGN w sytuacji początkowej

Je

śli jakiś warunek ograniczenia naprężeń (opisany poprzednio) nie zostanie spełniony, co

nale

ży uznać za stan niepożądany, należy dokonać sprawdzenia stanu granicznego nośno-

ści w sytuacji początkowej. Przyjmuje się założenia;
− wartość siły sprężającej oblicza się ze wzoru:

0

m

0

m

p

Sd

P

2

,

1

P

N

=

γ

=

− moment od ciężaru własnego

(

)

g

Sd

M

9

,

0

albo

1

,

1

M

=

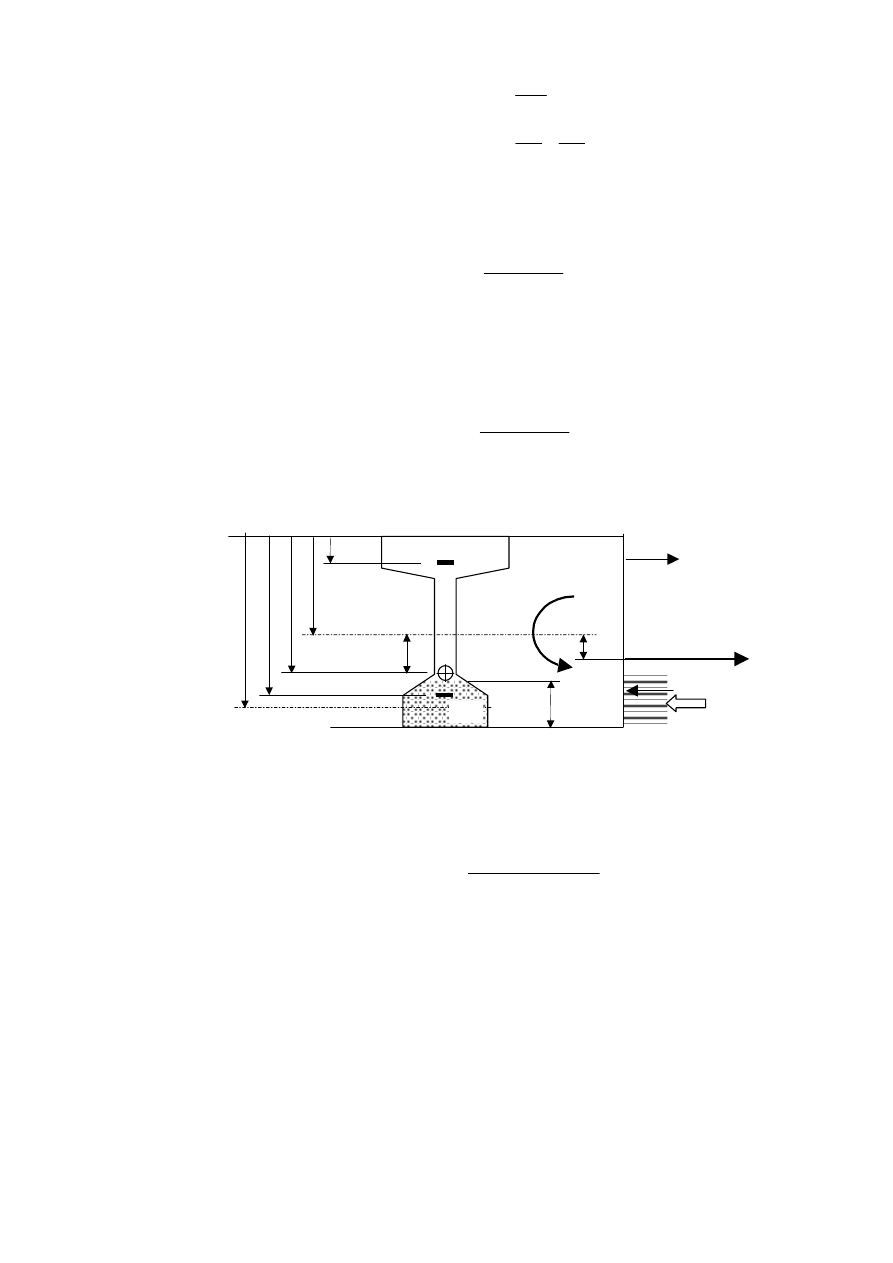
11

− mimośród statyczny oblicza się ze wzoru:

Sd

Sd

e

N

M

e

=

− wytrzymałość obliczeniowa betonu:

5

,

1

'f

'f

f

ck

c

ck

cd

=

γ

=

gdzie f’

ck

– napr

ężenia dopuszczalne wg punktu N7.1.7.1

Przekrój sprawdza si

ę jako ściskany mimośrodowo, pomijając możliwość wyboczenia

(

η = 1,0) i mimośrody przypadkowe (e

a

= 0,0):

i)

z warunku równowagi si

ł określić powierzchnię betonu ściskanego:

cd

yd

1

s

Sd

ct

f

f

A

N

A

−

=

i dalej wysoko

ść strefy ściskanej x

ct,eff

i po

łożenie środka ciężkości d

ct

,

ii)

sprawdzi

ć warunek równowagi momentów:

Sd

0

cs

1

s

yd

1

s

0

cs

ct

cd

ct

yd

1

s

cd

ct

Rd

M

)

d

d

(

f

A

)

d

d

(

f

A

f

S

f

S

M

≥

−

+

−

=

+

=

i je

śli jest spełniony, to element jest bezpieczny.

iii)

W przeciwnym wypadku, z warunku równowagi momentów obliczy

ć:

cd

yd

1

s

Sd

ct

f

f

S

M

S

−

=

i dalej pole przekroju strefy

ściskanej A

ct

i po

łożenie środka ciężkości d

ct

, wykorzy-

stuj

ąc związek:

)

d

d

(

A

S

0

cs

ct

ct

ct

−

=

A

ct

f

cd

A

s2

z

cp

d

s1

d

p

d

cs

0

d

s2

A

p

, A

d

M

Sd

x

ct

,e

ff

A

s1

d

ct

A

s1

f

yd

N

Sd

A

s2

f

yd

e

s

Rys. 6

Stan Graniczny No

śności przekroju w sytuacji początkowej

iv)

z warunku równowagi si

ł obliczyć wymagane pole przekroju zbrojenia rozciąganego

(górnego) A

s2,req

:

yd

Sd

yd

1

s

cd

ct

req

,

2

s

f

N

f

A

f

A

A

−

+

=

v)

sprawdzi

ć, czy założone zbrojenie A

s2

≥ A

s2,req

. Je

śli nie, to odpowiednio skorygować

jego ilo

ść.

• Sprawdzenie nośności i zaprojektowanie zbrojenia stref zakotwień

W strefach zakotwie

ń następuje przekazanie bardzo dużych sił występujących w napiętych

ci

ęgnach na ograniczoną powierzchnie betonu (tzw. kotwienie), co powoduje powstanie zło-

żonego, przestrzennego stanu naprężeń w betonie. Z punktu widzenia statycznego strefa
zakotwie

ń jest nazywana strefą zaburzeń obejmującą odcinek, poza którym rozkład od-

kszta

łceń i naprężeń jest rozkładem liniowym wynikającym z położenia wypadkowej wszyst-

kich zakotwie

ń (siły sprężającej). Jego długość jest równa w przybliżeniu wysokości belki. W

strefie tej powstaj

ą szczególnie niekorzystne poprzeczne naprężenia rozciągające, zależne

od warto

ści sił sprężających i konstrukcji zakotwień oraz kształtu strefy zakotwienia i roz-

mieszczenia ci

ęgien. W kablobetonie kotwienie odbywa się poprzez docisk zakotwień me-

chanicznych za

ś w strunobetonie przez przyczepność do betonu. Odmienność sposobu ko-

12

twienia powoduje istotne ró

żnice w sposobie sprawdzania i zbrojenia stref zakotwień w ka-

blobetonie i strunobetonie.




konstrukcje kablobetonowe
Przyk

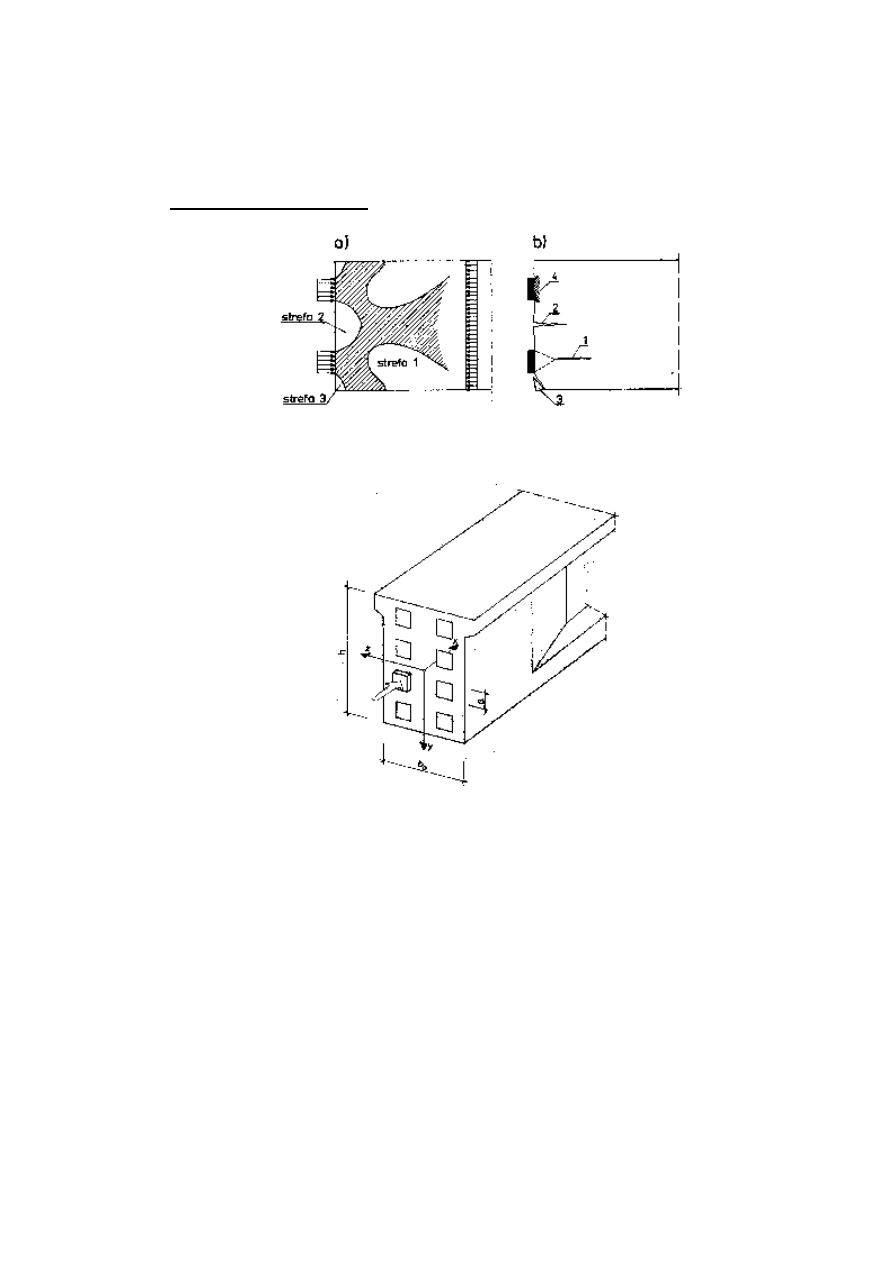
ładowy rozkład naprężeń i możliwe przyczyny uszkodzeń zakotwień ilustruje Rys. 7

Rys. 7

Mo

żliwe sposoby uszkodzenia strefy zakotwień w kablobetonie [1]

(1-roz

łupanie, 2-rozszczepienie, 3-odspojenie, 4-zmiażdżenie.)

P

di

Rys. 8

Uk

ład współrzędnych i płaszczyzn do sprawdzania stref zakotwień w kablobetonie [1]

Klasyczn

ą metodą obliczania naprężeń poprzecznych rozpatrującą łącznie wszystkie naprę-

żenia jest metoda Guyona. Przestrzenny rozkład naprężeń modeluje się tu za pomocą pła-
skich uk

ładów naprężeń w dwóch, wzajemnie prostopadłych płaszczyznach (pionowej XY i

poziomej XZ - Rys. 8). Wydziela si

ę odpowiednie kwadratowe bloki z o długości boku równej

2a (gdzie a – minimum odleg

łości od osi działania siły wypadkowej do bliższej krawędzi bel-

ki) i w poszczególnych w

ęzłach wpisanej w bloki siatki geometrycznej , za pomocą rozbudo-

wanych tablic, oblicza si

ę wartości naprężeń. Sposób ten szczegółowo omawiają pozycje [3],

[5], [12] i [13]. Stosowanie tej metody jest

żmudne i obliczeniowo niezbyt korzystne, ponie-

wa

ż zastępowanie obciążeń rozłożonych nawet na niewielkich powierzchniach zakotwień si-

łami skupionymi, zaczepionymi w poszczególnych węzłach siatki, daje w efekcie wartości
napr

ężeń poprzecznych znacznie większych niż w rzeczywistości.

Innym sposobem jest metoda kratownicowa: prosta, lecz wymagaj

ąca dużego doświadcze-

nia przy budowaniu teoretycznej kratownicy si

ł.

Metoda uproszczona zaprezentowana poni

żej analizuje odrębnie poszczególne przypadki

zniszczenia i daje w pe

łni zadawalające wyniki. Obliczenia prowadzi się także za pomocą

p

łaskich układów naprężeń. Jeśli rozmieszczenie zakotwień w płaszczyźnie spełnia postulat

liniowego rozk

ładu zakotwień tzn. każda siła wywołuje poza strefą zaburzeń sprężenie o

13

środku ciężkości leżącym w linii działania samej siły, to obliczenia można prowadzić zakła-
daj

ąc, ze poszczególne bloki odpowiadające zakotwieniom nie oddziaływają na siebie (Rys.

9).



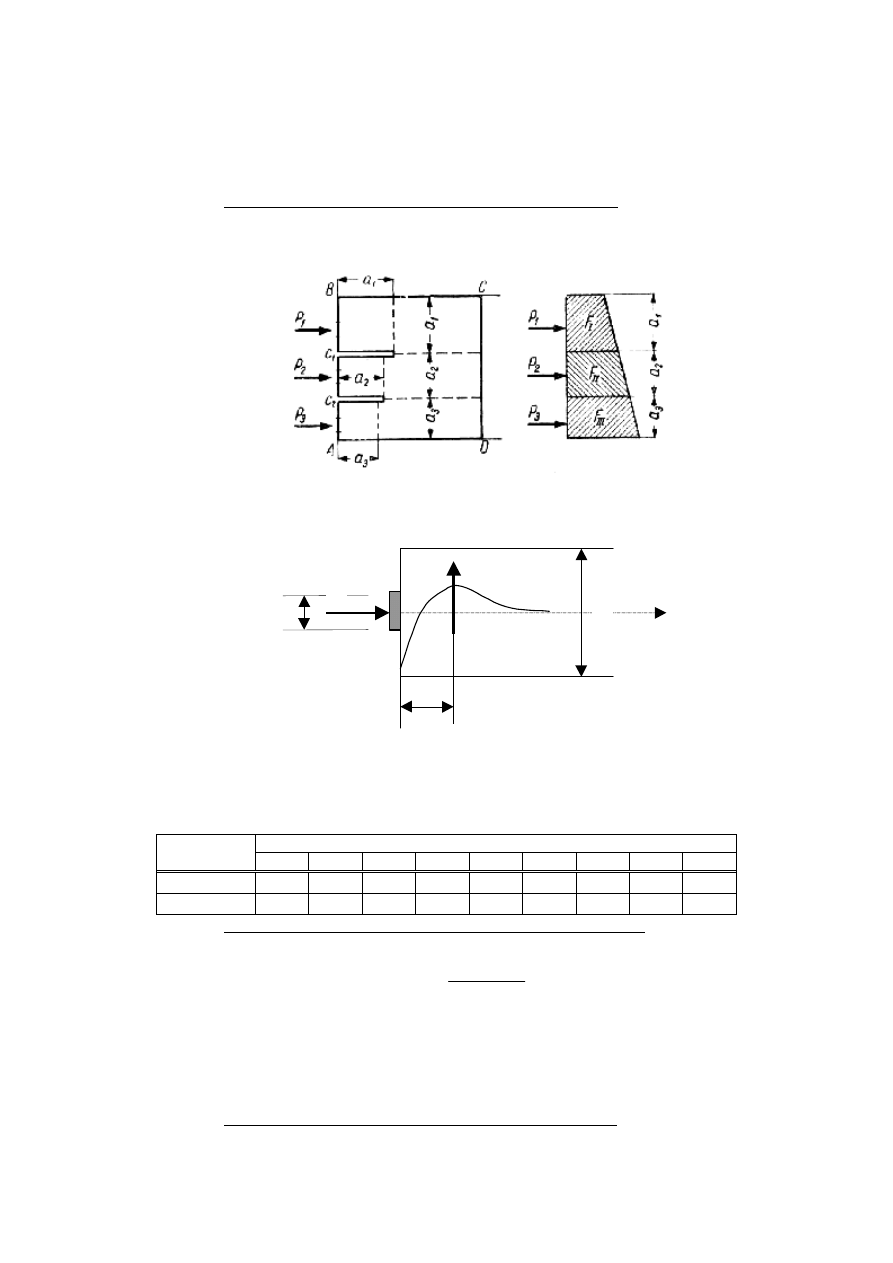
i)

poprzeczne napr

ężenia rozciągające wgłębne (Rys. 7b – 1)

W obliczeniach nale

ży przyjąć, że P

d

= F

pk

D

ługość boku pojedynczego bloku 2a to minimalna z wartości: odległości od osi działania si-

ły do krawędzi belki i połowa odległości od bliższego zakotwienia.

σ

cp

Rys. 9

Idea liniowego rozk

ładu zakotwień

2a

h

a

P

d

N

VSd

=c

1

P

d

x

0

=c

2

2a

x

Rys. 10

Rozk

ład wgłębnych naprężeń poprzecznych w osi zakotwienia i wypadowa rozciągań

Tab. 3 Wspó

łczynniki do obliczania zbrojenia wgłębnej strefy kotwienia

h

a

/2a

Wspó

ł-

czynnik

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

c

1

0,31

0,32

0,18

0,15

0,12

0,10

0,08

0,06

0,04

c

2

0,18

0,24

0,30

0,35

0,39

0,42

0,44

0,45

0,46

ii)

poprzeczne napr

ężenia rozciągające przyczołowe (Rys. 7b – 2)

Wypadkow

ą naprężeń pomiędzy warstwami zakotwień oblicza się ze wzoru:

(

)

dj

di

a

pij

a

pij

VSd

P

P

h

d

h

d

5

,

0

42

,

0

N

+

−

−

=

gdzie: d

pij

– odleg

łość pomiędzy rozpatrywanymi warstwami zakotwień,

h

a

– d

ługość rzutu zakotwienia na płaszczyznę

P

di

, P

dj

– si

ły w rozpatrywanych warstwach zakotwień

Zbrojenie nale

ży umieszczać jak najbliżej płaszczyzny czołowej (z zachowaniem wymaga-

nego otulenia pr

ętów i zagłębienia zakotwień

iii)

poprzeczne napr

ężenia rozciągające narożne (Rys. 7b – 3)

max

,

d

VSd

P

03

,

0

N

=

14

gdzie: P

d,max

, – najwi

ększa siła obciążająca czoło belki

iv)

zmia

żdżenie betonu (Rys. 7b – 4)

W

łaściwą metodą jest sprawdzenie na docisk (Rozdz. N5.8). W obliczeniach należy przyjąć

α

u

= 1, bo

σ

u,min

=

σ

u,max

konstrukcje strunobetonowe
Zasi

ęg strefy zakotwień (zaburzeń odkształceń i naprężeń) wyznacza długość rozkładu l

p,eff

,

obliczana ze wzoru (N155) przy za

łożeniu, że l

bpd

= 0,8l

bp

(z uwagi na intensywno

ść naprę-

żeń bardziej niekorzystna jest krótsza długość strefy zaburzeń). Rozłożony na długości zako-
twienia ci

ęgna przyrost siły sprężającej sprawia że w strunobetonie mogą wystąpić jedynie

uszkodzenia wywo

łane poprzecznymi naprężeniami rozciągającymi przyczołowymi (podob-

nie jak w kablobetonie przypadek ii)) oraz napr

ężeniami ścinające na styku niesprężonego

środnika i półki w której skupia się siła sprężająca. Wartość siły sprężającej należy przyjmo-
wa

ć: P

d

= P

0,max

i)

poprzeczne napr

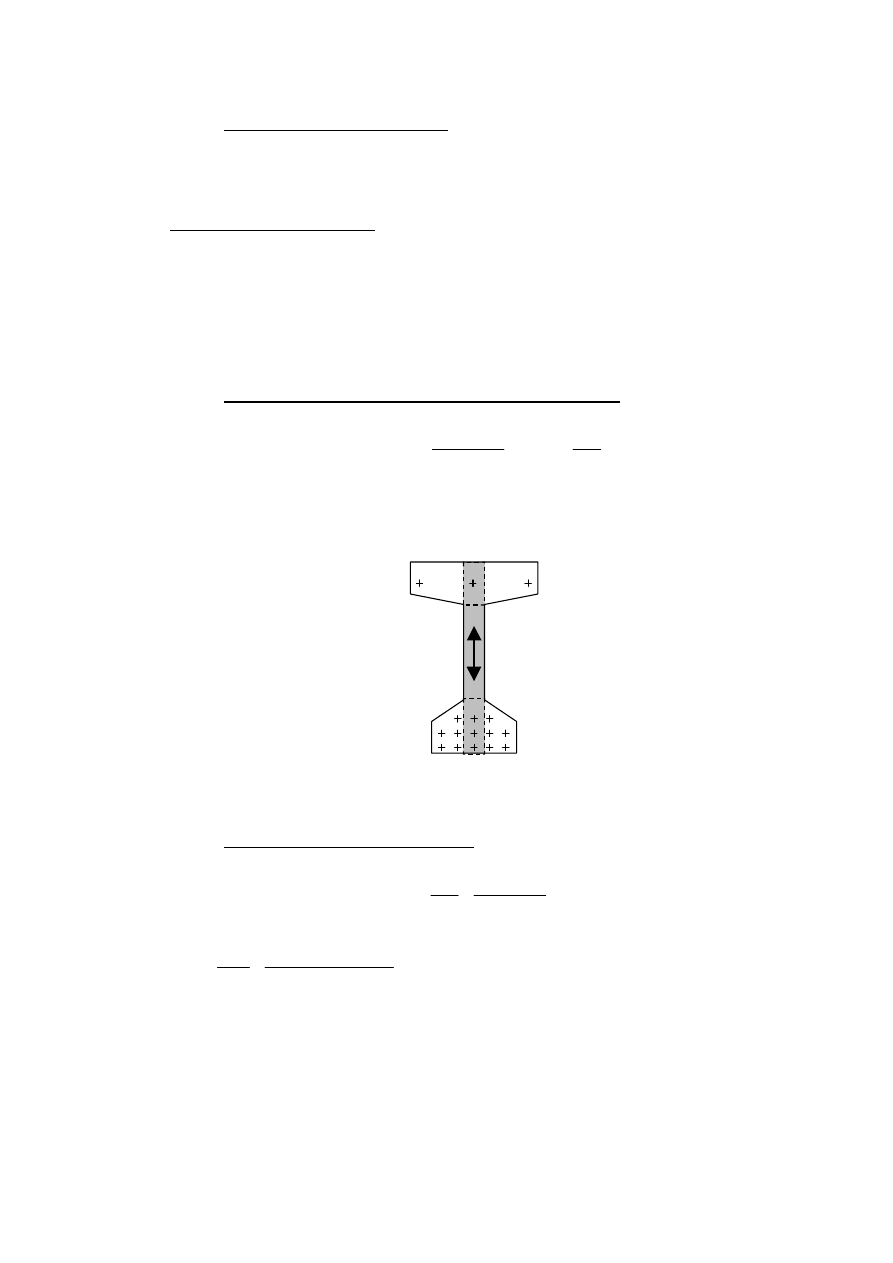
ężenia rozciągające przyczołowe (Rys. 11)

Wypadkow

ą naprężeń pomiędzy warstwami zakotwień oblicza się ze wzoru:

(

)

eff

,

p

2

d

1

d

12

p

12

pi

VSd

l

h

P

P

d

h

5

,

0

d

42

,

0

N

+

−

=

gdzie:

d

p12

– odleg

łość pomiędzy środkami ciężkości wypadkowych cięgien dolnych i

górnych,

P

d1

, P

d2

– si

ły sprężające w dolnej i górnej półce na szerokości środnika

N

VSd

Rys. 11

Analiza poprzecznych rozci

ągań przyczołowych

ii)

napr

ężenia rozwarstwiające (Rys. 12)

Wielko

ść siły rozwarstwiającej V

HSd

oblicza si

ę ze wzoru:

ct

eff

,

p

3

cp

1

cp

eff

,

p

1

d

HSd

A

l

2

l

P

V

σ

+

σ

−

=

,

gdzie napr

ężenia σ

cp3

na górnej kraw

ędzi dolnej półki oblicza się ze wzorów:

(

)

0

cs

1

0

cs

0

cp

d

0

cs

d

3

cp

J

h

d

h

z

P

A

P

−

−

+

=

σ

Obliczenie no

śności płaszczyzny styku i koniecznego zbrojenia prowadzi się tak jak w p.-cie

N5.5.4. przyjmuj

ąc we wzorach (N62) i (N63) za h

f

szeroko

ść środnika b

w

.

Je

śli belka nie ma wykształconej półki dolnej, wówczas jej umowną wysokość oblicza się ze

wzoru:

(

)

1

p

1

d

h

2

h

−

=

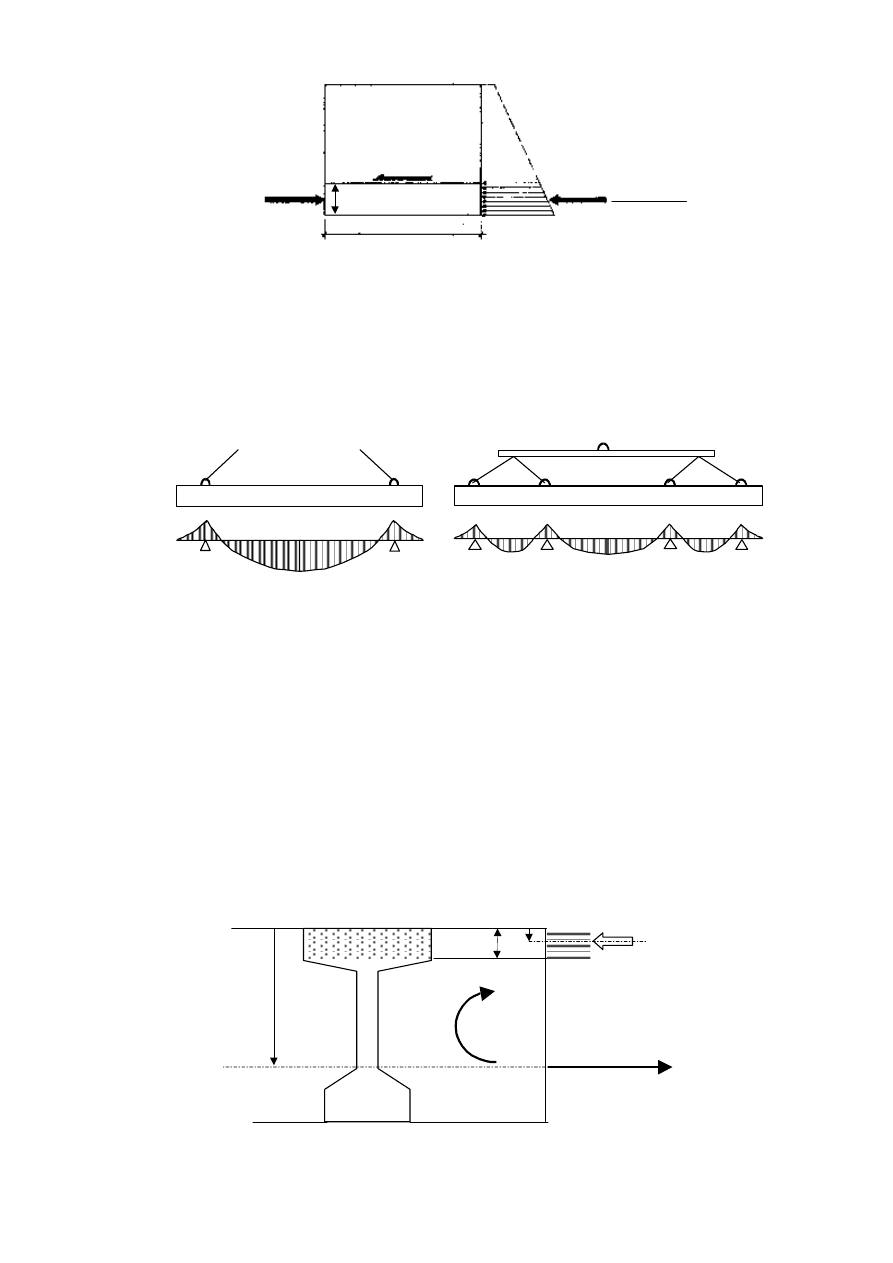
15

σ

cp1

P

d1

V

HSd

σ

cp1

σ

cp3

2

(σ

cp1

+

σ

cp3

)

A

ct

h

1

l

p,eff

Rys. 12 Wyznaczanie napr

ężeń rozwarstwiających

• Określenie sposobu składowania i transportu. Dobór haków montażowych

W projekcie nale

ży wskazać zasady składowania i transportu, kierując się względami tech-

nologicznymi (

środki transportu: dźwigi i zawiesia, naczepy, [15] i [16]), statycznymi (zgina-

nie, docisk, wyrwanie haka) i przepisami BHP. Sposób sk

ładowania i transportu może wywo-

łać odmienny od eksploatacyjnego stan naprężeń. Należy obliczeniowo wykazać, że stan ten
nie wywo

ła uszkodzenia elementu. Przy doborze haków należy kierować się zaleceniami

podanymi w [9] i [18].

Rys. 13

Momenty zginaj

ące w transporcie

7. Sprawdzenie SG w sytuacji monta

żowej

Sprawdzenie elementów w sytuacji monta

żowej dotyczy belek zespolonych, które mają różną no-

śność i sztywność przed i po zespoleniu, lub gdy występuje zmiana schematu statycznego (np.
podpory monta

żowe). Podpory montażowe, umieszczone w przęśle i odpowiednio rektyfikowane,

umo

żliwiają likwidację niepożądanych ugięć (pn. wynikających z małej sztywności elementu przed

zespoleniem).

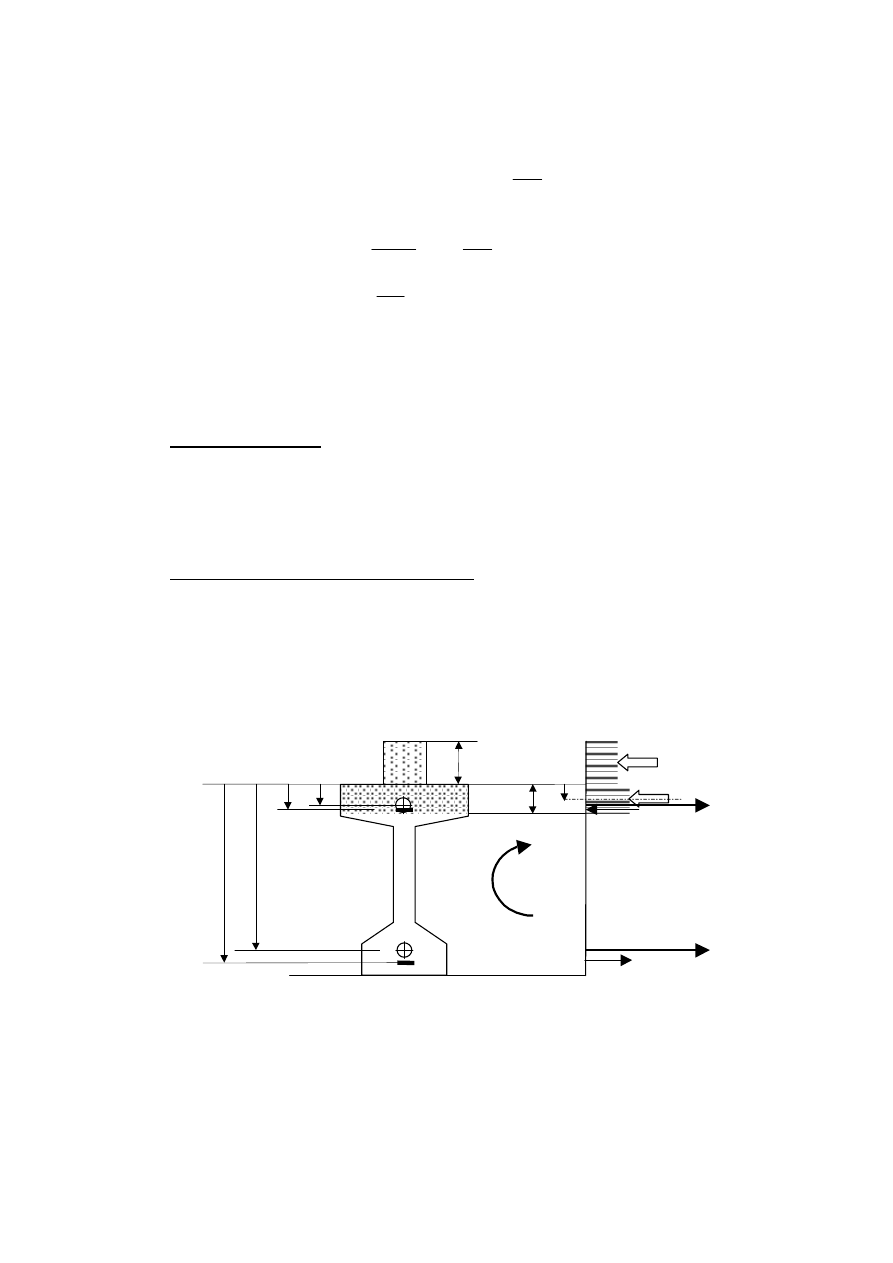
• SGN na zginanie

Poni

żej przedstawiono najbardziej uproszczoną metodę sprawdzania stanu granicznego no-

śności na zginanie. Przyjmuje się uproszczenia:
− prostokątny wykres naprężeń ściskających w betonie o wartości αf

cd.

(

α = 1)

− pominięcie zbrojenia miękkiego
− łączne zbrojenie sprężające o przekroju A

p

. = A

p1

+ A

p2

znajduje si

ę w swoim środku

ci

ężkości d

p

i osi

ąga pełną nośność: F

pd

= F

pd1

+ F

pd2

A

c

αf

cd

d

p

M

Rd

x

c,

e

ff

d

c

F

pd

16

Rys. 14

Stan Graniczny No

śności przekroju w sytuacji montażowej

Procedura oblicze

ń wygląda następująco:

i)

z warunku równowagi si

ł obliczyć:

cd

pd

eff

,

cc

f

F

A

α

=

ii)

z geometrii strefy

ściskanej wyznaczyć x

c,eff

i d

c

Dla prostok

ąta:

2

eff

,

cc

eff

b

A

x

=

2

x

d

eff

c

=

iii)

Sprawdzi

ć czy

lim

,

eff

p

eff

eff

d

x

ξ

≤

=

ξ

; gdzie

ξ

eff,lim

d

p

ze wzoru (N141) (we wzorze

(N143) mo

żna przyjąć, że f

pd

= F

pd1

/A

p1

a

σ

pmt

=

σ

pm0

), je

śli nie, to przyjąć x

eff

=

ξ

eff,lim

d

p

. i obliczy

ć d

c

i A

cc,eff

iv)

Obliczy

ć:

(

)

c

p

cd

eff

,

cc

Rd

d

d

f

A

M

−

α

=

v)

Sprawdzi

ć, czy M

Rd

≥ M

Sd

• SGN na ścinanie

Konstrukcje zespolone
Je

śli zgodnie z normą [N5] założymy, że beton zespalający nie współpracuje przy przeno-

szeniu si

ł poprzecznych to nośność konstrukcji na siły poprzeczne w sytuacji montażowej

(przed zespoleniem) nie b

ędzie się różnić od nośności konstrukcji w sytuacji trwałej (po ze-

spoleniu). Poniewa

ż siły poprzeczne wywołane obciążeniem obciążenia są z reguły większe

w sytuacji trwa

łej, stąd sprawdzenie przekrojów na ścinanie wykonuje się przy sprawdzaniu

elementu w sytuacji trwa

łej.

Konstrukcje ze zmian

ą schematu statycznego

Istnieje konieczno

ść sprawdzenia tej nośności w przekrojach, w których siła poprzeczna jest

wi

ększa niż w sytuacji trwałej. Metodę obliczeń omówiono dla sytuacji trwałej.

8. Sprawdzenie SG w sytuacji trwa

łej

• SGN na zginanie

Poni

żej przedstawiono metodę uproszczoną sprawdzania stanu granicznego nośności na

zginanie. Przyjmuje si

ę uproszczenia:

− prostokątny wykres naprężeń ściskających w betonie
− zbrojenie miękkie zgrupowane jest w poszczególnych warstwach

A

cc

αf

cd

d

p

2

x

c,

e

ff

d

c

σ

p2

A

p2

A

s2

d

p

1

d

s2

A

p1

M

Rd

A

s1

d

s1

A

s1

f

yd

F

pd1

A

s2

f

yd

h

n

A

p2

A

cn

αf

cdn

Rys. 15

Stan graniczny no

śności przekroju w sytuacji trwałej

Procedura oblicze

ń wygląda następująco:

i)

obliczy

ć naprężenia w cięgnach górnych:

[MPa]

400

0

pm

2

p

−

σ

=

σ

ii)

z warunku równowagi si

ł obliczyć:

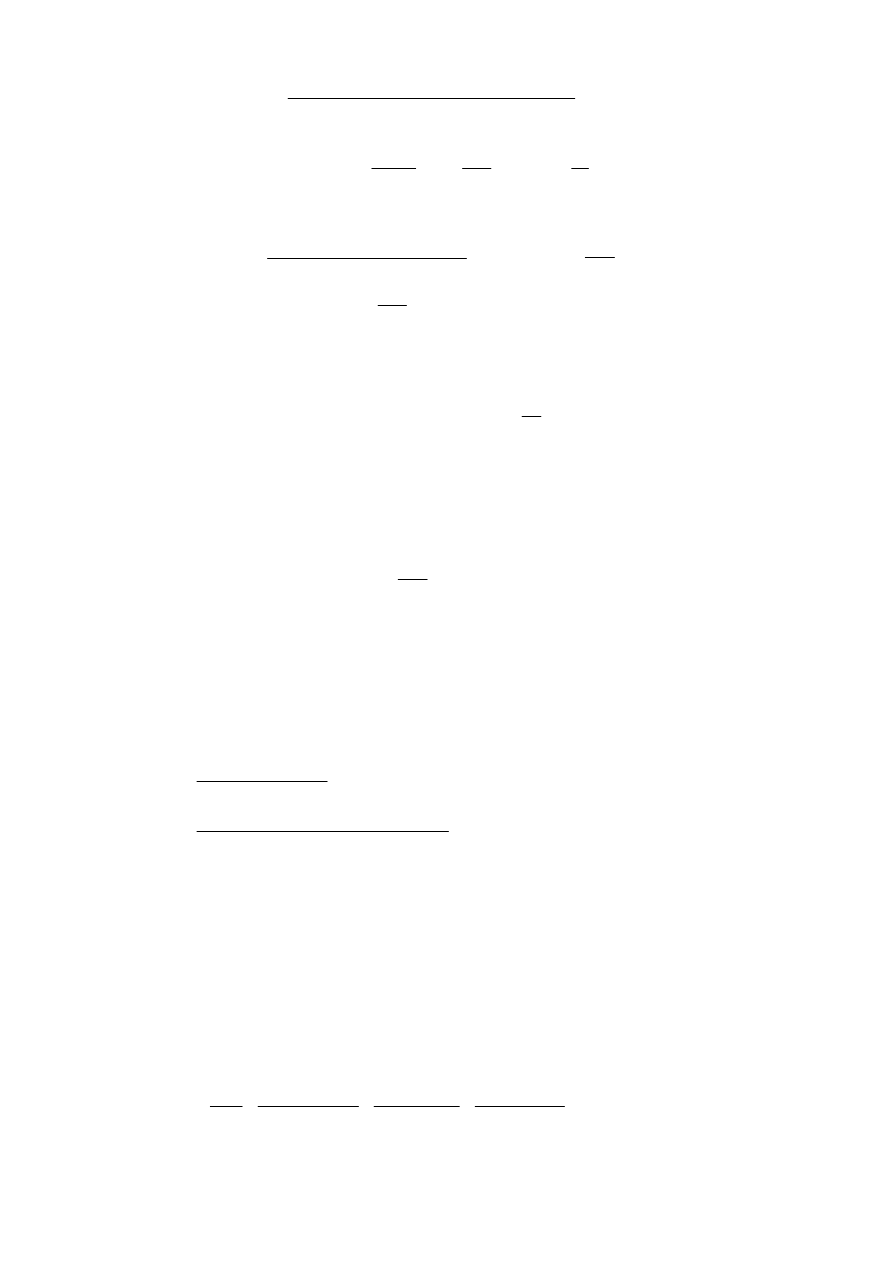
17

(

)

cd

cdn

cn

yd

2

s

1

s

2

p

2

p

1

pd

eff

,

cc

f

f

A

f

A

A

A

F

A

α

α

−

−

+

σ

+

=

iii)

z geometrii strefy

ściskanej wyznaczyć x

c,eff

i d

c

Dla prostok

ąta:

2

eff

,

cc

eff

b

A

x

=

2

x

d

eff

c

=

2

h

d

n

cn

=

Je

śli A

cc,eff

< 0 oznacza to,

że oś obojętna znajduje się w nadbetonie.

Wówczas nale

ży przyjąć: A

cc,eff

= 0; x

eff

= d

c

= 0, oraz obliczy

ć:

(

)

cdn

yd

2

s

1

s

2

p

2

p

1

pd

cn

f

f

A

A

A

F

A

α

−

+

σ

+

=

oraz

n

cn

n

cn

b

2

A

h

d

−

=

iv)

Sprawdzi

ć czy

lim

,

eff

p

eff

eff

d

x

ξ

≤

=

ξ

; gdzie

ξ

eff,lim

d

p

ze wzoru (N141) (we wzorze

(N143) mo

żna przyjąć, że f

pd

= F

pd1

/A

p1

), je

śli nie, to przyjąć x

eff

=

ξ

eff,lim

d

p

. i obliczy

ć

d

c

i A

cc,eff

v)

Obliczy

ć:

(

)

(

)

(

)

(

)

[

]

yd

1

s

p

1

s

2

s

p

2

s

2

p

p

2

p

2

p

n

p

cdn

cn

c

p

cd

eff

,

cc

Rd

f

d

d

A

d

d

A

d

d

A

2

h

d

f

A

d

d

f

A

M

−

+

−

−

−

σ

−













+

α

+

−

α

=

vi)

Sprawdzi

ć, czy M

Rd

≥ M

Sd

• SGN na ścinanie - dobór zbrojenia poprzecznego

Przekrój spr

ężony oblicza się tak jak przekrój żelbetowy, uwzględniając postanowienia punk-

tu N7.1.8.4 oraz przyjmuj

ąc

c

Sd

cp

A

N

=

σ

; gdzie

mt

Sd

P

9

,

0

N

=

.

Mo

żna uwzględnić zmniejszenie obciążenia przekroju siłą V

Sd

zgodnie ze wzorem (N168)

przyjmuj

ąc że kąt α

0

odpowiada warto

ści kąta φ(x) obliczonego wg Rys. 5 w przekroju, w któ-

rym obliczana jest si

ła V

Sd

.

Ponadto, w konstrukcjach kablobetonowych i z kablami bez przyczepno

ści należy uwzględ-

ni

ć osłabienie przekroju kanałami kablowymi. W przekrojach z kablami bez przyczepności

wype

łnienia kanałów kablowych nie uwzględnia się.

• Zabezpieczenie konstrukcji zespolonej przed rozwarstwieniem w płaszczyźnie zespolenia

We wzorze (N180) nale

ży przyjąć:

cdn

cn

cd

eff

,

cc

cdn

cn

f

A

f

A

f

A

+

=

β

(

)

cdn

cn

cd

eff

,

cc

cn

p

cdn

cn

c

p

cd

eff

,

cc

f

A

f

A

d

d

f

A

)

d

d

(

f

A

z

+

+

+

−

=

, lecz nie wi

ęcej niż 0,8d

p.

Przyj

ęte zbrojenia powierzchni styku może być związane z poprzecznym zbrojeniem prefa-

brykatu rozstawem pr

ętów lub wykorzystaniem np. pionowych gałęzi strzemion żeber. Po-

niewa

ż obciążenie powierzchni styku zmienia się podobnie jak siła poprzeczna, możliwe i

celowe jest ró

żnicowanie tego zbrojenia na długości styku, dokonując obliczeń w odpowied-

nich przekrojach.

• Sprawdzenie możliwości pojawienia się rys prostopadłych

O mo

żliwości pojawienia się rys prostopadłych decyduje wartość naprężeń na dolnej krawę-

dzi elementu

σ

c1

. Napr

ężenia te obliczać należy wykorzystując zasadę ich superpozycji, tzn,

obliczy

ć naprężenie będące efektem przyrostu obciążenia, sztywności belki i schematu sta-

tycznego w danej sytuacji (pocz

ątkowej, montażowej, trwałej), a następnie je zsumować.

Dzia

łające obciążenie jest wywołane oddziaływaniami długotrwałymi oraz przyjmuje wartości

obliczeniowe przy

γ

f

= 1,0, za

ś siła sprężająca wartość obliczeniową P

d

=P.

k,inf

= 0,9P

mt

.

W sytuacji trwa

łej:

(

)

(

)

(

)

cs

cs

Sd

0

cs

0

cs

Sd

0

cs

0

cs

0

cp

d

0

cs

d

1

c

J

d

h

M

J

d

h

M

J

d

h

z

P

A

P

−

∆

−

−

−

−

+

=

σ

,

gdzie: M

Sd

moment zginaj

ący w sytuacji montażowej

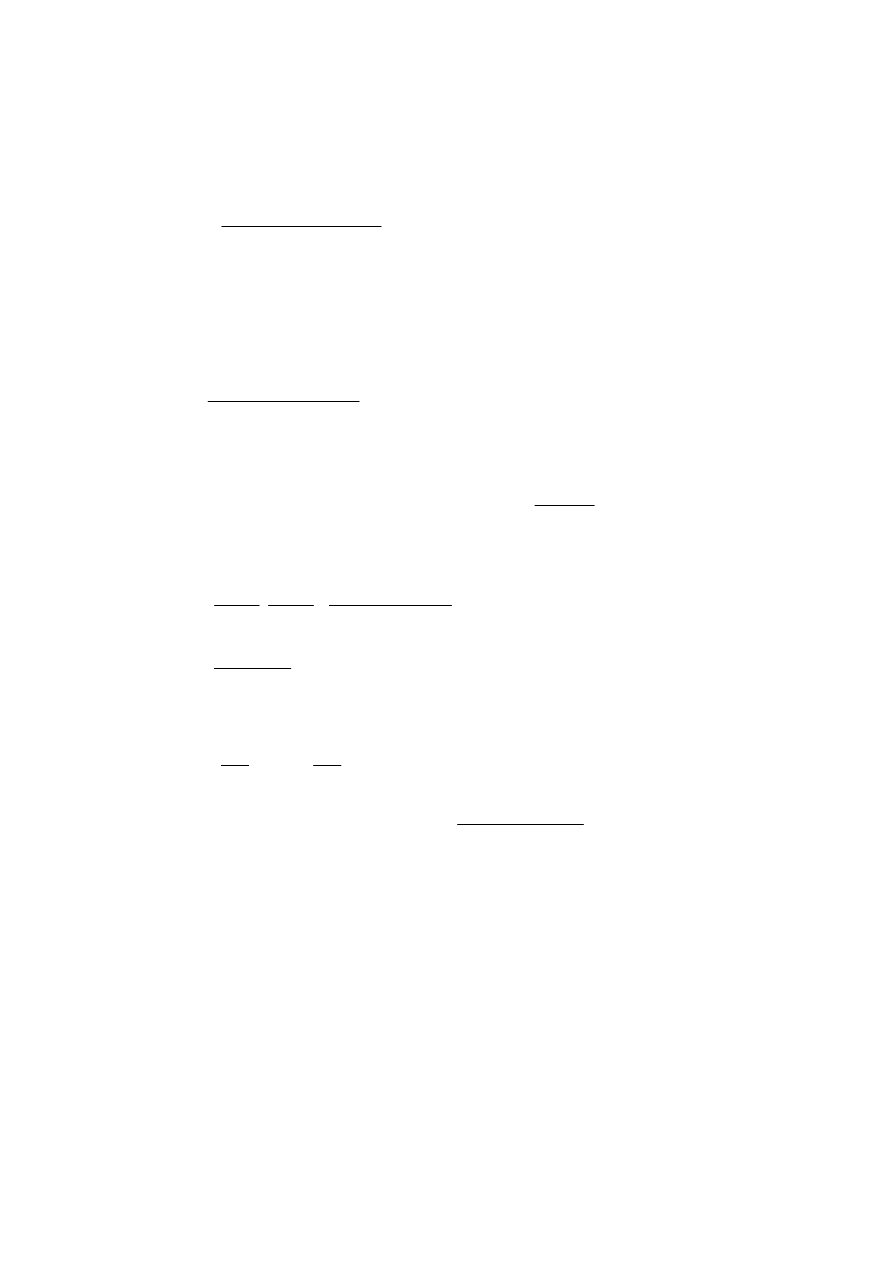
18

∆M

Sd

przyrost momentu zginaj

ącego wywołany pozostałymi obciążeniami (działają-

cymi d

ługotrwale)

Rysy nie wyst

ąpią, jeśli obliczone w powyższy sposób naprężenia (rozciągające) będą

mniejsze ni

ż f

ctm

:

ctm

1

c

f

−

≥

σ

, a zbrojenie w strefie rozci

ąganej spełnia warunek (N111), w

którym

σ

s,lim

nale

ży przyjąć uwzględniając zarówno cięgna jak i zbrojenie miękkie. Zastępczą

warto

ść naprężeń σ

s,lim

obliczy

ć ze wzoru:

1

s

1

p

lim

,

s

1

s

lim

,

s

1

p

lim

,

s

A

A

)

s

(

A

)

p

(

A

+

σ

+

σ

=

σ

gdzie: A

p1

, A

s1

– pole przekroju zbrojenia w strefie rozci

ąganej,

σ

s,lim

(p)i

σ

s,lim

(s) – warto

ść naprężenia w zbrojeniu z Tablicy N12, odpowiednio dla cię-

gien i zbrojenia zwyk

łego.

• Sprawdzenie SGU szerokości rozwarcia rys prostopadłych

Dokonujemy zgodnie z N7.1.9.3, uwzgl

ędniając cięgna (kable) i zbrojenie miękkie w dolnej

pó

łce.

We wzorze (N94) nale

ży przyjąć:

−

∑

∑

∑

∑

+

φ

+

φ

=

φ

p

s

p

p

p

1

s

s

s

1

1

n

n

n

k

n

k

k

,

gdzie: k

1s

φ

s

, k

1p

φ

p

- wsp. zale

żny od przyczepności i średnicy prętów,

Σn

s

,

Σn

s

- suma liczby pr

ętów

odpowiednio dla stali mi

ękkiej i cięgien,

− A

ct,eff

obliczy

ć na podstawie rys (N33) przyjmując

h

x

1

c

2

c

2

c

II

σ

−

σ

σ

=

, gdzie

σ

c1

i

σ

c2

napr

ężenia

odpowiednio na dolnej i górnej kraw

ędzi (w otoczeniu kabli, dla każdego kabla można przy-

j

ąć pole kwadratu o boku 300 mm)

Obliczenie momentu dekompresji przekroju:

(

)













−

+

−

=

0

cs

0

cs

cp

t

,

m

0

cs

t

,

m

cs

cs

de

J

d

h

z

P

9

,

0

A

P

9

,

0

d

h

J

M

Przyrost napr

ężeń w stali w przekroju zarysowanym:

(

)

z

A

A

M

M

1

s

1

p

de

Sd

s

+

−

=

σ

∆

gdzie z – rami

ę sił wewnętrznych, można przyjmować

1

p

d

)

90

.

0

85

.

0

(

z

÷

≅

Średnie odkształcenie zbrojenia wzór (N114):



























β

β

−

σ

∆

=

ε

∆

2

Sd

de

2

1

p

s

sm

M

M

1

E

gdzie

β

1

nale

ży obliczać ze wzoru

∑

∑

∑

∑

+

β

+

β

=

β

p

s

p

p

1

s

s

1

1

n

n

n

n

• Sprawdzenie SGU możliwości pojawienia się rys ukośnych

Dokona

ć należy w strefie przypodpoowej. Polega na wykazaniu, że rozciągające naprężenia

g

łówne nie przekroczą wytrzymałości betonu na ściskanie.

W belkach nale

ży sprawdzać w przekroju podporowym (A - A) i przy zmianie środnika – tak-

że w przekroju B – B (Rys. 16). W belkach strunobetonowych należy uwzględnić wartość siły
P

mt

(x) = wed

ług rysunku N37.

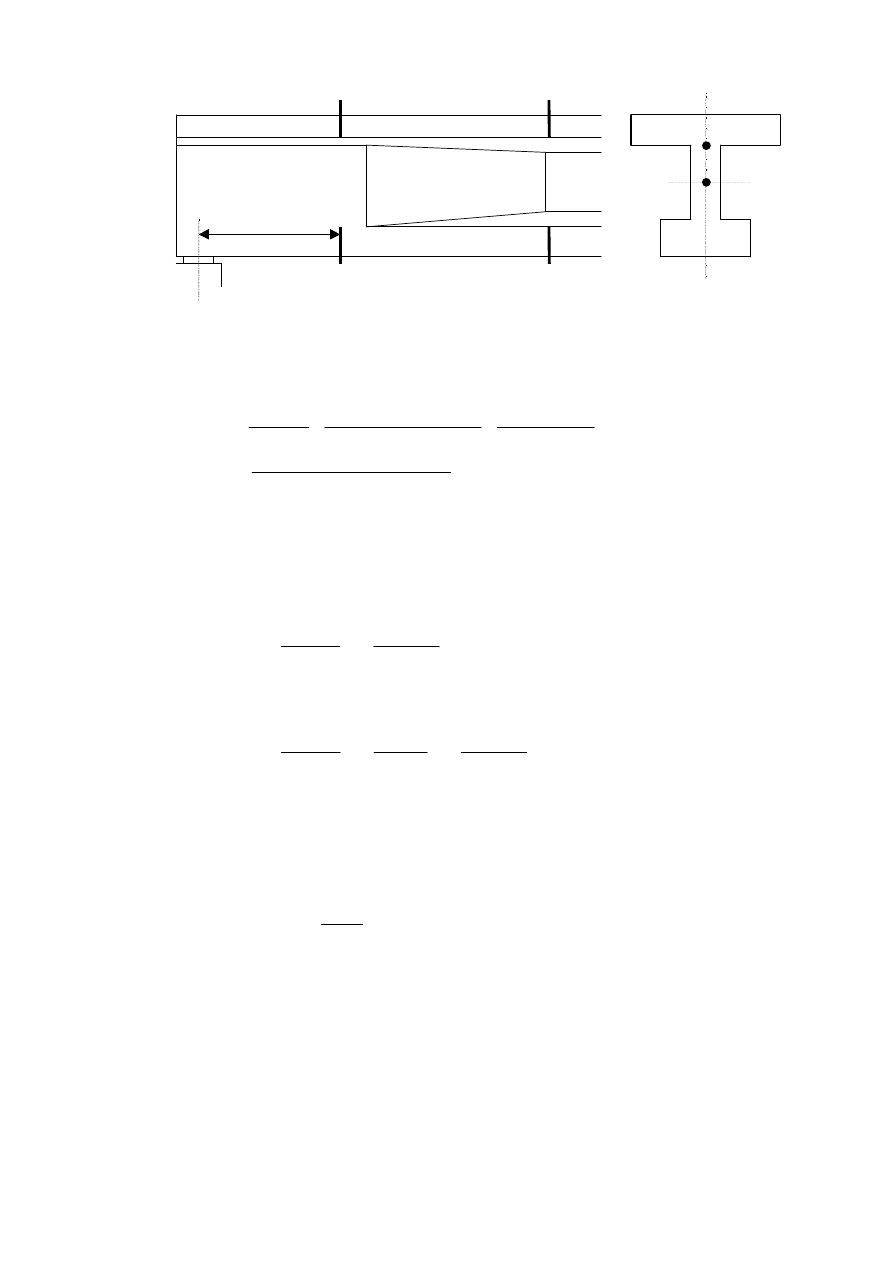
19

x = h

A

B

B

A

2

1

Rys. 16

Przekroje w których oblicza si

ę główne naprężenia rozciągające

Obliczenia napr

ężeń należy dokonać w poziomie 1 (na wysokości zmiany środnika) i 2

(w

środku ciężkości przekroju), wykorzystując wzór (N153), w którym:

(

)

(

)

cs

2

i

Sd

0

cs

2

i

0

cp

mt

0

cs

mt

x

J

y

d

)

x

(

M

J

y

d

)

x

(

z

)

x

(

P

9

,

0

A

)

x

(

P

9

,

0

−

−

−

+

=

σ

(

)

w

cst

co

mt

Sd

xy

b

J

S

)

x

(

sin

)

x

(

P

9

,

0

)

x

(

V

α

−

=

τ

Wzory powy

ższe zostały przedstawione w ogólnej postaci, uwzględniając odgięcie cięgien i

zmian

ę szerokości środnika (interpretacja wielkości b

w

!). Pionowe napr

ężenia normalne σ

y

zaleca si

ę pominąć.

• Sprawdzenie SGU ugięć

Ugi

ęcia w elementach niezarysowanych obliczać należy wykorzystując zasadę ich superpo-

zycji, tzn, obliczy

ć ugięcie będące efektem przyrostu obciążenia, sztywności belki i schematu

statycznego w danej sytuacji (pocz

ątkowej, montażowej, trwałej), a następnie je zsumować.

∑

α

−

∆

α

=

0

cs

c

2

eff

0

cp

pd

p

cs

c

2

eff

Sd

k

J

E

l

z

N

J

E

l

M

a

i

i

i

i

W przypadku konstrukcji zarysowanej mo

żna postąpić podobnie. Rozpatrując działanie przy-

rostu obci

ążenia w fazie zarysowanej, przyjąć zredukowaną sztywność belki B w sytuacji

dzia

łania sumy obciążenia (całość M

Sd

).

∑

α

−

∆

α

+

∆

α

=

0

cs

c

2

eff

0

cp

pd

p

Sd

2

eff

Sd

k

cs

c

2

eff

Sd

k

J

E

l

z

N

)

M

(

B

l

M

J

E

l

M

a

i

i

i

i

Przy obliczaniu ugi

ęć długotrwałych należy przyjąć efektywny moduł sprężystości betonu (z

uwzgl

ędnieniem współczynnika pełzania), i dla tej wartości obliczyć momenty bezwładności

przekroju w poszczególnych sytuacjach (zmiana wspó

łczynników α).

• Sprawdzenie SG zmęczenia (N7.2.)

Na wst

ępie należy sprawdzić zasadność sprawdzania konstrukcji w tej sytuacji:

6

,

0

M

M

k

pk

≥

∑

Nale

ży obliczyć stan naprężeń w przekroju w przypadku działania i braku działania obciąże-

nia wielokrotnie zmiennego przyjmuj

ąc charakterystyczne wartości obciążenia (ew. ze

wspó

łczynnikiem dynamicznym) i N

pd

= 1.1P

m,t

W wyniku tego, otrzymuje si

ę dwa wykresy naprężeń w betonie odpowiadające działaniu ob-

ci

ążeń stałych (lub minimalnych) oraz stałych i zmiennych (lub maksymalnych). Na podsta-

wie zmienno

ści naprężeń w skrajnych włóknach, należy przyjąć dopuszczalną wartość

σ

cR

.(Rys. 17)

20

σ

c

≤ 0,02maxσ

c

max

σ

c

≤ 0,18f

ck

σ

c

≤ 0,25f

ck

σ

c

≥ 0

STAN OBCI

ĄśEŃ STAŁYCH

(MINIMALNYCH)

STAN OBCI

ĄśEŃ PEŁNYCH

(MAKSYMALNYCH)

Rys. 17

Dopuszczane, maksymalne napr

ężenia w betonie przy działaniu obciążeń wielokrotnie

zmiennych

Je

śli zakres zmian naprężeń nie pozwala na odczytanie wartości σ

cR

, nale

ży skorzystać z

innej metody, cho

ć świadczy to o nadmiernym wytężeniu betonu. i wskazuje na celowość

zmiany koncepcji konstrukcji przekroju.
Ustalenie zmiany napr

ężeń w cięgnach sprężających lub w zbrojeniu pomocniczym moż-

na dokona

ć, wykorzystując poprzednie obliczenia:













σ

∆

−

σ

∆

+

σ

∆

α

=

σ

∆

h

d

2

c

1

c

1

p

2

c

p

1

p













σ

∆

−

σ

∆

+

σ

∆

α

=

σ

∆

h

d

2

c

1

c

1

s

2

c

s

1

s

gdzie

∆σ

c1

,

∆σ

c2

ró

żnice w naprężeniach w betonie, odpowiednio na dolnej i górnej

kraw

ędzi.

Ograniczenia wynikaj

ące z warunków ograniczenia naprężeń mogą spowodować ko-

nieczno

ść zmiany kształtu konstrukcji. Przesłanki byłyby następujące:

-

niespe

łnienie warunków ograniczenia naprężeń w betonie wskazuje na zmianę

gabarytów pó

łek (dolnej lub górnej) lub podniesienie wysokości konstrukcji. W sumie

– zwi

ększenie momentu bezwładności.

-

Przekroczenie dopuszczalnego zakresu zmian napr

ężeń w cięgnach wskazuje na

konieczno

ść zmniejszenia mimośrodu cięgien w stosunku do środka ciężkości prze-

kroju.

21

LITERATURA:

[1]

Ajdukiewicz A, Mames J.: „Konstrukcje spr

ężone". Warszawa ARKADY 1984.

[2]

Ajdukiewicz A, Mames J.: „Betonowe konstrukcje spr

ężone". Gliwice Wydawnictwo PŚ 2001

[3]

D

ąbrowski K., Stachurski W., Zieliński Z. A.: "Konstrukcje betonowe" Warszawa ARKADY 1982.

[4]

* Dyduch K.,: „Obliczanie konstrukcji spr

ężonych” Konf. N. – T. „Podstawy projektowania kon-

strukcji z betonu w uj

ęciu normy PN-B-03264:1998 w świetle Eurokodu 2”, Puławy 1998, ITB

Warszawa 1998

[5]

Grabiec K, Kampioni J.: „Betonowe konstrukcje spr

ężone". PWN Warszawa - Poznań 1982

[6]

* Grzegorzewski W. „Deski spr

ężone". Warszawa ARKADY 1965.

[7]

* Guyon Y. „Prestressed Concrete". Wiley & Sons, London 1953

[8]

Jasman S.: Projektowanie i wykonawstwo konstrukcji betonowych. Pol. Wroc

ławska Wrocław

1990.

[9]

Kledzik W., Kledzik B., Kot A.: „Wzory i tablice do projektowania konstrukcji

żelbetowych”. War-

szawa ARKADY 1982.

[10] * Ku

ś S „Konstrukcje sprężone kołowo - symetryczne". Warszawa ARKADY 1960.

[11] * Lin T.Y, Burns N.H.: „Design of Prestressed Concrete Structures", Wiley & Sons N.York 1982.
[12] Olszak i in. Teoria konstrukcji spr

ężonych T. I i II PWN Warszawa 1961.

[13] Pr. zbiorowa „Budownictwo betonowe". T. III Konstrukcje spr

ężone. Warszawa ARKADY 1965.

[14] Pr. zbiorowa „Poradnik in

żyniera i technika budowlanego". Tom V, Warszawa ARKADY 1996.

[15] Pr. zbiorowa „Poradnik kierownika budowy". Tom I i II, Warszawa ARKADY 1989.
[16] Pr. zbiorowa „Poradnik majstra budowlanego ". Warszawa ARKADY 1985.
[17] * Rossuee W., Graubner C.A., „Spannbetonbauwerke Teil l." Berlin Ernst & Sohn 1992.
[18] Starosolski W.: „Konstrukcje

żelbetowe, T. I i T. II”. PWN Warszawa 1996

[19] Zieli

ński Z. A.: Prefabrykowane betonowe dźwigary sprężone. Warszawa ARKADY 1962.

Normy,
[N1]. Aktualne normy obci

ążeniowe.

[N2]. PN-90/B-03000. Projekty budowlane - obliczenia statyczne.
[N3]. PN-80/B-01800. Antykorozyjne zabezpieczenia w budownictwie - konstrukcje betonowe i

żelbe-

towe - klasyfikacja i okre

ślenie środowisk.

[N4]. FIP-CEB Model Code 1980
[N5]. PN-B-03264:2002 konstrukcje betonowe,

żelbetowe i sprężone. Obliczenia statyczne i projek-

towanie.

22

ZA

ŁĄCZNIK 1. DANE WYBRANYCH SYSTEMÓW KABLI SPRĘśAJĄCYCH

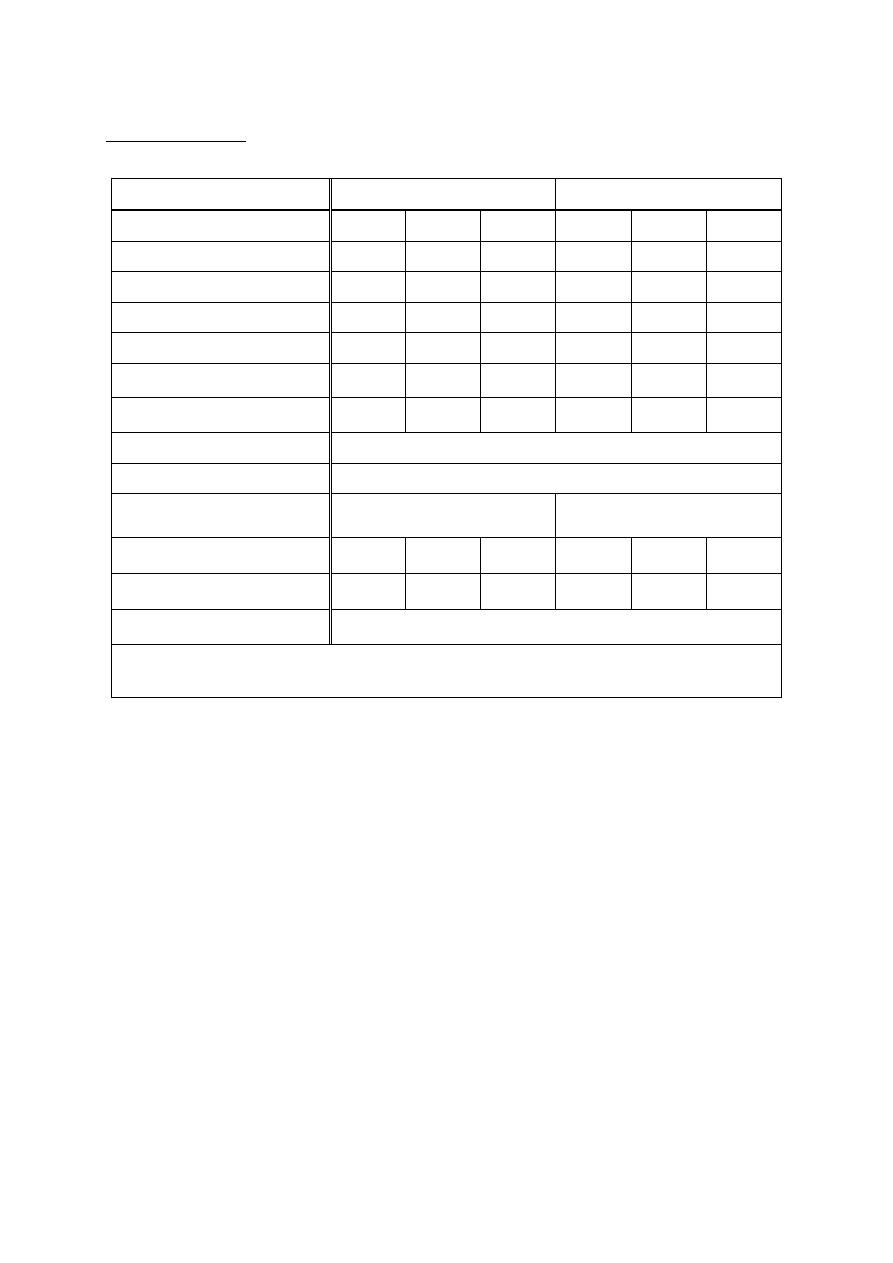
Pr

ęty i kable prętowe

Tab. 4 Pr

ęty sprężające żebrowane i gładkie. Kable z przyczepnością i bez przyczepności.

Klasa stali

835/1030

1080/1230

średnica pręta, mm

26

32

36

26

32

36

Przekrój,cm

2

5,31

8,04

10,18

5,31

8,04

10,18

Granica plastyczno

ści F

pyk

, kN

443,0

671,0

850,0

574,0

868,0

1099,0

No

śność F

pk

, kN

547,0

828,0

1049,0

653,0

989,0

1252,0

Kana

ł kablowy, ∅

zewn

mm

32/42

*)

38/46

*)

44/50

*)

32/42

*)

38/46

*)

44/50

*)

Min. promie

ń odgięcia spręży-

stego, m

15,9

19,5

21,9

8,75

10,75

12,1

Min promie

ń odgięcia plastycz-

nego, m

3,9

4,8

5,4

3,9

4,8

5,4

wsp. tarcia,

µ

0,25/0,05

*)

K

ąt falowania, rad/m

0,058

Po

ślizg cięgna w zakotwieniu,

mm

0,5/1,0

**)

1,0/1,5

**)

P

łytka kotwiąca

(wys.

× szer.), mm

120

×150 120×220 150×240 120×150 120×220 150×240

Min. rozstaw zakotwie

ń

(wys.

× szer.), mm

130

×200 130×300 160×280 130×200 130×300 160×280

Min. odleg

łość krawędzi zako-

twienia od kraw

ędzi betonu, mm

20

*)

– dla kabli bez przyczepno

ści

**)

– dla pr

ętów żebrowanych

Modu

ł sprężystości prętów i kabli prętowych E

p

= 200 GPa.

Kable pr

ętowe stosuje się jako kotwy, ściągi itp. Przydatne także do łączenia prefabrykowa-

nych elementów konstrukcyjnych, pe

łniąc role podobną do śrub sprężających. Ich zakotwienia gwin-

towe charakteryzuj

ą się bardzo małym poślizgiem, umożliwiając stosowanie tych kabli o bardzo ma-

łych długościach.

23

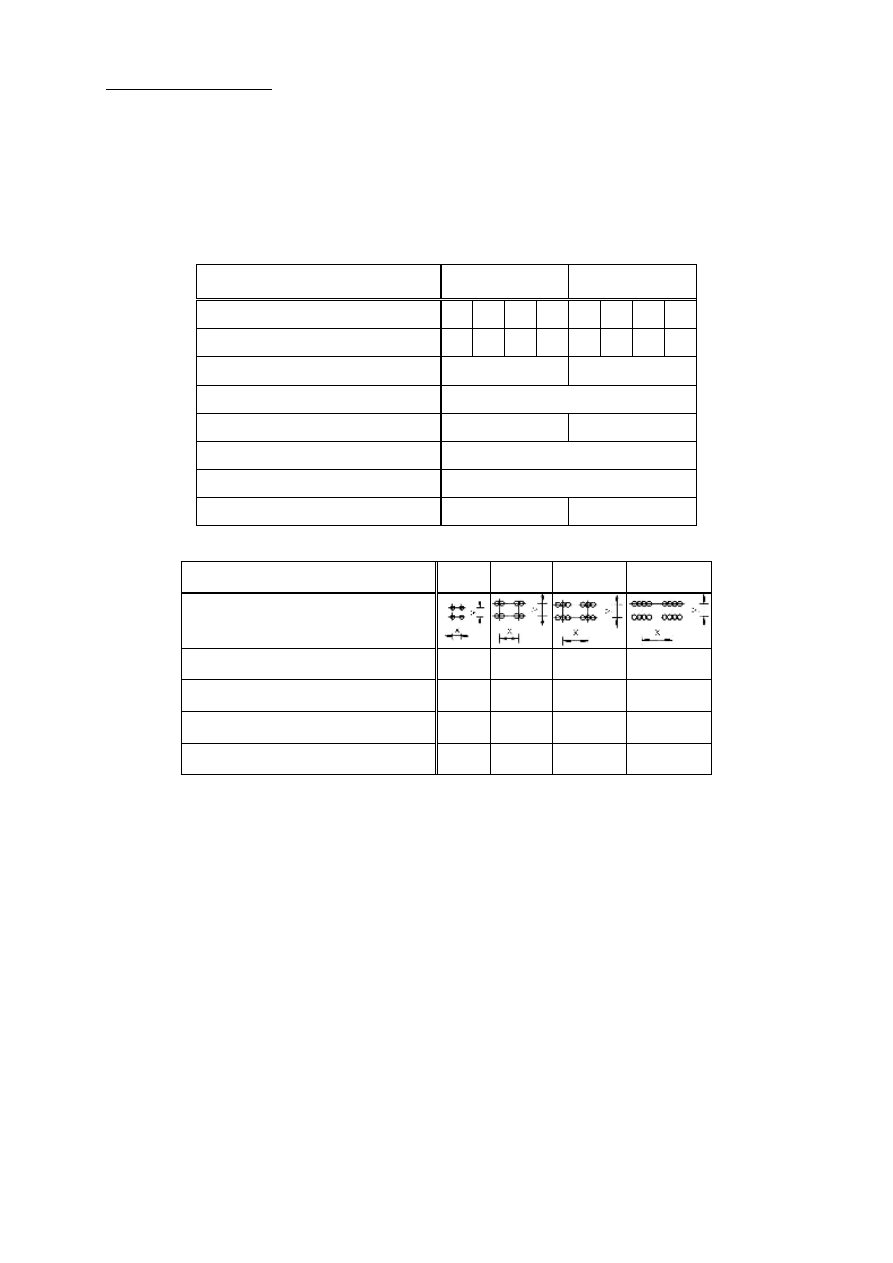
Kable bez przyczepno

ści

Stosowane do spr

ężania płyt ciągłych w popularnych systemach płytowo – słupowych, oraz do

obwodowego spr

ężania konstrukcji cylindrycznych (zbiorniki). Z uwagi na walory technologii, często

stosowane do wzmacniania konstrukcji. Kable te charakteryzuj

ą się bardzo niskim współczynnikiem

tarcia, dzi

ęki wprowadzeniu do przestrzeni kablowej środków smarnych i antykorozyjnych. W rezulta-

cie, si

ła sprężająca utrzymywane jest wyłącznie dzięki zakotwieniom, i nie prowadzi się kłopotliwych

technologicznie robót iniekcyjnych.

Poni

żej przedstawiono dane przykładowych rozwiązań kabli. Nośność kabli, powierzchnia

przekroju i inne dane zale

żą od rodzaju użytych cięgien (zgodnie z Tab. 2)

Tab. 5 Kable bez przyczepno

ści – dane przykładowe

Splot

∅ 16 mm

∅ 15,5 mm

∅ 13 mm

∅ 12,5 mm

Oznaczenie systemowe kabla

1/16 2/16 3/16 4/16 1/13 2/13 3/13 4/13

liczba splotów

1

2

3

4

1

2

3

4

Kana

ł kablowy, n×∅

zewn

mm

n

×20,5

n

×17,5

Max. rozstaw podpór kabli, m

1,0

Min promie

ń odgięcia R, m

2,5

2,0

wsp. tarcia,

µ

0,06

K

ąt falowania, rad/m

0,009

Po

ślizg cięgna w zakotwieniu, mm

5 - 7

4 – 6

Tab. 6 Kable bez przyczepno

ści –dane geometryczne

Liczba splotów

1

2

3

4

Konfiguracja kabli

Rozstaw kabli, mm:

x

y

45
45

80
60

100

60

120

60

P

łytka kotwiąca

(wys.

× szer.), mm

55

×130 130×180 130×180

140

×200

Min. rozstaw zakotwie

ń

(wys. / szer.), mm

100/190 160/240

180/260

200/280

Min. odleg

łość środka zakotwienia od

kraw

ędzi betonu, mm

70

100

110

120

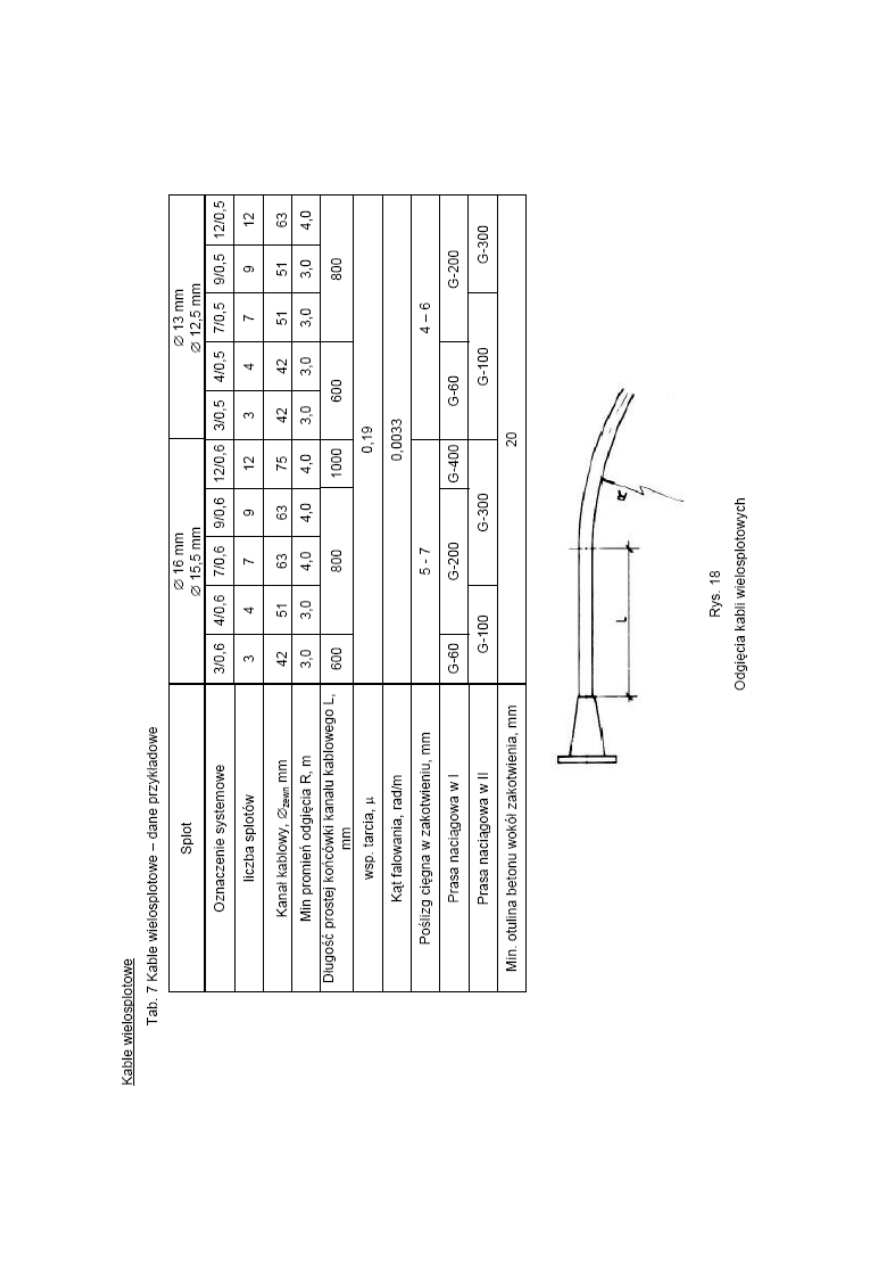
24

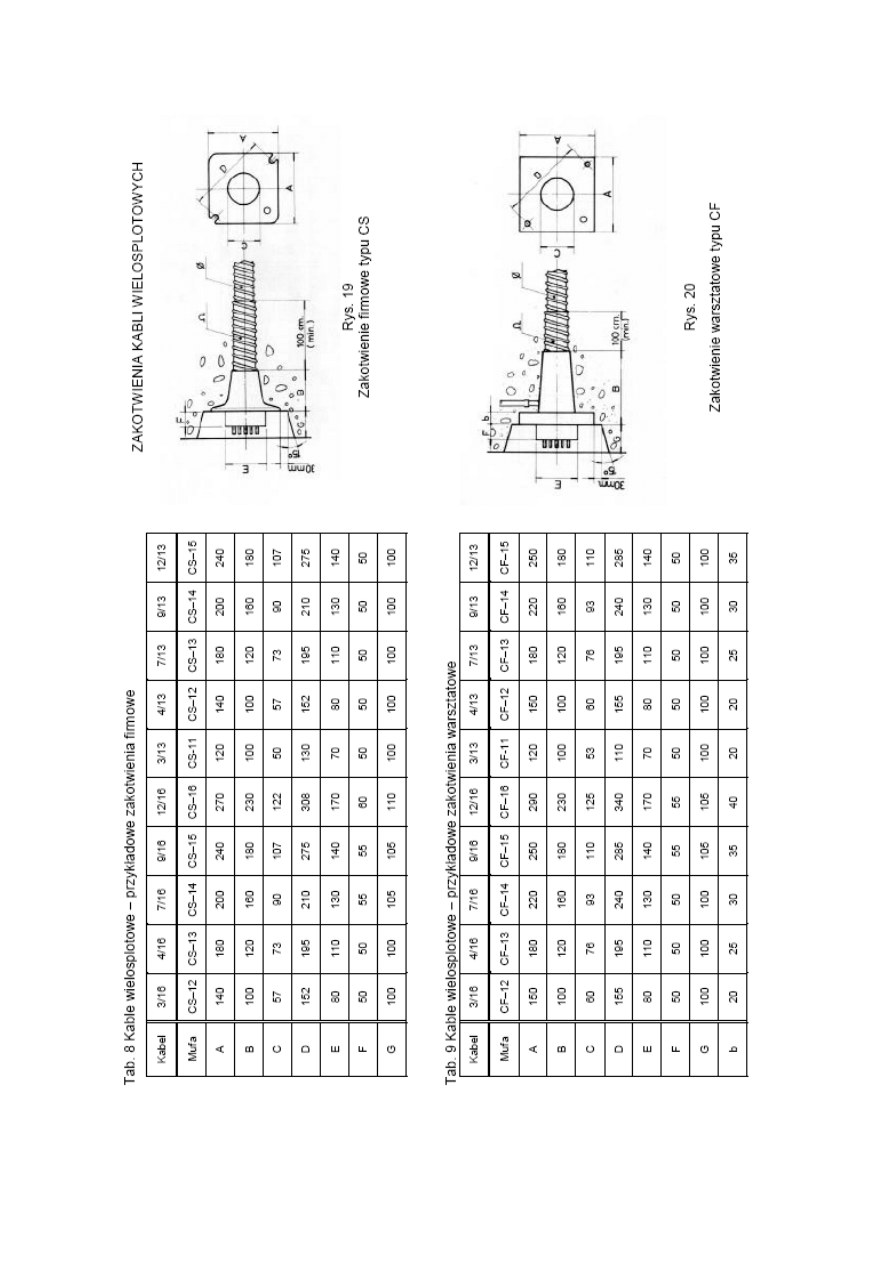
25

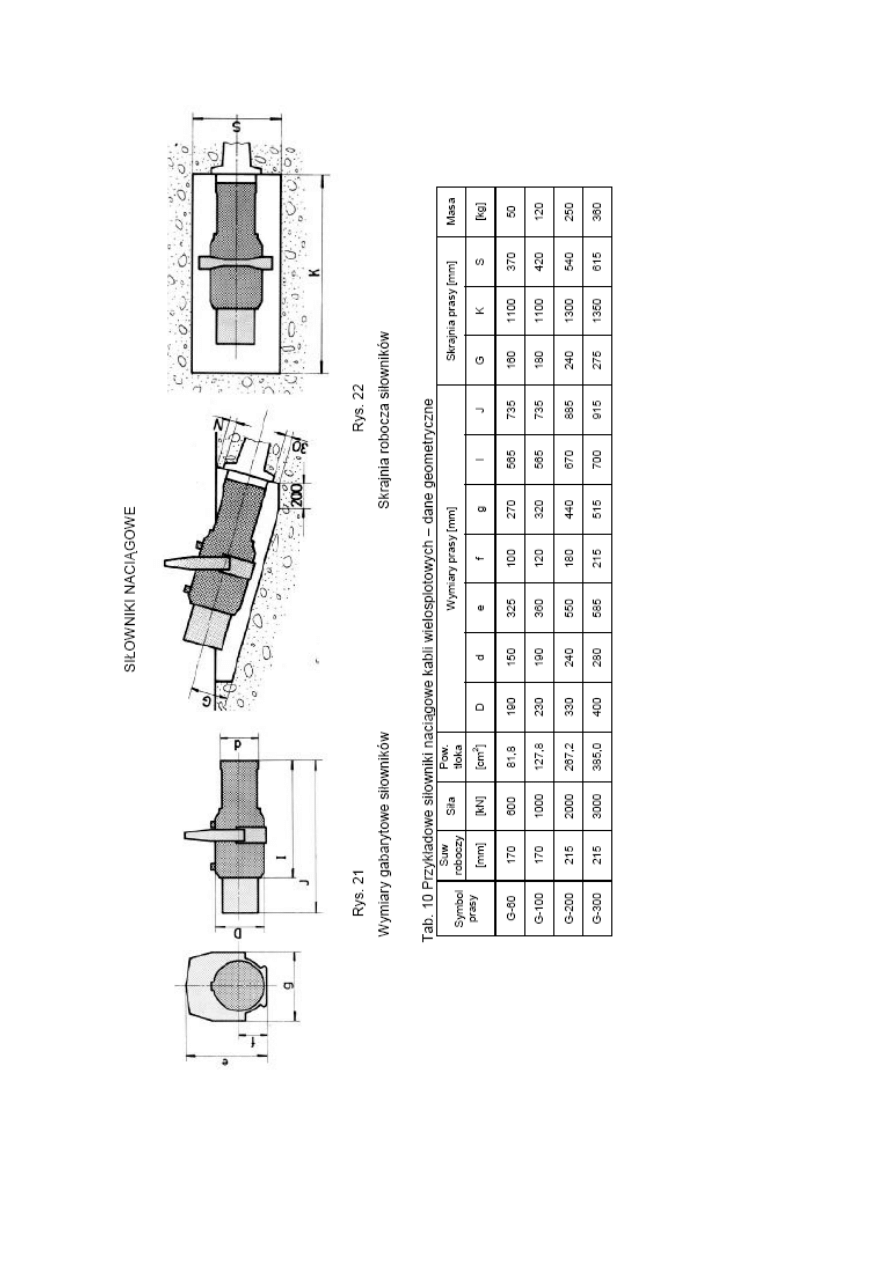
26

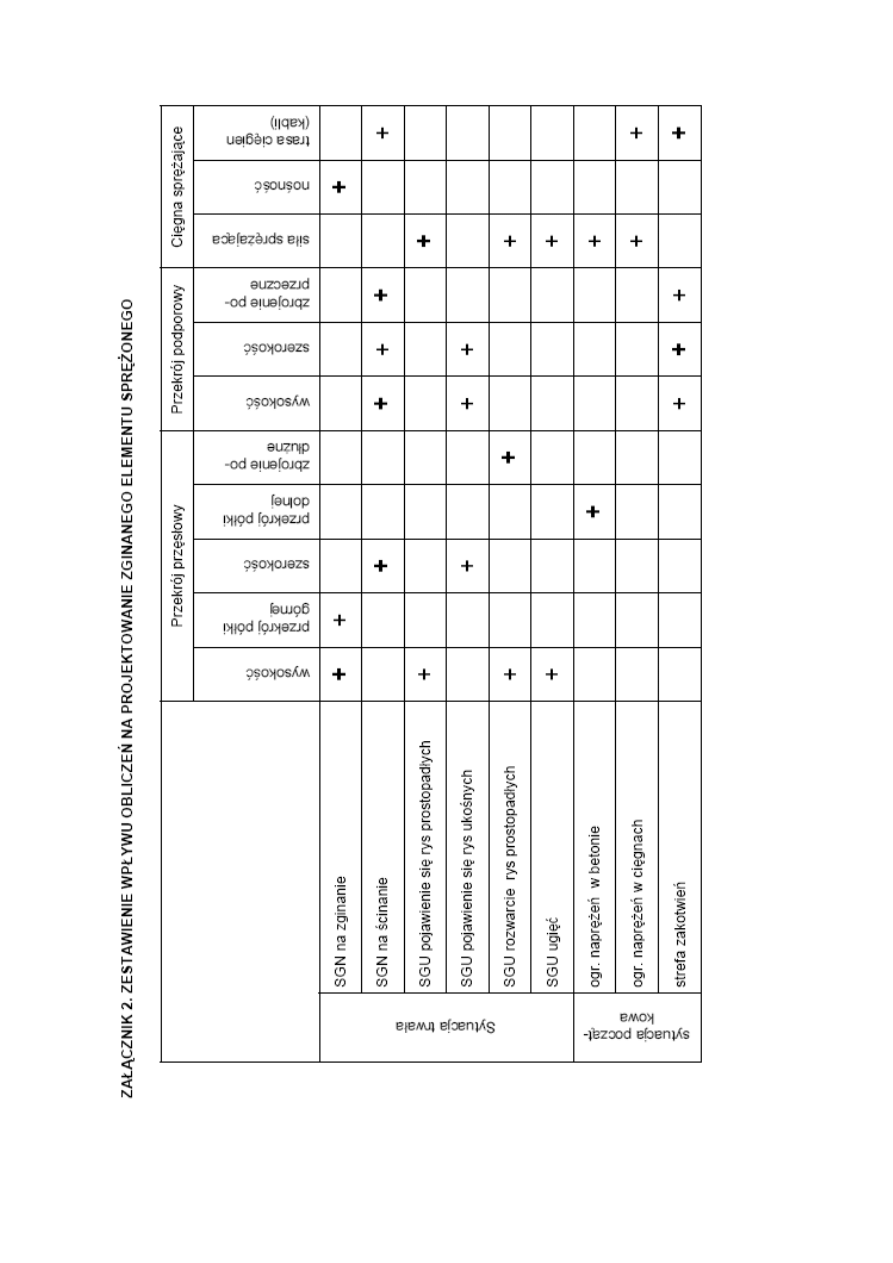
27

28

ZA

ŁĄCZNIK 3.

ZESTAWIENIE UWZGL

ĘDNIENIA OBCIĄśEŃ I SIŁY W CIĘGNACH W OBLICZENIACH

Obci

ążenia

ci

ęż

ar

w

ła

-

sn

y

st

ał

e

dł

ug

ot

rw

ał

e

ca

łko

w

ite

si

ła

w

ci

ęg

na

ch

SGN na zginanie

obl.

F

pd

,

σ

pc

SGN na

ścinanie

obl.

P

k,inf

SGU pojawienie si

ę rys

prostopad

łych

char.

P

k,inf

SGU pojawienie si

ę rys ukośnych

char.

P

k,inf

SGU rozwarcie rys prostopad

łych

char.

P

k,inf

S

yt

ua

cj

a

tr

w

ał

a

SGU ugi

ęć

char.

P

k,inf

pocz

ątkowe

P

o,max

st

ra

ty

reologiczne

char.

P

m,0

ogr. napr

ężeń w betonie

char.

P

k,sup

ogr. napr

ężeń w cięgnach

P

m0

P

m,t

syt

ua

cj

a

po

cz

ąt

-

ko

w

a

strefa zakotwie

ń

F

pk

- - kablob.

P

o,max

– strunob.