Temat:

Grafika inżynierska

Podstawy Inżynierii Wytwarzania



elementy przestrzeni



rzuty

Monge’a



aksonometria

WOJSKOWA AKADEMIA TECHNICZNA

Wydział Nowych Technologii i Chemii

KATEDRA ZAAWANSOWANYCH MATERIAŁÓW I TECHNOLOGII

Opracował: dr inż. Radosław Łyszkowski

T 1:

Informacje ogólne

Wojskowa Akademia Techniczna WTC KZMiT

2

http://www.wtc.wat.edu.pl/plany.html

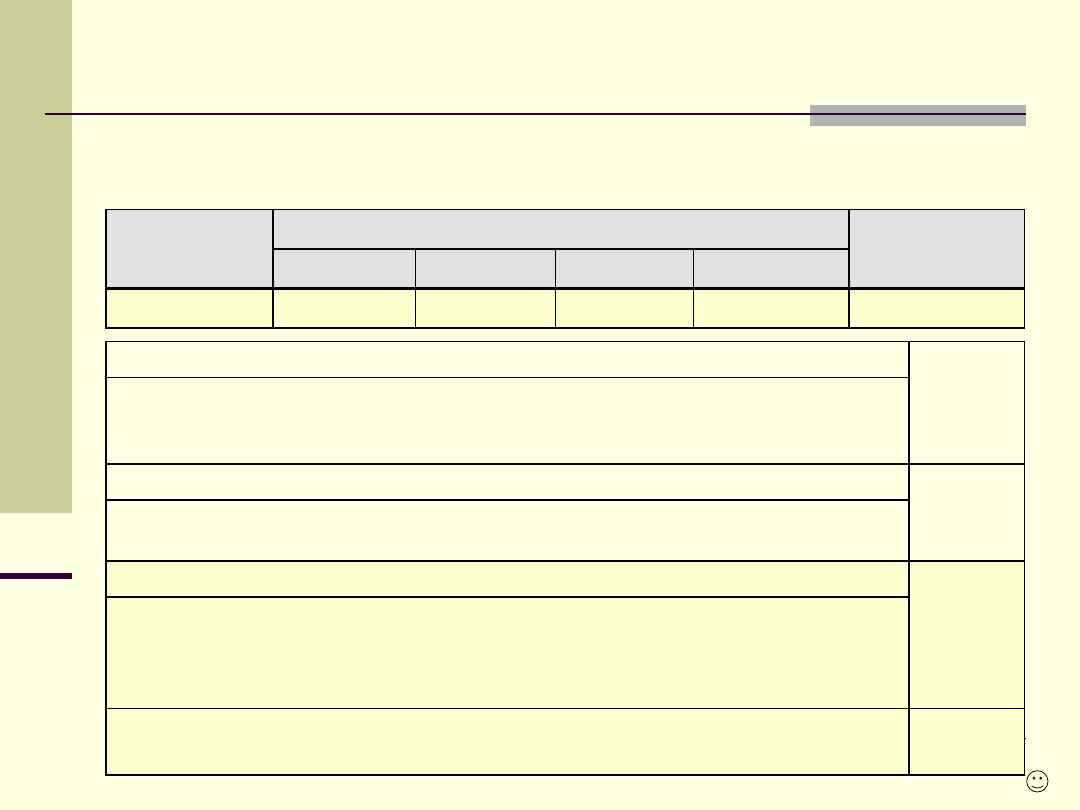
Semestr

Forma zajęć, liczba godzin (+ zaliczenie)

ECTS

razem

wykłady

ćwiczenia

laboratoria

I

60

24+

14+

22+

5

GRAFIKA INŻYNIERSKA

6

1.

Podstawowe elementy przestrzeni, podstawy rzutowania prostokątnego, rzuty
punktów, prostej, płaszczyzny, brył.

2.

Przekroje brył płaszczyznami rzutującymi, aksonometria.

PODSTAWY KONSTRUKCJI MASZYN

4

1.

Projektowanie i rysowanie części maszyn, podstawowe zasady obliczeń.

2.

Elementy projektowania węzłów konstrukcji.

METROLOGIA WIELKOŚCI GEOMETRYCZNYCH

4

1.

Metrologia wielkości geometrycznych, wzorce długości i kąta, przyrządy
suwmiarkowe, mikrometryczne i czujniki.

2.

Technika mierzenia, pomiary części maszyn o złożonym kształcie, zarządzanie
jakością w inżynierii wytwarzania.

MATERIAŁY INŻYNIERSKIE I TECHNIKI WYTWARZANIA

-

prowadzący dr inż. Dariusz ZASADA

10

Tematy ćwiczeń

Wojskowa Akademia Techniczna WTC KZMiT

3

TEMATY ĆWICZEŃ AUDYTORYJNYCH

7 x 2 =

14 godzin

1.

Rzuty prostokątne w rysunkach technicznych.

2.

Zasady zapisu kształtu części maszyn.

3.

Rysunki złożeniowe.

4. Schematy konstrukcji, normy rysunkowe.
5.

Komputerowe wspomaganie w projektowaniu inżynierskim (CAD).

6.

Zasady doboru materiałów.

7.

Dobór technik wytwarzania.

TEMATY ĆWICZEŃ LABORATORYJNYCH

11 x 2 =

22 godziny

1.

Obsługa systemu komputerowego wspomagania projektowania (CAD).

2. Projektowanie elementu maszyny - zapis konstrukcji z wykorzystaniem (CAD).

3.

Metody termicznego spajania materiałów.

4.

Sposoby obróbki skrawaniem.

5.

Pomiary przyrządami suwmiarkowymi i mikrometrycznymi.

6.

Pomiary mikroskopami.

7.

Pomiary przyrządami czujnikowymi.

8.

Stopy żelaza z węglem.

9.

Metale kolorowe.

10.

Obróbka cieplna.

11.

Właściwości mechaniczne materiałów inżynierskich.

Informacje ogólne

Wojskowa Akademia Techniczna WTC KZMiT

4

http://www.wtc.wat.edu.pl/kzmit/dydaktyka.html

ZASADY ZALICZANIA

– na podstawie:

• kolokwiów – pisane po odbyciu wykładów z bloków 1-3 (RŁ) oraz 4 (DZ);
• wykonanych prac domowych;
• uczestnictwa w wykładach, a zwłaszcza poprawności i jakości wykonanych notatek (rysunków).

Zaliczenie przedmiotu (uzyskanie wpisu) jest

możliwe po zaliczeniu wykładów z cz. I. (bloki

tematyczne 1-3) oraz cz. II (blok 4) a

także wcześniejszym zaliczeniu ćwiczeń

audytoryjnych i laboratoryjnych.

Literatura

A. Bieliński

Grafika inżynierska cz. I, Geometria wykreślna

W. Jakubiec, J. Malinowski

Metrologia wielkości geometrycznych

G. Wojnar, P.

Folęga, P. Czech

Graficzny zapis konstrukcji maszyn

L. Dobrzański

Materiały inżynierskie i projektowanie materiałowe

J. Dobrzański

Rysunek techniczny

A. Bober, M. Dudziak

Zapis konstrukcji

W. Szafrański

Materiały pomocnicze do projektowania konstrukcji

M. Gabrylewski

, J. Gąsienica-

Samek, I. Łosik

Mechaniczna Technologia Metali, ćwiczenia laboratoryjne

Pomoce rysunkowe

Wojskowa Akademia Techniczna WTC KZMiT

5

10 kartek

formatu

A4

HB (



1



)



0.5 mm

Wojskowa Akademia Techniczna WTC KZMiT

6

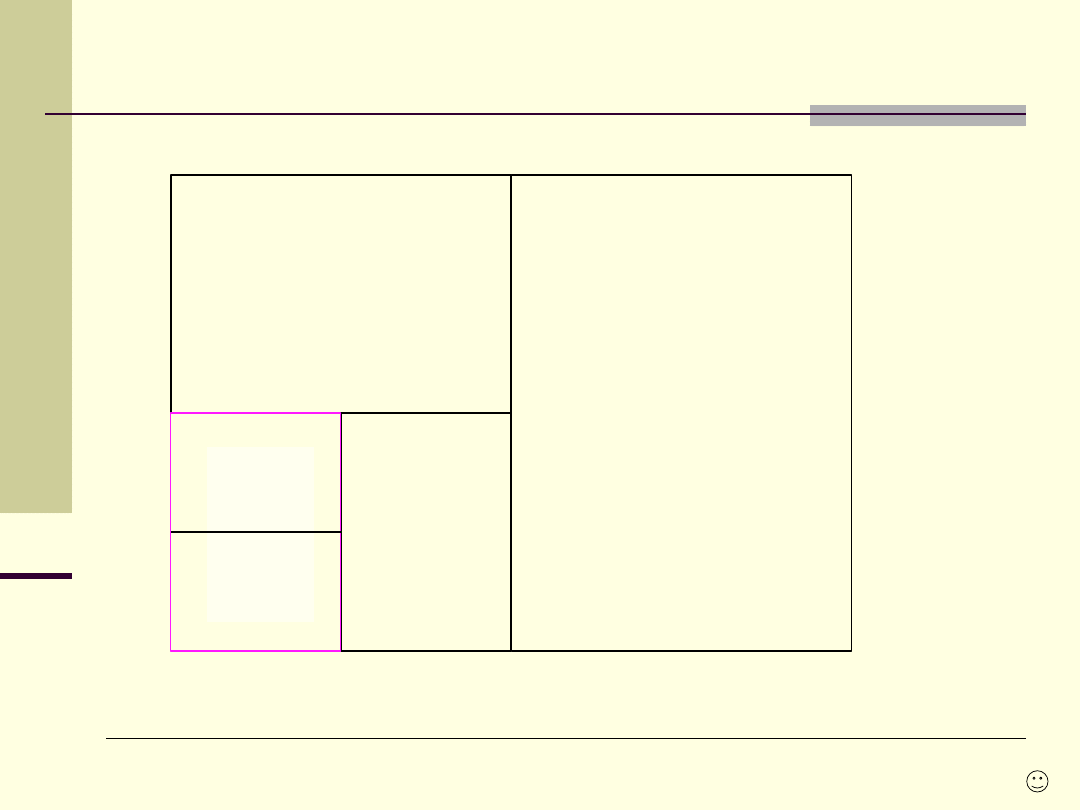
Formaty arkuszy rysunkowych

A4

A5

A5

A3

A2

A1

Wymiary:

A4 - 210 x 297

A5 - 148 x 210

A3 - 297 x 420

A2 - 420 x 594

A1 - 594 x 841

A0 - 841 x 1189

210 mm

29

7 m

m

Wojskowa Akademia Techniczna WTC KZMiT

7

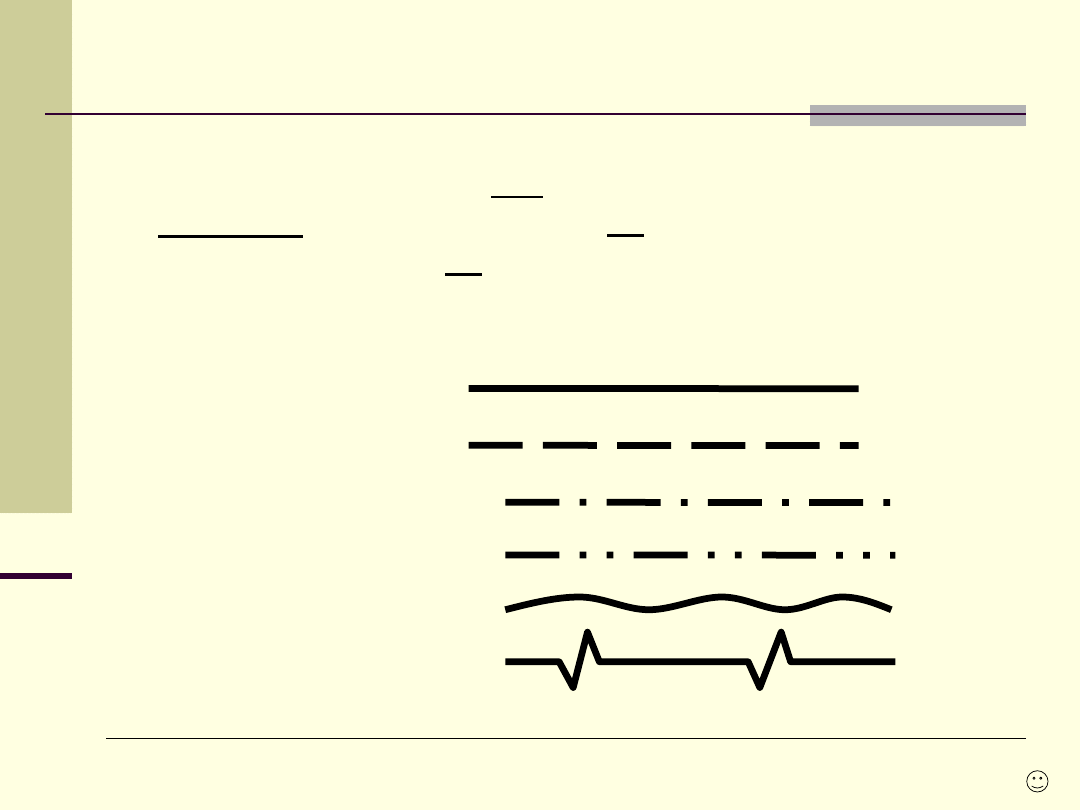
Linie rysunkowe

, wg PN-82/N-01616

1.

Linia cienka

2.

Linia gruba

3.

Linia bardzo gruba



ciągła



kreskowa



punktowa;



dwupunktowa



falista



zygzakowa

s

1

: s : s

2

= 1 : 2 : 4 (1 : 3 : 6)

– s

1

≥ 0.18 mm

– A3, A4 → s ≈ 0.5 ÷ 0.8 mm
– (1.0 ÷ 1.4 mm)

Wojskowa Akademia Techniczna WTC KZMiT

8







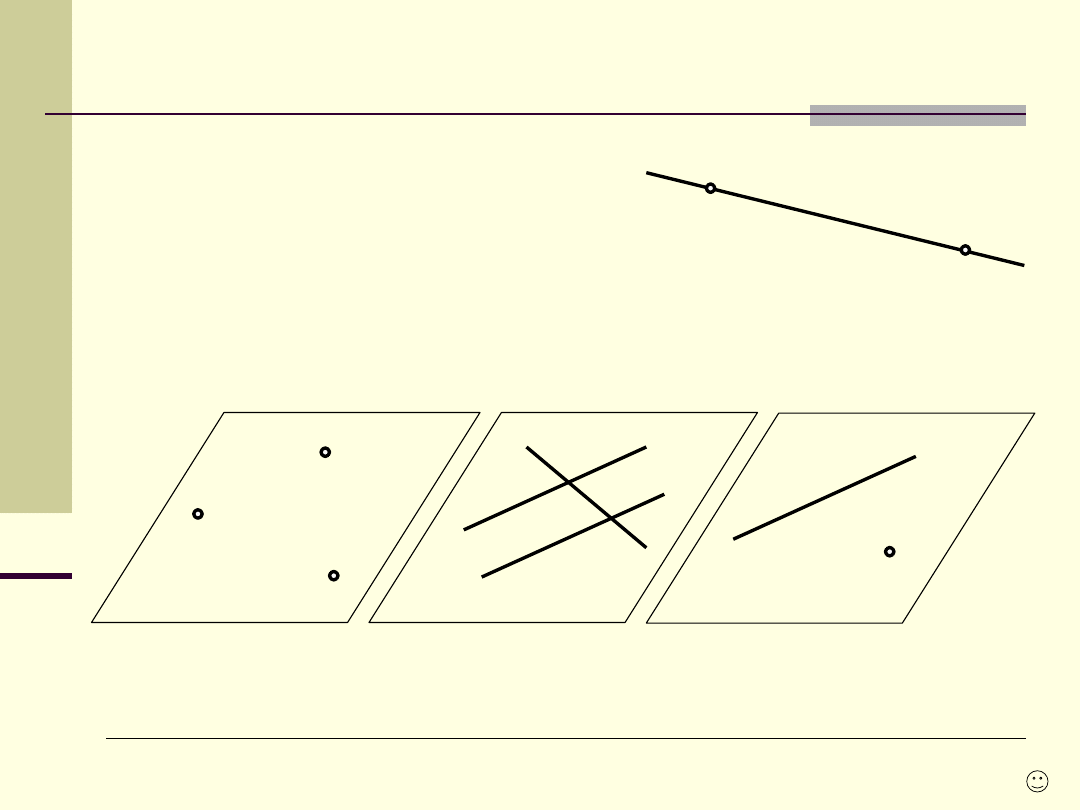
trzy punkty nie leżące na jednej prostej,



dwie nie pokrywające się proste równoległe,



dwie proste przecinające się,



prosta i nie leżący na niej punkt.

1.

Punkt

2.

Prosta

3.

Płaszczyzna

Elementy przestrzeni

A

B

A

B

C



a

b

c

B

a

→ dwa punkty

k

2

a

c

b

Wojskowa Akademia Techniczna WTC KZMiT

9

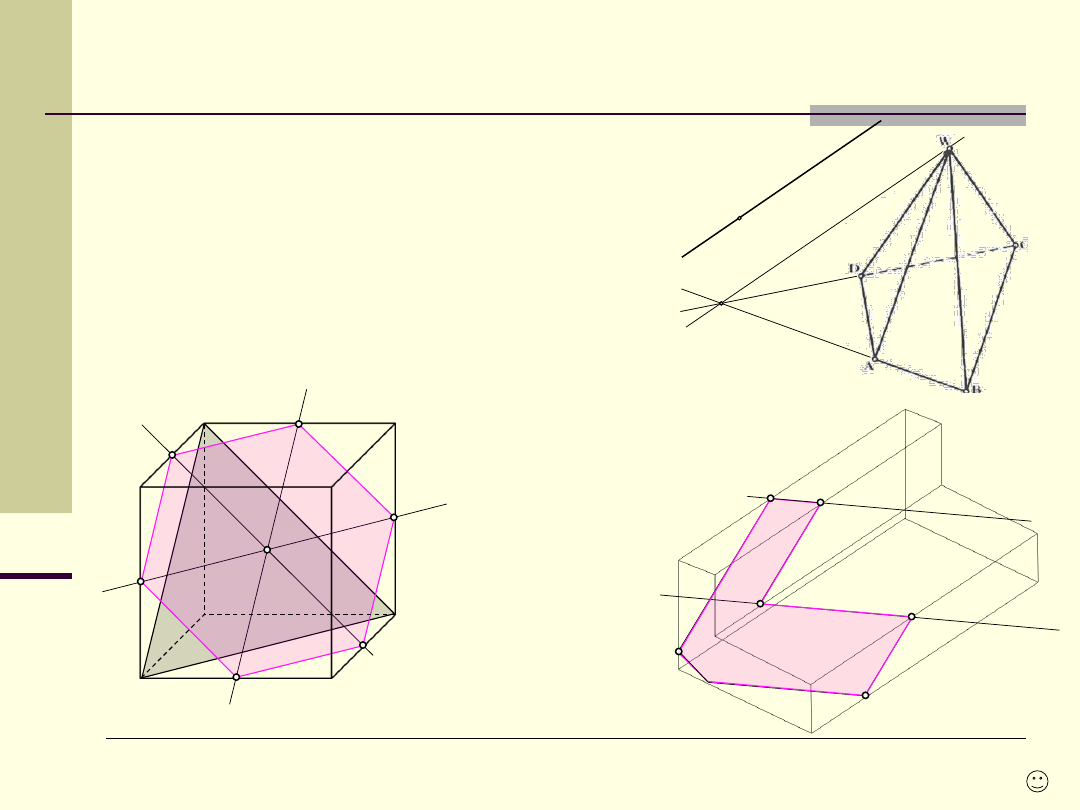
Przez dany punkt P

poprowadź prostą równoległą

do

ścian ABW i CDW ostrosłupa ABCDW

Elementy przestrzeni

- przykłady

B

Wyznaczyć przekrój sześcianu ABCDEFGH
płaszczyzną przechodzącą przez jego
środek i równoległą do płaszczyzny
wyznaczonej

wierzchołkami A, C i H.

E

P

O

A

C

D

E

F

G

H

P

R

K

L

N

M

Belkę o przekroju w kształcie
litery L

przeciąć płaszczyzną



wyznaczoną przez

punkty P, Q i R.

k

1

Q

R

P

S

U

T

Wojskowa Akademia Techniczna WTC KZMiT

10

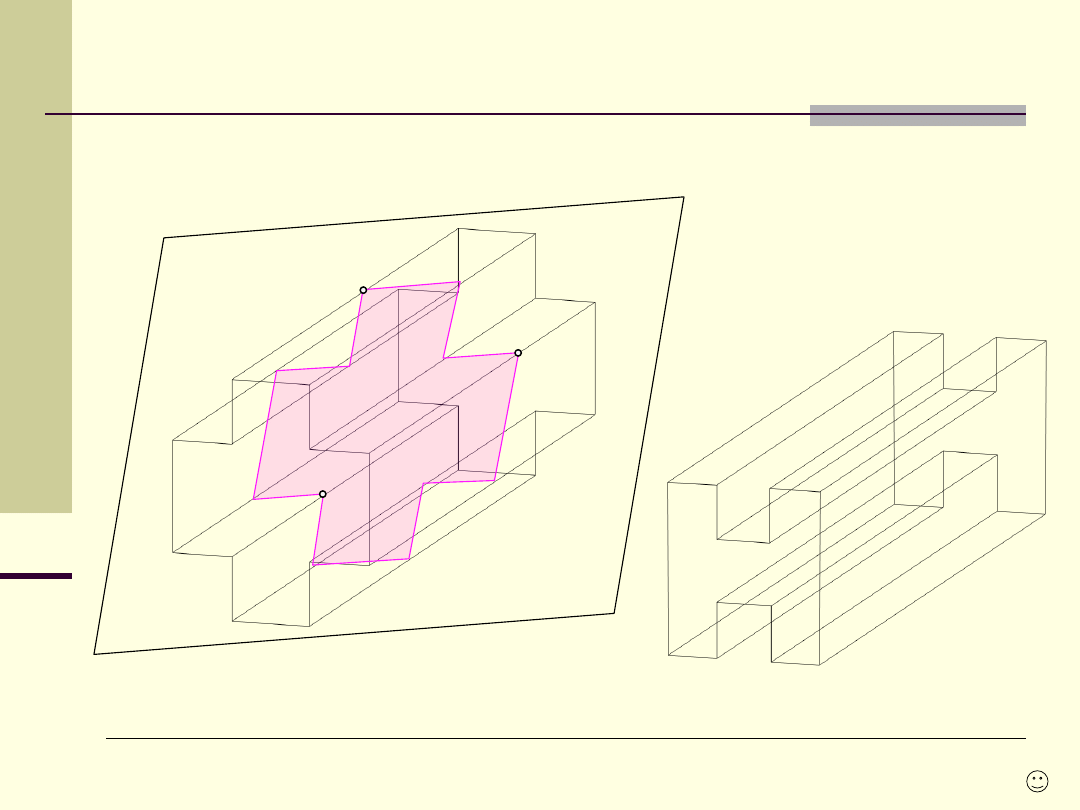
Zadanie domowe

Belkę o przekroju w kształcie litery H (+) przeciąć dowolną sieczną płaszczyzną

,

wyznaczoną przez punkty A, B i C.



Q

R

P





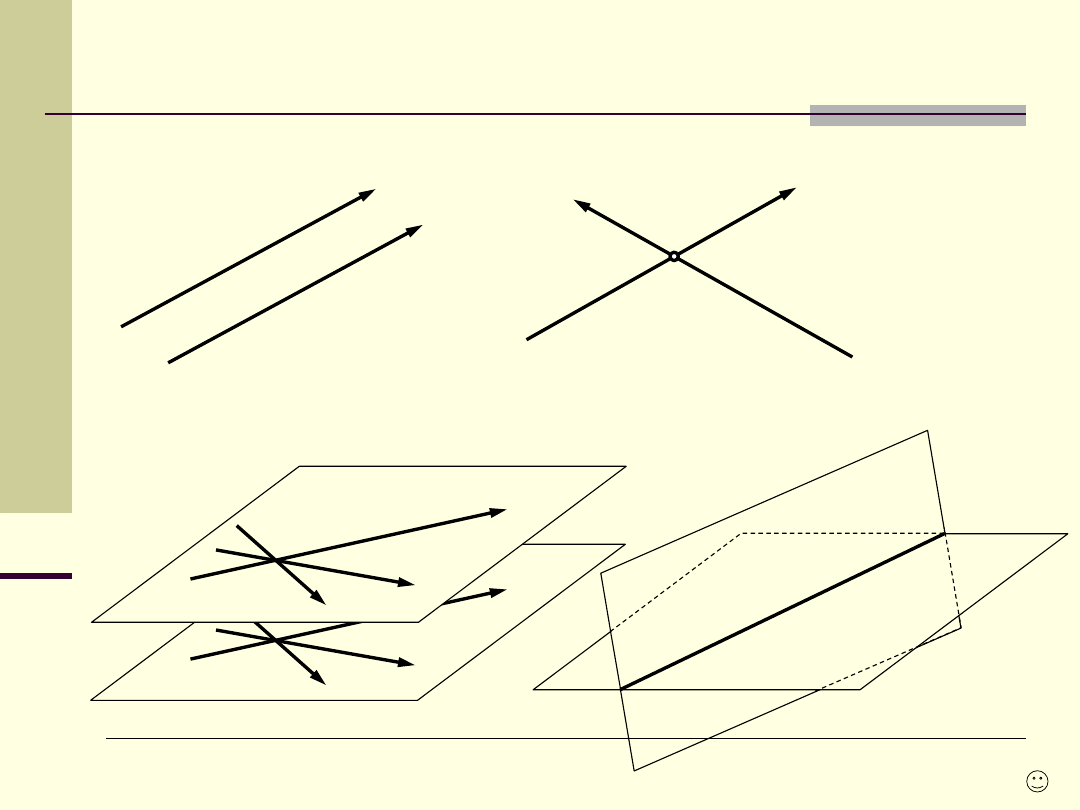
Odwzorowanie przestrzeni na płaszczyznę

Punkt

niewłaściwy

S



S



a

b

D

C



c

d

S



a

1



a

3



a

2



a

1

'



a

3

'



a

2

'





k

Wojskowa Akademia Techniczna WTC KZMiT

11

S



= a



b

S

= c



d

r



=

  

k

=

  

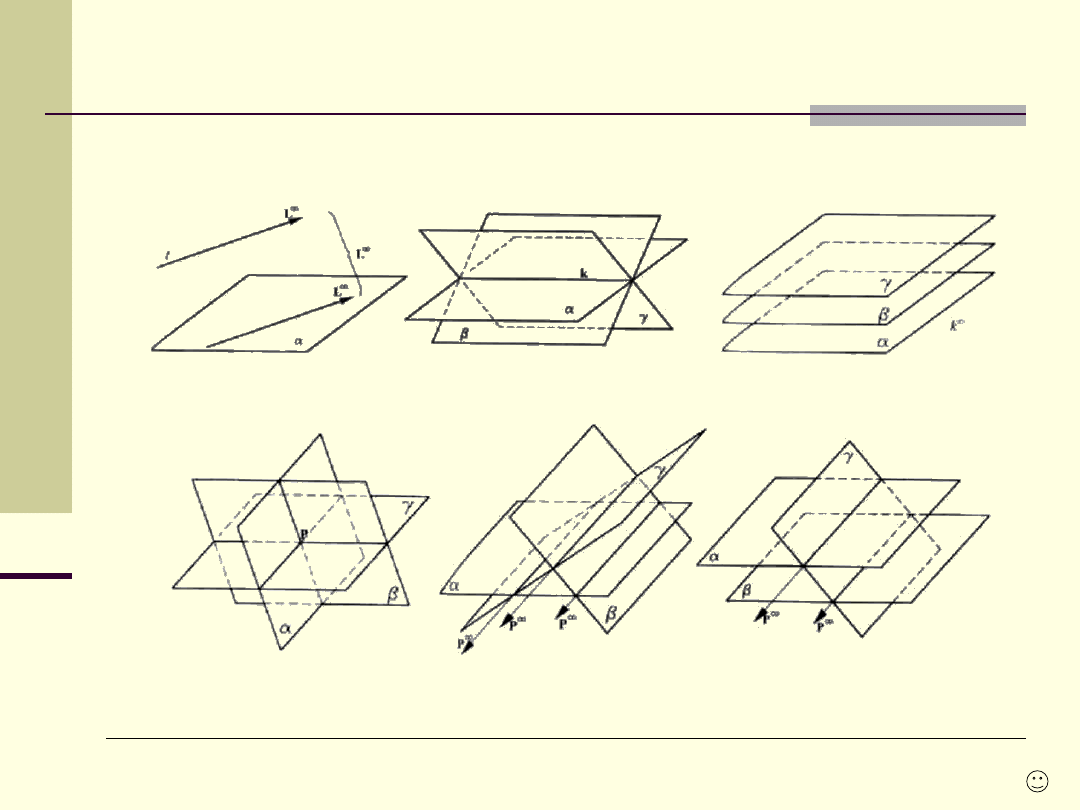
Punkt, prosta, płaszczyzna właściwa lub niewłaściwa

Wojskowa Akademia Techniczna WTC KZMiT

12

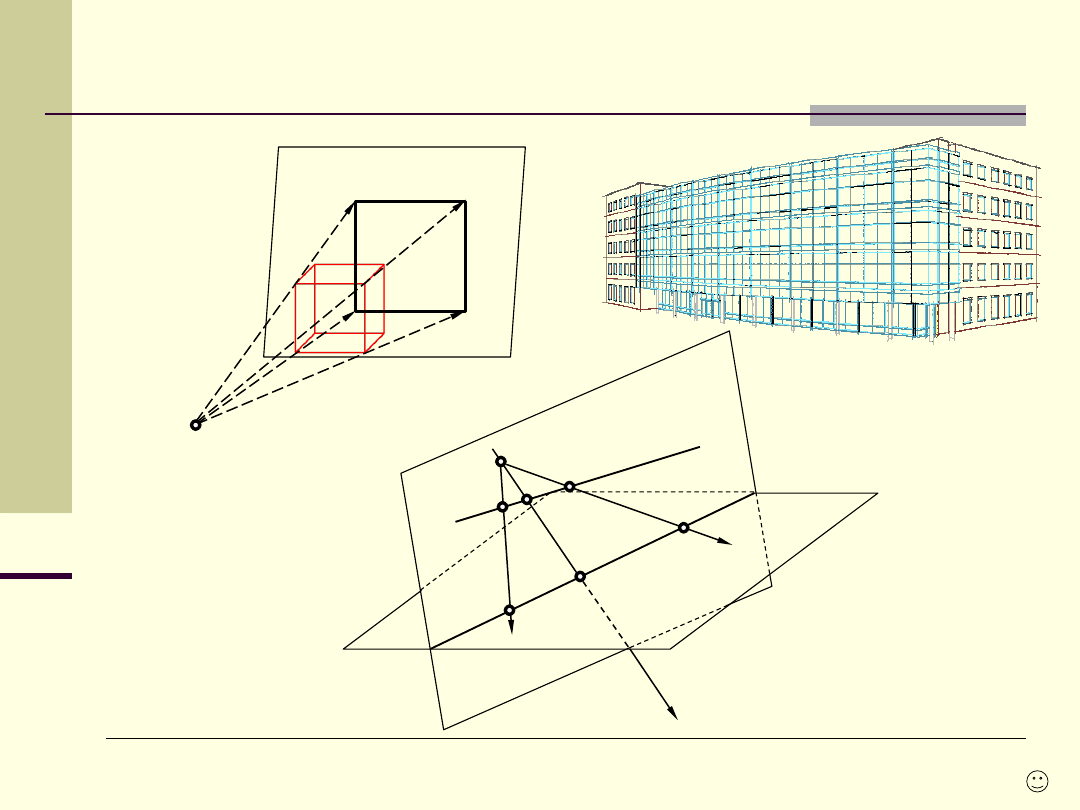
Rzutowanie środkowe (perspektywa)

p

A

p

m

m

'

A’ = S

A

’

S

C’

C

B

B’

A



m

Wojskowa Akademia Techniczna WTC KZMiT

13

p

- rzutnia

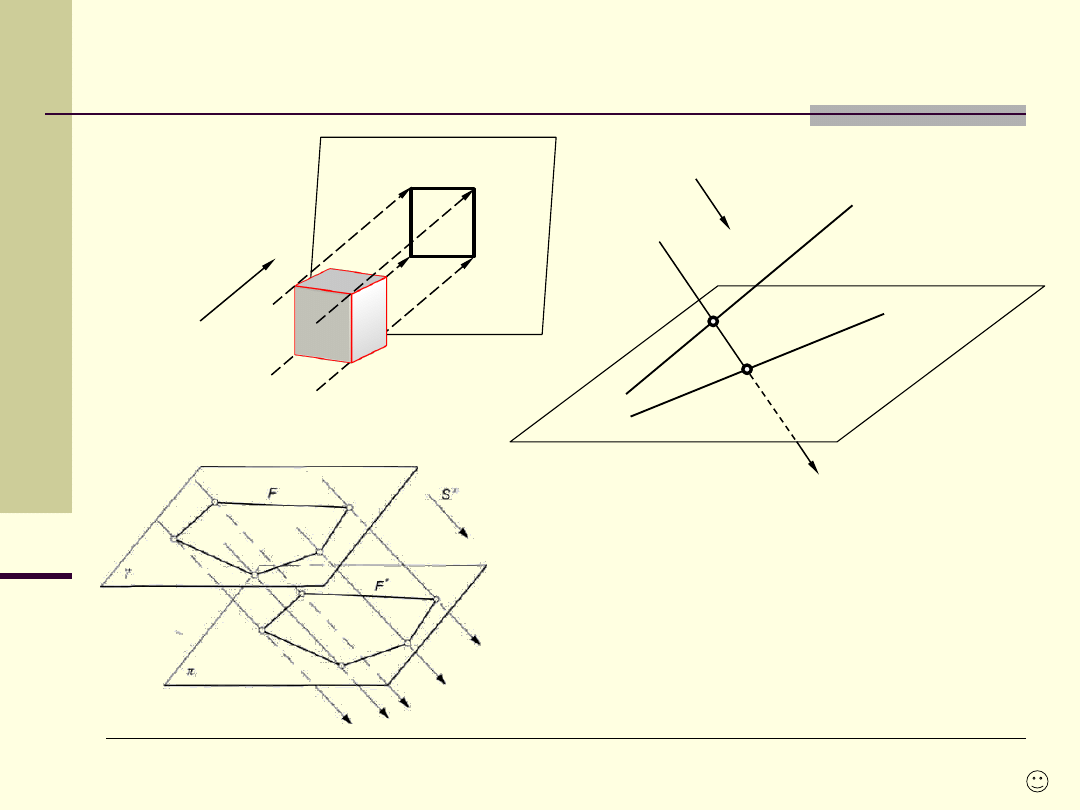
Rzutowanie równoległe ukośne

p

p

l

l

'

A’

A

S



Wojskowa Akademia Techniczna WTC KZMiT

14

A’ = S

A



p

Własności rzutu równoległego:
1. Rzutem punktu jest punkt, punkty rzutni

p

są swymi rzutami;

2. Rzutem prostej dowolnej jest prosta,

natomiast rzutem prostej

rzutującej jest

punkt;

3. Rzutem

płaszczyzny dowolnej jest cała

rzutnia

p

,

zaś rzutem płaszczyzny

rzutującej jest prosta.

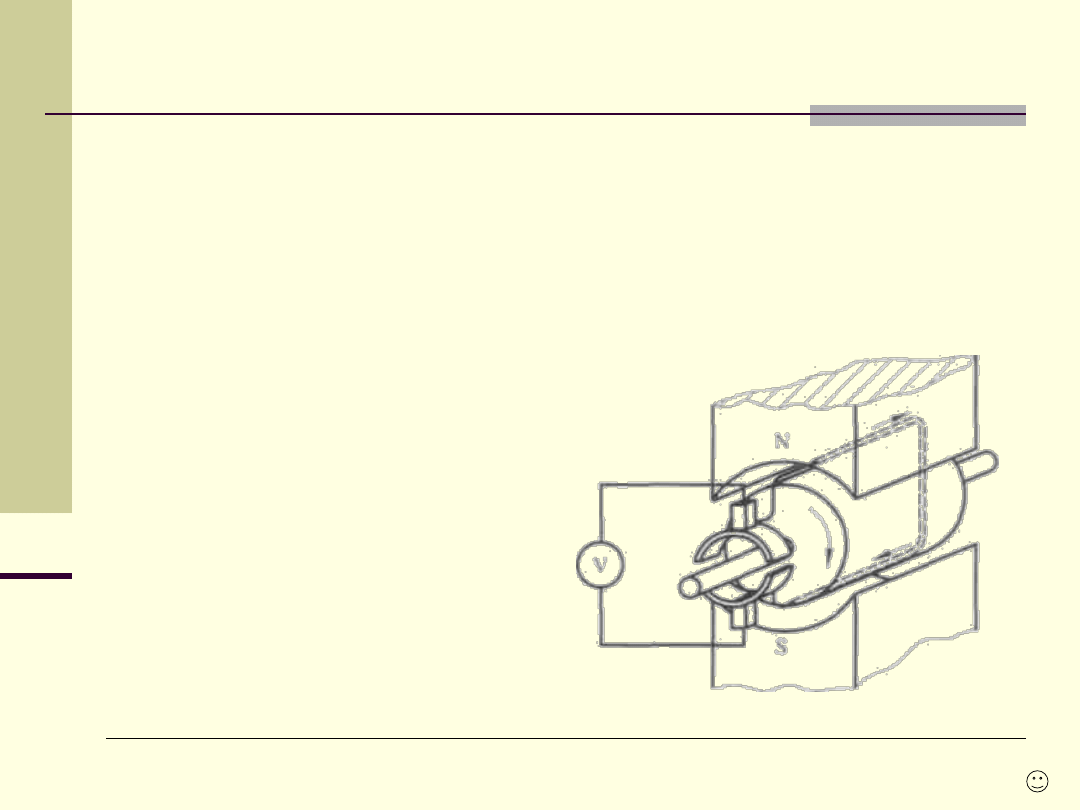
Rzutowanie równoległe ukośne

Wojskowa Akademia Techniczna WTC KZMiT

15

Niezmienniki rzutowania

– to pewne właściwości figur, które w trakcie rzutowania

nie

ulegają zmianom, czyli są przenoszone bez zmiany z figury na jej rzut.

Rzutowanie

równoległe zachowuje:

1.

Przynależność elementów;

2.

Współliniowość elementów;

3.

Równoległość prostych;

4. Stosunek

podziału odcinka przez punkt;

5. Stosunek

długości odcinków równoległych;

6.

Metrykę figur leżących w płaszczyznach

równoległych do rzutni.

Rzutowanie

równoległe

jest

odwzorowaniem

jednoznacznym

przestrzeni na

płaszczyznę. Każdy

punkt przestrzeni ma jeden obraz na
rzutni, ale nie odwrotnie.

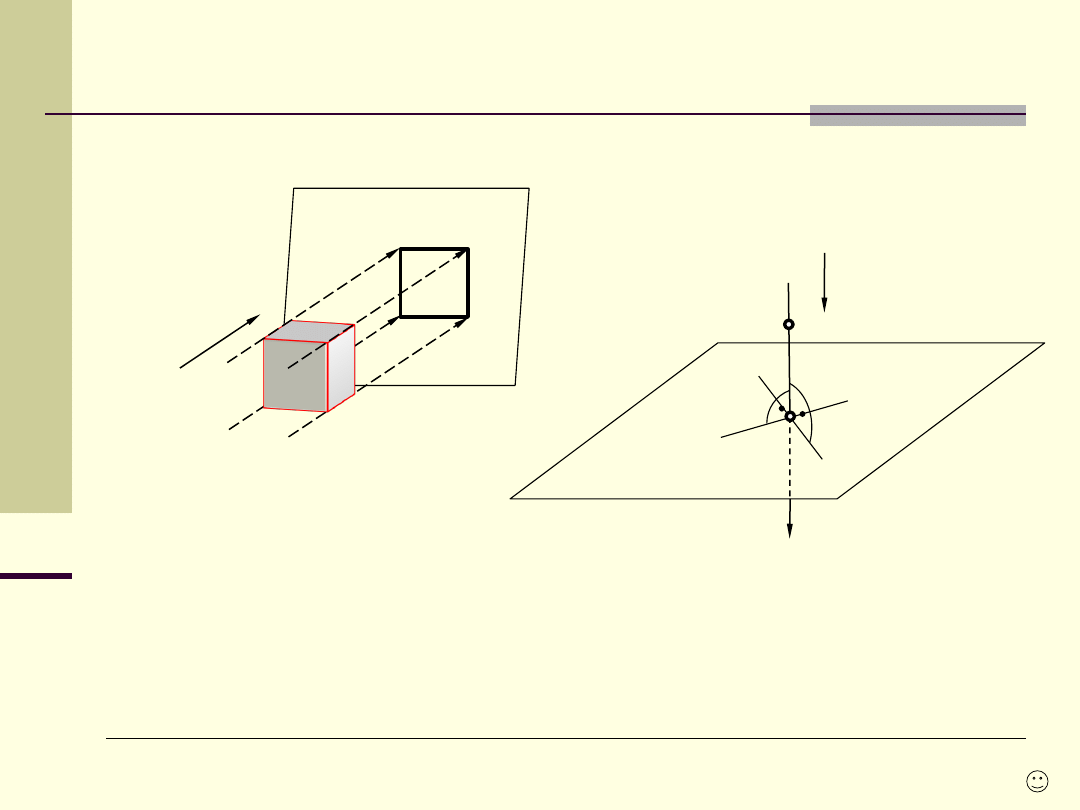
Rzutowanie prostokątne

p

p

A

S



A’

Wojskowa Akademia Techniczna WTC KZMiT

16

Rzutowanie

prostokątne

jest

szczególnym

przypadkiem

rzutowania

równoległego i posiada wszystkie jego własności (zachowuje dotychczasowe
niezmienniki) oraz

własność charakterystyczną (kierunek rzutowania jest

prostopadły do rzutni).

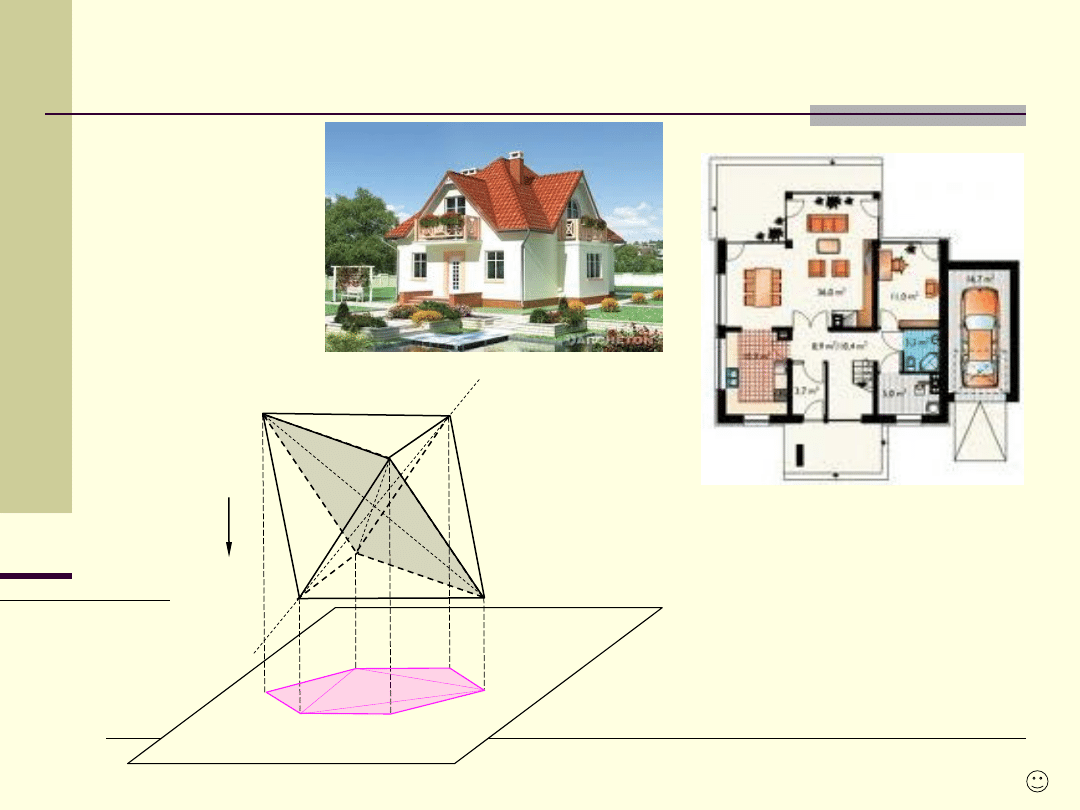
p

Rzutowanie prostokątne

Wojskowa Akademia Techniczna WTC KZMiT

17

Wykreślić rzut prostokątny
ośmiościanu foremnego o
danej

krawędzi a, którego

ściana ABF jest równoległa
do rzutni.

S



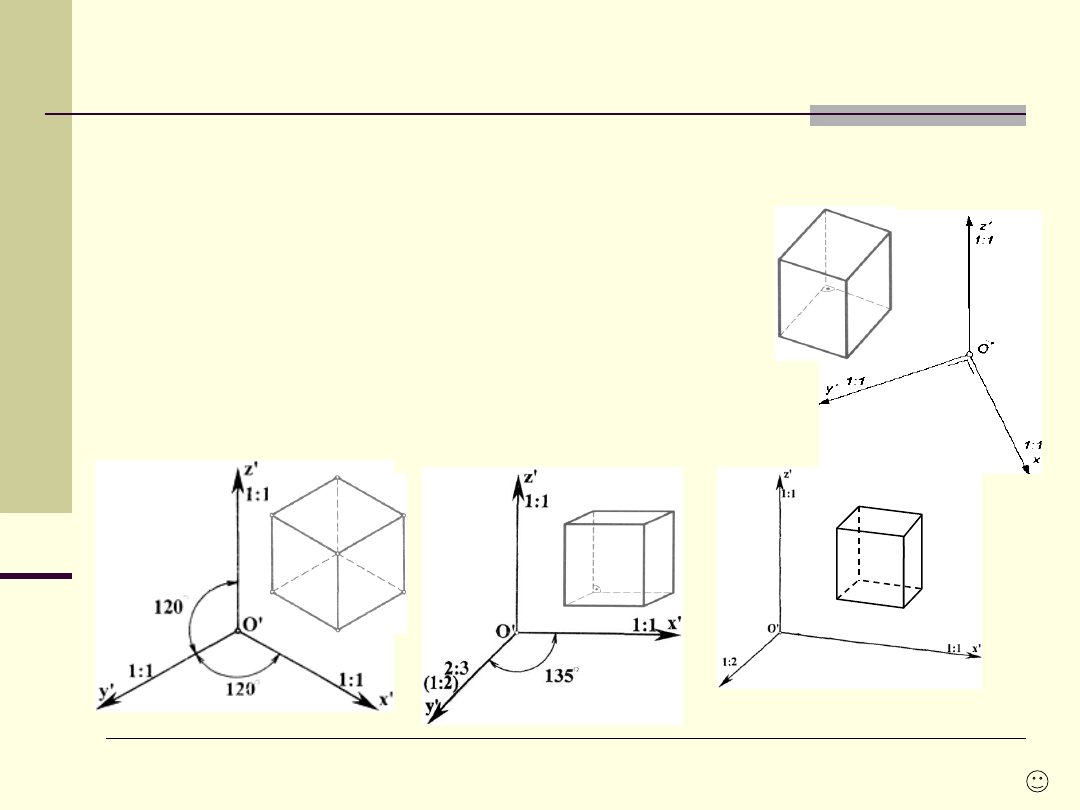
Aksonometryczne układy rzutowania

Izometria wojskowa - osie x' i y'

są



, skróty 1:1;

Izometria równokątna - osie x', y' i z' dzielą kąt pełny na
trzy równe części, skróty 1:1;
Dimetria kawalerska - osie x' i z'

są



, a oś y' jest

dwusieczną kąta, jaki tworzą osie x' i z', skróty osi y



2:3

lub 1:2;
Dimetria prawie prostokątna - osie x' i y' obrócone, skrót
osi y



1:2.

Wojskowa Akademia Techniczna WTC KZMiT

18

Dimetrią nazywamy układ aksonometryczny, w którym na dwóch osiach są
jednakowe

skróty, a izometrią układ o jednakowych skrótach na wszystkich trzech

osiach.

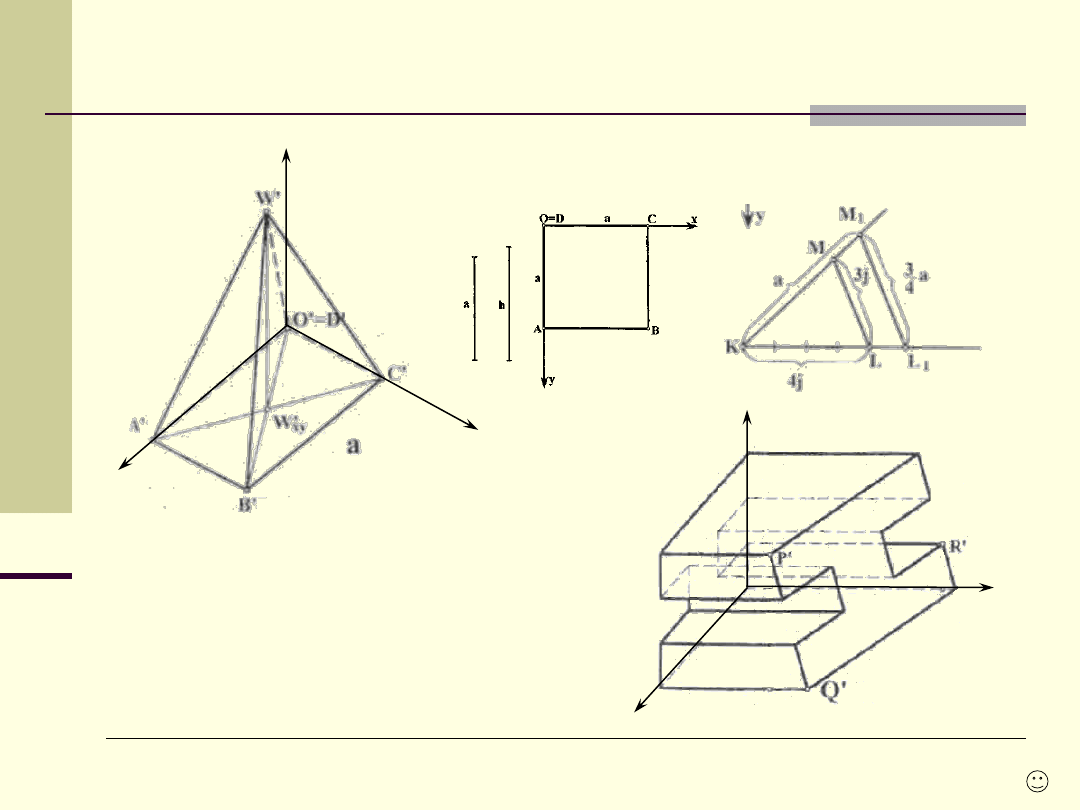
Aksonometria

- przykłady

Wojskowa Akademia Techniczna WTC KZMiT

19

W

przyjętym układzie aksonometrycznym, wykreślić obraz

ostrosłupa prawidłowego o wysokości h i boku a.

z’

1:1

x’

3:4

y’

1:1

W

przyjętym układzie aksonometrycznym,

wykreślić obraz belki o zadanym przekroju,
ograniczony

płaszczyzną

przekrój

przechodzącego przez punkty PRQ.

z’

1:1

x’

1:3

y’

1:1

Rzuty Monge'a

p

1

S

1



A’

A’’

A

p

2

x

I

III

II

IV

S

2



Wojskowa Akademia Techniczna WTC KZMiT

20

p

1

- rzutnia pozioma i

prostopadła do

niej rzutnia pionowa

p

2

.

x =

p

1



p

2

nazywamy

osią rzutów.

Rzutnie

p

1

i

p

2

dzielą przestrzeń na

cztery

ćwiartki.

Punkty przestrzeni rzutujemy

prostokątnie na rzutnie

p

1

i

p

2

,

wówczas punkt A' =

p

1



AS

1



jest rzutem poziomym punktu A,

a punkt A'' =

p

2



AS

2



jest rzutem pionowym.

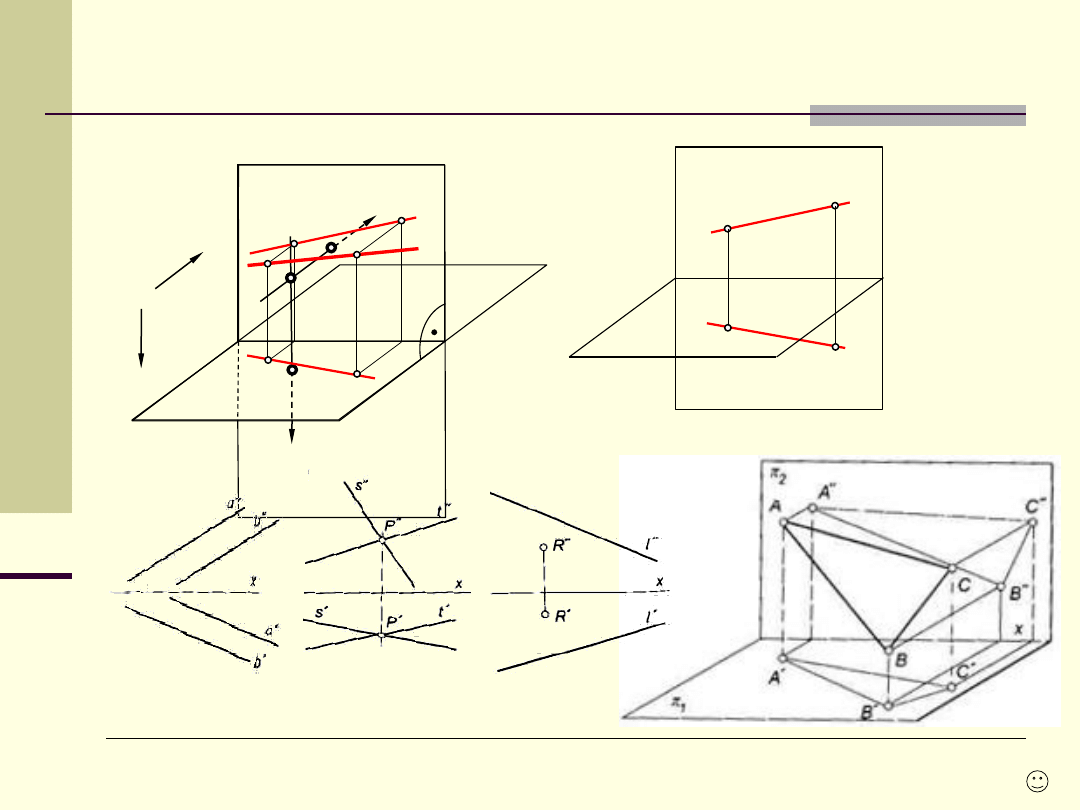
Odwzorowanie prostej i płaszczyzny

S

1



A’

A’’

A

I

III

II

IV

S

2



p

2

x

p

1

l”

l'

A’’

A’

B’’

B’

l

B

A

l”

l'

A’’

B’’

A’

B’

Wojskowa Akademia Techniczna WTC KZMiT

21

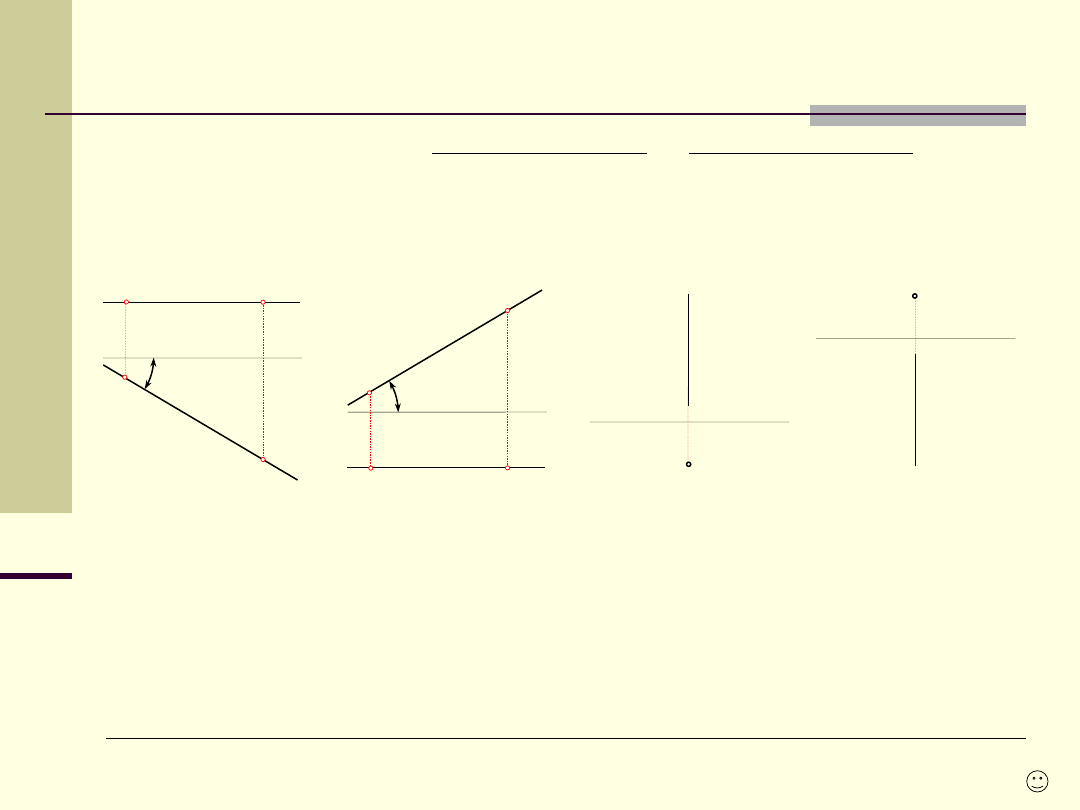
Szczególne położenia prostej

Wojskowa Akademia Techniczna WTC KZMiT

22

Prosta lub

płaszczyzna, która nie jest równoległa ani nie jest prostopadła do rzutni,

ma

położenie ogólne, w przeciwnym razie jest w położeniu szczególnym.

Prostą ‖ do rzutni poziomej nazywamy prostą poziomą, a ‖ do rzutni poziomej –
prostą czołową.

Prosta poziomo-

rzutująca (pionowa) – to prosta



do rzutni poziomej, jej rzutem

poziomym jest punkt, a pionowym prosta



do osi x.

Prosta pionowo-

rzutująca (celowa) – to prosta



do rzutni pionowej, jej rzutem

pionowym jest punkt, a poziomym prosta



do osi x.

B

''

A

'

B

'

x

p

'



A

''

p”

B

'

A

"

B

"

x

p

"



A

'

p'

m

'

x

m”

n

"

x

n'

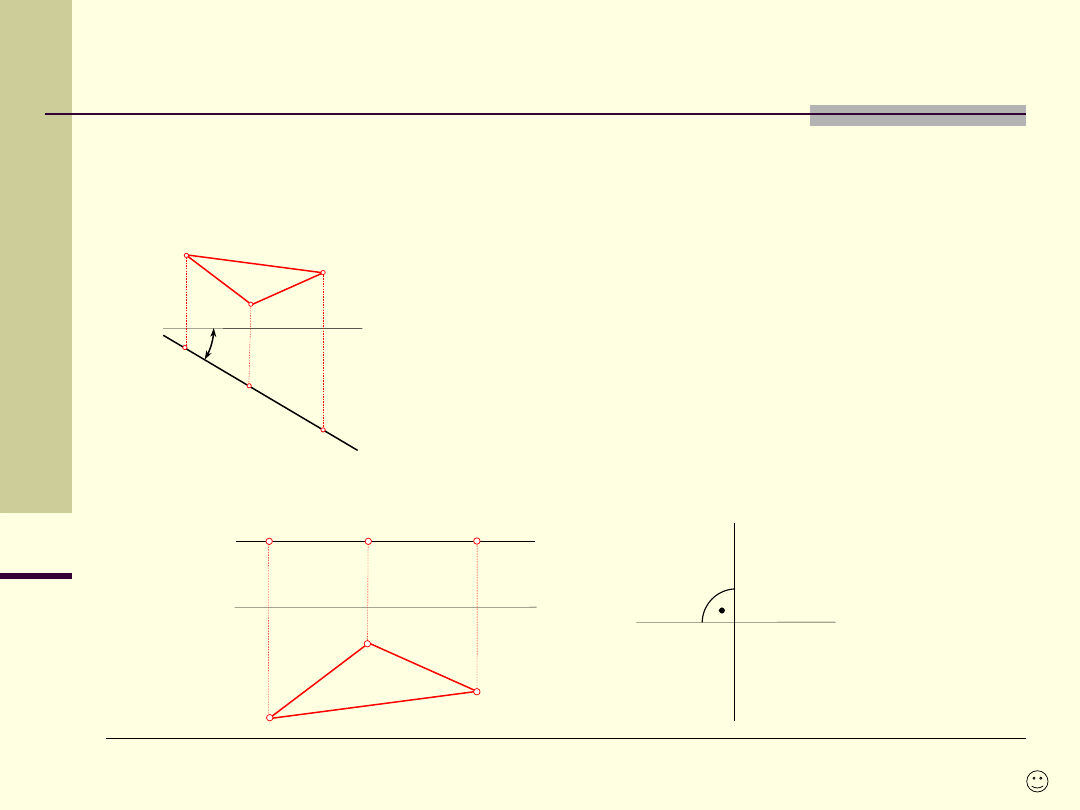
Szczególne położenia płaszczyzn

Wojskowa Akademia Techniczna WTC KZMiT

23

Płaszczyzna poziomo-rzutującą – to płaszczyzna



do rzutni poziomej, jej rzutem

poziomym jest prosta, a rzutem pionowym - rzutnia

p

2

.

Płaszczyznę





p

1

wyznacza

trójkąt ABC. Rzut poziomy



ABC jest odcinkiem prostej



'.

Kąt



utworzony przez

prostą



' i

oś x jest kątem, jaki płaszczyzna



tworzy z

rzutnią pionową.

C

''

B

''

A

'

B

'

C

'

x



'



A

''

Płaszczyznę ‖ do rzutni poziomej nazywamy

płaszczyzną poziomą, ‖ do rzutni pionowej -
płaszczyzną czołową, natomiast płaszczyznę



do

obu rzutni

– płaszczyzną profilową.

Płaszczyzna pionowo-rzutująca – to płaszczyzna



do rzutni pionowej, jej rzutem pionowym jest prosta.



"

C

'

B

'

A

"

B

"

C

"

x

A

'



' =



"

x



c



s

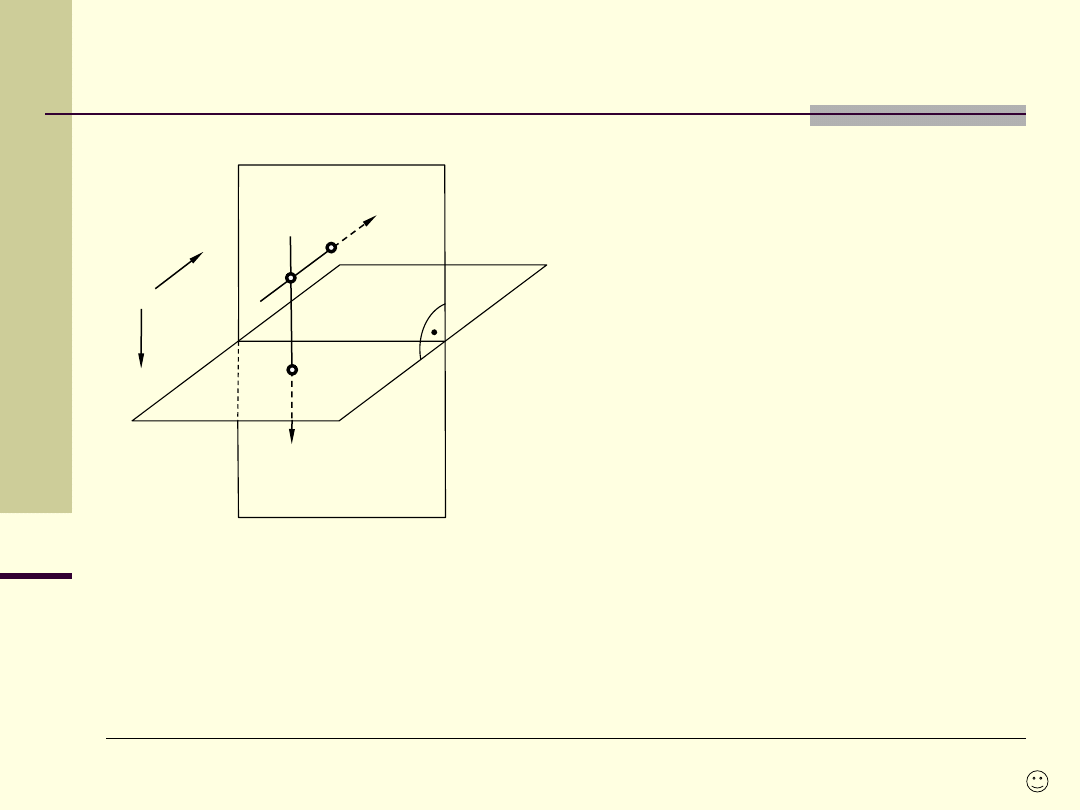
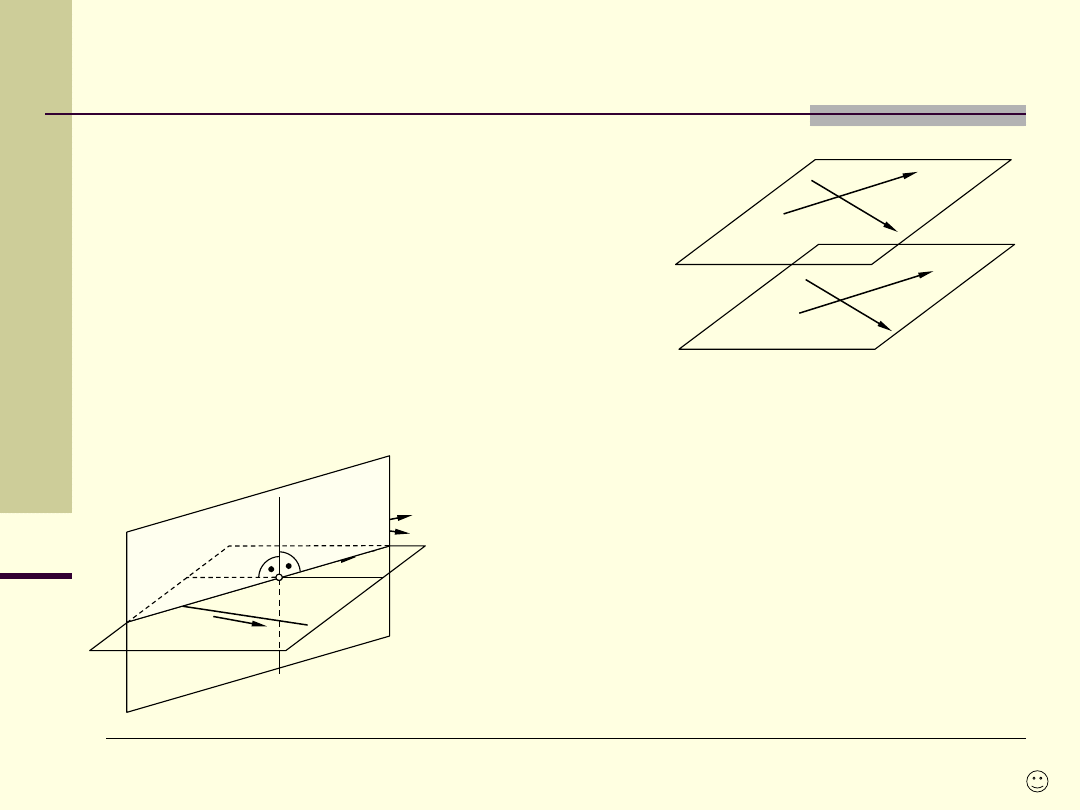
Równoległość, prostopadłość

Wojskowa Akademia Techniczna WTC KZMiT

24

Proste

mające wspólny punkt niewłaściwy (ten

sam kierunek)

są prostymi równoległymi.

Prosta i

płaszczyzna są II jeśli mają wspólny

punkt

niewłaściwy (istnieje na płaszczyźnie

taka prosta s

1

,

że jest II do s).

Płaszczyzny mające wspólną prostą niewłaściwą

są płaszczyznami II (dwie proste przecinające
się jednej płaszczyzny, muszą mieć II
odpowiedniki na drugiej).

Proste,

których punkty niewłaściwe tworzą kąt

prosty

są prostymi



.

Jeżeli prosta jest



do dwu dowolnych prostych

danej

płaszczyzny, to jest ona również



do tej

płaszczyzny.

Jeżeli płaszczyzna zawiera prostą



do drugiej

płaszczyzny, to są one



.

S



s

1



t

t

1

T



a

b

c



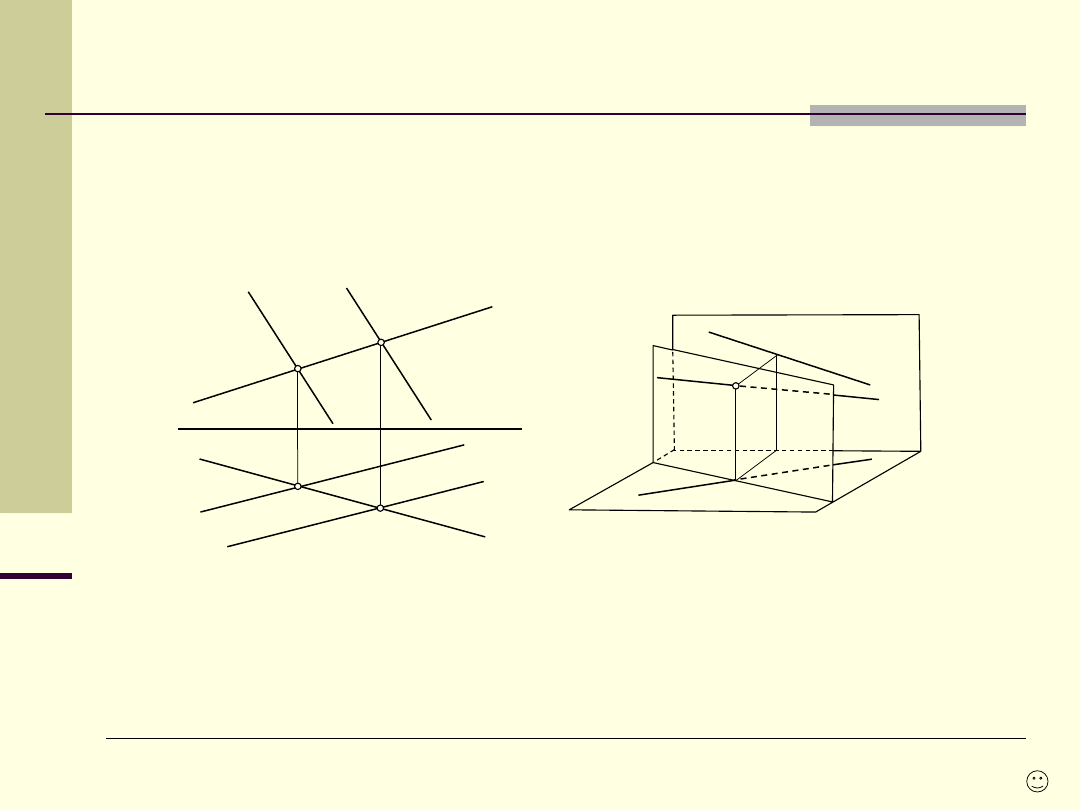
Wynik przebicia

Wojskowa Akademia Techniczna WTC KZMiT

25

Płaszczyzny rzutującej prostą
Niech dana

będzie płaszczyzna poziomo-rzutująca



i dowolna prosta l o rzutach

l’ i l".

Punkt P =





I

należy jednocześnie do płaszczyzny



i do prostej l, a

więc rzut

poziomy P' punktu P

leży w przecięciu



' i l' tzn. P' =



'



l'. Rzut pionowy P" punktu P

otrzymujemy przez odniesienie P' na rzut pionowy I" prostej l.

Płaszczyzny rzutującej płaszczyzną dowolną
Przyjmujemy

płaszczyznę poziomo-rzutującą



i

płaszczyznę dowolną wyznaczoną

prostymi

równoległymi l i ł.

Krawędź dwóch płaszczyzn wyznaczają dwa rożne punkty wspólne tych płaszczyzn.
Punkty P i Q

wyznaczają krawędź k płaszczyzny



i



,

której rzut poziomy k' pokrywa

się z rzutem poziomym



'

płaszczyzny



, a k"

wyznaczają punkty P" i Q".

l"

l'



p

1

p

2

x

l'

l"

x

P'

P"

l

P



'

P'

P"

l"

ł"

ł'

Q'

=

k'

k"

Q"

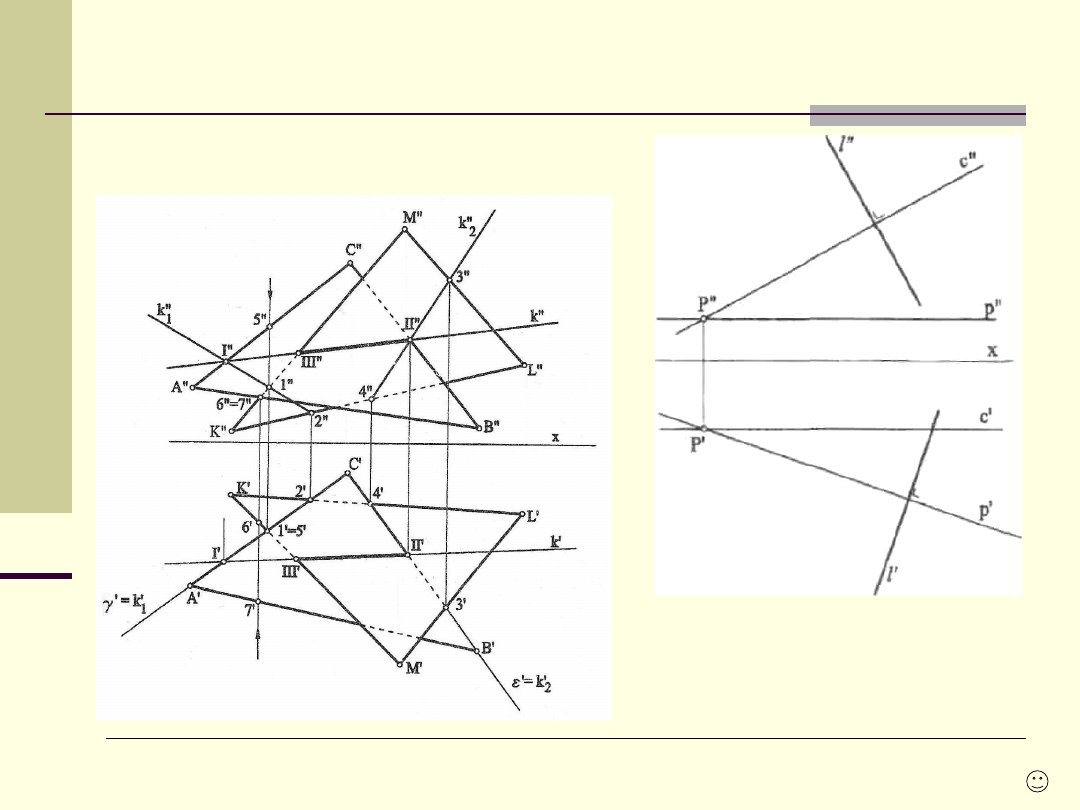
Elementy wspólne

Wojskowa Akademia Techniczna WTC KZMiT

26

Przez dany punkt P

poprowadzić płaszczyznę



prostopadłą do danej prostej l.

Wyznaczyć przenikanie się trójkątów
ABC i KLM.

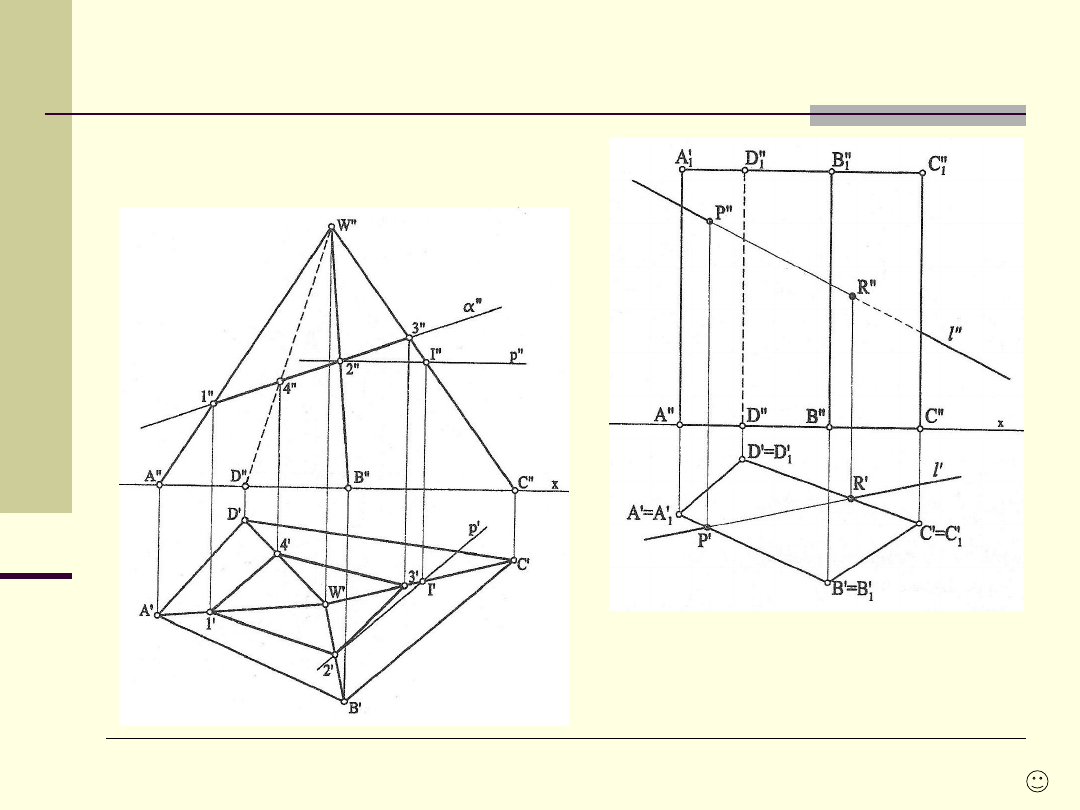
Przebicia i przekroje brył

Wojskowa Akademia Techniczna WTC KZMiT

27

Wyznaczyć punkt przebicia graniastosłupa

prostego

prostą l.

Przeciąć

ostrosłup

płaszczyzną

pionowo-

rzutująca.

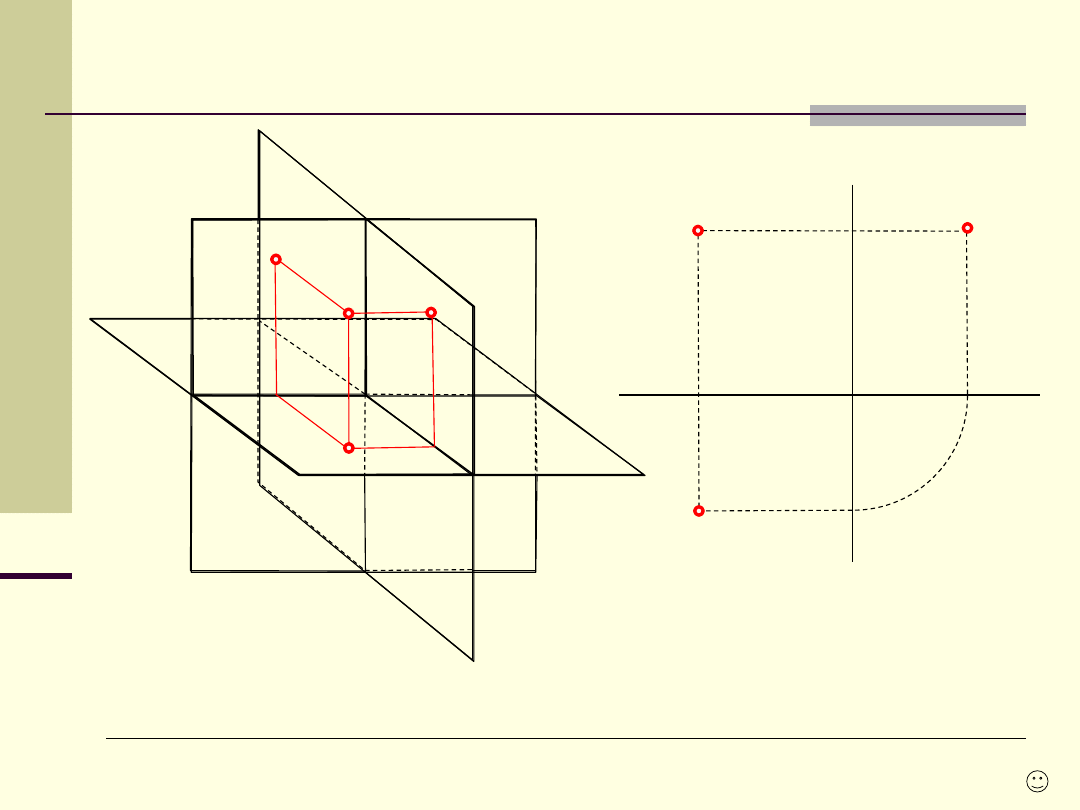
Trzy rzutnie

p

3

p

2

p

1

x

y

z

A

A’

A’’

A”’

x

y

z

y

A’’

A”’

A’

Wojskowa Akademia Techniczna WTC KZMiT

28

p

3

– rzutnia boczna

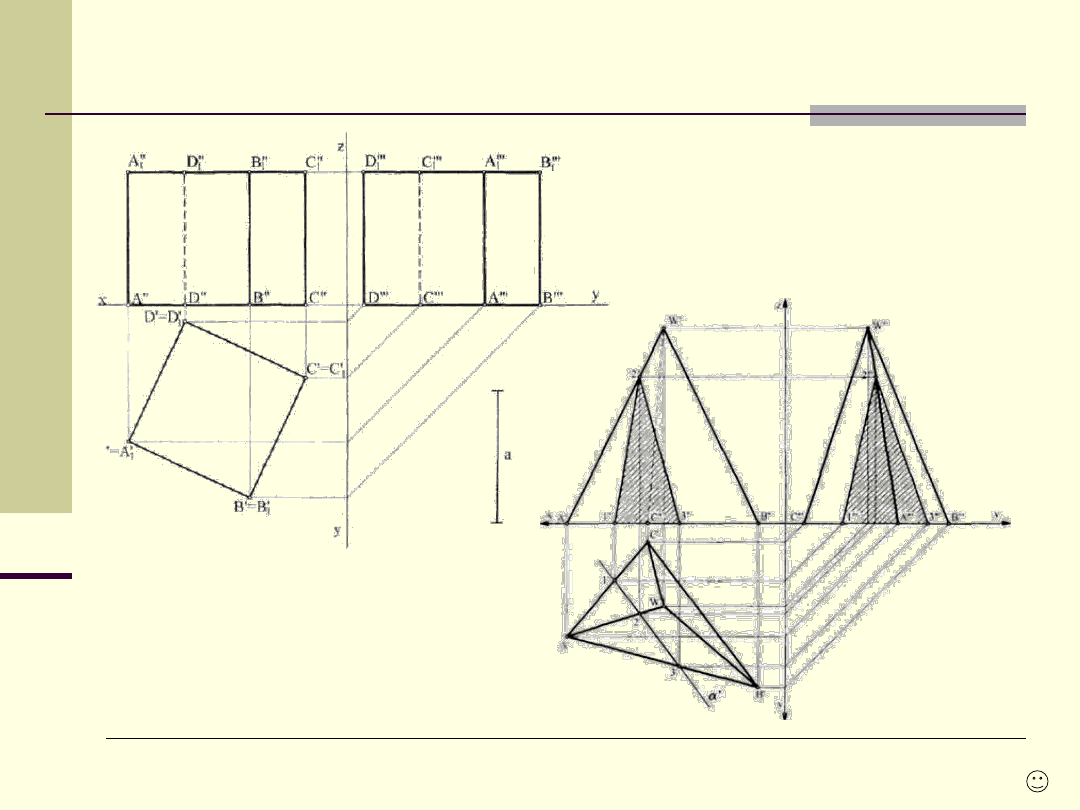
Rzuty figur

Wojskowa Akademia Techniczna WTC KZMiT

29

Wykreślić trzy rzuty sześcianu o
krawędzi a ustawionego na rzutni
poziomej.

Wykreślić

rzuty

ostrosłupa

o

podstawie na rzutni poziomej z
odciętą

płaszczyzną

poziomo-

rzutującą jego częścią.

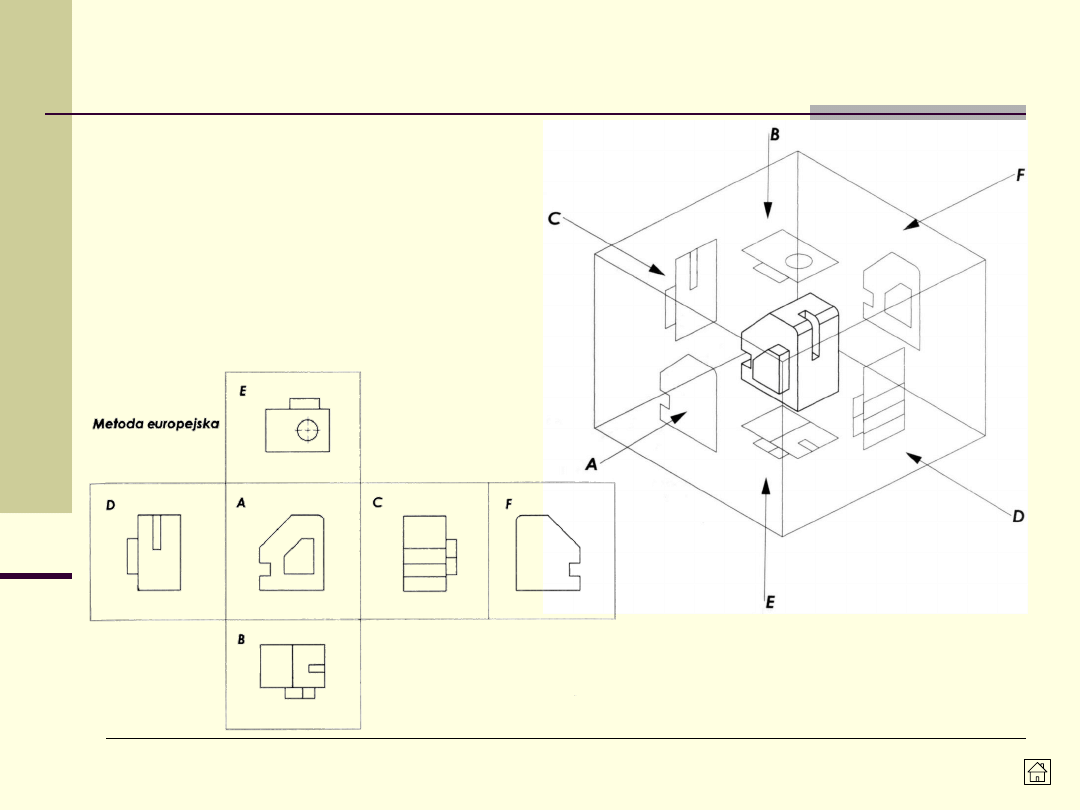
Rzutowanie metodą europejską

Wojskowa Akademia Techniczna WTC KZMiT

30