PKM II

gwinty, śruby,

mechanizmy śrubowe

Połączenia gwintowe

Ogólna charakterystyka połączeń gwintowych

•

Połączenia gwintowe to połączenia cierno-kształtowe,

rozłączne.

•

Zasadniczym elementem połączenia gwintowego jest

łącznik, składający się ze śruby i nakrętki. Skręcenie ze

sobą śruby i nakrętki tworzy połączenie gwintowe.

•

Połączenia gwintowe dzieli się na:

•

pośrednie – części maszyn łączy się za pomocą łącznika,

rolę nakrętki może również spełniać gwintowany otwór

w jednej z części;

•

bezpośrednie – gwint jest wykonany na łączonych

częściach.

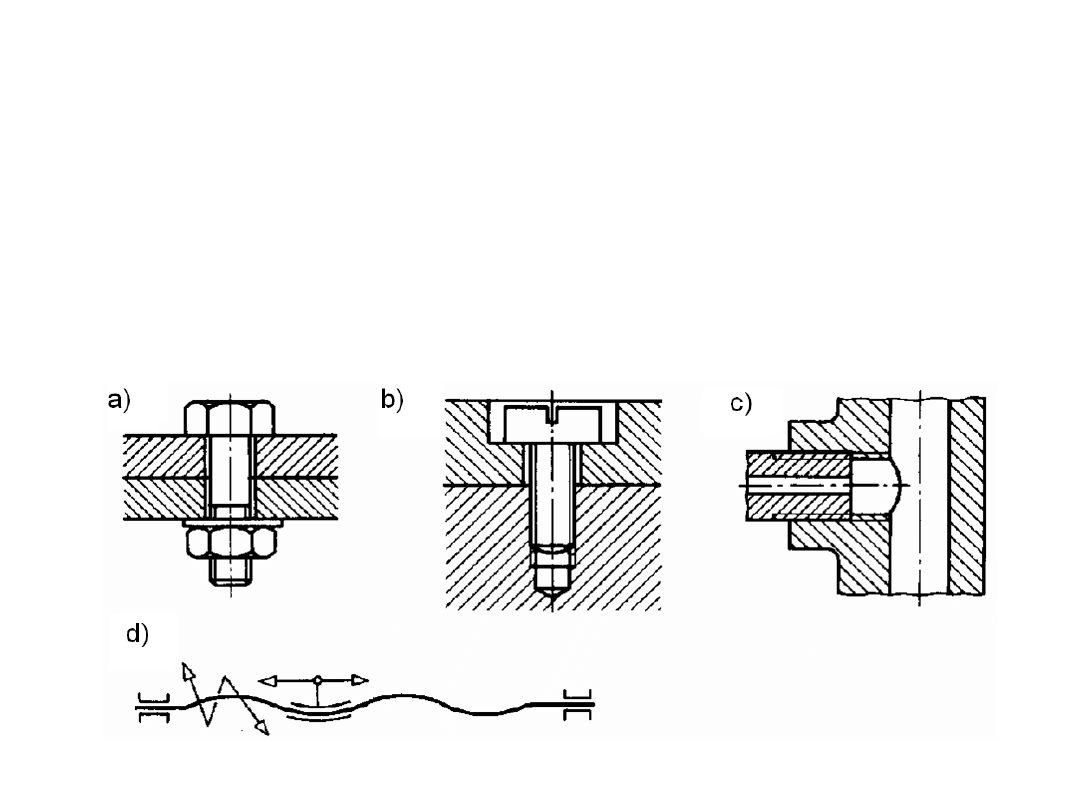
Połączenia gwintowe

• a),b) połączenia pośrednie
• c) połączenie bezpośrednie
• d) schemat mechanizmu śrubowego

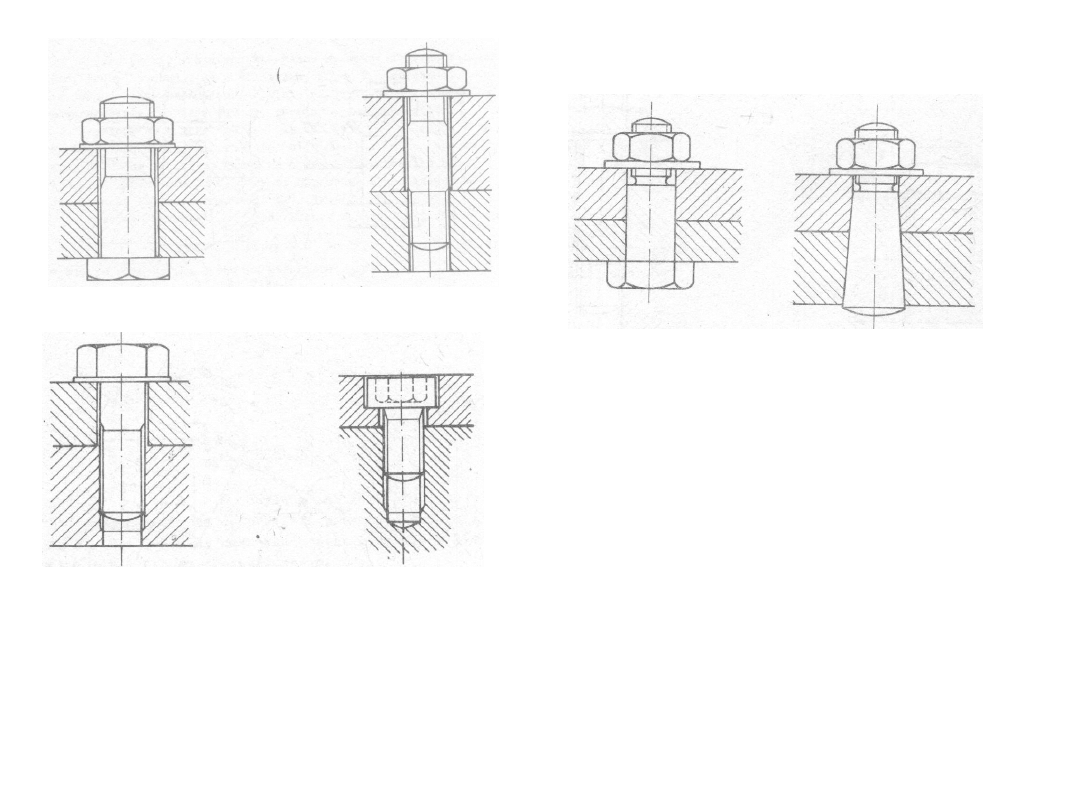
M. Dietrich – Podstawy Budowy Maszyn

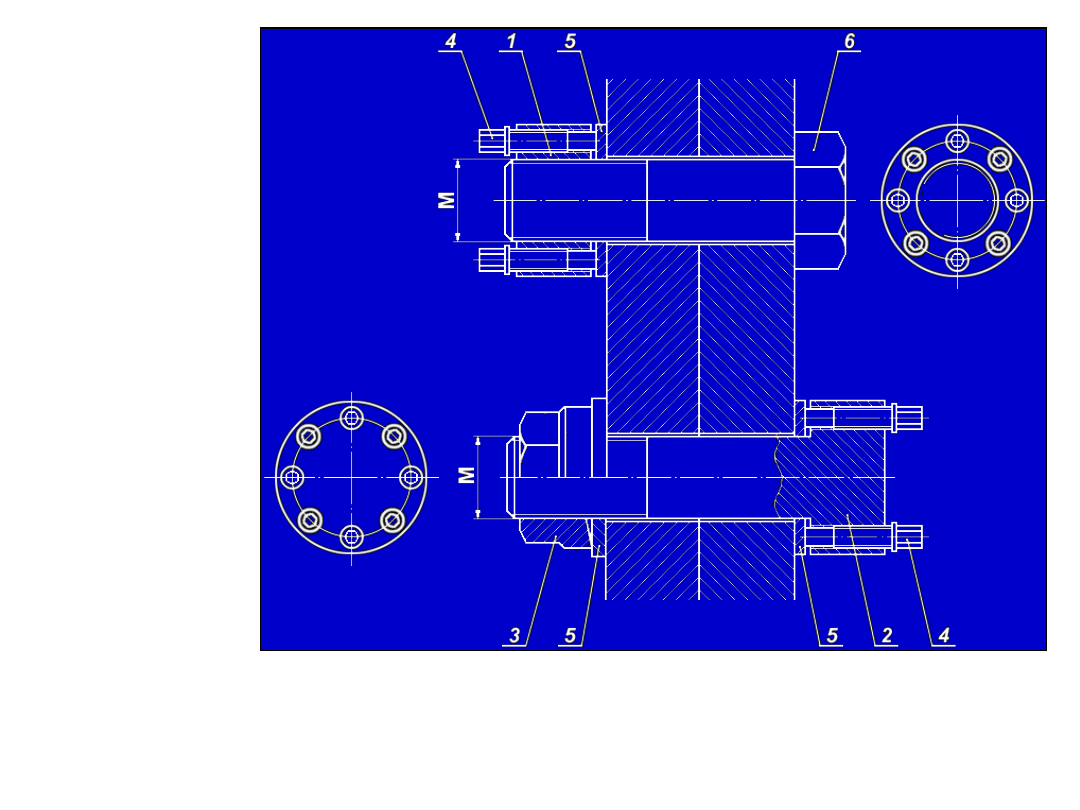
1. Korpus nakrętki

2. Korpus śruby

3. Nakrętka sprężysta

4. Śruba napinająca

5. Pierścień oporowy

6. Śruba standardowa

M – gwint główny

Dokręcanie śrub napinających (poz. 4) wywołuje nacisk na pierścień oporowy (poz. 5). Suma sił wywołanych
przez śruby napinające składa się na łączną siłę rozciągającą rdzeń śruby.

Podczas wkręcania śrub napinających, wraz ze zwiększającym się obciążeniem, elementy Superbolt
odkształcają się w taki sposób, że wszystkie nitki gwintu głównego są obciążone równomiernie.

Podstawowe cechy systemu Superbolt:
niskie momenty dokręcania - max. 860 Nm;
dowolne średnice i zarysy gwintów;
wysoka trwałość i niezawodność;
montaż w miejsce elementów standardowych;
zakres temperatur pracy od -250 do 630°C.

•

Korzyści ze stosowania elementów systemu Superbolt:

•

brak naprężeń skręcających rdzeń śruby i równomierne obciążenie wszystkich nitek
gwintu - przenoszenie wyższych naprężeń poosiowych przy tej samej średnicy gwintu

głównego, możliwość zastosowania elementów o mniejszych gabarytach;

•

brak ruchu obrotowego obciążonej nakrętki - wielokrotny montaż i demontaż bez oznak

zużycia nitek gwintu głównego;

•

średnica śrub napinających wielokrotnie mniejsza od średnicy gwintu głównego -

moment dokręcania śrub napinających od kilkunastu do kilkudziesięciu razy mniejszy

od momentu potrzebnego do wywołania analogicznego naprężenia w klasycznym

połączeniu gwintowym;

•

kompensacja nieprostopadłości osi śruby do powierzchni oporowej.

•

W połączeniach gwintowych napinanych elementami systemu Superbolt mogą

występować naprężenia wyższe od występujących w połączeniach klasycznych - zaleca

się zastępowanie nakrętek standardowych sprężystymi nakrętkami Superbolt.

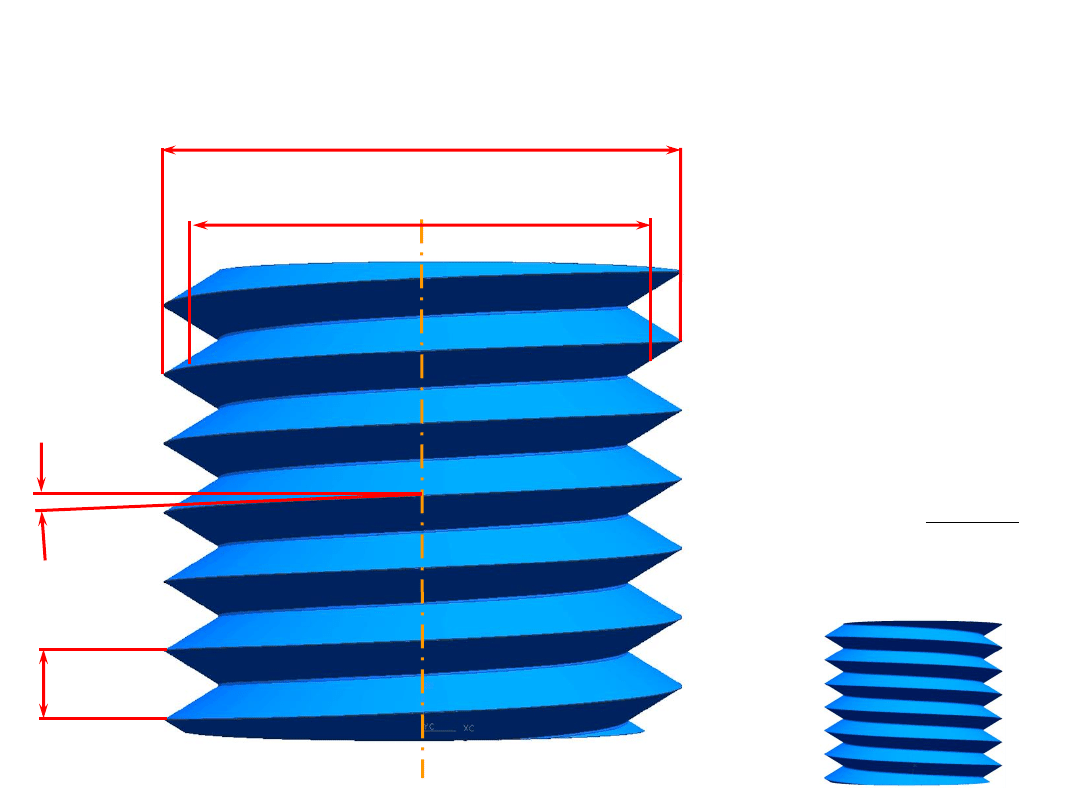
d

P

g

podstawowe parametry linii śrubowej – równia pochyła

2

tg

d

P



g



d -

średnica gwintu

(nominalna)

d

2

-

średnica

podziałowa

P - skok gwintu

g

- pochylenie linii

śrubowej

d

2

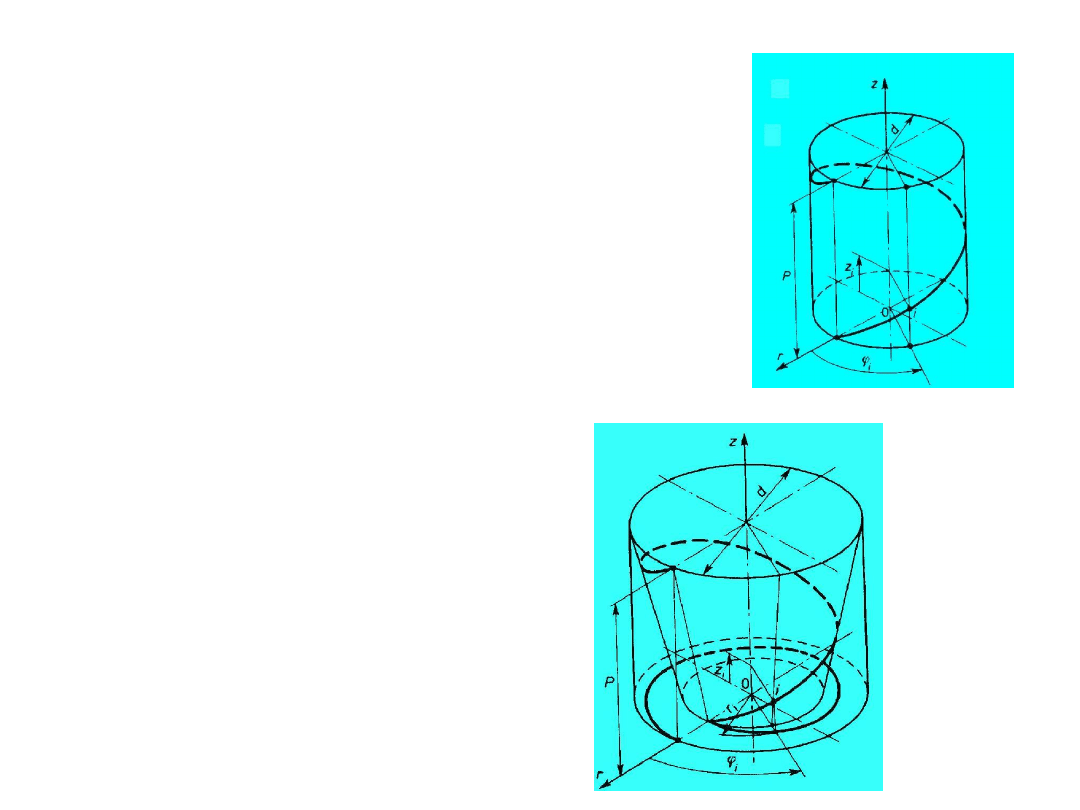
Gwint walcowy

Połączenia spoczynkowe i ruchowe

Gwint stożkowy

Tylko połączenia spoczynkowe –
umożliwia regulację nacisków
międzyzwojnych, skasowanie luzów i
uzyskanie szczelności – zastosowanie
w przewodach rurowych

Rodzaje gwintów

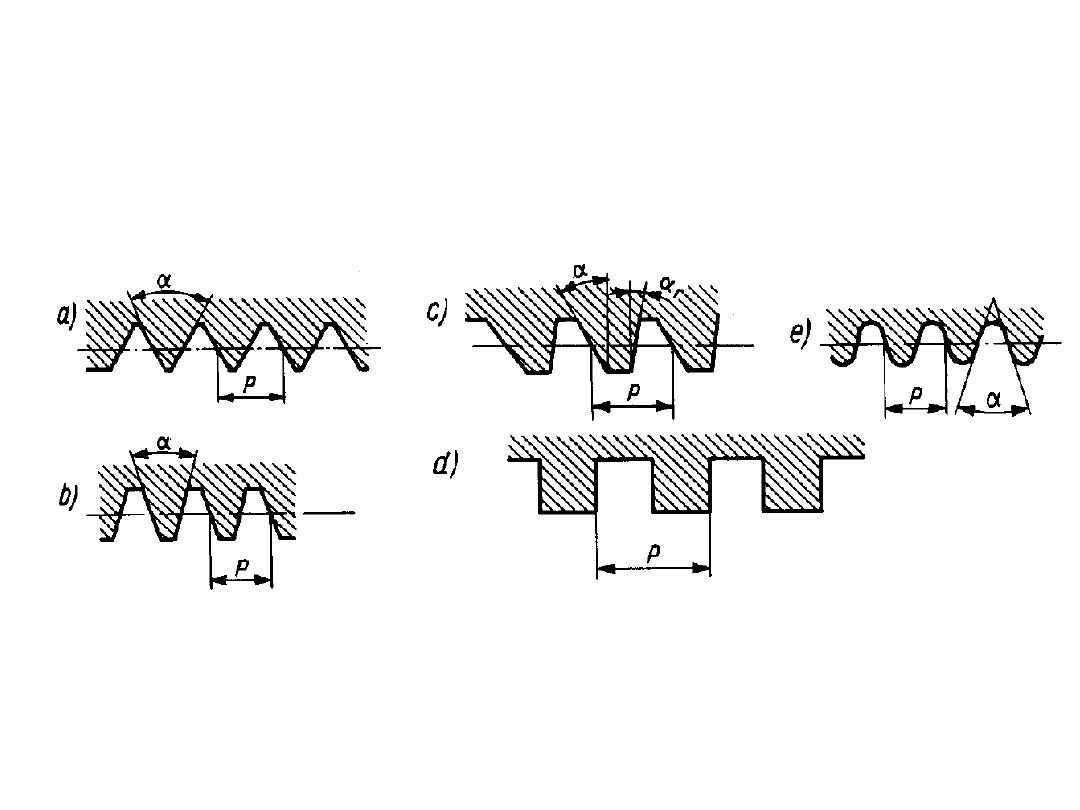
Rodzaje gwintów

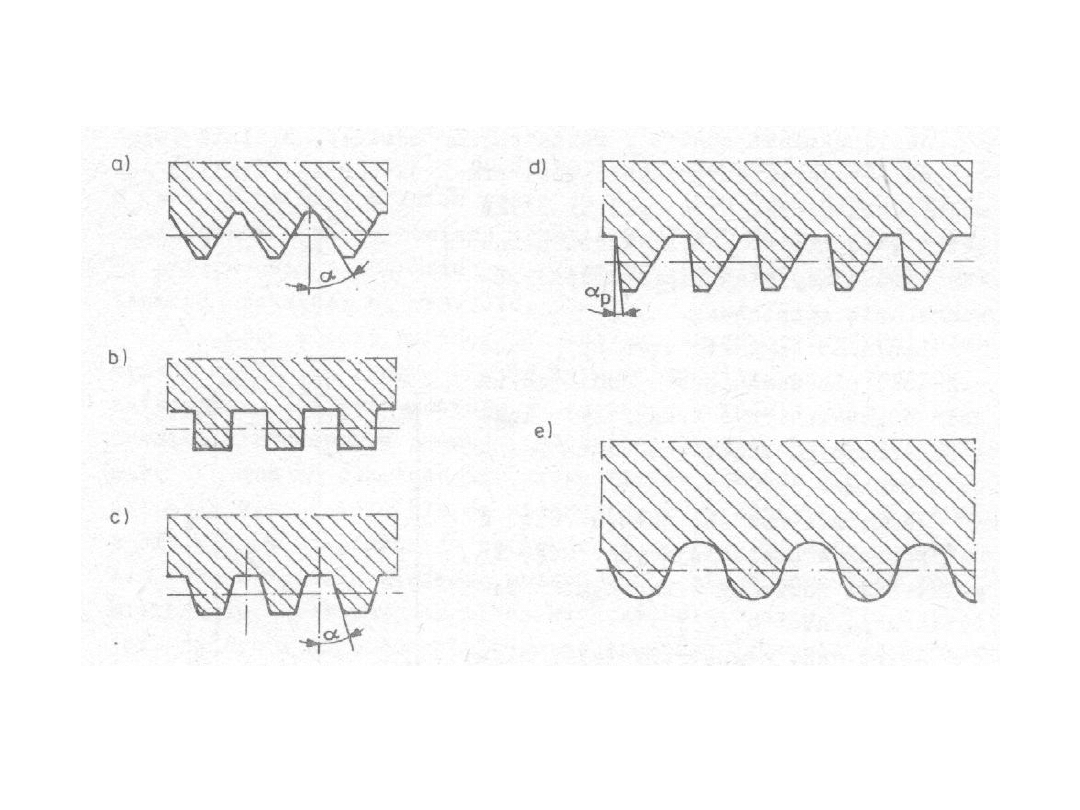
Rodzaje gwintów (trójkątne, prostokątne, trapezowe, okrągłe)

Gwint prawy – powszechnie stosowany

Gwint lewy – rzadziej stosowany, np. śruba
rzymska, zawory, gdy użycie gwintu prawego
sprzyja luzowaniu się złącza.

Gwint pojedynczy - powszechnie stosowany

Gwint wielokrotny (podziałka gwintu) –
mechanizmy, gdy wymagana jest duża
sprawność mechanizmu.

Gwint symetryczny- zmienny kierunek
obciążenia.

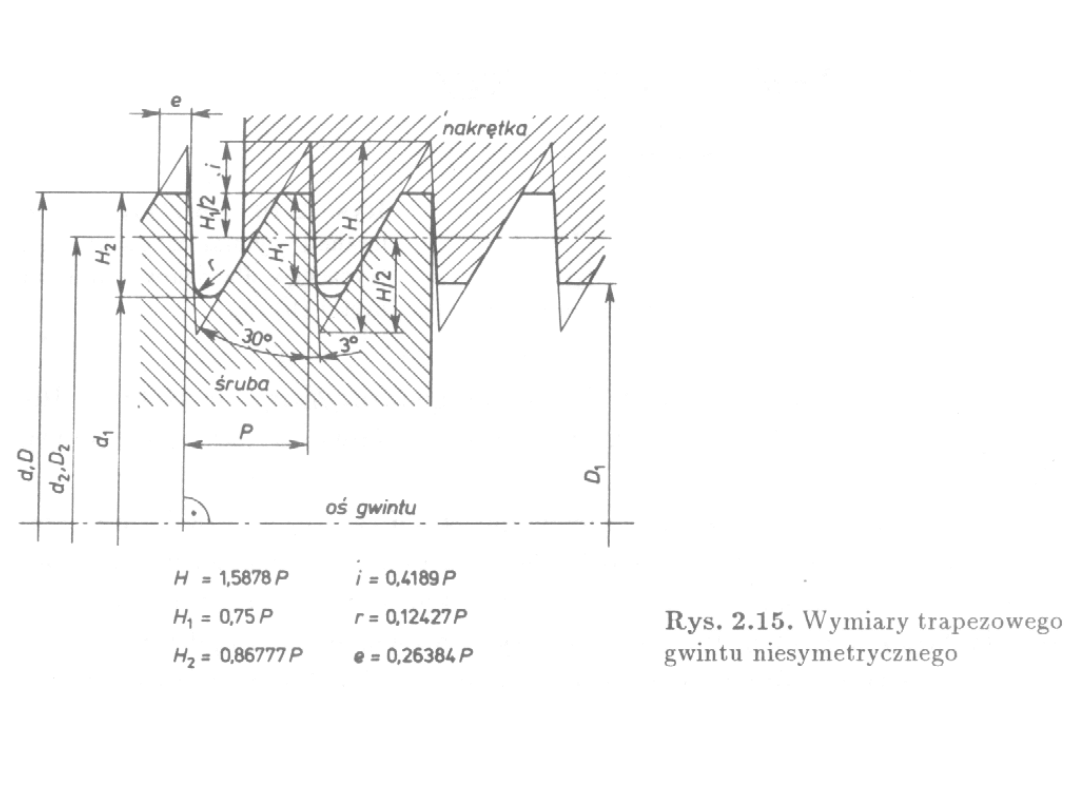
Gwint niesymetryczny – jednokierunkowe
obciążenie, w mechanizmach o wymaganej
dużej sprawności.

Gwint zwykły – normalny skok P – najczęściej występuje

Gwint grubozwojny – duży skok P – gdy o wytrzymałości złącza
decydują naciski na zwoje, a nie wytrzymałość rdzenia śruby, duże
obciążenia.

Gwint drobnozwojny – mały skok P – większa wytrzymałość statyczna
i zmęczeniowa rdzenia śruby, lepiej zabezpiecza złącze przed
luzowaniem się, ale wymaga większej dokładności – efekt karbu
wielokrotnego. Połączenia regulujące wzajemne położenie elementów.

Gwint okrągły – minimalizacja koncentracji naprężeń

Połączenia ruchowe – odporność na zużycie, duża
sprawność. Nie samohamowne i samohamowne.

Samohamowność połączenia gwintowego (np. gwinty
metryczne)

Umowny kąt pozornego tarcia

Połączenia spoczynkowe – wywołanie dużego nacisku w
polu styku elementów łączonych, zabezpieczenie przed
luzowaniem się złącza…Samohamowne

Połączenia szczelne – ciasne pasowania, gwinty
stożkowe.





















cos

arctg



g



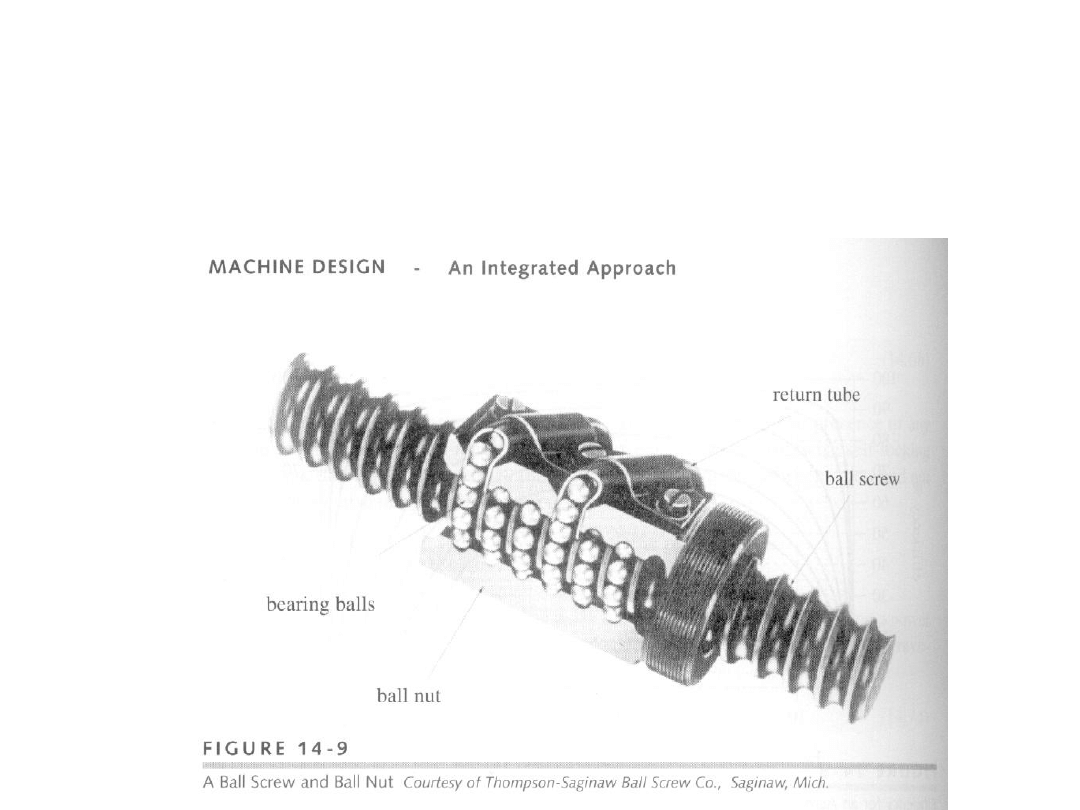
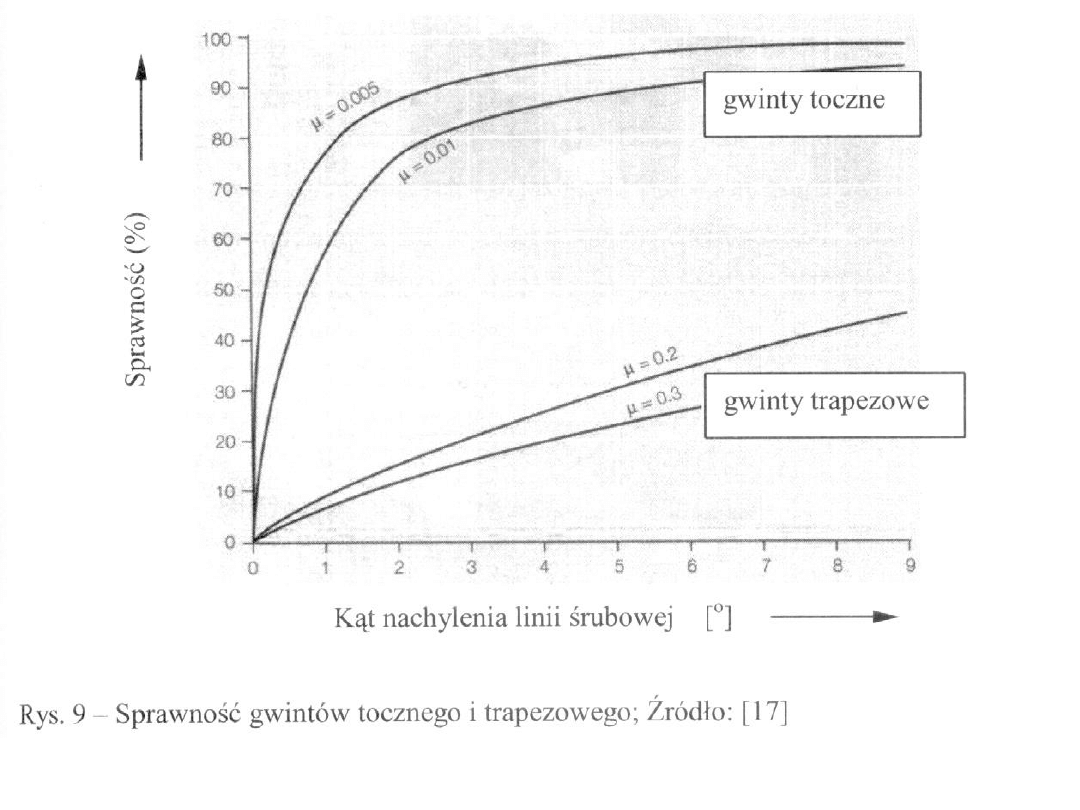
Gwint toczny

Bardzo duża sprawność, mogą przenosić duże obciążenia.

Zastosowania: podnośniki, napędy sterów w samolotach, mechanizmy
chowania i wypuszczania podwozia, mechanizmy sterowania w
samochodach, łóżkach szpitalnych …

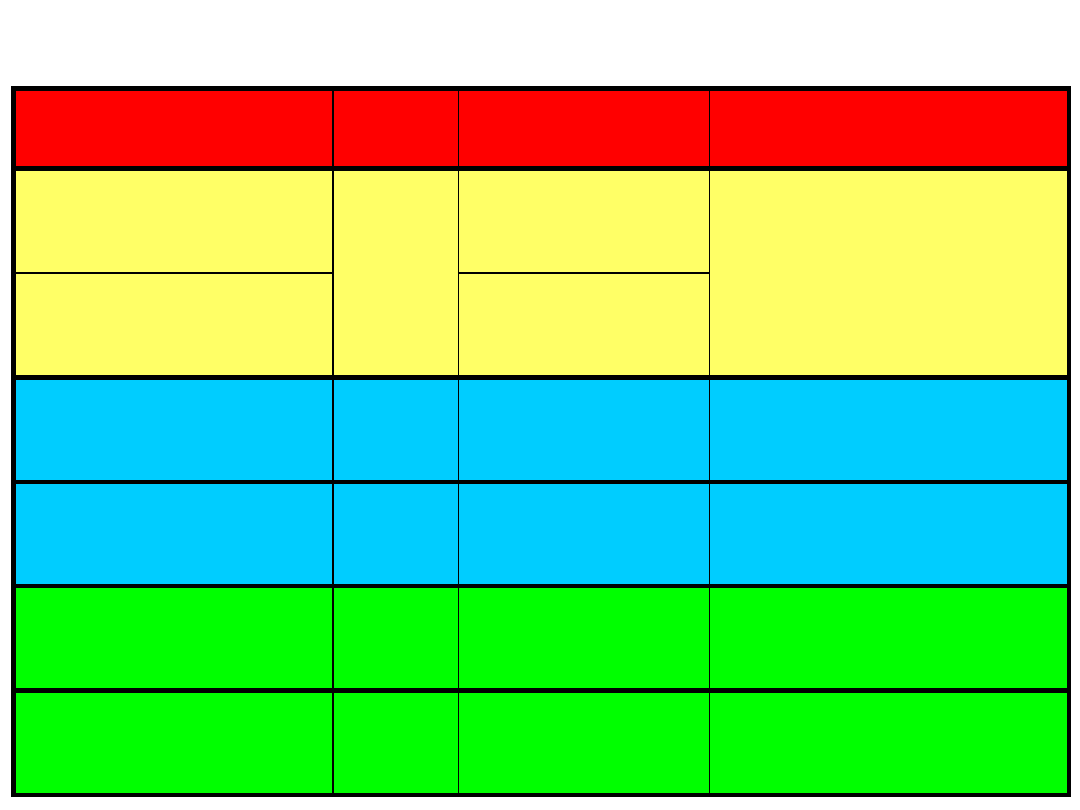
podstawowe rodzaje gwintów

nazwa

skrót oznaczenie opis dodatkowy

metryczny

zwykły

M

M24

gwinty trójkątne

o kącie zarysu

2



=60

metryczny

drobnozwojny

M24x1,5

calowy

(Whitworth’a)

-

3/4”

kąt zarysu 2



=55

rurowy

R

R3”

cylindryczne lub

stożkowe

trapezowy

symetryczny

Tr

Tr48x8

kąt zarysu 2



=30

trapezowy

niesymetryczny

S

S48x8

kąty zarysu



r

=3 ;



p

=30

Wybrane oznaczenia rodzajów gwintów

BSF - gwint calowy Whitwotha, drobnozwojny,
BSW - gwint calowy Whitwortha, zwykły,
E - gwint Edisona, sprzęt elektrotechniczny,
G - gwint rurowy Whitwortha, walcowy,
M - gwint metryczny zwykły i drobnozwojny,
NPT - gwint rurowy Briggsa, stożkowy
Pg - gwint specjalny instalacyjny, pancerny,
R - gwint rurowy Whitwortha, stożkowy, zewnętrzny,
Rc - gwint rurowy Whitwortha, stożkowy, wewnętrzny,
Rd - gwint okrągły, duża wytrzymałość rdzenia, mała wrażliwość na
zanieczyszczenia, np. w ściągach wagonów, w hakach dźwigów,
przewodach pożarniczych…
Rp - gwint rurowy Whitwortha, walcowy wewnętrzny,
RW, FG - gwint rowerowy,
S - gwint trapezowy niesymetryczny,
Tr - gwint trapezowy symetryczny,
UN - gwinty zunifikowane o skoku uprzywilejowanym,
UNC - gwint calowy, zunifikowany, zwykły,
UNEF - gwint calowy, zunifikowany, bardzo drobnozwojny,
UNF - gwint calowy, zunifikowany, drobnozwojny,
UNS - gwinty zunifikowane specjalne,
Ven, Vg - gwint wentylowy,
W - gwint stożkowy do zaworów gazowych,

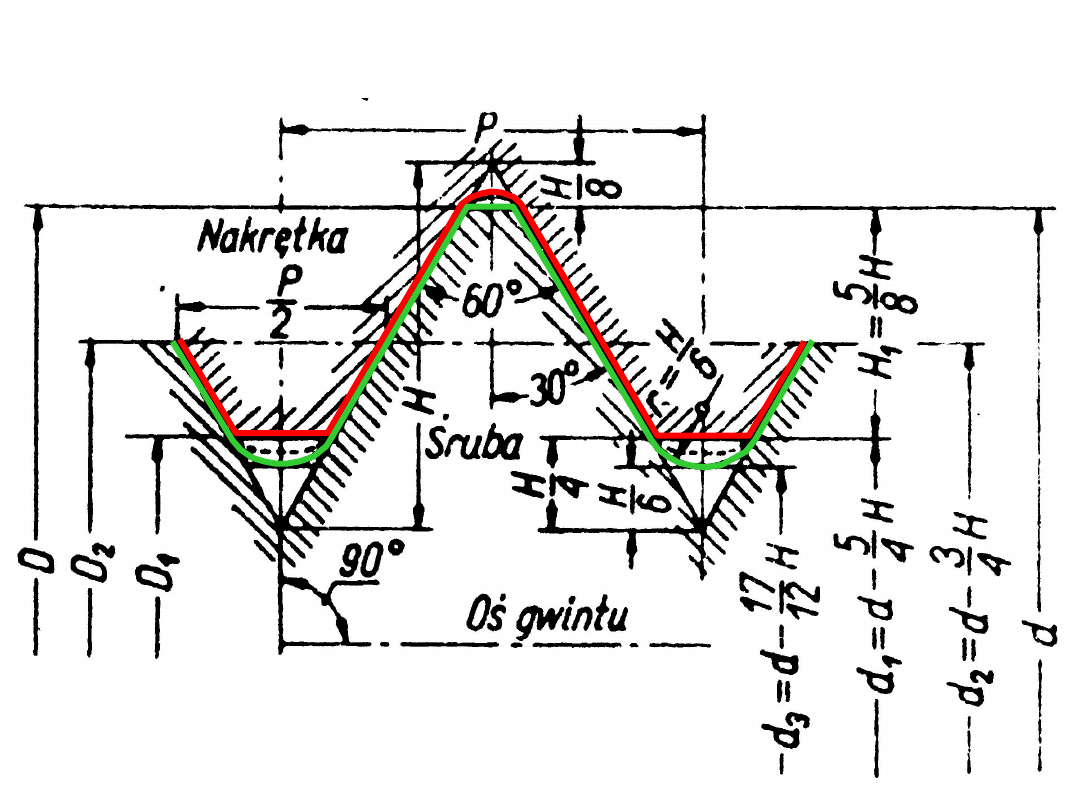
gwint metryczny zwykły

Gwinty są znormalizowane przez Polską Normę. Definiuje się w niej
gwinty metryczne, to znaczy takie, których średnica gwintu w
milimetrach jest typoszeregiem liczb naturalnych lub ich ułamków
dziesiętnych w przypadku gwintów drobnych.

Zgodnie z tym gwint metryczny koduje się Mn, gdzie n to średnica
gwintu w milimetrach np. M5, M20.

W gwintach, w których skok P jest inny niż by to wynikało z ogólnej
zasady, dodatkowo specyfikuje się ten parametr w kodzie gwintu
metrycznego, np. M20x2 (gwint metryczny o średnicy d = 20 mm i
skoku P = 2mm), M20x1.5, M20x1, M20x0.75. M20 posiada
normalny skok P = 2,5 mm.

szereg gwintów metrycznych

d=D

szeregi średnic

P

d

2

=

D

2

d

1

=

D

1

d

3

r

H

mm

2

gwint

1

2

3

zwy-

kły

drobno-

zwojny

24

3

2

1,5

1

0,75

22,051
22,701
23,026
23,351
23,513

20,752
21,835
22,376
22,918
23,188

20,319
21,546
22,160
22,773
23,080

0,433
0,259
0,217
0,144
0,108

1,624
1,083
0,812
0,541
0,406

324
365
386
407
419

25

2

1,5

1

23,701
24,026
24,351

22,835
23,376
23,918

22,546
23,160
23,773

0,289
0,217
0,144

1,083
0,812
0,541

399
421
444

26

1,5

25,026

24,376

24,160

0,217

0,812

458

27

3

2

1,5

1

0,75

25,051
25,701
26,026
26,351
26,513

23,752
24,835
25,376
25,918
26,188

23,319
24,546
25,160
25,773
26,080

0,433
0,259
0,217
0,144
0,108

1,624
1,083
0,812
0,541
0,406

427
473
497
522
535

4

2

3

d



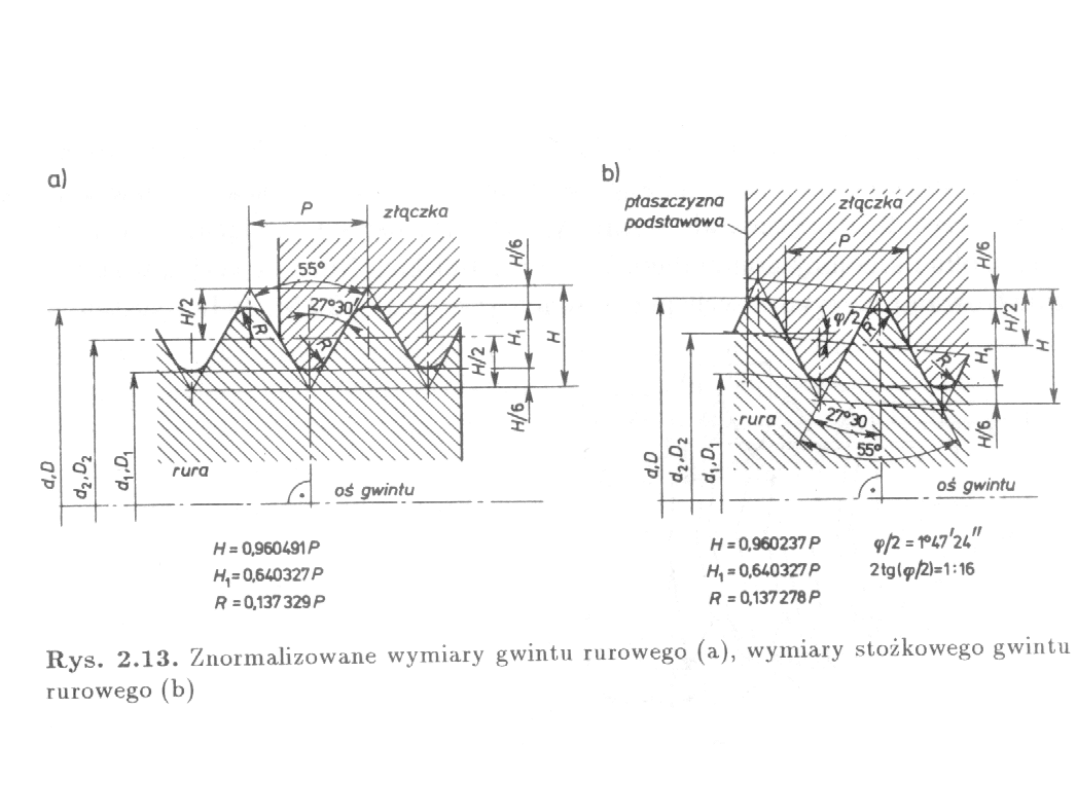
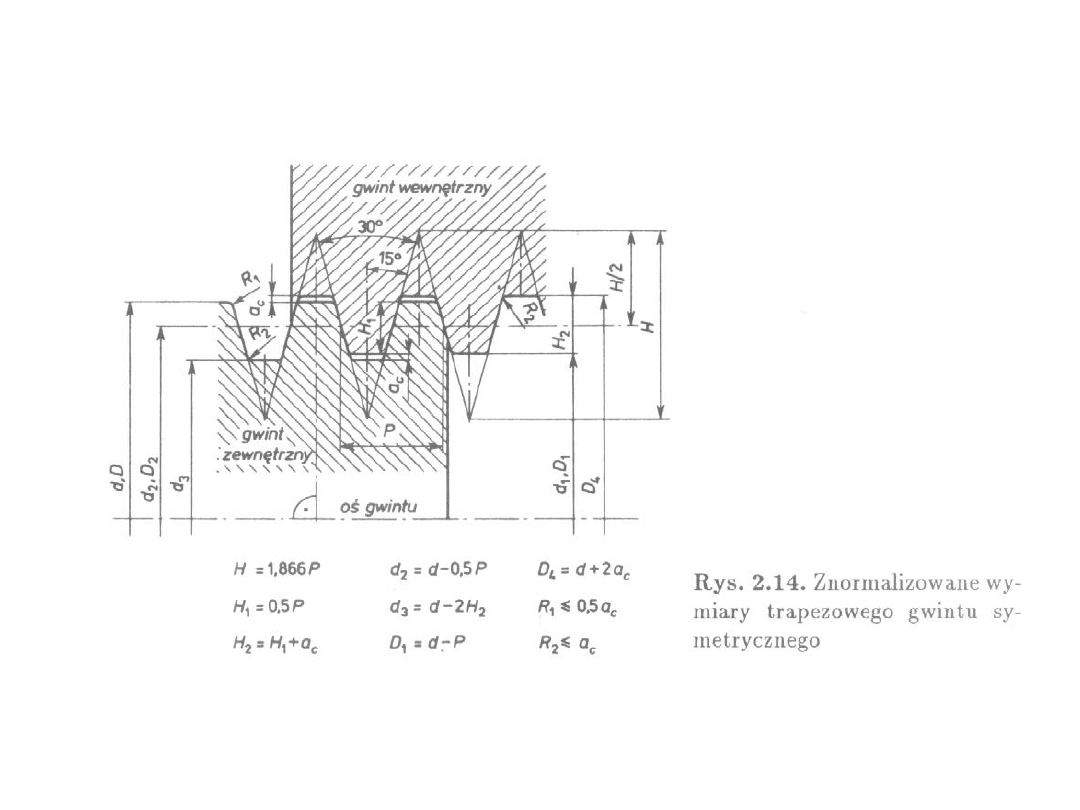
Mikołaj Piotrowski – pr. mgr.

γ

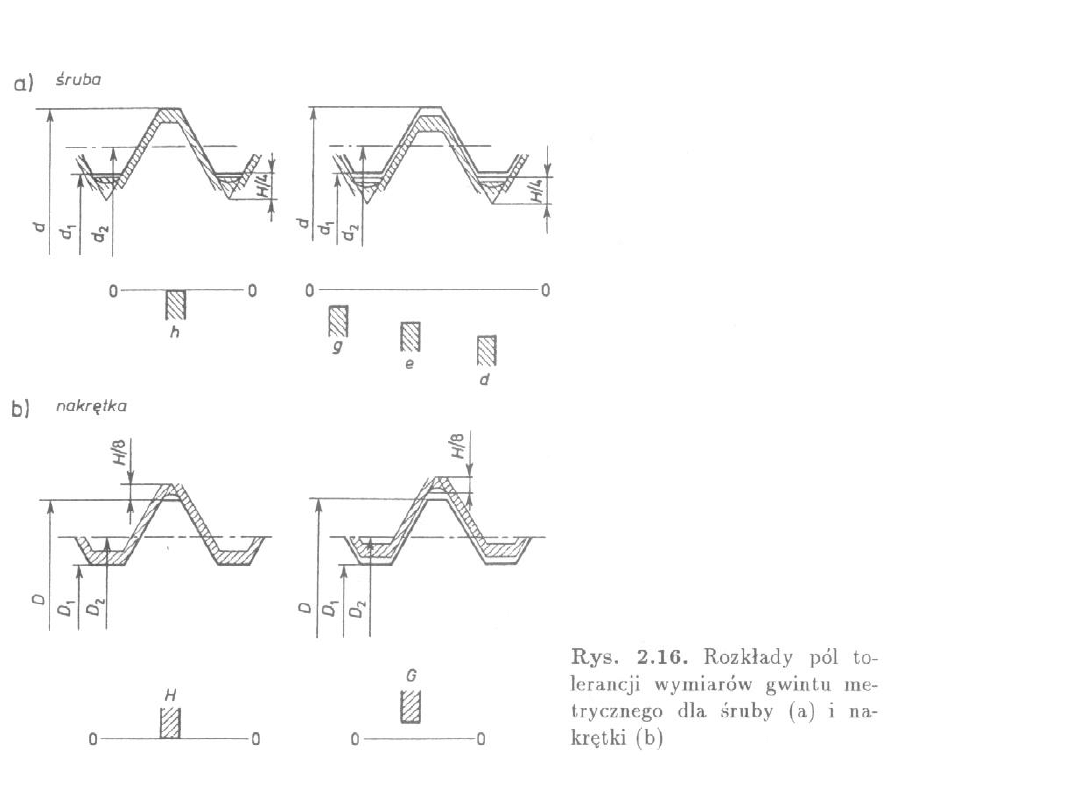
Tolerancje i pasowania gwintów – w głąb materiału

Suwliwe – połączenia
spoczynkowe, wymagane częste
złącznie i rozłączanie

Ciasne – połączenia
spoczynkowe, wymagane duże
siły tarcia, szczelność

Luźne – polączenia ruchowe

Technologia gwintów

Gwintowanie (narzynki i gwintowniki)

Frezowanie

Toczenie

Wygniatanie (walcowanie) – rolki, drewno, tworzywa
sztuczne

Wytłaczanie (np. gwintu E w mosiężnych rurkach)

Odlewanie pod ciśnieniem – metale nieżelazne, tworzywa
sztuczne

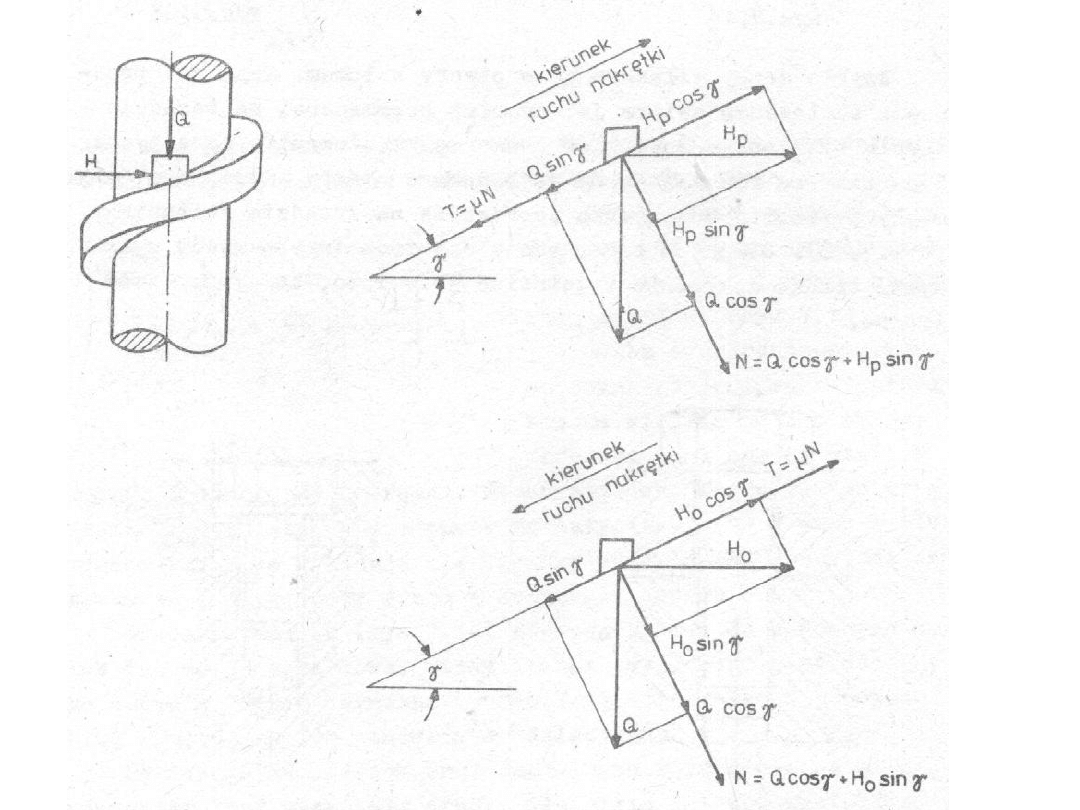
M. Dietrich – Podstawy Budowy Maszyn

T + Q sin γ = Hp cos γ

T = N μ = (Q cos γ + Hp sin γ) μ

Hp = Q tg (γ + ρ) przy podnoszeniu

μ = tg ρ

Ho = Q tg (γ - ρ) przy opuszczaniu

Jeżeli γ > ρ, czyli Ho > 0 to gwint jest niesamohamowny !!!

Jeżeli γ < ρ, czyli Ho < 0 to gwint jest samohamowny !!!

Dla gwintów nieprostokątnych – wzrost siły
tarcia:

Hp = Q tg (γ + ρ’) przy podnoszeniu

Ho = Q tg (γ – ρ’) przy opuszczaniu









cos

'

'

tg





M = 0.5 d

2

Q tg (γ

ρ’)

Moment nakrętka – śruba:

Sprawność (stosunek pracy użytecznej do pracy
włożonej):









cos

'

'

tg









'

tg

tg

2



g

g

















M

P

Q

P – skok gwintu

P = π d tg γ

Ruch do góry:





g



g





tg

'

tg

2













P

Q

M

Ruch w dół
(niesamohamowne):

obliczenia gwintów - wprowadzenie

całkowity moment oporów na śrubie:









n

n

D

d

Q

M





g











'

tg

2

2

Q -

siła osiowa

d

2

-

średnia średnica gwintu

γ

-

pochylenie linii śrubowej

ρ’ - kąt tarcia na gwincie

D

n

-

średnica tarcia nakrętki

μ

n

-

współczynnik tarcia nakrętki









cos

'

'

tg





obliczenia gwintów - wprowadzenie

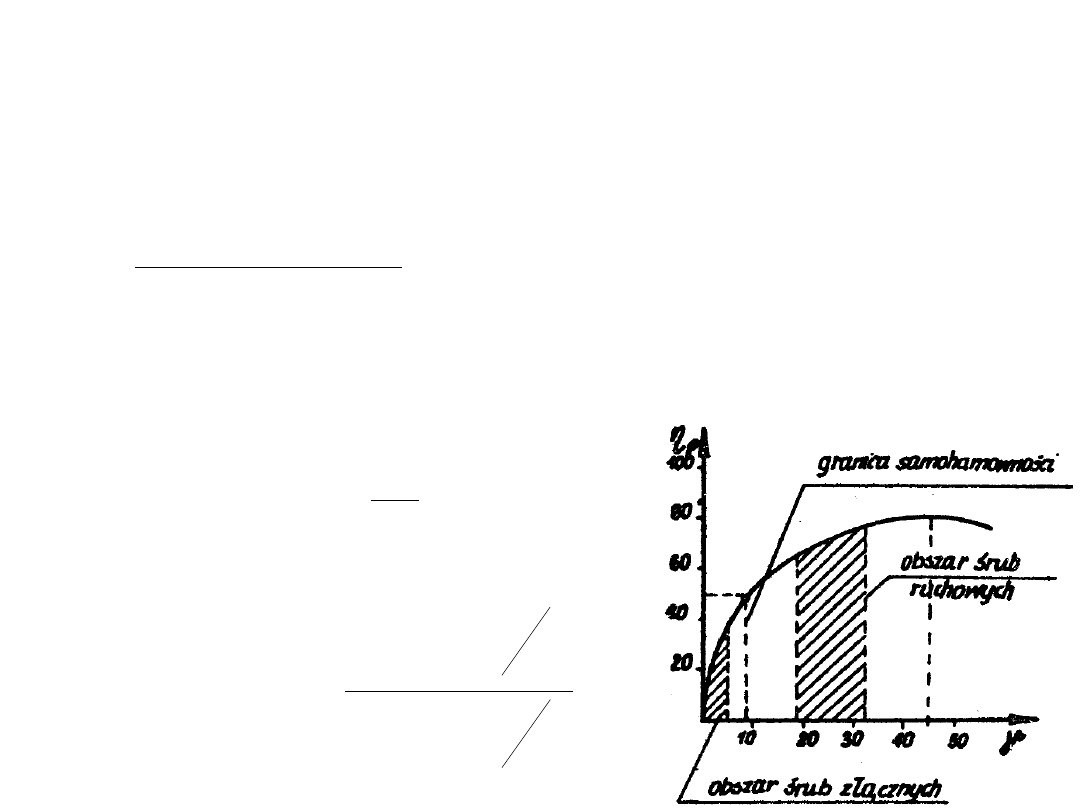
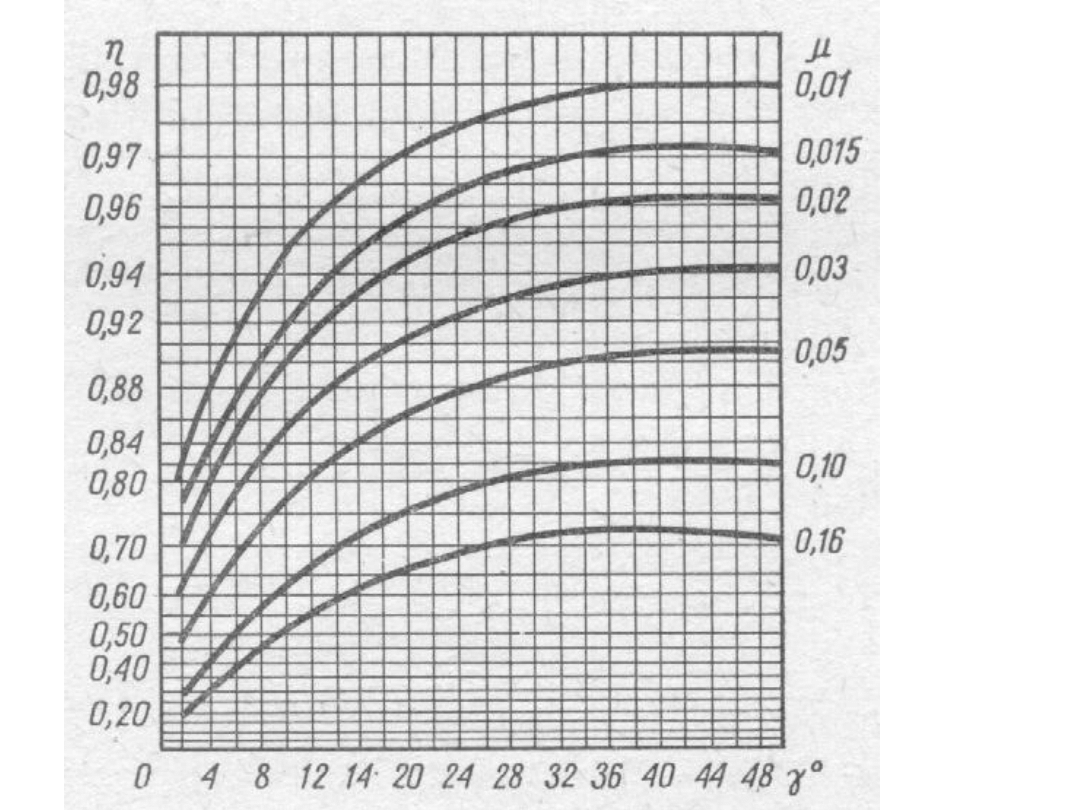
sprawność gwintu:





'

tg

tg



g

g







γ - pochylenie linii śrubowej

ρ’ - kąt tarcia na gwincie

2

'

45



g







opt



































2

'

45

tg

2

'

45

tg

max







dla

ρ’ = 5 40’ (μ=0,1)

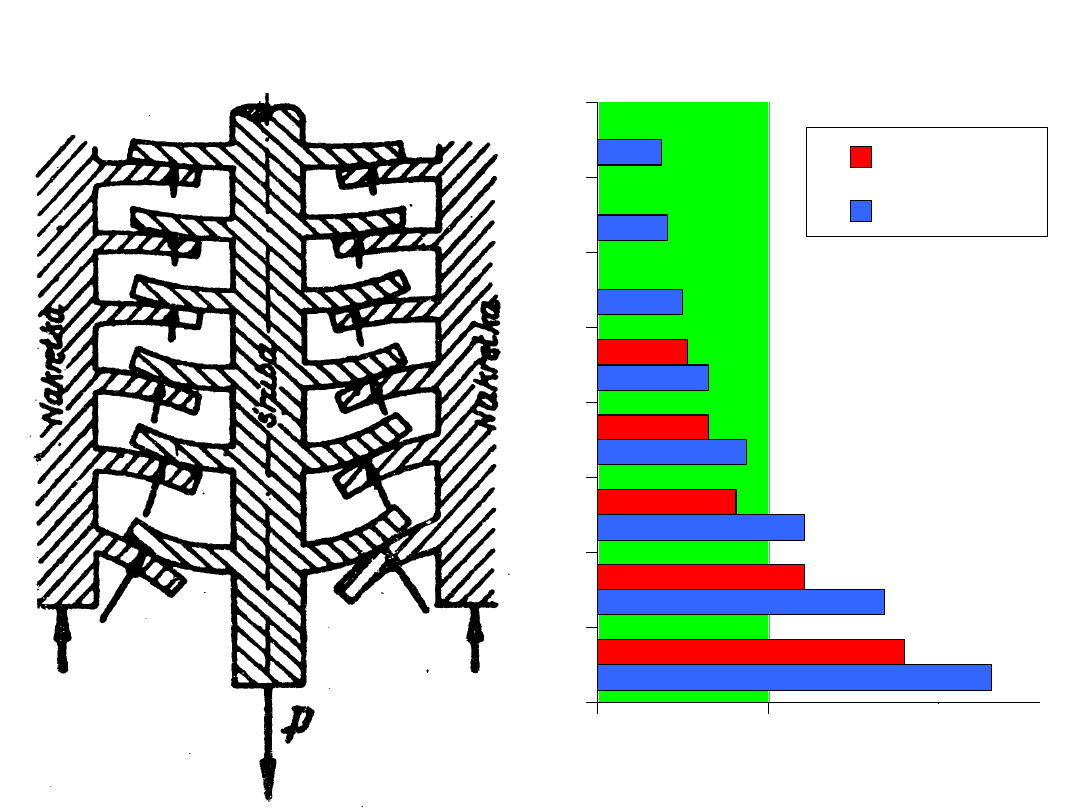
obciążenie poszczególnych nitek gwintu

231

168

121

87

65

50

41

37

180

121

81

65

53

0

100

200

1

2

3

4

5

6

7

8

5 zwojów

8 zwojów

obciążenie

%

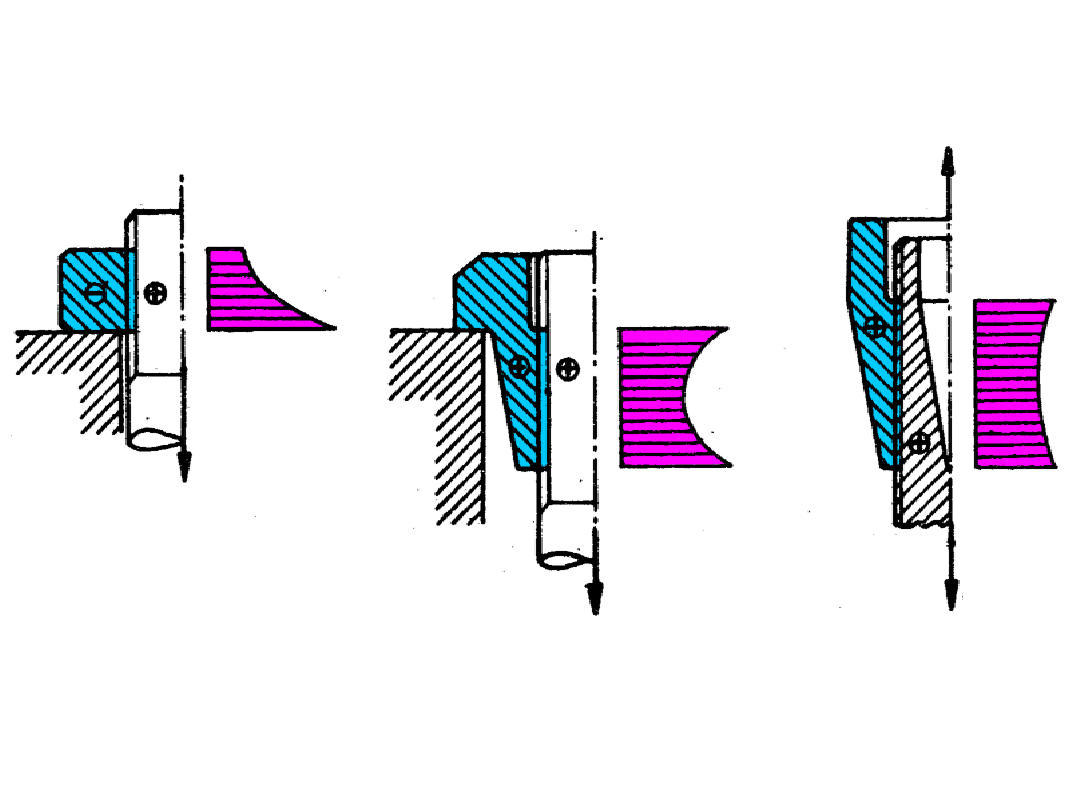
optymalizacja kształtu nakrętki

Q

Q

Q

Q

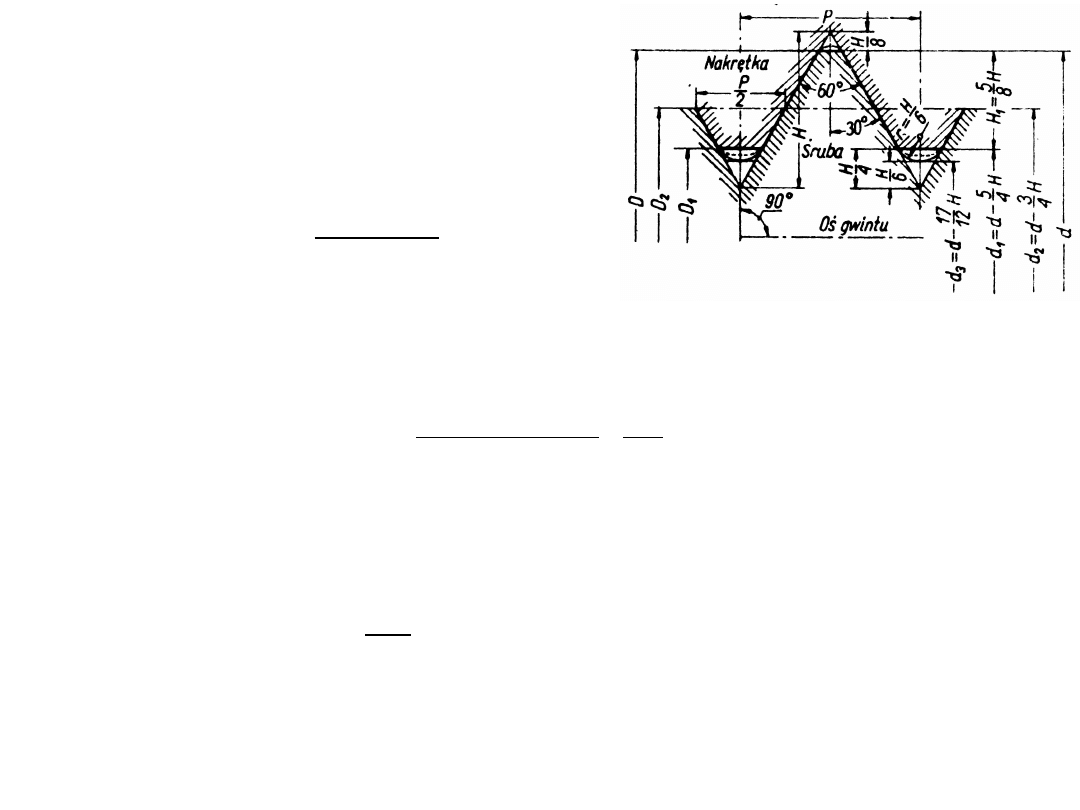
wytrzymałość gwintu

1.

rozciąganie rdzenia śruby

2.

nacisk na powierzchnię gwintu

3.

ścinanie gwintu

r

r

k

d

k

A

Q











4

2

3

3



dop

dop

p

p

P

m

d

d

p

i

A

Q

















4

)

(

2

1

2



t

t

t

t

k

h

d

P

m

k

A

Q















1



1.

warunek nacisku na powierzchnię gwintu

2.

warunek ścinania gwintu

wytrzymałość gwintu – wysokość nakrętki

d

m

p

P

m

d

d

k

d

Q

dop

r





















67

,

0

4

)

(

4

2

1

2

2

3









dop

p

d

d

P

Q

m









2

1

2

4



t

t

k

h

d

P

Q

m











1



d

m

k

P

m

h

d

k

d

Q

t

t

r





















48

,

0

4

1

2

3





sposoby obciążenia śruby

1.

czyste rozciąganie (ściskanie) siłą osiową

(np. hak)

2.

rozciąganie (ściskanie) siłą osiową oraz skręcanie

momentem skręcającym

(głównie mechanizmy gwintowe np. śruba pociągowa,
wrzeciono zaworu)

3.

obciążenie wstępne rozciągającą siłą osiową

i momentem skręcającym oraz obciążenie

robocze siłą osiową (stałą lub zmienną)

(typowe złącze śrubowe, np. pokrywka obciążona ciśnieniem)

4.

obciążenie wstępne rozciągającą siłą osiową

i momentem skręcającym oraz obciążenie

robocze siłą poprzeczną

(typowe złącza śrubowe np. sprzęgła kołnierzowe)

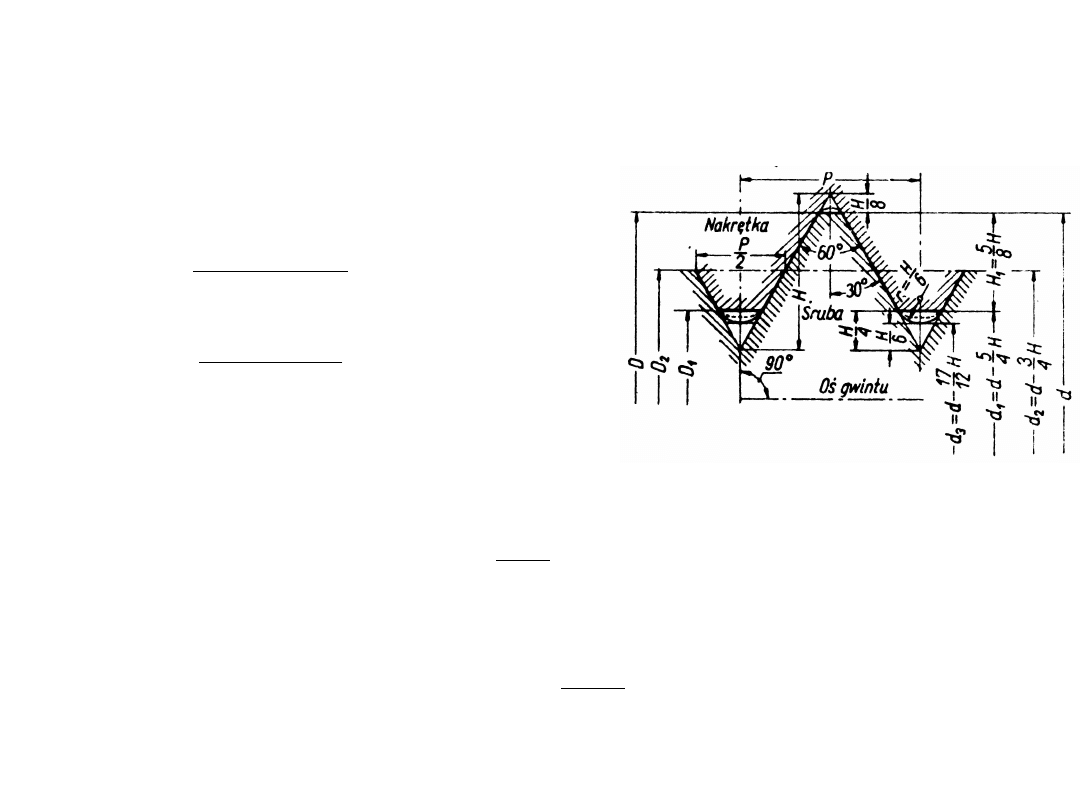
sposoby obciążenia śruby

1.

czyste rozciąganie (ściskanie) siłą osiową

r

r

k

d

Q







4

2

3





obciążenia statyczne:

obciążenia zmęczeniowe:

5

,

2

3

,

1

;







e

e

e

r

x

x

R

k

5

5

,

2

;







z

z

rj

r

x

x

Z

k

sposoby obciążenia śruby

2.

rozciąganie (ściskanie) siłą osiową oraz skręcanie

momentem skręcającym

4

2

3

d

Q









r

s

r

z

k

k

k



















2

2

2











16

'

tg

5

,

0

3

3

2

d

Q

d

















g



sposoby obciążenia śruby

4.

obciążenie wstępne rozciągającą siłą osiową

i momentem skręcającym oraz obciążenie

robocze siłą poprzeczną

• śruby pasowane:

• śruby z luzem:

t

k

d

T





4

2





dop

p

d

g

T

p

























r

w

k

d

Q

T

4

2

3

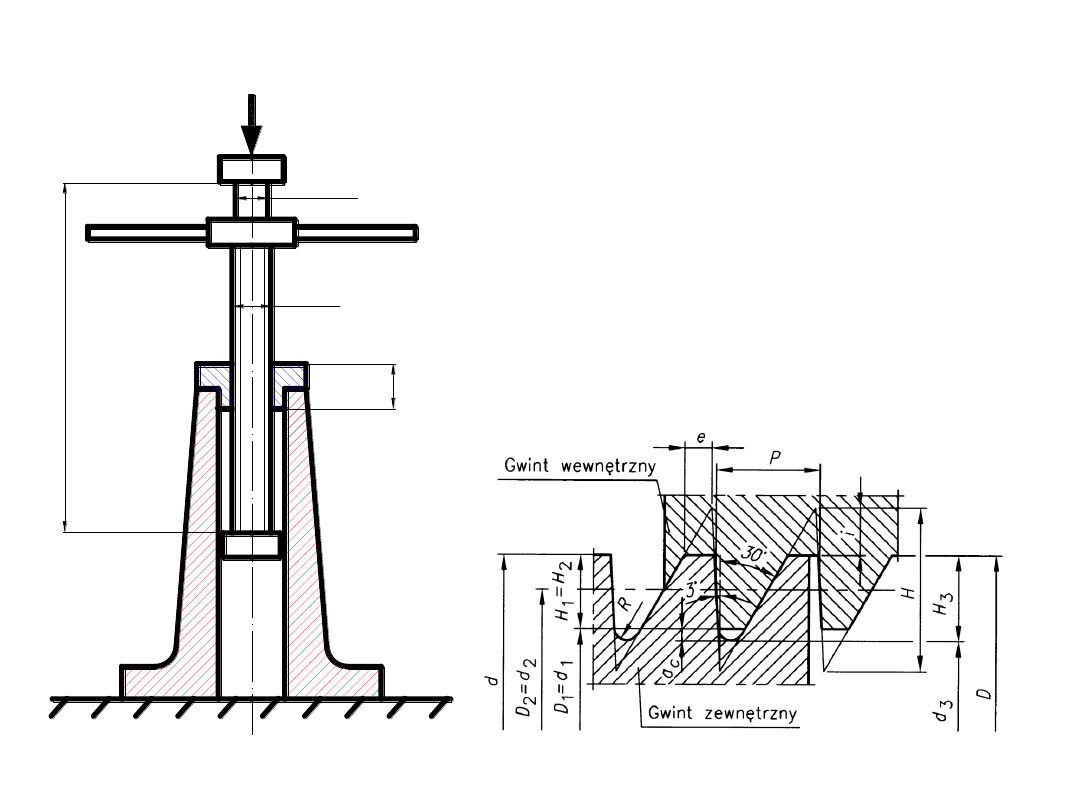
ZADANIE 1:

m

l

d

0

S40x6

Q

1.

Całkowity moment potrzebny do podniesienia masy jeśli
wsp. tarcia na gwincie wynosi



= 0,1,

zaś na głowicy

podnośnika



o

=0,15.

Średnica d

o

=30 mm;

2.Wykresy

składowych obciążenia śruby;

3.

Wysokość nakrętki m, jeśli dopuszczalne naciski na
zwojach gwintu

wynoszą p

dop

= 12 MPa;

4.

Maksymalne naprężenia w śrubie

5.

Sprawność

Podnośnik ze śrubą z gwintem S40x6 wykonaną ze
stali E360 podnosi

masę M = 4000 kg.

Wyznaczyć:

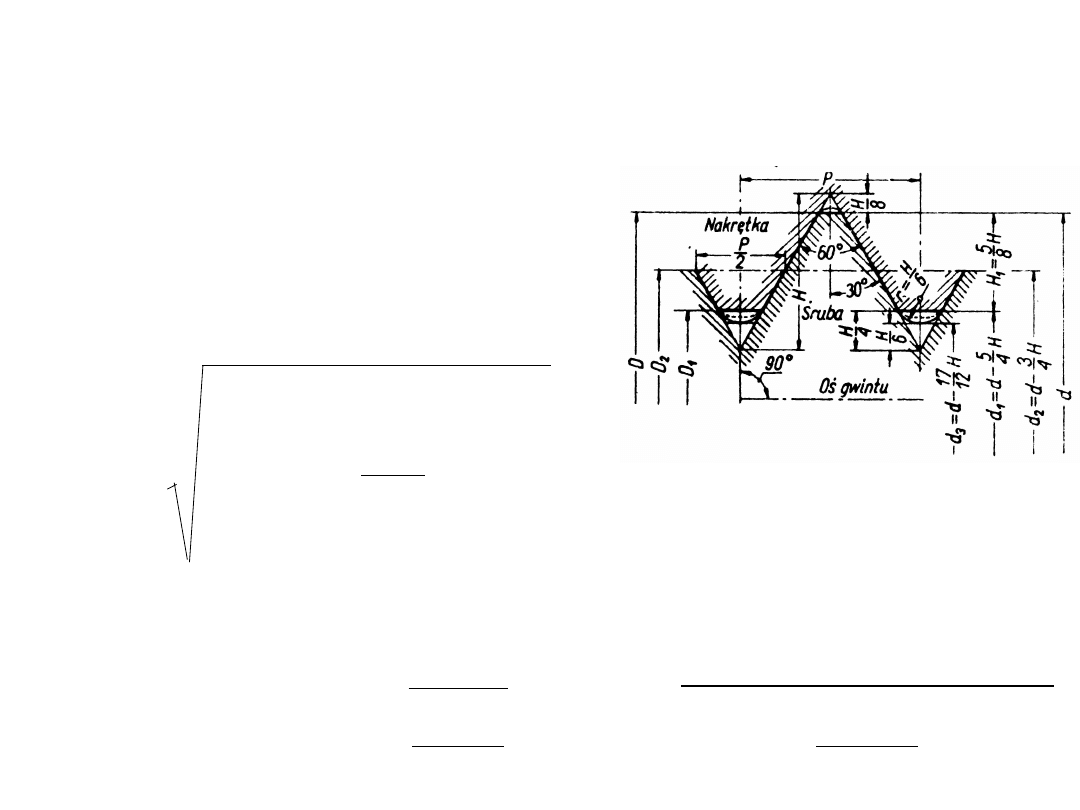
H=1,587911·P; H

1

=0,75 ·P; H

3

=H

1

+a

c;

a

c

=0,117767 ·P; d=D; d

2

=d-0,75 ·P; d

3

=d-2 ·H

3

; D

1

=d-1,5·P

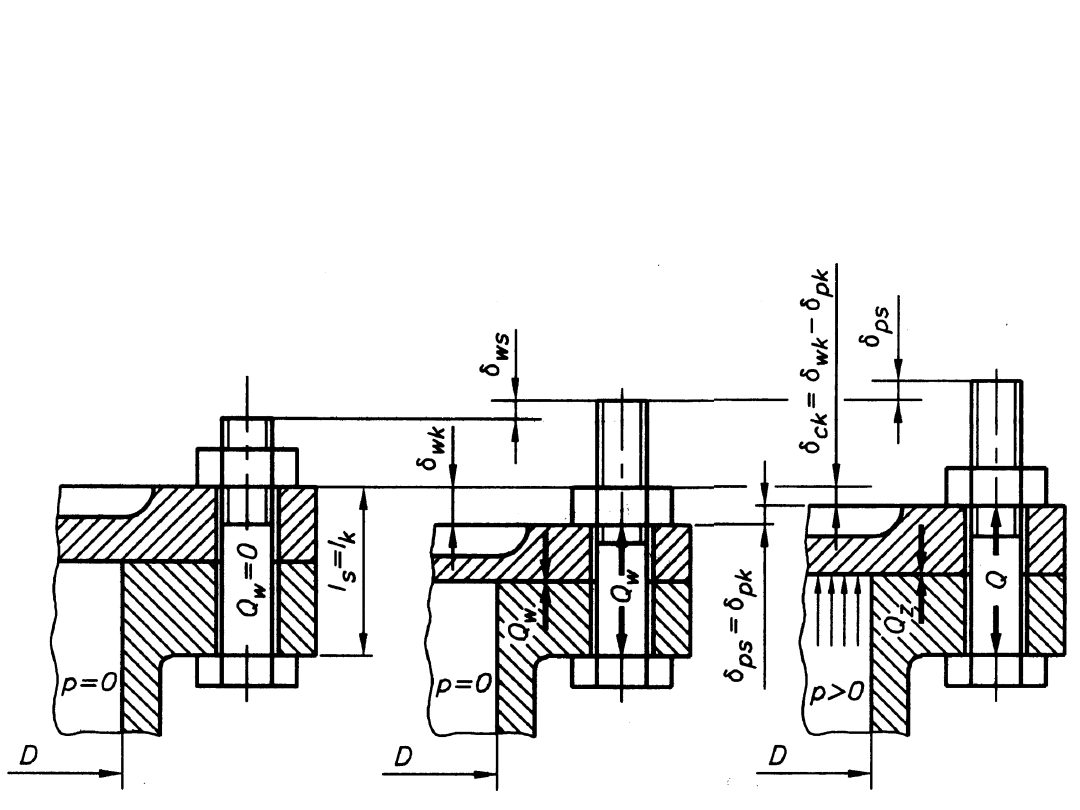
sposoby obciążenia śruby

3.

obciążenie wstępne rozciągającą siłą osiową

(i momentem skręcającym) oraz obciążenie

robocze siłą osiową (stałą lub zmienną)

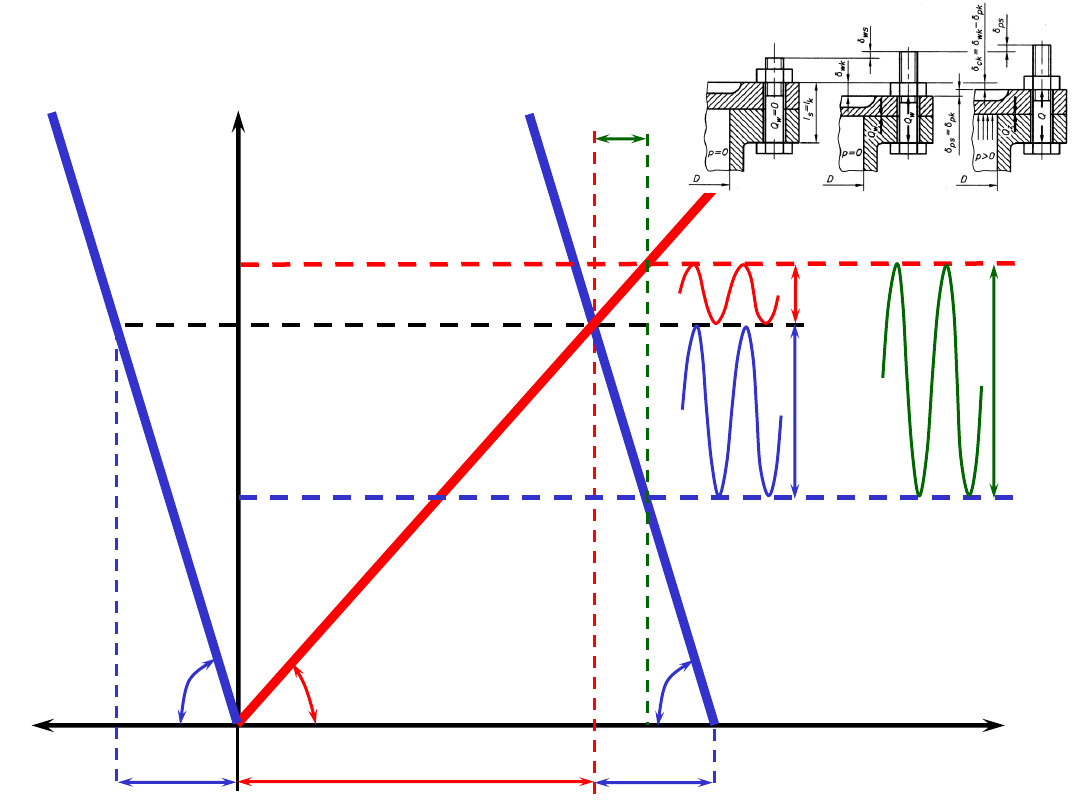
Δ

l

k

Δ

l

s

Q

Q

w

δ

ws

β

δ

wk

α

δ

ps

= δ

pk

Q

k

Q

s

ΔQ

p

ΔQ

ps

ΔQ

pk

δ

wk

β

śruby z naciągiem wstępnym

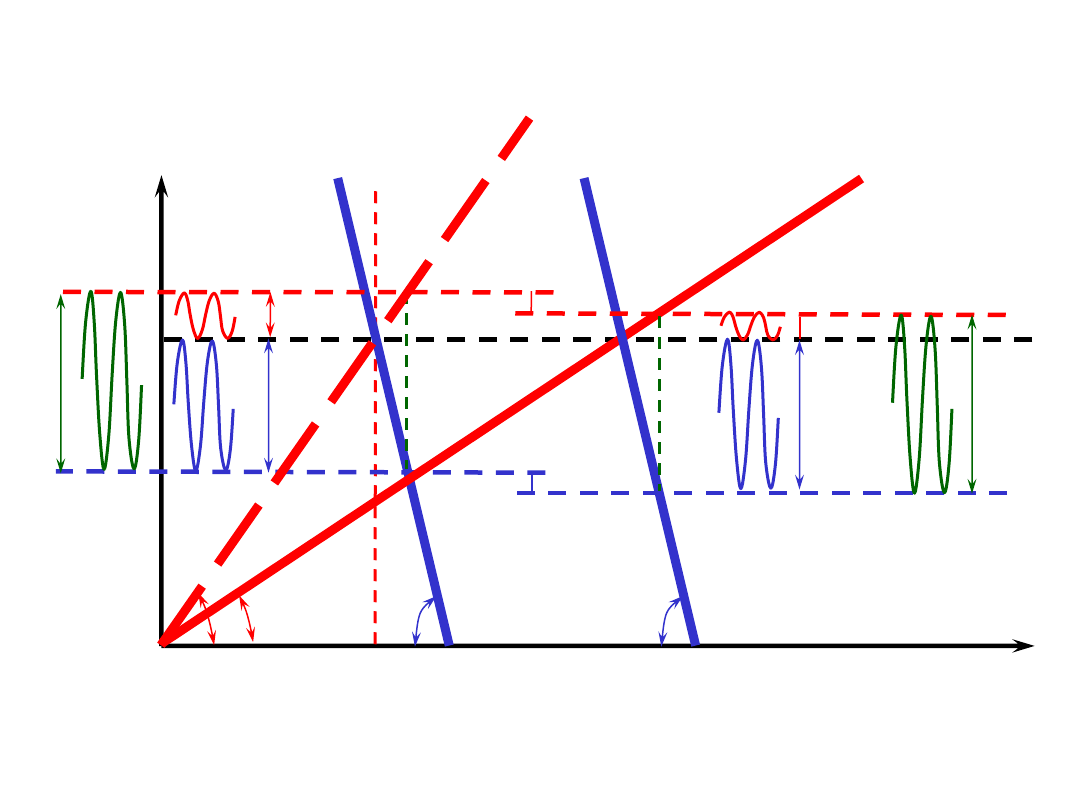
Δ

l

Q

Q

w

β

ΔQ

p

ΔQ

ps

ΔQ

pk

śruby z naciągiem wstępnym

– wzrost podatności śruby

β

ΔQ

p

ΔQ

ps1

ΔQ

pk1

ΔQ’

ps

< 0

ΔQ’

pk

> 0

α

1

α

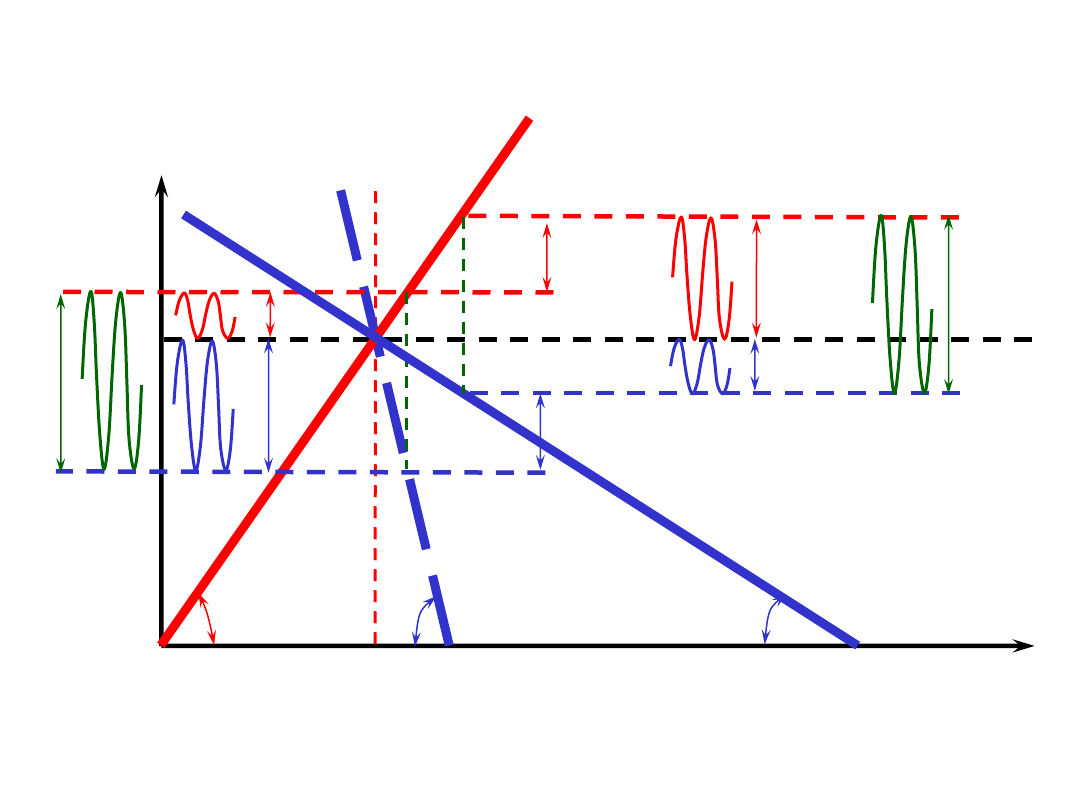
Δ

l

Q

β

α

ΔQ

p

ΔQ

ps

ΔQ

pk

śruby z naciągiem wstępnym

– wzrost podatności konstrukcji

β

2

ΔQ

p

ΔQ

ps2

ΔQ

pk2

ΔQ’’

ps

> 0

ΔQ’’

pk

< 0

Q

w

śruby z naciągiem wstępnym

– określanie sztywności

s

s

s

s

s

s

s

l

E

A

E

A

l

Q

Q

l

Q

Cs



































i

ki

ki

ki

i

ki

ki

ki

i

ki

E

A

l

E

A

l

Q

Q

l

Q

Ck

1

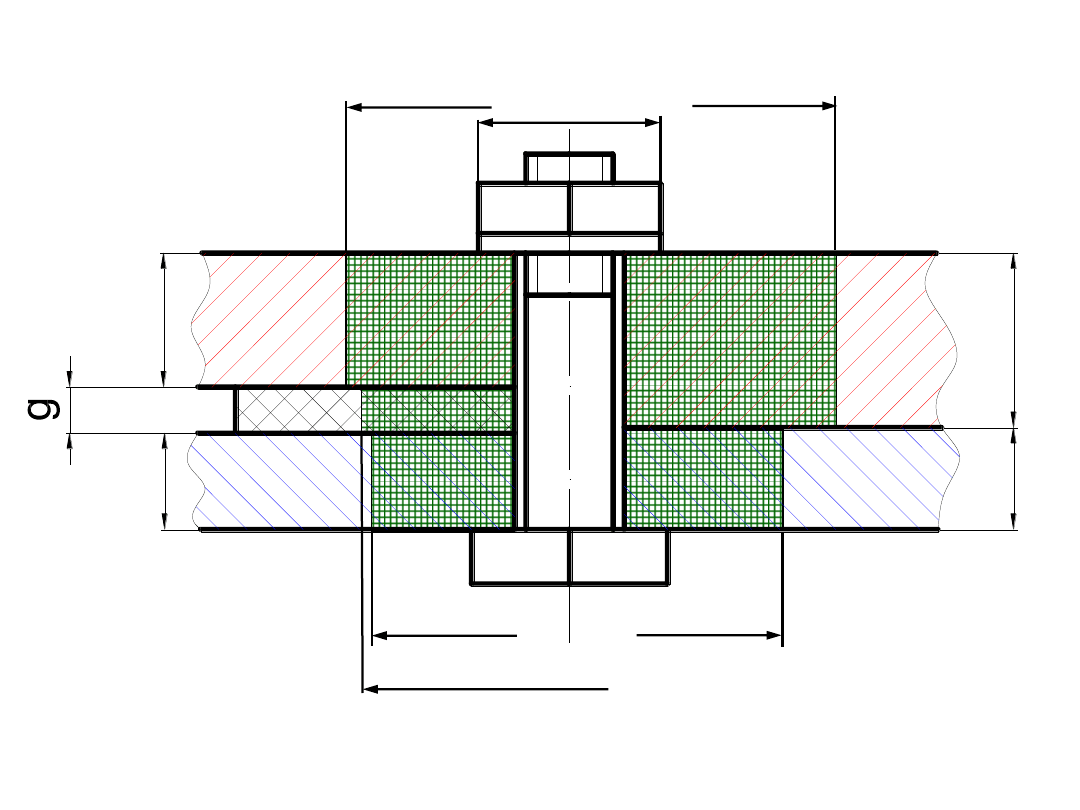
bez podkładki

z podkładką

śruby z naciągiem wstępnym

– określanie sztywności

g

1

+S

g

1

+S

g

2

+S

g

2

+S

(g

1

+g

2

)/2+S

S

g '

g '

g ''

g ''

1

2

p

1

2

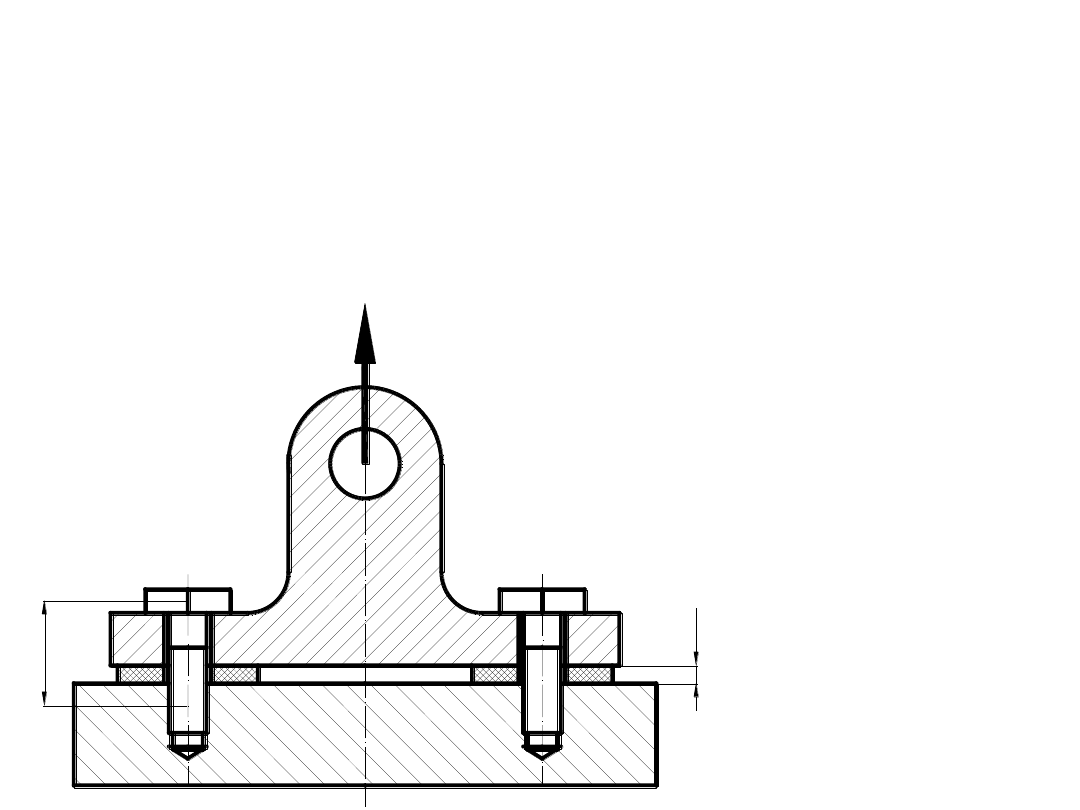
ZADANIE 2:

Okucie przedstawione na rysunku przymocowano do

podłoża dwiema stalowymi

śrubami M12x1,5 (E

s

=2,1

·10

5

MPa), o

długości czynnej l=20 mm, które podczas

montażu dokręcono, wywołując w każdej siłę naciągu wstępnego Q

w

=1,5 kN. Okucie

posadowiono na

podłożu na dwóch podkładkach o grubości g=5 mm, module Younga

E

p

=1

·10

3

MPa i powierzchni przekroju A

p

=15

·10

-4

m

2

.

Zakładając nieodkształcalność

okucia oraz

podłoża wyznaczyć:

1.

Maksymalną siłę Q

d1

którą można obciążyć okucie

aby nie

powstał luz pomiędzy okuciem a podkładką;

2.

Maksymalną siłę Q

d2

którą można obciążyć okucie

aby nie

powstał luz pomiędzy okuciem a łbem śruby;

3.

Wartość naciągu wstępnego śrub Q

wT

jeśli po

wprowadzeniu

naciągu wstępnego Q

w

temperatura

całej konstrukcji wzrośnie o ΔT=50 C, zaś wsp.

rozszerzalności liniowej okucia i śruby wynosi

α

s

=12

·10

-6

1/

ºC, a podkładki α

p

=24

·10

-6

1/

ºC

Przyjąć średnicę rdzenia
śruby d

r

=0,8

·d

g

l

Q

D

D

D
D

D

g

g

g

w

z

uw

uz

1

2

u

o

d

o

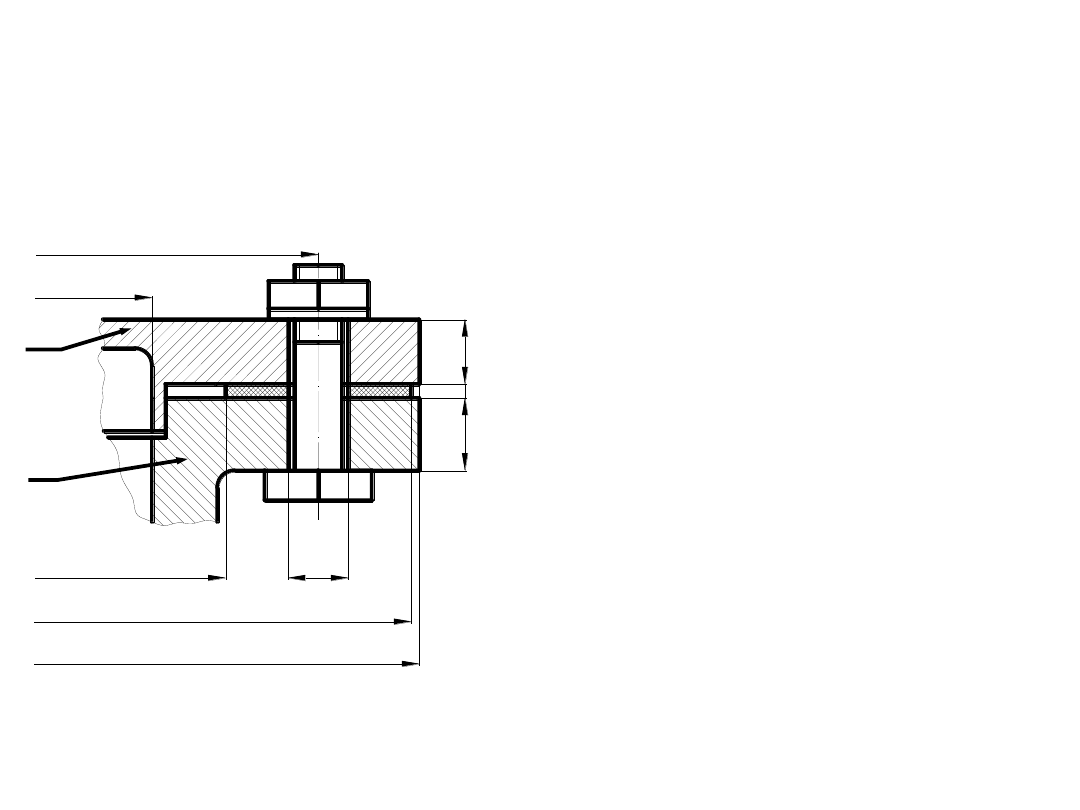
ZADANIE 3:

Pokrywa (1) otworu w zbiorniku

ciśnieniowym (2) dokręcona jest za pomocą N=16 śrub

M16, jak to przedstawiono na rysunku.

Śruby dokręcone zostały momentem M

s

=10 Nm

każda. Po zmontowaniu zbiornik wypełniony został parą po ciśnieniem. Współczynnik
tarcia

pomiędzy śrubą a nakrętką μ=0,1; pomiędzy nakrętką a podkładką μ

n

=0.

Obliczyć:

1.

Siłę naciągu wstępnego każdej ze śrub.

2. Maksymalne

ciśnienie

dopuszczalne

w

zbiorniku

p

max

takie,

aby

na

powierzchni uszczelki

pozostały naciski

resztkowe p

u

=2 MPa.

Pominąć wpływ

ciśnienia pary działającej na uszczelkę.

3. Maksymalne

naprężenia rozciągające

w

śrubie σ

r

przy

działaniu ciśnienia p

max

.

Założyć, że cała uszczelka o module Younga
E

u

=5

·10

3

MPa podlega jednakowemu

ściskaniu,

moduł Younga śruby wynosi E

s

=2,1

·10

5

MPa,

zaś zbiornik i pokrywa są nieodkształcalne.

D

0

=280 mm; D

w

=220 mm; D

z

=320 mm; D

uw

=245 mm; D

uz

=315 mm;

g

1

=12 mm; g

2

=14 mm; g

u

=3 mm; d

0

=18 mm;

dane gwintu: d=16 mm; P=2 mm; d

2

=14.701 mm; d

1

=13,835 mm; d

3

=13,546 mm

1

2

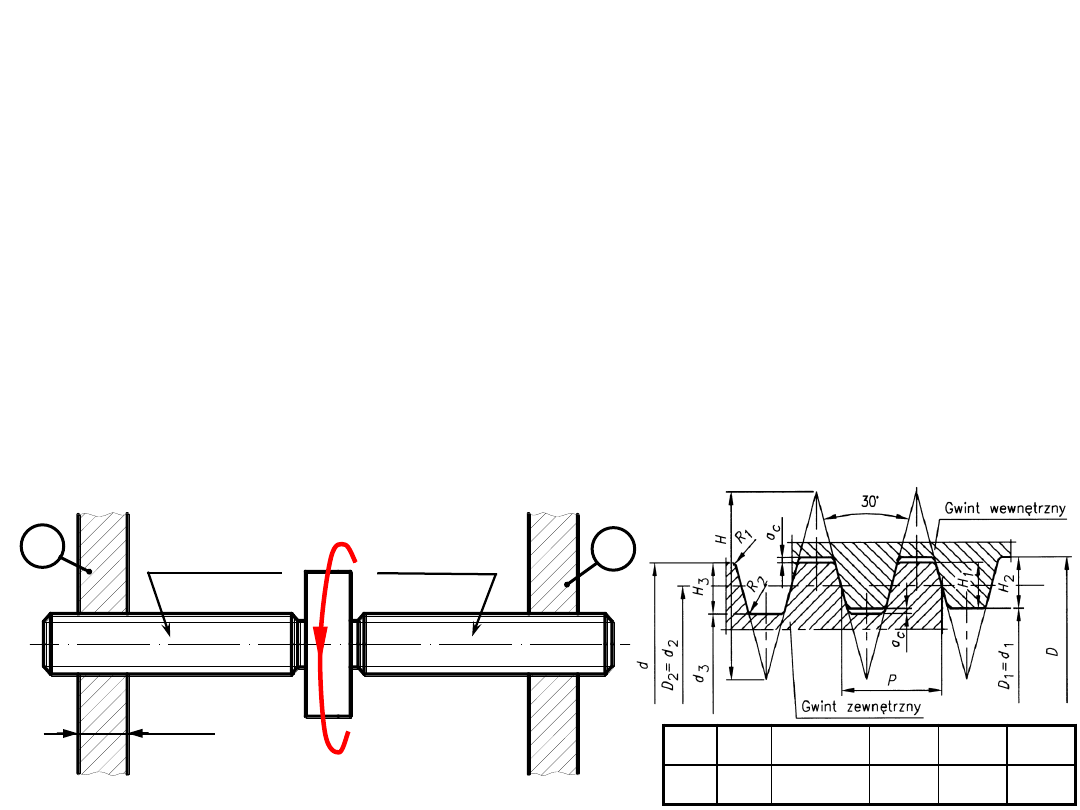
ZADANIE 4:

Pokazany na rysunku mechanizm

śrubowy składa się z dwóch płyt 1 i 2 oraz śruby o

gwintach jednozwojnych Tr32x6. Gwinty

są odpowiednio prawy i lewy jak zaznaczono

na rysunku. Wymiary gwintu podane

są na rysunku i w tabeli, współczynnik tarcia na

powierzchni gwintu

μ=0,1.

1.

Wyznaczyć moment M

s1

jakim

należy obracać śrubę aby siła normalna w śrubie

wynosiła Q

1

=-20 kN?

2.

Narysować wykres siły i momentu skręcającego w śrubie.

3.

Wyznaczyć maksymalne naprężenia zredukowane w śrubie.

4. Jakie

muszą być minimalne grubości płyt g aby naciski na powierzchnię gwintów nie

przekroczyły p

dop

=20 MPa?

5. Jak zmieni

się rozwiązanie jeśli oba gwinty będą prawoskrętne?

d

P

d

2

=D

2

d

3

D

1

D

32

6

29

25

26

33

1

2

gwint prawy

gwint lewy

M

s

g

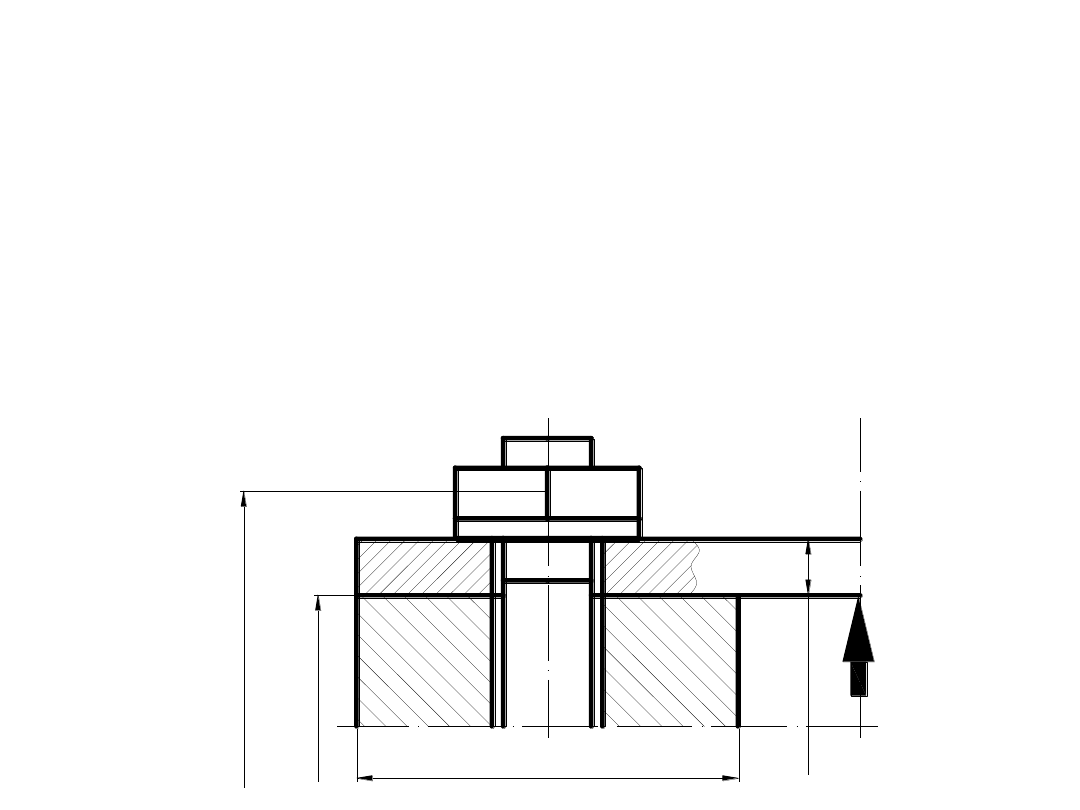
ZADANIE 5:

Prasa

tunelowa

o

schemacie

pokazanym

na

rysunku

składa

się

z

dwóch kolumn (1), dwóch trawers (2) i dwóch śrub (3). Wymiary śrub: d=120 mm,

d

3

=100 mm.

Montaż odbywa się tak, że śruby podgrzane do temp. T

1

=120

wkłada się w

otwory i

dokręca się nakrętki do skasowania luzów. Studzenie śrub powoduje powstanie

naciągu wstępnego w układzie. Temperatura prasy w trakcie pracy T

2

=20 .

Materiałem

kolumn i trawers jest

żeliwo Żl-35 (E

z

=1

·10

5

MPa,

α

z

= 10

·10

-6

1/ C).

Śruby wykonano ze

stali 45 (E

s

=2

·10

5

MPa,

α

s

= 120

·10

-6

1/ C).

Wyznaczyć zakres zmienności sił w śrubach gdy siła Q

d

zmienia

się od

0 do 1000 kN.

Uwaga: dla uproszczenia

przyjąć że trawersy są idealnie sztywne na zginanie i ściskanie.

g2=100

g1=300

kwadrat 200x200

ls=550

Qd