
Politechnika Śląska
Gliwice
Wydział Automatyki Elektroniki i Informatyki
Rok akademicki 2015/2016
Kierunek: Automatyka i Robotyka sem. 3
Semestr letni
Metody Numeryczne
Laboratorium
Ćw. 2: Przybliżone rozwiązywanie równań
całkowych
Wykonali:
Matthias Koziełło - Poklewski
Przemysław Zając
Grupa 5, Sekcja 2
Data odbycia ćwiczenia:
18.05.2016

1. Obliczenia analityczne:

2. Kod programu:
#include <iostream>
#include <fstream>
#include <math.h>
using namespace std;
double funkcja(double x)
{
return cos(x);
}
double jadro(double x, double t)
{
return sin(x-t);
}
double dokladna(double x)
{
return 1.0;
}
int main()
{
double a=0.0,b=1.0, lambda=1.0, deltaT = 0.0, suma=0.0;
int i=0, j=0, c=0, N=100, cykle = 10;
deltaT = (b-a)/(double)N;
double* y = new double[N];
double* yn = new double[N];
double* yd = new double[N];
double* xi = new double[N];
double* tj = new double[N];
double* roznica = new double[N];
ofstream wyniki;
wyniki.open("Wyniki.txt", ios::in | ios::out | ios::trunc);
for(i=0;i<N;i++)
{
xi[i] = i*deltaT;
tj[i] = i*deltaT;
y[i] = 0.0;
}
for(c=1;c<=cykle;c++)
{
for (int i = 0; i < N; i++)
{
suma = 0.0;

for (int j = 0; j <= i; j++)
{
suma += jadro(xi[i],tj[j])*y[j]*deltaT;
}
yn[i] = funkcja(xi[i]) + (lambda * suma);
yd[i] = dokladna(xi[i]);
roznica[i] = fabs(yn[i] - yd[i]);
}
for (int i = 0; i < N; i++)
{
y[i] = yn[i];
}
}
cout <<"x\t\ty\t\tyd\t\troznica\n";
wyniki <<"x\t\ty\t\tyd\t\troznica\n";
for (int i = 0; i < N; i++)
{
cout << xi[i] << "\t\t" << y[i] << "\t\t" << yd[i] << "\t\t" << roznica[i] << "\n";
wyniki << xi[i] << "\t\t" << y[i] << "\t\t" << yd[i] << "\t\t" << roznica[i] << "\n";
}
wyniki.close();
system("pause");
return 0;
}
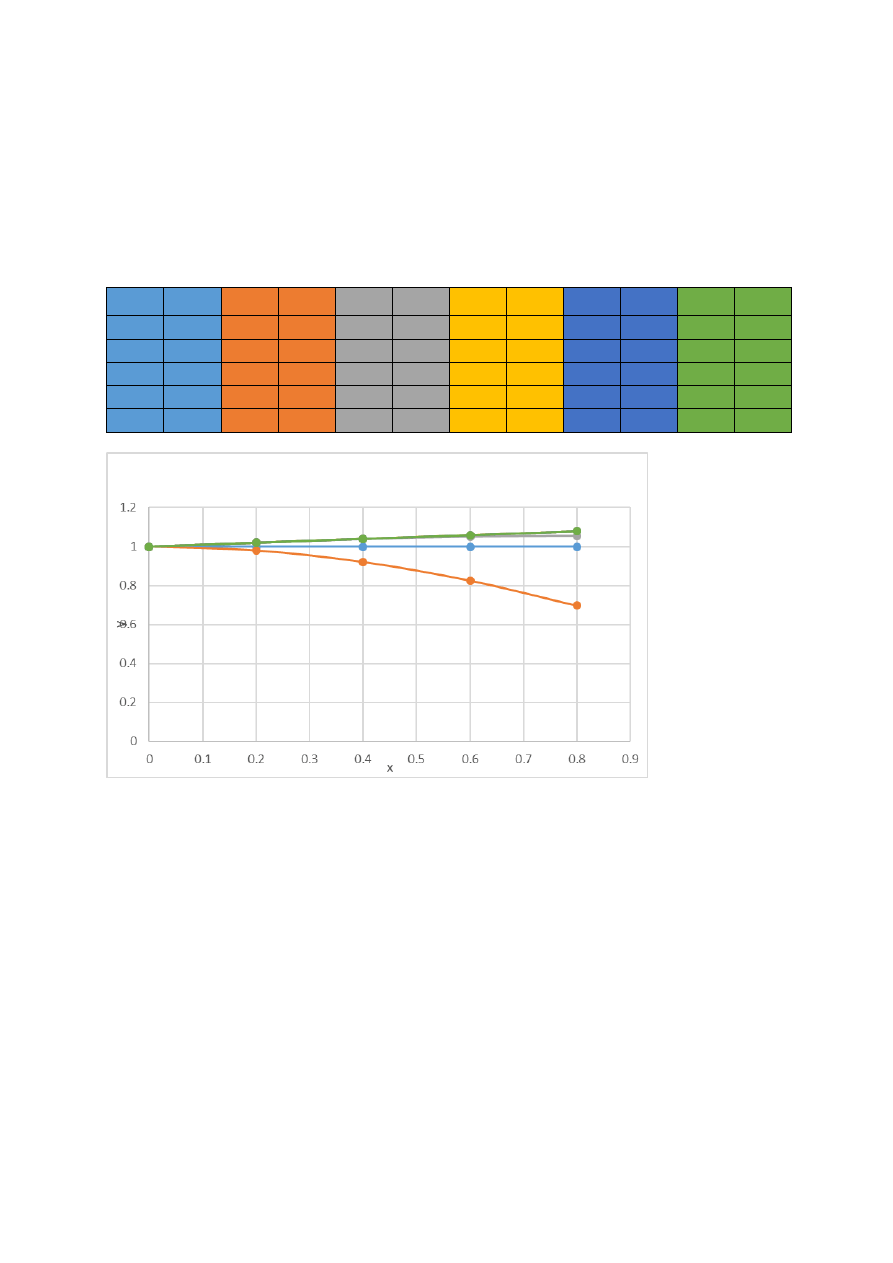
3. Wyniki i wykresy
2.1 funkcja o parametrach:
f(x)
= cos(x)
k(x,t) = sin(x-t)
λ = 1
a = 0
b = 1
a) wyniki dla 5 próbek(małych cykli) w dużym cyklu, kolejno dla 1, 2, 3, 5 i 10 dużych cykli.
x
y
dokładne
y
1
Δy
1
y
2
Δy
2
y
3
Δy
3
y
5
Δy
5
y
10
Δy
10
0
1
1
0
1
0
1
0
1
0
1
0
0.2
1 0.9801 0.0199 1.0198 0.0198 1.0198 0.0198 1.0198 0.0198 1.005 0.005
0.4
1 0.9211 0.0789 1.0379 0.0379 1.0395 0.0395 1.0395 0.0395
1.01
0.01
0.6
1 0.8253 0.1747 1.0512 0.0512 1.0589 0.0589 1.059 0.059 1.0149 0.0149
0.8
1 0.6967 0.3033 1.0554 0.0554 1.0779 0.0779 1.0784 0.0784 1.0199 0.0199
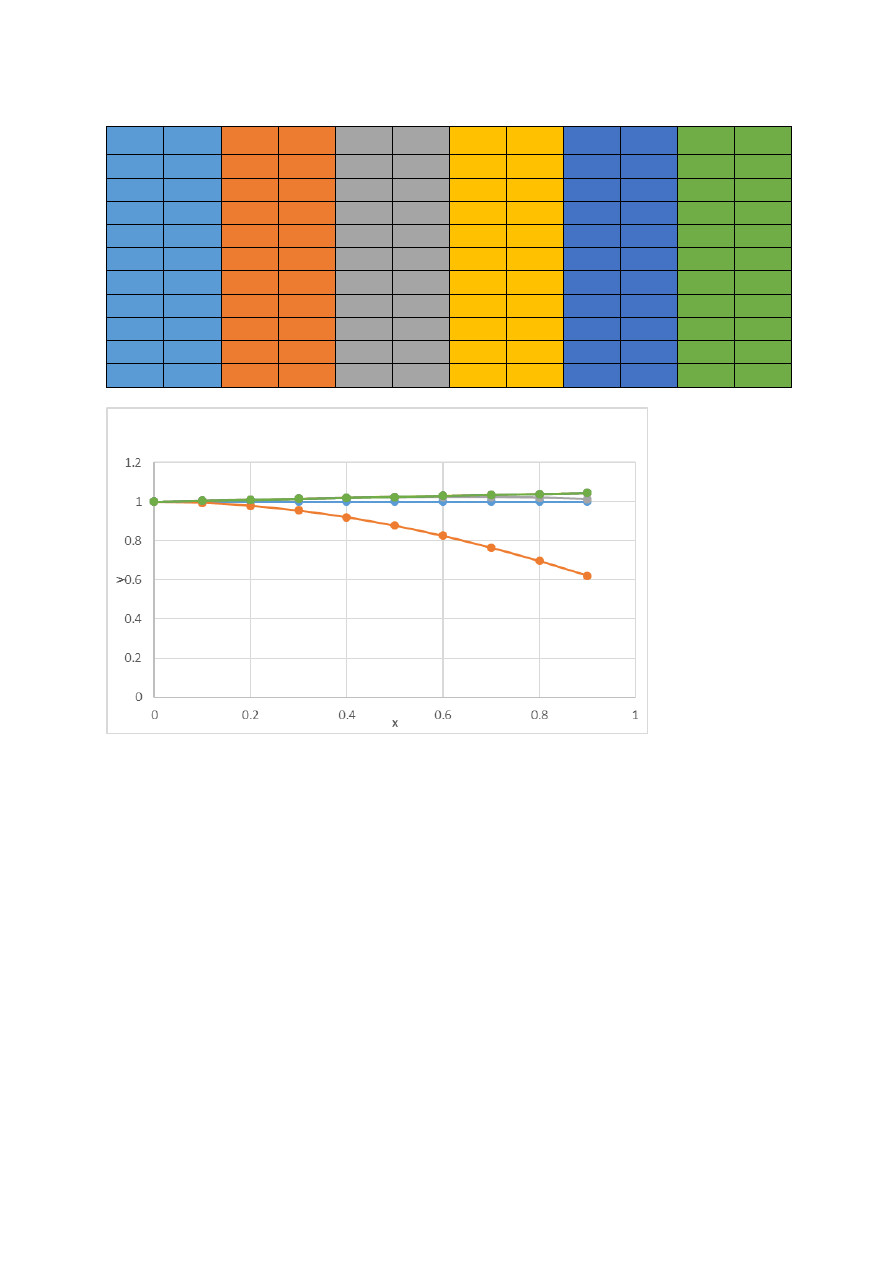
b) wyniki dla 10 próbek(małych cykli) w dużym cyklu, kolejno dla 1, 2, 3, 5 i 10 dużych cykli.
x
y
dokładne
y
1
Δy
1
y
2
Δy
2
y
3
Δy
3
y
5
Δy
5
y
10
Δy
10
0
1
1
0
1
0
1
0
1
0
1
0
0.1
1 0.995 0.005 1.005 0.005 1.005 0.005 1.005 0.005 1.005 0.005
0.2
1 0.9801 0.0199 1.0099 0.0099
1.01
0.01
1.01
0.01
1.01
0.01
0.3
1 0.9553 0.0447 1.0144 0.0144 1.0149 0.0149 1.0149 0.0149 1.0149 0.0149
0.4
1 0.9211 0.0789 1.0184 0.0184 1.0199 0.0199 1.0199 0.0199 1.0199 0.0199
0.5
1 0.8776 0.1224 1.0214 0.0214 1.0248 0.0248 1.0249 0.0249 1.0249 0.0249
0.6
1 0.8253 0.1747 1.023 0.023 1.0297 0.0297 1.0298 0.0298 1.0298 0.0298
0.7
1 0.7648 0.2352 1.0225 0.0225 1.0345 0.0345 1.0347 0.0347 1.0347 0.0347
0.8
1 0.6967 0.3033 1.0195 0.0195 1.0392 0.0392 1.0397 0.0397 1.0397 0.0397
0.9
1 0.6216 0.3784 1.0133 0.0133 1.0437 0.0437 1.0446 0.0446 1.0446 0.0446
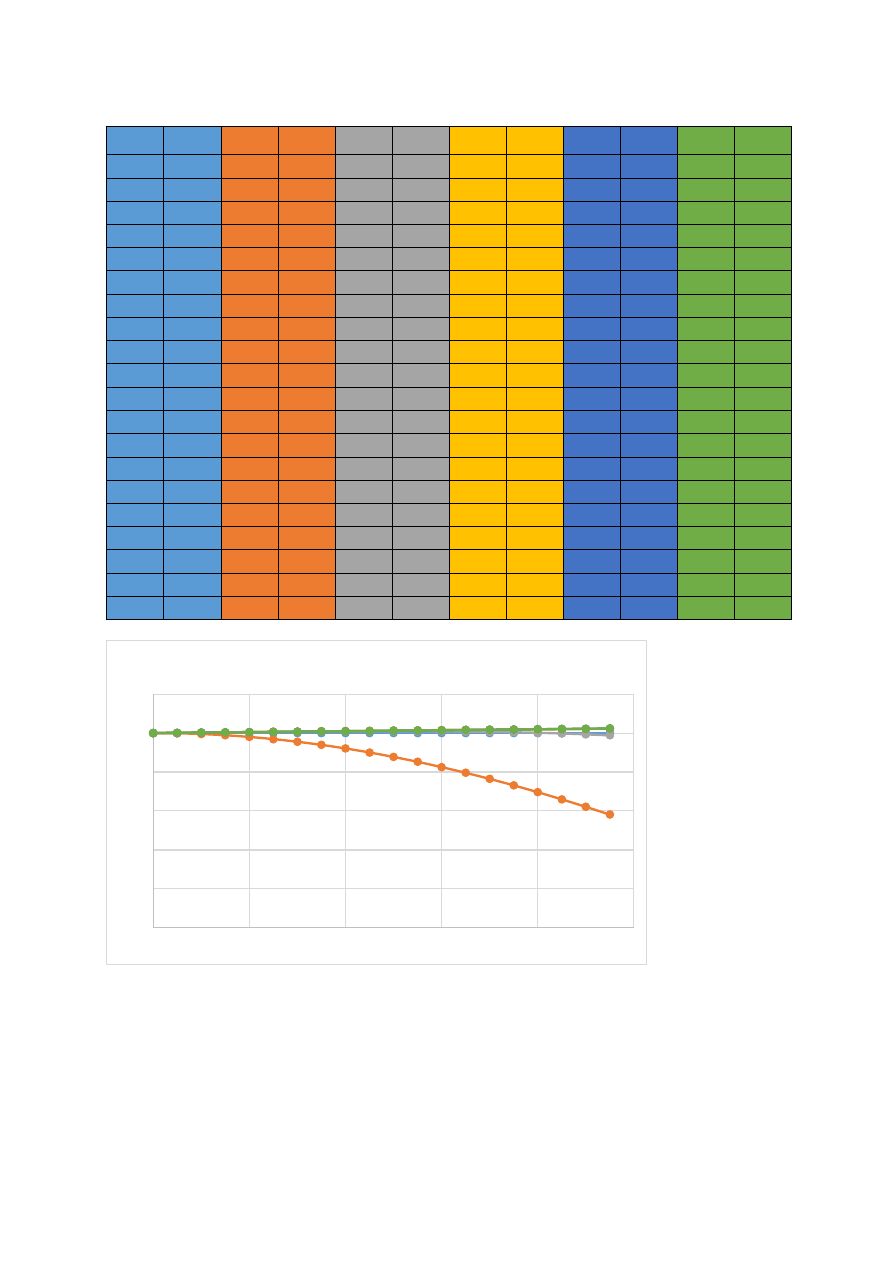
c) wyniki dla 20 próbek(małych cykli) w dużym cyklu, kolejno dla 1, 2, 3, 5 i 10 dużych cykli.
x
y
dokładne
y
1
Δy
1
y
2
Δy
2
y
3
Δy
3
y
5
Δy
5
y
10
Δy
10
0
1
1
0
1
0
1
0
1
0
1
0
0.05
1 0.9988 0.0012 1.0013 0.0012 1.0013 0.0012 1.0013 0.0012 1.0013 0.0012
0.1
1 0.995 0.005 1.0025 0.0025 1.0025 0.0025 1.0025 0.0025 1.0025 0.0025
0.15
1 0.9888 0.0112 1.0037 0.0037 1.0038 0.0037 1.0038 0.0037 1.0038 0.0037
0.2
1 0.9801 0.0199 1.0049 0.0049 1.005 0.005 1.005 0.005 1.005 0.005
0.25
1 0.9689 0.0311 1.006 0.006 1.0062 0.0062 1.0062 0.0062 1.0062 0.0062
0.3
1 0.9553 0.0447 1.0071 0.0071 1.0075 0.0075 1.0075 0.0075 1.0075 0.0075
0.35
1 0.9394 0.0606 1.008 0.008 1.0087 0.0087 1.0087 0.0087 1.0087 0.0087
0.4
1 0.9211 0.0789 1.0087 0.0087
1.01
0.01
1.01
0.01
1.01
0.01
0.45
1 0.9004 0.0996 1.0092 0.0092 1.0112 0.0112 1.0112 0.0112 1.0112 0.0112
0.5
1 0.8776 0.1224 1.0094 0.0094 1.0124 0.0124 1.0125 0.0125 1.0125 0.0125
0.55
1 0.8525 0.1475 1.0093 0.0093 1.0137 0.0137 1.0137 0.0137 1.0137 0.0137
0.6
1 0.8253 0.1747 1.0088 0.0088 1.0149 0.0149 1.015 0.015 1.015 0.015
0.65
1 0.7961 0.2039 1.0079 0.0079 1.0161 0.0161 1.0162 0.0162 1.0162 0.0162
0.7
1 0.7648 0.2352 1.0064 0.0064 1.0173 0.0173 1.0174 0.0174 1.0174 0.0174
0.75
1 0.7317 0.2683 1.0043 0.0043 1.0184 0.0184 1.0187 0.0187 1.0187 0.0187
0.8
1 0.6967 0.3033 1.0016 0.0016 1.0195 0.0195 1.0199 0.0199 1.0199 0.0199
0.85
1
0.66
0.34 0.9981 0.0019 1.0206 0.0206 1.0212 0.0212 1.0212 0.0212
0.9
1 0.6216 0.3784 0.9937 0.0063 1.0216 0.0216 1.0224 0.0224 1.0224 0.0224
0.95
1 0.5817 0.4183 0.9884 0.0116 1.0225 0.0225 1.0237 0.0236 1.0237 0.0236
0
0.2
0.4
0.6
0.8
1
1.2
0
0.2
0.4
0.6
0.8
1
y
x
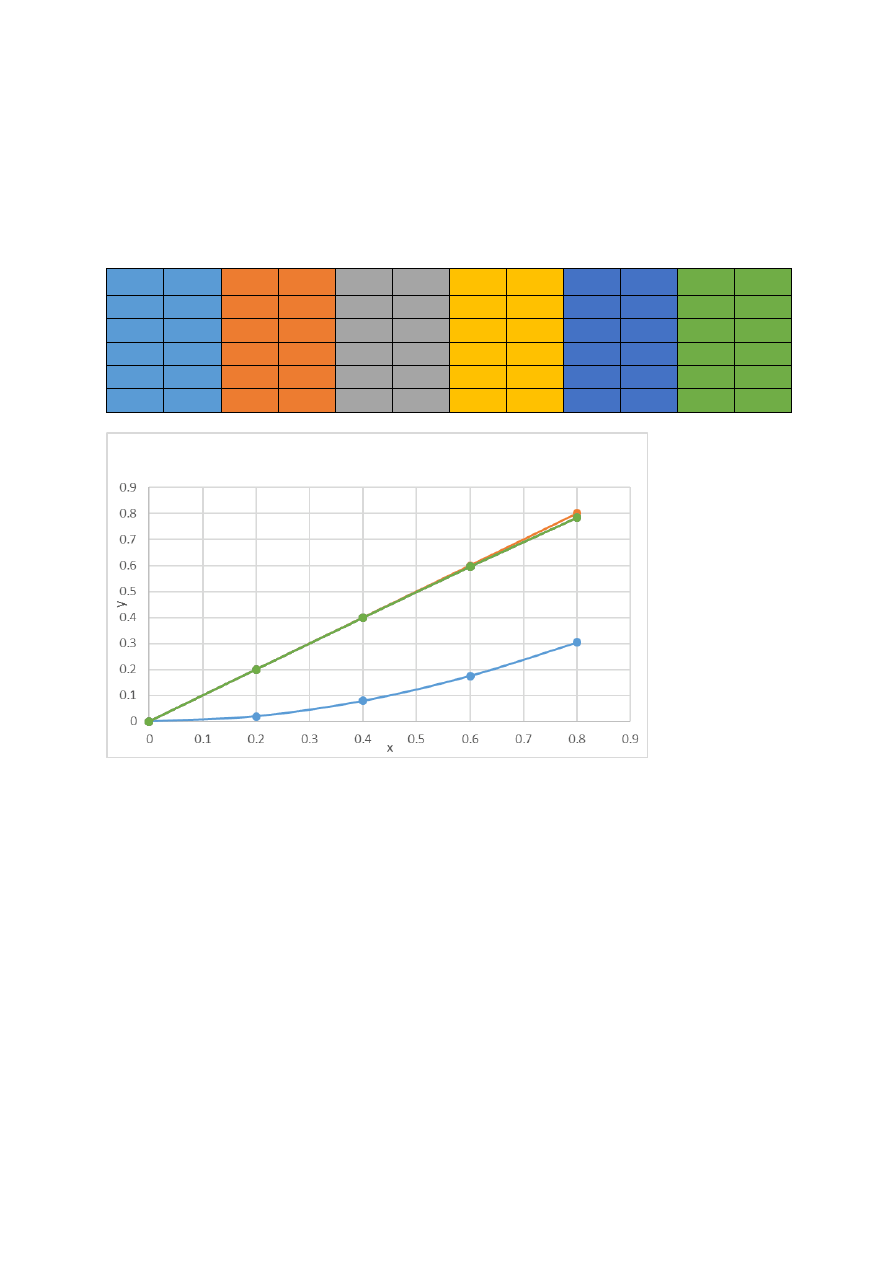
2.2 funkcja o parametrach:
f(x)
= x
k(x,t) = (1/2)*(x-t)^2
λ = -1
a = 0
b = 1
a) wyniki dla 5 próbek(małych cykli) w dużym cyklu, kolejno dla 1, 2, 3, 5 i 10 dużych cykli.
x
y
dokładne
y
1
Δy
1
y
2
Δy
2
y
3
Δy
3
y
5
Δy
5
y
10
Δy
10
0
0
0
0
0
0
0
0
0
0
0
0
0.2 0.0199
0.2 0.1801
0.2 0.1801
0.2 0.1801
0.2 0.1801
0.2 0.1801
0.4 0.0789
0.4 0.3211 0.3992 0.3203 0.3992 0.3203 0.3992 0.3203 0.3992 0.3203
0.6 0.1747
0.6 0.4253 0.5952 0.4205 0.5952 0.4205 0.5952 0.4205 0.5952 0.4205
0.8 0.3033
0.8 0.4967 0.784 0.4807 0.784 0.4807 0.784 0.4807 0.784 0.4807
b) wyniki dla 10 próbek(małych cykli) w dużym cyklu, kolejno dla 1, 2, 3, 5 i 10 dużych cykli.
x
y
dokładne
y
1
Δy
1
y
2
Δy
2
y
3
Δy
3
y
5
Δy
5
y
10
Δy
10
0
0
0
0
0
0
0
0
0
0
0
0
0.1 0.005
0.1 0.095
0.1 0.095
0.1 0.095
0.1 0.095
0.1 0.095
0.2 0.0199
0.2 0.1801
0.2
0.18
0.2
0.18
0.2
0.18
0.2
0.18
0.3 0.0447
0.3 0.2553 0.2997 0.255 0.2997 0.255 0.2997 0.255 0.2997 0.255
0.4 0.0789
0.4 0.3211 0.399 0.3201 0.399 0.3201 0.399 0.3201 0.399 0.3201
0.5 0.1224
0.5 0.3776 0.4975 0.3751 0.4975 0.3751 0.4975 0.3751 0.4975 0.3751
0.6 0.1747
0.6 0.4253 0.5948 0.4201 0.5948 0.4201 0.5948 0.4201 0.5948 0.4201
0.7 0.2352
0.7 0.4648 0.6902 0.455 0.6902 0.4551 0.6902 0.4551 0.6902 0.4551
0.8 0.3033
0.8 0.4967 0.7832 0.4799 0.7832 0.4799 0.7832 0.4799 0.7832 0.4799
0.9 0.3784
0.9 0.5216 0.873 0.4946 0.8731 0.4947 0.8731 0.4947 0.8731 0.4947
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.2
0.4
0.6
0.8
1
y
x
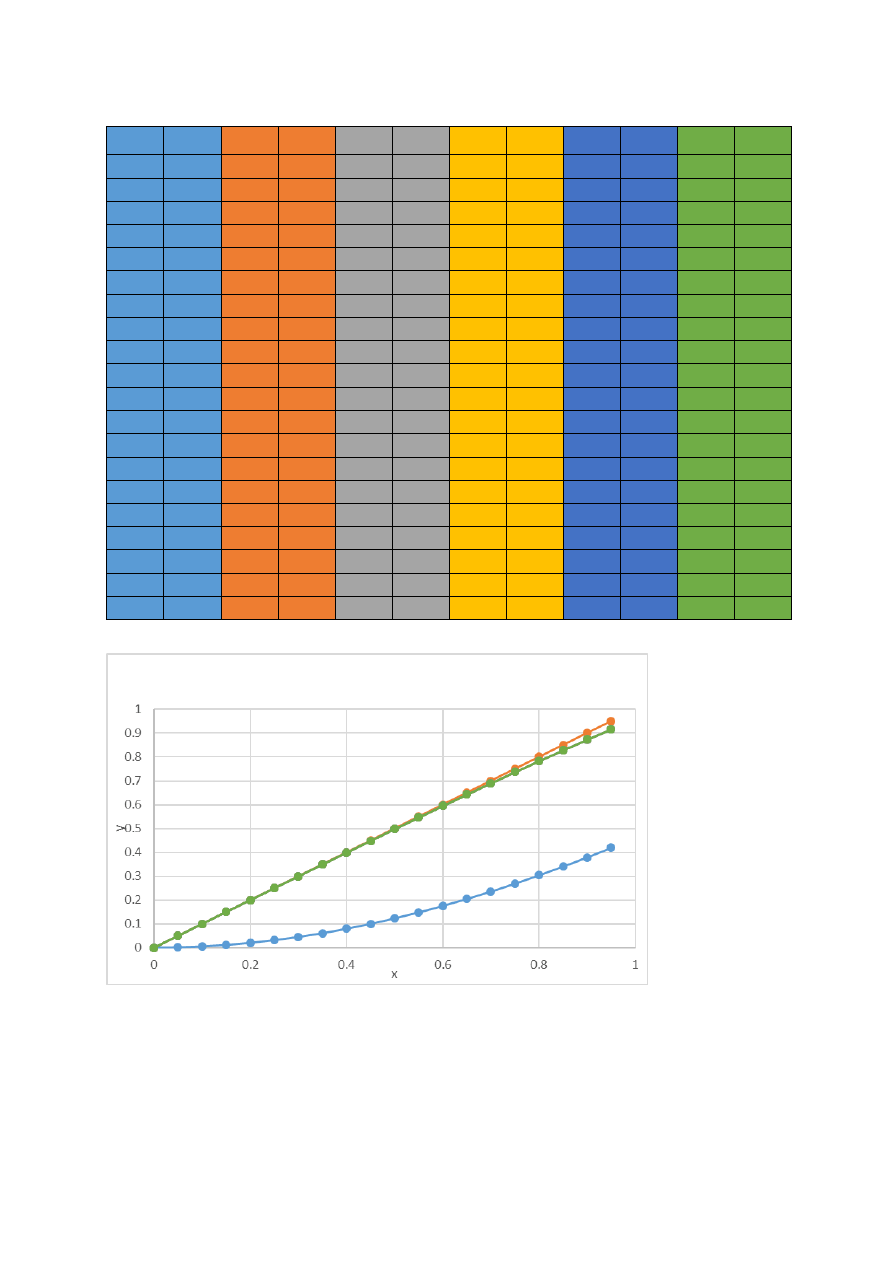
c) wyniki dla 20 próbek(małych cykli) w dużym cyklu, kolejno dla 1, 2, 3, 5 i 10 dużych cykli.
x
y
dokładne
y
1
Δy
1
y
2
Δy
2
y
3
Δy
3
y
5
Δy
5
y
10
Δy
10
0
0
0
0
0
0
0
0
0
0
0
0
0.05 0.0012
0.05 0.0488
0.05 0.0488
0.05 0.0488
0.05 0.0488
0.05 0.0488
0.1 0.005
0.1 0.095
0.1 0.095
0.1 0.095
0.1 0.095
0.1 0.095
0.15 0.0112
0.15 0.1388
0.15 0.1388
0.15 0.1388
0.15 0.1388
0.15 0.1388
0.2 0.0199
0.2 0.1801 0.1999
0.18 0.1999
0.18 0.1999
0.18 0.1999
0.18
0.25 0.0311
0.25 0.2189 0.2498 0.2188 0.2498 0.2188 0.2498 0.2188 0.2498 0.2188
0.3 0.0447
0.3 0.2553 0.2997 0.255 0.2997 0.255 0.2997 0.255 0.2997 0.255
0.35 0.0606
0.35 0.2894 0.3494 0.2888 0.3494 0.2888 0.3494 0.2888 0.3494 0.2888
0.4 0.0789
0.4 0.3211 0.399
0.32 0.399
0.32 0.399
0.32 0.399
0.32
0.45 0.0996
0.45 0.3504 0.4483 0.3488 0.4483 0.3488 0.4483 0.3488 0.4483 0.3488
0.5 0.1224
0.5 0.3776 0.4974 0.375 0.4974 0.375 0.4974 0.375 0.4974 0.375
0.55 0.1475
0.55 0.4025 0.5462 0.3987 0.5462 0.3987 0.5462 0.3987 0.5462 0.3987
0.6 0.1747
0.6 0.4253 0.5946
0.42 0.5946
0.42 0.5946
0.42 0.5946
0.42
0.65 0.2039
0.65 0.4461 0.6426 0.4387 0.6426 0.4387 0.6426 0.4387 0.6426 0.4387
0.7 0.2352
0.7 0.4648
0.69 0.4549 0.6901 0.4549 0.6901 0.4549 0.6901 0.4549
0.75 0.2683
0.75 0.4817 0.7369 0.4686 0.7369 0.4686 0.7369 0.4686 0.7369 0.4686
0.8 0.3033
0.8 0.4967 0.783 0.4797 0.783 0.4797 0.783 0.4797 0.783 0.4797
0.85
0.34
0.85
0.51 0.8283 0.4883 0.8284 0.4884 0.8284 0.4884 0.8284 0.4884
0.9 0.3784
0.9 0.5216 0.8727 0.4944 0.8728 0.4945 0.8728 0.4945 0.8728 0.4945
0.95 0.4183
0.95 0.5317 0.9162 0.4978 0.9163 0.498 0.9163 0.498 0.9163 0.498

4. Wnoiski
- W przypadku obu funkcji najdokładniejszy wynik otrzymaliśmy po 2 dużych cyklach, dla wiekszej liczby
cykli wyniki są bardzo zbliżone, błąd oscyluje wokół pewnej wartości
- Dla pierwszej funkcji zwiększenie ilości próbek(małych cykli) powodóje zwiększenie dokładności
metody, z koleji w przypadku drugiej funkcji dzieje się odwrotnie, im większa liczba próbek(małych
cykli) tym większy błąd metody.
Wyszukiwarka
Podobne podstrony:
lab106 2258 1395959527
lab106 19656 1462385132
106, LAB106M(1), ˙w.nr.106 Temat: Wyznaczanie stosunku H=Cp/Cv dla powietrza metod˙
lab106 19544 1462389000
lab106 19654 1462389421
więcej podobnych podstron