Metody numeryczne

Laboratorium

Temat ćwiczenia: Rozwiązywanie układów równań

liniowych

Grupa 4

sekcja 2, podsekcja 5

Mariusz Matyszkiewicz

Mateusz Odrobiński

1. Wstęp - metoda iteracji prostej

Metoda iteracji prostej umożliwia obliczanie przybliżonych wartości rozwiązań układów równań
liniowych za pomocą kolejnych aproksymacji.
Jest to powszechnie wykorzystywany sposób, ponieważ pozwala obliczyć wartość rozwiązania
znacznie szybciej niż w tradycyjny sposób. Obarczony jest jednak błędem, który powstaje w
wyniku kolejnych przybliżeń.

W technice zachodzi potrzeba rozwiązywania układów równań w jak najkrótszym czasie,
zaś dokładność obliczeń często nie jest tak ważna. Ograniczenie ilości wykonywanych obliczeń
jest szczególnie ważne w urządzeniach cyfrowych o małej mocy obliczeniowej
czy w urządzeniach mobilnych, w których co raz większe zapotrzebowanie na moc obliczeniową
przekłada się na zwiększenie poboru energii.

W metodzie iteracji prostej przekształcamy równanie

do postaci

wartość przybliżona kolejnego rozwiązania

wektor powstały z przekształceń wektora

wartość bieżącego rozwiązania

wektor powstały z przekształceń macierzy

Warunkiem dostatecznym zbieżności procesu jest:

Koniec procesu jest uwarunkowany kryterium stopu:

2. Wyniki działania algorytmu iteracji prostej zaimplementowanego w C++

Do obliczeń przyjęliśmy

I.

Układ równań

1. Parametry:

A =

[

]; b = [

]

detA = -42

2. Rozwiązania:

Metoda dokładna

[

] [

]

Metoda iteracji prostej

[

]

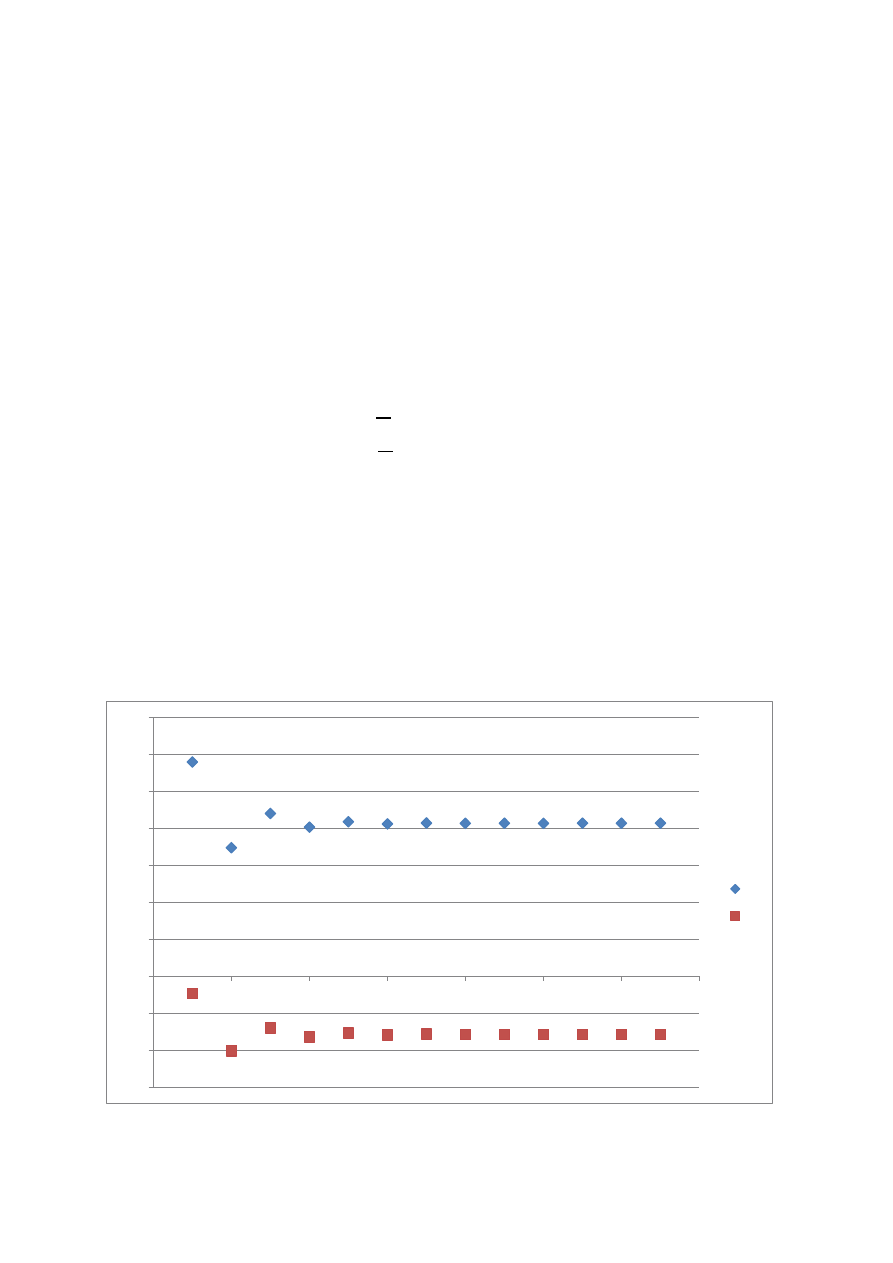
3. Ilość iteracji = 13

4. Błędy:

5. Wykres

-1,5

-1

-0,5

0

0,5

1

1,5

2

2,5

3

3,5

0

2

4

6

8

10

12

14

x1

x2

II.

Układ równań

1. Parametry:

A =

[

]; b = [

]

detA = 971

2. Rozwiązania:

Metoda dokładna

[

]

Metoda iteracji prostej

[

]

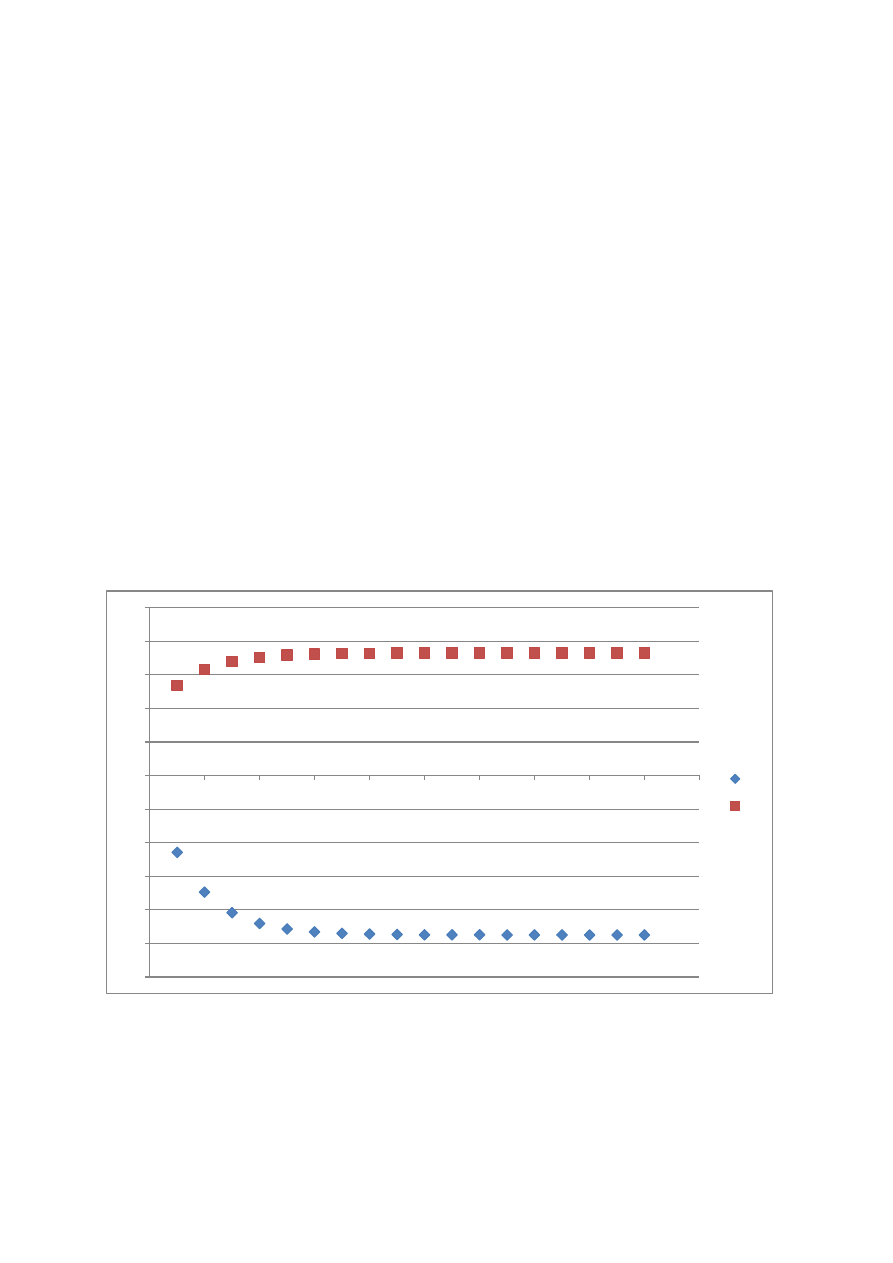
3. Ilość iteracji = 18

4. Błędy

5. Wykres

-12

-10

-8

-6

-4

-2

0

2

4

6

8

10

0

2

4

6

8

10

12

14

16

18

20

x1

x2

III.

Układ równań

1. Parametry:

A =

[

]; b = [

]

detA = 80,3026

2. Rozwiązania:

Metoda dokładna

[

]

Metoda iteracji prostej

[

]

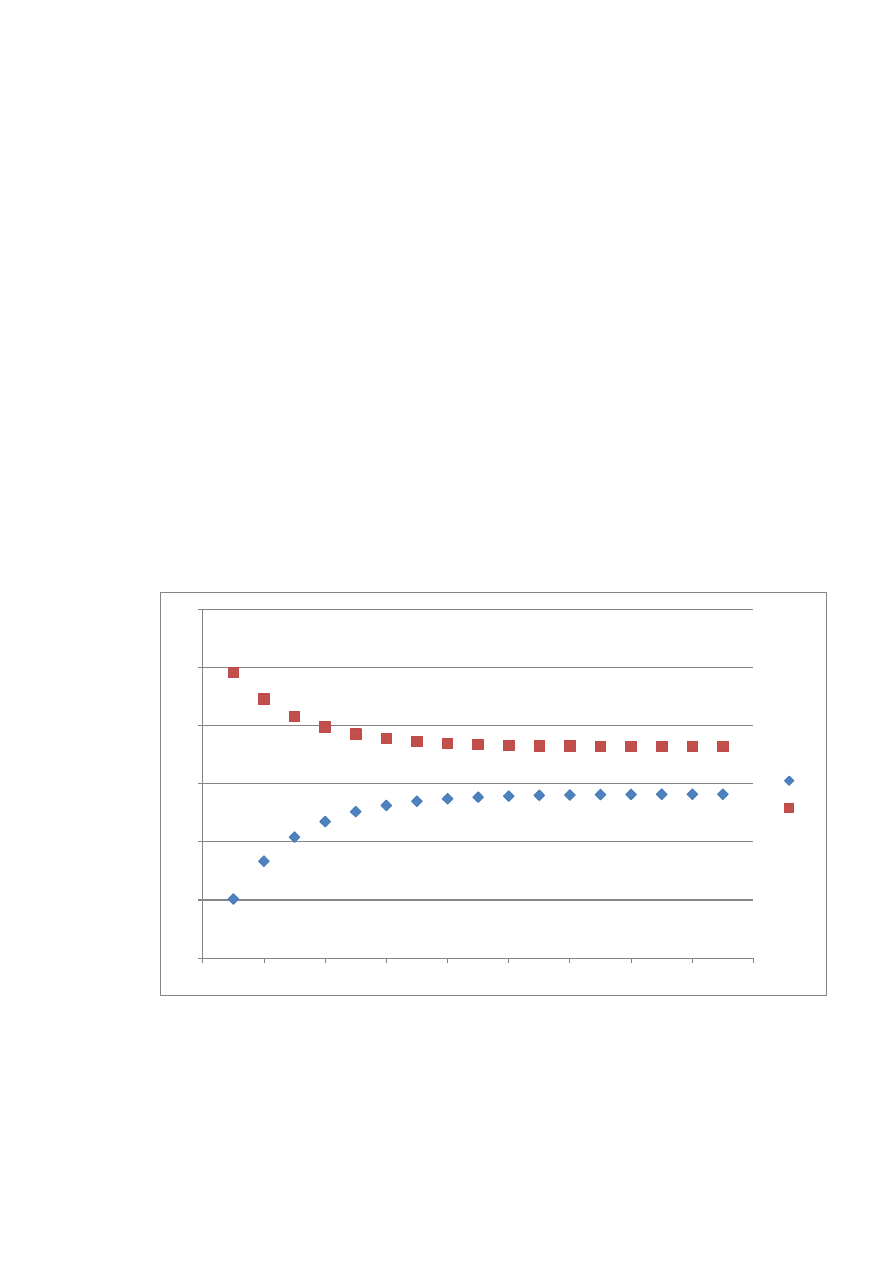
3. Ilość iteracji = 17

4. Błędy

5. Wykres

0

0,1

0,2

0,3

0,4

0,5

0,6

0

2

4

6

8

10

12

14

16

18

x1

x2

IV.

Układ równań

1. Parametry:

A =

[

]; b = [

] eps = 0.0001

detA = 838

2. Rozwiązania:

Metoda dokładna

[

];

Metoda iteracji prostej

[

]

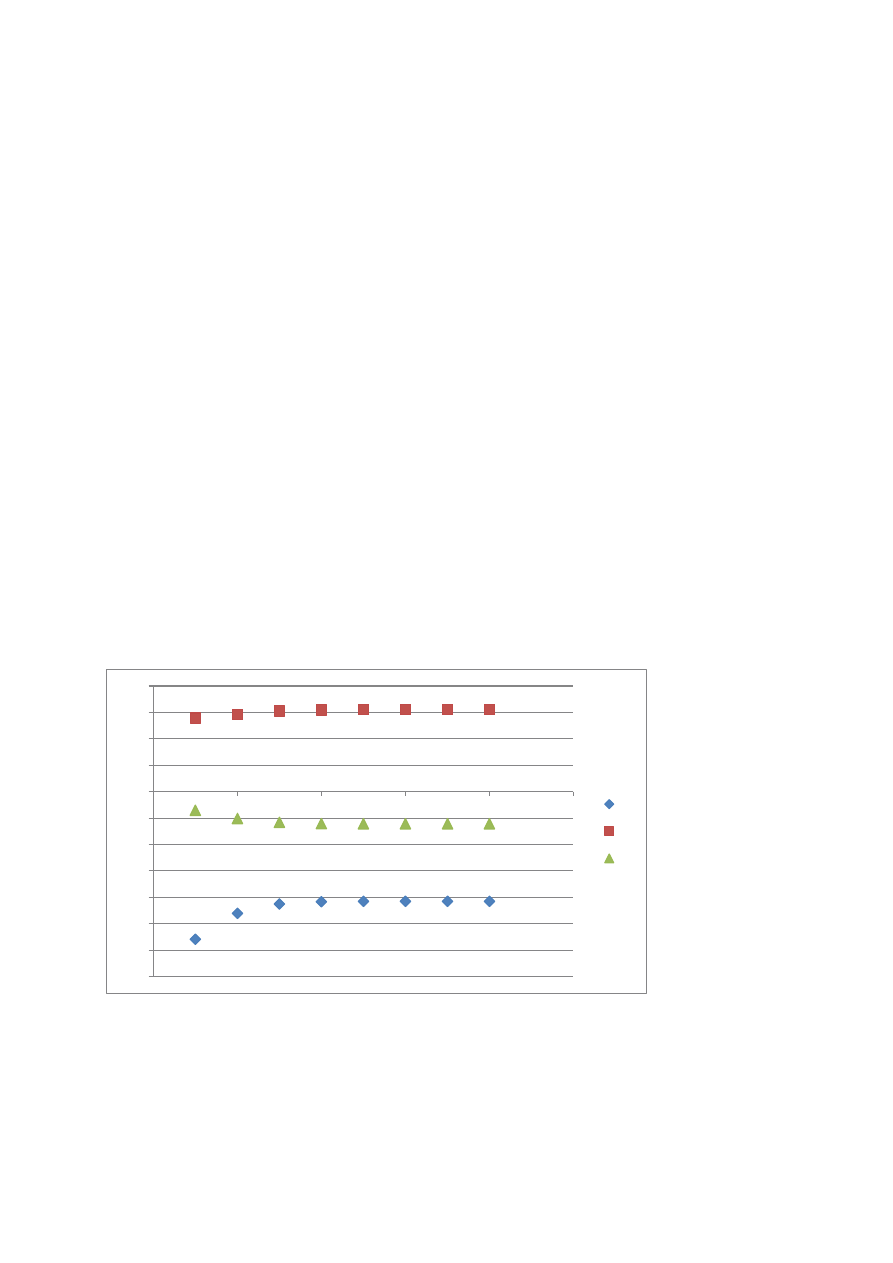
3. Ilość iteracji = 8

4. Błędy

5. Wykres

-1,4

-1,2

-1

-0,8

-0,6

-0,4

-0,2

0

0,2

0,4

0,6

0,8

0

2

4

6

8

10

x1

x2

x3

V.

Układ równań

1. Parametry:

A =

[

]; b = [

] eps = 0.0001

detA = 0.5846

Wyznacznik bliski 0.

2. Rozwiązania:

Metoda dokładna

[

]

Metoda iteracji prostej

[

]

3. Ilość iteracji = 2164

4. Błędy

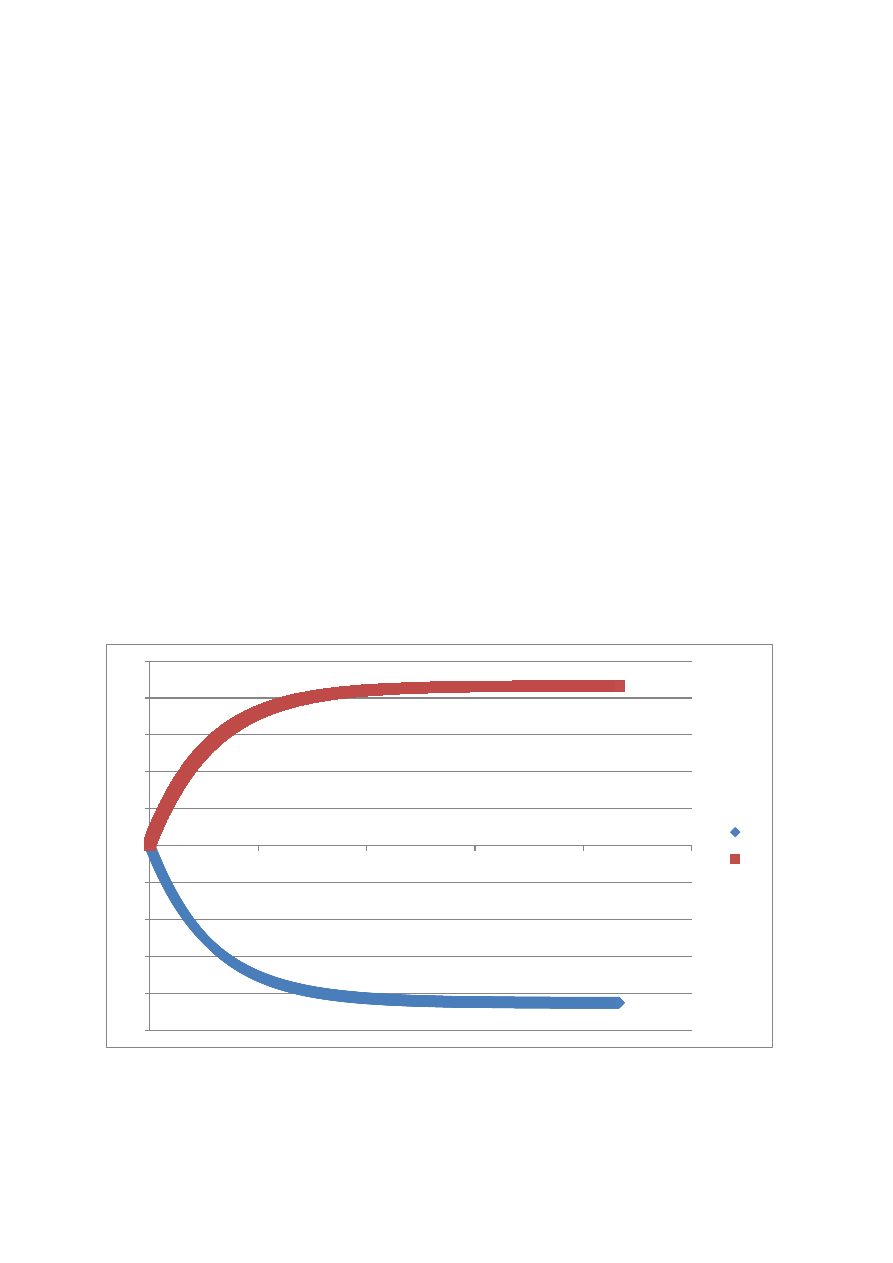
5. Wykres

-50

-40

-30

-20

-10

0

10

20

30

40

50

0

500

1000

1500

2000

2500

x1

x2

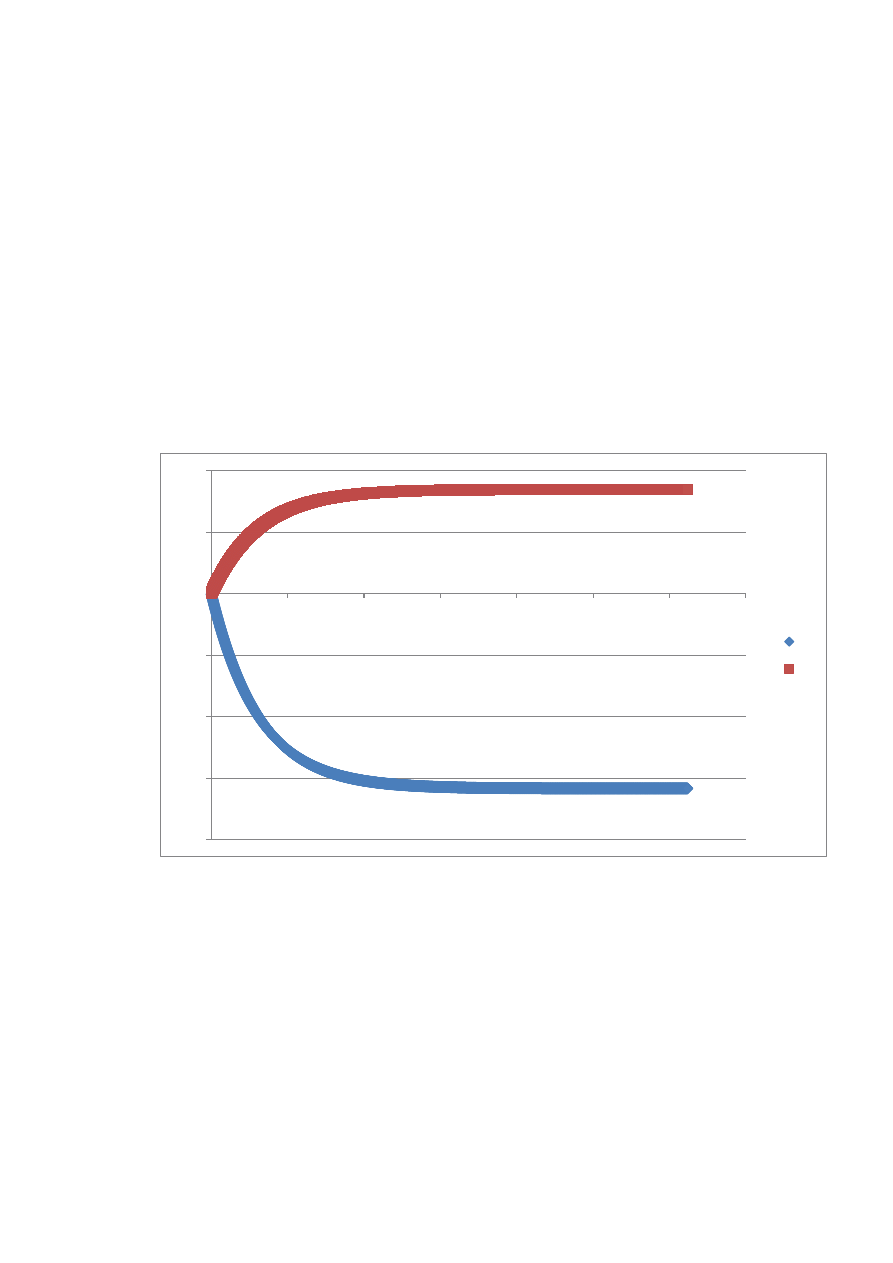
VI.

Układ równań dla którego nie spełnione są warunki zbieżności

1. Parametry:

A =

[

]; b = [

] eps = 0.0001

detA = 0,053

2. Rozwiązania:

Metoda dokładna

[

]

Metoda iteracji prostej

[

]

3. Ilość iteracji = 3118

-800

-600

-400

-200

0

200

400

0

500

1000

1500

2000

2500

3000

3500

x1

x2

3. WNIOSKI

W celu zbadania działania algorytmu przeprowadziliśmy obliczenia dla różnych danych
wejściowych. Wyniki działania programu porównaliśmy z dokładnymi rozwiązaniami,
należy jednak pamiętać, że nie zawsze są one idealne, ze względu na skończoną ilość cyfr
na których są zapisane. W przypadku układów równań od I do V różnice pomiędzy
otrzymanym wynikiem a dokładnym rozwiązaniem są pomijalnie małe.

Układ równań VI nie spełnia wymagań (norma macierzy H>1) dlatego program generuje
ostrzeżenie, celowo jednak nie przerwaliśmy jego działania – algorytm kończy działanie
dopiero po 3118 iteracjach, a otrzymane wyniki są diametralnie różne od prawidłowego
rozwiązania. Niewątpliwie jest to wada metody iteracji prostej.

Analizując wyniki stwierdziliśmy, że o ilości iteracji potrzebnych do otrzymania wyniku
spełniającego warunek stopu decyduje wyznacznik macierzy A. Jeśli jego wartość jest
bliska zeru (układ równań V), czas działania programu wzrasta około kilkaset razy, błędy
obliczeń również rosną, jednak można przypuszczać że wyznaczone rozwiązania
są wystarczająco dokładne w większości zastosowań. Zarówno dla ujemnych wartości
wyznacznika macierzy A, jak i dla dużych jego wartości nie zauważyliśmy wpływu na
ilość iteracji czy błędy otrzymanych wyników.

Ilość iteracji w przypadku układu 3 równań jest podobna jak w przypadku układu 2
równań.

Na podstawie wykresów można zauważyć, że w przypadku gdy wymagana jest mała
dokładność obliczeń, ilość wykonywanych operacji może być znacznie mniejsza, jednak
gdy wyznacznik macierzy A jest bliski zeru, ilość iteracji nadal musiałaby być bardzo
duża.

4. Kod programu

#include <iostream>
#include <math.h>
#include <fstream>

using namespace std;
#define N 2

int main()
{

ofstream file("wielomiany_wykresy.csv", ios::out);

ofstream file2("wielomiany_wyniki.csv", ios::out);

file << "Iteracja;" << "x1;" << "x2;" << "x...\n";

double a[N][N], b[N], x[N], h[N][N], g[N], suma, ilosc_iteracji = 0, suma_eps, xp, det, eps;

//Dane wejściowe

eps=0.0001;

a[0][0] = 15.43;

a[0][1] = 13.94;

a[1][0] = 10.5;

a[1][1] = 14.82;

b[0] = 9.42;

b[1] = 8.35;

if (N == 2) det = a[0][0] * a[1][1] - a[0][1] * a[1][0];

double sum;

for (int i = 0; i<N; ++i)

{

g[i] = b[i] / a[i][i];

x[i] = g[i];

sum=0;

for (int j = 0; j<N; ++j)

{

if (i == j)h[i][j] = 0;

else h[i][j] = -a[i][j] / a[i][i];

sum += fabs(h[i][j]);

}

if(sum>=1) cout << "Uklad rownan nie spelnia warunkow !";

}

do

{

file << ++ilosc_iteracji << ";";

suma_eps = 0;

for (int i = 0; i<N; i++)

{

suma = 0;

for (int j = 0; j<N; ++j) suma += (h[i][j] * x[j]);

xp = x[i];

x[i] = g[i] + suma;

suma_eps += powf(x[i] - xp, 2.0);

file << x[i] << ";";

}

file << endl;

suma_eps = powf(suma_eps, 0.5);

} while (suma_eps > eps);

for (int i = 0; i<N; ++i)

{

cout << x[i] << endl;

}

cout << "Iteracje "<< ilosc_iteracji <<endl;

cout <<"detA " << det <<endl;

file2 << "A=;" << a[0][0] << ";" << a[0][1] << endl << ";"<< a[1][0] << "; " << a[1][1] << endl;

file2 << "B=;" << b[0] << endl << ";" << b[1] <<endl;

file2 << "zadany eps=;" << eps << endl;

if (N == 2) file2 << "detA=;" << det << endl;

file2 << "x=;" << x[0] << endl << ";" << x[1]<<endl;

file2 << "Ilosc iteracji:;" << ilosc_iteracji << endl;

system("pause");

return 0;

}