1) Kierując się kryterium Akaike’a wybieramy model, dla którego wielkość 

tego kryterium będzie:
a) Najmniejsza z ujemnych
b) Najmniejsza z dodatnich
c) Najmniejsza co do wartości bezwzględnej
d) Najmniejsza

2) Selekcji modelu do prognozowania nie można dokonać wykorzystując 

a) Metodę Gaussa Seidla
b) Kryterium informacji Hannana-Quinna
c) Testu obejmowania Davidsona MacKinnona
d) Kryterium Cp Mallowsa

3) Modelu Wintersa nie stosuję się do prognozowania zjawiska 

charakteryzujących się
a) Występowaniem wyłącznie trendu i  wahań periodycznych
b) Występowaniem stałego poziomu
c) Występowaniem wahań periodycznych
d) Występowaniem trendu i wahań periodycznych

4) Wahania cykliczne to takie które:

a)pojawiają się w ciągu roku w ściśle określonych odstępach
b) pojawiają się w ciągu roku w dowolnych odstępach
c) pojawiają się w okresie powyżej roku w ściśle określonych 
odstępach
d) pojawiają się w dowolnych odstępach

5) Dekompozycja szeregu pozwala „oczyścić” go z:

a)  z trendu
b) ze stałej tendencji i wahań periodycznych

c) Z  trendu lub stałej tendencji oraz wahań periodycznych i 

przypadkowych

d) Tylko wahań sezonowych

Pytanie 1: Jakie kryterium można zastosować do wyboru odpowiedniego modelu 
ekonometrycznego (jakoś tak to brzmiało):
a) kryterium informacyjne (tu nie pamiętam, co było)
b) kryterium informacyjne Hannana-Quinna
c) kryterium informacyjne Schwarza-Bayesa
d) kryterium informacyjne (też nie pamiętam, co było)

Pytanie 2: Podane były wartości kryterium Akaike'a dla 3 modeli chyba jakichś 
autoregresyjnych i na ich podstawie trzeba było wybrać model, który możemy 
dalej badać (jakoś tak). Odpowiedzią powinien być podpunkt, w którym ten 
wskaźnik Akaike'a ma wartość najmniejszą.

Pytanie 3: Modelu Holta NIE stosuje się, gdy:
występują wahania czasowe/periodyczne (np. sezonowe)

Pytanie 5: Dekompozycja szeregu czasowego polega na:
identyfikacji trendu/stałego poziomu, wahań sezonowych oraz przypadkowych
Nic nie eliminujemy, musimy to po prostu znaleźć.

Pytanie 6: const+t (podana w pytaniu liczba odpowiadająca numerowi okresu)*to,
co w tabelce stoi pod t+odpowiedni współczynnik stojący pod zi (dla okresu 1, 5, 
9,..., będzie to z1; dla okresu 2, 6, 10, 14,..., będzie to z2; dla okresu 3, 7, 11, 
15,..., będzie to z3; dla okresu 4, 8, 12, 16,..., będzie to z4)

Pytanie 4: Coś z wahaniami sezonowymi, tylko nie pamiętam co.

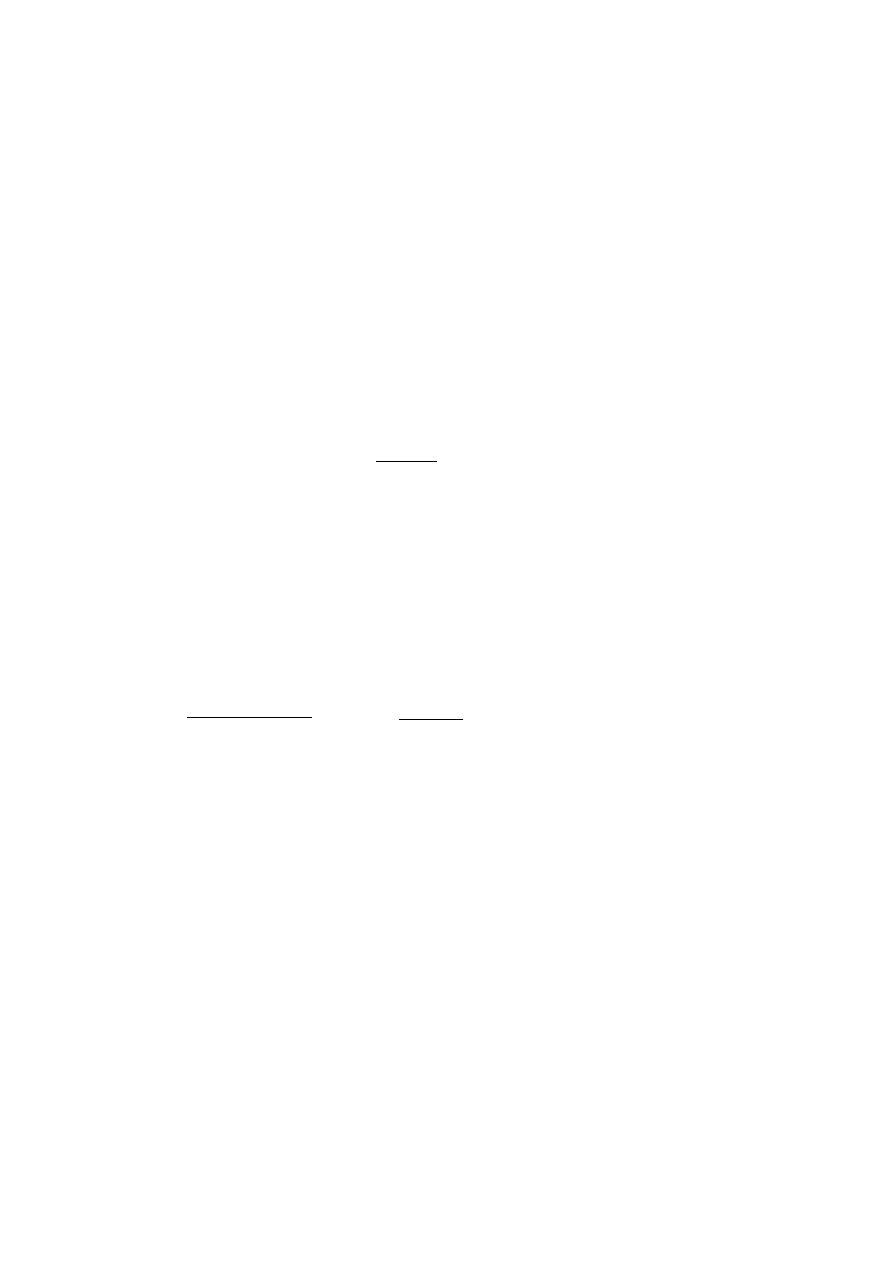
1.W ministerstwie Gospodarki Zasiedmiogrodu poddano analizie długość sieci 
wodociągowej w latach 2003-2012. Jednym z elementów tego badania była 
analiza trendu:

Ď

t

 = 20441 + 578t

(1648,7) (26,5)

Ď

t 

- długość sieci wodociągowej w roku t (w km), t – zmienna czasowa i= 1, 2... T

R

2 

= 0,983

S

e 

= 2413,4

(X

m

)

T

(X

T

*X)

-1

*x

m

* = 0,467

W nawiasach podano wartości błędów szacunku.

Jaka jest spodziewana długość sieci gazowej w Zasiedmiogrodzie na koniec roku 2013? 
Proszę wyznaczyć prognozę punktową i przedziałową długości sieci (dla prognozy 
przedziałowej proszę przyjąć poziom ufności równy 0,99). Uzyskane wyniki należy 
zinterpretować.

a) t=11

Ď

t 

= 20441 + 578 * 11 = 26799

Interpretacja: na 98,3% możemy sądzić, że długość sieci wodociągowej w 2013 roku 
wyniesie 26799 km.

b) Błąd predykcji: S

e 

= 2413,4

V =S

e

∗

√

(

X

m

)

T

(

X

TX

)

−

1

+

1=2413,4∗

√

0,467+1=2923,105

n = 10 – 2

t* = t

8,0,01

= 3,36 

Prognoza przedziałowa:

(Ď

t  

- t* * V ; Ď

t  

+ t* * V) = (26799 – 3,36 * 2923,105 ;  26799 – 3,36 * 2923,105) = 

(16977,3672 ; 36620,6328)

Interpretacja: Na 99% możemy stwierdzić, że długość sieci wodociągowej w 2013 roku 
będzie większa od 16977,3 i mniejsza od 36620,7.

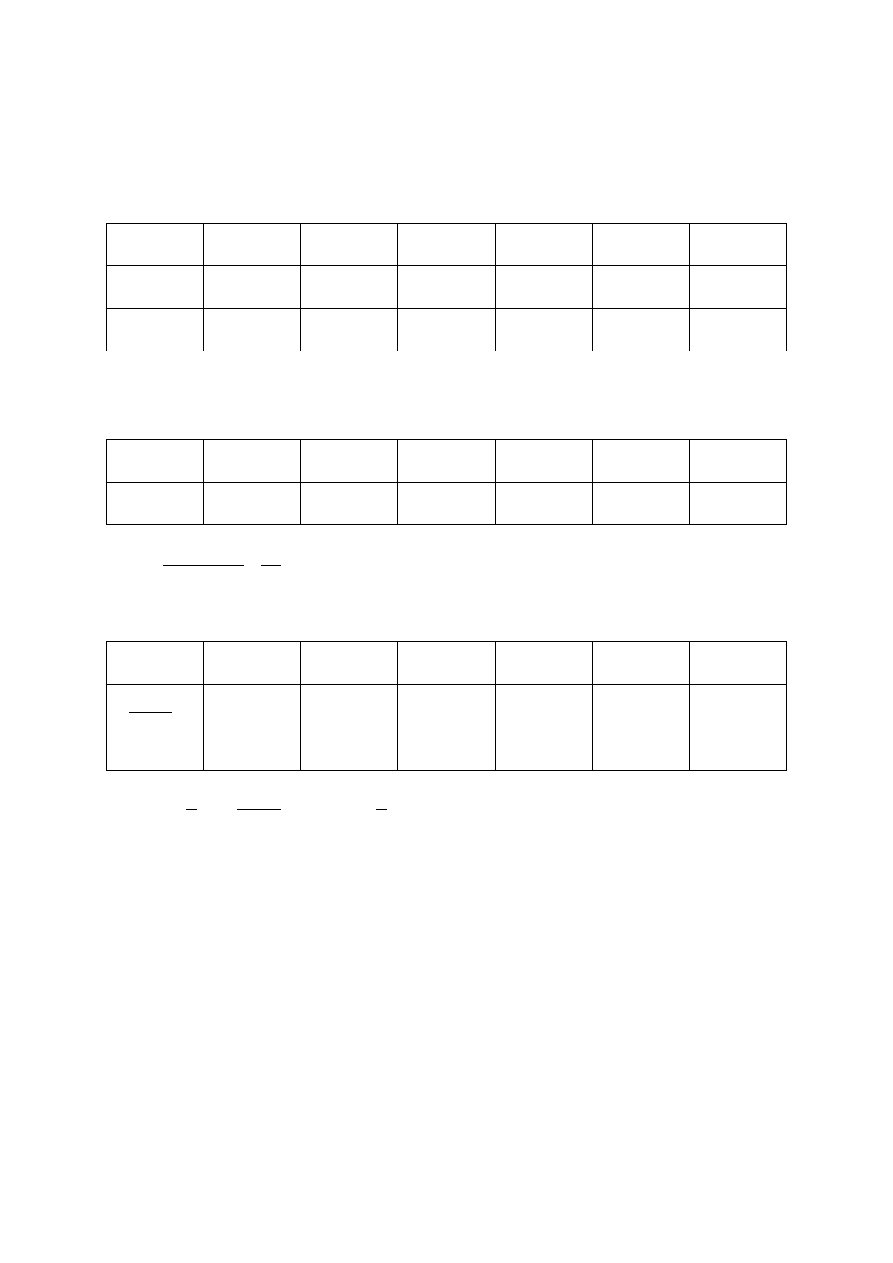
Zad 2

Za pomocą pewnego modelu wyznaczono prognozy liczby wypadków ubezpieczeniowych (w
tys.) dotyczących portfela ubezpieczeń OC pewnej firmy ubezpieczeniowej. Prognozy te oraz
wartości rzeczywiste wynosiły odpowiednio:

Rok

2000

2001

2002

2003

2004

2005

y_t

20

27

29

26

25

30

y_tp

18

24

30

25

27

29

Dokonaj oceny prognozy.

Wyznaczamy oceny prognozy:

Rok

2000

2001

2002

2003

2004

2005

|y

t

 - y

tp

|

2

3

1

3

2

1

ME =

∑

∣

y

t

−

y

tp

∣

n

=

12

6

=

2

Prognozy różniły się od wartości rzeczywistych o średnio 2 tys.

Rok

2000

2001

2002

2003

2004

2005

∣

y

t

− ̂

y

y

t

∣

2/20

3/27

1/29

3/28

2/25

1/30

MAPE=

1
n

∗

∑

∣

y

t

− ̂

y

y

t

∣

∗

100 proc=

1
6

∗

0,464∗100 proc=7,733 proc.

Średni absolutny błąd procentowy wynosi 7,733%. Prognozy różnią się średnio od wartości 
rzecz o około 8%.

Zad. 3

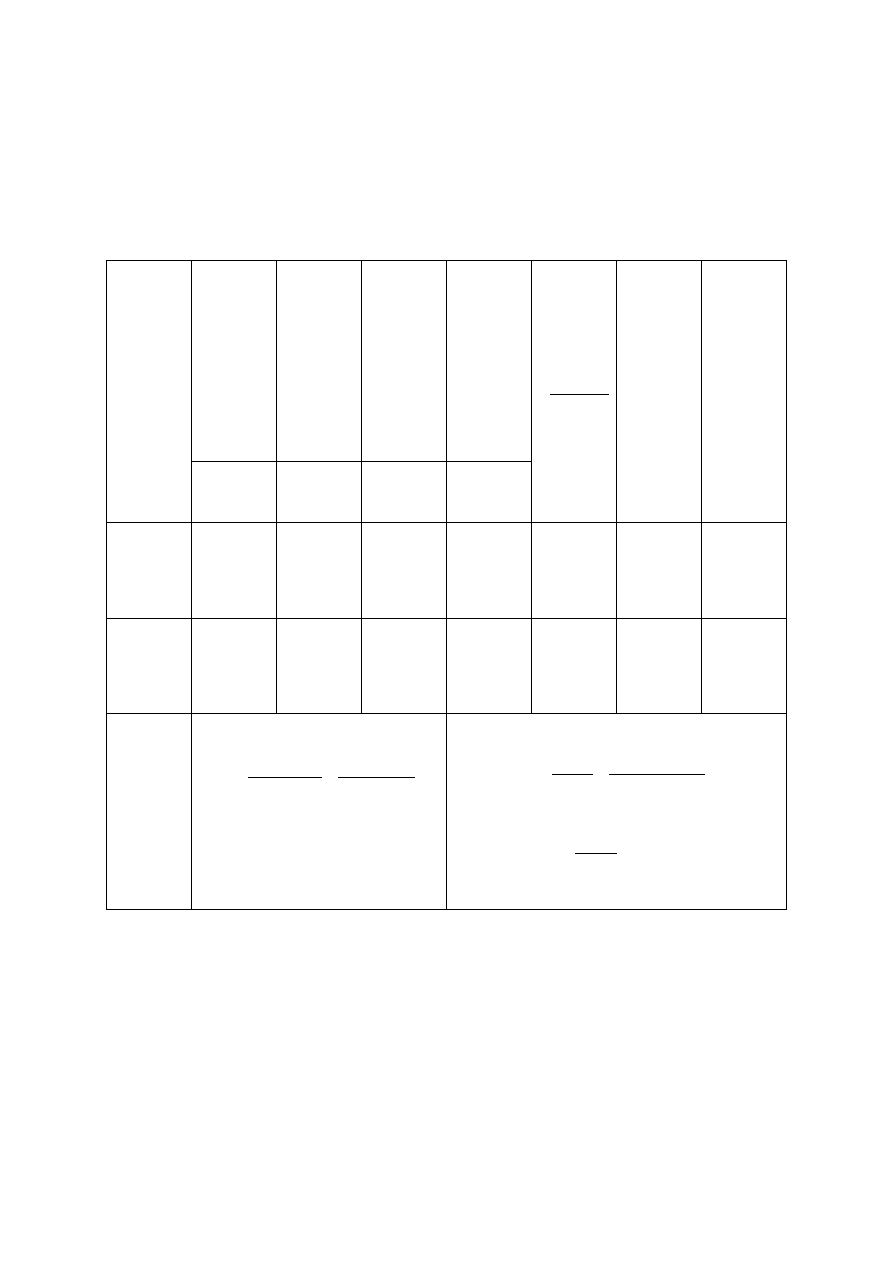
Analizie poddano półroczną sprzedaż w latach 2002-2011 (w tys. euro)siodełek rowerowych 
produkowanych przez pewną duńską firmę. Na podstawie danych zawartych w tabeli proszę 
wyznaczyć (analitycznie) i zinterpretować wskaźniki sezonowe g

i

(t).

Obliczenia cząstkowe

Suma 
wartości 
empirycz
nych

Suma 
wartości 
teoretycz
nych z 
modelu 
trendu 
liniowego

Suma 
wart. 
emp. Bez 
uwzględni
enia 
pierwszej 
i ostatniej
obserwacj
i

Suma 
wart. 
wygł. 
średnią 
ruchomą

S

i

∑

Y (t )

∑

̂

Y (t )

S

i

v

S

i 

* V

g

i

(t)

S

i

v

∗̄y −̄y

Y

t

̂

Y

t

Y

t

̆

Y

t

I półrocze 1567

1276,86

1447

1168

1567÷ 
1276,86 

= 1,227

1,227 * 
1,0035 

= 1,2313

291,207

II 
półrocze

951

1242,14

922

1196

951÷ 
1242,14

=0,766

0,766 * 
1,0035 

=0,76868

-291,232

̄y=

Y

t , I

+

Y

t , II

2

=

1567+951

2

̄y=1259

v=

L

∑

S

i

=

L

1,227+0,766

v=

2

1,993

=

1,0035

Surowe wskaźniki sezonowe wynoszą odpowiednio dla I i II półrocza 1,227 oraz 0,766. 
Skorygowane wskaźniki sezonowe odpowiednio 1,2313 oraz 0,76868. Absolutny poziom 
odchyleń sezonowych dla I półrocza wynosi 291,207, dla II półrocza -291,232