Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 1/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Pozycja 1.0 –belka podsuwnicowa
Obliczenia statyczne i wymiarowanie
1.0 Zestawienie danych przyjętej suwnicy oraz wymiarów przekroju poprzecznego
belki podsuwnicowej.
1.1 Suwnica.
Na podstawie danych wejściowych do projektu przyjęto suwnicę 1-hakową Spe1H o
udźwigu
]
[
125
kN
Q
. Pozostałe dane suwnicy:
rozpiętość
]
[
80
,
16
m
L
masa suwnicy
]
[
7
,
16
t
M
nacisk koła
]
[
121
max
kN
N
rozstaw kół
]
[
5
,
4
m
R
kabina mocowana na stałe z boku suwnicy
]
[
2
,
1
t
m
k
grupa natężenia pracy
4
A
GNP
Dane przyjęto na podstawie : W. Bogucki, M. Żyburtowicz: ‘Tablice do projektowania
konstrukcji metalowych’ ,W-wa. Arkady 1996 str.523
1.2 Szyna podsuwnicowa.
Przyjęto szynę SD 75 o parametrach:
wysokość
]
[
85
mm
h
masa
]
/
[
566
,
0
m
kN
m
sz
]
[
109
3
cm
W
x
]
[
101
3
cm
W
y
Na podstawie : W. Bogucki, M. Żyburtowicz: ‘Tablice do projektowania konstrukcji
metalowych’ ,W-wa. Arkady 1996 str.67
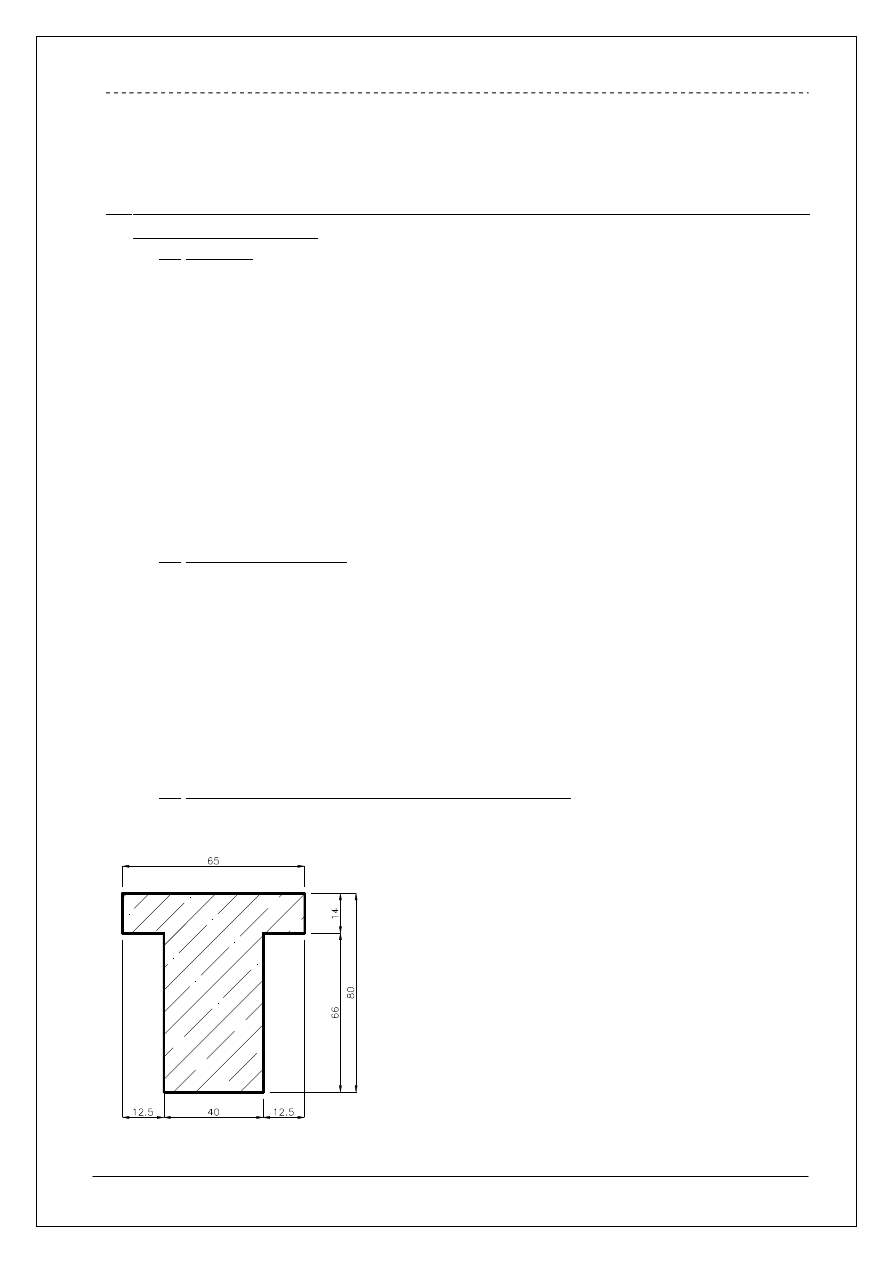
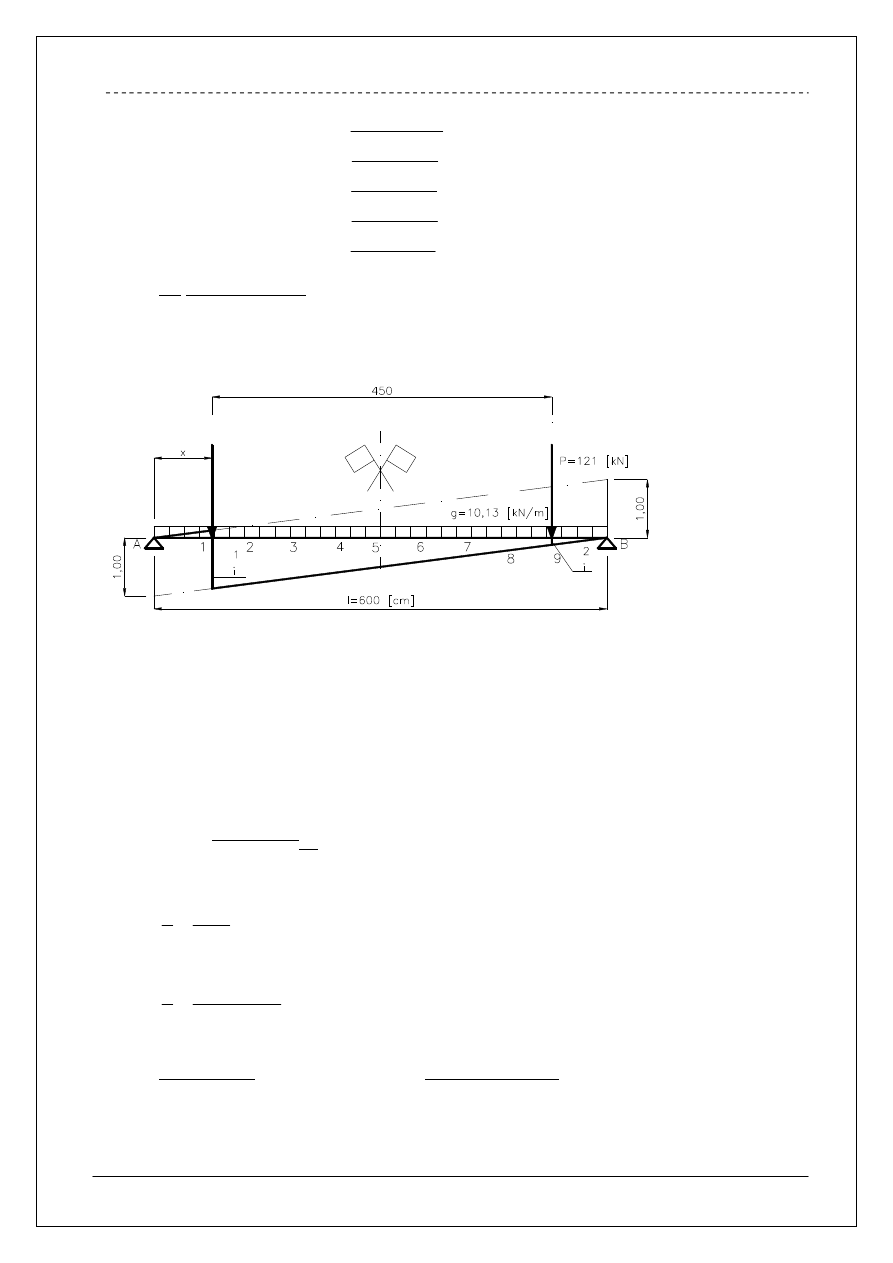
1.3 Belka podsuwnicowa geometria i schemat statyczny.
Rysunek pomocniczy
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 2/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
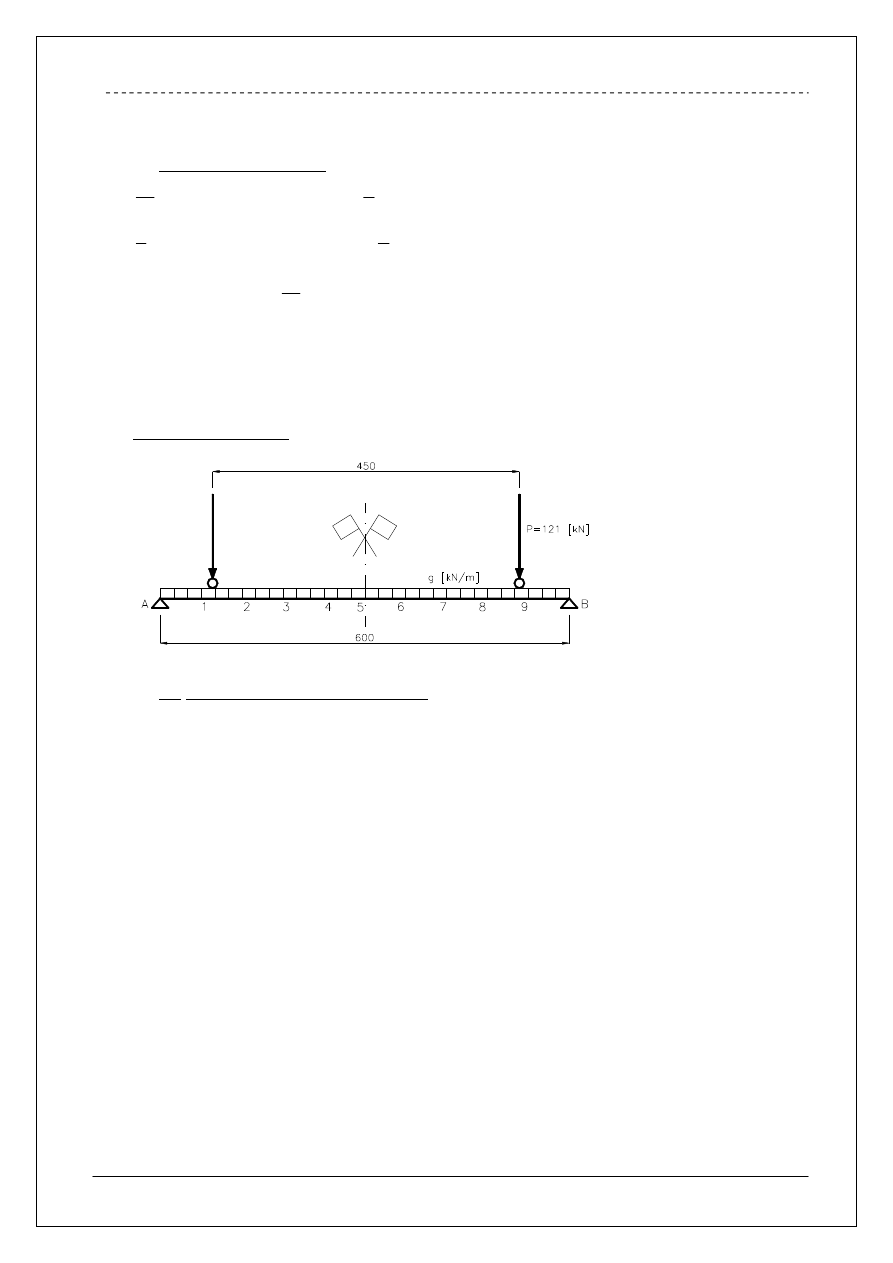
Zgodnie z danymi do projektu przyjęto belkę podsuwnicową o rozpiętości
]
[
0
,
6
m
L
i
geometrii jak na rysunku powyżej.
Sprawdzenie geometrii
a)
]
[
0
,
1
6
1
]
[
8
,
0
]
[
6
,
0
10
1
m
l
m
h
m
l
warunek spełniony
b)
]
[
4
,
0
2
1
]
[
4
,
0
]
[
267
,
0
3
1
m
h
m
b
m
h
warunek spełniony
c)
]
[
12
,
0
]
[
08
,
0
10
1
]
[
14
,
0
m
m
h
m
h
plyty
warunek spełniony
Warunki geometryczne sprawdzono wg zaleceń: J. Kobiak, W. Stachurski: ’Konstrukcje
żelbetowe’ Tom 2, W-wa Arkady 1987, str.198
Belka podsuwnicowa pracuje jako wolnopodparta obciążona dynamicznie suwnicą o
parametrach jak w pkt. 1.1.
Rysunek pomocniczy
1.4 Belka podsuwnicowa beton i stal.
Do projektu przyjęto beton B30. Parametry betonu B30:
]
[
30
,
MPa
f
G
cube
c
]
[
7
,
16
MPa
f
cd
]
[
2
,
1
MPa
f
ctd
]
[
0
,
25
MPa
f
ck
Na podstawie normy PN – B – B03264: 2002 tablica 2.
Do projektu przyjęto stal klasy AII gatunku 18G2-b o parametrach:
]
[
355
MPa
f
yk
]
[
310
MPa
f
yd
Na podstawie normy PN – B – B03264: 2002 tablica 5.
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 3/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
2.0
Zebranie obciążeń.
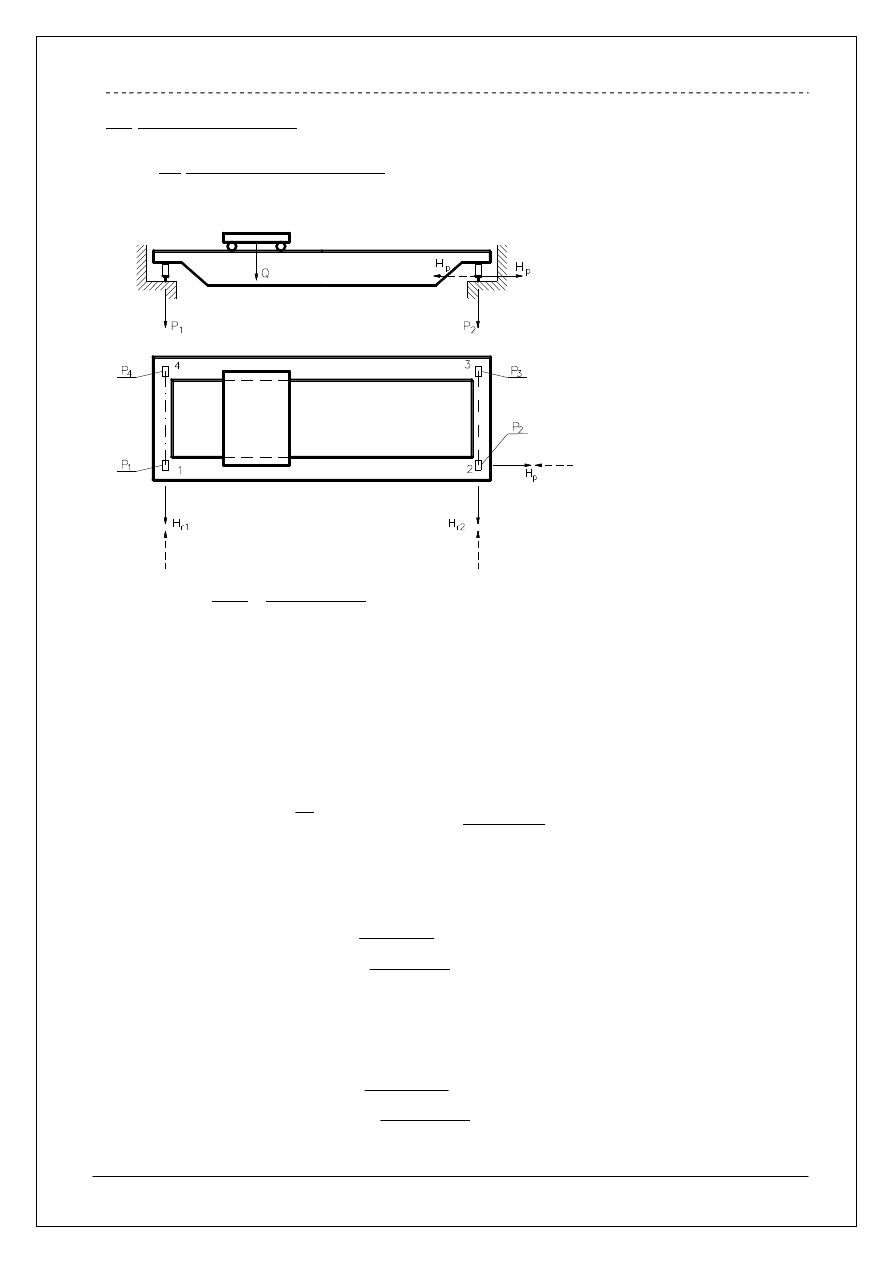
2.1 Obciążenia technologiczne.
Rysunek pomocniczy
2.1.1 Siły pionowe.
Maksymalne (charakterystyczne) siły pionowe od nacisku koła suwnicy dane są
wzorem:
ch
ch
i
P
V
min
max/
gdzie:
2
,
1
na podstawie na podstawie:
K.Grabiec: ’Konstrukcje betonowe’ ,Warszawa-
Poznań PWN 1992, tabela 5.1 dla suwnicy hakowej i GNP4.
ch
P
max
maksymalny nacisk koła na szyny podsuwnicowe, należy uwzględnić ciężar
kabiny sterowniczej z boku suwnicy:
]
[
5
,
126
11
5
,
0
121
12
11
5
,
0
max
max
kN
m
N
P
k
ch
ch
P
min
minimalny nacisk koła na szyny podsuwnicowe:
]
[
5
,
25
2
/
)
5
,
126
2
12
125
167
(
2
/
)
2
(
max
min
kN
P
m
Q
M
P
k
ch
Ostatecznie:
]
[
6
,
30
5
,
25
2
,
1
min
min
kN
P
V
ch
min (charakterystyczny) nacisk koła na szynę
]
[
8
,
151
5
,
126
2
,
1
max
max
kN
P
V
ch
max (charakterystyczny) nacisk koła na szynę
Dodatkowo chcąc wyznaczyć obliczeniową wartość siły pionowej, nacisku koła na szynę
należy uwzględnić współczynnik technologiczny
1
,
1
f
na podstawie:
K.Grabiec:
’Konstrukcje betonowe’ ,Warszawa-Poznań PWN 1992, tabela 5.1a dla GNP4 str.286
Zatem obliczeniowe siły mają wartości:
]
[
05
,
28
1
,
1
5
,
25
5
,
25
min
kN
P
f
]
[
15
,
139
1
,
1
5
,
126
5
,
126
max
kN
P
f
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 4/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
]
[
06
,
33
05
,
28
2
,
1
min
min
kN
P
V
]
[
98
,
166
15
,
139
2
,
1
max
max
kN
P
V
2.1.2 Siły poziome.
2.1.2.1 Siły poziome prostopadłe do toru suwnicy.
Uwzględniają uderzenia boczne i ukosowane suwnicy oraz siły
bezwładności, powstające w czasie rozruchu i hamowania wciągarki lub wciągnika na suwnicy.
max
P
k
H
p
gdzie:
]
[
15
,
139
max
kN
P
na podstawie pkt. 2.1.1
k
współczynnik dla suwnic z napędem mechanicznym, dobrany na podstawie:
K.Grabiec: ’Konstrukcje betonowe’ ,Warszawa-Poznań PWN 1992, rys 5.3
str.285
19
,
0
73
,
3
]
[
5
,
4
]
[
8
,
16
k
e
L
m
R
e
m
L
odczytano i przyjęto
]
[
44
,
26
15
,
139
19
,
0
max
kN
P
k
H
p
2.1.2.2 Siły poziome równoległe do toru suwnicy.
Uwzględniają siły bezwładności powstające w czasie rozruchu i
hamowania suwnicy.
max
12
,
0
P
H
r
gdzie:
]
[
15
,
139
max
kN
P
na podstawie pkt. 2.1.1
Na jedno koło przy hamowaniu przypada zatem:
]
[
70
,
16
15
,
139
12
,
0
1
kN
H
r
2.2 Obciążenia stałe
Obciążenia zebrano w tabeli 1.
Rodzaj obciążenia
Obciążenie
charakterystyczne
f
Obciążenie
obliczeniowe
[kN/m]
[-]
[kN/m]
ciężar własny belki żelbetowej
8,52
1,1
9,37
(0,4x0,66+0,65x0,14)x24
ciężar szyny z podkładkami
0,566
1,1
0,62
0,566
ciężar podkładki metalowej i złącza
0,12
1,1
0,13
0,12
9,21
10,13
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 5/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
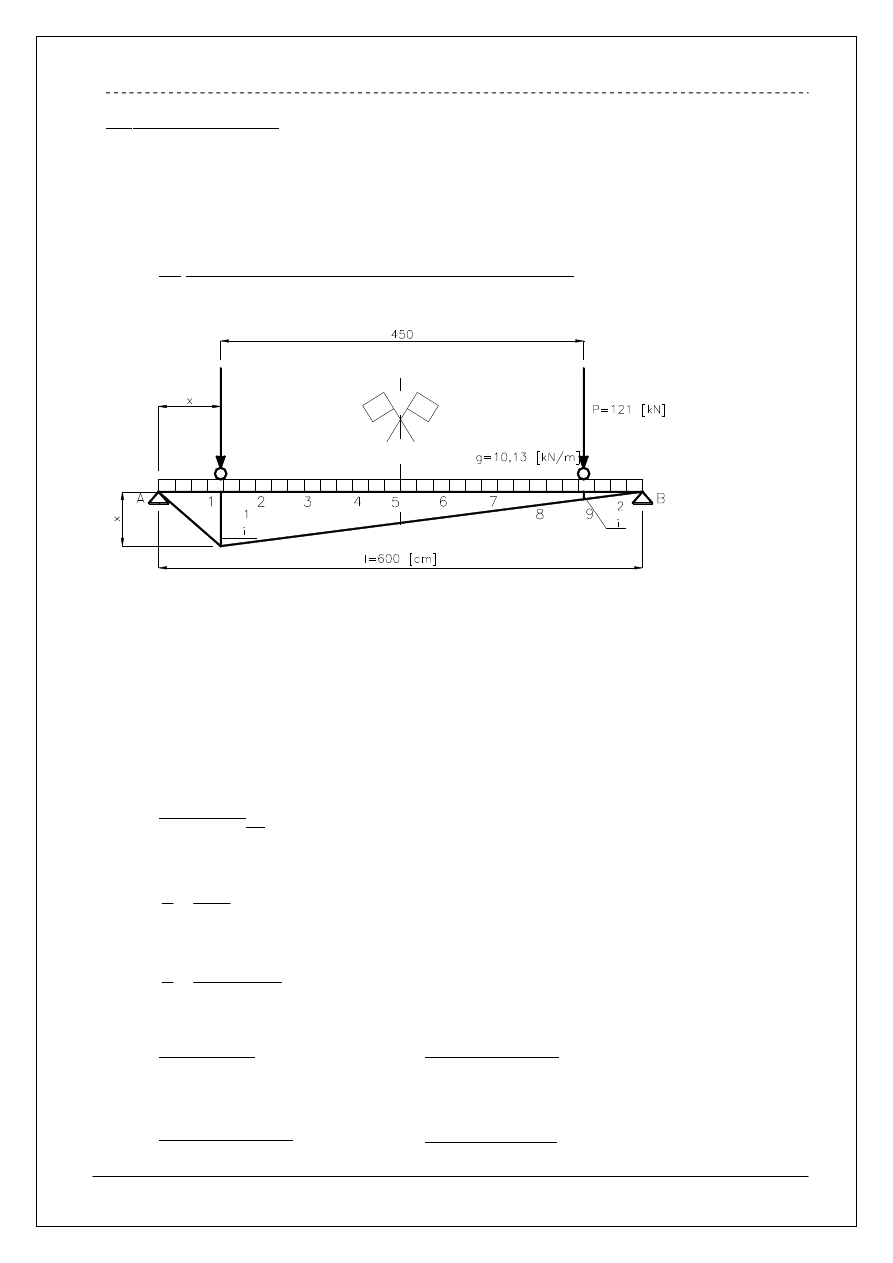
3.0 Siły wewnętrzne.
Przy projektowaniu belki podsuwnicowej obowiązuje wymiarowanie przekrojów wg
obwiedni momentów zginających i sił poprzecznych – obliczonych za pomocą linii
wpływowych. Wszystkie siły wewnętrzne obliczono w przekrojach co 60 cm. Dodatkowo
wykorzystano symetrię obciążenia i układu.
3.1 Obwiednie momentów zginających od sił pionowych.
Linia wpływowa momentu zginającego
Vi
gi
i
M
M
M
gdzie:
gi
M
moment zginający od obciążenia własnego
Vi
M
moment zginający od obciążenia technologicznego (nacisk kół suwnicy)
)
(
5
,
0
i
i
gi
x
l
x
g
M
i
Vi
V
M
gdzie:
]
[
98
,
166
kN
V
i
wg pkt. 2.1.1, maksymalny nacisk kół
i
rzędne pod siłami skupionymi odczytane z linii wpływu
Odczytanie
i
Rzędna
1
i
pod pierwszą siłą skupioną (pod pierwszym kołem)
6
/
)
6
(
6
6
1
1
x
x
x
x
i
i
Rzędna
2
i
pod drugą siłą skupioną (pod drugim kołem)
6
/
))
5
,
4
(
6
(
)
5
,
4
(
6
6
2
2
x
x
x
x
i
i
i
0
2
i
Ostatecznie zatem dla poszczególnych przekrojów:
0
x
x
A
]
[
6
,
0
1
m
x
x
0
1
A
54
,
0
6
/
6
,
0
)
6
,
0
6
(
1
1
0
2
A
09
,
0
6
/
6
,
0
))
6
,
0
5
,
4
(
6
(
2
1
]
[
2
,
1
2
m
x
x
]
[
8
,
1
3
m
x
x
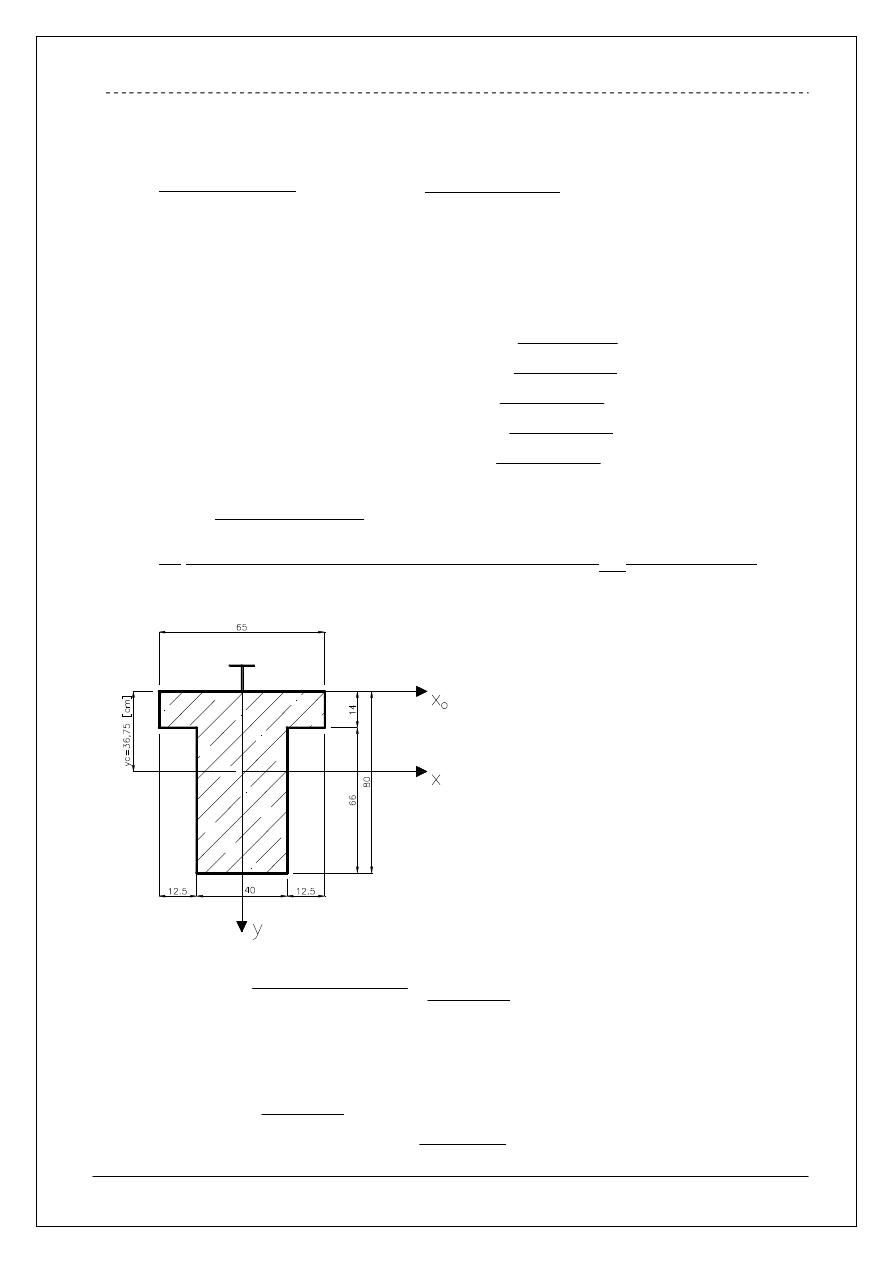
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 6/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
96
,
0
1
2
26
,
1
1
3
06
,
0
2
2
0
,
0
2
3
]
[
4
,
2
4
m
x
x
]
[
0
,
3
5
m
x
x
44
,
1
1
4
5
,
1
1
5
0
,
0
2
4
0
,
0
2
5
Zatem ostatecznie momenty zginające od sił pionowych mają wartość:
]
[
0
,
0
kNm
M
A
]
[
61
,
121
)
09
,
0
54
,
0
(
98
,
166
)
6
,
0
0
,
6
(
6
,
0
13
,
10
5
,
0
1
kNm
M
]
[
49
,
199
)
06
,
0
96
,
0
(
98
,
166
)
2
,
1
0
,
6
(
2
,
1
13
,
10
5
,
0
2
kNm
M
]
[
69
,
248
)
0
,
0
26
,
1
(
98
,
166
)
8
,
1
0
,
6
(
8
,
1
13
,
10
5
,
0
3
kNm
M
]
[
21
,
284
)
0
,
0
44
,
1
(
98
,
166
)
4
,
2
0
,
6
(
4
,
2
13
,
10
5
,
0
4
kNm
M
]
[
05
,
296
)
0
,
0
5
,
1
(
98
,
166
)
0
,
3
0
,
6
(
0
,
3
13
,
10
5
,
0
5
kNm
M
W zadanym układzie maksymalny moment występuje w przekroju 5 dla
]
[
0
,
3
m
x
]
[
05
,
296
5
kNm
M
3.2 Obwiednie momentów zginających od sił równoległych (
r
H ) do toru suwnicy.
Rysunek pomocniczy
Wyznaczenie środka ciężkości belki podsuwnicowej.
]
[
75
,
36
40
66
65
14
47
40
66
7
65
14
cm
y
c
Odległość położenia siły
r
H od główki szyny podsuwnicowej do środka ciężkości belki
podsuwnicowej obliczono jako wysokość szyny , podkładki oraz odległość
c
y .
]
[
25
,
46
1
5
,
8
75
,
36
cm
e
]
[
70
,
16
1
kN
H
r
na podstawie pkt. 2.1.2.2
]
[
72
,
7
463
,
0
70
,
16
kNm
e
H
M
r
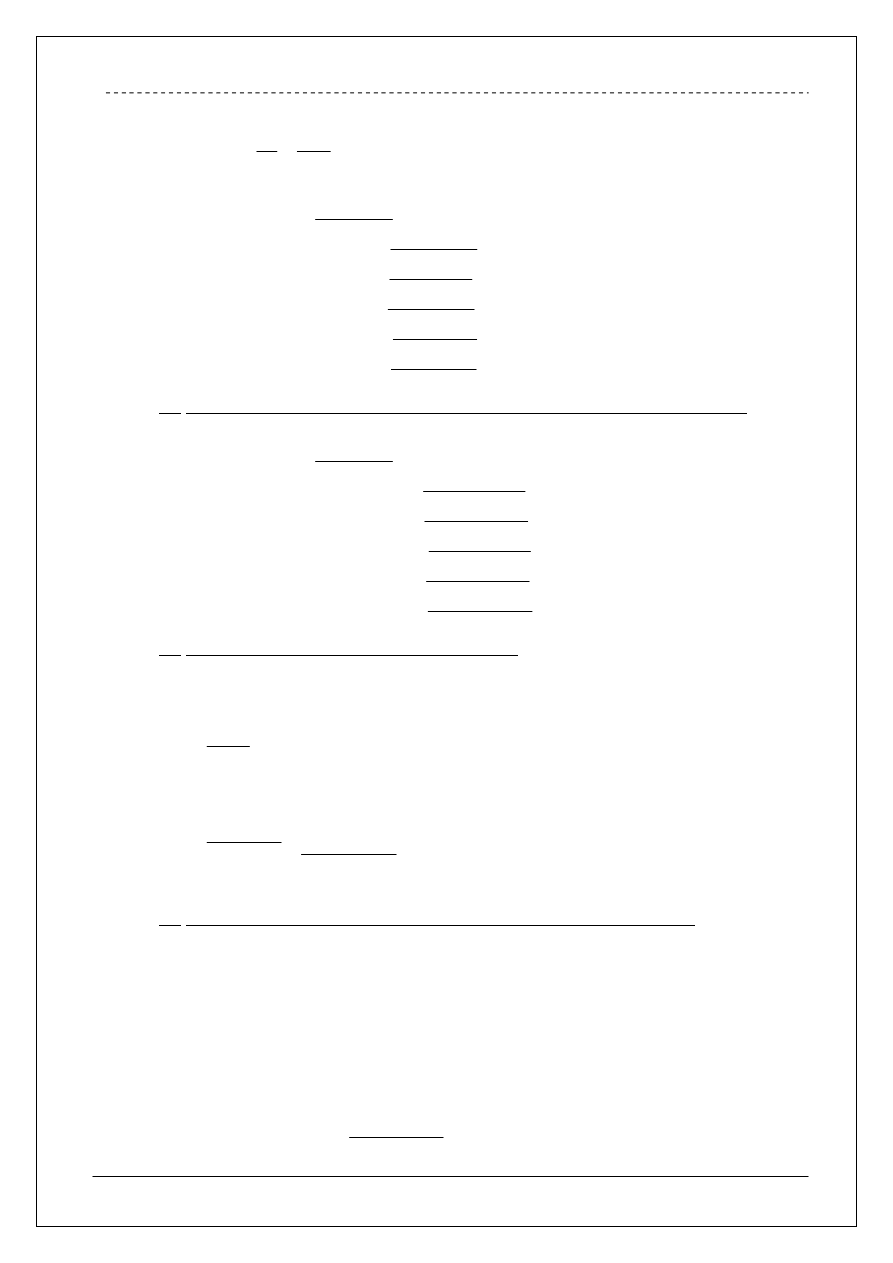
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 7/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Zatem siła poprzeczna na podporze:
]
[
29
,
1
6
72
,
7
kN
l
M
Q
A
Momenty zginające w poszczególnych przekrojach:
0
x
x
A
]
[
0
,
0
kNm
M
A
6
,
0
1
x
x
]
[
77
,
0
6
,
0
29
,
1
1
kNm
M
2
,
1
2
x
x
]
[
55
,
1
2
,
1
29
,
1
2
kNm
M
8
,
1
3
x
x
]
[
32
,
2
8
,
1
29
,
1
3
kNm
M
4
,
2
4
x
x
]
[
10
,
3
4
,
2
29
,
1
4
kNm
M
0
,
3
5
x
x
]
[
87
,
3
0
,
3
29
,
1
5
kNm
M
3.3 Sumaryczne wartości momentów zginających w poszczególnych przekrojach.
0
x
x
A
]
[
0
,
0
kNm
M
A
6
,
0
1
x
x
]
[
38
,
122
77
,
0
61
,
121
1
kNm
M
2
,
1
2
x
x
]
[
04
,
201
55
,
1
49
,
199
2
kNm
M
8
,
1
3
x
x
]
[
01
,
251
32
,
2
69
,
248
3
kNm
M
4
,
2
4
x
x
]
[
31
,
287
10
,
3
21
,
284
4
kNm
M
0
,
3
5
x
x
]
[
92
,
299
87
,
3
05
,
296
5
kNm
M
3.4 Momenty zginające w płaszczyźnie poziomej.
W obliczeniach uwzględniono jedynie moment maksymalny, który występuje w
przekroju 5- środek belki.
4
5
l
H
M
p
gdzie:
]
[
44
,
26
kN
H
p
na podstawie pkt. 2.1.2.1
Zatem:
]
[
66
,
39
4
0
,
6
44
,
26
5
kNm
M
Na ten moment zazbrojono belkę podsuwnicową na całej długości!
3.5 Momenty skręcające od sił poziomych prostopadłych do toru suwnicy.
Obliczeń dokonano na podstawie wartości współczynników
dla sił poprzecznych
tablica 10.73, K.Grabiec: ’Konstrukcje betonowe’ ,Warszawa-Poznań PWN 1992, str.560
dla
stosunku
0
,
0
/
l
R
, ponieważ w płaszczyźnie prostopadłej występuje tylko działanie jednej siły
poziomej
]
[
44
,
26
kN
H
p
na podstawie pkt. 2.1.2.1
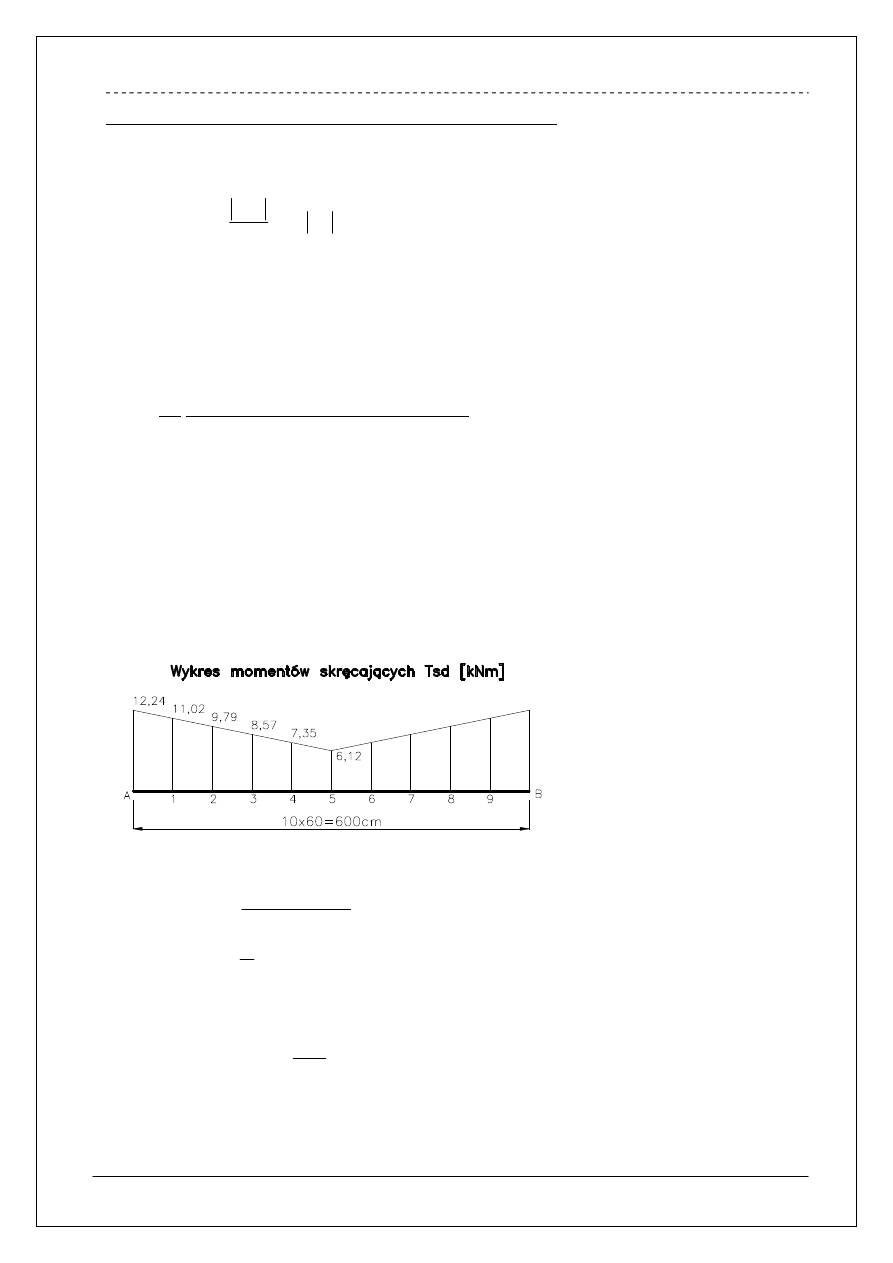
Moment skręcający obliczony wg wzoru:
e
H
M
p
i
ti
W poszczególnych przekrojach:
]
[
24
,
12
463
,
0
44
,
26
0
,
1
kNm
M
tA
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 8/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
]
[
02
,
11
463
,
0
44
,
26
9
,
0
1
kNm
M
t
]
[
79
,
9
463
,
0
44
,
26
8
,
0
2
kNm
M
t
]
[
57
,
8
463
,
0
44
,
26
7
,
0
3
kNm
M
t
]
[
35
,
7
463
,
0
44
,
26
6
,
0
4
kNm
M
t
]
[
12
,
6
463
,
0
44
,
26
5
,
0
5
kNm
M
t
3.6 Siły poprzeczne.
Siły poprzeczne obliczono na podstawie obciążania linii wpływowej
Rysunek pomocniczy
Vi
gi
i
Q
Q
Q
gdzie:
gi
Q
siła poprzeczna od obciążenia własnego
Vi
Q
siła poprzeczna od obciążenia technologicznego (nacisk kół suwnicy)
)
5
,
0
(
i
gi
x
l
g
Q
i
Vi
V
Q
gdzie:
]
[
98
,
166
kN
V
i
wg pkt. 2.1.1, maksymalny nacisk kół
i
rzędne pod siłami skupionymi odczytane z linii wpływu
Odczytanie
i
Rzędna
1
i
pod pierwszą siłą skupioną (pod pierwszym kołem)
6
/
)
6
(
6
1
6
1
1
x
x
i
i
Rzędna
2
i
pod drugą siłą skupioną (pod drugim kołem)
6
/
))
5
,
4
(
6
(
)
5
,
4
(
6
1
6
2
2
x
x
i
i
i
0
2
i
Ostatecznie zatem dla poszczególnych przekrojów:
0
x
x
A
]
[
6
,
0
1
m
x
x
0
,
1
1
A
9
,
0
6
/
)
6
,
0
6
(
1
1
25
,
0
2
A
15
,
0
6
/
))
6
,
0
5
,
4
(
6
(
2
1

Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 9/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
]
[
2
,
1
2
m
x
x
]
[
8
,
1
3
m
x
x
8
,
0
1
2
7
,
0
1
3
05
,
0
2
2
0
,
0
2
3
]
[
4
,
2
4
m
x
x
]
[
0
,
3
5
m
x
x
6
,
0
1
4
5
,
0
1
5
0
,
0
2
4
0
,
0
2
5
Do obliczenia siły poprzecznych z lewej strony rozpatrywanego przekroju wykorzystano
wartość
1
1
'
1
i
i
.
Zatem ostatecznie siły poprzeczne od sił pionowych mają wartość:
]
[
12
,
239
)
25
,
0
0
,
1
(
98
,
166
)
0
,
0
6
5
,
0
(
13
,
10
kN
Q
A
]
[
64
,
199
)
15
,
0
9
,
0
(
98
,
166
)
6
,
0
6
5
,
0
(
13
,
10
1
kN
Q
p
]
[
66
,
32
)
15
,
0
1
9
,
0
(
98
,
166
)
6
,
0
6
5
,
0
(
13
,
10
1
kN
Q
l
]
[
17
,
160
)
05
,
0
8
,
0
(
98
,
166
)
2
,
1
6
5
,
0
(
13
,
10
2
kN
Q
p
]
[
81
,
6
)
05
,
0
1
8
,
0
(
98
,
166
)
2
,
1
6
5
,
0
(
13
,
10
2
kN
Q
l
]
[
01
,
125
7
,
0
98
,
166
)
8
,
1
6
5
,
0
(
77
,
6
3
kN
Q
p
]
[
94
,
37
)
1
7
,
0
(
98
,
166
)
8
,
1
6
5
,
0
(
13
,
10
3
kN
Q
l
]
[
25
,
104
6
,
0
98
,
166
)
4
,
2
6
5
,
0
(
77
,
6
4
kN
Q
p
]
[
73
,
62
)
1
6
,
0
(
98
,
166
)
4
,
2
6
5
,
0
(
77
,
6
4
kN
Q
l
]
[
49
,
83
5
,
0
98
,
166
)
0
,
3
6
5
,
0
(
77
,
6
5
kN
Q
p
]
[
49
,
83
)
1
5
,
0
(
98
,
166
)
0
,
3
6
5
,
0
(
13
,
10
5
kN
Q
l
4.0
Wymiarowanie belki podsuwnicowej.
Stan graniczny nośności- SGN
4.1 Wymiarowanie przekroju na nośność-zginanie.
Do wyznaczenia zbrojenia głównego przeprowadzono obliczenia przy założeniu
prostokątnego rozkładu naprężeń w strefie ściskanej. Obliczenia zgodne z procedurą
wymiarowania określoną w normie PN-B-03264 (na maksymalny moment zginający).
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 10/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
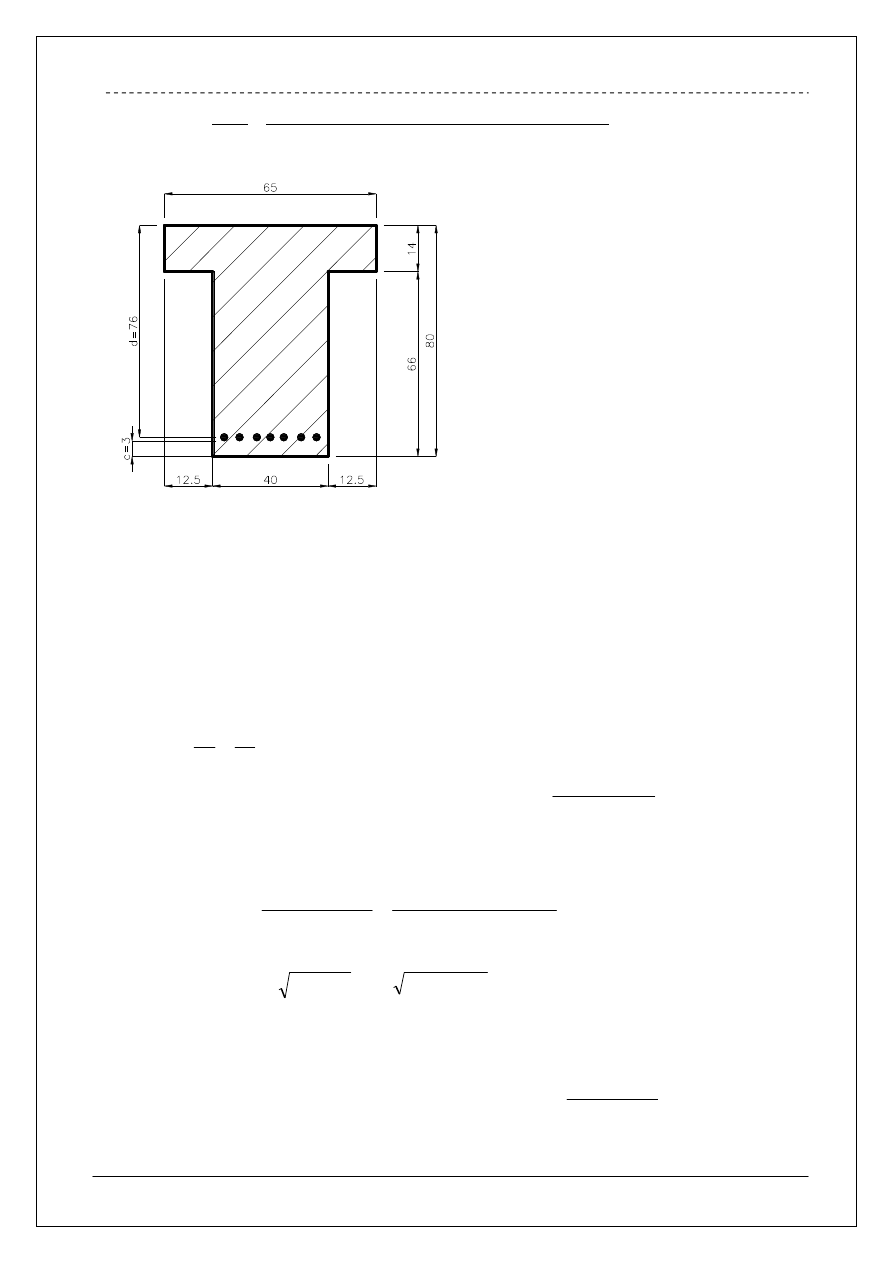
4.1.1 Wymiarowanie przekroju na zginanie w pionie.
Rysunek pomocniczy
- Wstępne przyjęcie średnicy prętów zbrojeniowych
Przyjęto pręty
]
[
25
mm
- Określenie minimalnej otuliny zbrojenia głównego
]
[
25
mm
c
oraz
mm
c
15
min
na podstawie tab. 21 PN-B-03264 dla przyjętej klasy środowiska 1
(hala przemysłowa)
Ostatecznie przyjęto otulinę
]
[
30
mm
c
- Określenie charakteru przekroju teowego
cd
eff
eff
RDP
f
b
d
M
2
,
5
,
0
1
,gdzie:
18
,
0
76
14
d
h
f
(
f
h
– grubość płyty)
]
[
0
,
1205
16700
0
,
1
65
,
0
76
,
0
18
,
0
5
,
0
1
18
,
0
2
,
kNm
M
eff
RDP
]
[
92
,
299
kNm
M
SD
na podstawie pkt. 3.3
]
[
0
,
1205
92
,
299
,
kNm
M
M
eff
RDP
SD
przekrój pozornie teowy
- Obliczenie współczynnika wejściowego-
eff
057
,
0
76
,
0
65
,
0
16700
0
,
1
92
,
299
2
2
d
b
f
M
eff
cd
SD
eff
- Obliczenie względnej wysokości strefy ściskanej-
eff
058
,
0
057
,
0
2
1
1
2
1
1
eff
eff
- Sprawdzenie czy przekrój wymaga dozbrojenia w strefie ściskanej tzn. zachodzi
warunek
lim
,
eff
eff
gdzie:
Na podstawie
tab. 9 PN-B-03264
dla stali klasy AII
55
,
0
lim
,
eff
55
,
0
058
,
0
lim
,
eff
eff
warunek spełniony przekrój zbrojony pojedynczo,
dołem
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 11/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
- Obliczenie pola powierzchni przekroju zbrojenia-
1
S
A
]
[
50
,
15
310000
16700
0
,
1
65
,
0
76
,
0
058
,
0
2
1
cm
f
f
b
d
A
yd
cd
eff
eff
S
- Dobór pola powierzchni zbrojenia
prow
S
A
,
1
Przyjęto zbrojenie
]
[
36
,
34
25
7
2
cm
prow
S
S
A
A
,
1
1
- Sprawdzenie warunku minimalnego pola powierzchni zbrojenia rozciąganego
w belce podsuwnicowej:
min
,
1
,
1
S
prow
S
A
A
gdzie:
]
[
36
,
34
69
,
5
0013
,
0
26
,
0
2
,
1
min
,
1
min
,
1
cm
A
A
d
b
d
b
f
f
A
prow
S
S
yk
ck
S
- Obliczenie rzeczywistego stopnia zbrojenia podłużnego-
S
%
0
,
2
%
13
,
1
76
,
0
40
,
0
36
,
34
,
1
d
b
A
prow
S
S
Wielkość zbrojenia przyjętego stanowi 222% zbrojenia wyliczonego dotychczas. Powiększenie
wynika z konieczności spełnienia warunku dla obciążeń wielokrotnie zmiennych.
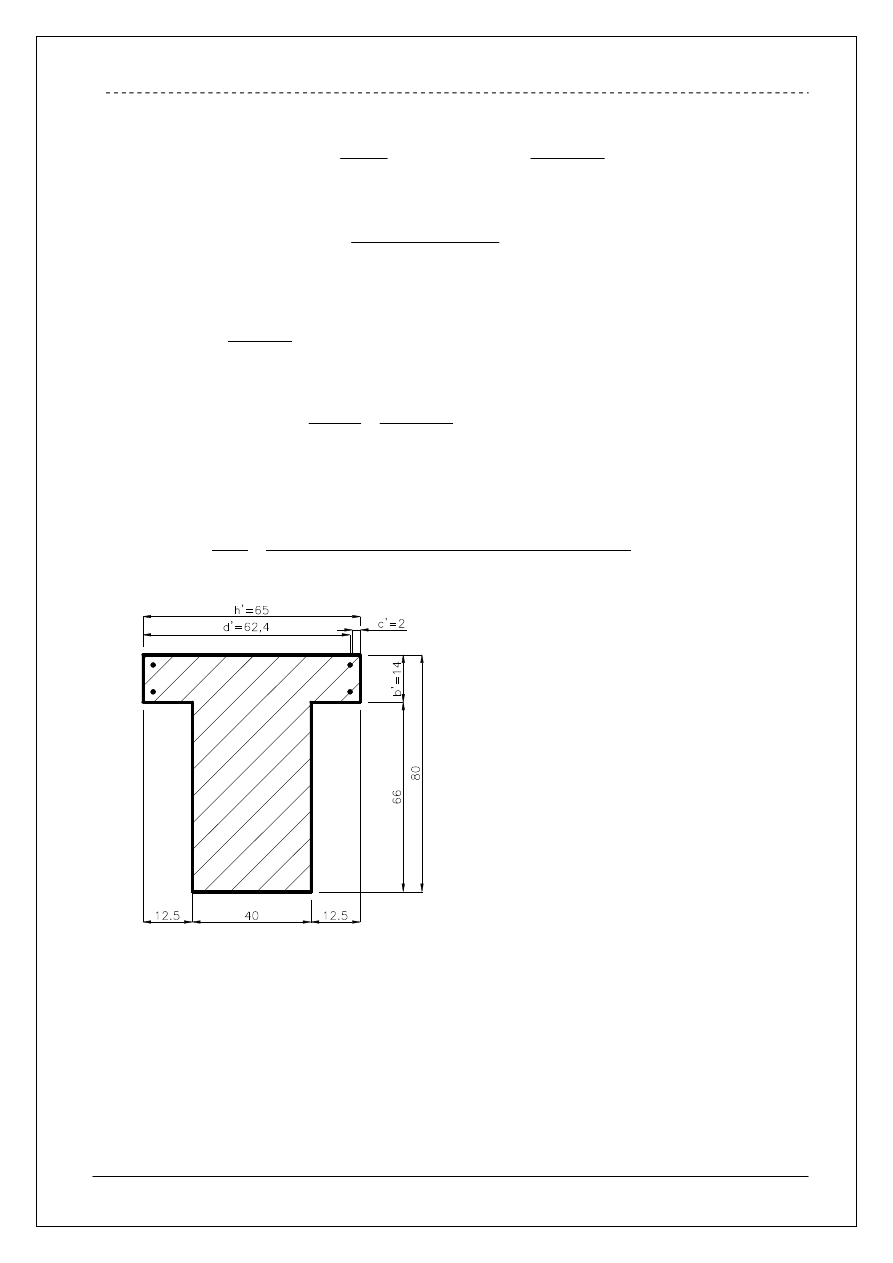
4.1.2 Wymiarowanie przekroju na zginanie w poziomie.
Rysunek pomocniczy
Obliczenie zbrojenia ze względu na moment od sił poziomych przy uwzględnieniu pracy
tylko przekroju
'
' xb
h
jako prostokątnego.
- Wstępne przyjęcie średnicy prętów zbrojeniowych
Przyjęto pręty
]
[
12
mm
- Określenie minimalnej otuliny zbrojenia głównego
]
[
12
mm
c
oraz
mm
c
15
min
na podstawie
tab. 21 PN-B-03264
dla przyjętej klasy środowiska 1
(hala przemysłowa)
Ostatecznie przyjęto otulinę
]
[
20
mm
c
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 12/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
- Obliczenie współczynnika wejściowego-
eff
044
,
0
624
,
0
14
,
0
16700
0
,
1
66
,
39
)
'
(
'
2
2
d
b
f
M
eff
cd
SD
eff
- Obliczenie względnej wysokości strefy ściskanej-
eff
045
,
0
044
,
0
2
1
1
2
1
1
eff
eff
oraz
55
,
0
045
,
0
lim
,
eff
eff
warunek spełniony
- Obliczenie pola powierzchni przekroju zbrojenia-
1
S
A
]
[
12
,
2
310000
16700
0
,
1
14
,
0
624
,
0
045
,
0
'
'
2
1
cm
f
f
b
d
A
yd
cd
eff
eff
S
- Obliczenie teoretycznego stopnia zbrojenia podłużnego-
teor
%
24
,
0
4
,
62
14
12
,
2
'
'
1
d
b
A
eff
S
teor
- Dobór pola powierzchni zbrojenia
prow
S
A
,
1
Przyjęto zbrojenie
]
[
26
,
2
12
2
2
cm
prow
S
S
A
A
,
1
1
- Sprawdzenie warunku minimalnego pola powierzchni zbrojenia rozciąganego
w „płycie” belki podsuwnicowej:
min
,
1
,
1
S
prow
S
A
A
gdzie:
]
[
26
,
2
66
,
1
'
'
0013
,
0
'
'
26
,
0
2
,
1
min
,
1
min
,
1
cm
A
A
d
b
d
b
f
f
A
prow
S
S
eff
eff
yk
ck
S
- Obliczenie rzeczywistego stopnia zbrojenia podłużnego-
S
%
2
%
27
,
0
4
,
62
14
26
,
2
'
'
,
1
d
b
A
eff
prow
S
S
Obliczenia belki podsuwnicowej zostały przeprowadzone w przekroju przęsłowym na
maksymalny moment zginający w płaszczyźnie poziomej i pionowej.
4.2 Sprawdzenie nośności belki przy uwzględnieniu działania obciążeń wielokrotnie
zmiennych.
Maksymalny moment zginający w tym przypadku określa się od obciążeń
charakterystycznych z uwzględnieniem współczynnika dynamicznego.
]
[
92
,
299
5
max
kNm
M
M
na podstawie pkt. 3.3
Wartość charakterystyczna określono zatem na podstawie wzoru:
]
[
65
,
272
1
,
1
92
,
299
max
max
kNm
M
M
f
ch
Minimalna charakterystyczna wartość momentu zginającego została obliczona tylko dla
ciężaru własnego belki podsuwnicowej:
]
[
45
,
41
)
0
,
3
0
,
6
(
0
,
3
21
,
9
5
,
0
min
kNm
M
ch
Sprawdzamy konstrukcję w fazie 2 (po zarysowaniu) ale przy zachowaniu liniowej
zależności
. Warunki normowe:
maksymalny zakres zmian naprężeń w stali nie jest większy od zakresu
dopuszczalnego:
sR
s
s
s
min
max
max
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 13/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Przyjęto średnice odgięć
]
100
15
MPa
sR
na podstawie
tablicy 19,
PN-B-03264
maksymalne naprężenie normalne w betonie obliczone przy założeniu
liniowego rozkładu naprężeń w przekroju i
Ecm
E
s
e
nie jest większe od
naprężenia dopuszczalnego:
ck
cR
c
f
25
,
0
max
.
Warunki normowe na podstawie
pkt. 7.2.2 PN-B-03264.
Obliczenie momentu bezwładności przekroju sprowadzonego belki podsuwnicowej.
1.
Określenie współczynnika
e
56
,
6
5
,
30
200
cm
s
e
E
E
,gdzie
cm
s
E
E ,
moduły sprężystości odpowiednio stali oraz
betonu na podstawie normy żelbetowej.
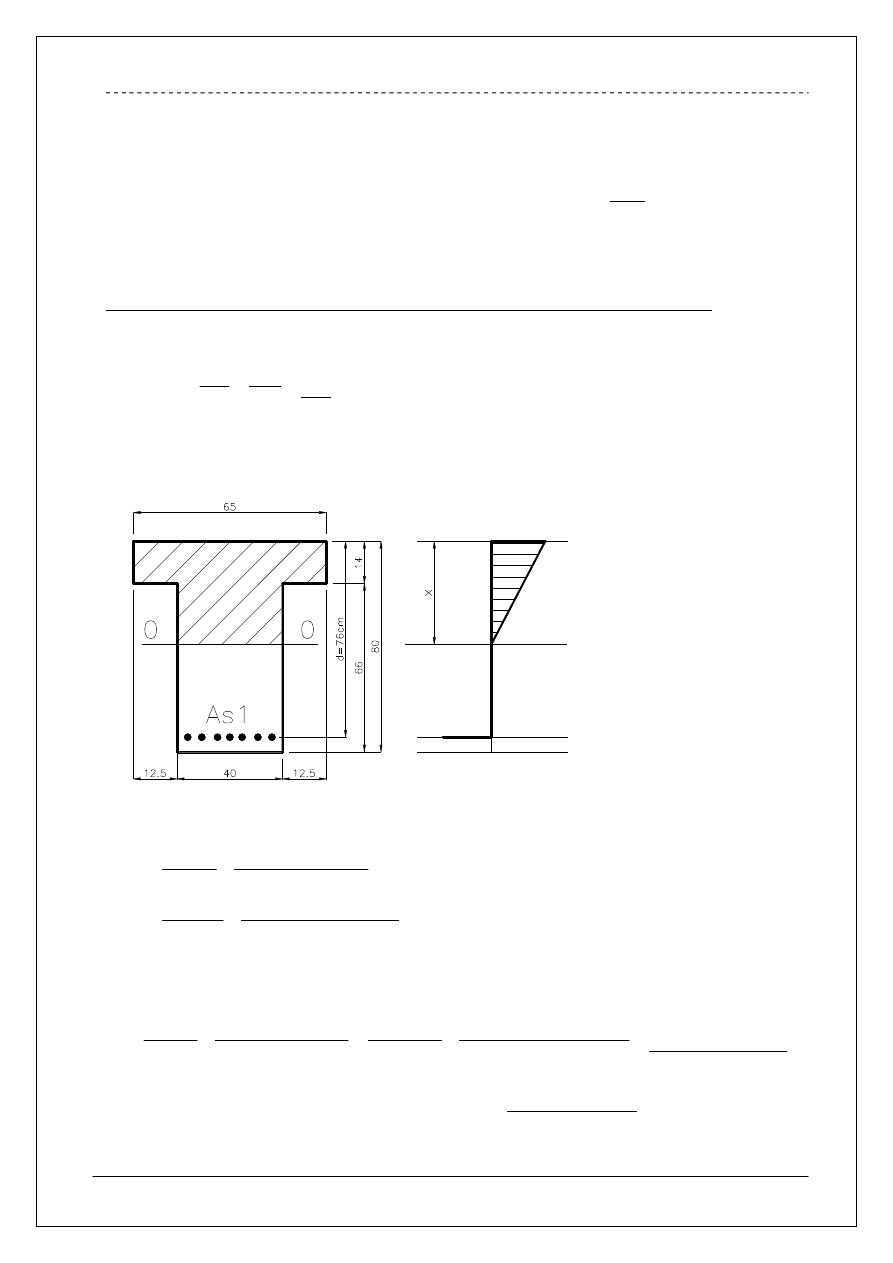
2.
Określenie położenia osi obojętnej.
Rysunek pomocniczy.
0
0
0
M
0
2
2
1
2
2
x
d
A
h
x
b
b
x
b
s
e
f
w
eff
eff
0
76
,
0
003436
,
0
56
,
6
2
14
,
0
4
,
0
65
,
0
2
65
,
0
2
2
x
x
x
Rozwiązując równanie kwadratowe otrzymano położenie osi obojętnej czyli wartość
]
[
0
,
20
cm
x
.
3.
Moment bezwładności pracującego przekroju betonowego.
]
[
001715333
,
0
3
14
,
0
2
,
0
4
,
0
65
,
0
3
2
,
0
65
,
0
3
3
4
3
3
3
3
m
h
x
b
b
x
b
I
f
w
eff
eff
c
4.
Moment bezwładności zbrojenia
]
[
00706577
,
0
2
,
0
76
,
0
003436
,
0
56
,
6
4
2
2
1
m
x
d
A
I
s
e
s
5.
Sprowadzony moment bezwładności.

Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 14/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
]
[
008781101
,
0
00706577
,
0
001715333
,
0
4
m
I
I
I
s
c
cs
Sprawdzenie naprężeń w betonie.
]
[
21
,
6
]
[
63
,
6209
2
,
0
008781101
,
0
65
,
272
max
MPa
kPa
x
I
M
cs
ch
c
]
[
25
,
6
25
25
,
0
25
,
0
]
[
21
,
6
max
MPa
f
MPa
ck
cR
c
warunek spełniony,
]
[
25
MPa
f
ck
dla betonu B30 (PN-B-03264)
Sprawdzenie naprężeń w stali.
)
45
,
41
65
,
272
(
008781101
,
0
2
,
0
76
,
0
56
,
6
min
max
max
min
max
ch
ch
cs
e
s
s
s
M
M
I
x
d
]
[
69
,
96
]
[
63
,
96686
MPa
kPa
]
[
0
,
100
]
[
69
,
96
max
MPa
MPa
sR
s
warunek spełniony
Przyjęte zbrojenie oraz zaprojektowany przekrój belki podsuwnicowej spełnia wszystkie
normowe warunki dotyczące zmęczenia konstrukcji wg
7.2.2 PN-B-03264.
4.3 Wymiarowanie przekroju na ścinanie.
Warunek normowy:
Rd
Sd
V
V
, gdzie
Sd
V
obliczeniowa ,bezwzględna wartość siły
poprzecznej,
Rd
V
nośność obliczeniowa, równa jednej z trzech granicznych sił poprzecznych:
2
1
,
Rd
Rd
V
V
lub
3
Rd
V
;
wg 5.5.1.2 PN-B-03264.
Określenie rodzajów odcinków wyznaczenie
1
Rd
V
.
Sprawdzenie warunku na nośność ze względu na rozciąganie ukośnego krzyżulca w
elemencie bez zbrojenia poprzecznego:
d
b
f
k
V
w
cp
I
ctd
Rd
]
15
,
0
40
2
,
1
35
,
0
[
1
; gdzie:
k
współczynnik wyznaczany ze wzoru:
1
6
,
1
d
k
]
[
20
,
1
MPa
f
ctd
dla betonu B30 wg
tablicy 2, PN-B-03264
w
I
b
d ,
,
na podstawie pkt. 4.1.1
]
[
0
kPa
cp
naprężenia wywołane od siły podłużnej
]
[
29
,
204
76
,
0
4
,
0
01
,
0
40
2
,
1
10
2
,
1
0
,
1
35
,
0
(
3
1
kN
V
Rd
Maksymalna siła poprzeczna
]
[
12
,
239
kN
V
Q
Sd
A
]
[
29
,
204
12
,
239
1
kN
V
V
Rd
Sd
warunek niespełniony, w belce podsuwnicowej
występują odcinki pierwszego i drugiego rodzaju.
Sprawdzenie odcinków pierwszego rodzaju.
Nośność na ścinanie ukośnego krzyżulca betonowego, sprawdzenie warunku:
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 15/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Sd
Rd
V
V
2
;gdzie:
z
b
f
V
w
cd
Rd
5
,
0
2
gdzie
54
,
0
250
25
6
,
0
250
6
,
0
ck
f
współczynnik zmniejszający wytrzymałość
betonu na ściskanie
d
z
9
,
0
]
[
66
,
1233
76
,
0
9
,
0
4
,
0
16700
54
,
0
5
,
0
2
kN
V
Rd
]
[
12
,
239
]
[
66
,
1233
2
kN
V
kN
V
Sd
Rd
warunek spełniony
Wyznaczenie maksymalnego rozstawu strzemion na odcinkach pierwszego rodzaju .
Na podstawie
9.3.1.5 PN-B-03264
przyjęto:
]
[
400
75
,
0
max
mm
d
s
przyjęto rozstaw strzemion:
]
[
8
,
56
]
[
76
75
,
0
75
,
0
max
cm
cm
d
s
;oraz
]
[
40
max
cm
s
.
Dodatkowo zbrojenie musi spełniać warunki określone warunkiem
(209)
.
Sprawdzenie minimalnego stopnia zbrojenia
%
17
,
0
240
25
08
,
0
08
,
0
min
,
yk
ck
w
f
f
dla betonu B30 oraz stali A-I.
]
[
56
,
29
40
0017
,
0
01
,
2
min
,
1
max
,
1
cm
b
A
s
w
w
sw
przyjęto
]
[
26
1
cm
s
Wyznaczenie długości odcinków drugiego rodzaju.
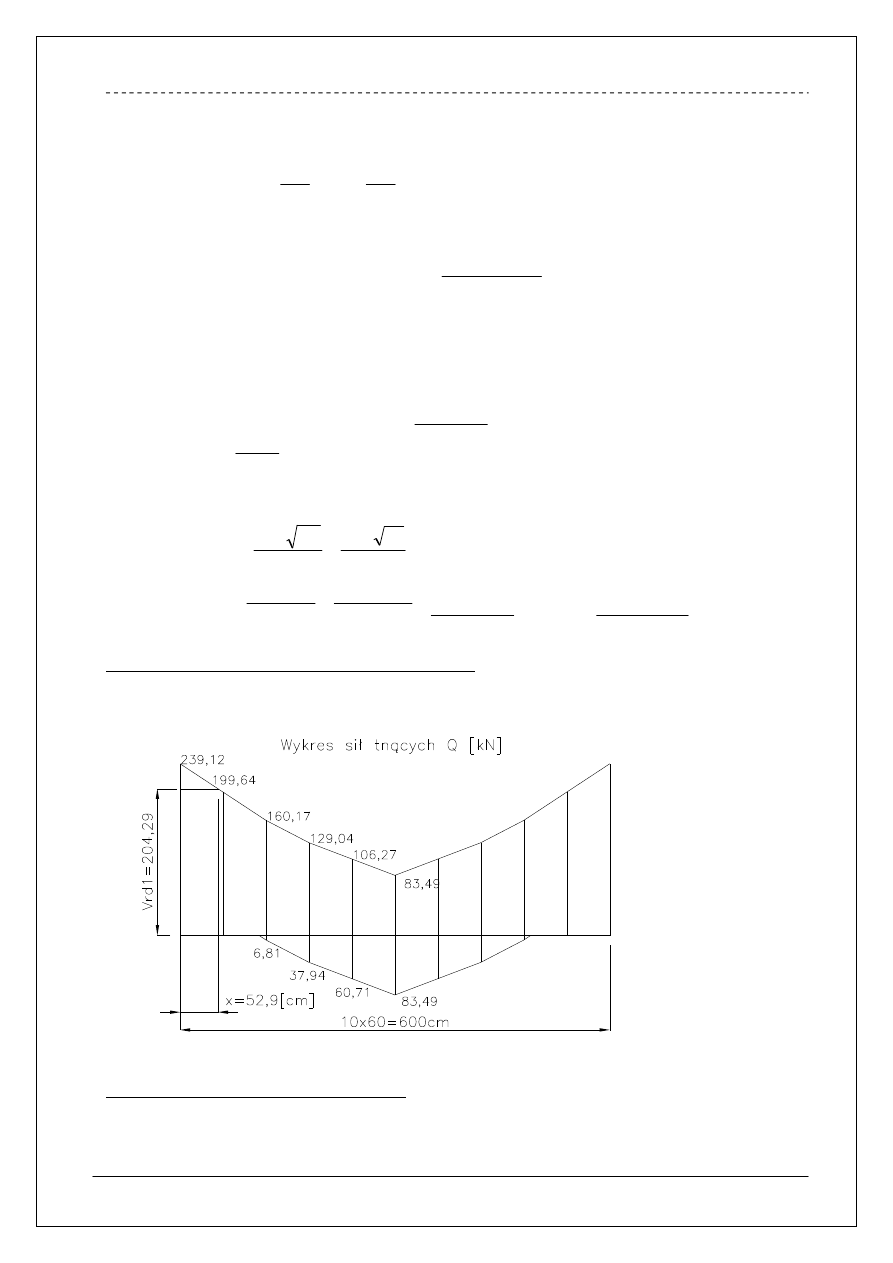
W celu określenia długości odcinków drugiego rodzaju sporządzono wykres sił tnących.
Rysunek pomocniczy.
Długość odcinka drugiego rzędu odczytano z wykresu i przyjęto
]
[
9
,
52
cm
x
.
Sprawdzenie odcinków drugiego rodzaju.
Sprawdzenie polega na spełnieniu warunku:
)
,
min(
3
2
Rd
Rd
Sd
V
V
V
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 16/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Założenie:
Przyjęto i obliczono zbrojenie na ścinanie w postaci strzemion prostopadłych.
- Nośność na ścinanie ukośnego krzyżulca betonowego, sprawdzenie warunku:
Sd
Rd
V
V
2
;gdzie:
2
2
1 ctg
ctg
z
b
f
V
w
cd
Rd
;gdzie:
45
- kąt nachylenia krzyżulca betonowego
Pozostałe dane i oznaczenia jak w pkt. powyżej.
Zatem:
]
[
66
,
1233
45
1
45
76
,
0
9
,
0
4
,
0
16700
54
,
0
2
2
kN
ctg
ctg
V
Rd
]
[
12
,
239
]
[
66
,
1233
2
kN
V
kN
V
SD
Rd
warunek spełniony.
Wyznaczenie maksymalnego rozstawu strzemion na odcinkach drugiego rodzaju.
Patrz jak dla odcinków pierwszego rodzaju. Przyjęto s
max
= 26 cm.
Nośność na rozciąganie zbrojenia poprzecznego, sprawdzenie warunku
Sd
Rd
V
V
3
;gdzie:
ctg
z
s
f
A
V
ywd
sw
Rd
1
1
1
3
]
[
01
,
2
503
,
0
4
2
1
cm
A
sw
- przyjęto strzemiona z prętów 48mm ze stali
St3SX-b (czterocięte na podstawie
pkt. 9.3.1.5 PN-B-03264
)
]
[
210
1
MPa
f
ywd
wytrzymałość obliczeniowa strzemion
1
s
rozstaw strzemion prostopadłych do osi żebra
Obliczenie rozstawu maksymalnego strzemion do spełnienia powyższego warunku:
]
[
121
,
0
45
76
,
0
9
,
0
12
,
239
210000
10
01
,
2
4
1
1
max
,
1
m
ctg
ctg
z
V
f
A
s
Sd
ywd
SW
Do projektu przyjęto strzemiona 48mm w rozstawie
]
[
12
1
cm
s
.
Ostatecznie:
]
[
60
,
240
45
76
,
0
9
,
0
12
,
0
210000
10
01
,
2
4
3
kN
ctg
V
Rd
]
[
12
,
239
]
[
60
,
240
3
kN
V
kN
V
Sd
Rd
warunek spełniony, poprawnie
zaprojektowane zbrojenie poprzeczne (na ścinanie)
Sprawdzenie minimalnego stopnia zbrojenia
0017
,
0
0042
,
0
40
12
01
,
2
min
,
1
w
w
sw
w
b
s
A
warunek spełniony.
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 17/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Sprawdzenie stanu granicznego nośności zbrojenia głównego.
Na podstawie pkt. 5.5.3.2 PN-B-03264
1
S
td
F
F
;gdzie:
ctg
V
z
M
F
Sd
Sd
td
5
,
0
; gdzie:
Sd
Sd
V
M
,
siły wewnętrzne na podporze wg pkt. 3.3 i 3.6
yd
S
S
f
A
F
1
'
1
; gdzie:
]
[
73
,
14
91
,
4
3
25
3
2
1
'
cm
A
S
analizowana część zbrojenia głównego.
]
[
50
,
456
310000
001473
,
0
]
[
56
,
119
45
12
,
239
5
,
0
0
,
0
kN
kN
ctg
F
td
Warunek spełniony.
4.4 Wymiarowanie przekroju na skręcanie.
Na podstawie
pkt. 5.7.2 PN-B-03264
obliczeniowy moment skręcający powinien spełniać
następujące warunki:
1.
1
Rd
Sd
T
T
2.
2
Rd
Sd
T
T
, gdzie:
Sd
T
obliczeniowy moment skręcający na podstawie pkt. 3.5, oraz
Sdi
ti
T
M
2
1
,
Rd
Rd
T
T
nośność na skręcanie ze względu na maksymalny moment skręcający, który
może być przeniesiony odpowiednio: przez ściskane krzyżulce betonowe, przez zbrojenie.
Rysunek pomocniczy.
Wyznaczenie
1
Rd
T
oraz sprawdzenie warunku normowego.
tg
A
t
f
T
k
cd
Rd
cot
2
1
gdzie:
u
A
t
gdzie
]
[
32
,
0
8
,
0
4
,
0
2
m
A
przekrój wewnątrz obwodu zewnętrznego
]
[
4
,
2
8
,
0
2
4
,
0
2
m
u
obwód zewnętrzny
]
[
13
,
0
4
,
2
32
,
0
m
t
równoważna grubość ścianki
]
[
6
2
13
cm
c
t
przyjęto
]
[
181
,
0
13
,
0
8
,
0
13
,
0
4
,
0
8
,
0
)
4
,
0
(
2
m
t
t
A
k
powierzchnia
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 18/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
zawarta wewnątrz linii środkowej
54
,
0
)
200
25
1
(
6
,
0
)
250
1
(
6
,
0
ck
f
współczynnik zmniejszający
wytrzymałość betonu na ściskanie
45
nachylenie krzyżulców betonowych (jak wyżej)
]
[
19
,
212
45
45
cot
181
,
0
13
,
0
16700
54
,
0
2
1
kNm
tg
T
Rd
Zatem:
]
[
19
,
212
]
[
24
,
12
1
kNm
T
kNm
T
Rd
Sd
warunek spełniony
Sprawdzenie jednoczesnego skręcania i ścinania belki podsuwnicowej
Na podstawie
pkt. 5.7.3 PN-B-03264
sprawdzono warunek
1
2
2
2
1
Rd
Sd
Rd
Sd
V
V
T
T
Wszystkie dane na podstawie pkt. 4.3 i 4.4.
1
041
,
0
66
,
1233
12
,
239
19
,
212
24
,
12
2
2
warunek spełniony.
Norma dopuszcza przyjęcie minimalnego zbrojenia na skręcanie i ścinanie gdy spełnione
są następujące warunki:
5
,
4
w
Sd
Sd
b
V
T
1
5
,
4
1
Rd
w
Sd
Sd
Sd
V
b
V
T
V
Warunki zostały sprawdzone w przekrojach co 60 [cm] (od A do 5- symetria) w tabeli 2.
Tabela 2.
Przekrój
T
Sd
V
Sd
b
w
/4,5 T
Sd
V
Sd
b
w
/4,5 V
Sd
[1+(4,5T
Sd
)/(V
Sd
b
w
) V
Rd1
V
Sd
[1+(4,5T
Sd
)/(V
Sd
b
w
)V
Rd1
[kNm] [kNm]
[-]
[kN]
[kN]
[-]
A
12,24
21,26
spełniony
376,82
204,29
nie spełniony
1
11,02
17,75
spełniony
323,62
204,29
nie spełniony
2
9,79
14,24
spełniony
270,31
204,29
nie spełniony
3
8,57
11,47
spełniony
225,45
204,29
nie spełniony
4
7,35
9,45
spełniony
188,96
204,29
spełniony
5
6,12
7,42
spełniony
152,34
204,29
spełniony
Zatem w przekrojach od 4 do 5 jedynym warunkiem na przyjęcie strzemion na ścinanie i
skręcanie jest tablica 32 PN-B-03264 dotycząca minimalnego zbrojenia poprzecznego. Ponieważ
warunki te zachodzą dla samego ścinania, po dołożeniu dodatkowego zbrojenia ze względu na
skręcanie, warunek minimalnego stopnia zbrojenia spełniony definicyjnie i sprawdzenie
przeprowadzone poniżej wykonane zostało jedynie ze względów projektowych..
Maksymalny rozstaw strzemion
t
s ze względu na czyste skręcanie.
Obliczenia na podstawie
pkt. 5.7.3 PN-B-03264:

Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 19/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Dla przekrojów od A do 1 oraz od 9do B.
cot
2
2
S
A
f
A
T
sw
ywd
k
Rd
dla
]
[
24
,
12
2
kNm
T
T
Sd
Rd
wyznaczono max
s
]
[
24
,
31
45
cot
24
,
12
503
,
0
210000
181
,
0
2
cot
2
2
1
cm
T
A
f
A
s
Rd
sw
ywd
k
A
Przyjęto
]
[
0
,
31
1
cm
s
A
.
Zatem warunek
2
Rd
Sd
T
T
dla przyjętego przekroju spełniony definicyjnie.
Dla przekrojów od 1 do 9.
]
[
02
,
11
1
kNm
T
]
[
70
,
34
45
cot
02
,
11
10
503
,
0
210000
181
,
0
2
cot
2
4
2
9
1
cm
T
A
f
A
s
Rd
sw
ywd
k
Przyjęto
]
[
0
,
34
9
1
cm
s
.,
Ostateczne przyjęcie strzemion ze względu na skręcanie i ścinanie.
Wprowadzono
jednolite
zbrojenie
w
postaci
strzemion
czterociętych
]
[
01
,
2
503
,
0
4
8
4
2
cm
ze stali AI (St3SX-b).
1.0
Odcinek belki, na którym występuje odcinek drugiego rodzaju, przekroje
od A do 1 oraz od 9 do B.
Obliczenie niezbędnego zbrojenia strzemionami ze względu na:
ścinanie
m
cm
A
V
sw
2
77
,
16
12
,
0
503
,
0
4
:
skręcanie
m
cm
A
T
sw
2
62
,
1
31
,
0
503
,
0
:
Obliczenie maksymalnego rozstawu wg pkt 4.3 i 4.4.
m
cm
A
sw
2
01
,
20
62
,
1
2
77
,
16
]
[
1
,
10
]
[
101
,
0
01
,
20
01
,
2
cm
m
s
I
przyjęto
]
[
0
,
10
cm
S
I
2.0
Odcinek belki na którym występuje odcinek pierwszego rodzaju, przekrój
od 1 oraz od 9.
Obliczenie niezbędnego zbrojenia strzemionami ze względu na:
ścinanie
m
cm
A
V
sw
2
73
,
7
26
,
0
503
,
0
4
:
skręcanie
m
cm
A
T
sw
2
48
,
1
34
,
0
503
,
0
:
Obliczenie maksymalnego rozstawu wg pkt 4.3 i 4.4.
m
cm
A
sw
2
69
,
10
48
,
1
2
73
,
7
]
[
80
,
18
]
[
1880
,
0
69
,
10
01
,
2
cm
m
s
II
przyjęto
]
[
18
cm
S
II
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 20/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Sprawdzenie minimalnego stopnia zbrojenia,
tablica 32 PN-B-03264
Sprawdzenia dokonano jedynie w przekroju od 1 do 9, dla rzadszego rozstawu
strzemion.
0018
,
0
min
,
w
dla betonu B30 oraz stali AI (St3SX-b).
0017
,
0
0028
,
0
40
18
01
,
2
min
,
w
w
II
sw
w
b
S
A
warunek spełniony. Wszystkie
obliczane przekroje spełniają warunek minimalnego stopnia zbrojenia poprzecznego.
Przyjęcie dodatkowego zbrojenia podłużnego na skręcanie.
Na podstawie
5.7.2 PN-B-03264:
cot
2
2
k
k
Rd
yld
st
A
u
T
f
A
gdzie:
]
[
33
,
12
45
cot
31
,
0
10
503
,
0
210000
181
,
0
2
cot
2
4
2
kN
S
A
f
A
T
sw
ywd
k
Rd
]
[
88
,
1
13
,
0
8
,
0
2
13
,
0
4
,
0
2
m
u
k
obwód powierzchni
k
A
]
[
10
05
,
3
45
cot
210000
181
,
0
2
88
,
1
33
,
12
2
4
m
A
st
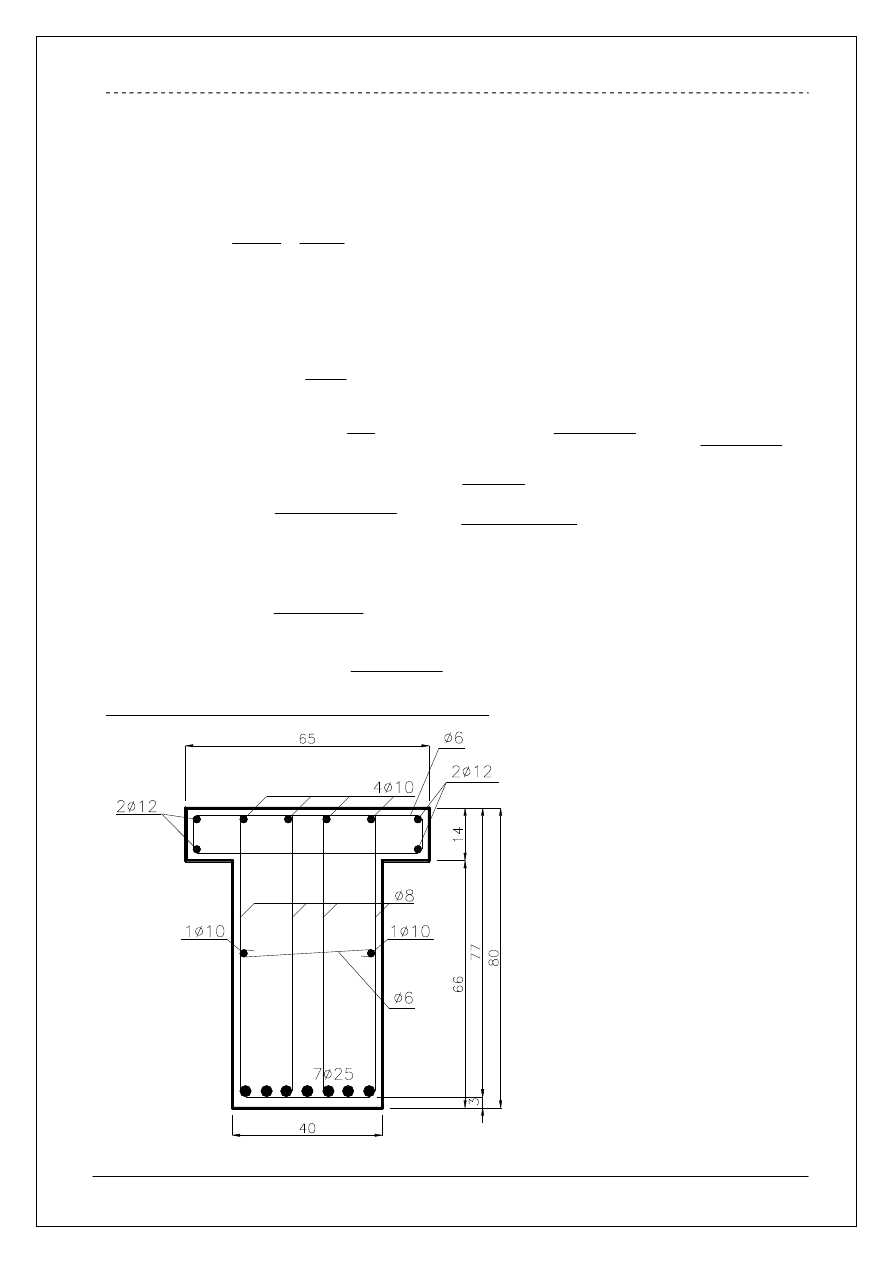
Przyjęto na wysokości belki z każdej strony
10
1
o
]
[
57
,
1
2
cm
A
. Dołem jest nadmiar
zbrojenia wynikający z projektowania belki podsuwnicowej na obciążenia wielokrotnie zmienne
]
[
86
,
18
50
,
15
36
,
34
2
1
cm
A
s
. Górą przewidziano dodatkowe zbrojenie montażowe
]
[
14
,
3
10
4
2
cm
. Ostatecznie zatem całkowite zbrojenie na skręcanie ma wartość:
]
[
05
,
3
]
[
57
,
23
14
,
3
86
,
18
57
,
1
2
2
cm
cm
A
st
warunek spełniony
Ostateczne zbrojenie ma postać-rysunek pomocniczy
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 21/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Stan graniczny użytkowalności- SGU
Obliczenia dokonano na długotrwałych wartościach obciążeń.
4.5 Sprawdzenie szerokości rys ukośnych.
Szerokość
k
w rys ukośnych w elementach zginanych obliczymy na podstawie
6.4
PN-B-03264.
lim
,
k
k
w
w
;gdzie:
ck
S
w
k
f
E
w
2
4
d
b
V
w
SD
'
naprężenia ścinające od obciążenia długotrwałego
2
2
2
1
1
1
3
1
W
W
;
sin
2
2
1
1
2
1
w
SW
w
SW
w
w
W
b
s
A
b
s
A
ponieważ przyjęto zbrojenie na ścinanie w
postaci strzemion , zatem
1
2
0
w
w
w
2
1
,
współczynniki określające przyczepność betonu do odpowiednio:
strzemion i prętów odgiętych, dla prętów gładkich 1,0 oraz dla żebrowanych 0,7.
2
1
,
odpowiednio: średnica strzemion i prętów odgiętych
]
[
3
,
0
lim
,
mm
w
k
przyjęto na podstawie
pkt. 6.4 PN-B-03264
Pozostałe oznaczenia bez zmian jak wyżej.
Obliczenia przeprowadzono dla strefy podporowej – największe naprężenia styczne.
Naprężenia styczne przy ścinaniu
W tym przypadku siłę ścinającą wyznaczono dla kombinacji obciążeń
długotrwałych, czyli zastosowano współczynnik
6
,
0
d
dla obciążenia zmiennego i
współczynniki
0
,
1
f
dla obciążenia własnego belki. Zatem na podstawie pkt. 2.2 i 3.6
otrzymano:
]
[
87
,
152
)
25
,
0
0
,
1
(
98
,
166
6
,
0
)
0
,
0
6
5
,
0
(
21
,
9
'
kN
Q
A
]
[
503
,
0
]
[
86
,
502
76
,
0
4
,
0
87
,
152
'
MPa
kPa
d
b
V
w
SD
Stopień zbrojenia
]
[
00503
,
0
40
10
01
,
2
1
1
w
I
Sw
w
w
b
s
A
Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 22/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
Współczynnik
]
[
530
8
0
,
1
00503
,
0
3
1
3
1
1
1
1
mm
W
Obliczenie rozwarcia rys ukośnych i sprawdzenie warunku normowego.
]
[
3
,
0
]
[
0213
,
0
25
10
200
00503
,
0
530
503
,
0
4
4
3
2
1
2
mm
mm
f
E
w
ck
S
w
k
warunek spełniony.
Ponieważ warunek rozwarcia rys ukośnych spełniony jest dla maksymalnej siły
poprzecznej zatem cała belka podsuwnicowa spełnia powyższy warunek
lim
,
k
k
w
w
.
4.6 Sprawdzenie ugięcia belki podsuwnicowej.
Ugięcia sprawdzono w przęśle, przekrój 5 wg
tab. 13 i pkt. 6.5 PN-B-03264.
Obliczenie naprężeń w zbrojeniu rozciąganym dokonano przy uwzględnieniu części
długotrwałej obciążenia (zastosowano tak jak wyżej współczynniki
6
,
0
d
dla
obciążenia zmiennego i współczynniki
0
,
1
f
dla obciążenia własnego belki).
Ostatecznie na podstawie 2.2 i 3.6 otrzymano:
d
A
M
S
s
1
'
5
gdzie
]
[
73
,
191
)
0
,
0
5
,
1
(
98
,
166
6
,
0
)
0
,
3
0
,
6
(
0
,
3
21
,
9
5
,
0
'
5
kNm
M
moment maksymalny od obciążeń długotrwałych
80
,
0
dla
%
0
,
1
na podstawie
załącznika D PN-B-03264
Pozostałe dane jak w pkt. 4.1.1
]
[
78
,
91
76
,
0
10
36
,
34
8
,
0
73
,
191
4
MPa
s
Obliczenie stosunku rozpiętości obliczeniowej
eff
l
do wysokości użytecznej
d
.
89
,
7
76
,
0
0
,
6
d
l
eff
Interpolacja liniowa stosunku
d
l
eff
na podstawie PN-B-03264 tablica 15.
Dla belki swobodnie podpartej:
A
s1
/bd
s
=250 [MPa]
s
=250 [MPa]
B15
B25
B30(interpolowane)
1,0
18
19
20
1,25
17
18
19

Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 23/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
48
,
19
48
,
0
0
,
19
0
,
19
48
,
0
13
,
1
25
,
1
0
,
1
25
,
1
19
20
x
d
l
x
x
eff
Interpolacja stosunku
%
13
,
1
d
l
eff
dla
]
[
78
,
91
MPa
S
(wg
pkt. 6.5 PN-B-03264
)
06
,
53
78
,
91
250
48
,
19
78
,
91
%
13
,
1
MPa
eff
S
d
l
Sprawdzenie maksymalnej wartości stosunku
d
l
eff
,dla której nie trzeba sprawdzać
ugięć,
tablica 13 PN-B-03264
d
l
d
l
eff
MPa
eff
S
78
,
91
%
13
,
1
89
,
7
06
,
53
warunek spełniony, sprawdzenie ugięcia nie jest konieczne.
4.7 Sprawdzenie szerokości rys prostopadłych.
Rysy sprawdzono w przekroju 5 (maksymalne naprężenia rozciągające w stali), na podst.
zał. D PN-B-03264. Do sprawdzenia rys niezbędny jest współczynnik zbrojenia podłużnego
S
na podstawie pkt.4.1.1 oraz naprężenia rozciągające w stali
S
wg pkt. 4.6.
%
13
,
1
s
]
[
78
,
91
MPa
s
Na podstawie analizy tabeli D PN-B-03264 wynika że największa możliwa średnica pręta
zbrojeniowego w przekroju 5 dla
%
13
,
1
s
i
]
[
78
,
91
MPa
s
to
mm
32
. Największa
zaprojektowana średnica pręta zbrojeniowego to
mm
25
, zatem szerokość rys prostopadłych w
elementach zginanych nie przekroczy szerokość rysy granicznej
mm
w
3
,
0
lim
.
5.0 Sprawdzenie warunków dodatkowych.
5.1 Sprawdzenie belki na transport.
Wzięto pod uwagę możliwość transportu belki w pozycji odwróconej. Założono, że beton
osiągnął 70% wytrzymałości gwarantowanej. Przyjęto podpory w odległości 0,1 [m] od końców
belki, czyli:
]
[
8
,
5
1
,
0
2
0
,
6
m
l
Maksymalny moment zginający od ciężaru własnego belki podsuwnicowej wg
tabeli 1 (obciążenia obliczeniowe).
]
[
60
,
42
8
8
,
5
13
,
10
8
2
2
kNm
l
q
M
T
Określenie zbrojenia niezbędnego do przeniesienia obciążenia.

Katedra Konstrukcji Betonowych i Technologii Betonu PG Pomoce dydaktyczne
str. 24/24 Przykład obliczeniowy żelbetowej belki podsuwnicowowej
aktualizacja, PP: 12.2009
015
,
0
775
,
0
4
,
0
16700
7
,
0
0
,
1
60
,
42
)
(
2
2
d
b
f
M
eff
cd
T
eff
Obliczenie względnej wysokości strefy ściskanej-
eff
015
,
0
015
,
0
2
1
1
2
1
1
eff
eff
Sprawdzenie czy przekrój wymaga dozbrojenia w strefie ściskanej tzn. zachodzi
warunek
lim
,
eff
eff
gdzie:
Na podstawie
tab. 9 PN-B-03264
dla stali klasy AII
55
,
0
lim
,
eff
55
,
0
015
,
0
lim
,
eff
eff
warunek spełniony
Obliczenie pola powierzchni przekroju zbrojenia-
1
S
A
]
[
51
,
2
310000
16700
0
,
1
4
,
0
775
,
0
015
,
0
'
'
2
1
cm
f
f
b
d
A
yd
cd
eff
eff
S
Ponieważ
przyjęto
już
dodatkowe
zbrojenie
montażowe
górą
w
postaci
]
[
14
,
3
10
4
2
cm
zatem przekrój jest już wystarczająco dozbrojony.
5.2 Obliczenie uchwytów transportowych ze stali AI gatunku St3SX-b.
Przyjęto dwa uchwyty transportowe w odległości 1,0 [m] od końców belki. Wymagany
przekrój uchwytów dla ciężaru własnego (obliczeniowego) belki podsuwnicowej wg tabeli 1.
]
[
45
,
1
210000
2
0
,
6
13
,
10
2
2
'
cm
f
l
q
A
yd
T
Dodatkowo uwzględniono współczynnik zwiększający przekrój ze względu na podryw
prefabrykatu
0
,
2
dyn
]
[
9
,
2
2
45
,
1
2
'
cm
A
A
dyn
T
T
Przyjęto uchwyty z pręta
]
[
54
,
1
14
2
cm
zatem
]
[
9
,
2
]
[
08
,
3
14
2
2
2
cm
cm
( uchwyt dwucięty) warunek spełniony.
Wyszukiwarka
Podobne podstrony:
belka podsuwnicowa algorytm cz7
belka podsuwnicowa algorytm cz2
belka podsuwnicowa algorytm cz3
belka podsuwnicowa algorytm stara norma(1)
belka podsuwnicowa algorytm cz5
belka podsuwnicowa algorytm calosc
belka PODSUw mój
Belka podsuwnicowa
belka podsuwnicowa algorytm cz4
belka podsuwnicowa algorytm cz1[1]
belka podsuwnicowa algorytm stara norma
belka podsuwnicowa algorytm cz7
belka podsuwnicowa algorytm cz2
belka podsuwnicowa algorytm stara norma
więcej podobnych podstron