Opis ruchu

1. Układ odniesienia, położenie i tor punktu materialnego.

2. Przemieszczenie.

3. Prędkość i przyśpieszenie.

cinew

- kineo (poruszam się)

kinematyka – nauka o ruchu (bez wskazania przyczyny ruchu)

1. Układ odniesienia – ciało lub układ ciał, względem których opisywane jest
położenie badanego ciała (z wybranym układem odniesienia wiąże się na ogół układ
współrzędnych).

2. Ruch – zmiana położenia ciała względem innego ciała (układu odniesienia).

3. Punkt materialny – punkt obdarzony masą. Jest modelem obiektu fizycznego,
którego rozmiary pomijamy. Ciało traktujemy jako punkt materialny wtedy, kiedy
odległości pokonywane przez to ciało są o wiele większe od jego rozmiarów, a jego
struktura wewnętrzna nie ma znaczenia dla opisu jego zachowania.

4. Tor – linia zakreślana przez obrany punkt poruszającego się ciała w danym
układzie odniesienia.

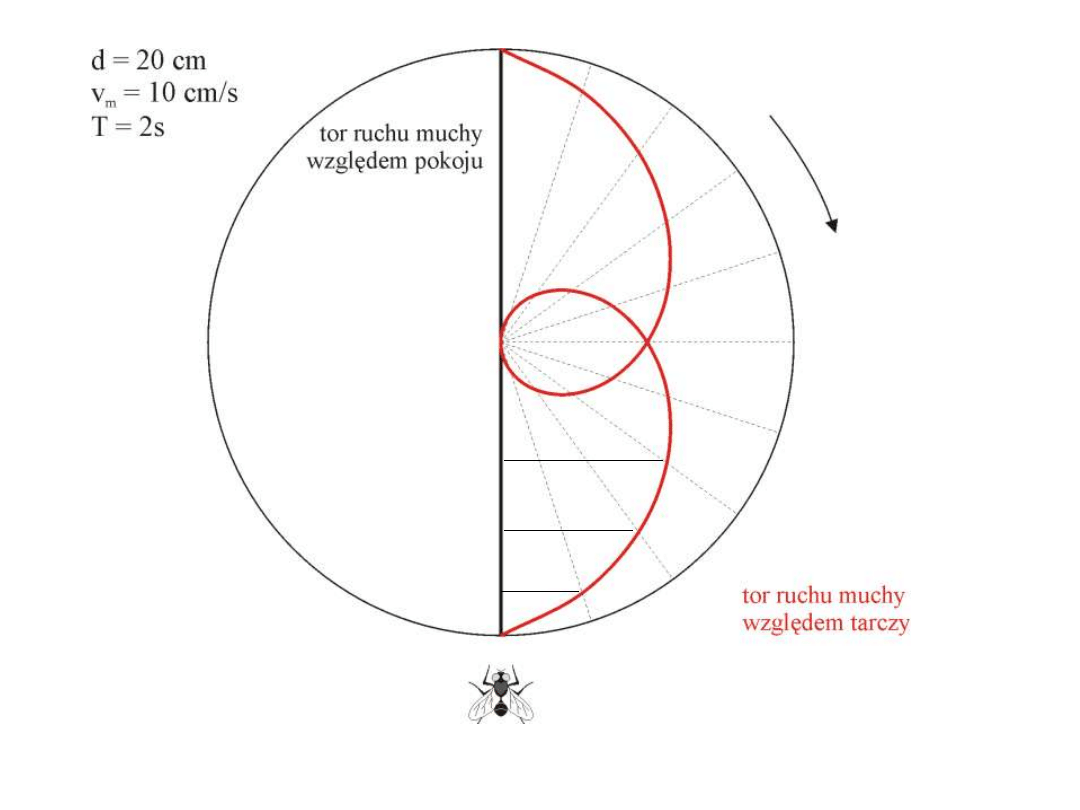
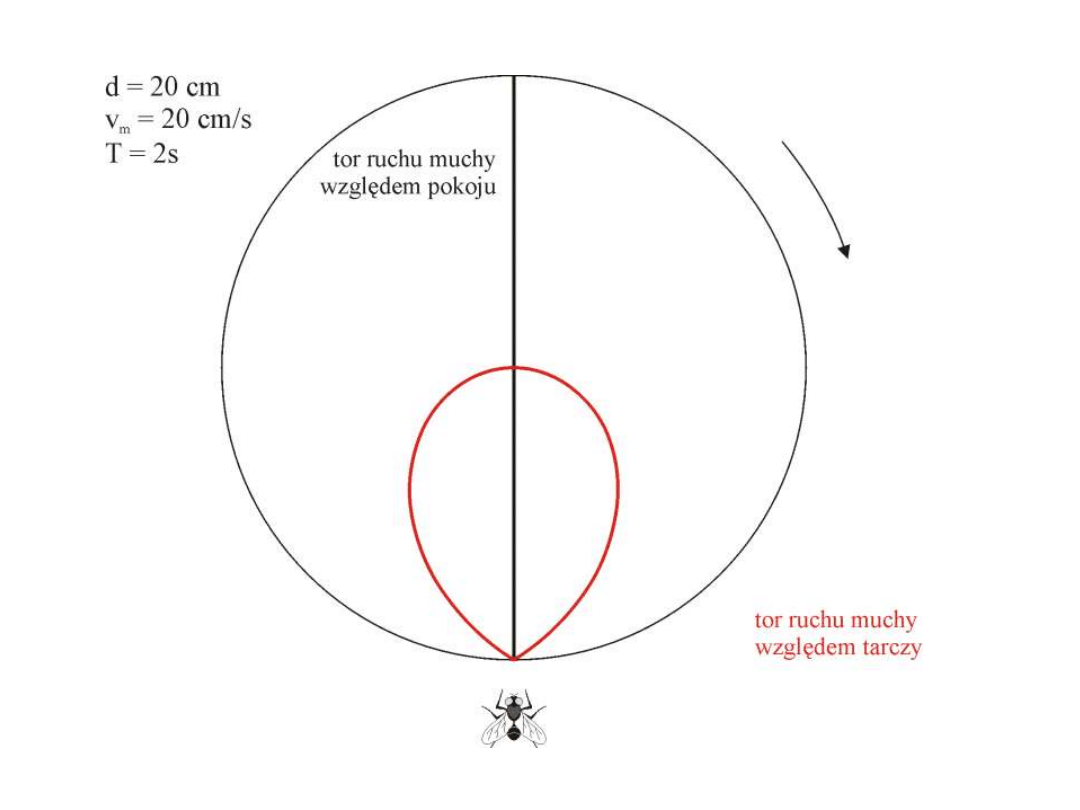
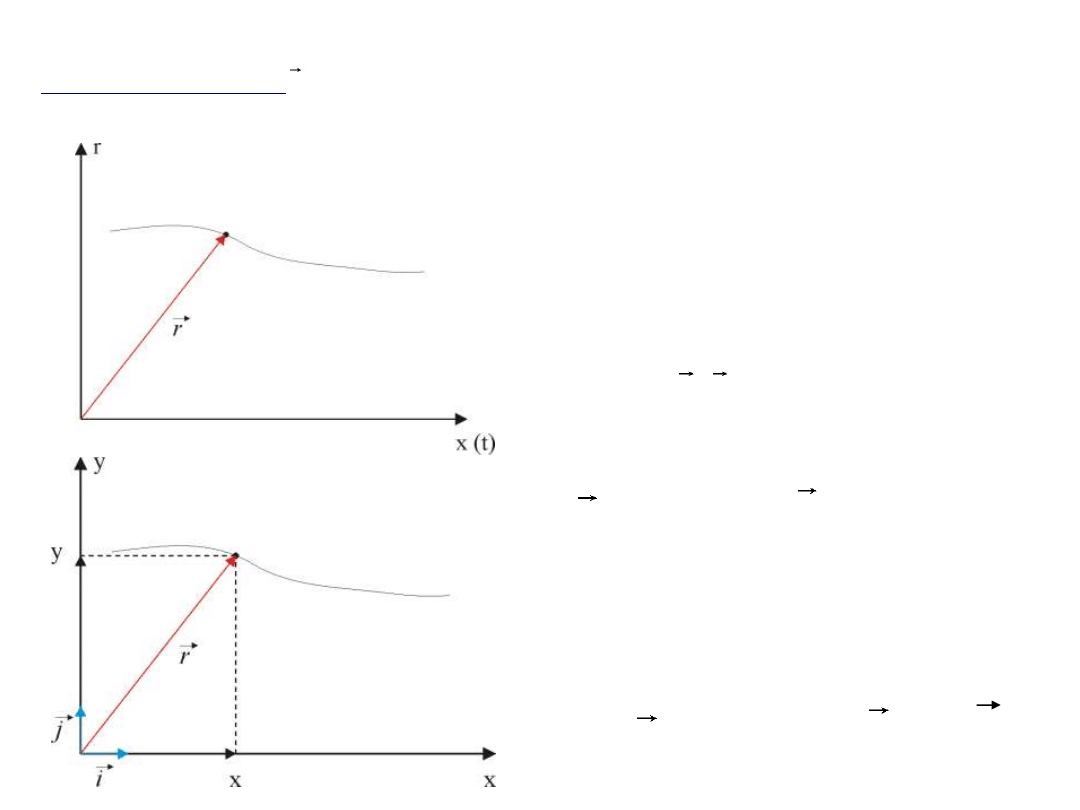
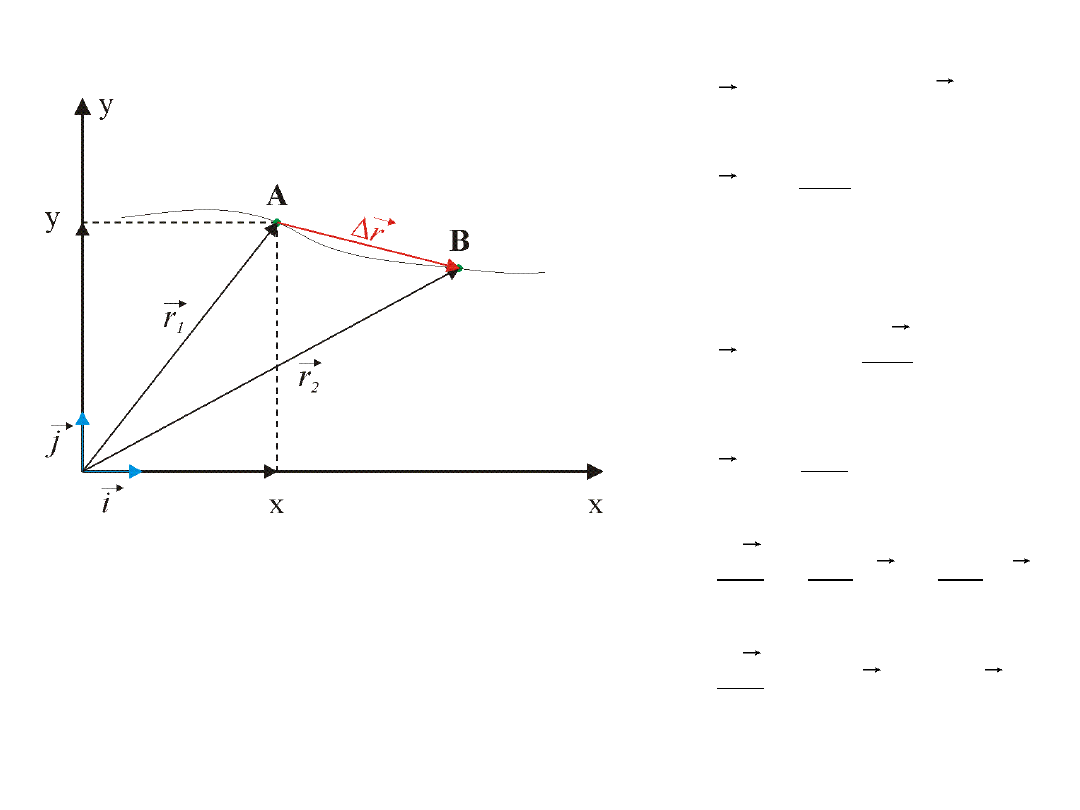
Wektor położenia - wektor, którego początek znajduje się w początku
układu współrzędnych, a koniec w punkcie położenia ciała w danej chwili.

r

( )

r

f t



- wektory

jednostkowe

,

i j

W przestrzeni trójwymiarowej:

r

x i

y j

   

r

x i

y j k z

     

z

.

k

0

0

lim

śr

ch

t

ch

x

y

r

x i

y j

r

v

t

t

r

v

t

dr

v

dt

dr

dx

dy

i

j

dt

dt

dt

dr

v i

v

j

dt



   



















 





 



t



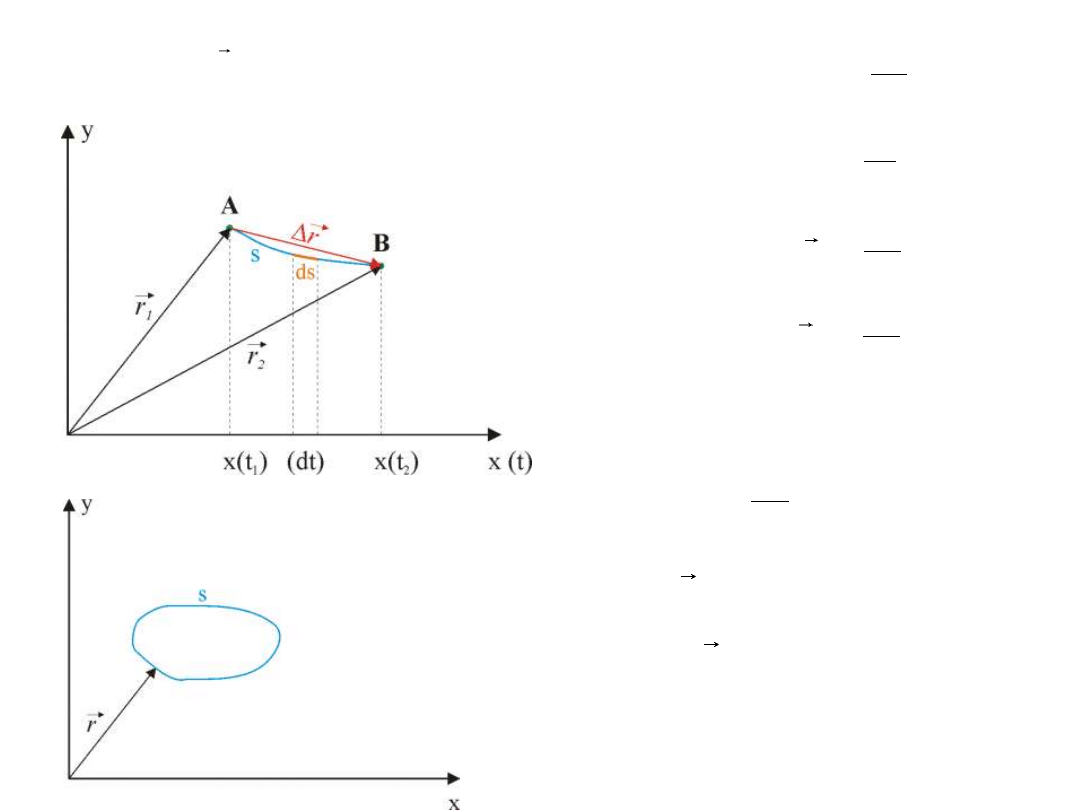
Przemieszczenie - wielkość wektorowa
Droga

s

– wielkość skalarna (długość toru)

r



Szybkość średnia:


Szybkość chwilowa:


Prędkość średnia:


Prędkość chwilowa:

śr

s

v

t





0

0

śr

śr

s

v

t

v

r







 

ch

ds

v

dt



śr

r

v

t







śr

dr

v

dt



ch

0

lim

ch

t

y

x

x

y

v

dv

a

t

dt

dv

dv

dv

a

i

j

dt

dt

dt

a a i

a j

 













 



  



śr

v

a

t







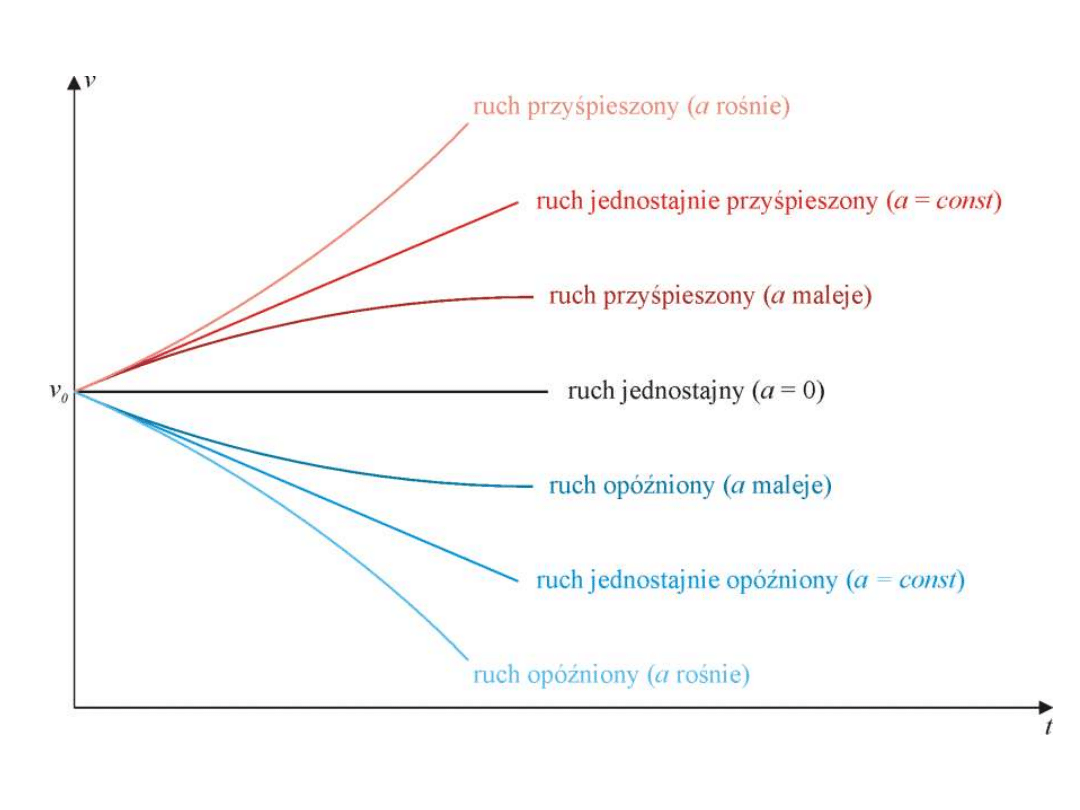
Przyśpieszenie średnie:


Przyśpieszeni chwilowe:

ch

dv

a

dt



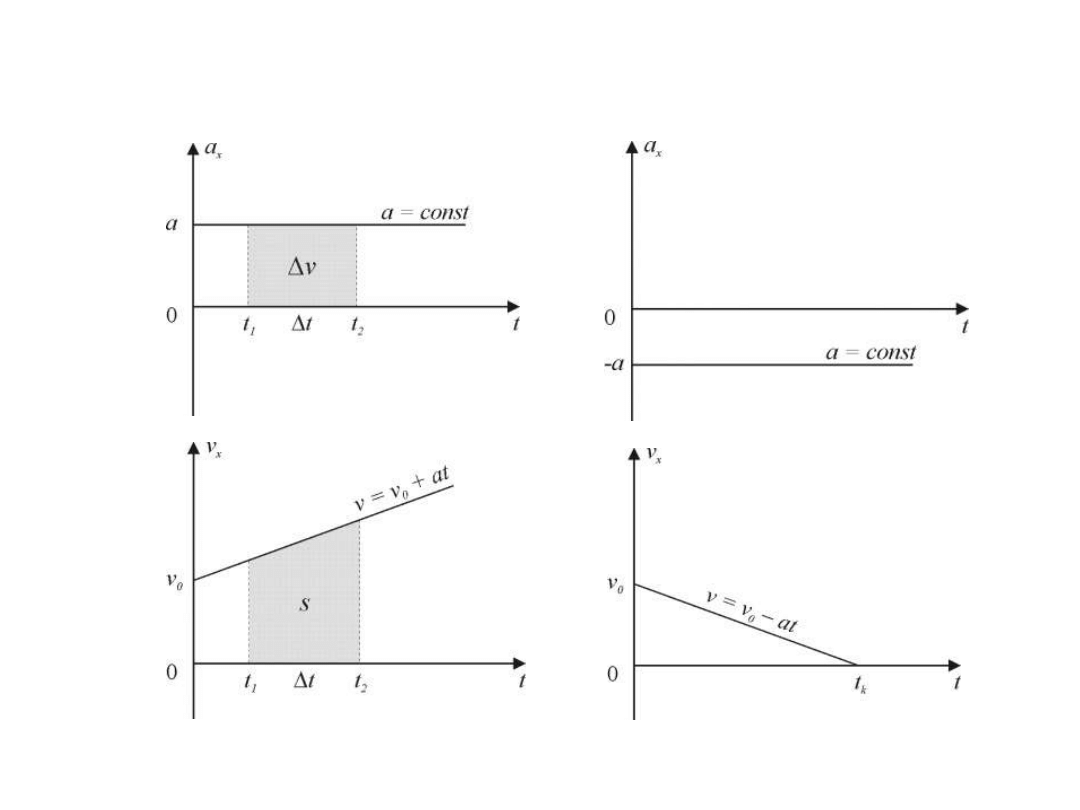
Ruch jednostajnie przyśpieszony

Ruch jednostajnie opóźniony

v=a

.

t

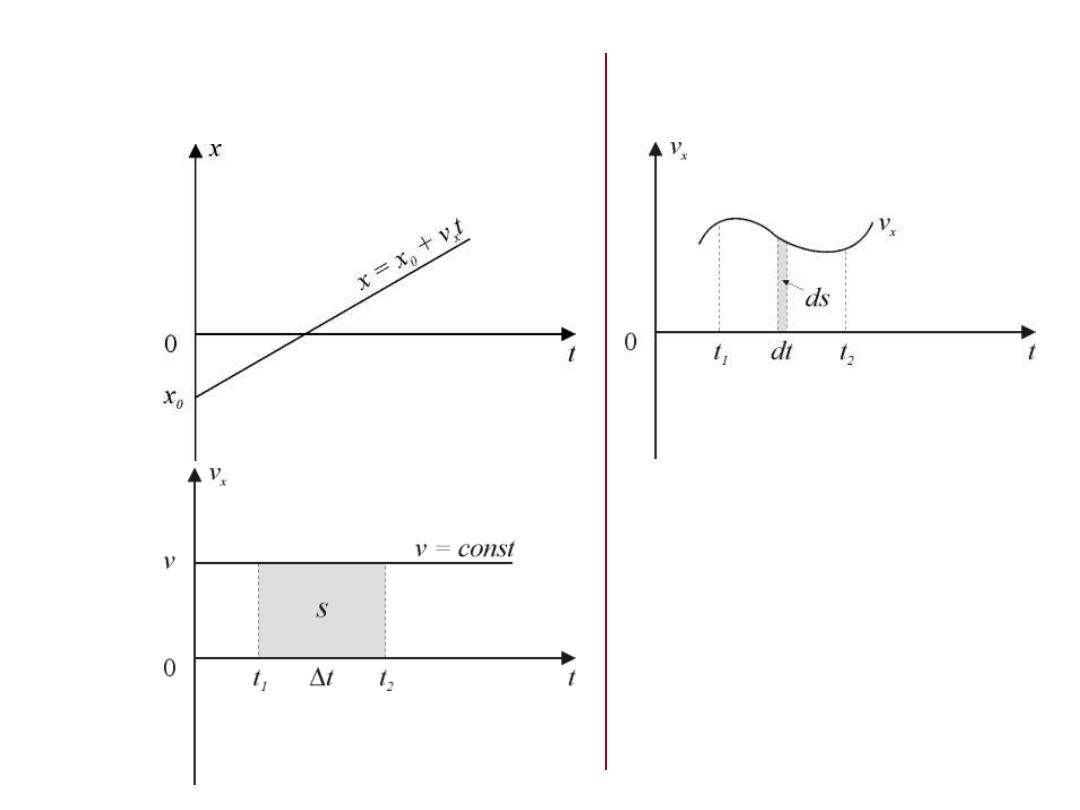
Ruch jednostajny, prostoliniowy

v=const

Ruch niejednostajny, prostoliniowy

vconst

s=v

.

t

dt

v

ds

x











2

1

t

t

x

dt

v

s

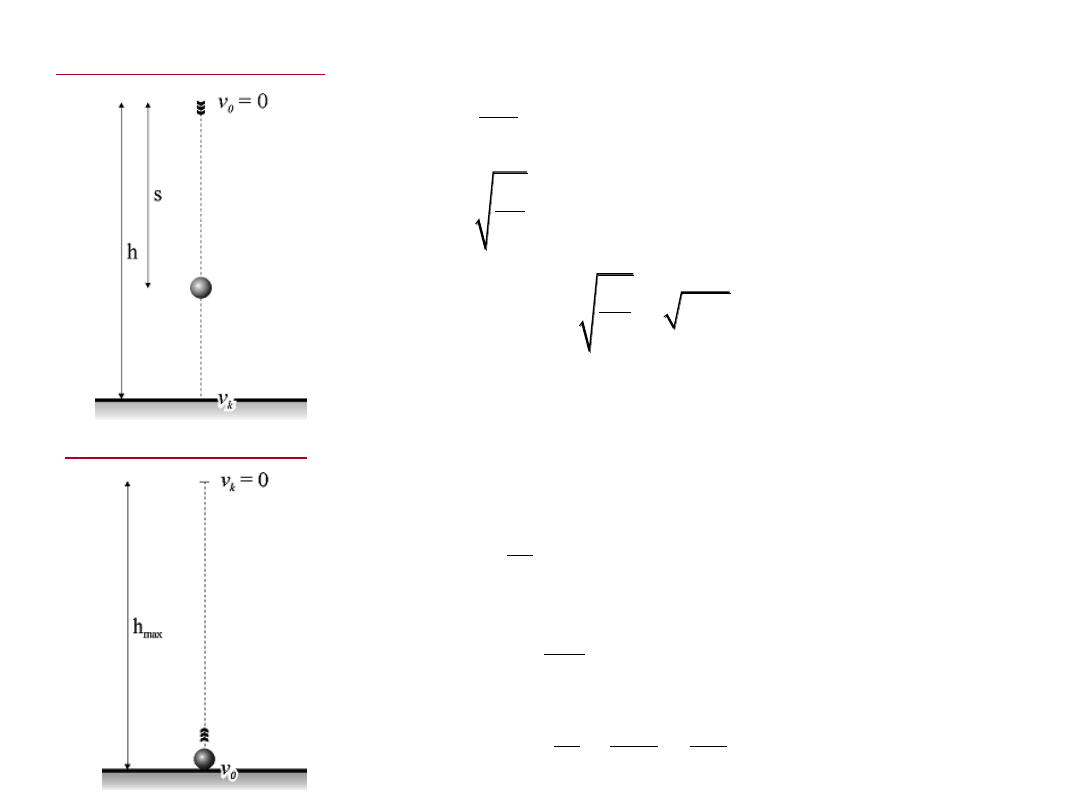
Swobodny spadek ciał

2

2

2

2

2

k

a g

gt

s

s

t

g

h

v

g t g

gh

g







  



Rzut pionowy do góry

0

0

2

0

2

2

0

0

0

max

0

2

0

2

2

2

k

wzn

wzn

a

g

v

v

gt

v

t

g

gt

s v t

v

gv

v

h

v

g

g

g

 -

 -







-

 

-



2

0

2

0

0

0

2

0

0

2

0

2

0

1

2

1

2

1

2

2

y

y

gt

y y

gt

x v t

x

t

v

x

y y

g

v

g

y y

x

v

- 



-





 



-

 

 



-

równanie paraboli

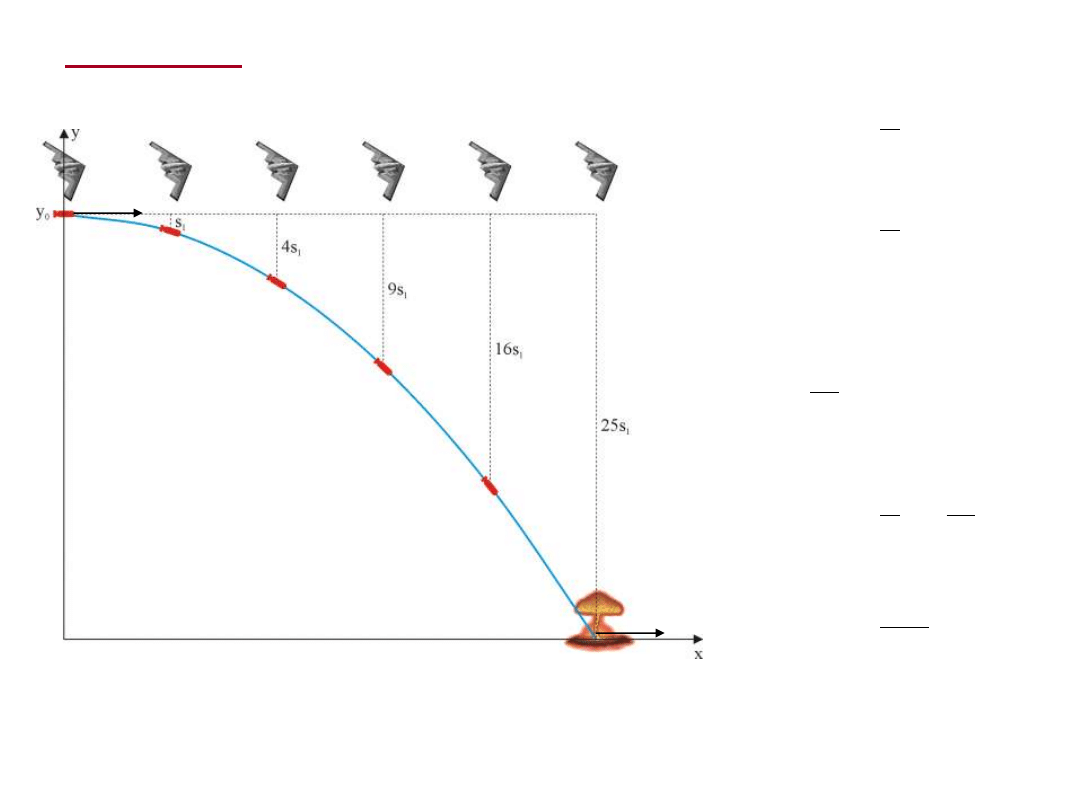
Rzut poziomy

v

0

v

0

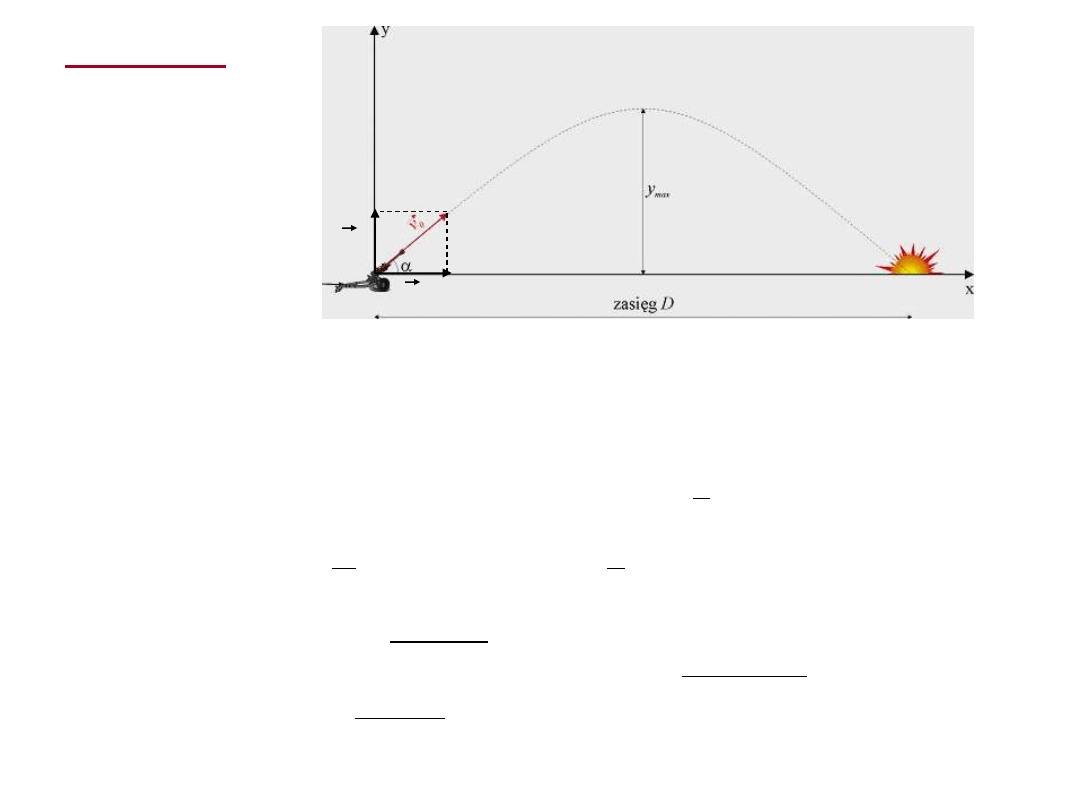
Rzut ukośny

0

0

cos
sin

ox

oy

v

v

v

v





 
 

2

0

( )

1

( )

2

x

ox

y

oy

a

x t

v t

a

g

y t

v t

gt









 -





 -

2

0

max

sin 2

(

)

4

v

D

D

g













2

2

0

max

sin

2

v

y

g





Składowe prędkości
początkowej:

Składowe przyśpieszenia:

Zasięg:

Wzniesienie maksymalne:

Czas trwania ruchu:

0

2 sin

v

t

g





równanie paraboli

2

2

2

0

tg

2 cos

g

y

x

x

v





 -

 



v

0y

v

0

x

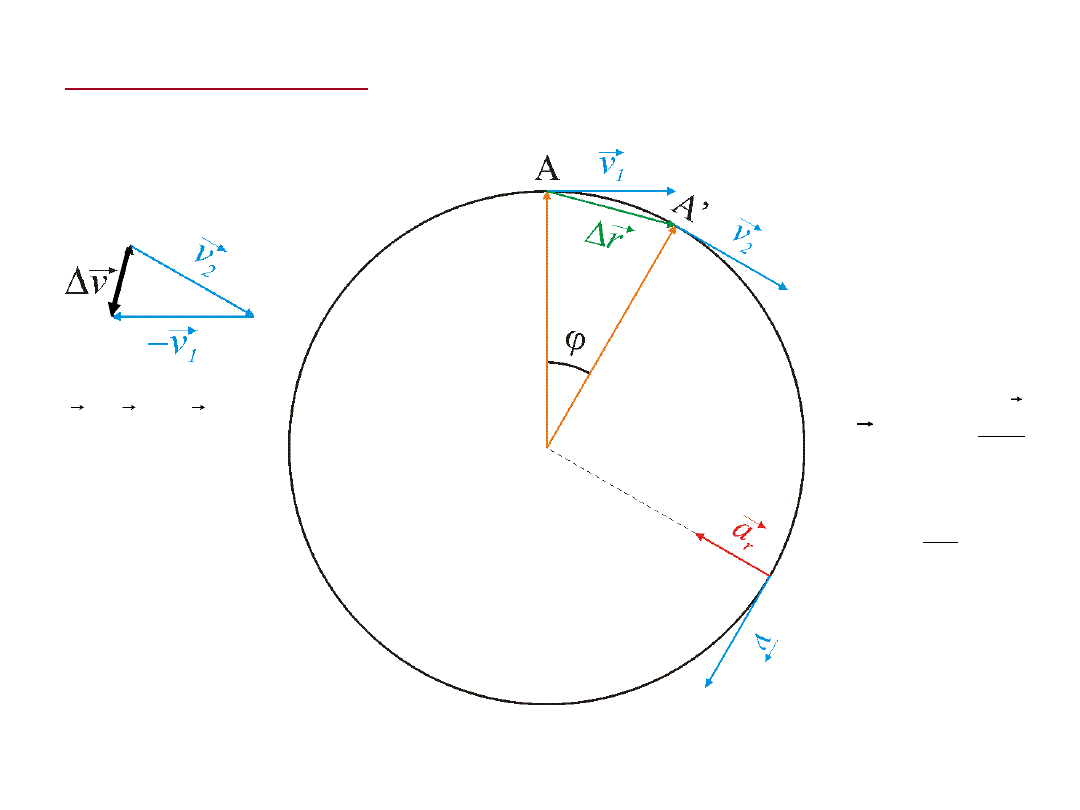
Ruch jednostajny po okręgu

2

1

v v

v

-  

1

2

v

v

v const





0

2

lim

r

t

r

v

a

t

v

a

t

 









r

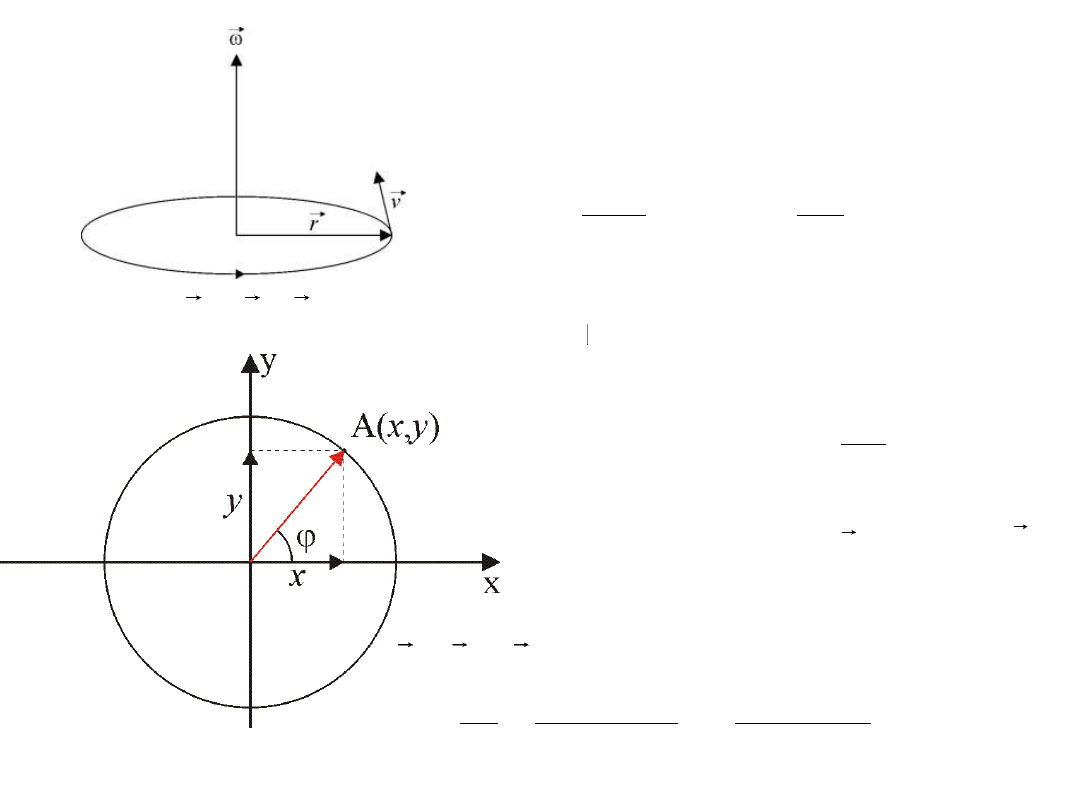
v

r

w

 

v – prędkość liniowa

w – prędkość kątowa
T - okres

2

2

r

v

T

T

v

r





w

w







t

t

d

dt

d

dt



 w

 w



w







cos

sin

x r

r

x i

y j

y r







   



( cos )

(cos

)

sin

cos

x

y

x

y

v

v

v

dx

d r

d

t

v

r

r

t

dt

dt

dt

v

r

t



w

w

w

w

w











 -



~

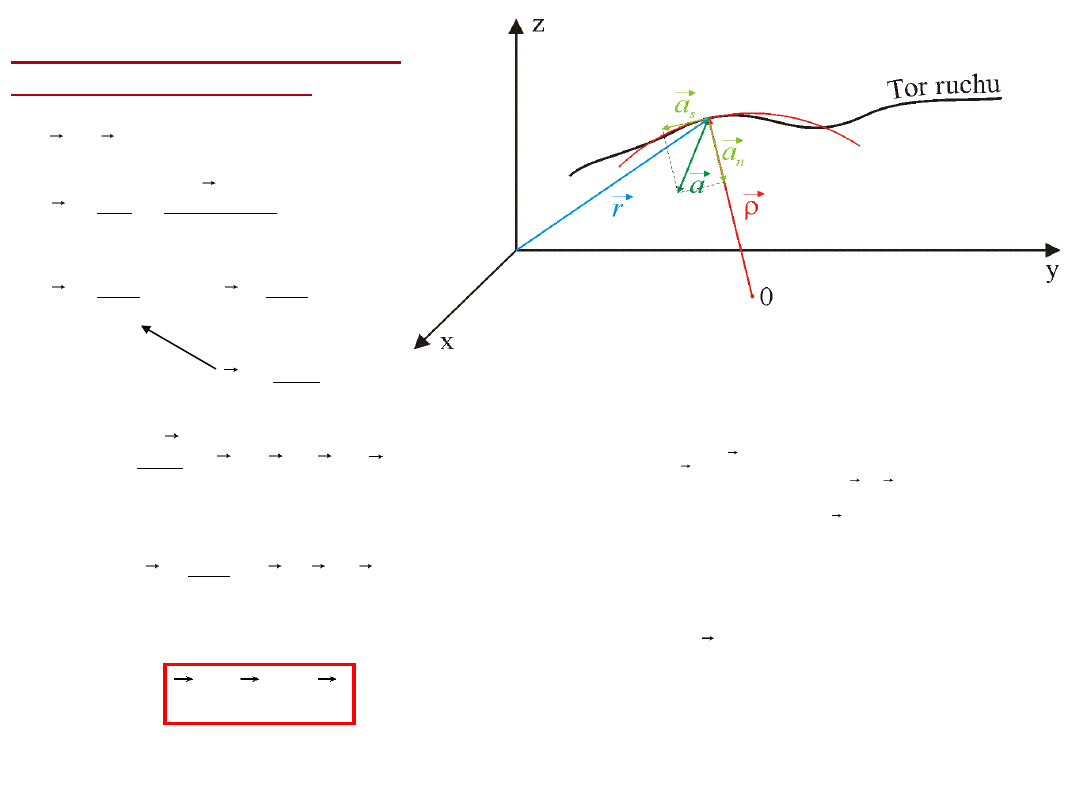
Przyśpieszenie styczne i normalne
w ruchu krzywoliniowym

(

)

v

dv

d

a

dt

dt

d

d

a

dt

dt

w 

w 

w



 w

 









  

d

dt

w

e



s

d

a

dt

w  e 

   

e

w



e 



v

n

d

v a

dt



w

w



  

przyśpieszenie
kątowe

przyśpieszenie
styczne

kierunek i jest do
płaszczyzny ruchu, więc
ma ten sam kierunek co

przyśpieszenie
normalne

leży w płaszczyźnie
ruchu i ma ten sam
kierunek co promień
krzywizny , a zwrot
zawsze przeciwny



s

n

a a

a

 

Przyśpieszenie dośrodkowe w ruchu po okręgu

2

2

2

(

)

(

)

(

)

0, gdyż

n

n

n

n

n

r

a

v

r

a

r

r

r

r

a

r

v

a

a

r

v

r



w

w w

w w

w w

w

w

w

w

w



   



 

 - 



 



 -











)

(

)

(

)

(

b

a

c

c

a

b

c

b

a























-











przyspieszenie dośrodkowe