1

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

1

transport masy

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

2

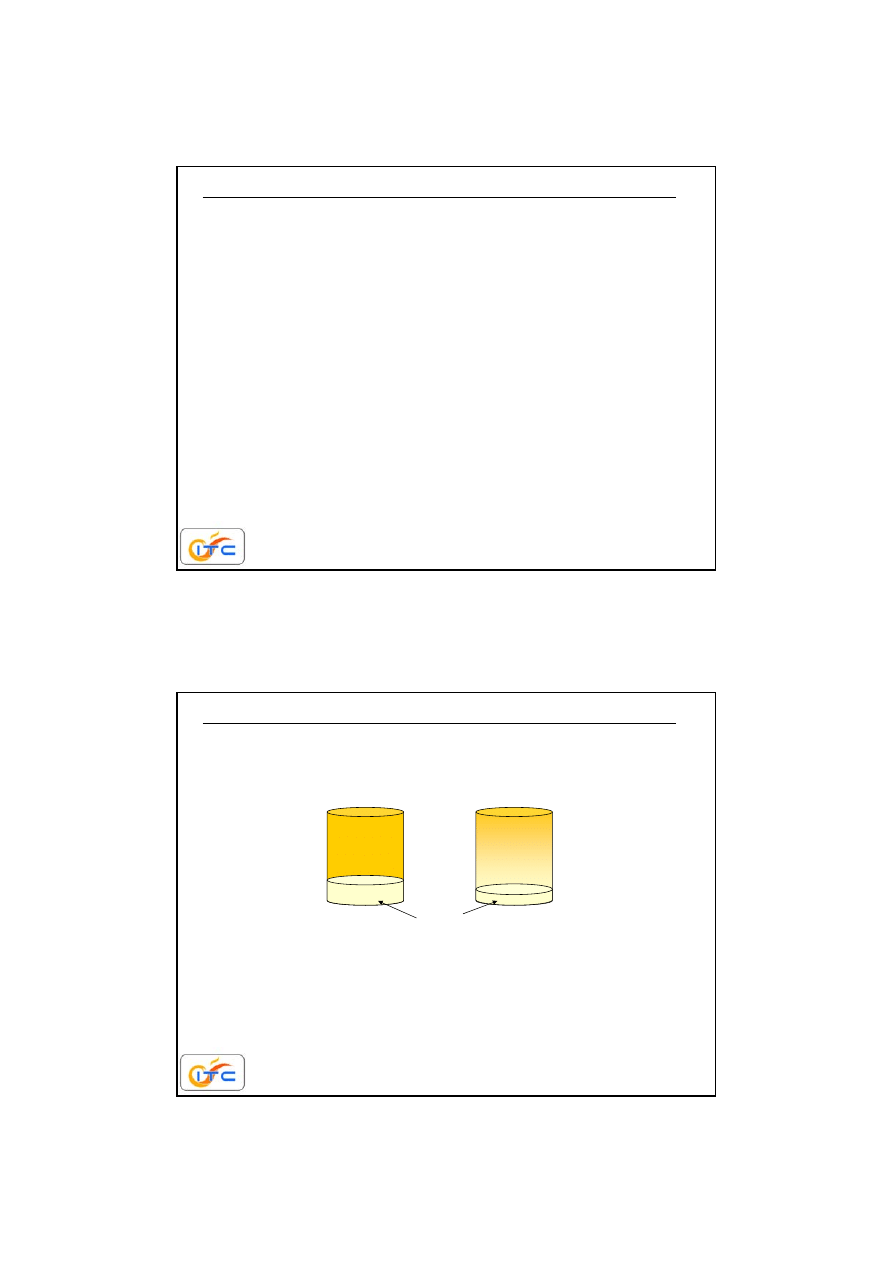
herbata

herbata
z cukrem

dyfuzja jest samorzutnym, nieodwracalnym procesem mieszania

wywołanym różnicą stężeń

natura dąży do wyrównania istniejących różnic stężeń. Proces
odwrotny wymaga nakładu pracy. Proces dyfuzji jest w wielu
aspektach

podobny do transportu ciepła

. Opis dyfuzji będzie

bazować na wykorzystaniu istniejących analogii

cukier

2

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

3

różne rodzaje dyfuzji

Transport masy może być wywołany przez

• różnicę stężeń

-

zwykła dyfuzja

(w skrócie

dyfuzja

)

• różnicę ciśnień

–

dyfuzja ciśnieniowa

istotna tylko przy bardzo dużych

różnicach ciśnień np. w ultrawirówkach przy separacji izotopów

•

siły inne niż różnica ciśnień- dyfuzja wymuszona.

Np. ruch

cząstek naładowanych lub namagnesowanych w polu elektromagnetycznym

•

gradient temperatury-termodyfuzja

(efekt Soreta)

Dyfuzja w porach o rozmiarach mniejszych niż średnia droga swobodna
cząsteczki –

dyfuzja Knudsena

Dyfuzja w porach o rozmiarach porównywalnych z rozmiarami cząsteczki –

dyfuzja powierzchniowa

, zaadsorbowane cząsteczki poruszają się wzdłuż

ścian porów
Ruch cząstek o wymiarach poniżej 1

m (sadza, mgła) -

ruchy Browna

na ogół efekty te są pomijalne.
W ramach tego kursu nie będą omawiane

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

4

wektor strumienia masy i-tego składnika kg/m

2

s





dSd

dm

i

i

j

i

m

masa i-tego składnika wyrażona w kg

S

powierzchnia

analogiem wektora gęstości strumienia ciepła

q

jest wektor

gęstości strumienia masy

j



czas

i

im

i

im

i

w

D

D

















j

analogiem prawa Fouriera jest prawo Ficka

im

D

współczynnik dyfuzji i-tego składnika przez mieszaninę
innych składników. m

2

/s

i



gęstość i-tego składnika kg/m

3

V

m

i

i

/





V

objętość

System oparty na kilogramie

masę można wyrażać w kg lub kmol.

i

w

ułamek masowy i-tego składnika



gęstość mieszaniny kg/m

3

3

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

5

wektor strumienia masy i-tego składnika kmol/m

2

s





dSd

dn

i

i

J

i

n

masa i-tego składnika wyrażona w kmol

S

powierzchnia

analogiem wektora gęstości strumienia ciepła

q

jest wektor

gęstości strumienia masy

J



czas

i

im

i

im

i

y

cD

c

D













J

analogiem prawa Fouriera jest prawo Ficka

im

D

współczynnik dyfuzji i-tego składnika przez mieszaninę
innych składników. m

2

/s

i

c

koncentracja molowa i-tego składnika kmol/m

3

V

n

c

i

i

/



V

objętość

System oparty na kilomolu

i

y

ułamek molowy i-tego składnika

c

gęstość molowa (koncentracja) mieszaniny kmol/m

3

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

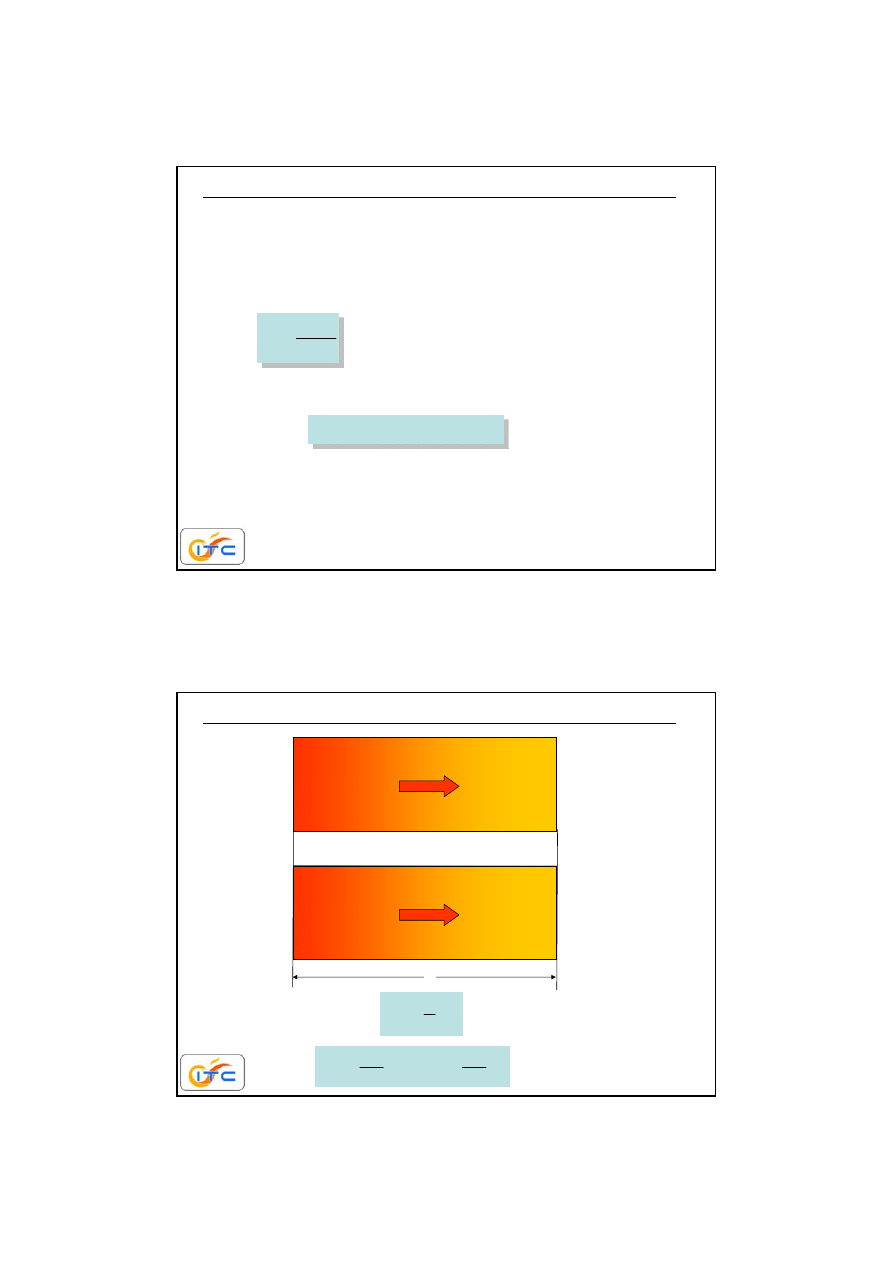
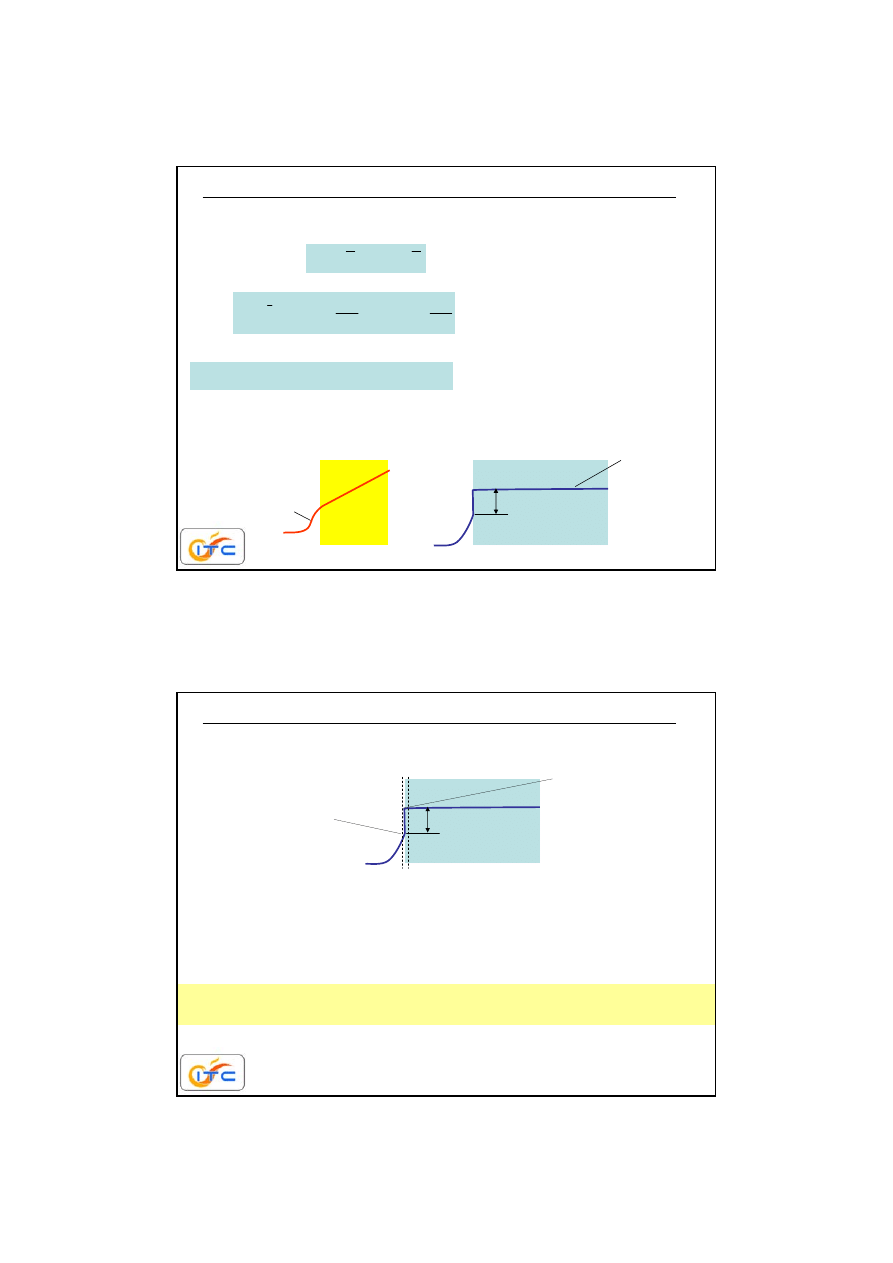
6

przewodzenie
ciepła

T

L

=90

0

C

T

r

=10

0

C

strumień ciepła

T

S

S

Q









 q

w

L

=90

%

w

r

=10

%

strumień masy
i-tego składnika

i

im

i

i

SD

S

m









 j

Q

S

T









im

im

i

i

i

i

D

D

m

S

n

S

c













przewodzenie
ciepła

dyfuzja masy



dyfuzja
masy

4

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

7

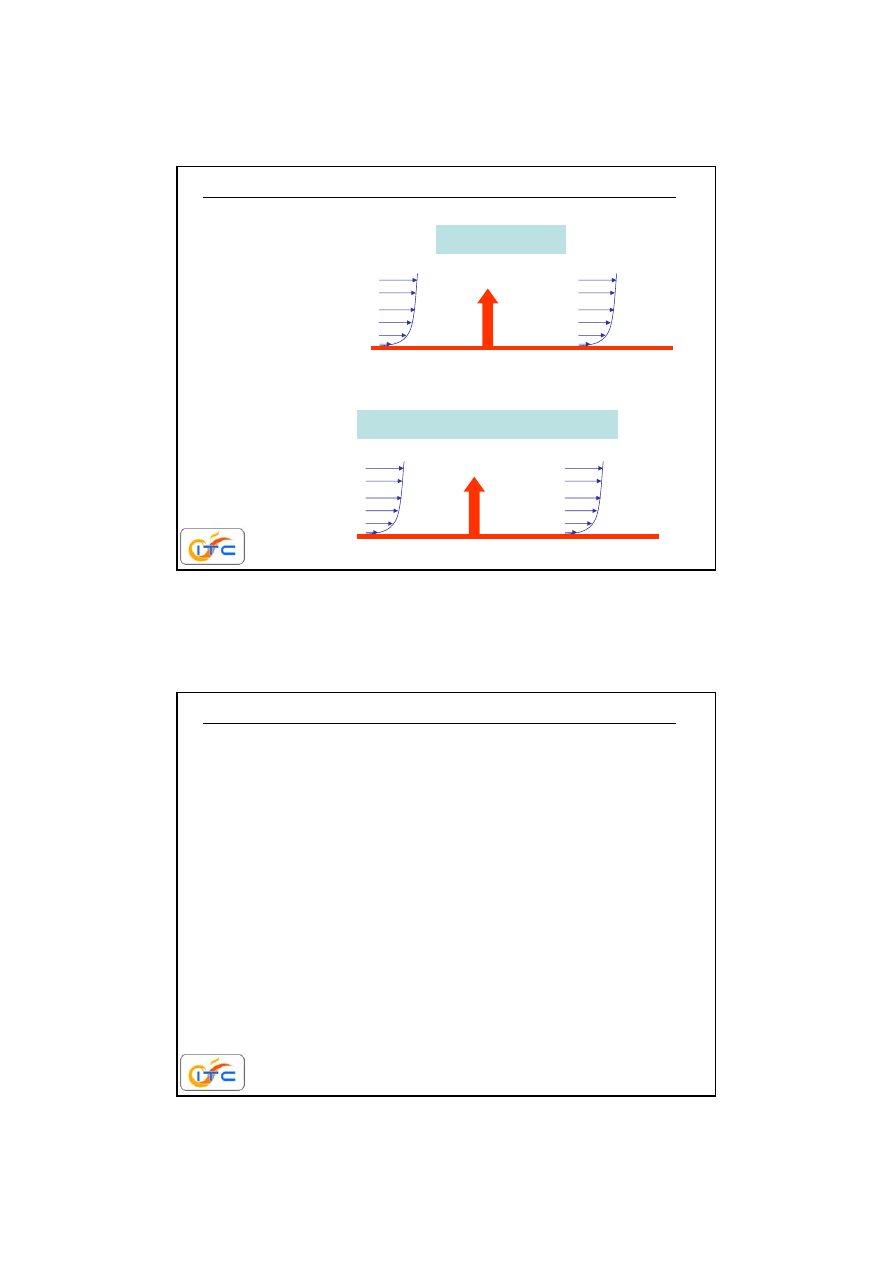
konwekcyjny transport ciepła

konwekcyjny
strumień ciepła

)

(









T

T

S

Q

w

C

T

w

0

100



C

T

0

10





konwekcyjny
strumień masy

)

(

)

(





















y

y

S

S

m

w

w

i

100%

w

y



%

10





y

gaz

powierzchnia
cieczy

gaz

konwekcyjny transport masy



warstwa
przyścienna

warstwa
przyścienna

ścianka

współczynnik
wnikania ciepła
W/m

2

K



współczynnik
wnikania masy
m/s

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

8

radiacyjny transport ciepła

brak odpowiednika w transporcie masy

5

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

9

Równanie transportu masy w poruszającym się płynie

’

’





n’

J

i

R

i

'

'd '

d '

dif

i

i

i

n

J







 

 











J n

strumień masy i-tego składnika transportowany przez dyfuzję

d

gen

i

i

n

R













d

acc

i

i

n

c

























J

i

–

wektor gęstości strumienia masy

, kmol/m

2

s, J

i

-

składowa normalna

R

i

– wydajność reakcji chemicznych

tworzących i-ty składnik kmol/s m

3

prędkość tworzenie i-tego składnika na skutek reakcji

'

'd '

d '

adv

i

i

i

n

c

c







 

 













v n

strumień masy i-tego składnika transportowany przez adwekcję

prędkość akumulacji masy w objętości kontrolnej

'

i

i

J

 

J n

v

–

wektor prędkości płynu

, m/s -



składowa normalna

'

 

v n



transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

10

bilans masy

acc

dif

adv

gen

i

i

i

i

n

n

n

n











'

'

'

'

'

'

'

'

i

i

i

Jd

c d

R d

d

c













 

  

 













wprowadzając definicję strumieni

zamieniając całki powierzchniowe na objętościowe (tw. Gaussa o dywergencji)

'

(

)

'

0

i

i

i

i

c

R

d

c









  

 

 













J

v

słuszne dla dowolnej objętości kontrolnej, tylko wtedy gdy

(

)

i

i

i

i

c

R

c



  







J

v

wstawiając prawo Fick’a

[

]

(

)

i

im

i

i

i

D

c

c

R

c





  







v

prawo zachowania masy
i-tego składnika

i

im

i

D

c

 



J

6

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

11

2

2

2

2

2

2

(

)

(

)

(

)

i

i

y

i x

i z

i

i

i

im

i

c v

c v

c v

c

c

c

D

R

x

y

z

x

y

z

c























































w współrzędnych kartezjańskich przy stałym współczynniku dyfuzji

dla nieruchomego ośrodka i stałego wsp. dyfuzji

2

2

2

2

2

2

i

i

i

i

im

i

c

c

c

D

R

x

y

z

c





































dla nieruchomego ośrodka, stałego wsp. dyfuzji i braku reakcji chemicznych

2

2

2

2

2

2

i

i

i

i

im

c

c

c

D

x

y

z

c



































dla nieruchomego ośrodka, stałego wsp. dyfuzji, braku reakcji chemicznych i 1D

2

2

i

i

im

c

D

x

c











dla nieruchomego ośrodka, stałego wsp. dyfuzji, braku reakcji chemicznych, 1D

i stanu ustalonego

2

2

d

0

d

i

c

x



transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

12

reakcje chemiczne – źródło substancji i-tego składnika

1

j

j

R

k c



1

i

k

j

R

k c c



1

1

r

i

i

j

R

k c

k c

 



1

1

r

i

k l

i

j

R

k c c

k c c





i

j



k

j

i

 

i

j



k

l

i

j







2

1

i

j

R

k c



2 j

i



przykładowe równanie reakcji

równanie kinetyki reakcji tworzenia produktu

składnik i bierze udział w jednej reakcji

1

1

i

i

R

k c

 

1

2

1

i

k

R

k c



1

1

1

r

i

i

j

R

k c

k c

 



i

j



i

j



1

2

1

i

i

R

k c

 

2i

j



przykładowe równania reakcji

równania kinetyki reakcji

składnik i bierze udział w dwu reakcjach

i

j

k

 

i

j

k

l







k

i



i

j

k

 

2

2

i

i

j

R

k c c

 

2

2

2

r

i

i

j

k l

R

k c c

k c c





2k

i



2

2

2

r

i

k

i

R

k c

k c





2

2

2

r

i

i

j

k

R

k c c

k c

 



źródło jest sumą równań kinetycznych każdej z reakcji

w której bierze udział i-ty składnik

1

M

m

i

i

m

R

R







m

kolejny numer reakcji w której bierze udział i-ty składnik

M

liczba takich reakcji

7

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

13

uwaga 1:

równanie reakcji nie musi odpowiadać równaniu kinetyki.

Często wzory opisujące kinetykę wyznacza się empirycznie.
W procesach biochemicznych często występuje równanie

uwaga 2:

stałe reakcji odwracalnych są powiązane przez równowagę chemiczną.

Np. dla

1

1

r

i

k l

i

j

R

k c c

k c c





1

1

r

k l

i

j

k c c

k c c



w stanie równowagi sumaryczna prędkość reakcji jest zerowa

1

1

r

k

K k



ponieważ

i

j

k l

c c

K

c c



stała równowagi chemicznej

1

2

1

i

i

i

k c

R

k c

 



Michaelisa-Mentena

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

14

transport masy na drodze dyfuzji może występować w gazie,

cieczy lub ciele stałym

Wartości współczynników dyfuzji otrzymuje się

eksperymentalnie

•gaz przez gaz – rząd 10

-5

m

2

/s

są wzory teoretyczne

•ciecz przez ciecz – rząd 10

-9

m

2

/s

•gaz przez ciało stałe – rząd od 10

-10

do 10

-25

m

2

/s

współczynniki zależą silnie od temperatury i
ciśnienia – dla gazów

p

T

D

ij

/

2

/

3



dla cieczy i ciał stałych rosną z temperaturą
np. wsp. dyfuzji węgla w stali przy wzroście temperatury
z 500 do 1000C rośnie 6000 razy.

8

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

15

warunki brzegowe

• zadane stężenie 1-go rodzaju (Dirichlet)

• zadana składowa normalna gęstości strumienia masy

2-go rodzaju (Neumann)

warunek konwekcyjny 3-go rodzaju (Robin)

i

i

i

i

c

c

y

y





dn

dc

D

J

dn

dy

D

j

j

i

im

i

i

im

i

i











)

(

)

(

















c

c

J

y

y

j

w

i

w

i

temperatura na powierzchni brzegowej jest funkcją ciągłą,

stężenie najczęściej doznaje skoku na powierzchni międzyfazowej

gaz

ścianka

temperatura

ułamek
masowy H

2

0

(w fazie
ciekłej
y

h20

=1)

woda

powietrze

skok stężenia

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

16

powietrze
p=92kPa
T=15C

skok stężenia

definiując zadane stężenie brzegowe,

trzeba dodatkowo podać której z faz dotyczy

0185

.

0

,

powietrze

2



O

H

y

1

,

woda

2



O

H

y

woda
T=15C

wartości stężeń po obu stronach powierzchni międzyfazowej

związane są przez warunek równowagi termodynamicznej

warunek 1 rodzaju (Dirichleta)

9

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

17

odparowanie cieczy – krzywa nasycenia

)

(

,

,

gaz

gaz

T

f

y

p

p

i

i







absorpcja gazu w cieczy

ciecz

gaz

gaz

,

,

,

i

i

i

Hy

y

p

p







H

stała Henry’ego wyrażona w paskalach zależy praktycznie tylko od temperatury

duży zbiór wartości stałej Henry’ego dostępny jest w sieci www.henrys-law.org

Prawo Henry’ego - małe stężenia (gazy słabo rozpuszczalne w cieczach)

Prawo Raoulta - duże stężenia (gazy dobrze rozpuszczalne w cieczach
np. amoniak w wodzie)

)

(

,

,

,

ciecz

gaz

gaz

T

p

y

y

p

p

si

i

i

i







p

si

ciśnienie nasycenia i-tego składnika

sublimacja ciała stałego – krzywa nasycenia

)

(

,

,

gaz

gaz

T

f

y

p

p

i

i







transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

18

gaz

stale

cialo

,

,

i

i

p

c







dyfuzja gazu przez ciało stałe



rozpuszczalność kmol/m

3

Pa

dyfuzja cieczy przez ciało stałe

ciecz

stale

cialo

,

,

i

i

c

c









stała równowagi rozpuszczania (bezwymiarowa)

rozpuszczanie ciała stałego w cieczy

ciecz

,

( )

i

T



 



rozpuszczalność kg/m

3

Uwaga: stałe równowagi występujące w tych równaniach np. stała
Henry’ego, rozpuszczalność mogą być wyrażane w innych jednostkach

ciecz

gaz

,

ciecz

gaz

,

ciecz

gaz

,

,

,

,

i

yc

i

i

cc

i

i

yy

i

c

H

y

c

H

c

y

H

y







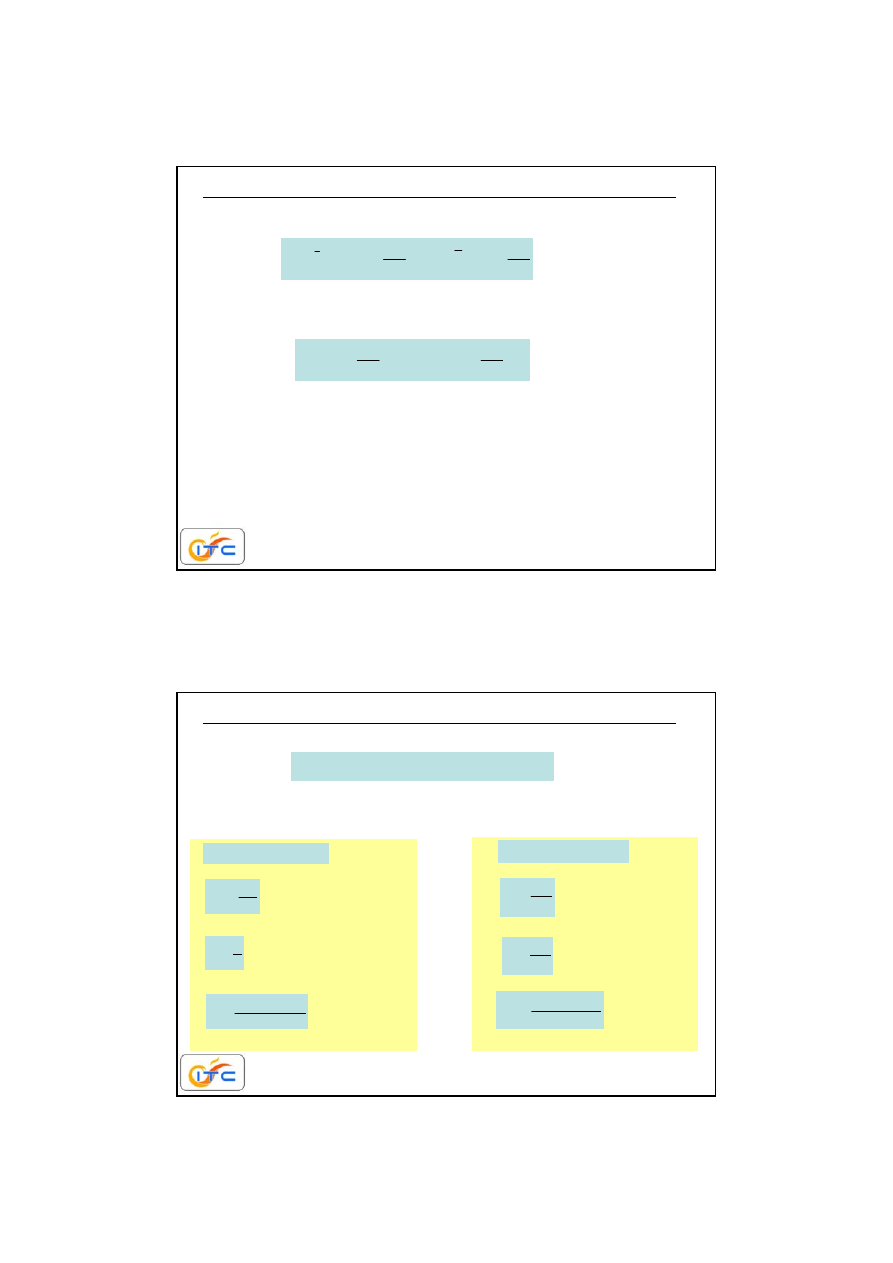
cialo stale

gaz

,cialo stale

gaz

,

,

,

cc

yc

i

i

i

i

c

c

y

c

  

 

10

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

19

warunek 2 rodzaju (Neumanna)

najczęściej warunek nieprzepuszczalności ścianki

dn

dc

D

J

J

dn

dy

D

j

j

i

im

i

i

i

im

i

i













0

0

0

0













dn

dc

J

dn

dy

j

i

i

i

i

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

20

warunek 3 rodzaju (Robina)

)

(

)

(

















c

c

J

y

y

j

w

i

w

i

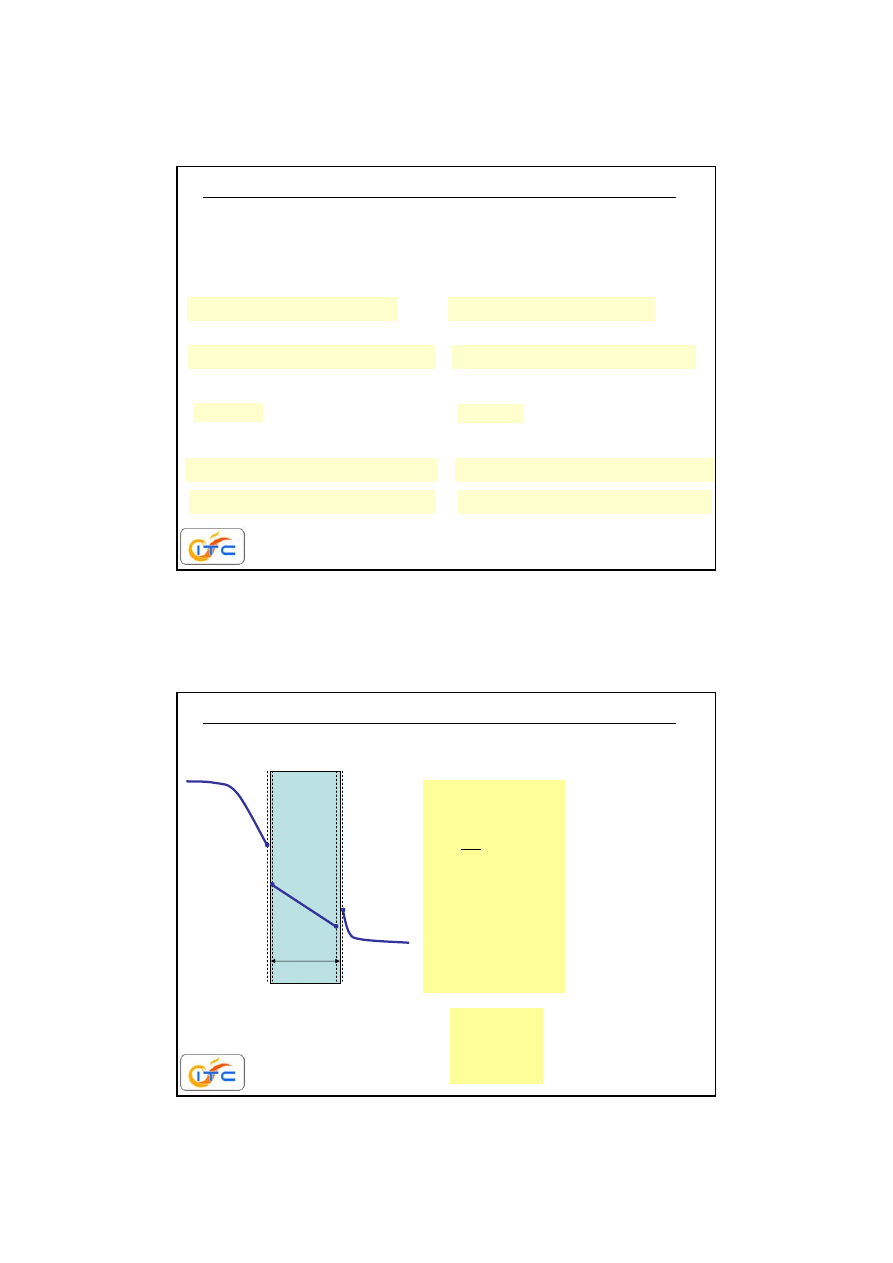
wartość współczynnika wnikania masy



otrzymuje się z równań

kryterialnych analogicznych do równań występujących w konwekcyjnym
transporcie ciepła

)

Gr

Pr,

(Re,

Nu

f



)

Gr

,

Sc

(Re,

Sh

m

f









L

Nu

im

D

L





Sh

liczba Sherwooda

a





Pr

im

D





Sc

liczba Schmidta

liczba Nusselta

liczba Prandtla

2

3

)

(

Gr











L

T

T

g

s

liczba Grashofa

liczba Grashofa

2

3

m

)

(

Gr













L

g

w

 współczynnik

rozszerzalności
objętościowej

 współczynnik

wnikania masy

ruch ciepła

ruch masy

11

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

21

6

.

0

Pr

Pr

Re

664

.

0

Nu

3

/

1

5

.

0





analogia między ruchem masy i ciepła – równania kryterialne są często
(nie zawsze!) podobne. Analogia dotyczy małych strumieni dyfundującej
masy (wpływ na prędkość głównego strumienia), gładkich powierzchni

5

.

0

Sc

Sc

Re

664

.

0

Sh

3

/

1

5

.

0





przepływ laminarny wzdłuż płaskiej płyty

Re<5 10

5

160

Pr

7

.

0

Pr

Re

023

.

0

Nu

4

.

0

8

.

0







160

Sc

7

.

0

Sc

Re

023

.

0

Sh

4

.

0

8

.

0







przepływ turbulentny w rurze

Re>10

5

w pełni rozwinięty przepływ laminarny w rurze

Re<2300

66

.

3

Nu



konwekcja swobodna z pionowej ścianki

66

.

3

Sh



9

5

4

/

1

10

Pr

Gr

10

Pr)

Gr

(

59

.

0

Nu







9

m

5

4

/

1

m

10

Pr

Gr

10

)

Sc

Gr

(

59

.

0

Sh







13

9

3

/

1

10

Pr

Gr

10

Pr)

Gr

(

1

.

0

Nu







13

m

9

3

/

1

m

10

Pr

Gr

10

)

Sc

Gr

(

1

.

0

Sh







transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

22

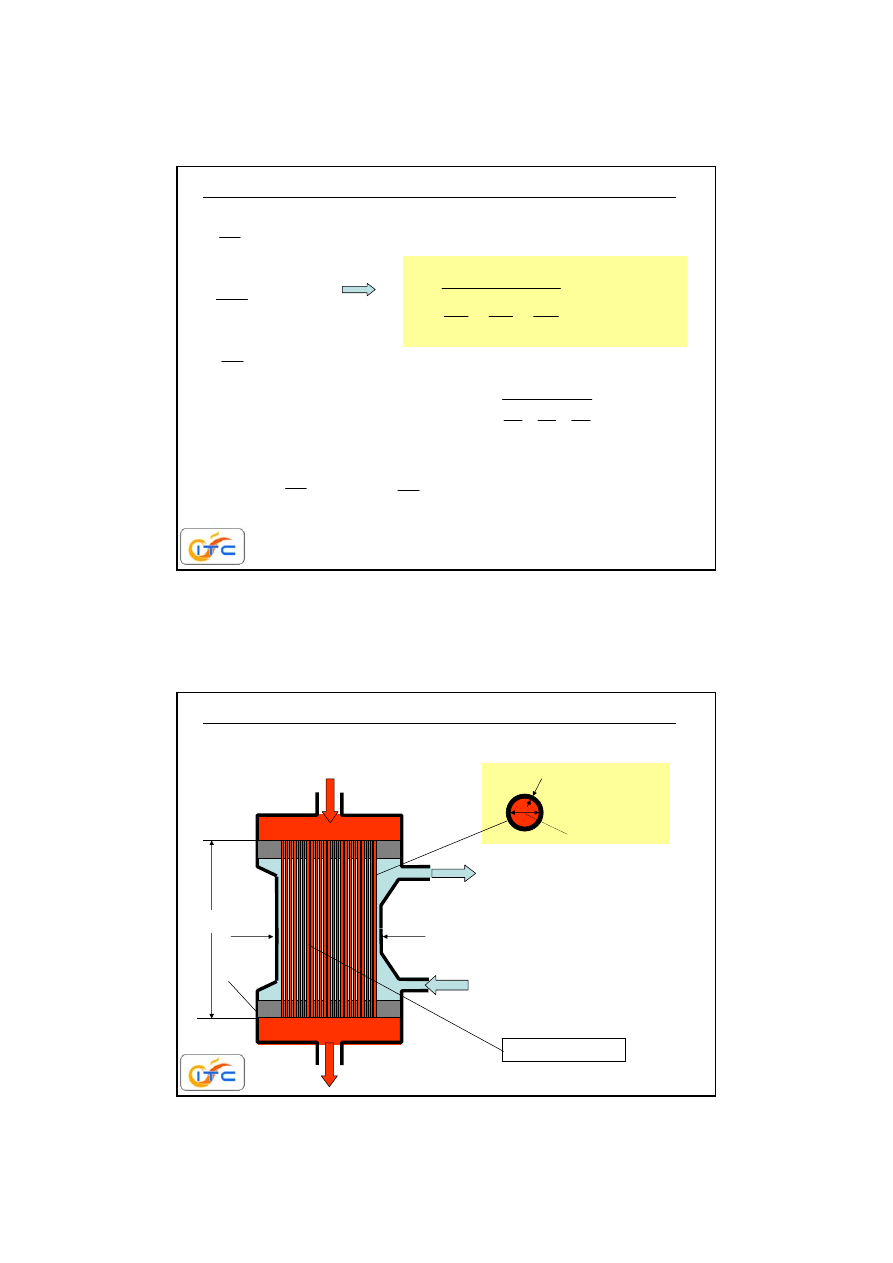
ustalone przenikanie masy przez membranę

układ ciecz-membrana-ciecz

L

c



ciecz

membrana

ciecz

L

w

c

L

m

c

R

m

c

R

w

c

R

c



L



R



)

(

L

w

L

L

c

c

J









)

(

R

m

L

m

c

c

D

J







)

(

R

R

w

R

c

c

J









wnikanie od cieczy do

membrany

dyfuzja w membranie

wnikanie z membrany

do cieczy

L

m

L

L

w

c

c





R

m

R

R

w

c

c





warunki równowagi

na obu brzegach

membrany

L

m

L

w

c

c





R

m

R

w

c

c





w biotechnologii ciecz po

obu stronach membrany

zwykle zbliżona do wody,

stałe równowagi

praktycznie te same



dla uproszczenia zapisu opuszczono

indeks transportowanego czynnika

12

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

23

L

w

L

L

c

c

J









L

R

w

w

J

c

c

D







R

R

w

R

c

c

J









)

(

1

1

R

L

m

R

L

R

L

c

c

k

D

c

c

J



























R

L

m

D

k













1

1

1

sumowanie oporów transportu masy –

analogicznie jak w ruchu ciepła

współczynnik przenikania masy

L

L

L

w

J

c

c









wartości stężeń na brzegach membrany





/

L

w

L

m

c

c

R

R

R

w

J

c

c













/

R

w

R

m

c

c

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

24

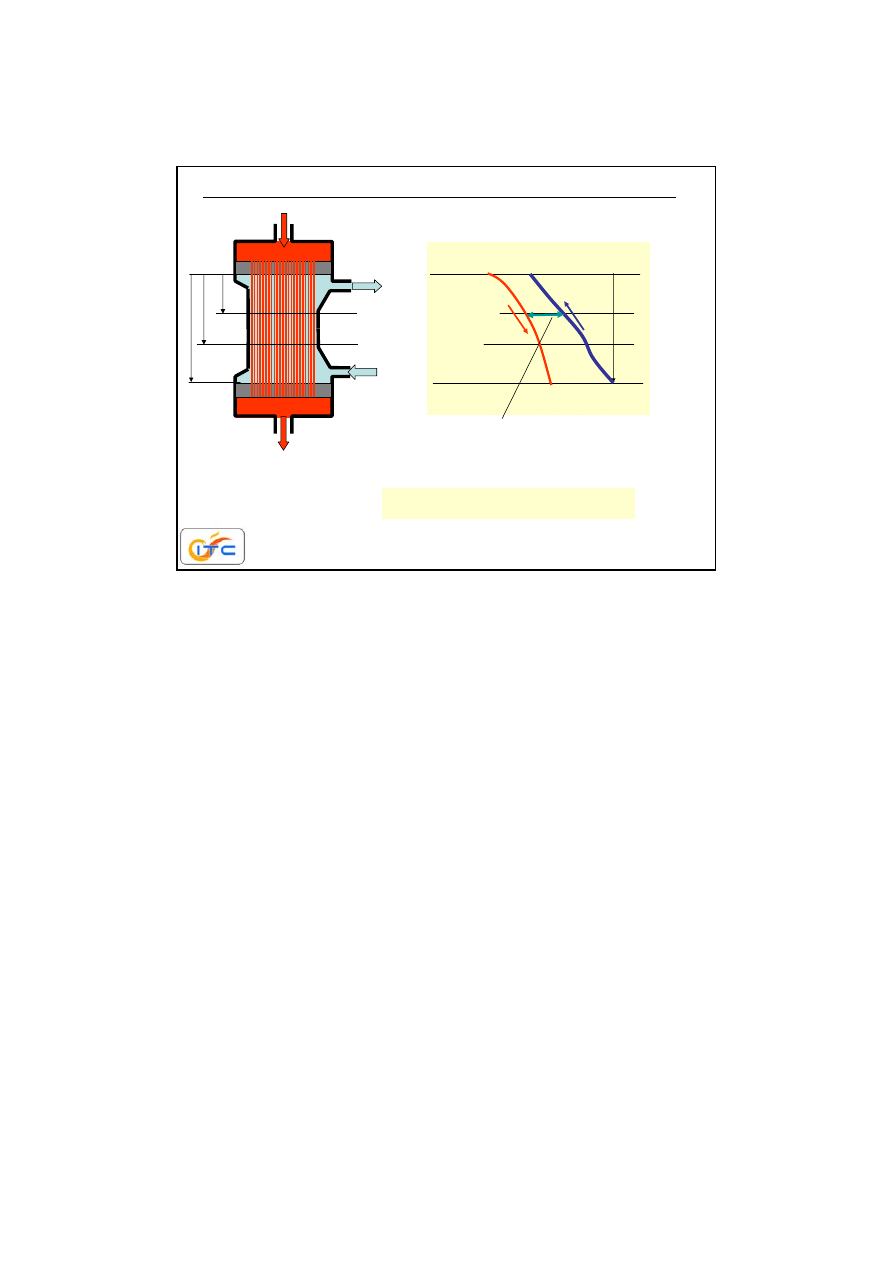
sztuczna nerka

krew +

metabolity

krew oczyszczona

dializat

(woda+sole)

dializat

(woda+sole+metabolity)

20 cm

4 cm

200

m

30

m przekrój

przez

kapilarę

ok. 10 tys kapilar

dno
sitowe

13

transport ciepła i masy

dyfyzyjny

dyfyzyjny

ruch masy

ruch masy

©Ryszard A. Białecki

25

out

B

c



)]

'

(

)

'

(

)[

'

(

z

c

z

c

z

k

dS

dJ

D

B

m









różniczkowy strumień metabolitów usuniętych z krwi

poprzez różniczkową powierzchnię

dS

kapilar

z

'

z

L

'

z

z

L

in

D

c



out

D

c



in

B

c



out

B

c



rozkład stężeń metabolitów

w sztucznej nerce

in

B

c



in

D

c



out

D

c



)

'

(

)

'

(

z

c

z

c

D

B







siła napędowa wymiany

masyw przekroju z’

całkowanie wzdłuż kapilar daje całkowity strumień usuniętych

metabolitów