1

Opracował: Szymon Skibicki

Projekt stropu oraz słupów hali magazynowej w konstrukcji stalowej
1.Dane ogólne:

Rodzaj stropu: WPS/140
Do wykonania stopu przyjęto stal St4VX:

dla t<16

2

d

dv

2

d

cm

kN

0

,

14

MPa

140

f

58

,

0

f

cm

kN

5

,

23

MPa

235

f

=

=

=

=

=

dla t

∈

(16,40)

2

d

dv

2

d

cm

kN

5

,

13

MPa

135

f

58

,

0

f

cm

kN

5

,

22

MPa

225

f

=

=

=

=

=

Rozmiary stropu:

Szerokość hali:

15,90 m

Długość hali:

22,50 m

Wysokość:

5,70 m

2.Obciążenia dla belki stropu WPS.

(Założono wstępnie dwuteownik NP200)

Lp.

Rodzaj obci

ąż

enia

Obci

ąż

enie

charakterystyczne

q

k

[kN/m

2

]

γ

f

Obci

ąż

enie

obliczeniowe

q

o

[kN/m

2

]

1.

plytki ceramiczne gr. 2cm

0,02x21=0,42

0,42

1,2

0,504

2.

wylewka cementowa gr. 5cm

0,05x21=1,05

1,05

1,3

1,365

3.

keramzyt gr. 12cm 0,12x7=0,84

0,84

1,3

1,092

4.

ci

ęż

ar własny dwuteownika NP200

26,3kg/m:1,4m=18,79kg/m2=0,19kN/m2

0,19

1,1

0,209

5.

ci

ęż

ar własny płyty WPS

1,2

1,1

1,32

6.

tynk cementowo- wapienny

0,015x19=0,285kN/m2

0,285

1,3

0,3705

Obci

ąż

enie stałe

Σ

Σ

Σ

Σ

q

k

3,99

4,86

Obci

ąż

enie zmienne(u

ż

ytkowe) p

5,5

1,3

7,15

Σ

Σ

Σ

Σ

p+q

9,49

12,01

2

2.1. Obciążenia na 1 m bieżący stropu:

a)

charakterystyczne:

m

kN

286

,

13

m

4

,

1

)

q

p

(

k

k

=

×

+

b)

obliczeniowe

m

kN

81

,

16

m

4

,

1

)

q

p

(

o

o

=

×

+

2.2. Założony układ statyczny jako składający się z belek jednoprzęsłowych
wolnopodpartych.

2.3. Rozpiętość efektywna(obliczona wg teorii mechaniki ogólnej):

cm

543

cm

530

025

,

1

l

025

,

1

l

o

eff

=

×

=

×

=

o

l - rozpiętość w świetle elementu.

2.4.Moment maksymalny dla belki stropu WPS:

kNm

96

,

61

8

l

)

q

p

(

M

2

eff

o

o

max

=

×

+

=

2.3.Siły tnące dla belki stropu WPS:

kNm

64

,

45

2

l

)

q

p

(

R

R

T

eff

o

o

B

A

max

=

×

+

=

=

=

1.

Obliczenia belki stropu WPS:

Belka stropu WPS pracuje na zginanie jednokierunkowe.

2.4.orientacyjne wymiary przekroju belki:

x

d

d

x

W

M

f

f

W

M

=

⇒

≤

=

ς

(naprężenia na zginanie)

⇓

d

x

f

M

W

=

⇓

3

x

cm

66

,

263

MPa

235

kNm

96

,

61

W

=

=

(potrzebny wskaźnik wytrzymałości)

Przyjęto dwuteownik NP220 (

x

W

= 278

3

cm

)

2.5.Sprawdzenie klasy przekroju dla NP220(klasa przekroju zależy od jego smukłości):

3

a)

Ś

rodnik(pracuje jako element zginany):

g

h

s

=

λ

(wzór na smukłość)

ε

<

=

×

−

×

−

=

−

−

=

λ

66

15

,

22

81

,

0

)

81

,

0

2

(

)

22

,

1

2

(

22

g

r

2

t

2

h

Ś

rodnik jest w klasie I.

95

,

0

235

215

f

215

d

=

=

=

ε

b)

Półka(sprawdzana jest górna półka, która pracuje na ściskanie):

t

s

1

=

λ

ε

<

=

×

−

−

=

−

−

=

λ

9

02

,

3

2

,

12

2

)

1

,

8

2

(

1

,

8

98

t

2

r

2

g

s

Półka jest w klasie I.

Z obliczeń wynika, że cały element jest w klasie I.

2.6.Sprawdzanie nośności na zginanie:

Przekrój znajduje się w pierwszej klasie więc do nośności

R

M

należy doliczyć

współczynnik rezerwy plastycznej

07

,

1

p

=

α

0

,

1

L

=

ϕ

(współczynnik zwichrzenia występujący w strefie ściskanej, jest równy 1 ponieważ

strefa ściskana w przypadku rozpatrywanego stropu została usztywniona)

1

M

M

R

L

p

≤

×

ϕ

×

α

(Nośność)

kNm

33

,

65

kNcm

6533

cm

278

cm

kN

5

,

23

W

f

M

2

2

x

d

R

=

=

×

=

×

=

1

89

,

0

90

,

69

96

,

61

kNm

33

,

65

0

,

1

07

,

1

kNm

96

,

61

M

M

R

L

p

<

=

=

×

×

=

×

ϕ

×

α

Przekrój przeniesie obciążenia.

2.7.Sprawdzania nośności na ścinanie środnika:

max

2

dv

v

R

T

kN

9

,

232

MPa

140

cm

087

,

17

f

A

V

>

=

×

=

×

=

(nośność na ścinanie nie została

przekroczona)

2

v

cm

087

,

17

g

)

r

2

t

2

h

(

A

=

×

−

−

=

(pole przekroju czynnego przy ścinaniu)

4

2

d

dv

cm

kN

0

,

14

MPa

140

f

58

,

0

f

=

=

=

(wytrzymałość obliczeniowa stali na ścinanie)

2.8. Sprawdzenie Stanu Granicznego Użytkowalności belki (Sprawdzenie Ugięcia):

Sprawdzenie wg założeń mechaniki ogólnej oraz wg wartości normowych dla danego

elementu:

lim

max

a

a

<

cm

17

,

2

250

543

250

l

a

eff

lim

=

=

=

(wg normy)

lim

x

4

eff

k

k

max

a

cm

73

,

1

I

E

384

l

)

q

p

(

5

a

<

=

×

×

×

+

×

=

WARUNEK SPEŁNIONY

E = 205GPa (współczynnik sprężystości)

4

x

cm

4250

I

=

(moment bezwładności przekroju)

3.Obciążenia na blachownicę.

3.1.Rozpiętość efektywna blachownicy(wg teorii mechaniki ogólnej):

m

53

,

11

cm

1153

cm

1125

025

,

1

l

025

,

1

l

o

eff

=

=

×

=

×

=

o

l - rozpiętość w świetle elementu.

3.2.Ciężar własny blachownicy

m

kN

8

,

15

m

N

05

,

1575

85

,

0

)

m

53

,

11

100

700

(

85

,

0

)

l

100

700

(

C

eff

=

=

×

×

+

=

×

×

+

=

Lp.

Rodzaj obci

ąż

enia

Obci

ąż

enie

charakterystyczne

q

k

[kN/m]

γ

f

Obci

ąż

enie

obliczeniowe

q

o

[kN/m]

1.

ci

ęż

ar własny blachownicy

1,58

1,1

1,738

2.

obci

ąż

enie od stropu

qxl(5,30m)

3,99kN/m2x5,30m

=21,15

-

4,86kN/mx5,30m

=25,76

Obci

ąż

enie stałe

Σ

Σ

Σ

Σ

q

k

22,73

27,50

Obci

ąż

enie zmienne(u

ż

ytkowe) p

29,15(5,5x5,30)

1,3

37,9

ΣΣΣΣ

p+q

51,88

65,40

5

3.3.Moment maksymalny działający na blachownicę

kNm

79

,

1086

8

l

)

q

p

(

M

2

eff

o

o

max

=

×

+

=

3.4.Siły tnące dla belki stropu WPS:

kNm

03

,

377

2

l

)

q

p

(

R

R

T

eff

o

o

B

A

max

=

×

+

=

=

=

5.Blachownica – obliczenia.

5.1.Ustalenie przekroju blachownicy.

Przyjęto:

=

w

t

1cm (grubość środnika)

=

w

h

85cm (wysokość środnika)

=

f

t

2cm (grubość półki)

=

f

b

24cm (szerokość półki)

cm

86

,

76

cm

3

,

115

l

15

1

10

1

h

eff

w

−

=













−

=

cm

85

t

f

M

h

w

d

w

=

×

α

=

(

2

,

1

=

α

)

mm

10

h

3

7

t

w

w

=

+

=

(h należy wstawić w metrach)

cm

33

,

28

cm

17

h

3

1

5

1

b

w

f

−

=













−

=

cm

67

,

1

b

F

t

f

f

=

=

2

w

w

w

x

cm

07

,

43

6

t

h

h

W

F

=

×

−

=

(wzór na pole wyprowadzony z wzoru Steinera)

5.2.Sprawdzenie klasy przekroju dla blachownicy(klasa przekroju zależy od jego smukłości):

a)

Ś

rodnik(pracuje jako element zginany):

w

w

t

h

=

λ

(wzór na smukłość)

6

ε

<

=

=

λ

105

85

1

85

Ś

rodnik jest w klasie III.

95

,

0

235

215

f

215

d

=

=

=

ε

b)

Pas(sprawdzany jest pas górny, który pracuje na ściskanie):

f

f

t

b

=

λ

ε

<

=

=

λ

14

12

2

24

Pas jest w klasie III.

Z obliczeń wynika, że cały element jest w klasie III.

5.3.Wielkości charakterystyczne przekroju.

a)

Moment bezwładności(obliczane ze wzoru Steinera)

4

2

f

w

3

f

f

3

f

w

w

x

cm

5

,

209655

A

2

t

2

h

12

t

b

2

12

)

t

2

h

(

t

I

=















×













−

+

×

+

−

=

b)

Wskaźnik wytrzymałości

3

w

x

x

cm

4933

h

5

,

0

I

W

=

=

5.4.

Sprawdzanie nośności na zginanie:

0

,

1

L

=

ϕ

(współczynnik zwichrzenia występujący w strefie ściskanej, jest równy 1 ponieważ

strefa ściskana w przypadku rozpatrywanego stropu została usztywniona)

1

M

M

R

L

≤

×

ϕ

(Nośność)

kNm

1159

kNcm

115900

cm

4933

cm

kN

5

,

23

W

f

M

2

2

x

d

R

=

=

×

=

×

=

1

937

,

0

kNm

1159

0

,

1

kNm

79

,

1086

M

M

R

L

<

=

×

=

×

ϕ

Przekrój przeniesie obciążenia.

7

5.5.Sprawdzania nośności na ścinanie środnika:

max

2

dv

v

R

T

kN

1104

MPa

140

cm

81

f

A

V

>

=

×

=

×

=

(nośność na ścinanie nie została

przekroczona)

2

w

f

w

v

cm

81

t

)

t

2

h

(

A

=

×

−

=

(pole przekroju czynnego przy ścinaniu)

2

d

dv

cm

kN

0

,

14

MPa

140

f

58

,

0

f

=

=

=

(wytrzymałość obliczeniowa stali na ścinanie)

5.6. Sprawdzenie Stanu Granicznego Użytkowalności belki (Sprawdzenie Ugięcia):

Sprawdzenie wg założeń mechaniki ogólnej oraz wg wartości normowych dla danego

elementu:

lim

max

a

a

<

cm

29

,

3

350

1153

350

l

a

eff

lim

=

=

=

(wg normy)

lim

x

4

eff

k

k

max

a

cm

78

,

2

I

E

384

l

)

q

p

(

5

a

<

=

×

×

×

+

×

=

WARUNEK SPEŁNIONY

E = 205GPa (współczynnik sprężystości)

4

x

cm

5

,

209655

I

=

(moment bezwładności przekroju)

6.Słup.

6.1 Obciążenia na słup.

Są sumą reakcji z dwóch przęseł blachownicy wraz z ciężarem własnym.

kN

4

,

754

kN

3

,

0

03

,

377

03

,

377

C

R

R

R

w

2

1

=

+

+

=

+

+

=

6.2 Orientacyjne pole przekroju słupa:

1

N

N

Rc

≤

×

ϕ

8

,

0

6

,

0

−

=

ϕ

(współczynnik wyboczenia)

⇓

1

A

f

N

d

≤

×

×

ϕ

⇓

8

d

f

N

A

×

ϕ

≥

cm

71

,

53

A

≥

lub

cm

28

,

40

A

≥

Zgodnie z orientacyjnym polem przekroju przyjęto dwa ceowniki NP200 (A=32,2cm

2

)

6.3 Parametry przyjętych kształtowników(NP200):

cm

5

,

7

s

cm

01

,

2

e

cm

148

I

cm

1910

I

cm

14

,

2

i

cm

7

,

7

i

cm

2

,

32

A

0

0

4

0

y

4

0

x

0

y

0

x

2

0

=

=

=

=

=

=

=

6.4 Nośność w płaszczyźnie x-x:

1

N

N

Rc

x

≤

×

ϕ

kN

4

,

1513

A

2

f

N

0

d

Rc

=

×

×

=

a)

obliczenie współczynnika wyboczenia:

zależy on od smukłości zastępczej (

x

λ

)

026

,

74

cm

7

,

7

cm

570

i

l

0

x

x

x

=

=

=

λ

(smukłość)

cm

570

cm

570

0

,

1

H

l

x

=

×

=

×

µ

=

(

0

,

1

=

µ

ponieważ zakładamy połączenia przegubowe

podstawy i głowicy słupa z innymi elementami stropu)

346

,

80

235

215

84

f

215

84

d

p

=

=

=

λ

(smukłość porównawcza)

921

,

0

p

x

x

=

λ

λ

=

λ

(smukłość zastępcza, na jej podstawie odczytujemy z tabeli

współczynnik wyboczeniowy

ϕ

)

625

,

0

=

ϕ

(odczytany z krzywej c)

9

b)

sprawdzenie nośności

1

N

N

Rc

≤

×

ϕ

1

80

,

0

kN

4

,

1513

625

,

0

kN

4

,

754

N

N

Rc

≤

=

×

=

×

ϕ

6,5 Nośność w płaszczyźnie y-y:

1

N

N

Rc

)

b

(

≤

×

ϕ

ψ

1

0

d

Rc

A

2

f

N

ϕ

×

×

×

=

a)

określenie smukłości względem osi y-y (tak zwanej smukłości nie materiałowej)

y

y

y

i

l

=

λ

cm

570

l

l

x

y

=

=

A

I

i

y

y

=

(promień bezwładności dla całego układu)

Moment bezwładności (

y

I ) dla całego układu policzymy stosując wzór Steinera:



























+

=

2

0

0

y

y

2

e

A

I

2

I

Najpierw należy jednak określić e czyli odległość miedzy środkami kształtowników.

b)

określanie odległości miedzy środkami (e):

Aby układ pracował w dwóch kierunkach to musi być spełnione równanie:

y

x

I

I

1

,

1

=

×

0

x

x

I

2

I

×

=



























+

=

2

0

0

y

y

2

e

A

I

2

I

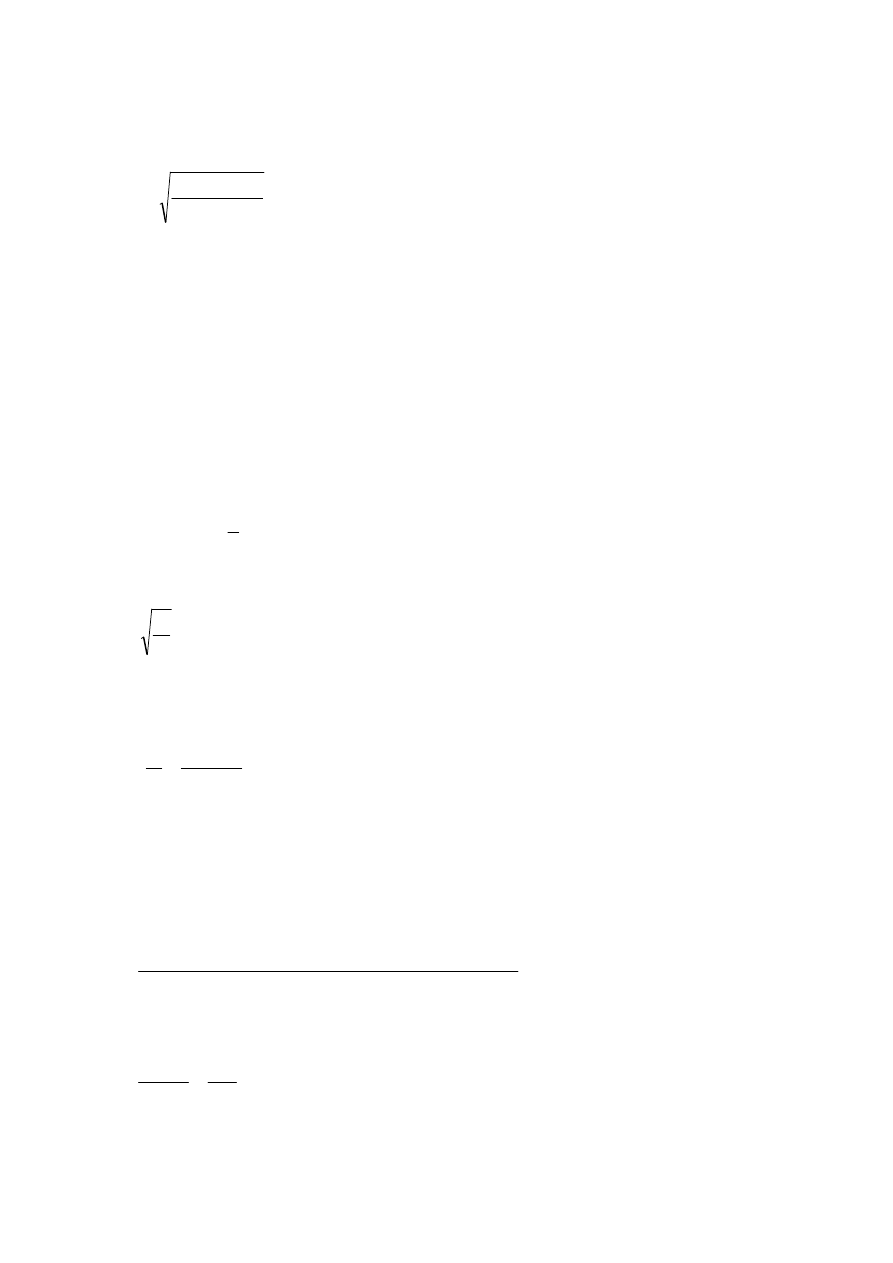
10

Z przekształcenia wzoru:

cm

576

,

15

A

I

I

1

,

1

2

e

0

0

y

0

x

=

−

×

×

=

Sprawdzenie odległości d(odległość ta wynosi minimum 10 cm ze względu na potrzebę
konserwacji elementów):

1

1

s

2

e

2

e

d

−

+

=

d = 4,6 cm (d za małe należy zmienić odległość aby wymagania wobec

długości d były spełnione)

Dla e = 21 cm , d = 10,02 cm a więc wymagania będą spełnione

Przyjęto e = 21 cm

c)

określenie momentu bezwładności przekroju w płaszczyźnie y-y

4

2

0

0

y

y

cm

7396

2

e

A

I

2

I

=



























+

=

d)

promień bezwładności przekroju w płaszczyźnie y-y

A

I

i

y

y

=

= 10,12cm

e)

smukłość w płaszczyźnie y-y

19

,

53

cm

12

,

10

cm

570

i

l

y

y

y

=

=

=

λ

6.5 Dobór ilości oraz rozstawu przewiązek.

a)

rozstaw przewiązek

−

1

l

rozstaw przewiązek

)

a

nieparzyst

.

zawsze

(

mi

przewiazka

.

miedzy

.

pól

.

liczha

)

podstawy

.

i

.

glowicy

.

bez

(

slupa

.

dlugosc

l

1

=

Założono orientacyjna wysokość głowicy jako 20 cm a podstawy jako 40 cm.

cm

23

,

39

13

510

13

60

H

l

1

=

=

−

=

b)

smukłość postaciowa dla przewiązek:

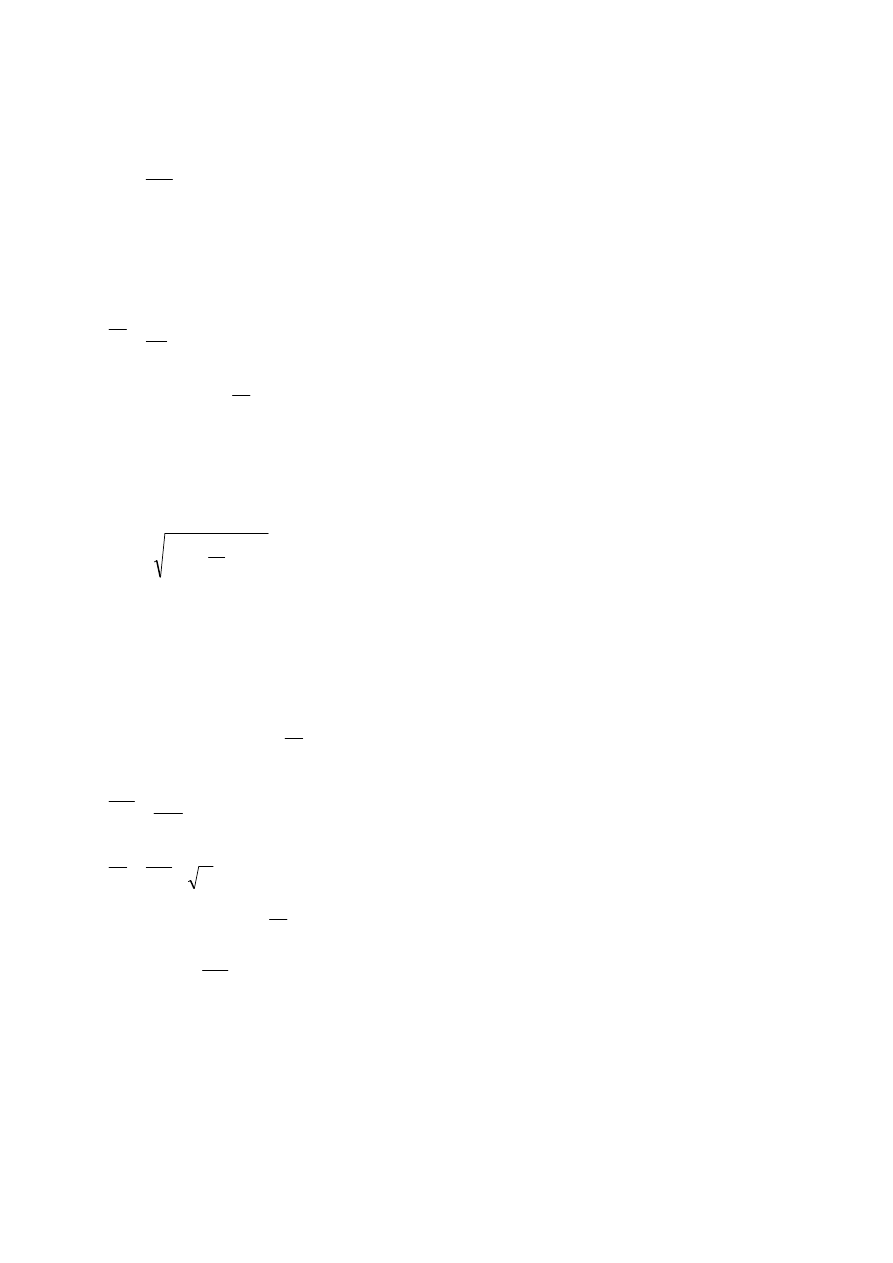
11

55

,

42

8

,

0

y

=

λ

y

min

1

8

,

0

33

,

18

i

l

λ

<

=

=

λ

ν

−

=

0

y

min

i

i

najmniejszy promień bezwładności(z promieni dla kształtowników)

c)

smukłość postaciowa zastępcza (dla przewiązek):

228

,

0

p

=

λ

λ

=

λ

ν

ν

W zależności od

ν

λ

dobieramy

1

ϕ

z krzywej c.

=

ϕ

1

0,976

6.6 Smukłość zastępcza dla całego przekroju.

=

λ

+

+

λ

=

λ

ν

2

2

y

my

2

m

56,259

m – liczba elementów przez które nie przechodzi rozpatrywana płaszczyzna (w tym
przypadku m = 2)

=

λ

my

56,259 >

19

,

53

y

=

λ

więc dobieramy

)

b

(

ψ

ϕ

z krzywej b i traktujemy przekrój jako

klasę IV

6.7 Smukłość zastępcza

y

λ

dla całego przekroju.

7

,

0

p

my

my

=

λ

λ

=

λ

=

ψ

×

λ

=

λ

my

y

0,692

1

ϕ

=

ψ

(wynikające z

ν

λ

)

W oparciu o

my

λ

dobieramy

)

b

(

ψ

ϕ

z krzywej b

847

,

0

)

b

(

=

ϕ

ψ

6.8 Sprawdzenie nośności w płaszczyźnie y-y

12

1

603

,

0

A

2

f

N

N

N

1

0

d

)

b

(

Rc

)

b

(

≤

=

ϕ

×

×

×

×

ϕ

=

×

ϕ

ψ

ψ

Słup przeniesie zadane obciążenia.

6.9 Sprawdzenie nośności przewiązek:
a) nośność przewiązek obliczamy na zastępczą siłę poprzeczną działającą w słupie

=

×

×

=

×

×

=

d

0

d

f

A

2

012

,

0

f

A

012

,

0

Q

18,16kN

A-przekrój poprzeczny słupa

b) Siła poprzeczna działająca wzdłuż osi słupa

=

−

×

=

e

)

1

m

(

n

l

Q

V

1

Q

16,96kN

m = 2 (liczba gałęzi słupa)

n = 2 (liczba płaszczyzn przewiązek przeciętych osią y)

1

l

= 39,23cm osiowy rozstaw przewiązek

e = 21 cm ( osiowy odstęp gałęzi słupa)

d)

Moment zamocowania przewiązki

=

×

×

=

n

m

l

Q

M

1

Q

1,78 kNm

e)

dobranie przekroju przewiązek pośrednich:

p

t - grubość przewiązki

p

b - wysokość przewiązki

p

a - szerokość przewiązki

=

p

a

200 mm

100mm

≤

p

p

a

4

3

b

≤

⇒ 100mm

≤

p

b

≤

150mm ⇒ przyjęto

p

b = 120mm

6mm

≤

p

t

≤

15

b

p

p

t ⇒

≤

mm

8

p

t ⇒ przyjęto

p

t =10mm

f)

sprawdzenie smukłości elementu:

ε

≤

=

=

15

12

10

120

t

b

p

p

⇒ przekrój zalicza do klasy 3

g)

nośność obliczeniowa przewiązki przy zginaniu:

=

×

×

=

×

=

d

2

p

p

d

px

R

f

6

b

t

f

W

M

5,64 kNm

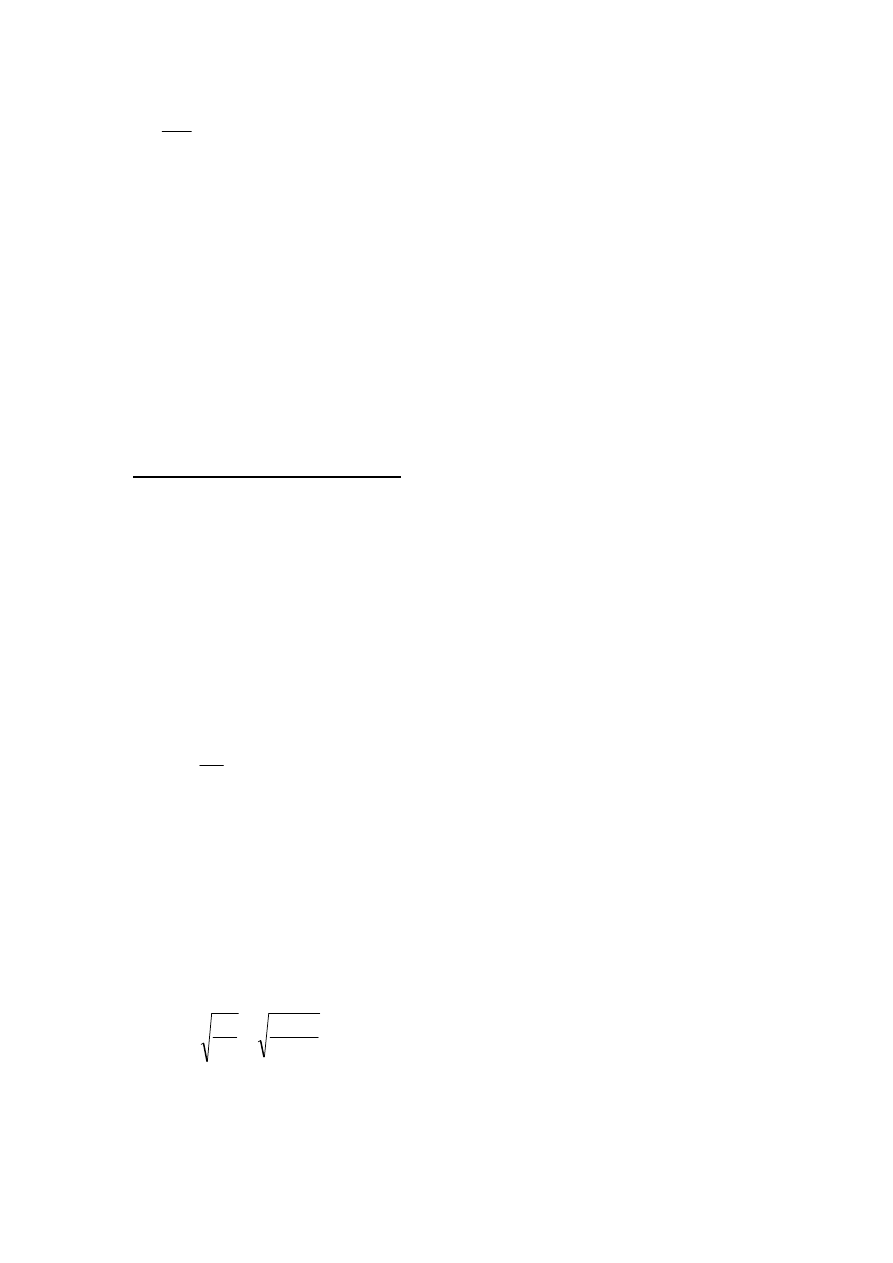
13

1

316

,

0

M

M

R

Q

<

=

przewiązka przeniesie moment zamocowania

h)

nośność obliczeniowa przewiązki przy ścinaniu:

ν

ν

×

=

d

R

f

A

V

=0,9

dv

p

p

f

t

b

×

×

×

=147,2 kN

R

Q

V

3

,

0

V

<

⇒ nie należy brać pod uwagę wpływu ścinania.

f)

dobór wymiarów przewiązek skrajnych:

przewiązki skrajne muszą mieć wysokość

p

b = 1,5

p

b przewiązki pośredniej więc

p

b dla

przewiązki skrajnej jest równe = 180mm.

7 Obliczenia podstawy słupa.:

a)

Założono stopę fundamentową o rozmiarach 120 cm x 120 cm i wysokości 60 cm z
betonu B20(

=

cd

f

10,6MPa).

Założony blachę poziomą o wymiarach a = 41 cm na b = 30 cm.

2

d

cm

1230

b

a

A

=

×

=

(powierzchnia blachy podstawy słupa)

b)

Naprężenia na docisk z podstawy słupa.

N = 754,4kN (obciążenie przenoszone ze słupa na fundament)

=

=

σ

d

d

A

N

6,13MPa (naprężenia na docisk)

c)

określenie powierzchni rozdziału

cm

101

60

41

h

a

a

r

=

+

=

+

=

cm

90

60

30

h

b

b

r

=

+

=

+

=

h – wysokość fundamentu

d)

współczynnik rozdziału

2

b

a

a

a

A

A

r

r

d

r

u

≤

×

×

=

=

ω

⇒

=

ω

u

2,68 > 2 więc przyjmuje

=

ω

u

2,0

e)

zakładamy, że stalowe podkładki między blachą podstawy o słupem zajmują więcej
niż 25% powierzchni docisku, zakładamy wykonanie podlewki gr.3cm z zaprawy
cementowej M8, w naszym fundamencie jest także zbrojenie na docisk, z naszych

14

założeń przyjmujemy współczynnik

=

β

1,0 oraz liczymy

cud

f

(wytrzymałość

obliczeniowa betonu na docisk) z wzoru:

cd

cu

cud

f

f

×

γ

×

β

=

gdzie

(

)

1

f

u

cd

cmu

u

cu

−

ω

σ

−

ω

=

γ

=

×

=

σ

r

r

cmu

b

a

N

0,83MPa (średnie naprężenia na powierzchni rozdziału)

cd

cu

cud

f

f

×

γ

×

β

=

=10,75MPa >

MPa

13

,

6

d

=

σ

więc beton wytrzyma docisk od

słupa.

f)

dobór grubości blachy poziomej, (ustalamy to w zależności od współczynników

ω

dla danych pól podstawy)

ω

- współczynnik określający wpływ momentu zginającego w rozpatrywanej płycie

umownej

Pole A(wspornik o wysięgu l=42 mm):

Dla wsporników

l

73

,

1

×

=

ω

więc

cm

27

,

7

=

ω

Pole B(płyta umowna oparta na 3 krawędziach), dobieramy współczynnik

ω

z tabeli(wg PN-

B-03215) i w zależności od stosunku

l

b

4

,

0

200

80

l

b

=

=

⇓

=

ω

l

0,595 (odczytane z tabeli)

⇓

=

ω

11,9cm

Pole B(płyta umowna oparta na 4 krawędziach), dobieramy współczynnik

ω

z tabeli(wg PN-

B-03215) i w zależności od stosunku

l

b

858

,

0

233

200

5

,

8

2

250

200

l

b

=

=

×

−

=

⇓

15

=

ω

l

0,524 (odczytane z tabeli)

⇓

=

ω

12,2cm

g) obliczenie grubości blachy poziomej(przyjmuje największy wyliczony współczynnik
określający wpływ momentu czyli

cm

2

,

12

=

ω

)

mm

7

,

19

cm

97

,

1

235

13

,

6

2

,

12

f

t

d

d

p

=

=

×

=

σ

×

ω

=

Przyjęto grubość blachy podstawy równą

mm

20

t

p

=

g)

przyjęcie śrub kotwiących:

przyjęto śruby średnicy d = 25 mm wg wytycznych normowych

przyjęto głębokość kotwienia = 20d wg wytycznych normowych

8

Przyjęcie blach trapezowych:

Wysokość blach trapezowych obliczymy z warunku nośności pionowych spoin
pachwinowych:

a)

dobranie grubości spoin pachwinowych łączących blachy trapezowe z słupem

wg wymagań normowych:

a < 0,7

min

t

a > 0,2

max

t

min

t

= 8 mm

max

t

= 11,5 mm

a

∈

(2,3mm; 5,6mm)

przyjęto grubość spoin a = 4mm

b)

wyliczenie grubości spoin spoin:

d

||

f

)

l

a

(

N

×

α

≤

×

Σ

=

τ

(warunek nośności spoin wg PN-90/B-03200)

⇓

=

×

α

×

×

=

d

||

f

a

8

N

l

12,54 cm

8

,

0

||

=

α

(wg tablicy 18 w PN-90/B-03200)

16

l < 100a wiec l < 40 cm

WARUNEK SPEŁNIONY

l > 10a więc l > 4cm

WARUNEK SPEŁNIONY

l > b więc l > 7,5 cm

WARUNEK SPEŁNIONY

b < 30t


c) na podstawie potrzebnej długości spoiny przyjęto blachę trapezową wysokości 14 cm i
grubości 0,8 cm

Opracował:

Szymon Skibicki