ROK WYD. LXV

앫 ZESZYT 2/2006

3 9

Dr in˝. Iwona Oprz´dkiewicz pracuje w Katedrze Auto-

matyzacji Procesów AGH w Krakowie.

Stale wzrastajàca niezawodnoÊç i moc obliczeniowa

systemów sterowania wykorzystujàcych sterowniki
PLC sk∏ania do coraz szerszego zastosowania ich
w przemyÊle. Systemy te realizujà bardzo odpowie-
dzialne zadania, a wspó∏czesna technologia stawia
coraz powa˝niejsze wymagania zwiàzane przede
wszystkim z zagwarantowaniem czasu najd∏u˝sze-
go cyklu sterowania [1, 2]. To w∏aÊnie zmusza do
przeprowadzenia szczegó∏owej analizy mo˝liwoÊci
stosowanych systemów pod wzgl´dem minima-
lizownia czasu cyklu. Istniejà mechanizmy pozwala-
jàce na pomiar czasu ka˝dego cyklu sterownika.
Mo˝na równie˝ zadaç maksymalny czas trwania
tego cyklu, którego przekroczenie jest sygnalizowa-
ne. Dlatego istotne ze wzgl´du na prac´ w systemach
czasu rzeczywistego jest opracowanie optymal-
nego czasowo oprogramowania, czyli takiego, które
cechuje si´ maksymalnym skróceniem czasu cyklu
bez utraty w∏aÊciwoÊci funkcjonalnych. Analizujàc
przyczyny zmiennoÊci czasu trwania cyklu sterownika
nale˝y wziàç pod uwag´:

Problemy oszacowania parametrów statystycznych
rozk∏adów czasów cyklu sterowników PLC

IWONA OPRZ¢DKIEWICZ

쐌 Typ sterownika – poszczególne sterowniki ró˝nià

si´ mi´dzy sobà nie tylko szybkoÊcià wykonywania
instrukcji, ale i liczbà dost´pnych instrukcji. Dlatego
rozwiàzujàc problem nale˝y wziàç pod uwag´ fakt,
˝e w jednym sterowniku do rozwiàzania zadania mo˝e
wystarczyç jedna instrukcja, podczas gdy w innym
konieczne jest zastosowanie ciàgu instrukcji.

쐌 Z∏o˝onoÊç programu u˝ytkownika – rozwiàzu-

jàc zadanie nale˝y dà˝yç do zastosowania jak naj-
mniejszej liczby instrukcji o najkrótszym czasie wy-
konywania (czasy te sà podawane przez producentów
sterowników). W praktyce najcz´Êciej musimy wy-
braç, czy korzystniejsze b´dzie zastosowanie jednej
instrukcji bardziej skomplikowanej (o d∏ugim czasie
wykonania), czy sekwencji instrukcji prostszych. Du˝e
znaczenie majà tak˝e typy danych, na jakich wyko-
nywane sà poszczególne operacje. Przyk∏adowo,
operacje na zmiennych typu REAL trwajà znacznie
d∏u˝ej ni˝ na zmiennych typu DINT o tej samej
precyzji.

쐌 Liczb´ po∏àczeƒ z urzàdzeniami peryferyjnymi

i innymi sterownikami – obs∏uga tych urzàdzeƒ mo˝e
zajmowaç znaczàcà cz´Êç czasu trwania cyklu ste-

ROK WYD. LXV

O ZESZYT 2/2006

4 0

rownika, dlatego skrócenie czasu cyklu mo˝na uzys-
kaç, ograniczajàc w programie liczb´ tych po∏àczeƒ
lub (je˝eli b´dzie to korzystne) rozdzielajàc czas
transmisji na kilka kolejnych cykli. Istnieje równie˝
mo˝liwoÊç ustalenia w sterowniku maksymalnego
czasu niezb´dnego do obs∏ugi urzàdzeƒ peryferyj-
nych (w procentach wartoÊci czasu cyklu). Wa˝ne jest
tak˝e wy∏àczenie nieu˝ywanych wejÊç i wyjÊç w mo-
du∏ach oraz ich poprawna konfiguracja (np. roz-
dzielczoÊç przetworników A/C).

Czas trwania cyklu sterownika ma decydujàcy

wp∏yw na dzia∏anie uk∏adów czasu rzeczywistego.
Jednym z g∏ównych warunków poprawnego wyko-
rzystania programu w tego typu systemach jest
warunek nieprzekraczania wczeÊniej narzuconej
wartoÊci czasu cyklu. Konsekwencjà przekroczenia
tego czasu mo˝e byç nawet wstrzymanie pracy ste-
rownika. Dà˝y si´ równie˝ do zmniejszenia fluktuacji
czasu trwania cyklu. W tym celu w wielu sterowni-
kach istnieje mo˝liwoÊç ustawienia minimalnego
czasu cyklu.

Z przedstawionych informacji wynika, ˝e tworzàc

oprogramowanie na konkretnym sterowniku, spe∏-
niajàce wymagania czasu rzeczywistego nale˝y zwró-
ciç szczególnà uwag´ na liczb´ i rodzaj u˝ytych in-
strukcji oraz na efektywnà obs∏ug´ urzàdzeƒ pery-
feryjnych, gdy˝ najwi´kszy wp∏yw na czas trwania
cyklu ma czas wykonywania programu u˝ytkowego.

Czas wykonywania cyklu przez sterownik

Spe∏nienie za∏o˝eƒ czasu rzeczywistego w czasie

pracy sterownika wymaga, aby podczas cyklicznego
wykonania programu czas cyklu nie przekracza∏ na-
rzuconej wartoÊci. Jest to g∏ówne kryterium oceny
poprawnoÊci wykonywania programu. Dlatego czas
cyklu sterownika jest wa˝nym czynnikiem, który
nale˝y omówiç.

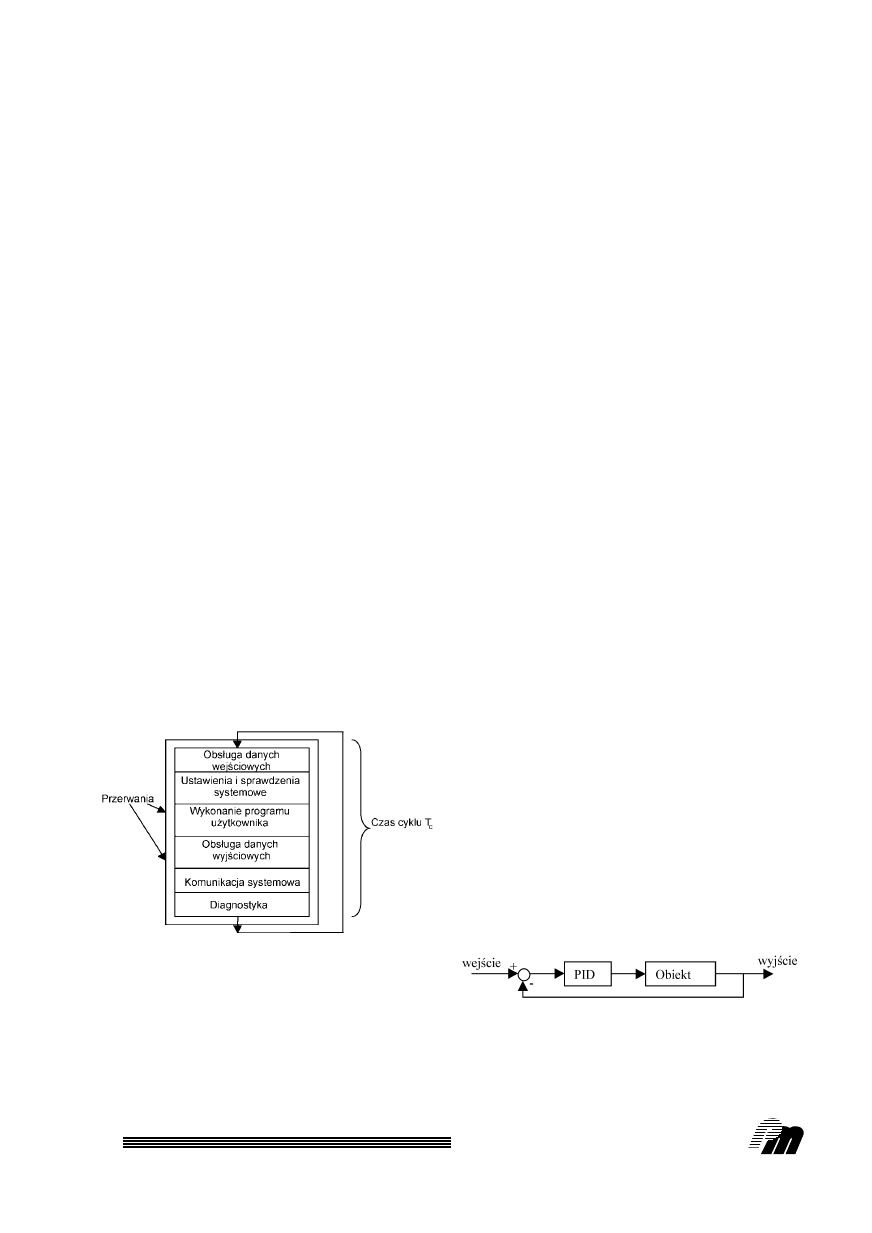
Czas trwania cyklu T

c

to czas, który up∏ywa podczas

jednego cyklu programu (rys. 1). Na jego d∏ugoÊç
wp∏ywajà:

I ustawienia systemowe i sprawdzenie magistrali

wejÊç/wyjÊç, pami´ci, autotest CPU itp. (czas sta∏y dla
danego typu sterownika),

I czas obs∏ugi danych wejÊciowych i wyjÊciowych

(dla danego typu sterownika sta∏a),

I czas wykonywania programu u˝ytkownika (war-

toÊç zmienna),

I czas obs∏ugi urzàdzeƒ peryferyjnych.

Teoretyczne oszacowanie czasu cyklu mo˝na zrea-

lizowaç na podstawie danych dostarczonych przez
producenta konkretnego typu sterownika. B´dzie
to oczywiÊcie oszacowanie dla najmniej korzyst-
nej sytuacji, czyli rzeczywiste pomiary konkretnych
czasów powinny byç krótsze od wartoÊci obliczonej
[3, 4].

Czas cyklu nie jest wartoÊcià sta∏à, lecz zale˝y np.

od liczby i rodzaju przerwaƒ oraz szybkoÊci komu-
nikacji systemowej. Szacujàc jego wartoÊç nale˝y
uwzgl´dniç [5]:

T

c

=

T

R

+

T

os

+

T

u

+

T

w

+

T

Di

+

T

Do

+

T

t

+

T

DP

(1)

gdzie:

T

R

,

T

w

– czas odczytu i zapisu odpowiednio

wejÊç i wyjÊç,

T

u

– czas wykonania programu u˝ytkownika,

T

os

– czas wykonania systemu operacyjnego

sterownika,

T

Di

,

T

Do

– czas opóênienia zwiàzanego z od-

czytem/zapisem wejÊç/wyjÊç,

T

t

– czas wykonania cykli (timerów) u˝ytych

w programie,

T

DP

– czas komunikacji z siecià.

W zaproponowanym wzorze nie uwzgl´dniono

czasu przeznaczonego na diagnostyk´, gdy˝ jest on
pomijalnie ma∏y w stosunku do pozosta∏ych czasów.

Wyznaczanie Êrednich

i maksymalnych cyklów sterowników PLC

Badania doÊwiadczalne zosta∏y wykonane na ste-

rownikach PLC SIEMENS SIMATIC S7-300 z jed-
nostkami centralnymi: 312 IFM oraz 315. Na ka˝dej
z tych jednostek uruchomiono procedury testowe
realizujàce nast´pujàce typowe zadania sterowania:

I sterowanie logiczne (procedura P1),

I sterowanie ciàg∏e z wykorzystaniem algorytmu

PID (procedura P2),

I sterowanie z zakresu robotyki (zagadnienie kine-

matyki prostej)(procedura P3).

Sterowanie logiczne zrealizowano w procedurze P1

obs∏ugujàcej zadajnik cyfrowy (ang. thumbwheel
switch) [1]. Umo˝liwia on wprowadzanie do ste-
rownika kolejno cyfr z poszczególnych segmentów
zadajnika. Aby odczytaç wartoÊci z zadajnika, ko-
nieczne by∏o napisanie procedury z „kroczàcà je-
dynkà”, która umo˝liwi∏a odczytanie kolejnych wyjÊç.
Realizacja tej procedury wymaga∏a obs∏ugi wy∏àcz-
nie wejÊç i wyjÊç binarnych przez sterownik.

Do testów algorytmu regulacji ciàg∏ej wykorzysta-

no typowy uk∏ad regulacji (sterowanie w uk∏adzie
zamkni´tym) z regulatorem PID w g∏ównej linii re-
gulacji (procedura P2), którego schemat blokowy
przedstawiono na rys. 2. Celem stawianym uk∏adowi

Rys. 1. Etapy cyklu sterownika

Rys. 2. Schemat blokowy uk∏adu regulacji wykorzystanego
w procedurze P2

regulacji by∏o takie sterowanie napi´ciem zasilajà-
cym wentylatory, aby wirujàca masa (osiem meta-
lowych ∏opatek osadzonych na rdzeniu) osiàgn´∏a
˝àdanà pr´dkoÊç obrotowà [6]. Realizacja procedury

ROK WYD. LXV

O ZESZYT 2/2006

4 1

P2 wymaga∏a obs∏ugi wejÊç i wyjÊç zarówno binar-
nych, jak i analogowych (do modu∏u SM 334 pod-
∏àczono wentylatory sterujàce). Funkcj´ czujnika
pr´dkoÊci obrotowej spe∏nia∏ enkoder firmy Omron
(E6C2-CWZ6C) i zosta∏ on pod∏àczony do jednostki
centralnej CPU.

W systemach rzeczywistych relacja mi´dzy wejÊ-

ciem a wyjÊciem jest reprezentowana przez czas
odpowiedzi, który w zale˝noÊci od momentu zadzia-
∏ania sygna∏u wejÊciowego w stosunku do czasu
cyklu zmienia si´ w granicach od 1,5 do 2. W dalszych
rozwa˝aniach ograniczono si´ tylko do czasu cyklu,
gdy˝ ma on istotny wp∏yw na d∏ugoÊç czasu odpo-
wiedzi i mo˝na go w prosty sposób zmierzyç.

Proste zagadnienie kinematyki jest to zadanie sta-

tyczno-geometryczne polegajàce na obliczaniu pozy-
cji i orientacji cz∏onu roboczego manipulatora. Majàc
dane wszystkie wspó∏rz´dne konfiguracyjne, nale˝y
obliczyç pozycj´ danego punktu zwiàzanego z ro-
botem wzgl´dem globalnego uk∏adu wspó∏rz´d-
nych. Przy uwzgl´dnieniu wymagaƒ czasu rzeczy-
wistego jest to problem wymagajàcy wielokrotnego
wykorzystania czasoch∏onnych funkcji trygonomet-
rycznych (procedura P3). Realizacja tej procedury
wymaga∏a obs∏ugi wejÊç i wyjÊç binarnych i ana-
logowych.

Cykl programowy w ka˝dej procedurze testujàcej

wykonywany jest zgodnie ze schematem z rys. 1.

Ârednie i maksymalne czasy cyklu sterowników

wyznaczano korzystajàc z

Module Information dost´p-

nego w pakiecie Step 7

[7]. Z uwagi na bardzo krótki

czas wykonania pojedynczej instrukcji (rz´du

µ

s)

i w zwiàzku z tym na niemo˝liwoÊç jego precyzyjnego
odczytu, zdecydowano si´ na pomiar czasu cyklu dla
tysiàckrotnego wykonania danej procedury w p´tli.

Rezultaty przeprowadzonych badaƒ

Przeprowadzone badania mia∏y na celu oszacowa-

nie czasów cyklów w poszczególnych procedurach
sterowania w oparciu o dane udost´pnione przez
producenta sterowników SIEMENS [2], a nast´pnie
zweryfikowanie ich podczas pracy rzeczywistego
systemu sterowania.

Do wyznaczenia oszacowaƒ wykorzystano wzór (1).

Po wst´pnych oszacowaniach okaza∏o si´, ˝e decy-
dujàcy wp∏yw na d∏ugoÊç czasu cyklu ma z∏o˝onoÊç
(rodzaj i liczba u˝ytych instrukcji) procedury steru-
jàcej. Suma czasów:

T

os

(czas wykonania systemu

operacyjnego sterownika),

T

R

,

T

w

(czas odczytu i za-

pisu odpowiednio wejÊç i wyjÊç),

T

Di

,

T

Do

(czas

opóênienia zwiàzanego z odczytem/zapisem wejÊç/
wyjÊç) oraz

T

DP

(czas komunikacji z siecià) w obu

u˝ytych sterownikach wynosi∏a oko∏o 2 ms. Tabela
zawiera oszacowania maksymalnych czasów cyklu

w pierwszej fazie badaƒ zaj´to si´ wyznaczaniem tych
w∏aÊnie czasów.

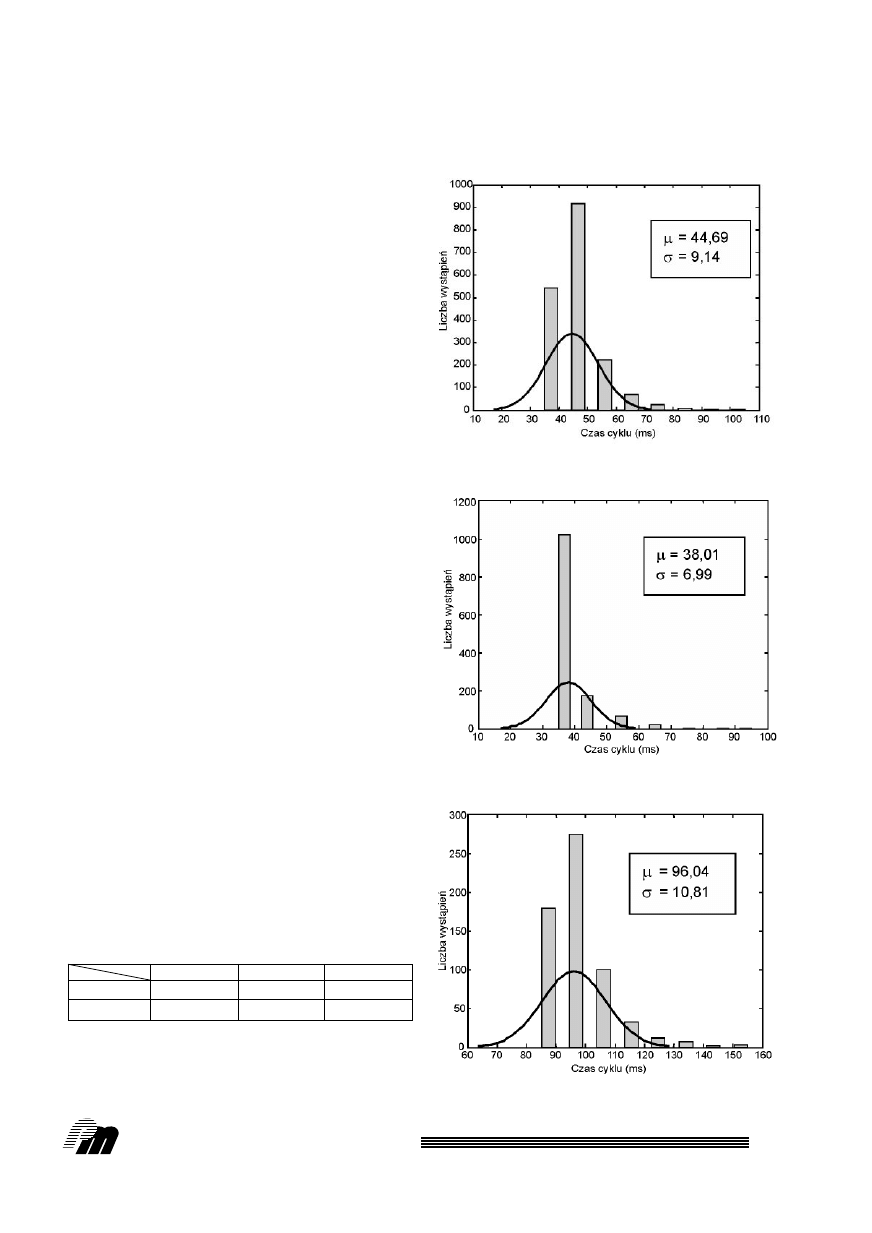
Na rys. 3 – 8 przedstawiono histogramy wystàpieƒ

poszczególnych Êrednich czasów cyklów, przy czym
czasy cyklów mierzono z dok∏adnoÊcià do 10 ms. Na
podstawie analizy histogramów (dla procedur P1, P2,

Rys. 3. Ârednia liczba wystàpieƒ poszczególnych czasów
cyklów sterownika 312 IFM dla procedury P1

Rys. 4. Ârednia liczba wystàpieƒ poszczególnych czasów
cyklów sterownika 315 dla procedury P1

Oszacowanie maksymalnych czasów cyklów dla procedur
testujàcych typowe zadania sterowania P1, P2, P3

P1

P2

P3

312 IFM

ok. 200 ms

ok. 3400 ms

ok. 3000 ms

315

ok. 100 ms

ok. 3400 ms

ok. 2900 ms

Rys. 5. Ârednia liczba wystàpieƒ poszczególnych czasów
cyklów sterownika 312 IFM dla procedury P2

dla analizowanych procedur na podstawie danych
dotyczàcych czasów wykonania poszczególnych in-
strukcji, podanych przez producenta sprz´tu [8].

Aby zorientowaç si´, ile czasu Êrednio trwa cykl

sterownika przy realizacji analizowanych procedur,

ROK WYD. LXV

O ZESZYT 2/2006

4 2

P3) mo˝na stwierdziç, ˝e zmienna losowa, jakà jest
czas cyklu, jest opisana rozk∏adem normalnym. Z tego
wzgl´du podj´to prób´ aproksymacji otrzymanych
rozk∏adów rozk∏adem normalnym i okreÊlenia pa-
rametrów tych rozk∏adów, wykorzystujàc do tego celu

Rys. 6. Ârednia liczba wystàpieƒ poszczególnych czasów
cyklów sterownika 315 dla procedury P2

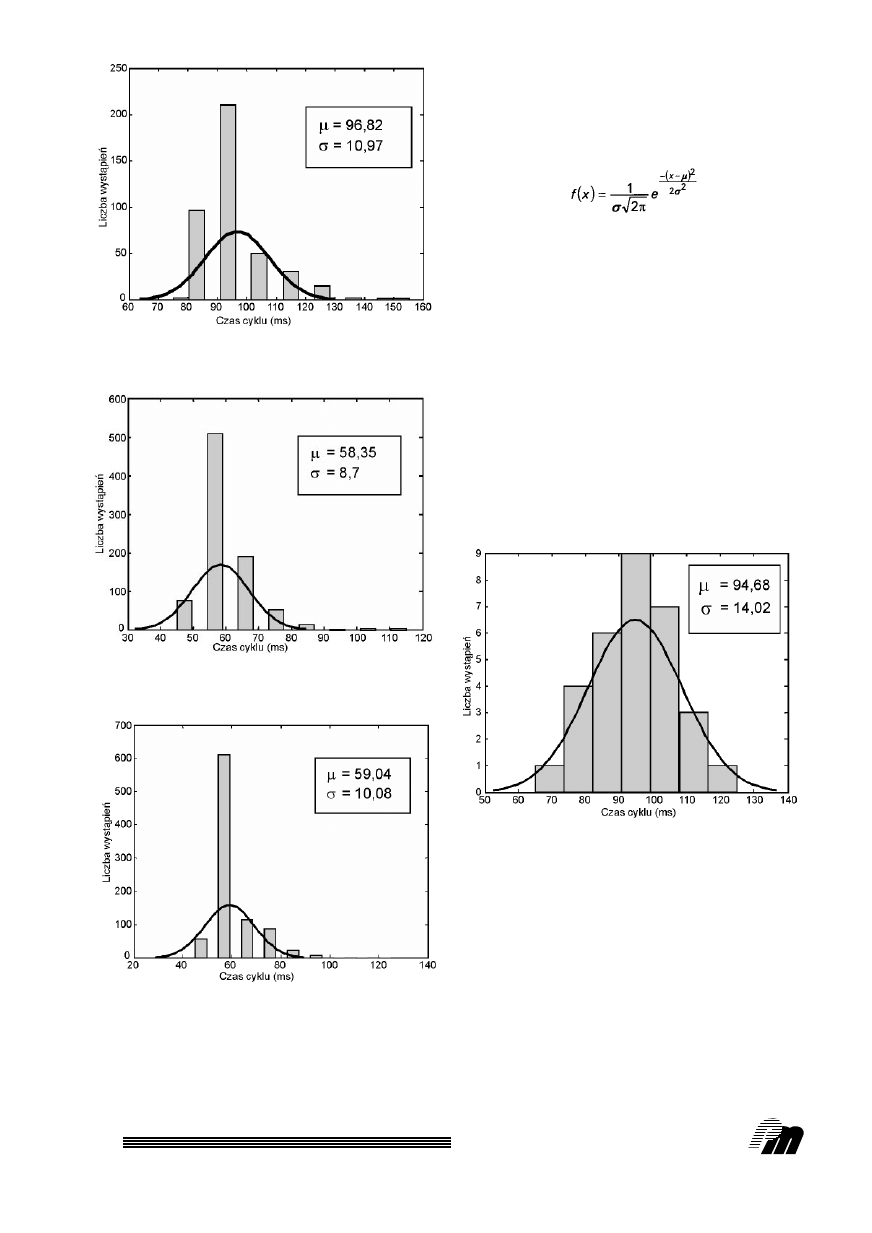
Rys. 7. Ârednia liczba wystàpieƒ poszczególnych czasów
cyklów sterownika 312 IFM dla procedury P3

Rys. 8. Ârednia liczba wystàpieƒ poszczególnych czasów
cyklów sterownika 315 dla procedury P3

Rys. 9. Ârednia liczba wystàpieƒ maksymalnych czasów cyklów
sterownika 312 IFM dla procedury P1

pakiet Matlab. Na ka˝dym rysunku linià zaznaczono
rozk∏ad g´stoÊci wyznaczonego rozk∏adu normalnego.

Funkcja g´stoÊci dla rozk∏adu normalnego ze

Êrednià

µ

i odchyleniem standardowym

σ

jest

przyk∏adem funkcji

Gaussa zdefiniowanej za pomocà

nast´pujàcego wzoru:

(2)

Ârednie czasy cyklów wyznaczone w wyniku ba-

daƒ doÊwiadczalnych okaza∏y si´ znacznie krótsze,
ni˝ wynika to z teoretycznych oszacowaƒ. Wyniki
przedstawiono na rys. 3 – 8. Obok siebie zestawiono
wyniki otrzymane dla tej samej procedury realizo-
wanej dla dwóch ró˝nych jednostek centralnych
312 IFM i 315.

Maksymalny czas cyklu sterownika jest istotniej-

szy przy projektowaniu systemów sterowania pra-
cujàcych w czasie rzeczywistym ni˝ czas Êredni cyklu,
który pozwala tylko na oszacowanie najcz´Êciej wy-
st´pujàcego czasu cyklu sterownika. Wià˝e si´ to
z faktem, ˝e projektant musi zagwarantowaç nie-
przekraczalny czas pojedynczego cyklu w nawet
najbardziej niekorzystnej sytuacji.

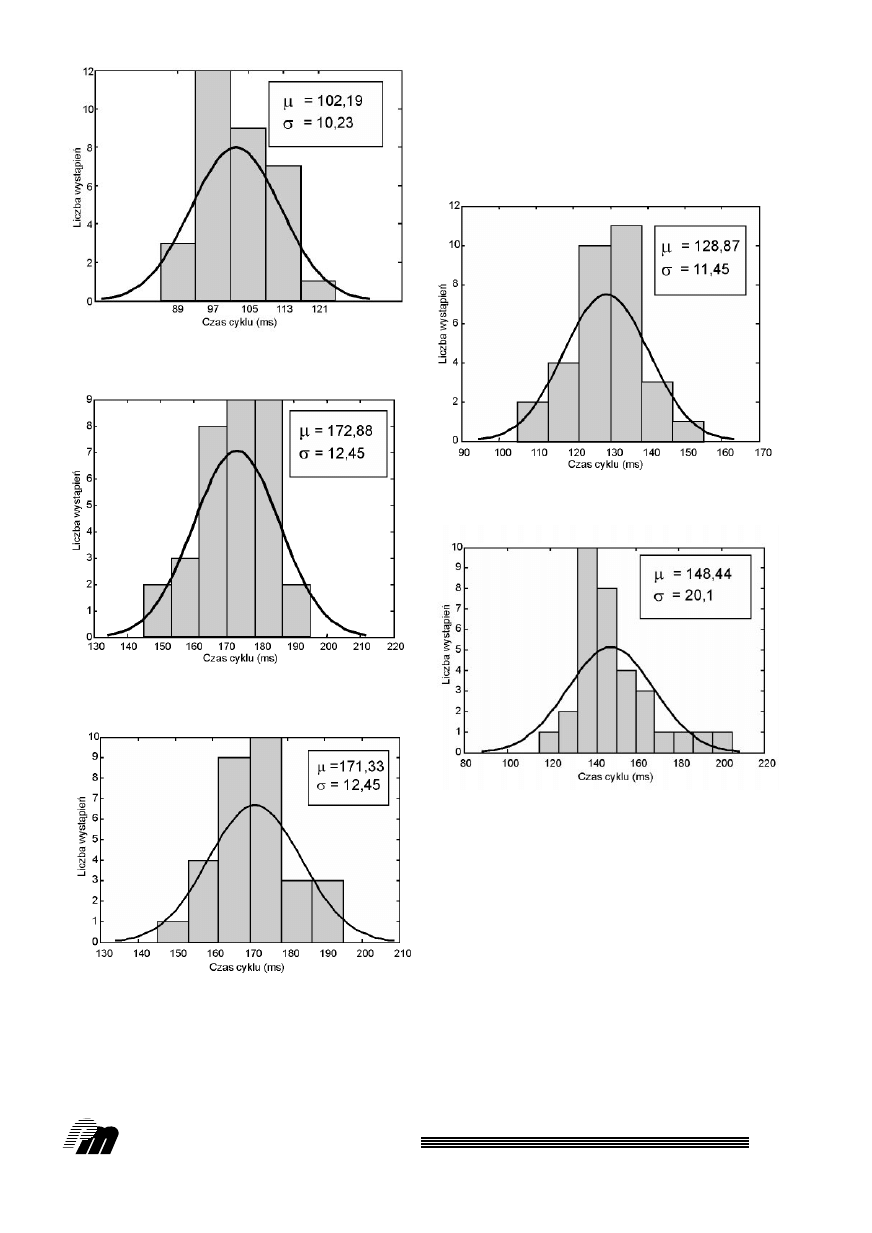
Przedstawiono wyniki badaƒ przeprowadzone dla

tych samych co poprzednio procedur testujàcych
(rys. 9 – 14). Maksymalne czasy cyklów wyznaczano

dla 10-sekundowych (czas bardzo d∏ugi w stosunku
do czasu cyklu) okresów pracy analizowanej pro-
cedury sterujàcej, a nast´pnie badano liczb´ wystà-
pieƒ tych czasów w poszczególnych przedzia∏ach
(co 10 ms). Dla otrzymanych histogramów równie˝
wyznaczono odpowiadajàce im rozk∏ady normalne.

Wnioski

Przeprowadzone badania Êwiadczà o tym, ˝e teo-

retyczne oszacowanie czasu cyklu mo˝na traktowaç
jako bardzo zawy˝ony, maksymalny mo˝liwy czas
cyklu. W praktyce, rzeczywiste czasy cyklów naj-
cz´Êciej sà kilka-, a nawet kilkunastokrotnie krótsze.
Wynika to z faktu, ˝e producent podaje najd∏u˝szy

ROK WYD. LXV

O ZESZYT 2/2006

4 3

Rys. 10. Ârednia liczba wystàpieƒ maksymalnych czasów
cyklów sterownika 315 dla procedury P1

Rys. 11. Ârednia liczba wystàpieƒ maksymalnych czasów
cyklów sterownika 312 IFM dla procedury P2

Rys. 12. Ârednia liczba wystàpieƒ maksymalnych czasów
cyklów sterownika 315 dla procedury P2

Rys. 13. Ârednia liczba wystàpieƒ maksymalnych czasów
cyklów sterownika 312 IFM dla procedury P3

Rys. 14. Ârednia liczba wystàpieƒ maksymalnych czasów
cyklów sterownika 315 dla procedury P3

mo˝liwy czas wykonania danej instrukcji. Z zamiesz-
czonych histogramów wynika, ˝e stosujàc jednost-
k´ CPU 315 mo˝na znaczàco skróciç czasy cyklów
(w stosunku do jednostki 312 IFM), zw∏aszcza w od-
niesieniu do procedur logicznych (rys. 4). Wniosek ten

potwierdzajà równie˝ histogramy cz´stoÊci wystà-
pieƒ maksymalnych czasów cyklów dotyczàcych
procedury P1 (rys. 9 i 10). Czasy cyklów w proce-
durach realizujàcych sterowanie ciàg∏e oraz rozwià-
zujàcych proste zadanie kinematyki sà zbli˝one i to
zarówno w oszacowaniach teoretycznych, jak i wyz-
naczonych doÊwiadczalnie.

Przedstawione w pracy aproksymacje otrzymanych

wyników rozk∏adem normalnym nale˝y uznaç za
poprawne i dobrze odzwierciedlajàce cz´stoÊç wy-
stàpieƒ poszczególnych czasów cyklów. Zaprezen-
towane wyniki oszacowaƒ teoretycznych i prak-
tycznych mogà u∏atwiç poprawny dobór typu ste-
rownika do okreÊlonych zadaƒ pod wzgl´dem spe∏-
nienia wymagaƒ czasu rzeczywistego.

LITERATURA

1.

KwaÊniewski J.: Programowalne sterowniki przemys∏owe
w systemach sterowania. Kraków 1999.

2. Siemens. Simatic S7-300 Programmable Controller. Instruc-

tion List.

3

Tadeusiewicz R.: Modelowanie komputerowe i obliczenia
wspó∏czesnych uk∏adów automatyzacji

. Wyd. AGH, Kraków

2004.

E

ROK WYD. LXV

앫 ZESZYT 2/2006

4 4

4.

Berger

H

.: Automating with STEP7 in STL and SCL. SIMATIC

S7-300/400

.

Programmable Controllers. Publicis MCD Cor-

porate Publishing, 2001.

5.

Kwiecieƒ

A.,

Sidzina

M.: Metody skracania czasu wymian

wyzwalanych w sieciach przemys∏owych typu MASTER-
-SLAVE. XI Konferencja Systemów Czasu Rzeczywistego.
Ustroƒ, 13 – 16 wrzeÊnia 2004.

6.

Doniec ¸

.: Stabilizacja obrotów obiektu z elementem elas-

tycznym o du˝ej podatnoÊci

.

Praca dyplomowa magisterska.

Wydzia∏ In˝ynierii Mechanicznej i Robotyki. AGH, Kraków
2004.

7. Siemens. Simatic S7-300 Programmable Controller. Manual.

Edition 03/99. Installation and Hardware.

8.

Oprz´dkiewicz

K.:

Spe∏nienie wymagaƒ czasu rzeczywistego

w Êrodowisku sprz´towo-programowym soft PLC podczas
realizacji predyktora Smitha. Informatyka teoretyczna i sto-
sowana. Instytut Matematyki i Informatyki, Politechnika
Cz´stochowska, rocznik 4, nr 7/2004.

Dokoƒczenie z 43 str.