Dynamika ruchu obrotowego bryły sztywnej 

Wyznaczanie momentu bezwładności 

Ćw.2 

 

Cel ćwiczenia 

Sprawdzenie słuszności równania dynamiki ruchu obrotowego 

ε = M/I oraz wyznaczenie momentu 

bezwładności przyrządu do badania ruchu obrotowego. 

 

Zakres obowiązującego materiału teoretycznego 

Kinematyka i dynamika ruchu obrotowego. Moment bezwładności, moment siły, moment pędu, środek 

masy, twierdzenie Steinera. Zasada zachowania momentu pędu. 

 

Przyrządy użyte w ćwiczeniu 

Suwmiarka, sekundomierz, przyrząd do badania ruchu obrotowego (PBRO). 

 

Wprowadzenia i aparatura 

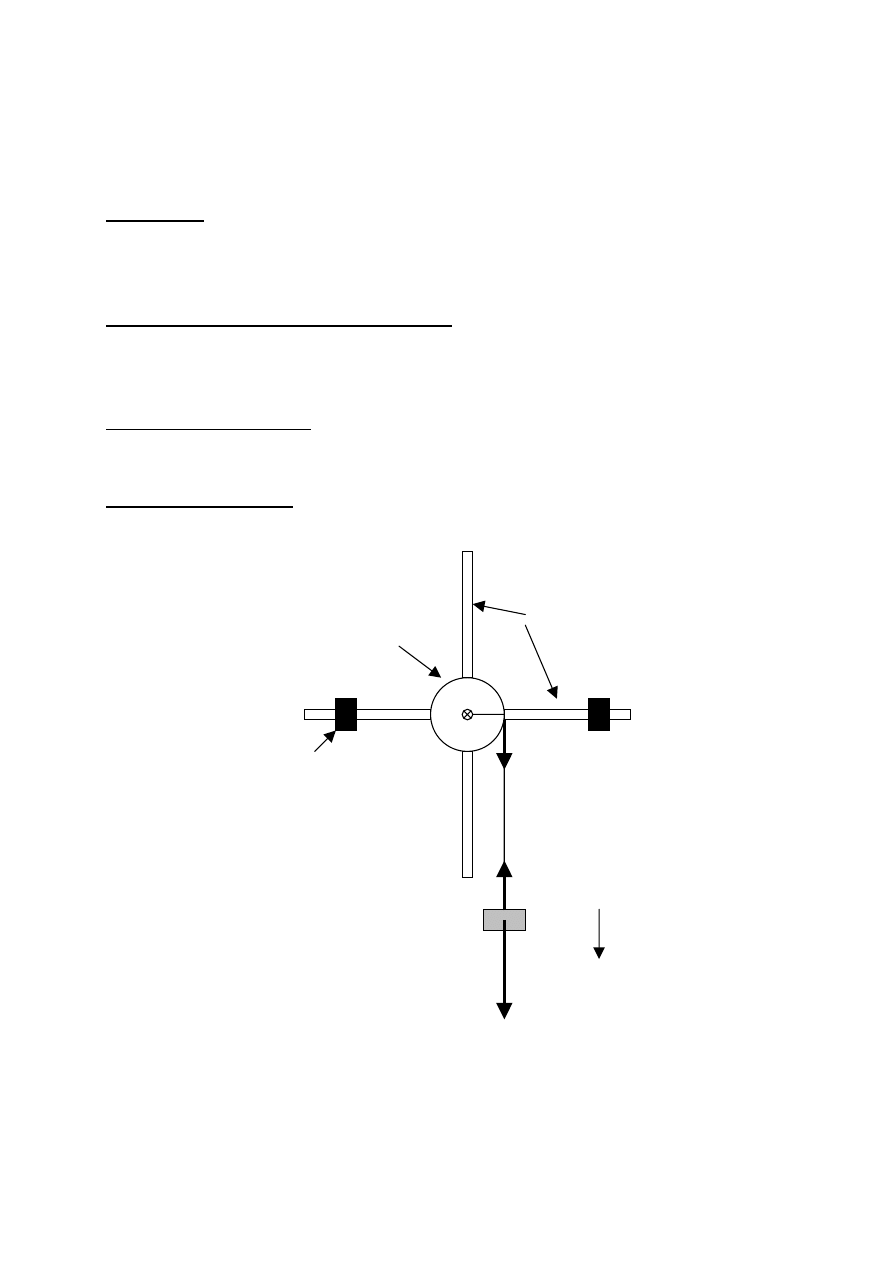
W doświadczeniu posługujemy się przyrządem do badania ruchu obrotowego, zilustrowanym na rys.1  

M

r

Q

r

N

r

ar

N

r

P 

C 

W 

a=F/m 
 
F=Q-N 
Q=mg 
 

r

1

 

Rys.1 

Walec metalowy C jest osadzony na łożyskach kulkowych i może obracać się wokół osi OO'. Z 

walcem połączone są cztery pręty stalowe P, na których osadzone są walce W. Walce W można 

przemieszczać wzdłuż prętów i zmieniać w ten sposób moment bezwładności urządzenia. Chcąc 

wprowadzić przyrząd w ruch obrotowy obciążamy nić masą m.  

Druga zasada dynamiki Newtona dla ruchu obrotowego ma postać: 

 

I

M

=

ε

 

 

(1) 

Gdzie: 

M - moment wypadkowy działających sił 

I - moment bezwładności urządzenia PBRO 

ε- przyspieszenie kątowe 

 

Sprawdzenie słuszności równania (1), co jest głównym celem ćwiczenia, dokonujemy w następujący 

sposób. Dla warunków doświadczalnych wynikających z geometrii i dynamiki urządzenia PBRO 

wyliczamy na drodze teoretycznej wartości: 

1 - momentu wypadkowego działających sił M 

2 - momentu bezwładności urządzenia PBRO - I 

3 - przyspieszenia kątowego 

ε urządzenia PBRO.  

Wyliczone wartości I, M oraz 

ε podstawiamy do równania (1) otrzymując wyrażenie, którego słuszność 

potwierdzamy na drodze doświadczalnej. 

 

Moment siły T 

W omawianym przypadku, moment siły naciągu N jest momentem obrotowym M i wyraża się wzorem: 

N

r

M

1

=

;         

N

ma

mg

−

=

 

(2) 

Gdzie: 

r

1

 - promień tej części walca C na której nawinięta jest nić. 

N - siła naciągu nici. 

m - masa ciężarka. 

 

Moment bezwładności urządzenia PBRO 

Moment bezwładności urządzenia PBRO jest sumą:  

- 

momentu bezwładności walca C - I

c

; 

- 

momentu bezwładności czterech prętów P - 4I

p

;  

- 

momentu bezwładności dwóch ruchomych walców W równego 2I

w

 + 2m

w

(d/2)

2

 

Masa walca W oznaczona jest symbolem m

w

, a d jest odległością przeciwległych walców. I

w

 jest 

momentem bezwładności walca ruchomego względem osi przechodzącej przez jego środek masy i 

wynikającym z twierdzenia Steinera.  

Całkowity moment bezwładności urządzenia PBRO wynosi wiec: 

 

2

d

m

I

2

I

4

I

I

2

w

w

p

c

+

+

+

=

 

(3) 

 

a wprowadzając oznaczenie 

w

p

c

o

I

2

I

4

I

I

+

+

=

 

 

otrzymamy 

2

d

m

I

I

2

w

o

+

=

 

(3) 

I

o

 - ma wartość stałą. 

 

Przyspieszenie kątowe urządzenia PRBO 

Przyspieszenie kątowe 

ε urządzenia PBRO obliczamy na podstawie pomiaru czasu przebycia znanej 

drogi przez ciężarek obciążający nić. 

 

2

at

s

2

=

;   

   (prędkość początkowa wynosi 0) 

1

r

a

ε

=

 

(4) 

 

Gdzie: s, a - droga i przyspieszenie ciężarka obciążającego nić. 

Stąd: 

2

1

t

r

s

2

=

ε

 

 

(5) 

 

Podstawiając wyrażenia (3), i (5) do równania (1) otrzymujemy po prostych przekształceniach: 















+

+

=

m

r

I

1

g

s

2

d

mg

r

sm

t

2

1

o

2

2

1

w

2

 

 

(7) 

 

W układzie współrzędnych prostokątnych, w którym na osi y odkładamy  t

2

, a na osi x wartości  d

2

, 

równanie (7) jest równaniem prostej 

 

B

Ax

y

+

=

 

(8) 

 

Gdzie: stale A i B można wyrazić następująco: 

 

mg

r

sm

A

2

1

w

=

 

 

(9) 

 













+

=

m

r

I

1

g

s

2

B

2

1

o

 

 

(10) 

 

Doświadczalnie potwierdzony prostoliniowy przebieg zależności t

2

 = f(d

2

) jest dowodem słuszności 

równania (1). 

 

Część doświadczalna 

W celu sprawdzenia słuszności równania dynamiki ruchu obrotowego dokonujemy pomiarów czasu t 

opadania ciężarka m ze stałej wysokości s=1,5 m w zależności od odległości d przeciwległych walców 

W. Zmieniając położenie ciężarków W zmieniamy moment bezwładności. Pomiary wykonujemy dla 4 

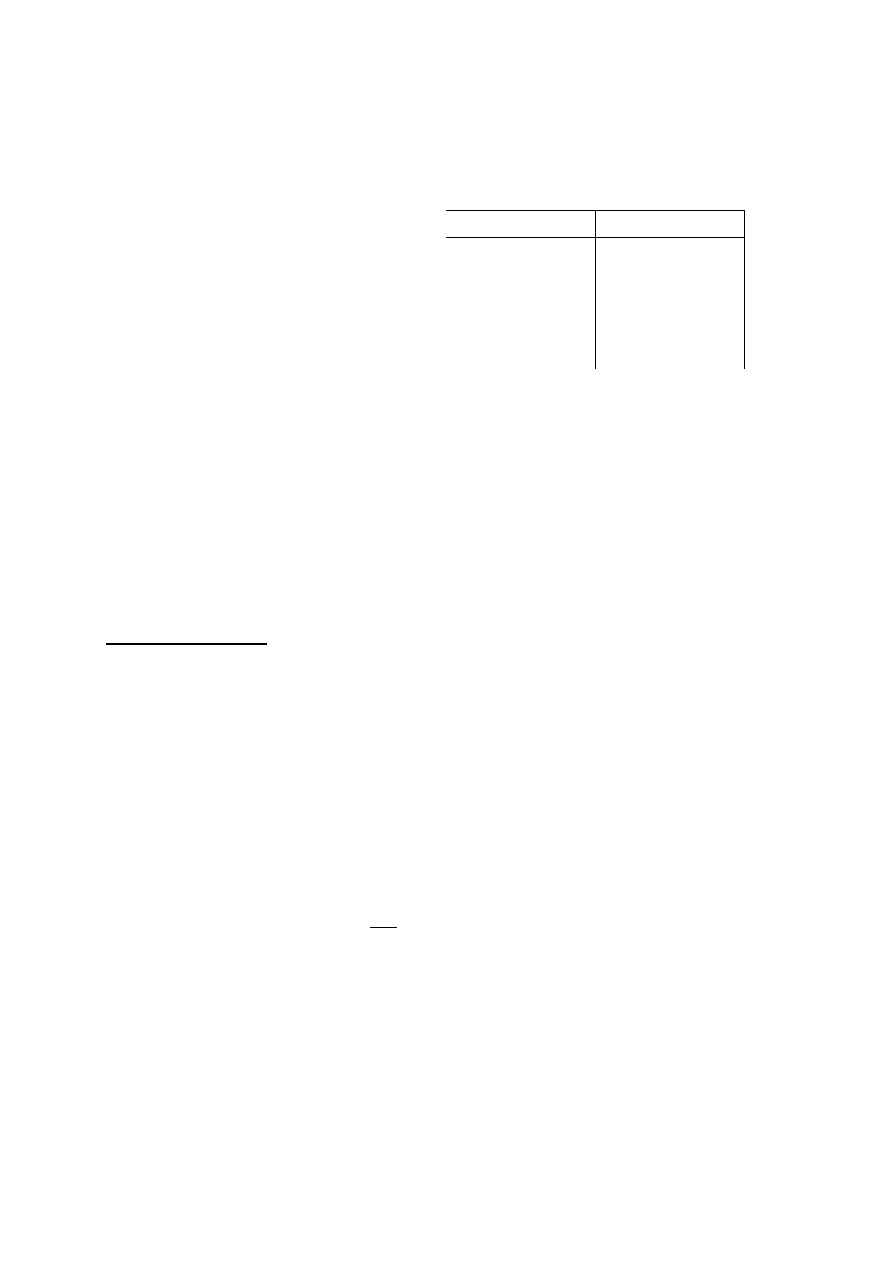
wartości odległości d, w zakresie (8,5-20)·10

-2

m. Wyniki liczbowe zamieszczamy w tabeli. Dla każdej 

wartości d, dokonujemy 6 pomiarów czasu opadania ciężarka t, biorąc do obliczeń wartość średnią. 

 

Tabela 1  

d [m] 

t [sek.] 

d

2

 [m

2

] t

2

 [sek

2

 ] 

d

1

 

t

1, 

…….. t

6

 

 

 

d

2

  

. 

. 

d

n 

 . 

. 

  

. . 

 

 

 

 

 

Wykreślamy zależność t

2

(d

2

), która zgodnie z równaniem (7) powinna być zależnością prostoliniową, 

opisywaną ogólnym równaniem prostej (8). Z wykresu t

2

(d

2

) dokonujemy oceny wartości stałych A i B.  

Dokładne wartości współczynników  A i B wyznaczamy korzystając ze statystycznej metody 

opracowania wyników pomiarów (metoda najmniejszych kwadratów). Podstawy teoretyczne tej 

metody wraz z konkretnym przykładem jej zastosowania zamieszczone są w instrukcji nr 17. 

Wartości współczynników  A i B wyznaczone z metody najmniejszych kwadratów porównujemy z 

wartościami współczynników A i B wyznaczonymi na wykresie zależności t

2

(d

2

). W przypadku braku 

zgodności sprawdzić obliczenia. 

 

Opracowanie wyników 

Sprawozdanie powinno zawierać:  

1. Określenie celu ćwiczenia i podanie podstawowych zależności. 

2. Sporządzić wykres zależności t

2

(d

2

) z wyników pomiarów zamieszczonych w Tabeli 1 (układ 

SI). 

2.1. Wykorzystując metodę najmniejszych kwadratów w odniesieniu do zależności t

2

(d

2

) 

wyznaczamy wartości stałych  A i B z równania (10). Z wartości stałej  B obliczamy 

moment bezwładności I

0

 dla urządzenia PBRO; 

2.2. Podać wartości momentu bezwładności  I

o

 urządzenia PBRO z uwzględnieniem błędu 

bezwzględnego ∆I

o

 (I

o

±∆I

o

) oraz obliczyć błąd względny 

 

%

100

I

I

o

o

×

∆

 

 

 

 
3. Wnioski 

końcowe.