Kompresja informacji

Kierunek

Specjalność

Rok studiów Symbol grupy lab.

Elektronika i Telekomunikacja

Telekomunikacja

4

CZ/P, 13:15

Temat

Numer lab.

Kwantowanie liniowe, kwantowanie dynamiczne i kwantowanie

nieliniowe w oparciu o krzywą

µµµµ

Ć

wiczenie nr 2

Skład grupy ćwiczeniowej

Uwagi

Ocena

1. Cel

ć

wiczenia

Celem ćwiczenia było zapoznanie się z procesem kwantowania liniowego i nieliniowego
w oparciu o krzywą

µ

.

2. Kwantyzacja liniowa

Pierwszym zadaniem było sprawdzenie działania oraz analizę otrzymanych wyników procesu
kwantyzacji liniowej. Proces kwantyzacji liniowej polega na podzieleniu nieskończonego
zbioru wartości próbek na zbiór o skończonej liczbie elementów. Zbiór możliwych wartości
zostaje podzielony na obszary, którym zostaje przyporządkowana jedna wartość. W procesie
kwantyzacji liniowej wszystkie zbiory są jednakowe co do długości. Liczba możliwych
wartości, jakie może przyjąć próbka jest ściśle związana z ilością bitów przetwornika, jest to
zależność:

k

przedział

liczba

2

_

=

,

gdzie:
k – liczba bitów przetwornika.

W tej części ćwiczenia należało wyznaczyć stosunek sygnał/szum (SQNR) dla różnej

ilości bitów przetwornika. SQNR można charakteryzować jako stosunek mocy sygnału do
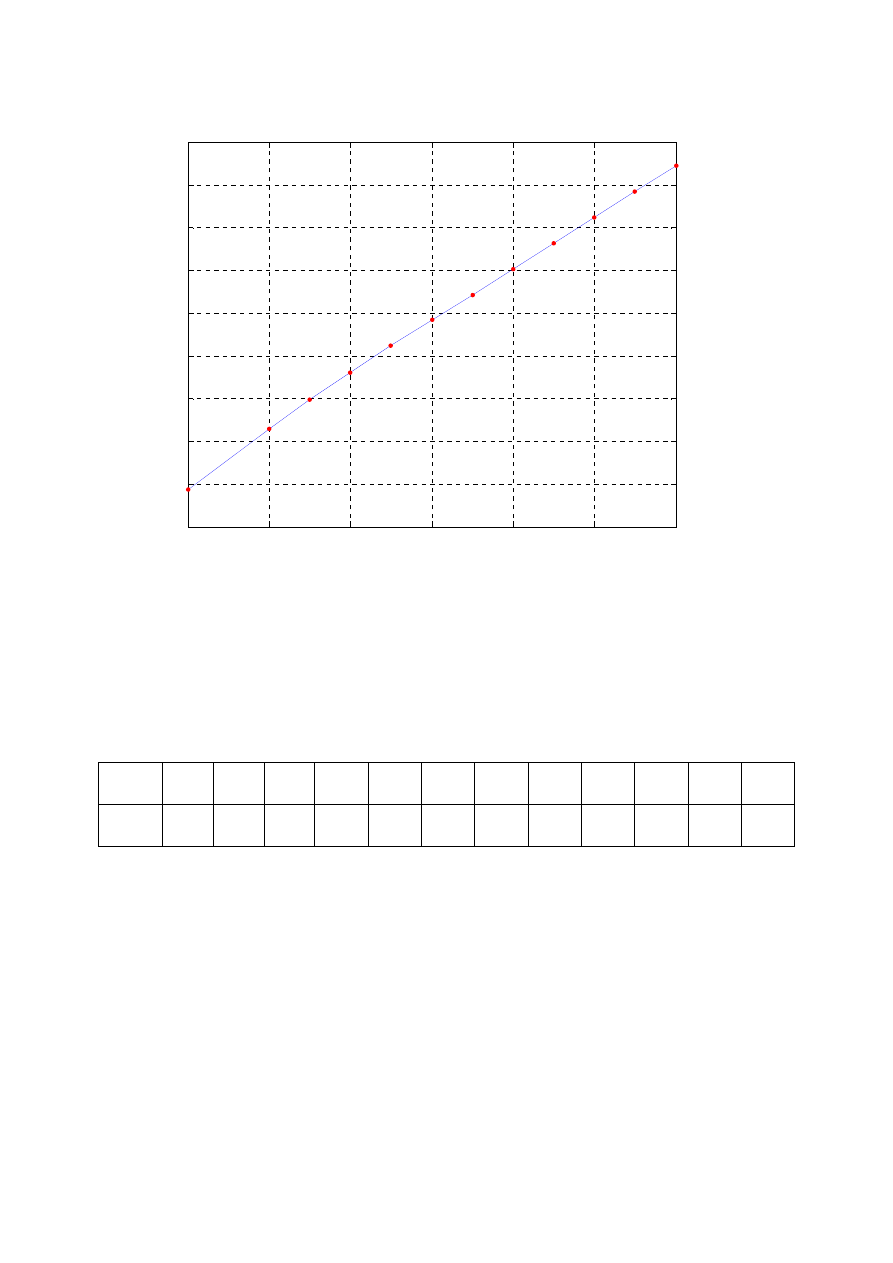
mocy szumu. Dla sygnału mowy „mowa.wav” wykreślono zależność stosunku sygnał/szum
od liczby bitów przetwornika. Zależność pokazano na poniższym rysunku (rys. 1).

4

6

8

10

12

14

16

-20

-10

0

10

20

30

40

50

60

70

Wykres zaleznosci SQNR od liczby bitów przetwornika

liczba bitów przetwornika

S

Q

N

R

[

d

B

]

Rysunek 1 Zależność SQNR od liczby bitów przetwornika

Jak łatwo zauważyć wykres powyższy jest w przybliżeniu linią prostą (szczególnie

widać to dla liczby bitów >10), wobec czego łatwo można sprawdzić o ile zwiększa się
SQNR, gdy do przetwornika doda się jeden bit. W poniższej tabeli (tab. 1) przedstawiono
dokładne wartości SQNR dla poszczególnych liczby bitów.

Tab. 1

liczba

bitów

4

6

7

8

9

10

11

12

13

14

15

16

SQNR

[dB]

-11.46

2.69

9.59 15.99 22.12 28.17 34.11 40.19 46.21 52.19 58.20 64.29

Po dodaniu kolejnego bitu do przetwornika stosunek sygnał/szum zwiększa się. Dzięki

skorzystaniu z metody regresji liniowej za pomocą programu komputerowego wyznaczono
współczynnik nachylenia prostej. Wynosi on 6,21 [dB/bit]. Dla projektowania przetworników
wystarczy założyć, że wzrost SQNR wynosi 6 [dB/bit]. Jest to bardzo ważna informacja i
pozwala dobrać odpowiednią liczbę bitów w przetworniku w zależności od oczekiwanego
SQNR.

Poniżej przedstawiono tabele (tab. 2), która przedstawia wyniki badań odsłuchowych

dla przetwornika o różnej ilości bitów.

Tab. 2

Liczba

bitów

1

2

3

4

5

6

7

8

Wrażenia

odsłucho

we

Brak

zrozumia-

łości

dźwięku

B. duże

szumy, b.

niewyra-

ź

ny

dźwięk

Duże

szumy,

niewyra-

ź

ny

dźwięk

Duże

szumy,

zniekszta-

cony

dźwięk

Duże

szumy,

wyra-

ź

ny

dźwięk

Duże

szumy,

wyra-

ź

ny

dźwięk

Słyszal-

ne

szumy,

wyraźny

dźwięk

Słyszal-

ne

szumy,

wyraźny

dźwięk

Liczba

bitów

9

10

11

12

13

14

15

16

Wrażenia

odsłucho

we

Lekkie

szumy,

wyraźny

dźwięk

Czysty i

wyraźny

dźwięk

Czysty i

wyraźny

dźwięk

Czysty i

wyraźny

dźwięk

Czysty i

wyra-

ź

ny

dźwięk

Czysty i

wyra-

ź

ny

dźwięk

Czysty i

wyraźny

dźwięk

Czysty i

wyraźny

dźwięk

Po wykonaniu badań odsłuchowych stwierdzono, że szumy zaczynają być słyszalne

gdy przetwornik posiada poniżej 10 bitów (początkowa wartość wynosiła 16 bitów). Jednak
mowa jest nadal zrozumiała.

3. Kwantyzacja dynamiczna

W tym ćwiczeniu badano jakość kwantyzera dynamicznego oraz porównanie go
z kwantyzerem liniowym 4-bitowym. Podczas działania kwantyzera dynamicznego
wyznaczono współczynnik nmse (normalized mean square error) – czyli znormalizowany
błąd średniokwadratowy.

Działanie tego kwantyzera przetestowano na tym samym sygnale co poprzednio

(mowa.wav), wynik działania 4-bitowego kwantyzera dynamicznego przedstawiono poniżej.

nmse – 0.0078,
SQNR – 21.0906 [dB].

Jak łatwo zauważyć, jest to wartość dużo wyższa niż osiągnięta przy kwantyzerze

liniowym 4-bitowym (-11.46 [dB]). Różnica wynosi ~ 32.5 [dB].

Badania odsłuchowe wykazały, ze sygnał skwantowany kwantyzerem dynamicznym

4-bitowym, odpowiada kwantowaniu 9-bitowemu dla kwantyzacji liniowej. Dla kwantowania
liniowego dla przetwornika 9 bitów SQNR= 22.12[dB]. Zaletą kwantyzerów dynamicznych
jest to, że można uzyskać wyższy SQNR niż za pomocą kwantyzerów liniowych, jednak
kosztem większej ilości operacji matematycznych wykonywanych na sygnale.

4. Kwantyzacja nieliniowa

•

Charakterystyka kompresora typu µ

Rodzina krzywych typu

µ

, to krzywe o różnym współczynniku. Są używane m. in. do tego,

aby próbki o małych amplitudach mogły być dokładniej kwantowane. Działanie kompresora
opiera się na przemnożeniu kolejnych próbek sygnału przez odpowiedni współczynnik, dzięki
temu próbki o małych amplitudach na czas kwantowania posiadają większe amplitudy.
Rodzinę krzywych typu

µ

kompresora przedstawiono poniżej (rys. 2). Współczynniki

wynoszą odpowiednio: [1,2,10,25,50,100,150,200,250,300]. Im współczynnik większy tym
bardziej krzywa jest „zagięta”.

-1

-0 . 8

-0 . 6

-0 . 4

-0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

-1

-0 . 8

-0 . 6

-0 . 4

-0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

c h a ra k t e ry s t y k a k o m p re s o ra t y p u u

w e js c ie

w

y

js

c

ie

Rysunek 2 Charakterystyka kompresora typu u

•

Charakterystyka dekompresora typu µ

Po kwantowaniu sygnał musi powrócić do swojej pierwotnej postaci, wobec czego

trzeba go przemnożyć przez współczynnik krzywej dekompresora. Ta krzywa musi mieć
ś

ciśle określony przebieg, aby sygnał mógł być odtworzony poprawnie. Na poniższym

rysunku (rys. 3) przedstawiono rodzinę krzywych dekompresora.

-1

-0 . 8

-0 . 6

-0 . 4

-0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

-1

-0 . 8

-0 . 6

-0 . 4

-0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

c h a ra k t e ry s t y k a d e k o m p re s o ra t y p u u

w e js c ie

w

y

js

c

ie

Rysunek 3 Charakterystyka dekompresora typu u

Poprawne dobranie krzywej gwarantuje prawidłowe odtworzenie przebiegu.

5. Rozkład amplitudy dla sygnału mowy

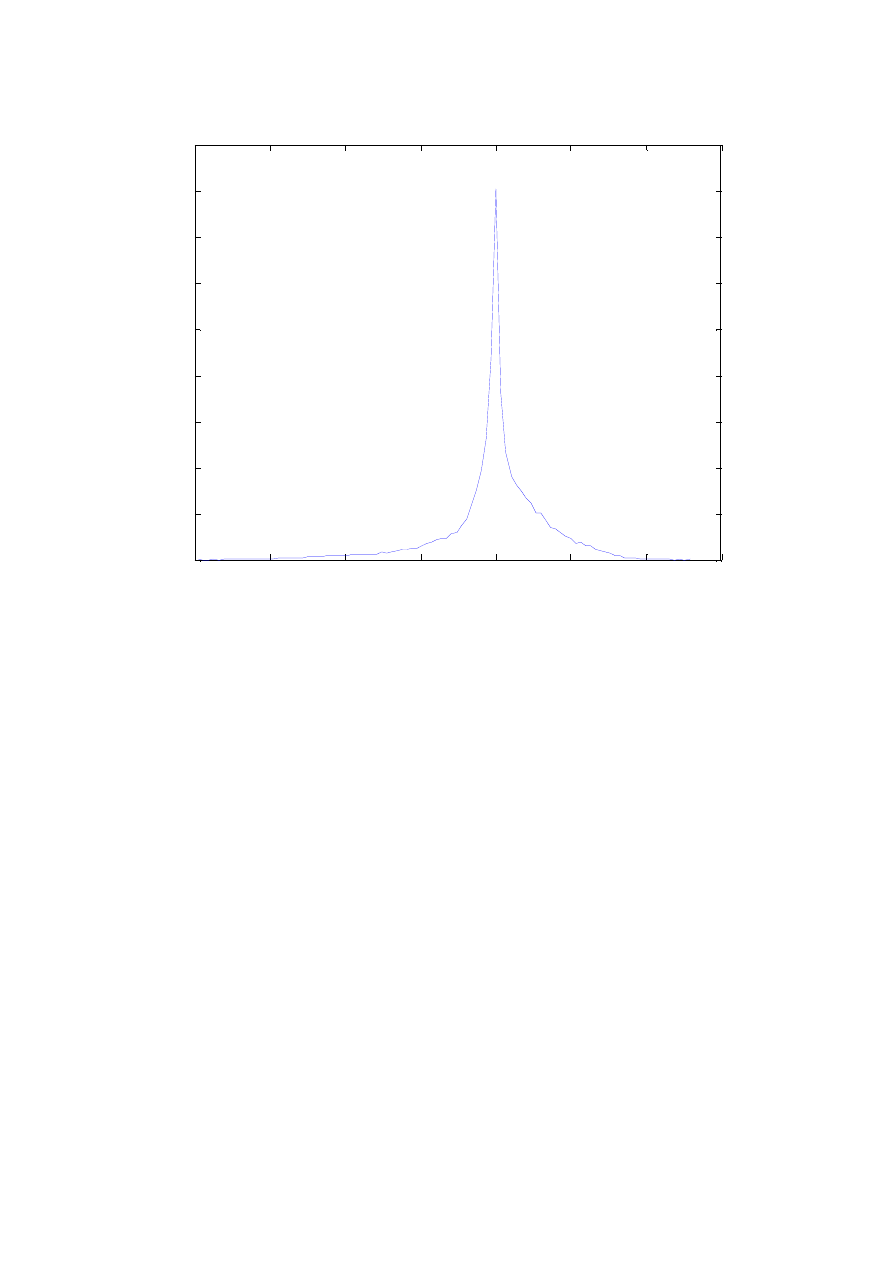
Kolejnym krokiem tego ćwiczenia było wykreślnie histogramu rozkładu amplitudy dla
badanego sygnału mowy (mowa.wav). Taki histogram utworzono dla 100 przedziałów
i zgodnie z teorią wartości próbek skupiły się w okolicach 0. Poniżej (rys. 4) przedstawiono
otrzymany histogram.

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0

1000

2000

3000

4000

5000

6000

7000

8000

9000

histogram rozkladu amplitudy dla sygnalu mowy

amplituda

il

o

s

c

p

ró

b

e

k

Rysunek 4 Histogram rozkładu amplitudy dla sygnału mowy

6. Kwantyzacja dla ró

ż

nych warto

ś

ci parametru µ

Kolejnym krokiem było przeprowadzenie kwantowania nieliniowego dla różnych ilości bitów
przetwornika oraz różnych wartości współczynnika µ. Takie doświadczenia pozwala
zaobserwować wpływ współczynnika krzywej na SQNR sygnału mowy. Do analizy
zastosowano ten sam sygnał mowy (mowa.wav), aby możliwe było porównanie wyników.

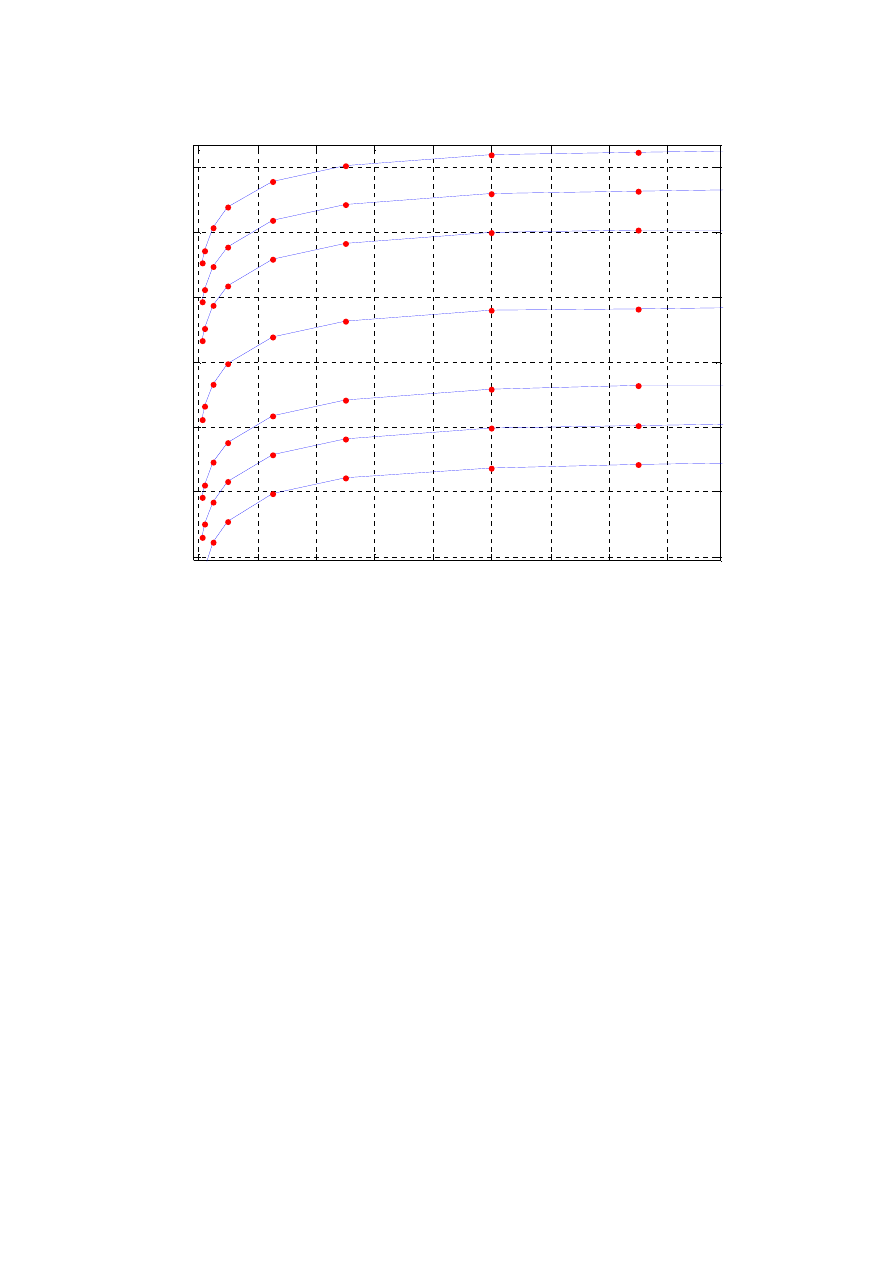
Dzięki wcześniejszym badaniom odsłuchowym możliwe było stwierdzenie, że dla

SQNR=28 [dB] szum nie jest słyszalny. Na poniższym rysunku (rys. 5) przedstawiono wynik
symulacji.

0

20

40

60

80

100

120

140

160

10

20

30

40

50

60

70

wartosc wspolczynnika u

S

Q

N

R

[

d

B

]

zaleznosc SQNR od wartosci wspolczynnika krzywej u dla roznych ilosci bitow przetwornika

Rysunek 5 Zależność SQNR od wartości współczynnika u

Po przeanalizowaniu wyników symulacji można zauważyć, że wymagany poziom

(około 28[dB]) można osiągnąć dzięki przetwornikowi 7-bitowemu po zastosowaniu krzywej
µ o współczynniku powyżej 50. Ewentualnie skorzystać można z przetwornika 8-bitowego
i zastosować współczynnik krzywej większy od 15.

Łatwo można zauważyć, że po przekroczeniu współczynnika o wartości 100 nie

następuje dalszy widoczny wzrost SQNR, wiec nie ma dalszej poprawy jakości.

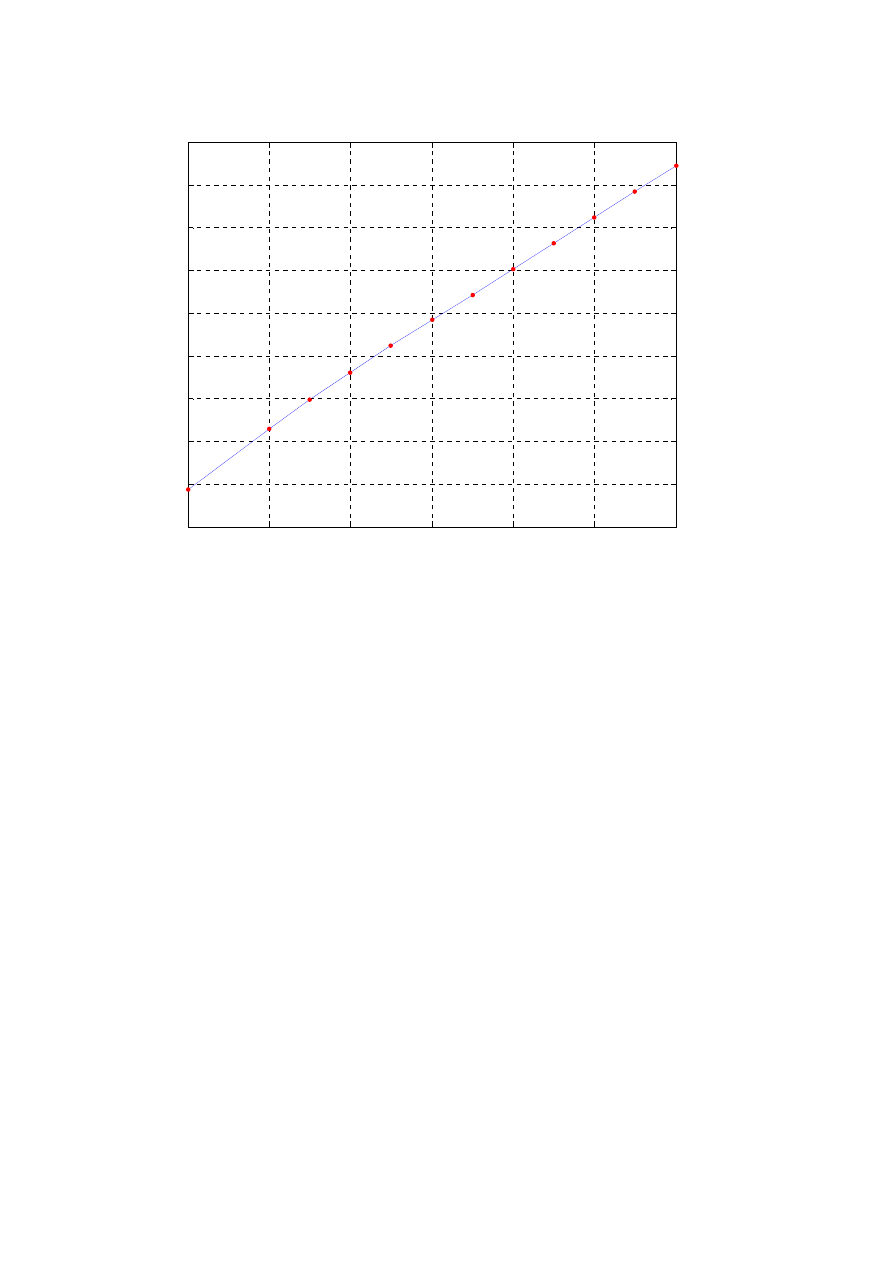
Dla porównania wyników przytoczono wykres z ptk. 1 i naniesiono na niego

wymagany SQNR dla niezaszumionego dźwięku.

4

6

8

10

12

14

16

-20

-10

0

10

20

30

40

50

60

70

Wykres zaleznosci SQNR od liczby bitów przetwornika

liczba bitów przetwornika

S

Q

N

R

[

d

B

]

Rysunek 6 zależność SQNR od liczby bitów przetwornika

7. Wnioski

Przeprowadzone ćwiczenie miało na celu przybliżenie działania operacji kwantyzacji,
zarówno liniowej jak i nieliniowej. Kwantyzacja nieliniowa nie zakłada jednakowych
przedziałów kwantyzacji, wobec czego czasami może dawać lepsze wyniki. Kwantyzacja
nieliniowa jest pożądana w sytuacjach, gdy rozkład prawdopodobieństwa występowania
próbek nie jest jednostajny (np. tak jest dla sygnału mowy – próbki o małych amplitudach
występują częściej co można zaobserwować na przedstawionym histogramie). Dla
odpowiednich sygnałów taki sposób kwantyzacji da lepsze wyniki w postaci większego
SQNR.

Sygnał mowy jest jednym w typów sygnałów, dla którego zalecane jest stosowanie

kwantyzera nierównomiernego z krzywa typu µ, co znacznie zwiększa SQNR.

Kwantyzery dynamiczne są zalecane dla kwantyzacji sygnału o przetwornikiem o

małej liczbie bitów (2-5), gdyż daje to lepsze rezultaty niż ta sama operacja na przetworniku
liniowym. Jednak kosztem jest duża złożoność operacyjna, przez to ten typ kwantyzacji nie
jest dobrym rozwiązaniem dla kwantowania sygnału za pomocą przetwornika o liczbie bitów
większej niż 5.