Laboratorium nr 3 

1/3 

y

min

 

y

max

 

(0,0) 

x

min

 

x

max

 

 

1) 

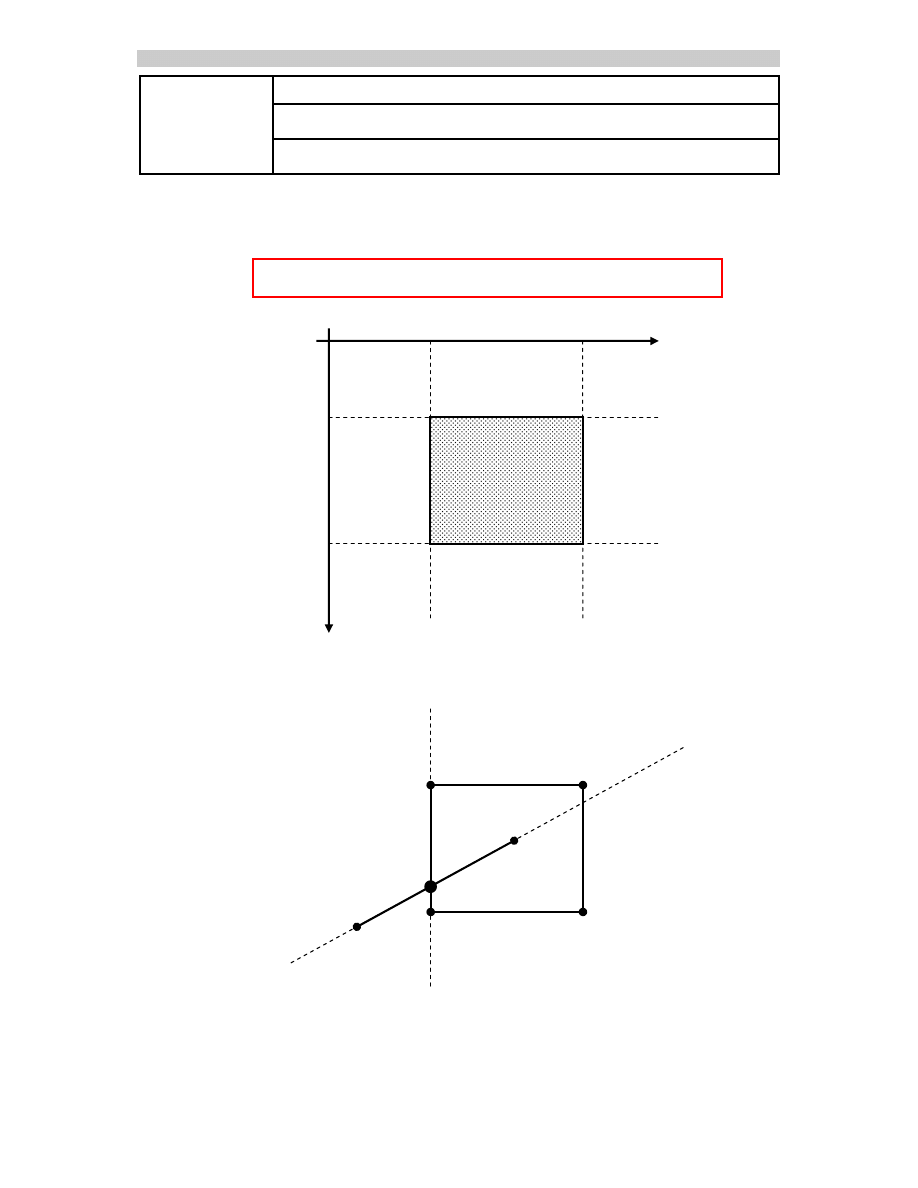
Obcinanie odcinków do prostokąta 

 

Prostokąt obcinający jest figurą regularną o bokach  

 równoległych do osi układu współrzędnych 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.1) 

Punkt przecięcia dwóch prostych 

 

 

 

 

 

 

 

 

 

 

 

b

ax

y

+

=

 - równanie prostej przechodzącej przez punkt P

0

 i P

1

 

d

cx

y

+

=

 - równanie prostej przechodzącej przez punkt A i B 

 

Grafika Komputerowa 2D 

Temat: Obcinanie odcinków do prostokąta 

 

Instrukcja 

laboratoryjna 

3 

Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota 

P

0

(x

0

,y

0

) 

P

1

(x

1

,y

1

) 

A(x,y) 

B(x,y) 

d

cx

y

+

=

 

P

2

(x

2

,y

2

) 

b

ax

y

+

=

 

Laboratorium nr 3 

2/3 

W  celu  obliczenia  punktu  przecięcie  między  dwoma  prostymi  rozwiązujemy  układ 

równań: 







+

=

+

=

d

cx

y

b

ax

y

 

 

1.2) 

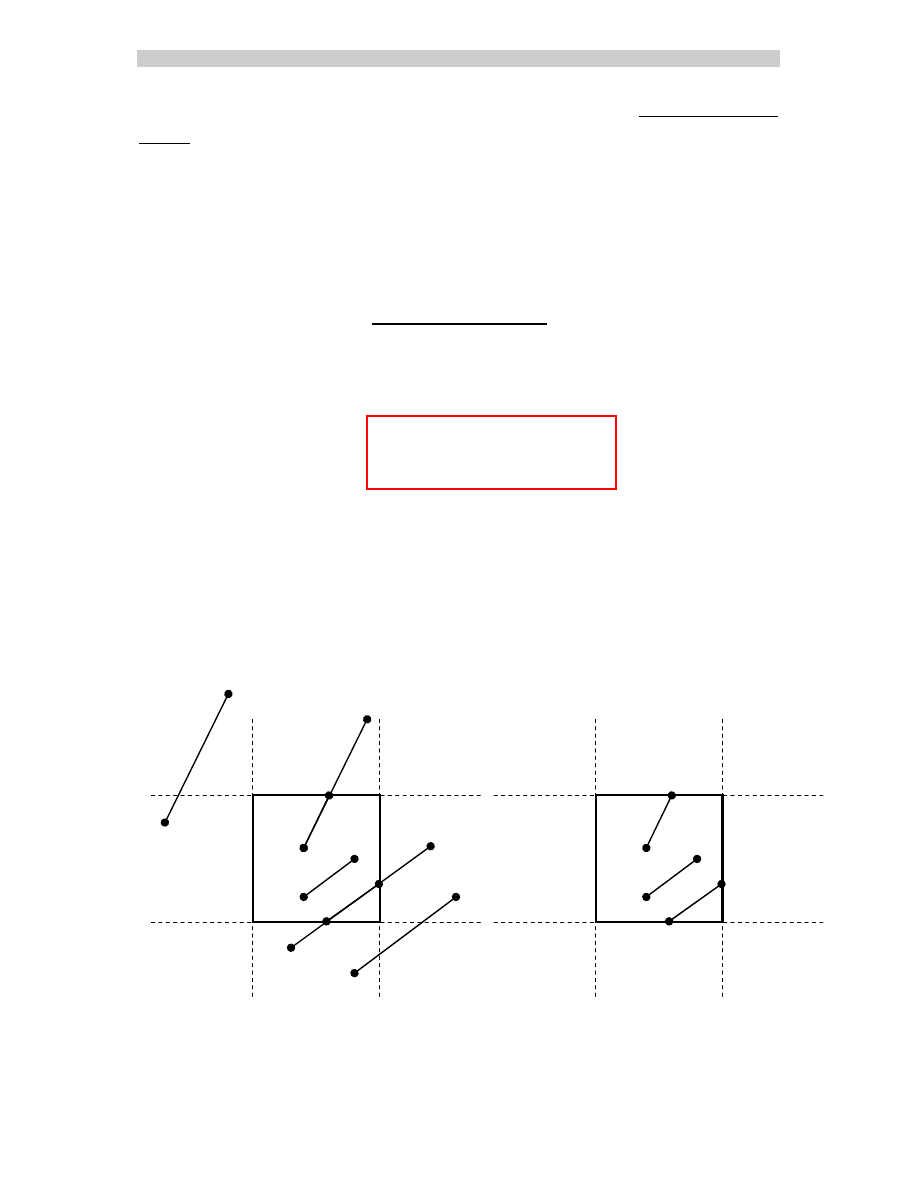
Obcinanie punktów 

 

Jeżeli  współrzędnymi 

x  prostokąta  obcinającego  są  x

min

  i  x

max

,  a  granicznymi 

współrzędnymi 

y  są  y

min

  i  y

max

  to  na  to,  żeby  punkt 

A(x,y)  był  wewnątrz  prostokąta 

obcinającego, muszą być spełnione cztery nierówności: 

 

max

min

x

x

x

≤

≤

 

max

min

y

y

y

≤

≤

 

 

Jeżeli jedna z tych czterech nierówności nie jest spełniona, to punkt leży, na zewnątrz 

prostokąta obcinającego. 

 

1.3) 

Obcinanie odcinków 

 

 

 

 

B 

A 

C 

D 

C’ 

E 

F 

G 

H 

G’ 

H’ 

I 

J 

B 

A 

C 

C’ 

G’ 

H’ 

Laboratorium nr 3 

3/3 

W celu obcięcia odcinka musimy wziąć pod uwagę tylko jego 

punkty końcowe, a nie 

nieskończenie  wiele  punktów  wewnętrznych.  Jeżeli  oba  punkty  końcowe  odcinka  leżą 

wewnątrz prostokąta obcinającego, to cały odcinek leży wewnątrz prostokąta obcinającego i 

może  być  bezpośrednio  zaakceptowany.  Jeżeli  jeden  koniec  odcinka  leży  wewnątrz 

prostokąta  obcinającego,  a  drugi  na  zewnątrz,  to  odcinek  przecina  prostokąt  obcinający  i 

musimy  obliczyć 

punkt  przecięcia.  Jeżeli  oba  końce  odcinka  leżą  na  zewnątrz  prostokąta 

obcinającego,  to  odcinek  może  (nie  musi)    przecinać  prostokąt  obcinający  i  musimy 

przeprowadzić dalsze obliczenia w celu ustalenia, czy są inne przecięcia, a jeśli są to gdzie 

się znajdują. 

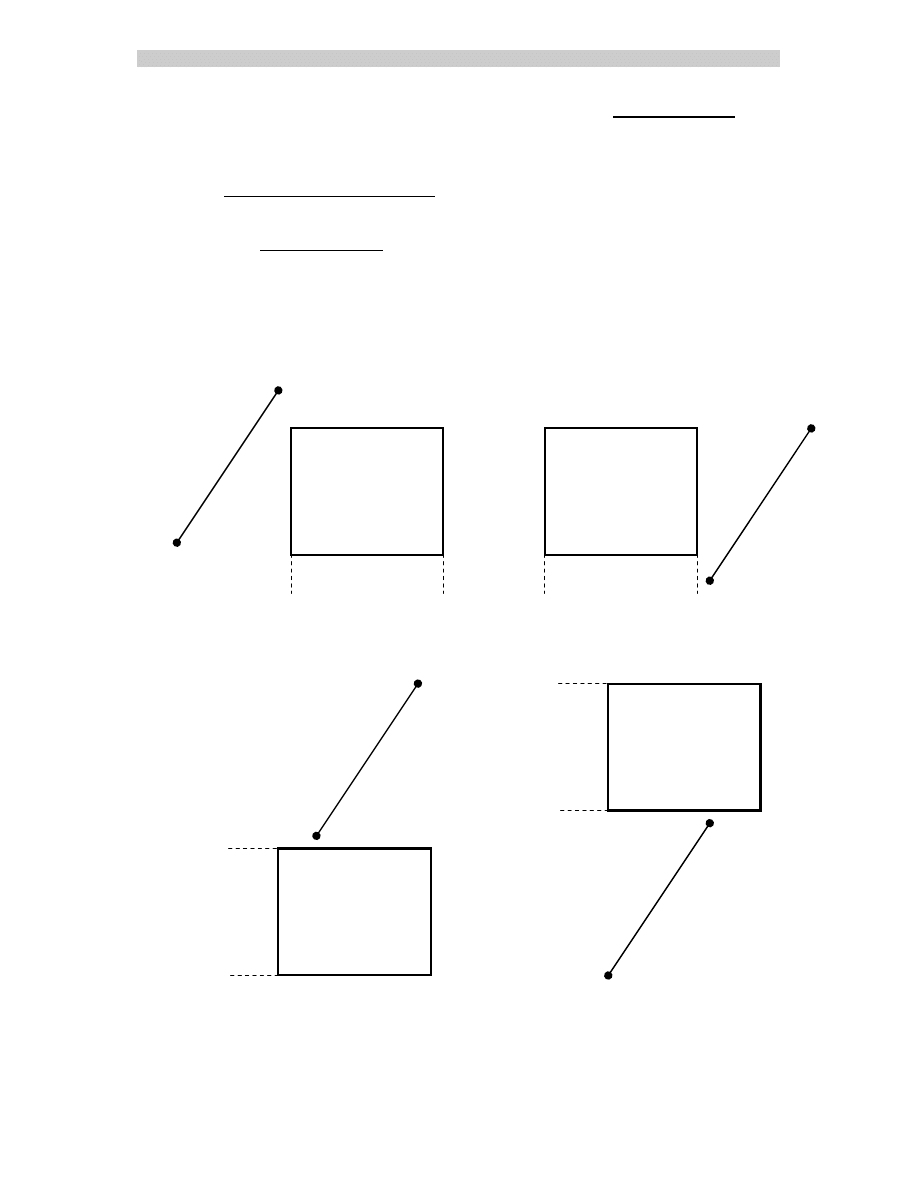
Przypadki dla których nie dokonujemy obcinania: 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

0

(x

0

,y

0

) 

x

min

 

x

max

 

X

0

, X

1

 < X

min 

P

1

(x

1

,y

1

) 

P

0

(x

0

,y

0

) 

x

min

 

x

max

 

X

0

, X

1

 > X

max 

P

1

(x

1

,y

1

) 

P

0

(x

0

,y

0

) 

y

min

 

y

max

 

Y

0

, Y

1

 < Y

min 

P

1

(x

1

,y

1

) 

P

0

(x

0

,y

0

) 

y

min

 

y

max

 

Y

0

, Y

1

 > Y

max 

P

1

(x

1

,y

1

)