JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

Zależność liniowa

(regresja II rodzaju dla dwóch zmiennych)

JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

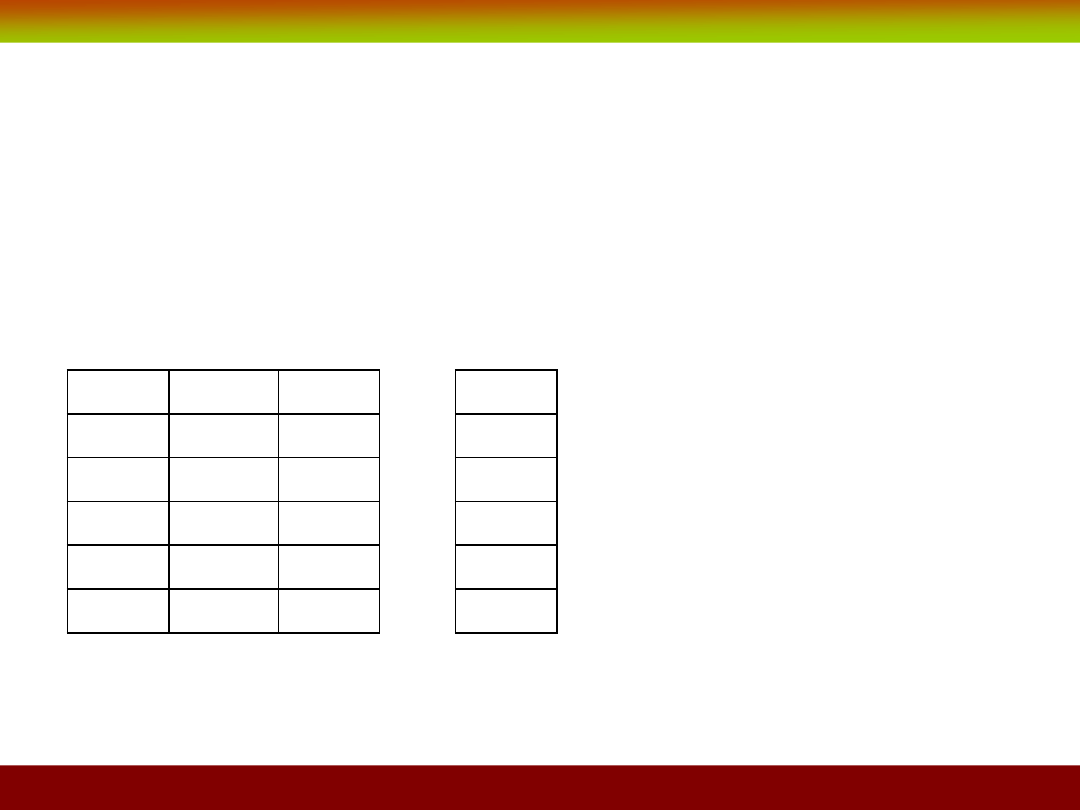
Przykład

Niech zmienna X oznacza staż pracy (w latach), a zmienna Y – wiek (również
w latach).

Mamy 5

– osobową populację, dla której wartości zmiennych X i Y przedstawia

tabela:

Lp.

X

Y

1

12

30

2

2

25

3

4

20

4

10

40

5

15

35

E(X|Y)

12

2

4

10

15

Regresja średnich ma tyle
wartości, ile zmienna Y.

W tym przypadku

– jest tyle

wartości, ile osób w populacji.
MODEL NICZEGO NIE
UPRASZCZA, więc nie wiadomo,
po co go stosować

JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

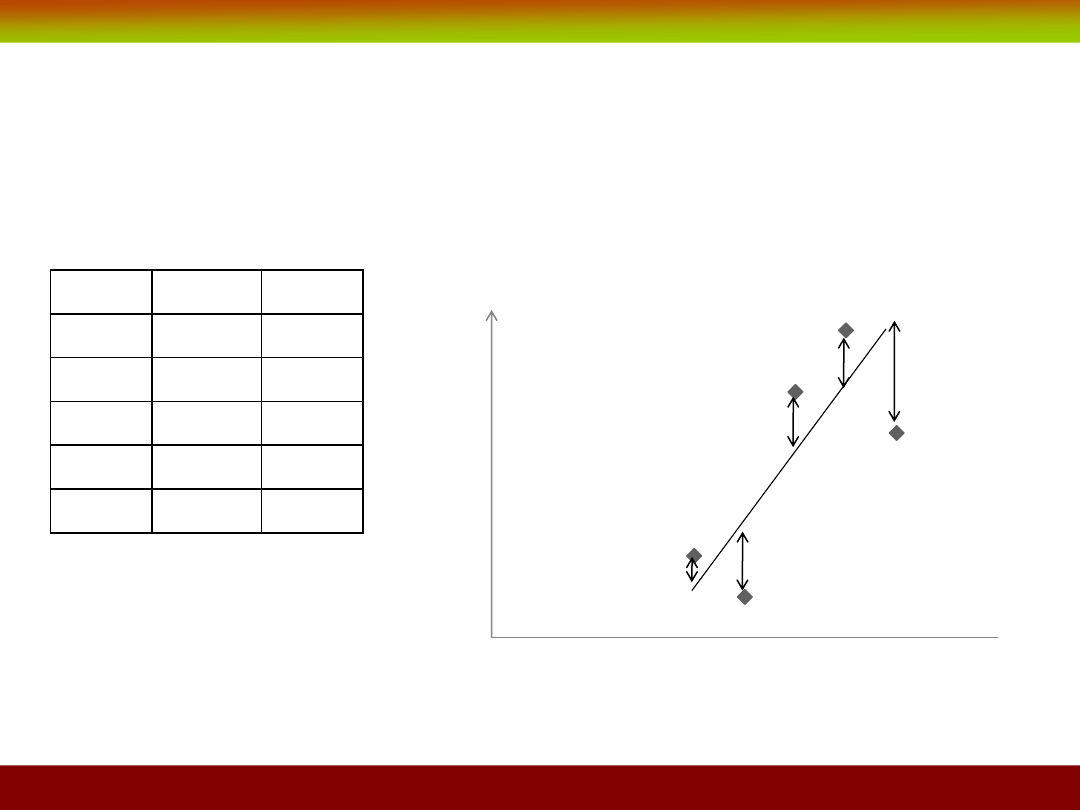
Przykład

X -

staż pracy (w latach), a zmienna Y – wiek (również w latach).

Lp.

X

Y

1

12

30

2

2

25

3

4

20

4

10

40

5

15

35

0

2

4

6

8

10

12

14

16

0

10

20

30

40

50

Rozwiązaniem jest zastosowanie modelu liniowego

JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

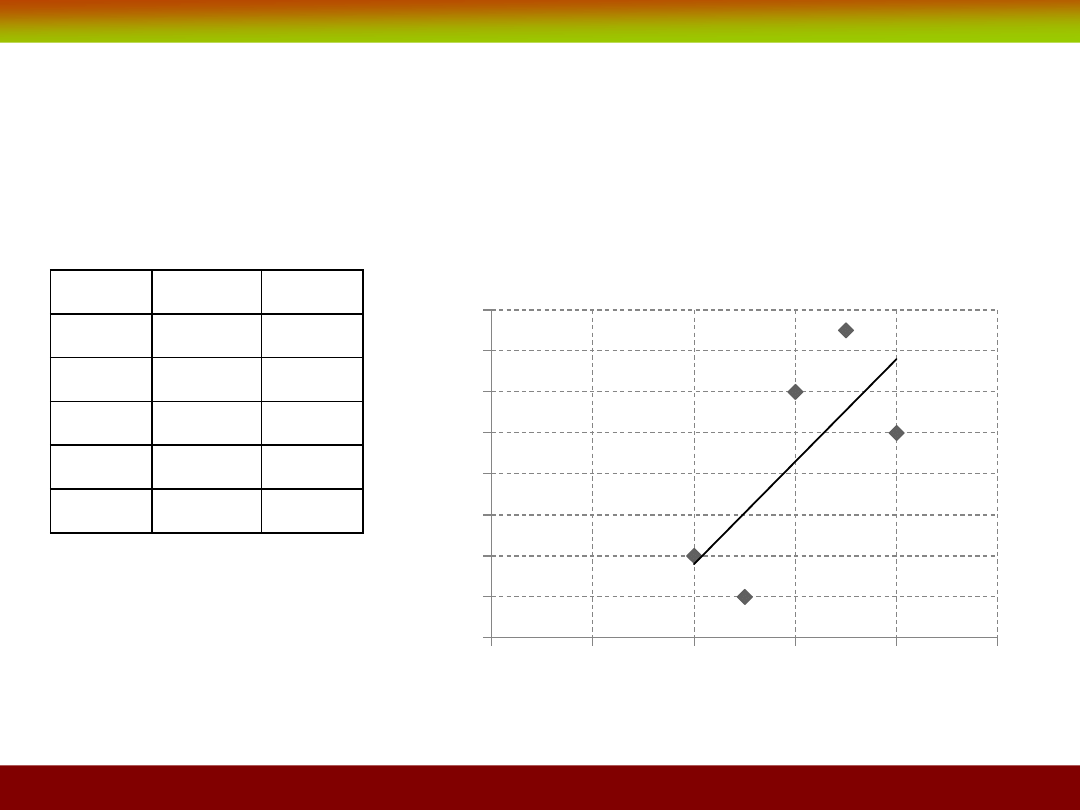
Przykład

X -

staż pracy (w latach), a zmienna Y – wiek (również w latach).

Lp.

X

Y

1

12

30

2

2

25

3

4

20

4

10

40

5

15

35

x = 0,5y - 6,4

0

2

4

6

8

10

12

14

16

0

10

20

30

40

50

Prosta ma spełniać warunek minimalizacji średniego kwadratu błędu

JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

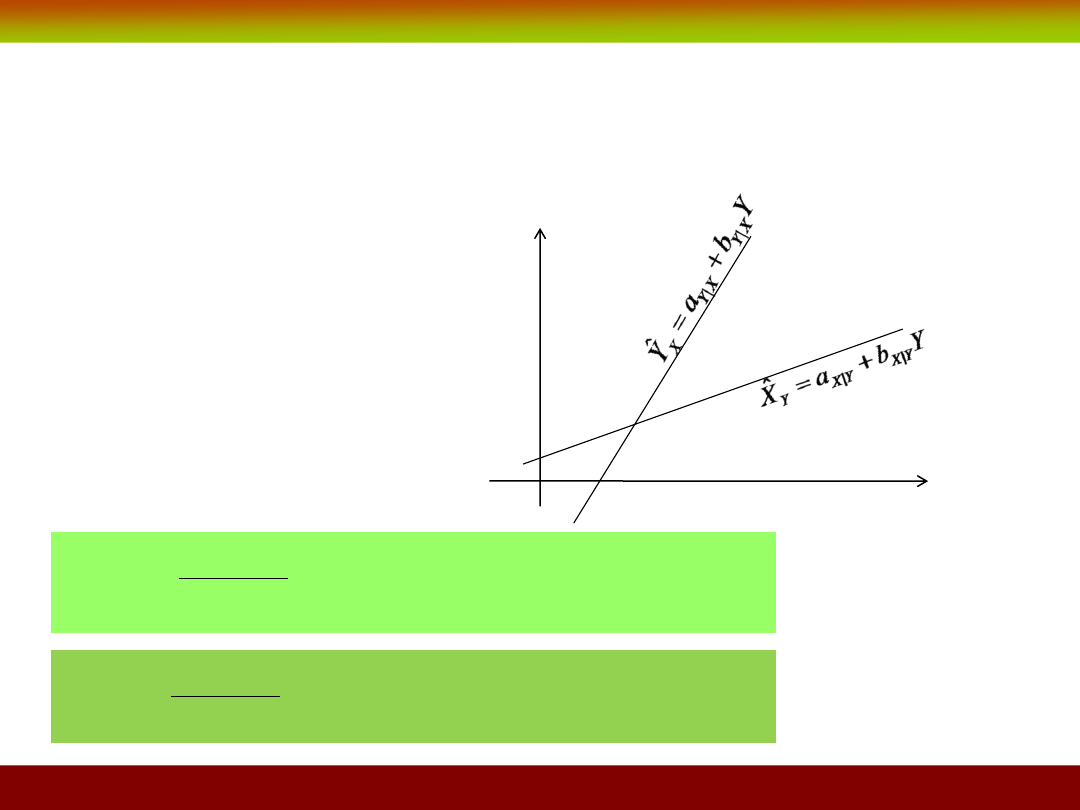
Regresja liniowa (najmniejszych kwadratów)

Linear regression (least square regression)

Y

b

a

X

Y

X

Y

X

Y

|

|

ˆ





Y

b

a

Y

X

Y

X

Y

X

|

|

ˆ





X

X

Y

,

ˆ

Y

Y

X

,

ˆ

)

(

)

,

(

2

|

Y

D

Y

X

c

b

Y

X



)

(

)

,

(

2

|

X

D

Y

X

c

b

X

Y



)

(

)

(

|

|

Y

E

b

X

E

a

Y

X

Y

X





)

(

)

(

|

|

X

E

b

Y

E

a

X

Y

X

Y





JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

Przykład

X -

staż pracy (w latach), a zmienna Y – wiek (również w latach).

Lp.

X

Y

1

12

30

2

2

25

3

4

20

4

10

40

5

15

35

Wyznaczmy regresję liniową X od Y

Y

b

a

X

Y

X

Y

X

Y

|

|

ˆ





Interpretacja współczynników równania:

Y

X

Y

5

,

0

4

,

6

ˆ







0,5

– jeśli porównamy 2 osoby różniące się wiekiem o 1 rok, to przewidujemy, że

osoba starsza będzie miała staż pracy dłuższy o 0,5 roku;

-6,4

– hipotetyczny przewidywany staż pracy osoby, której wiek wynosiłby 0 lat.

JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

Przykład

X -

staż pracy (w latach), a zmienna Y – wiek (również w latach).

Lp.

X

Y

1

12

30

2

2

25

3

4

20

4

10

40

5

15

35

Y

X

Y

5

,

0

4

,

6

ˆ







Każda zmienna zostaje poddana standaryzacji, a dopiero potem wyznaczane jest
równanie regresji. Równanie regresji w wersji standaryzowanej ma wyraz wolny
równy 0. Dlaczego?

Ze względu na to, że „wyraz wolny” w równaniu
regresji stwarza niekiedy trudności
interpretacyjne, stosuje się często
standaryzowaną postać równania regresji

JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

Standaryzowana postać równania regresji

U

– standaryzowana zmienna X (staż pracy)

W

– standaryzowana zmienna Y (wiek)

Lp.

X

Y

U

W

1

12

30

0,696347

0

2

2

25

-1,35173

-0,70711

3

4

20

-0,94212

-1,41421

4

10

40

0,286731 1,414214

5

15

35

1,310771 0,707107

Y

X

Y

5

,

0

4

,

6

ˆ







Interpretacja równania w wersji standaryzowanej:

Współczynnik stojący przy zmiennej zależnej, to współczynnik korelacji (Pearsona)

Jeśli porównamy 2 osoby różniące się wiekiem o 1 odchylenie standardowe, to przewidujemy,
że osoba starsza będzie się miała staż pracy dłuższy o 0,72 odchylenia standardowego.

W

U

W

72

,

0

ˆ



JOANNA KONIECZNA-SAŁAMATIN

Statystyka dla socjologów

Collegium Civitas

Miernik siły zależności przy regresji liniowej

(Kwadrat współczynnika korelacji liniowej)

Lp.

X

Y

1

12

30

2

2

25

3

4

20

4

10

40

5

15

35

)

(

)

ˆ

(

)

(

)

ˆ

(

)

(

2

2

2

2

2

2

,

X

D

X

D

X

D

X

X

E

X

D

Y

Y

Y

X











)

(

)

(

)

,

(

2

2

2

2

,

Y

D

X

D

Y

X

c

Y

X





Miernik ten pokazuje, jaką część zróżnicowania zmiennej X udało się odtworzyć
za pomocą modelu liniowego.
A zatem mierzy on:
•

liniowość zależności

•

siłę zależności liniowej