Deterministyczne Modele

Badań Operacyjnych

Jesień 2011

Egzamin, II termin

14 lutego 2012

Imię, nazwisko i numer indeksu:

Zadanie

1

2

Łącznie

Punkty do zdobycia

10

15

25

Punkty uzyskane

1. (Uczta na Wawelu) Książę Krak postanowił uczcić uratowanie Baltazara Gąbki

przez Smoka Wawelskiego i jego kompanów wyprawieniem wystawnej kolacji. Bar-

tolini Bartłomiej herbu Zielona Pietruszka otrzymał zadanie przygotowania odpo-

wiedniego menu dla każdego z gości: księcia Kraka, Smoka Wawelskiego i Baltazara

Gąbki. Nadworny kuchmistrz postanowił ograniczyć się jedynie do dwóch posiłków:

pieczonej jagnięciny i żabich udek. W ciągu godziny pracy Bartolini jest w stanie

przyrządzić 3 kg jagnięciny albo 1 kg żabich udek. Kolacja musi być przygotowana

według określonych zasad. Wiadomo, że:

1. Bartolini może poświęcić co najwyżej 10 godzin na przygotowanie uczty;

2. według dworskiej etykiety książę Krak musi zjeść łącznie co najmniej o 50%

więcej niż Baltazar Gąbka. Ponadto, nie może dojść do sytuacji, w której

prof. Gąbka zje więcej francuskich przysmaków niż książę;

3. Smok Wawelski nie może zjeść więcej każdego z posiłków niż pozostali goście

łącznie;

4. według diety nadwornego astrologa Onufrego Arkadiusza Paralaksy optymalna

dieta dla prof. Gąbki to łączna konsumpcja 2 kg uczty i odpowiednio 2.5 kg

w przypadku księcia Kraka. Jakiekolwiek odstępstwo, niezależnie czy w posta-

ci niedoboru czy nadmiaru, od optymalnego planu żywieniowego jest wysoce

niewskazane;

5. w celu uniknięcia kontrowersji i posądzenia przez lud o zbyt wystawne życie

księcia, łączna ilość żabich udek musi stanowić co najwyżej połowę spożywanej

jagnięciny.

Dla księcia Kraka najważniejsze są dwa cele: 1. nagrodzenie Smoka Wawelskiego

możliwie największą porcją jedzenia (dla smoka liczy się łączna ilość spożywanego

pokarmu, a nie proporcje); 2. konsumpcja Kraka i Gąbki powinna jak najmniej

odbiegać od optymalnej diety w jakąkolwiek ze stron. Cel 1. jest o 50% ważniejszy niż

cel 2. Zaproponuj optymalne menu dla każdego z gości mając na uwadze spełnienie

ograniczeń 1–5.

(a)

(1p.)

Zdefiniuj zmienne decyzyjne.

(b)

(4p.)

Podaj warunki ograniczające zadania w postaci ograniczeń liniowych.

(c)

(3p.)

Zdefiniuj funkcję celu rozważanego problemu w postaci funkcji liniowej.

(d)

(2p.)

Podaj optymalne menu dla każdego z bohaterów.

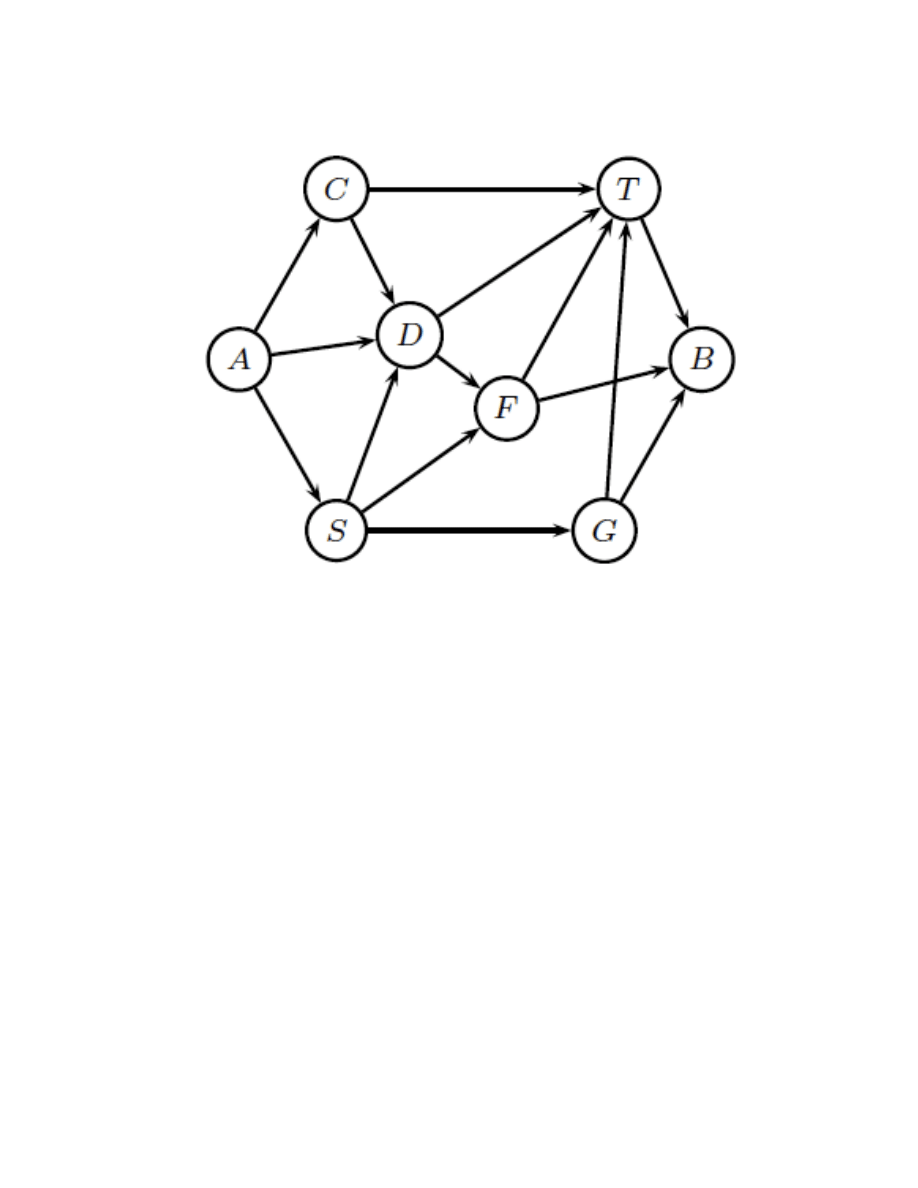
2. (Top secret) Wywiad MI6 dysponuje mapą tras dostaw pomiędzy punktami przesy-

łowymi przedstawioną na rysunku poniżej. Tabelka poniżej podaje przepustowość

każdej części trasy (w liczbie przesyłek), koszt przesłania jednej przesyłki oraz praw-

dopodobieństwo przechwycenia przesyłki przez wrogi wywiad.

Dla każdego z poniższych punktów podaj funkcję celu i ograniczenia oraz znajdź za

pomocą programowania liniowego:

(a)

(4p.)

najtańszą drogę przesłania 1 przesyłki z punktu A do punktu B (wraz z min

kosztem).

(b)

(3p.)

najtańszą drogę przesłania 5 przesyłek z punktu A do punktu B (wraz z min

kosztem).

(c)

(3p.)

największą liczbę przesyłek, które mogą być przesłane z punktu A do B (mak-

symalny przepływ).

(d)

(5p.)

najmniej awaryjną ścieżkę od A do B: prawdopodobieństwa przechwycenia są

niezależne dla różnych łuków na trasie (wskazówka: przyjmij, że przesyłasz

jedną przesyłkę; iloczyn prawdopodobieństw to to samo co suma logarytmów

prawdopodobieństw; przyjmij −ln(1 − p

i

) jako koszt dla łuku i, p

i

oznacza

prawdopodobieństwo przechwycenia przesyłki na łuku i; po wyliczeniu opty-

malnej wartości funkcji celu f można przejść z powrotem na prawdopodobień-

stwo przejścia przesyłki bez przechwycenia za pomocą e

−f

).

Page 2

Page 3

Page 4