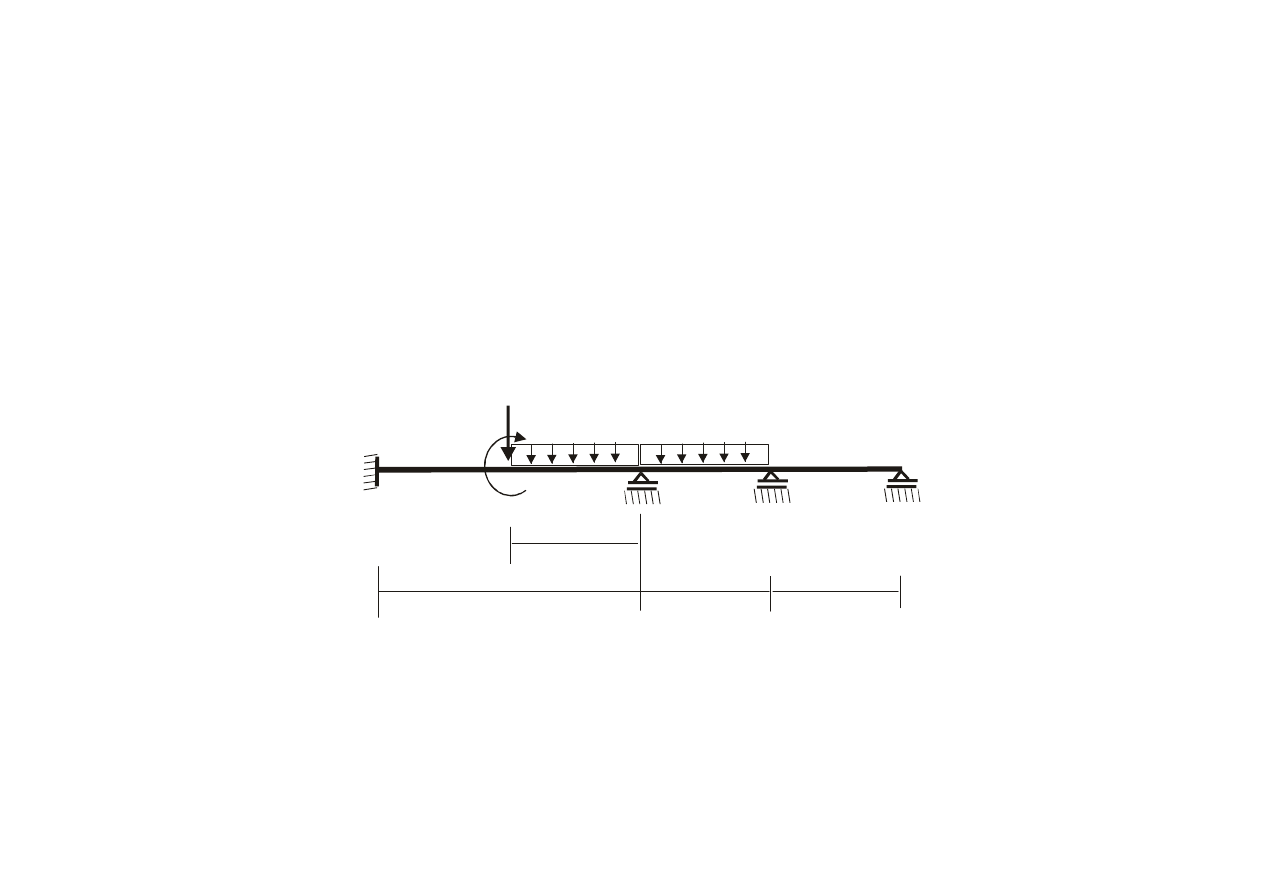
Przykład 5
Wyznaczyć wykresy sił wewnętrznych
2l
l
l
l
EJ=const
q
P
M
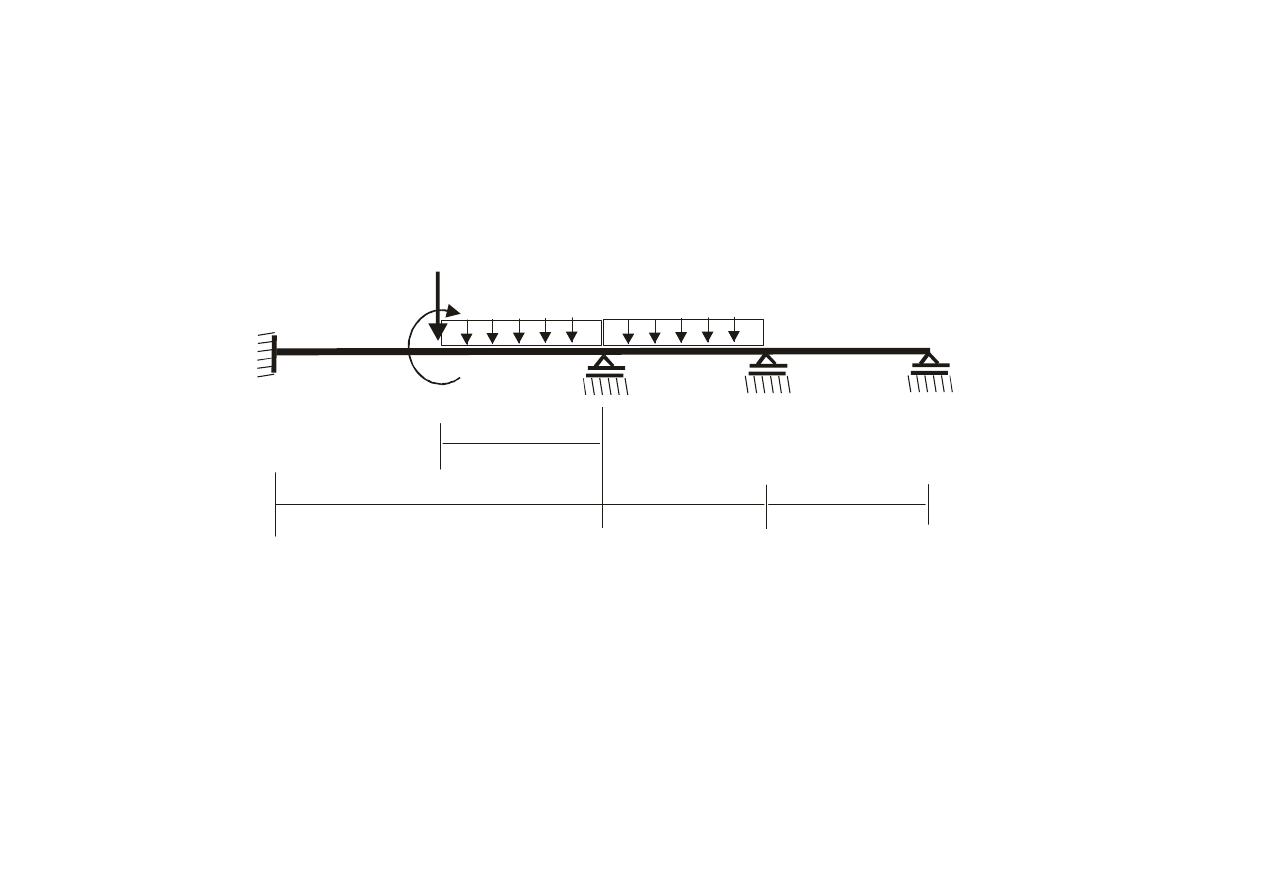
dane
2l
l
l
l
EJ=const
q
P
M
P=10kN
M=10kNm
q=3kN/m
l =10m
EJ=10000kNm
2
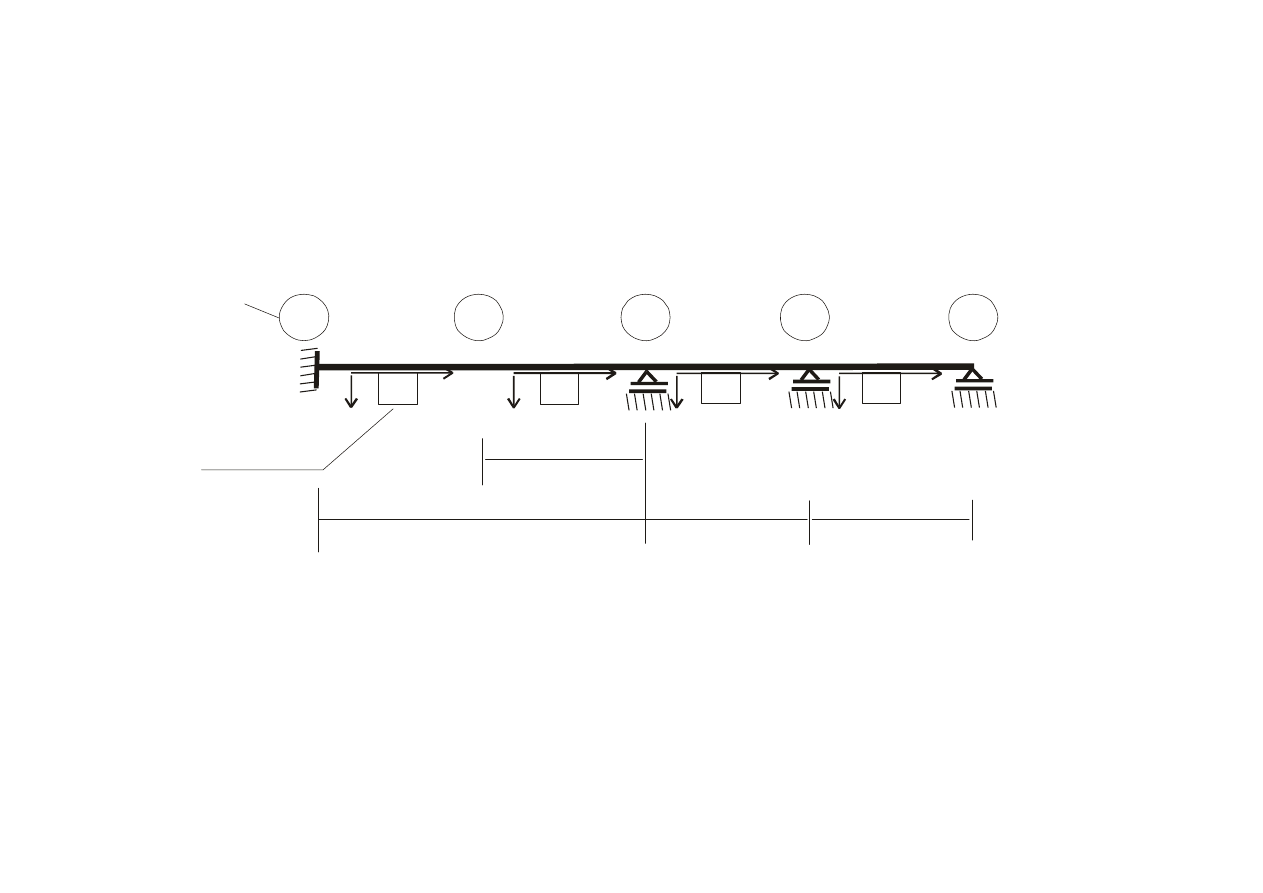
dyskretyzacja
x
x
x
x
y
y
y
y
1
1
2
3
4
5
2
3
4
2l
l
l
l
EJ=const
węzły
elementy
Wektor przemieszczeń
1
2
3
4
q
2
q
3
q
4
q
5
q
1
[
]
1
2
3
4
5
T
q
q
q
q
q
q
=
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....1
6
4
6
2
.....2
....0
12
6
12
6
....3
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....1
6
4
6
2
.....2
....0
12
6
12
6
....3
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
Macierze sztywności elementów
1
2
3
4
q
2
q
3
q
4
q
5
q
1
1
v
a
ϕ
a
ϕ
b
v
b
2
v
a
ϕ
a
ϕ
b
v
b
3
v
a
ϕ
a
ϕ
b
v
b
4
v
a
ϕ
a
ϕ
b
v
b
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....0
....1
12
6
12
6
....2
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....0
....1
12
6
12
6
....2
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....3
....0
12
6
12
6
....4
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....3
....0
12
6
12
6
....4
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....4
....0
12
6
12
6
....5
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....4
....0
12
6
12
6
....5
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
modyfikacja
0 0 1 2
1 2 0 3
0 3 0 4
0 4 0 5
Agregacja globalnej
Macierzy sztywnosci
1
2
3
4
q
2
q
3
q
4
q
5
q
1
3
2
3
2
22
3232
22
.....0
6
4
6
2
.....0
....1
1261
2
6
....2
62
64
aa
bb
llllv
E
J
E
J
E
J
E
J
llll
v
E
JE
JE
JE
J
llll
E
JE
JE
JE
J
llll
ϕ
ϕ
⎢⎥
⎢⎥⎡⎤
⎢⎥
−
⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥
−−
−⎢
⎥
⎢⎥⎣⎦
⎢⎥
⎢⎥
−
⎣⎦
3
2
3
2
22
3232
22
.....
6
4
6
2
.....
....0
126126
....
6264
aa
bb
llll
v
E
J
E
J
E
J
E
J
llll
v
E
JE
JE
JE
J
llll
E
JE
JE
JE
J
llll
ϕ
ϕ
−
⎢⎥
⎢⎥⎡
⎢⎥
−
⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥
−
−−
⎢⎥
⎢⎥⎣
⎢⎥
⎢⎥
−
⎣⎦
3232
22
323
2
22
126126
...
6462
...
...
126126
...
6264
a
abb
E
JE
JE
JE
J
llll
v
E
JE
JE
JE
J
llll
v
EJEJEJEJ
llll
E
JE
JE
JE
J
llll
ϕ
ϕ
⎡⎤
−
⎢⎥
⎢⎥⎡
⎢⎥
−
⎢⎥
⎢⎥
⎢⎥
⎢⎥⎢⎥
⎢⎥
−
−−
⎢⎥
⎢⎥⎣
⎢⎥
⎢⎥
−
⎣⎦
3232
22
3232
22
126126
.....
0
6
4
6
2
....
.4
....
0
12612
6
....
5
6264
a
abb
E
JE
JE
JE
J
llllv
E
JE
JE
JE
J
llllv
E
JE
JE
JE
J
llll
E
JE
JE
JE
J
llll
ϕ
ϕ
⎡⎤
−
⎢⎥
⎢⎥⎡⎤
⎢⎥
−⎢
⎥
⎢⎥
⎢⎥
⎢⎥⎢⎥
⎢⎥
−−
−⎢
⎥
⎢⎥⎣⎦
⎢⎥
⎢⎥
−
⎣⎦
3
2
3
2
22
3232
22
.....0
6
4
6
2
.....0
....1
1261
2
6
....2
62
64
aa
bb
llllv
E
J
E
J
E
J
E
J
llll
v
E
JE
JE
JE
J
llll
E
JE
JE
JE
J
llll
ϕ
ϕ
⎢⎥
⎢⎥⎡⎤
⎢⎥
−
⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥
−−
−⎢
⎥
⎢⎥⎣⎦
⎢⎥
⎢⎥
−
⎣⎦
3
2
3
2
22
3232
22
.....
6
4
6
2
.....
....0
126126
....
6264
aa
bb
llll
v
E
J
E
J
E
J
E
J
llll
v
E
JE
JE
JE
J
llll
E
JE
JE
JE
J
llll
ϕ
ϕ
−
⎢⎥
⎢⎥⎡
⎢⎥
−
⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥
−
−−
⎢⎥
⎢⎥⎣
⎢⎥
⎢⎥
−
⎣⎦
3232
22
323
2
22
126126
...
6462
...
...
126126
...
6264
a
abb
E
JE
JE
JE
J
llll
v
E
JE
JE
JE
J
llll
v
EJEJEJEJ
llll
E
JE
JE
JE
J
llll
ϕ
ϕ
⎡⎤
−
⎢⎥
⎢⎥⎡
⎢⎥
−
⎢⎥
⎢⎥
⎢⎥
⎢⎥⎢⎥
⎢⎥
−
−−
⎢⎥
⎢⎥⎣
⎢⎥
⎢⎥
−
⎣⎦
3232
22
3232
22
126126
.....
0
6
4
6
2
....
.4
....
0
12612
6
....
5
6264
a
abb
E
JE
JE
JE
J
llllv
E
JE
JE
JE
J
llllv
E
JE
JE
JE
J
llll
E
JE
JE
JE
J
llll
ϕ
ϕ
⎡⎤
−
⎢⎥
⎢⎥⎡⎤
⎢⎥
−⎢
⎥
⎢⎥
⎢⎥
⎢⎥⎢⎥
⎢⎥
−−
−⎢
⎥
⎢⎥⎣⎦
⎢⎥
⎢⎥
−
⎣⎦
1
2
3
4
5
1234
5
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....0
....1
12
6
12
6
....2
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....1
6
4
6
2
.....2
....0
12
6
12
6
....3
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....3
....0
12
6
12
6
....4
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....4
....0
12
6
12
6
....5
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....0
....1
12
6
12
6
....2
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....1
6
4
6
2
.....2
....0
12
6
12
6
....3
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....3
....0
12
6
12
6
....4
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
.....0
6
4
6
2
.....4
....0
12
6
12
6
....5
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
v
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
EJ
l
l
l
l
ϕ
ϕ
⎡
⎤
−
⎢
⎥
⎢
⎥ ⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎣
⎦
⎢
⎥
⎢
⎥
−
⎣
⎦
1
0
0
1
0
0
0
1
0
2
0
4
2
3
0
4
2
3
3
1
0
0
0
1
0
0
0
4
2
5
3
4
2
5
3
4
5
1
2
3
4
5
Macierz sztywności układu
1
2
3
4
q
2
q
3
q
4
q
5
q
1
3
2
2
24
6
0
0
0
8
2
0
0
0
6
2
8
2
0
2
8
2
0
0
2
4
0
0
0
EJ
EJ
l
l
EJ
EJ
l
l
EJ
EJ
EJ
EJ
l
l
l
l
EJ
EJ
EJ
l
l
l
EJ
EJ
l
l
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Wyznaczenie wektora obciążenia
2l
l
l
l
EJ=const
q
P
M
2
2
2
12
2
12
ql
ql
ql
ql
⎡
⎤
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
0
3
0
4
2
2
0
,
,0,
,0
2
12
12
T
ql
ql
ql
⎡
⎤
= −
−
⎢
⎥
⎣
⎦
R
[
]
, ,0,0,0,0
T
P M
=
R
2
0
2
2
25
35
12
0
0
0
0
25
0
0
12
0
ql
P
ql
M
ql
⎡
⎤
−
⎢
⎥
⎡ ⎤
⎡
⎤
⎢
⎥
⎢ ⎥
⎢
⎥
⎢
⎥
−
⎢ ⎥
⎢
⎥
⎢
⎥
⎢ ⎥
⎢
⎥
=
−
=
−
=
⎢
⎥
⎢ ⎥
⎢
⎥
⎢
⎥
−
⎢ ⎥
⎢
⎥
⎢
⎥
⎢ ⎥
⎢
⎥
⎢
⎥
⎣ ⎦
⎣
⎦
⎢
⎥
⎢
⎥
⎣
⎦
P
R
R
P=10kN
M=10kNm
q=3kN/m
l =10m
EJ=10000kNm
2
2
2
2
12
2
12
ql
ql
ql
ql
⎡
⎤
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
1
2
0
3
Obliczenie sił w elemencie nr 1
2l
l
l
l
EJ=const
q
P
M
0.1337
0.0073
q= -0.0118
-0.0002
0.0001
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
0
0
-11.6464
6
4
6
2
0
0
-65.5592
12
6
12
6
0.1337
0
11.6464
0.0073
0
-5
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
T
EJ
EJ
EJ
EJ
M
l
l
l
l
T
EJ
EJ
EJ
EJ
l
l
l
l
M
EJ
EJ
EJ
EJ
l
l
l
l
⎡
⎤
−
⎢
⎥
⎢
⎥
⎡
⎤
⎡
⎤ ⎡ ⎤
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢ ⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
=
+
=
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎢ ⎥
⎢
⎥ ⎣
⎦ ⎣ ⎦
⎣
⎦
⎢
⎥
−
⎢
⎥
⎣
⎦
0.9046
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Wektor
przemieszczeń:
Siły w 1
elemencie:
Obliczenie sił w elemencie 2, 3
0.1337
0.0073
q= -0.0118
-0.0002
0.0001
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
0.13370
15
-1.6464
6
4
6
2
0.0073
25
60.9
12
6
12
6
0
15
-0.0118
25
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
T
EJ
EJ
EJ
EJ
M
l
l
l
l
T
EJ
EJ
EJ
EJ
l
l
l
l
M
EJ
EJ
EJ
EJ
l
l
l
l
⎡
⎤
−
⎢
⎥
⎢
⎥
−
⎡
⎤
⎡
⎤
⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
=
+
=
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎣
⎦
⎣
⎦
⎣
⎦
⎢
⎥
−
⎢
⎥
⎣
⎦
046
-28.3536
72.6316
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
0
15
-22.2039
6
4
6
2
-0.0118
25
-72.6316
12
6
12
6
0
15
-
-0.0002
25
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
T
EJ
EJ
EJ
EJ
M
l
l
l
l
T
EJ
EJ
EJ
EJ
l
l
l
l
M
EJ
EJ
EJ
EJ
l
l
l
l
⎡
⎤
−
⎢
⎥
⎢
⎥
−
⎡
⎤
⎡
⎤
⎡
⎤
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
=
+
=
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
−
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥ ⎣
⎦
⎣
⎦
⎣
⎦
⎢
⎥
−
⎢
⎥
⎣
⎦
7.7961
0.5921
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
2l
l
l
l
EJ=const
q
P
M
Siły w 2
elemencie:
Siły w 3
elemencie:
Obliczenie sił w elemencie 4
0.1337
0.0073
q= -0.0118
-0.0002
0.0001
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
3
2
3
2
2
2
3
2
3
2
2
2
12
6
12
6
0
0
-0.0592
6
4
6
2
-0.0002
0
-0.5921
12
6
12
6
0
0
0.0592
0.0001
0
0
6
2
6
4
a
a
b
b
EJ
EJ
EJ
EJ
l
l
l
l
T
EJ
EJ
EJ
EJ
M
l
l
l
l
T
EJ
EJ
EJ
EJ
l
l
l
l
M
EJ
EJ
EJ
EJ
l
l
l
l
⎡
⎤
−
⎢
⎥
⎢
⎥
⎡
⎤
⎡
⎤ ⎡ ⎤ ⎡
⎢
⎥
−
⎢
⎥
⎢
⎥ ⎢ ⎥ ⎢
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥ ⎢
=
+
=
⎢
⎥
⎢
⎥
⎢
⎥ ⎢ ⎥ ⎢
⎢
⎥
−
−
−
⎢
⎥
⎢
⎥ ⎢ ⎥
⎢
⎥ ⎣
⎦ ⎣ ⎦ ⎣
⎣
⎦
⎢
⎥
−
⎢
⎥
⎣
⎦
⎤
⎥
⎥
⎥
⎢
⎥
⎦
2l
l
l
l
EJ=const
q
P
M
Siły w 4
elemencie:
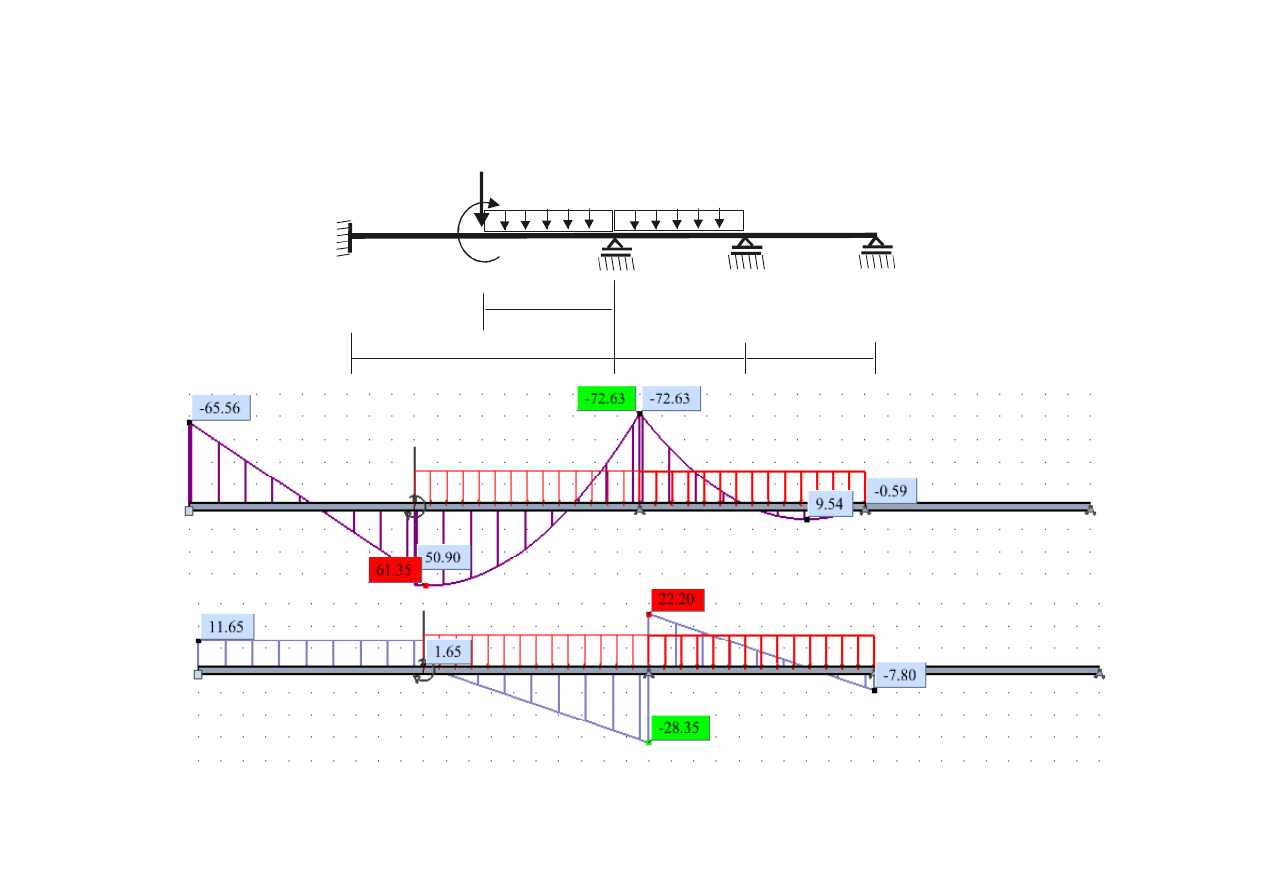
Wykresy sił wewnętrznych
-0.0592
-0.5921
0.0592
0
a
a
b
b
T
M
T
M
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
=
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎣
⎦
⎣
⎦
2l
l
l
l
EJ=const
q
P
M
-11.6464
-65.5592
11.6464
-50.9046
a
a
b
b
T
M
T
M
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
-1.6464
60.9046
-28.3536
72.6316
a
a
b
b
T
M
T
M
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
=
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎣
⎦
⎣
⎦
-22.2039
-72.6316
-7.7961
0.5921
a
a
b
b
T
M
T
M
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
=
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
⎣
⎦
⎣
⎦
1
2
3
4
Wyszukiwarka
Podobne podstrony:
Egzamin Praktyczny Czerwiec 2007 Przykładowe Zrzuty Ekranu (Zadanie 2)
Egzamin Praktyczny Czerwiec 2007 Przykładowe Zrzuty Ekranu (Zadanie 4)
2007 przyklad RAMA
Egzamin Praktyczny Czerwiec 2007 Przykładowe Zrzuty Ekranu (Zadanie 1)
2007 przyklady 1 MB II
2007 przykład arkusz Operon
Egzamin zawodowy praktyczny technik spedytor czerwiec 2007 (przykładowe rozwiązanie)
Egzamin Praktyczny Czerwiec 2007 Przykładowe Zrzuty Ekranu (Zadanie 2)
2007 przyklady 1 MB II
2007 czerwiec zad 1,2,3,4 Egzamin praktyczny przykład rozwiązania
1 Przykładowe rozwiązanie zad pratycznego -Technik mechanik, Technik mechanik - egzamin zawodowy, 20
06 Czy zdobywanie przez bakterie odporności na antybiotyki można uznać za przykład ewolucji (2007)
2007 czerwiec zad 3 Egzamin praktyczny przykład rozwiązania
więcej podobnych podstron