1

w w w. o p e r o n . p l

Modele odpowiedzi do arkusza Próbnej Matury z OPERONEM

Fizyka i astronomia

Poziom rozszerzony

Listopad 2010

W klu czu są pre zen to wa ne przy kła do we pra wi dło we od po wie dzi. Na le ży rów nież uznać od po wie dzi ucznia, je śli
są ina czej sfor mu ło wa ne, ale ich sens jest sy no ni micz ny wo bec sche ma tu, oraz in ne od po wie dzi, nie prze wi dzia -
ne w klu czu, ale po praw ne.

Numer

zadania

Prawidłowa odpowiedź

Liczba

punktów

1.

1.1.

1 pkt – obliczenie momentu bezwładności bloczka

2 10

I

m R

2

1

kg m

0

0

2

5

2

$

$

=

=

-

0–13

1.2.

1 pkt – wykorzystanie zasady zachowania energii

1 pkt – wykorzystanie zależności pomiędzy prędkością liniową a kątową

1 pkt – wyznaczenie wzoru na prędkość końcową ciężarka o masie

v

mgh

m

I

2

2

2

0

2

~

=

+

v

R

$

s

=

m

v

mR

I

gh

1

2

k

2

0

=

+

1.3.

1 pkt – wykorzystanie wzoru na drogę w ruchu jednostajnie przyspieszonym
bez prędkości początkowej

1 pkt – wykorzystanie wzoru na przyspieszenie liniowe

1 pkt – wyznaczenie wzoru na czas spadku

Wypełnienie prawidłowo tabeli – 2 pkt, 1 błąd – 1 pkt, więcej niż jeden błąd – 0 pkt.

Lp.

1
2
3

h

at

2

2

=

v

v

a

t

t

k

D

D

=

=

v

t

h

2

k

=

t s

6

@

v

s

m

k

9 C

m g

6

@

0,91

4,4

50

0,78

5,1

100

0,74

5,4

150

1.4.

2 pkt – wyznaczenie wzoru i obliczenie przyspieszenia liniowego dla

2 pkt – wyznaczenie wzoru i obliczenie przyspieszenia kątowego

v

0 s

m

0

=

,

,

,

,

v

a

t

t

mR

I

gh

1

1

2

18

1

1

0 5 0 15

2 10

2 9 81 2

0 35

s

m

s

m

2

0

2

5

2

2

$

$

$

$

.

D

=

=

+

=

+

-

,

,

,

R

a

0 15

0 35

2 3 1

s

2

f

=

=

=

2

w w w. o p e r o n . p l

Fizyka i astronomia. Poziom rozszerzony

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Numer

zadania

Prawidłowa odpowiedź

Liczba

punktów

2.

2.1.

1 pkt – wyznaczenie długości fali stojącej

Odległość pomiędzy węzłami fali stojącej

, stąd

1 pkt – wykorzystanie wzoru na prędkość fali dźwiękowej

1 pkt – wyznaczenie i obliczenie częstotliwości kamertonu

2

0,8

L

m

m

=

=

L

2

1

m

=

v

f

$

m

=

,

425

v

f

0 8

340 Hz

Hz

m

= =

=

0–11

2.2.

1 pkt – wyznaczenie zależności między długościami fali w dwóch ośrodkach

1 pkt – obliczenie zmiany długości fali

v

v

f

f

p

w

p

w

m

m

=

,

v

v

340

1480

4 35

w

p

w

p

p

p

.

m

m

m

m

=

=

2.3.

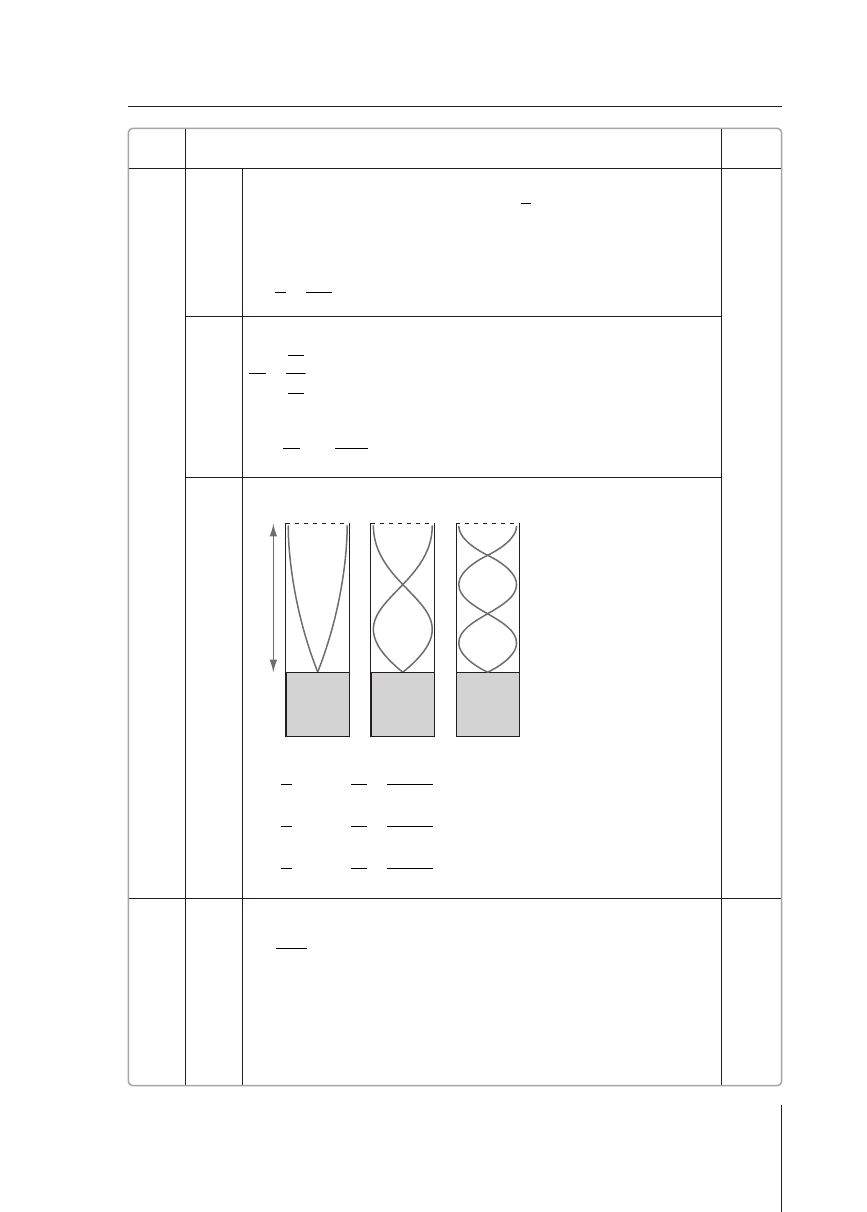
3 pkt – narysowanie 3 poprawnych rysunków ukazujących powstawanie fali
stojącej w słupie powietrza nad wodą

3 pkt – obliczenie kolejnych częstotliwości dźwięku

,

,

,

H

=

5

2

c

m

,

163,5

v

f

4 0 52

340 Hz

Hz

1

1

$

.

m

=

=

H

4

1

1

m

=

,

,

v

f

4 0 52

3 340

490 4

Hz

Hz

2

2

$

$

.

m

=

=

H

4

3

2

m

=

,

817,3

v

f

4 0 52

5 340 Hz

Hz

3

3

$

$

.

m

=

=

H

4

5

3

m

=

3.

3.1.

1 pkt – obliczenie kąta padania na pierwszą wewnętrzną powierzchnię
pryzmatu

,

,

1 pkt – obliczenie kąta padania na drugą wewnętrzną powierzchnię pryzmatu

,

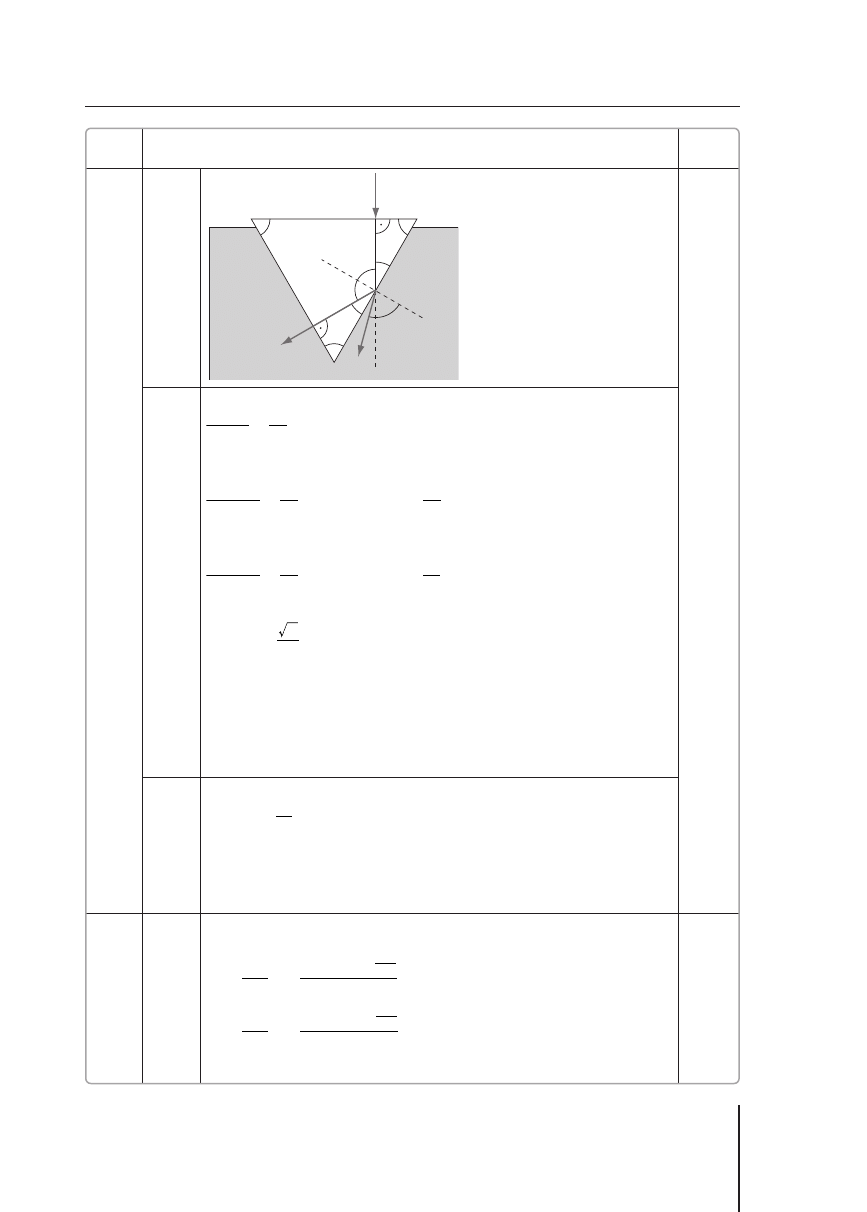
2 pkt – poprawne narysowanie rysunku. Zadbanie o to, aby kąt padania był
równy kątowi odbicia na pierwszej wewnętrznej powierzchni pryzmatu (1 pkt)
oraz aby kąt załamany

był większy od kąta padania , ponieważ

(1 pkt).

°

°

90

60

a

d

=

- =

°

°

°

180

90

30

d

c

=

-

- =

°

°

3

180

60

c

=

=

°

0

2

a

=

°

°

180

90

{

c

d

=

- - =

n

n

>

s

w

a

b

0–12

3

w w w. o p e r o n . p l

Fizyka i astronomia. Poziom rozszerzony

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Numer

zadania

Prawidłowa odpowiedź

Liczba

punktów

n

p

n

w

n

s

c

c

c

z

a

d

d

a

b

3.2.

1 pkt – zapisanie prawa załamania światła na granicy szkło–woda

1 pkt – obliczenie kąta granicznego promienia padającego na powierzchnię
szkło–woda

, stąd

1 pkt – obliczenie kąta granicznego promienia padającego na powierzchnię
szkło–powietrze

, stąd

1 pkt – obliczenie wartości

2 pkt – porównanie wartości sinusów kątów i stwierdzenie, czy zajdzie zjawisko
całkowitego odbicia światła:
a) szkło–woda:

, więc

– zjawisko całkowitego odbicia

światła nie zajdzie w tym wypadku
b) szkło–powietrze:

, więc

– zjawisko całkowitego

odbicia światła zajdzie w tym wypadku

sin

sin

n

n

s

w

b

a =

]

]

g

g

0,917

sin

n

n

gr

s

w

.

a

=

_ i

°

sin

sin

n

n

90

gr

s

w

a

=

]

_

g

i

0,6

sin

n

n

89

gr

s

p

.

a

=

_ i

°

sin

sin

n

n

90

gr

s

p

a

=

]

_

g

i

°

sin 60

^

h

°

,

sin 60

2

3

0 866

=

=

]

g

>

gr

a

a

sin

sin

>

gr

a

a

_

]

i

g

<

gr

a

a

sin

sin

<

gr

a

a

_

]

i

g

3.3.

1 pkt – wyznaczenie wzoru na współczynnik ośrodka

stąd
1 pkt – obliczenie współczynnika załamania światła ośrodka

sin

n

n

gr

s

o

a

=

_ i

sin

n

n

o

s

gr

a

=

_ i

,

°

,

,

,

sin

n

1 45

60

1 45 0 866

1 255

o

$

=

=

=

]

g

4.

4.1.

2 pkt – obliczenie indukcji pola magnetycznego w miejscach znajdowania się
przewodów

2 pkt – zaznaczenie na rysunku wektorów indukcji magnetycznej

,

B

a I

2

2 0 2

1 4 10

3

3 10

m

A

N

A

T

1

0

1

7

6

2

$

$

$

$

$

r

r

r

nn

=

=

=

-

-

,

B

a I

2

2 0 2

1 4 10

1

10

m

A

N

A

T

2

2

7

6

0

2

$

$

$

$

r

r

r

nn

=

=

=

-

-

0–14

4

w w w. o p e r o n . p l

Fizyka i astronomia. Poziom rozszerzony

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Numer

zadania

Prawidłowa odpowiedź

Liczba

punktów

4.2.

1 pkt – obliczenie siły wzajemnego oddziaływania

lub wzór

1 pkt – poprawne narysowanie sił na rysunku i stwierdzenie, że przewodniki
będą się przyciągały

,

°

10

3

2

1

6 10

sin

sin

F

F

B I L

B L

a

I

I L

2

90

T

A

m

N

2

1

2 1

0 2

1

6

6

$

$

$

$

r

nn

=

=

=

=

=

=

-

-

_

]

i

g

F

F

a

I I

L

2

2

1

0 2 1

r

nn

=

=

4.3.

1 pkt – zapis superpozycji pól magnetycznych

1 pkt – zauważenie, że jeśli wypadkowe pole magnetyczne ma mieć wartość
równą , to:

lub

1 pkt – poprawny zapis powyższego równania względem pierwszego
przewodnika

1 pkt – wyznaczenie wzoru i obliczenie

B

B

B

1

2

=

+

0

B

B

1

2

=

B

B

0

1

2

-

=

x

I

a x

I

2

2

0

0 1

0 2

$

$

r

r

nn

nn

-

- =

]

g

x

15

x

I

I

I a

a

4

3

cm

1

2

1

=

+ =

=

4.4.

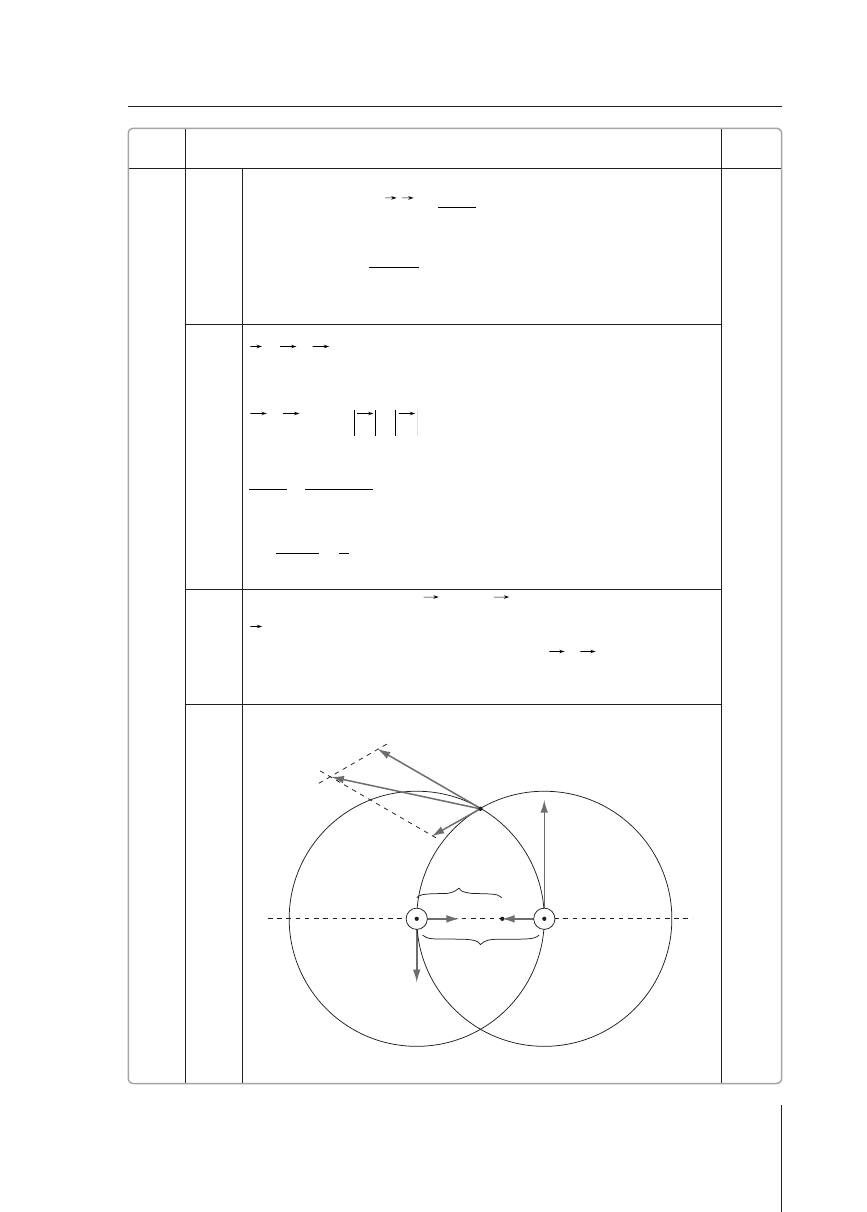
3 pkt – narysowanie wektora

(1 pkt),

(1 pkt) i wektora wypadkowego

(1 pkt)

1 pkt – zachowanie proporcji pomiędzy wektorami

i

B

2

B

1

B

B

2

B

1

B

B

3

1

2

=

Wspólny rysunek do każdego podpunktu

a

P

B

I

1

B

2

F

1

A

F

2

"

"

"

"

"

"

"

B

1

I

2

x = a

B

1

B

2

3
4

–

5

w w w. o p e r o n . p l

Fizyka i astronomia. Poziom rozszerzony

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Numer

zadania

Prawidłowa odpowiedź

Liczba

punktów

5.

5.1.

1 pkt – obliczenie różnicy mas przed i po reakcji

1 pkt – obliczenie

1 pkt – wyznaczenie wzoru na częstotliwość promieni

, stąd

1 pkt – przeliczenie energii na

1 pkt – obliczenie częstotliwości

,

,

,

,

m

m

m

m

2

9 01210

2 4 00150

1 00866

0 00044

u

u

u

u

n

Be

$

D

=

-

+

=

-

+

=

=

a

^

]

h

g

E

D

0,00044 931,5

0,41

E

m c

c

c

MeV

MeV

2

2

2

$

$

$ .

D

D

=

=

c

h

E

o

D

=

h

E

o

D

=

J

0,41

0,41 10 1,602 10

6,57 10

E

MeV

J

J

6

19

14

$

$

$

$

.

D

=

=

-

-

6,63 10

6,57 10

9,91 10

J s

J

Hz

34

14

19

$

$

$

$

.

o

=

-

-

0–10

5.2.

1 pkt – obliczenie defektu mas cząsteczki

1 pkt – obliczenie energii wiązania

1 pkt – obliczenie energii wiązania przypadającej na nukleon

a

,

,

,

,

m

m

m

m

2

2 1 00728

1 00866

4 00150

0 0304

u

u

u

u

p

n

.

D

=

+

-

=

+

-

a

_

]

i

g

,

,

,

E

m c

c

c

0 0304 931 5

28 3

MeV

MeV

2

2

2

$

$

$ .

D

D

=

=

7,075

E

4

MeV

.

D

5.3.

1 pkt – określenie proporcji
Ponieważ

waży

i znajduje się w nim

(liczba Avogadra)

atomów, to w

jest ich

, stąd:

1 pkt – obliczenie liczby atomów

N

N

m

N m

A

Be

$

=

9,0121

6,02 10

1

,

N

6 68 10

mol

g

mol

1

g

23

22

$

$

$

.

=

1 mol ( )

Be

9,0121 g

N

A

1 g