1

Otoczenie i Sąsiedztwo

Niech

x

0

∈ R

oraz

δ > 0

.

• Przedział

( x

0

− δ , x

0

+ δ )

nazywamy otoczeniem punktu

x

0

o promieniu

δ

i oznaczamy

U (x

0

, δ)

.

• Przedział

h x

0

, x

0

+ δ )

nazywamy otoczeniem prawostronnym

punktu

x

0 o promieniu

δ

.

• Przedział

( x

0

− δ , x

0

i

nazywamy otoczeniem lewostronnym

punktu

x

0 o promieniu

δ

.

Zauważmy, że

x ∈ U (x

0

, δ) ⇐⇒ | x − x

0

| < δ

2

• Przedział

( x

0

, x

0

+ δ )

nazywamy sąsiedztwem prawostronnym

punktu

x

0 o promieniu

δ

.

• Przedział

( x

0

− δ , x

0

)

nazywamy sąsiedztwem lewostronnym

punktu

x

0 o promieniu

δ

.

• Sumę tych dwóch przedziałów nazywamy sąsiedztwem punktu

x

0

o promieniu

δ

i oznaczamy

S(x

0

, δ)

, tj.

S(x

0

, δ) = ( x

0

− δ , x

0

) ∪ ( x

0

, x

0

+ δ ) = ( x

0

− δ , x

0

+ δ )r{ x

0

}

Zauważmy, że

x ∈ S(x

0

, δ) ⇐⇒ 0 < | x − x

0

| < δ

3

• Przedział

( δ , +∞ )

nazywamy otoczeniem plus nieskończoności.

• Przedział

( −∞ , δ )

nazywamy otoczeniem minus nieskończoności.

• W tym przypadku otoczenie i sąsiedztwo są tymi samymi zbiorami.

4

Granica funkcji

f : D → R,

D ⊂ R

x

0

∈ D

lub

∃

{x

n

}∈D

x

n

−→ x

0

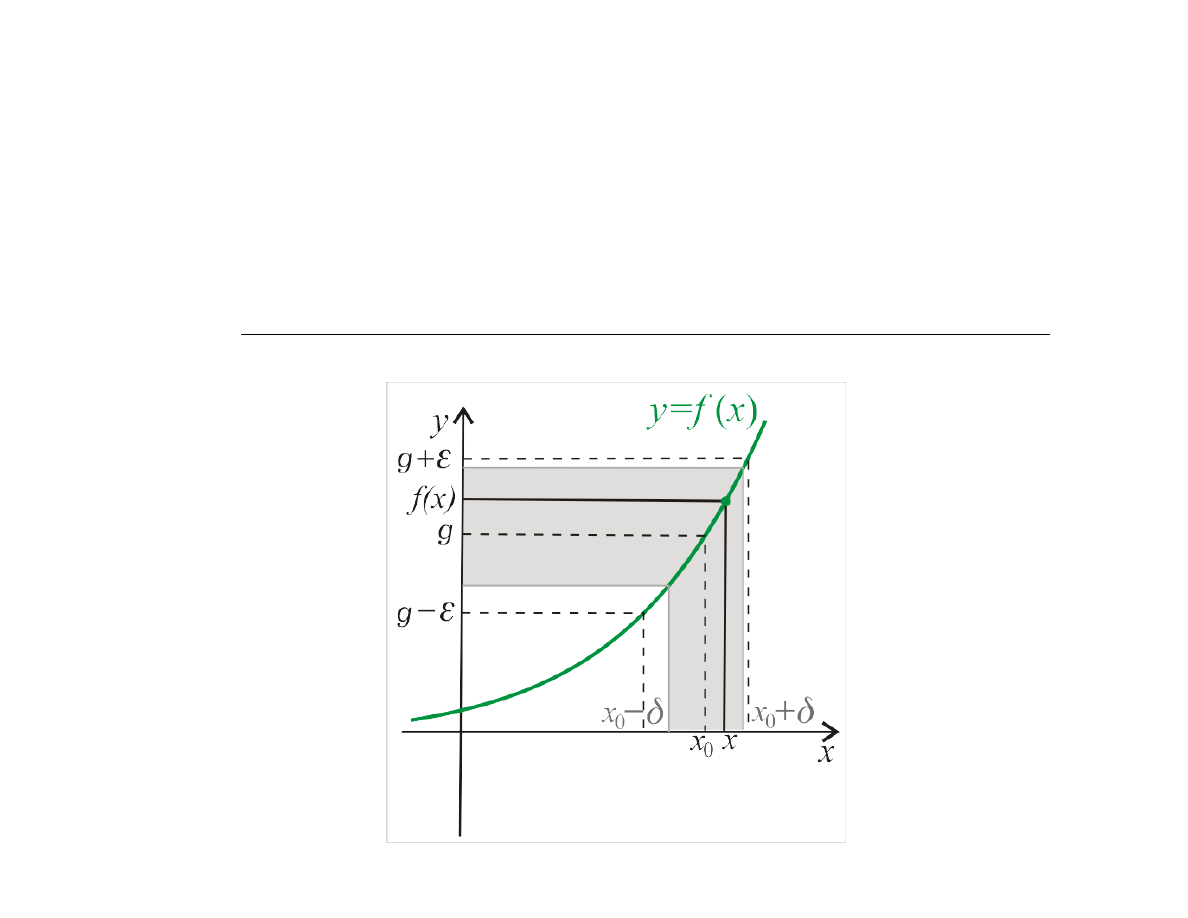
Definicja

Niech

f

będzie określona przynajmniej w sąsiedztwie

punktu

x

0 . Funkcja

f

ma w punkcie

x

0 granicę

g

, co zapisujemy

lim

x→x

0

f (x) = g,

gdy dla dowolnego otoczenia

U

punktu

g

istnieje sąsiedztwo

S

punktu

x

0 takie, że dla każdego

x ∈ S

wartość

f (x)

należy do

otoczenia

U

.

5

• Jeżeli

x

0

∈ R

i

g ∈ R

, to mamy:

lim

x→x

0

f (x) = g

⇐⇒

∀

ε>0

∃

δ>0

∀

x∈D

0 < | x − x

0

| < δ

⇒

| f (x) − g | < ε

( Definicja Cauchy’ego granicy właściwej w punkcie )

6

• Jeżeli

x

0

= +∞

i

g ∈ R

, to mamy:

lim

x→+∞

f (x) = g

⇐⇒

∀

ε>0

∃

K>0

∀

x∈D

x > K

⇒

| f (x) − g | < ε

( Definicja Cauchy’ego granicy właściwej w plus nieskończoności )

• Napisz definicję Cauchy’ego granicy właściwej w minus nieskończoności.

• Jeżeli

x

0

∈ R

i

g = −∞

, to mamy:

lim

x→x

0

f (x) = −∞

⇐⇒

∀

M <0

∃

δ>0

∀

x∈D

0 < | x − x

0

| < δ

⇒

f (x) < M

( Definicja Cauchy’ego granicy niewłaściwej (

= −∞

) w punkcie )

• Napisz definicję Cauchy’ego granicy niewłaściwej (

= +∞

) w punkcie.

7

• Jeżeli

x

0

= +∞

i

g = +∞

, to mamy:

lim

x→+∞

f (x) = +∞

⇐⇒

∀

M >0

∃

K>0

∀

x∈D

x > K

⇒

f (x) > M

( Definicja Cauchy’ego granicy niewłaściwej (

= +∞

)

w plus nieskończoności )

• Napisz definicję Cauchy’ego granicy niewłaściwej (

= +∞

) w minus

nieskończoności.

• Napisz definicję Cauchy’ego granicy niewłaściwej (

= −∞

) w plus

nieskończoności.

• Napisz definicję Cauchy’ego granicy niewłaściwej (

= −∞

) w minus

nieskończoności.

8

Przykład

Wykaż, korzystając z definicji Cauchy’ego granicy

funkcji, że

lim

x→1

( 2x − 7 ) = −5.

Definicja Heinego granicy

Definicja

g

(

g ∈ R

lub

g = ±∞

) jest granicą funkcji

f

w

x

0

(

x

0

∈ R

lub

x

0

= ±∞

) wtedy i tylko wtedy, gdy dla

dowolnego ciągu

{ x

n

}

, takiego, że

x

n

∈ S(x

0

) ⊂ D

, zachodzi

lim

n→∞

x

n

= x

0

=⇒

lim

n→∞

f (x

n

) = g.

9

Przykład

Wykaż, korzystając z definicji Heinego granicy funkcji,

że

lim

x→2

3x + 1

5x + 4

=

1

2

.

Twierdzenie

Definicje: Cauchy’ego i Heinego granicy funkcji są

równoważne.

10

Fakt

Jeżeli istnieją ciągi

(

x

0

n

)

i

(

x

00

n

)

spełniające warunki:

•

lim

n→∞

x

0

n

= x

0 , przy czym

x

0

n

6= x

0 dla

n ∈ N

oraz

lim

n→∞

f (x

0

n

) = g

0

,

•

lim

n→∞

x

00

n

= x

0 , przy czym

x

00

n

6= x

0 dla

n ∈ N

oraz

lim

n→∞

f (x

00

n

) = g

00

,

•

g

0

6= g

00

,

to granica

lim

x→x

0

f (x)

nie istnieje.

Przykład

Wykaż, że granica funkcji

f (x) = cos x

w plus

nieskończoności nie istnieje.

11

Wnioski z definicji Heinego granicy

Twierdzenie

(Arytmetyka granic funkcji)

Jeżeli funkcje

f

i

g

mają granice właściwe w

x

0 , to

•

lim

x→x

0

( f (x) ± g(x) ) =

lim

x→x

0

f (x) ±

lim

x→x

0

g(x)

,

•

lim

x→x

0

( c · f (x) ) = c ·

lim

x→x

0

f (x)

,

gdzie

c ∈ R

,

•

lim

x→x

0

( f (x) · g(x) ) =

lim

x→x

0

f (x) ·

lim

x→x

0

g(x)

,

•

lim

x→x

0

f (x)

g(x)

=

lim

x→x0

f (x)

lim

x→x0

g(x)

,

o ile

lim

x→x

0

g(x) 6= 0

.

Twierdzenie

lim

x→x

0

f (x) = 0

⇐⇒

lim

x→x

0

| f (x) | = 0

12

Twierdzenie

Załóżmy, że funkcje

f

i

g

są określone w

sąsiedztwie

x

0 . Jeżeli granica funkcji

f

w

x

0

jest równa

0

,

a funkcja

g

jest ograniczona, to

lim

x→x

0

f (x) · g(x) = 0.

Twierdzenie

Załóżmy, że funkcja

f

jest określona w sąsiedztwie

x

0 . Wówczas

lim

x→x

0

f (x) = +∞ (−∞)

=⇒

lim

x→x

0








1 +

1

f (x)








f (x)

= 0.

13

Twierdzenie

(O trzech funkcjach)

Jeżeli funkcje

f, g

i

h

, określone co najmniej w sąsiedztwie

S(x

0

)

punktu

x

0 , spęłniają warunki:

•

f (x) 6 g(x) 6 h(x)

dla każdego

x ∈ S(x

0

)

•

lim

x→x

0

f (x) =

lim

x→x

0

h(x) = p

,

to

lim

x→x

0

g(x) = p

.

Przykład

Korzystając z powyższych twierdzeń wykaż, że

lim

x→0

sin x

x

= 1

.

Fakt

lim

x→0

sin x

x

= 1

lim

x→0

tg x

x

= 1

14

Przykład

Oblicz granice:

a)

lim

x→1

x

2

−2x+1

x

2

−1

b)

lim

x→∞






3x

4

−1

√

x

8

+3x+4

+

√

x

2

+ 1 − x






c)

lim

x→−∞

x

√

x

2

+1

d)

lim

x→3





1

x−3

−

6

x

2

−9





e)

lim

x→−∞

sin x

x

2

f )

lim

x→0








x

sin 3x

+

x

cos πx

−

tg

3

√

x

4

2x








g)

lim

x→−∞






3x

3

+2

3x

3

−6






−x

3

h)

lim

x→0

√

1+sin x−

√

1−sin x

tg x

i)

lim

x→−∞

arcctg x

x

j)

lim

x→0

arcsin x+arctg x

sin x

15

Granice jednostronne funkcji

Definicja

Załóżmy, że funkcja

f

jest określona w pewnym

prawostronnym (lewostronnym) sąsiedztwie punktu

x

0

∈ R

. Funkcja

f

ma w punkcie

x

0

granicę prawostronną (lewostronną)

g

, co

zapisujemy

lim

x→x

+

0

f (x) = g

(

lim

x→x

−

0

f (x) = g ),

gdy dla dowolnego otoczenia

U

punktu

g

istnieje sąsiedztwo

prawostronne (lewostronne)

S

+

(

S

−

) punktu

x

0

takie, że dla

każdego

x ∈ S

+ (

x ∈ S

−

) wartość

f (x)

należy do otoczenia

U

.

16

• Definicja Cauchy’ego granic jednostronnych

lim

x→x

+

0

f (x) = g

⇐⇒

∀

ε>0

∃

δ>0

∀

x∈D

x

0

< x < x

0

+ δ

⇒

| f (x) − g | < ε

lim

x→x

−

0

f (x) = g

⇐⇒

∀

ε>0

∃

δ>0

∀

x∈D

x

0

− δ < x < x

0

⇒

| f (x) − g | < ε

• Definicja Heinego granic jednostronnych

lim

x→x

+

0

f (x) = g

⇐⇒

∀

{x

n

}, x

n

>x

0

lim

n→∞

x

n

= x

0

⇒

lim

n→∞

f (x

n

) = g

17

lim

x→x

−

0

f (x) = g

⇐⇒

∀

{x

n

}, x

n

<x

0

lim

n→∞

x

n

= x

0

⇒

lim

n→∞

f (x

n

) = g

Ćwiczenie

Napisz definicje granic jednostronnych w przypadku,

gdy

g = +∞

lub

g = −∞

.

Twierdzenie

(Warunek dostateczny istnienia granicy)

Dla istnienia granicy

g

funkcji

f

w punkcie

x

0

∈ R

potrzeba

i wystarcza, by istniały obie granice jednostronne w punkcie

x

0

i

żeby były sobie równe. Ponadto wówczas

lim

x→x

0

f (x) =

lim

x→x

+

0

f (x) =

lim

x→x

−

0

f (x).

18

Uwaga

Twierdzenia sformułowane dla granic funkcji są również

prawdziwe dla granic jednostronnych.

Przykład

Oblicz granice jednostronne:

a)

lim

x→2

+

x

2

−2x+1

x

2

−4

b)

lim

x→2

−

x

2

−2x+1

x

2

−4

c)

lim

x→0

+

8

3

s

8+8

− 1

x

d)

lim

x→0

−

8

3

s

8+8

− 1

x

e)

lim

x→0

+

arccos






tg x

|x|






f )

lim

x→0

−

arccos






tg x

|x|






19

Ciągłość funkcji

f : D → R,

D ⊂ R

x

0

∈ D

Definicja

(Ciągłości funkcji w punkcie)

Niech

f

będzie

określona przynajmniej w otoczeniu punktu

x

0

∈ R

. Funkcja

f

jest ciągła w punkcie

x

0 wtedy i tylko wtedy, gdy

lim

x→x

0

f (x) = f (x

0

).

Definicja

Mówimy, że funkcja

f

jest ciągła w swojej dziedzinie,

jeżeli

f

jest ciągła dla każdego punktu

x

0

∈ D

.

20

Definicja

(Ciągłości jednostronnej funkcji w punkcie)

• Niech

f

będzie określona przynajmniej w otoczeniu prawostronnym

punktu

x

0

∈ R

. Funkcja

f

jest prawostronnie ciągła w punkcie

x

0 wtedy i tylko wtedy, gdy

lim

x→x

+

0

f (x) = f (x

0

).

• Niech

f

będzie określona przynajmniej w otoczeniu lewostronnym

punktu

x

0

∈ R

. Funkcja

f

jest lewostronnie ciągła w punkcie

x

0 wtedy i tylko wtedy, gdy

lim

x→x

−

0

f (x) = f (x

0

).

Twierdzenie

Funkcja jest ciągła w punkcie wtedy i tylko wtedy, gdy

jest w tym punkcie ciągła lewostronnie i prawostronnie.

21

Własności funkcji ciągłych

Twierdzenie

Jeżeli dwie funkcje

f

i

g

określone w tym samym

zbiorze

D

są ciągłe w punkcie

x

0

∈ D

, to w punkcie

x

0 ciągłe są

funkcje

f + g

,

f − g

,

f · g

oraz

f

g

(ta ostatnia przy założeniu

g(x

0

) 6= 0

).

Twierdzenie

Złożenie funkcji ciągłych jest funkcją ciągłą.

Uwaga Mówimy, że funkcja

f

określona na przedziale domkniętym

[a, b]

jest ciągła, jeżeli:

•

f

jest ciągła dla każdego

x ∈ (a, b)

•

f

jest prawostronnie ciągła dla

x = a

•

f

jest lewostronnie ciągła dla

x = b

.

22

Twierdzenie Założmy, że funkcja

f

określona w pewnym przedziale

(otwartym lub domkniętym) jest ciągła i odwracalna. Wówczas funkcja

odwrotna do funkcji

f

jest funkcją ciągłą.

Wniosek

Funkcje cyklometryczne są funkcjami ciągłymi.

Uwaga

Wszystkie funkcje elementarne są funkcjami ciągłymi (w

swoich dziedzinach).

Uwaga

(Wykorzystanie ciągłości do obliczania granic)

Założmy, że określona jest funkcja złożona

f (g(x))

oraz, że funkcja

f

jest ciągła w punkcie

lim

x→x

0

g(x)

. Wówczas

lim

x→x

0

f (g(x)) = f ( lim

x→x

0

g(x)).

23

Przykład

Oblicz granice jednostronne e) i f ) z poprzedniego

przykładu.

Przykład

Wiedząc, że

lim

x→x

0

f (x)

=

a > 0

oraz

lim

x→x

0

g(x) = b

oblicz granicę:

lim

x→x

0

f (x)

g(x)

.

Przykład

Zbadaj ciągłość funkcji:

f (x) =







































































































x − arccos 0

x 6 0

arctg ln x

0 < x

6 e

2

e < x 6 4

1

(x−4)

2

x > 4

24

Rodzaje punktów nieciągłości

• Funkcja

f

ma w punkcie

x

0

nieciągłość pierwszego rodzaju,

jeżeli itnieją granicę jednostronne

f

w tym punkcie, ale

lim

x→x

+

0

f (x) 6=

lim

x→x

−

0

f (x)

nieciągłość I rodzaju nieusuwalna (”skok”)

albo

lim

x→x

+

0

f (x) =

lim

x→x

−

0

f (x)

i

lim

x→x

0

f (x) 6= f (x

0

)

nieciągłość I rodzaju usuwalna (”luka”)

.

• Funkcja

f

ma w punkcie

x

0

nieciągłość drugiego rodzaju,

jeżeli przynajmniej jedna z granic jednostronnych funkcji

f

w

tym punkcie nie istnieje.

25

Twierdzenie

( Weierstrassa)

Jeżeli funkcja

f : [a, b] → R

jest ciągła, to jest ograniczna.

Ponadto wówczas istnieją takie argumenty

c

1

, c

2

∈ [a, b]

, że

f (c

1

)

jest najmniejszą wartością funkcji, a

f (c

2

)

- największą.

Twierdzenie

( Darboux o przyjmowaniu wartości pośrednich)

Jeżeli funkcja

f : [a, b] → R

jest ciągła oraz

f (a) 6= f (b)

, to dla

każdego

w ∈ ( f (a) , f (b) )

istnieje

c ∈ (a, b)

takie, że

f (c) = w.

26

Twierdzenie

( Darboux o miejscach zerowych funkcji)

Jeżeli funkcja

f : [a, b] → R

jest ciągła oraz

f (a) · f (b) < 0

,

to istnieje

c ∈ (a, b)

takie, że

f (c) = 0.

Przykład Wyznacz z dokładnościa do

0, 1

przybliżenie pierwiastka

wielomianu

f (x) = x

4

− 2x − 1

zawartego w przedziale

[−1, 0]

.