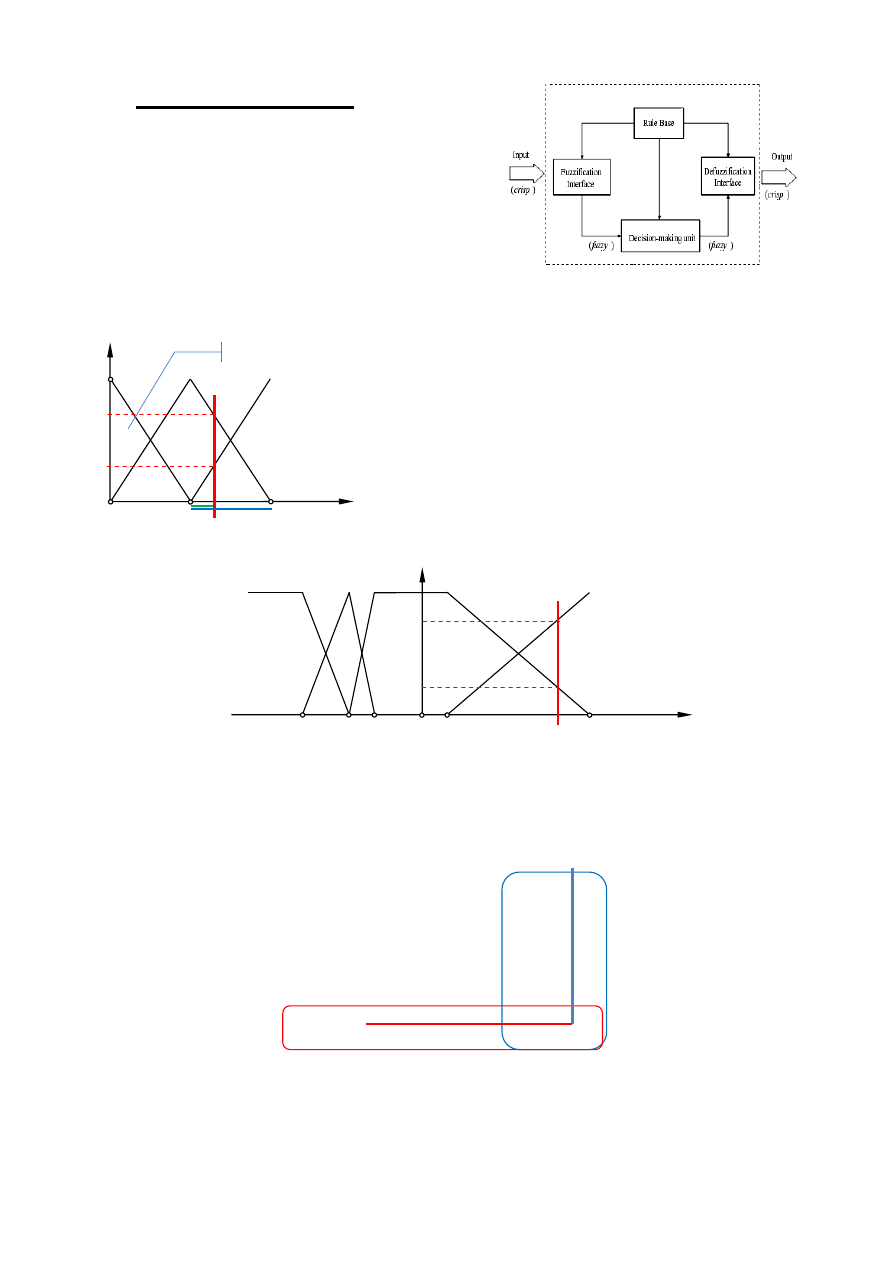
Regulator rozmyty

Ireneusz Dominik KAP AGH

Rys. 1. Regulator rozmyty

a)

fuzzyfikacja

Rys.2. Rozkład funkcji przynależności dla1-go wejścia SV

ZawWE:

2,5

– 2 =

0,5

SzerPrzedz: 4-2=

2

Przyn_SV[0] =2,5mm in FP niska: 1-(

0,5

/

2

)=3/4

Przyn_SV[1] =2,5mm in FP srednia: 1-3/4=1/4

Rys.2. Rozkład funkcji przynależności dla 2-go wejścia e

b) wyliczanie wartości wyjściowej dla danych: SV =

2,5

[mm], PV= 1,8 [mm], obliczone e =

0,7

[mm],

output MV=?

Fig. 4. Baza reguł

MV = ¾ *1/7*50 + ¾*6/7*60 + ¼*1/7* 80 + ¼*6/7*85 =

3/28*50 + 18/28*60 + 1/28*80 + 6/28*85 = 65 [A]

-0

.5

(A

) D

uz

y_

m

-

- 0

.3

(B

) M

aly

_m

-0

.2÷

0.1

(C

) z

er

o

0.8

(D

) M

aly

_p

 (1) 0

!"#$% (2) 2

#&!"% (3) 4

(

10

15

20

25

30

40

50

60

70

75

80

85

+

u (e)

1

- 0.5

Duzy_m

(A)

- 0.3 - 0.2

0.1

0.8

0

0

Maly_m

(B)

zero

(C)

Maly_p

(D)

[mm]

0,7

6/7

1/7

0

2 4

niska (2)

u (SV)

1

zero (1)

[mm]

2,5

srednia (3)

3/4

1/4

error e

se

t

v

a

lu

e

S

V

(* Wprowadzanie parametrow bazy reguł *)

(*

X := 0;*)

Sing[0] := 10;

Sing[1] := 30;

Sing[2] := 70;

(*

X := 1;*)

Sing[3] := 15;

Sing[4] := 40;

Sing[5] := 75;

(*

X := 2;*)

Sing[6] := 20;

Sing[7] := 50;

Sing[8] := 80;

(*

X := 3;*)

Sing[9] := 25;

Sing[10] := 60;

Sing[11] := 85;

(* Położenie granic FP dla wybranych wejść*)

(* Granice FP dla wejścia 1 - dla uchybu*)

We[0] := e_Duzy_m; (* A -0,5*)

We[1] := e_Maly_m; (* B -0,3*)

We[2] := e_Zero_m; (* C -0,2*)

We[3] := e_Zero_p; (* C 0,1*)

We[4] := e_Maly_p; (* D 0,8*)

(* Granice FP dla wejścia 2 - dla wartości zadanej*)

We[5] := INT_TO_REAL(SV_Zero); (* 1 +0*)

We[6] := INT_TO_REAL(SV_Niska); (* 2 +2*)

We[7] := INT_TO_REAL(SV_Srednia); (* 3 +4*)

(* Rozmywanie e *)

if e > We[0] then

if e < We[1] then

ZawWE := e - We[0];

SzerPrzedz := We[1] - We[0];

Przyn_e[1] := ZawWE / SzerPrzedz;

Przyn_e[0] := 1,0 - Przyn_e[1];

X := 0;

elsif e < We[2] then

ZawWE := e - We[1];

SzerPrzedz := We[2] - We[1];

Przyn_e[1] := ZawWE / SzerPrzedz;

Przyn_e[0] := 1,0 - Przyn_e[1];

X := 1;

elsif e <= We[3] then

Przyn_e[0] := 1,0;

Przyn_e[1] := 0,0;

X := 2;

elsif e < We[4] then

ZawWE := e - We[3];

SzerPrzedz := We[4] - We[3];

Przyn_e[1] := ZawWE / SzerPrzedz;

Przyn_e[0] := 1,0 - Przyn_e[1];

X := 2;

else

Przyn_e[0] := 1,0;

Przyn_e[1] := 0,0;

X := 3;

end_if;

else

Przyn_e[0] := 1,0;

Przyn_e[1] := 0,0;

X := 0;

end_if;

(* Rozmywanie SV *)

if SV > We[5] then

if SV < We[6] then

ZawWE := SV - We[5];

SzerPrzedz := We[6] - We[5];

Przyn_SV[1] := ZawWE / SzerPrzedz;

Przyn_SV[0] := 1,0 - Przyn_SV[1];

Y := 0;

elsif SV < We[7] then

ZawWE := SV - We[6];

SzerPrzedz := We[7] - We[6];

Przyn_SV[1] := ZawWE / SzerPrzedz;

Przyn_SV[0] := 1,0 - Przyn_SV[1];

Y := 1;

else

Przyn_SV[1] := 0,0;

Przyn_SV[0] := 1,0;

Y := 2;

end_if;

else

Przyn_SV[0] := 1,0;

Przyn_SV[1] := 0,0;

Y := 0;

end_if;

(* Wnioskowanie i wyostrzanie (wyznaczanie wartości wyjściowej *)

out := Przyn_e[0] * Przyn_SV[0] * INT_TO_REAL(Sing[Y + 3 * X])

+ Przyn_e[0] * Przyn_SV[1] * INT_TO_REAL(Sing[Y + 1 + 3 * X])

+ Przyn_e[1] * Przyn_SV[0] * INT_TO_REAL(Sing[Y + 3* (X + 1)])

+ Przyn_e[1] * Przyn_SV[1] * INT_TO_REAL(Sing[Y + 1 + 3 * (X + 1)]);