Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

1

12.



12. WPROWADZENIE DO DYNAMIKI BUDOWLI

12.1. Wstęp

Dynamika jest działem mechaniki zajmującym się układami odkształcalnymi będącymi w ruchu, w

których uwzględniamy wpływ działających sił. Przy rozpatrywaniu zagadnień dynamicznych zakładamy, że
przemieszczenia są bardzo małe i charakteryzują się zmiennością w czasie. Przemieszczenia te mają charakter
oscylacyjny. W rozważaniach zajmować się będziemy drganiami harmonicznymi.

Kolejnym założeniem jest sposób określenia współczynników uogólnionych. Każde ciało posiada stopnie
swobody dynamicznej, czyli liczbę współczynników uogólnionych, które jednoznacznie określają położenie
ciała w przestrzeni oraz możliwość ruchu.

Aby dobrze zrozumieć zagadnienia dynamiki budowli, należałoby wyjaśnić kilka pojęć:

1. Punkt materialny – to ciało, którego położenie w przestrzeni daje się określić w taki sam sposób, jak

położenie punktu geometrycznego (masa bez wymiarów).

2. Ciało materialne – to układ oddzielnych punktów materialnych lub też zbiór punktów wypełniających daną

część przestrzeni w sposób ciągły. Belka jest traktowana jako zbiór punktów materialnych i ma
nieskończenie wiele stopni swobody dynamicznej. Należy przez to rozumieć, że każdy z punktów belki
ugina się inaczej. Możemy w tym przypadku posłużyć się aproksymacją sprowadzając opis belki do dwóch
końcowych jej punktów.

3. Siła – to działanie wywierane na ciało celem wyprowadzenia go ze stanu spoczynku. Siła jest wielkością

kierunkową, czyli wektorem.

4. Masa – to pewna wielkość, charakteryzująca zachowanie się dynamiczne ciała, niezależna ani od stanu

ruchu, ani też od stanu fizycznego ciała. Masa jest wielkością bezkierunkową, czyli skalarem.

12.2. Zasada d'Alemberta

Na poszczególne punkty układu materialnego działają siły czynne P oraz siły bierne (opory ruchu) 

W ;

siły te nadają poszczególnym punktom materialnym o masach m przyspieszenia a . Wprowadzając fikcyjne

siły B=−m⋅a , zwane siłami bezwładności, sprowadzamy zagadnienie układu materialnego będącego w

ruchu do ststycznego zagadnienia równowagi sił. Stan ruchu układu materialnego określamy twierdzeniem:

W każdym położeniu poruszającego się układu materialnego siły bezwładności równoważą się z siłami

zewnętrznymi, o ile siły wewnętrzne nawzajem się znoszą.

PB=0

(12.1)

12.3. Drgania własne układu o jednym stopniu swobody dynamicznej

Rozpatrzmy ruch masy

m o jednym stopniu swobody dynamicznej (rys. 12.1), która jest zamocowana

sprężyście (podpora o sztywności

k). Zakładamy możliwość swobodnego ruchu tylko w jednym kierunku.

Wartość przemieszczenia opisuje funkcja czasu

q(t).

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

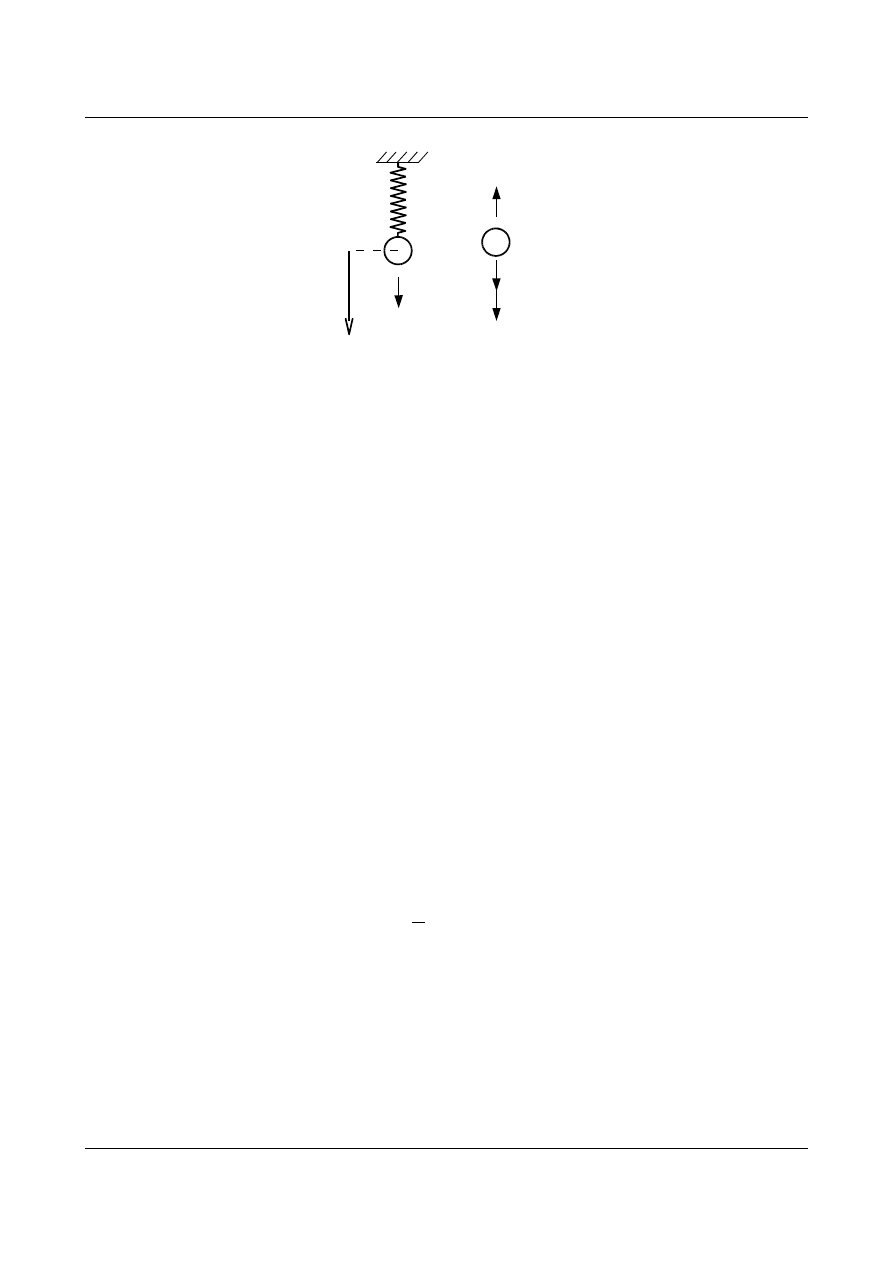
Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

2

m

q(t)

k [N/m]

P(t)

P(t)

B(t)

m

Q(t)

Rys. 12.1. Układ o jednym stopniu swobody dynamicznej

Zgodnie z zasadą d'Alemberta możemy zapisać równanie równowagi:

P



t



B



t



−Q



t



=0

(12.2)

gdzie siła bezwładności:

B



t



=−m⋅¨q



t



(12.3)

a siła sprężystości:

Q



t



=k⋅q



t



(12.4)

Po podstawieniu wyrażeń (12.3) i (12.4) do równania (12.2), otrzymujemy:

m

⋅¨q



t



k⋅q



t



=P



t



(12.5)

Dla układu, na który nie działa zewnętrzna siła wymuszająca



P

t=0



otrzymujemy równanie jednorodne.

m

⋅¨q



t



k⋅q



t



=0

(12.6)

Równanie (12.6) jest nazywane równaniem różniczkowym zwyczajnym ruchu. Dzieląc to równanie

obustronnie przez masę i podstawiając wyrażenie na częstość kołową drgań własnych

 :



2

=

k

m

(12.7)

otrzymujemy:

¨q



t





2

⋅q



t



=0

(12.8)

Równanie różniczkowe (12.8) można wyliczyć przyjmując funkcję rozwiązującą w postaci:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

3

q



t



=C

1

⋅sin  tC

2

⋅cos  t

(12.9)

lub w innej formie:

q



t



= A⋅sin



 t



(12.10)

gdzie

 jest przesunięciem fazowym.

Wykorzystując zależności trygonometryczne możemy wyznaczyć relację pomiędzy C

1

i C

2

, a stałymi A

i

 .

q



t



=A⋅sin



 t



= A⋅

[

sin

 t⋅cos cos  t⋅sin 

]

Przyrównując do siebie wyrażenia (12.9) i (12.10) otrzymujemy:

A

⋅

[

sin

 t⋅cos cos  t⋅sin

]

=C

1

⋅sin  tC

2

⋅cos  t

C

1

=A⋅cos

(12.11)

C

2

=A⋅sin

(12.12)

Znając warunki początkowe możemy wyznaczyć wartości stałych równania (12.10). Nie należy mylić

warunków początkowych z warunkami brzegowymi, ponieważ te pierwsze dotyczą czasu, a drugie
przestrzeni. Przykładowo dla chwili początkowej t

=0 :

1) przemieszczenie ma wartość q



0



=a

2) prędkość jest równa ˙q



0



=0

Z warunków tych otrzymujemy:

˙q



0



= A⋅cos



0



=0

cos

=0

=



2

(12.13)

oraz:

q



0



=A⋅sin



0



=a

A

⋅sin =a

A

⋅sin



2

=a

A

=a

(12.14)

Zatem dla powyższych warunków początkowych otrzymujemy pełne rozwiązanie postaci:

q



t



=a⋅sin



 t



2



=A⋅cos  t

(12.15)

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

4

Zgodnie z rozwiązaniem (12.15) kulka o masie

m zamocowana sprężyście powróci do położenia

początkowego po czasie odpowiadającemu kątowi 2

 . Podstawmy zatem tę wartość do równania (12.15).

q



t



= A⋅cos



 t2



=A⋅cos

[





t



2







]

=A⋅cos

[





t

T



]

(12.16)

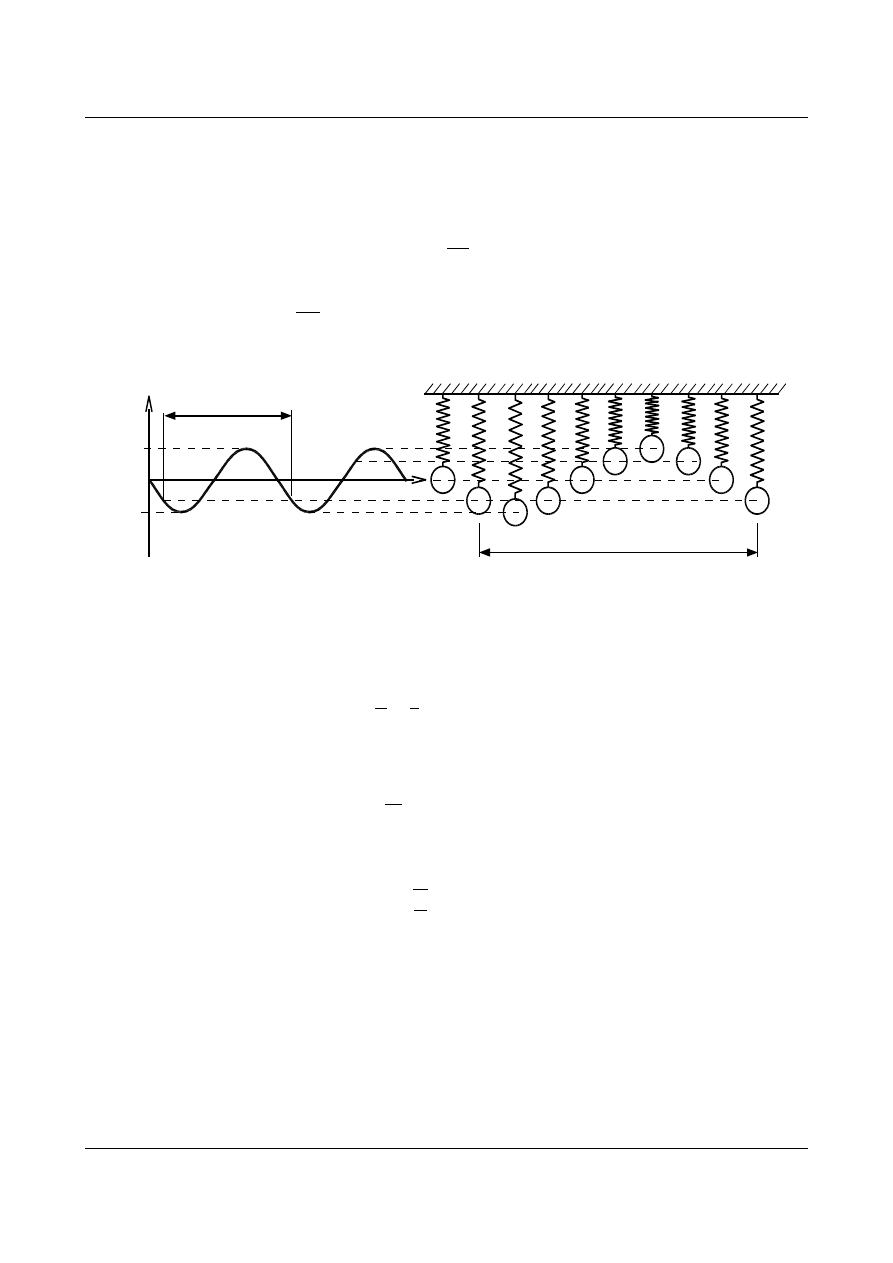
Wprowadzone oznaczenie T

=

2





jest okresem drgań, czyli czasem dzielącym dwa identyczne położenia

rozpatrywanego ciała (rys. 12.2).

q(t)

t

T

k [N/m]

A

A

T

Rys. 12.2. Położenie ciała w zależności od czasu

Mając zdefiniowany okres drgań możemy na jego podstawie określić częstotliwość i częstotliwość techniczną.

1. Częstotliwość (częstość fizyczna) – to ilość pełnych cykli wykonanych w jednostce czasu.

f

=

1

T

[

1

s

=Hz

]

(12.17)

2. Częstotliwość techniczna – to ilość pełnych cykli wykonanych w ciągu jednej minuty.

n

=

60

T

[

Hz

]

(12.18)

Powróćmy jeszcze do wzoru (12.7) na częstość kołową drgań własnych:

=



k

m

gdzie:

k – sztywność [kN/m], jest to siła jaką należy przyłożyć, aby wywołać jednostkowe przemieszczenie,

m – masa [kg].

Oznacza to, że jeśli chcemy poznać częstość kołową drgań własnych konstrukcji, to przy prostych
schematach, przybliżonych jedną masą drgającą wystarczy, że wyznaczymy sztywność konstrukcji. Omówimy
to zagadnienie na kilku przykładach.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

5

Przykład 1

Znaleźć częstość kołową drgań własnych dla wspornika przedstawionego na rysunku 12.3.

l

EJ

m

Rys. 12.3. Model belki z jedną masą na końcu

Zadanie rozwiążemy korzystając z twierdzenia o pracy wirtualnej. Określimy współczynnik podatności, który
jest odwrotnością sztywności.

1⋅=

∫

0

l

M

P



M

EJ

ds

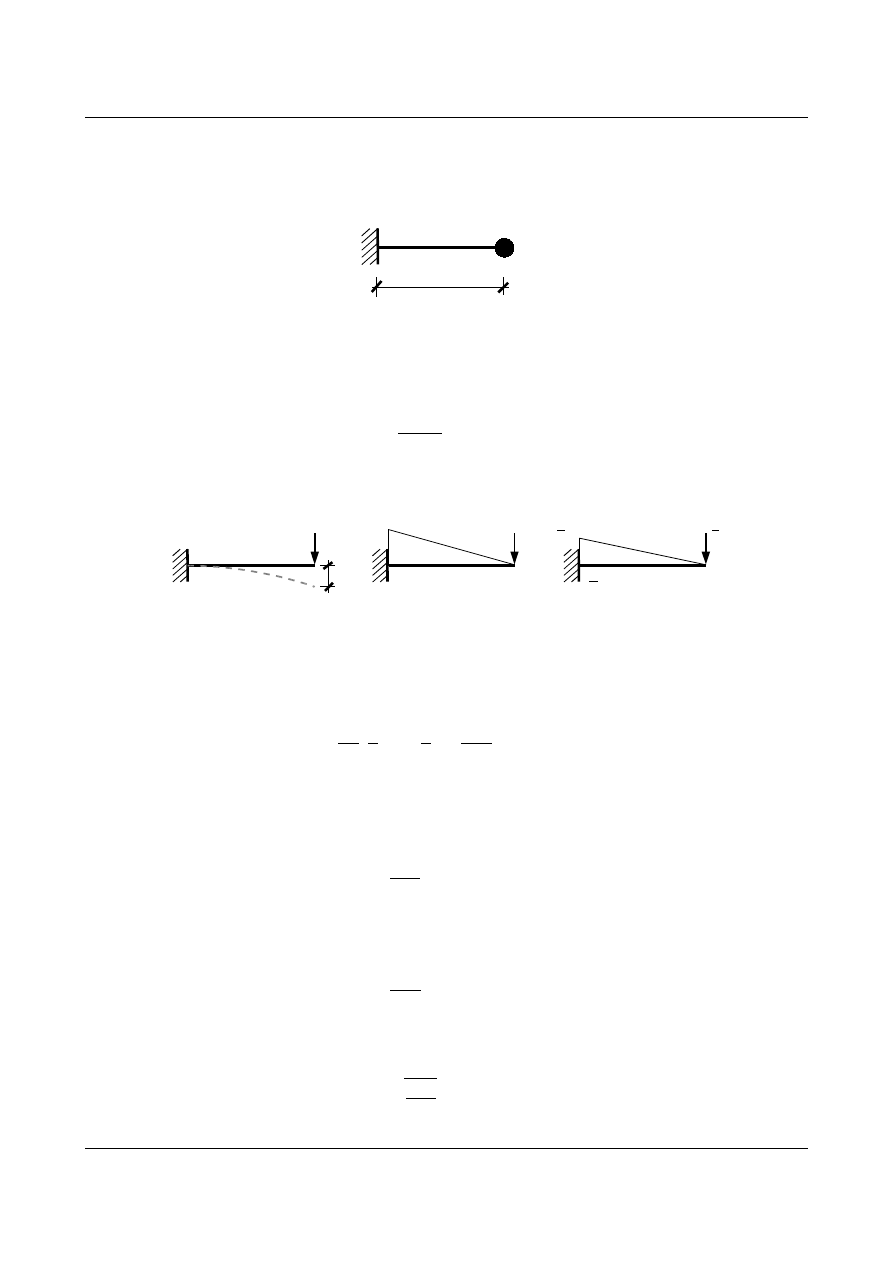
Narysujmy najpierw wykresy momentów od siły rzeczywistej

P i wirtualnej 1 .

Pl

1

P

P = ?

δ=1

M

P

M

1·l

Rys. 12.4. a) Linia ugięcia belki, b) Wykres momentów od siły P, c) Wykres momentów od 1

Przemieszczenie wyznaczamy z twierdzenia Wereszczegina-Mohra, czyli wymnażając wykresy

M

P

i 

M . Po

przekształceniach i uproszczeniu przez jedynkę wirtualną otrzymujemy:

=

1

EJ



1
2

⋅P⋅l⋅l⋅

2
3

⋅l



=

Pl

3

3 EJ

Wiemy, że sztywność [kN/m] to siła jaką należy przyłożyć, aby wywołać jednostkowe przemieszczenie. Zatem
wyznaczone przemieszczenie przyrównujemy do jedynki.

=

Pl

3

3 EJ

=1

Z tego możemy wyznaczyć siłę

P powodującą przemieszczenie δ = 1, inaczej sztywność.

P

=

3 EJ

l

3

=k

Po podstawieniu otrzymanej sztywności do wzoru (12.7) otrzymujemy częstość kołową drgań własnych belki.

=



3 EJ

ml

3

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

6

Przykład 2

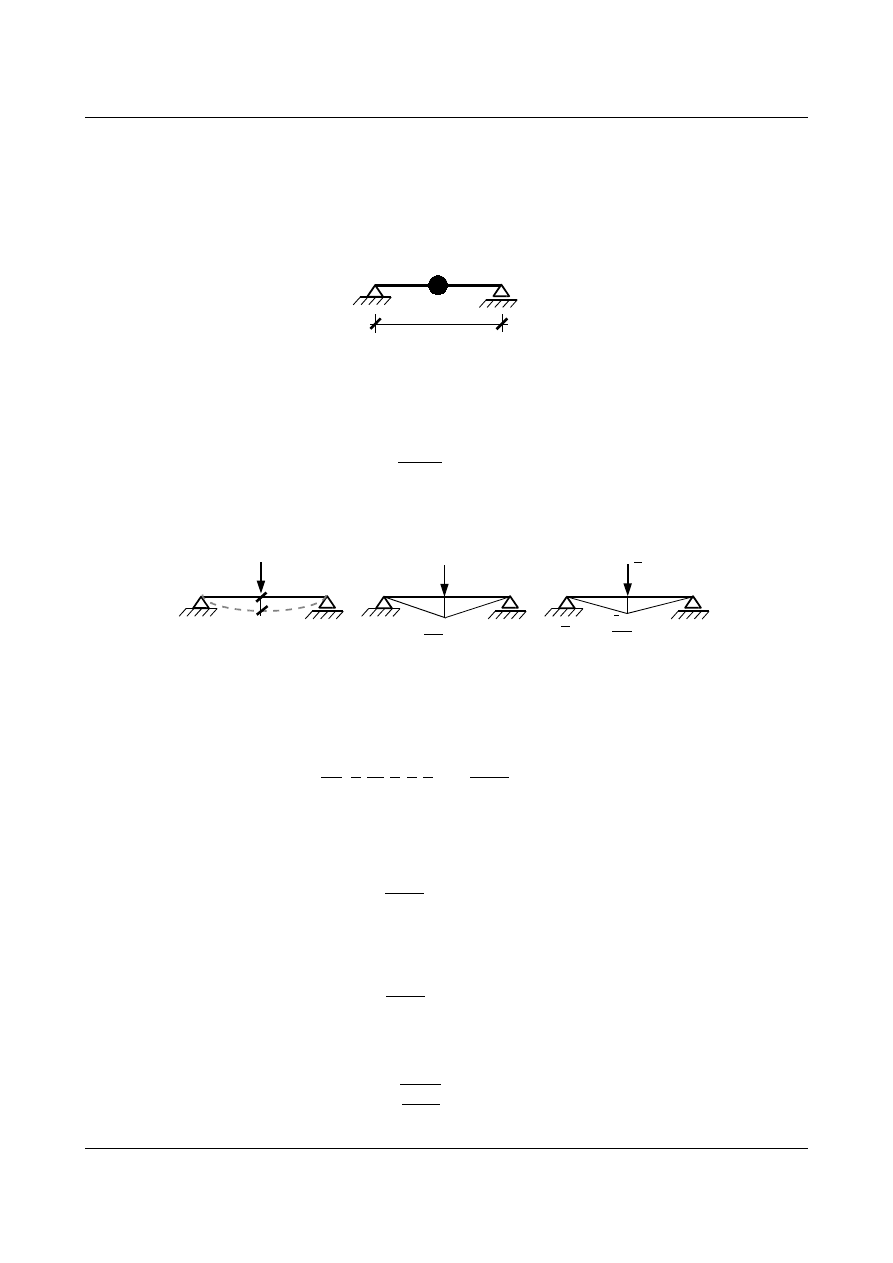
Znaleźć częstość kołową drgań własnych dla belki wolnopodpartej (rys. 12.5).

EJ

l

m

Rys. 12.5. Belka wolnopodparta z masą w środku rozpiętości

Zadanie rozwiążemy analogicznie jak poprzednie, również korzystając z twierdzenia o pracy wirtualnej.

1⋅=

∫

0

l

M

P



M

EJ

ds

Po narysowaniu wykresów momentów od siły rzeczywistej

P i wirtualnej 1 .

Pl

1

P

P = ?

δ = 1

M

P

M

4

4

1·l

Rys. 12.6. a) Linia ugięcia belki, b) Wykres momentów od siły P, c) Wykres momentów od 1

wyznaczmy przemieszczenie

δ

=

1

EJ



1
2

⋅

Pl

4

⋅

l

2

⋅

2
3

⋅

l

4



⋅2 =

Pl

3

48 EJ

Skoro sztywność to siła jaką należy przyłożyć, aby wywołać jednostkowe przemieszczenie, to możemy zapisać

=

Pl

3

48 EJ

=1

Z tego wyznaczamy siłę

P równą sztywności układu

P

=

48 EJ

l

3

=k

a następnie częstość kołową drgań własnych belki ze wzoru (12.7)

=



48 EJ

ml

3

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

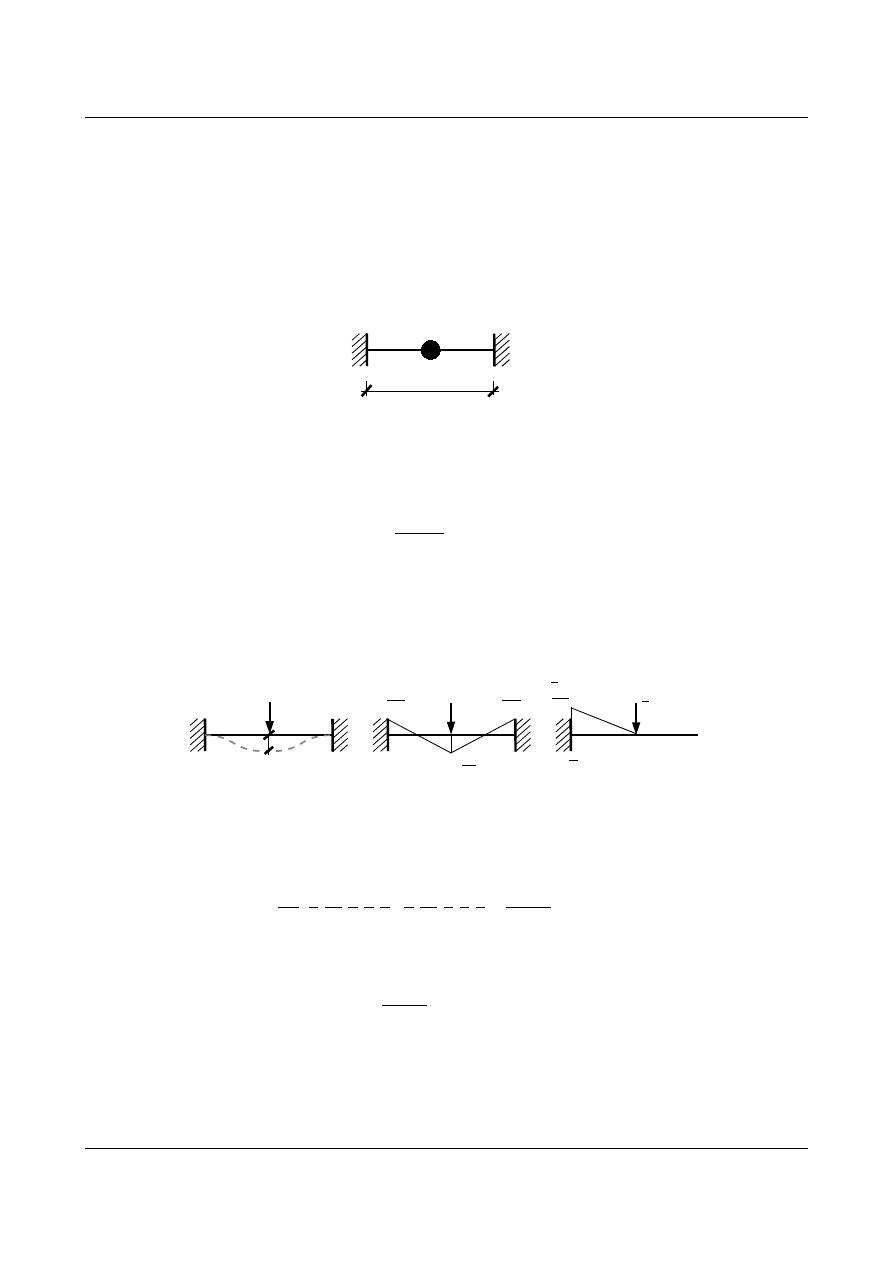
Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

7

Aby poznać wartość liczbową częstości drgań własnych musimy określić sztywność giętną belki EJ, znać
wartość masy przyłożonej w środku rozpiętości i długość belki.

Przykład 3

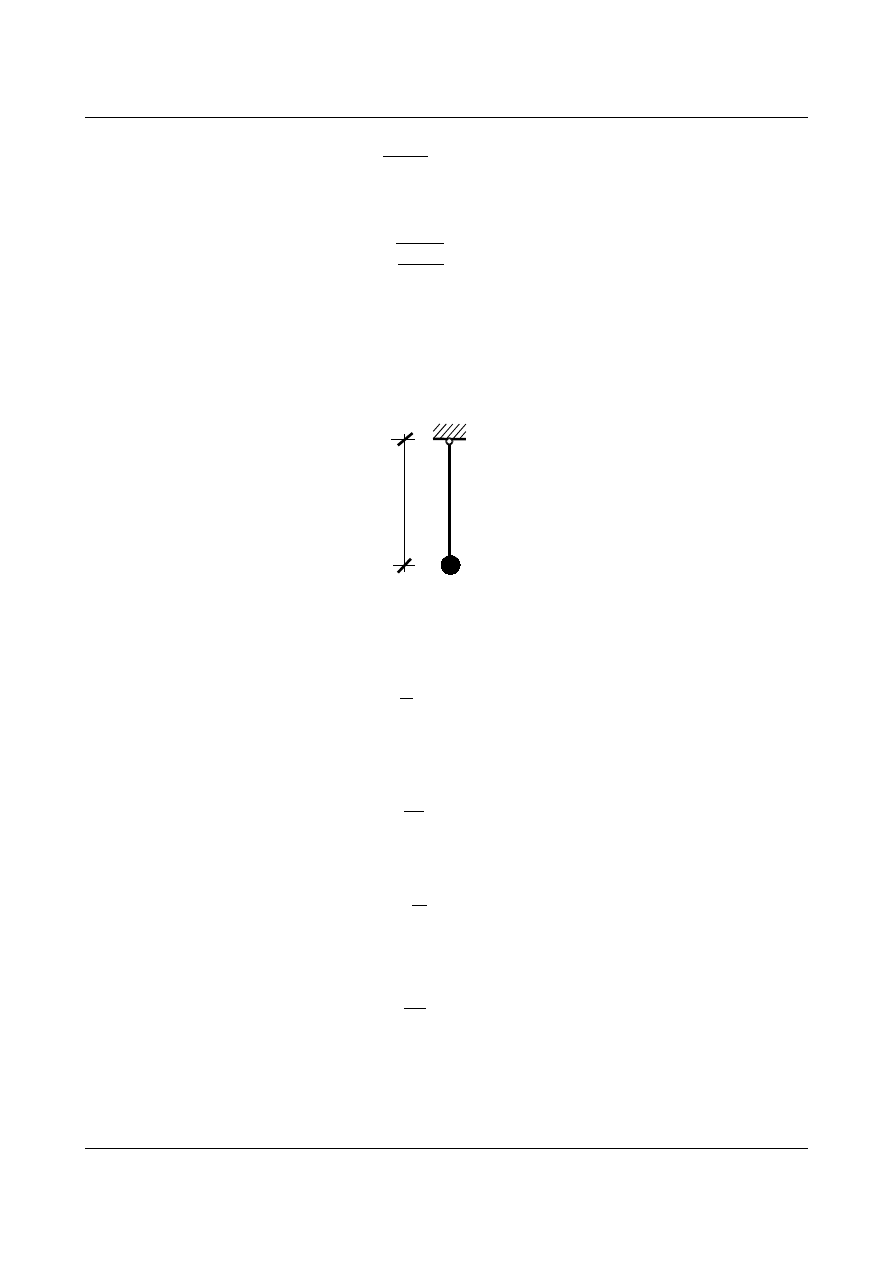
Znaleźć częstość kołową drgań własnych dla belki obustronnie utwierdzonej (rys. 12.7).

l

EJ

m

Rys. 12.7. Belka obustronnie utwierdzona – przybliżona masą w środku rozpiętości

Ponieważ jest to układ statycznie niewyznaczalny, dlatego należy rozwiązać go korzystając z twierdzenia
redukcyjnego.

1⋅=

∫

0

l

M

P



M

o

EJ

ds

gdzie:

M

P

- wykres momentów od siły

P w układzie statycznie niewyznaczalnym,



M

o

- wykres momentów od siły 1 w układzie podstawowym.

Pl

1

P

P = ?

δ = 1

M

P

M

8

Pl

8

Pl

8

2

1·l

Rys. 12.8. a) Linia ugięcia belki, b) Wykres momentów od siły P, c) Wykres momentów od 1

Wyznaczmy przemieszczenie od siły

P:

=

1

EJ



1
2

⋅

Pl

8

⋅

l

2

⋅

2
3

⋅

l

2

−

1
2

⋅

Pl

8

⋅

l

2

⋅

1
3

⋅

l

2



=

Pl

3

192 EJ

i przyrównajmy je do jedynki

=

Pl

3

192 EJ

=1

Następnie wyznaczamy sztywność (siłę

P dla której δ = 1)

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

8

P

=

192 EJ

l

3

=k

Po podstawieniu otrzymanej sztywności do wzoru (12.7) otrzymujemy częstość kołową drgań własnych belki.

=



192 EJ

ml

3

Przykład 4

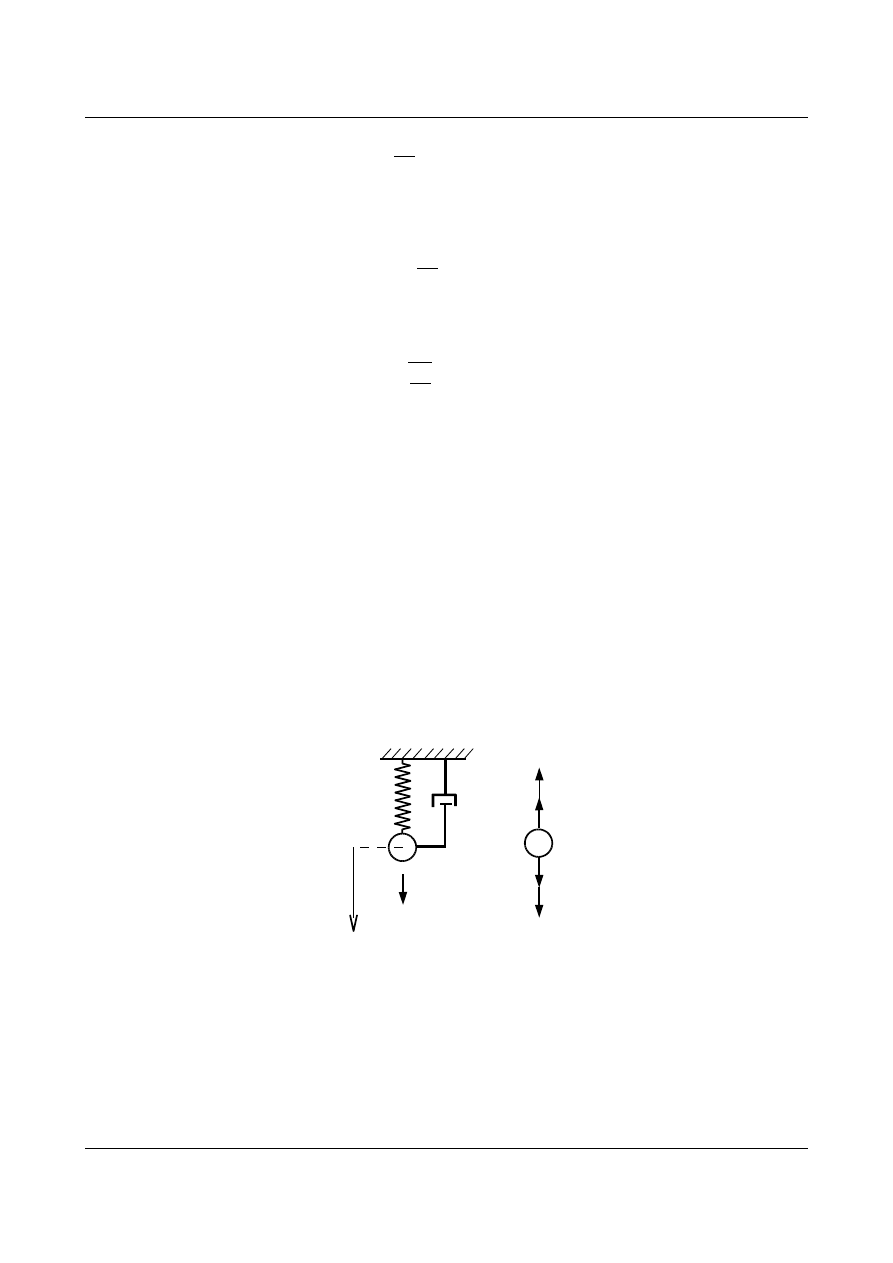
Znaleźć częstość kołową drgań własnych dla schematu jak na poniższym rysunku (rys. 12.9).

l

EJ

m

Rys. 12.9. Pręt pionowy zamocowany przegubowo

Zgodnie z prawem Hooke'a odkształcenie jest wprost proporcjonalne do naprężenia, które je spowodowało:

=

1

E

⋅

Poza tym odkształcenie pręta jest równe wydłużeniu względnemu (przyrost długości

Δl do długości l):

=

l

l

Wiedząc, że



N

=

N

A

na podstawie powyższych zależności możemy zapisać

l=

N

EA

⋅l

Szukamy siły

N, która wywoła jednostkowe wydłużenie pręta, zatem przyrównajmy Δl do jedynki:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

9

l=

N

EA

⋅l=1

Jest to inaczej sztywność podłużna tego pręta,

k

=N =

EA

l

na podstawie której możemy wyliczyć częstość kołową drgań własnych konstrukcji (12.27)

=



EA

ml

Należy zwrócić uwagę na fakt, że drgania (przemieszczenia) odbywają się wzdłuż osi pręta.

12.4. Drgania własne tłumione

Tłumienie drgań jest wynikiem działania na ciało sił oporu oznaczanych jako R . W tłumieniu lepkim

(wiskotycznym), siły te są proporcjonalne do prędkości ruchu ciała.

R

≃c⋅˙qt

(12.19)

Na rys. 12.10 przedstawiono drgające ciało o masie

m i jednym stopniu swobody, którego ruch jest tłumiony

wiskotycznie. Przemieszczenia (drgania) opisuje funkcja

q(t).

m

q(t)

k [N/m]

tłumik

c

P(t)

P(t)

B(t)

R(t)

Q(t)

m

Rys. 12.10. Model układu drgającego z tłumieniem

Zgodnie z zasadą d' Alemberta możemy zapisać równanie drgań własnych tłumionych jako równowagę sił:

P



t



B



t



−Q



t



−R



t



=0

Dla układu nieobciążonego



P

t =0



można zapisać:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

10

m

⋅¨q



t



c⋅˙q



t



k⋅q



t



=0

(12.20)

W równaniu (12.20) wielkość

c jest stałą tłumienia.

Dzieląc obustronnie równanie (12.20) przez masę drgającego ciała otrzymujemy równanie:

¨q



t



2 ⋅˙q



t





2

⋅q



t



=0

(12.21)

w którym

=

c

2 m

, to współczynnik tłumienia drgań,



2

=

k

m

to częstość drgań własnych.

Rozwiązaniem, całką ogólną równania ruchu (12.21) jest funkcja wykładnicza:

q

t = A e

rt

(12.22)

której pochodne wynoszą:

˙qt =A r e

rt

¨qt=A r

2

e

rt

Podstawiamy funkcję (12.22) i jej pochodne do równania ruchu (12.21). Po przekształceniach otrzymujemy

równanie charakterystyczne postaci:

r

2

2  r

2

=0

(12.23)

W zależności od wielkości tłumienia (parametr

c) mamy trzy możliwe, różne rozwiązania równania

charakterystycznego:

1. Małe tłumienia



0



– rozwiązaniem są dwa pierwiastki zespolone, sprzężone,

2. Duże tłumienia



0



– rozwiązaniem są dwa pierwiastki rzeczywiste,

3.

=0 – rozwiązaniem są dwa pierwiastki podwójne,

gdzie:

=



2





2

−4⋅

2

=4⋅

2

−4⋅

2

=4

2

−

2



Znak wyrażenia

 zależy od stosunku  do  , dla  mamy 0 .

Przeanalizujmy rozwiązania:

Ad 1. Zajmijmy się teraz przypadkiem, gdy tłumienia są małe

 (tłumienie podkrytyczne). Możliwe są

dwa rozwiązania (pierwiastki zespolone, bo

0 ):

r

1

=−i





2

−

2

r

2

=i





2

−

2

(12.24)

Ostatecznie funkcję rozwiązującą można zapisać w postaci:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

11

q



t



=A e

−t

sin





1

t





(12.25)

która jest równoważna (przez analogię do poprzednich rozważań) wyrażeniu:

q



t



=e

−t



C

1

⋅cos 

1

t

C

2

⋅sin 

1

t



(12.26)

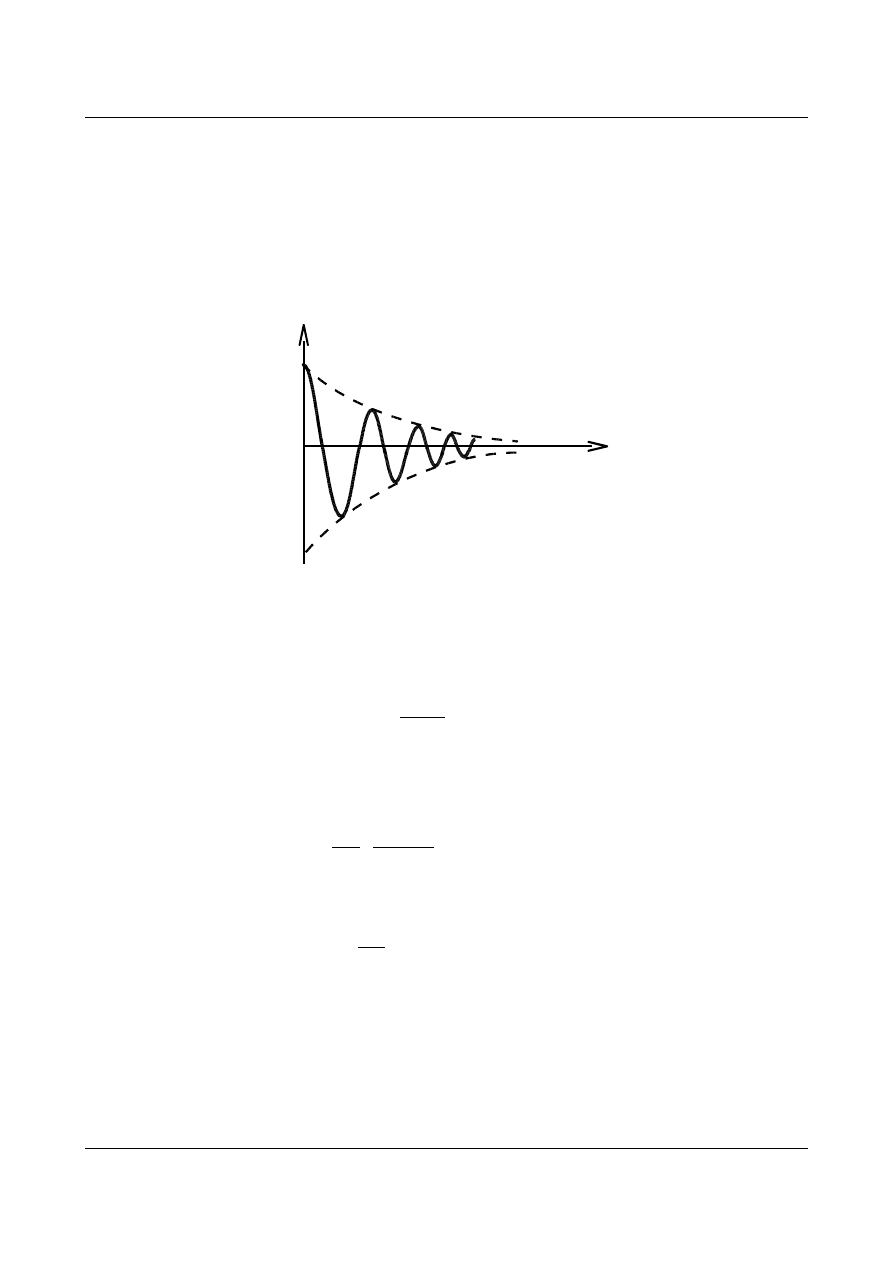
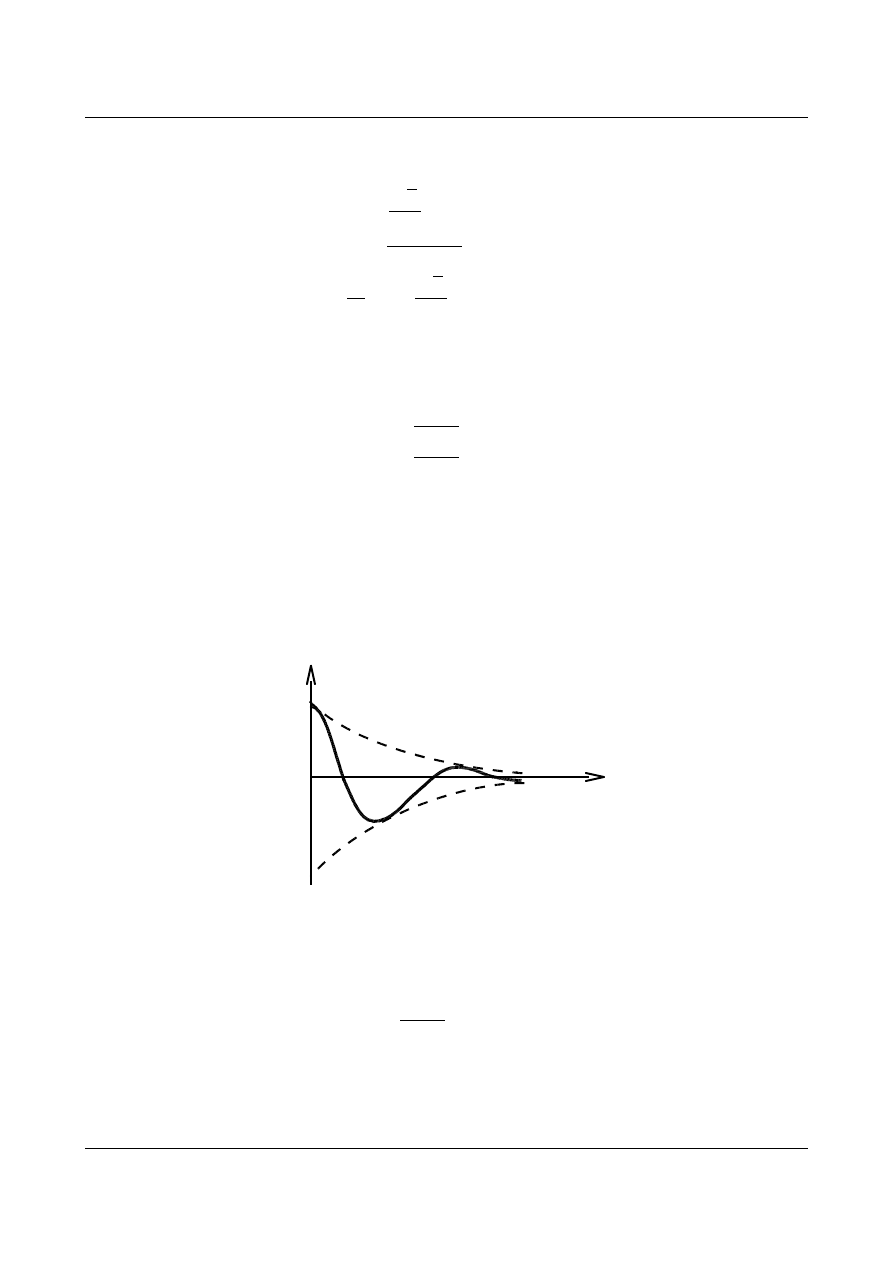
Na rys. 12.11 przedstawiono wykres funkcji rozwiązującej (12.26).

q(t)

t

e

-ρt

Rys. 12.11. Funkcja rozwiązująca (tłumienie podkrytyczne)

Na rysunku 12.11 widzimy, że drgania oscylują, następuje redukcja amplitudy przemieszczenia

(zmniejsza się do zera). Okres drgań T

1

jest większy w tym przypadku, ponieważ częstość kołowa



1

drgań

tłumionych jest mniejsza w porównaniu z drganiami nietłumionymi -



1

 .



1

=





2

−

2

(12.27)

Miarą tłumienia jest logarytmiczny dekrement tłumienia

λ, który oblicza się ze stosunku amplitud

kolejnych przemieszczeń:

q

n

1

q

n

=

A e

−



t

T

1



A e

− t

=e

−T

1

czyli:

=ln

∣

q

n

1

q

n

∣

=ln

∣

e

−T

1

∣

=T

1

(12.28)

Na podstawie wyrażenia (12.28) można powiedzieć, że logarytmiczny dekrement tłumienia to logarytm

naturalny ze stosunku dwóch amplitud oddalonych od siebie o okres. Jest on wprost proporcjonalny do
współczynnika tłumienia.

=T

1

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

12

Zadanie 1

Kolejne amplitudy drgań własnych maleją dwukrotnie, znaleźć relacje pomiędzy

ω

1

a

ω oraz określić

logarytmiczny dekrement tłumienia

λ.

=ln

∣

A e

−



t

T

1



A e

−t

∣

gdzie:

A e

−t

- amplituda po czasie

t,

A e

−



t

T

1



- kolejna amplituda po czasie

t + T

1

.

Ponieważ kolejne amplitudy drgań maleją dwukrotnie, to:

A e

−



t

T

1



A e

−t

=

1
2

A zatem logarytmiczny dekrement tłumienia wynosi:

=ln

∣

1
2

∣

Ze wzoru (12.28) wiemy, że

=T

1

=ln

∣

1
2

∣

Skoro

T

1

=

2





1

to

2





1

=ln

∣

1
2

∣

=



1

2



⋅ln

∣

1
2

∣

Na podstawie wzoru (12.27) możemy wyznaczyć relację między

ω

1

a

ω:



1

2

=

2

−





1

2



⋅ln

∣

1
2

∣



2

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

13



1

2

[

1





ln

∣

1
2

∣

2





2

]

=

2





1

=



1





ln

∣

1
2

∣

2





2

Ad 2. Rozpatrzmy teraz przypadek, gdy tłumienia są duże

 (tłumienie nadkrytyczne). Wówczas również

otrzymujemy dwa rozwiązania (tym razem rzeczywiste) równania charakterystycznego:

r

1

=−−





2

−

2

r

2

=−





2

−

2

(12.29)

Funkcja rozwiązująca dla tego przypadku ma następującą postać:

q



t



=e

−t





C

1

⋅sinh 



1

t

 

C

2

⋅cosh 



1

t



(12.30)

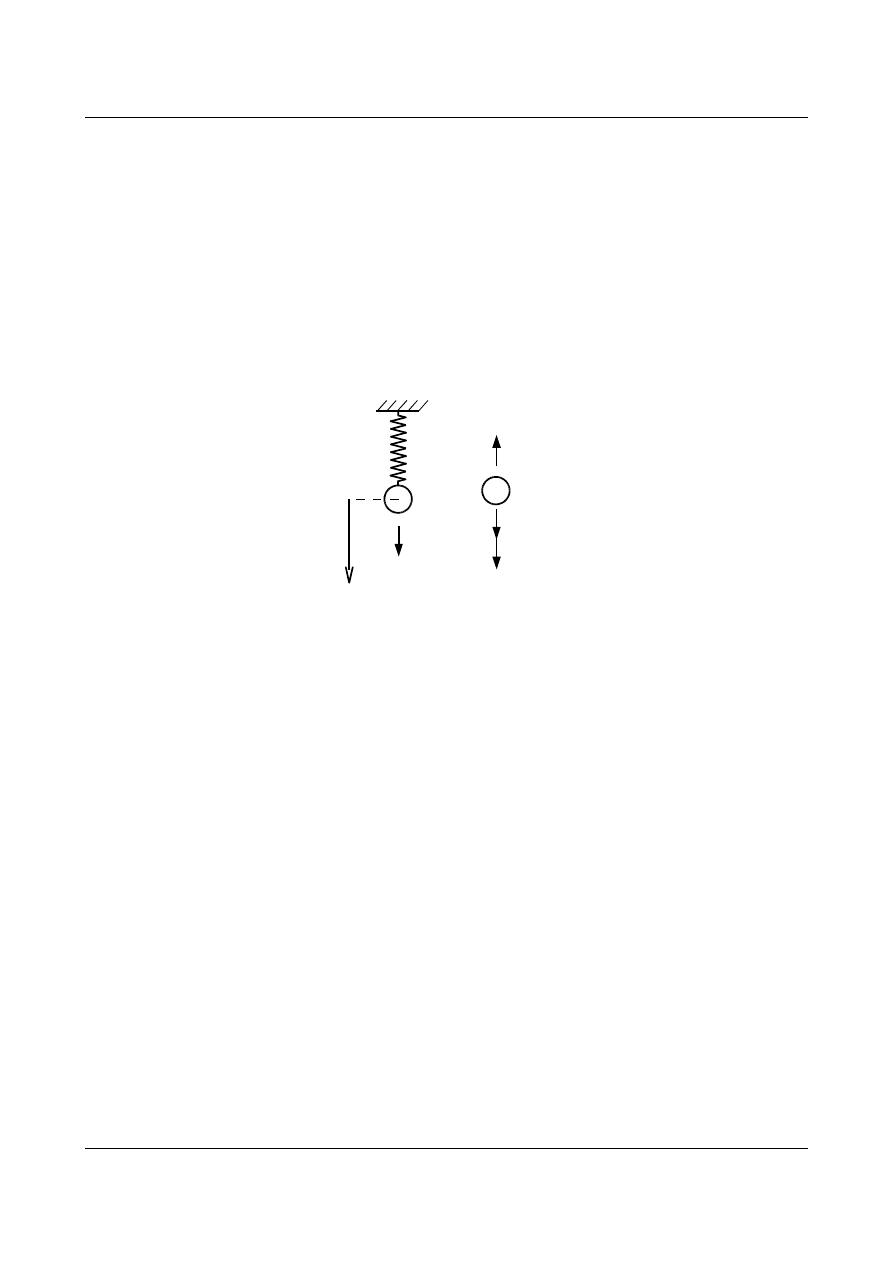
Na rys. 12.12 przedstawiono wykres funkcji rozwiązującej (12.30).

q(t)

t

Rys. 12.12. Funkcja rozwiązująca (tłumienie nadkrytyczne)

Z rys. 12.12 wynika, że drgania z tłumieniem nadkrytycznym szybko zanikają i nie mają charakteru
oscylacyjnego. Częstość kołowa drgań własnych wynosi:





1

=





2

−

2

(12.31)

Ad 3. W przypadku tłumienia krytycznego, tzn. gdy

= , rozwiązanie przyjmuje postać funkcji:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

14

q



t



=e

− t





C

1

⋅t 

C

2



(12.32)

której przebieg drgań jest bardzo podobny do drgań nadkrytycznych.

12.5. Drgania wymuszone nietłumione

Rozpatrzmy układ o jednym stopniu swobody dynamicznej, zamocowany sprężyście, w którym siła

wymuszająca jest harmonicznie zmienna w czasie (rys. 12.13).

m

q(t)

k [N/m]

P(t)

P(t)

B(t)

m

Q(t)

Rys. 12.13. Model układu o jednym stopniu swobody

Zgodnie z zasadą d'Alemberta możemy zapisać równanie równowagi:

P



t



B



t



−Q



t



=0

Po podstawieniu zależności (12.3) i (12.4) mamy:

m

⋅¨q



t



k⋅q



t



=P



t



(12.33)

gdzie P

t jest siłą wymuszającą zmienną w czasie, której wartość w przypadku drgań harmonicznych

można zapisać jako sumę:

P



t



=P

1

sin pt

P

2

cos pt

=P sin



pt





(12.34)

gdzie:

p – częstość kołowa drgań wymuszonych,

P – amplituda siły wymuszającej,

 – kąt przesunięcia fazowego.

Wprowadzając do równania równowagi (12.33) wyrażenie opisujące częstość kołową drgań własnych (12.7)
otrzymujemy po przekształceniach:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

15

¨q



t





2

⋅q



t



=

P

m

⋅sin



pt





(12.35)

Dalej stosunek amplitudy siły wymuszającej do masy oznaczamy symbolem

Q:

Q

=

P

m

(12.36)

Rozwiązaniem równania różniczkowego (12.35) jest funkcja, będąca sumą całki ogólnej i całki szczególnej:

q



t



=C

1

⋅sin  tC

2

⋅cos t

Q



2

− p

2

⋅sin



pt





(12.37)

gdzie wyrażenia:

C

1

⋅sin  tC

2

⋅cos  t

- to całka ogólna równania różniczkowego, którą otrzymujemy poprzez rozwiązanie

równania różniczkowego jednorodnego

¨q



t





2

⋅q



t



=0

,

Q



2

− p

2

⋅sin



pt





- to całka szczególna równania różniczkowego, wyznaczyć ją możemy w prosty sposób

stosując metodę przewidywań.

Jeżeli przyjmiemy przesunięcie fazowe

=0 oraz dobierzemy takie warunki początkowe, aby wartości

stałych całkowania C

1

=C

2

=0 , to funkcja rozwiązująca będzie miała postać:

q



t



=

Q



2

− p

2

⋅sin pt=

Q



2

1

−

p

2



2

⋅sin pt

(12.38)

W wyrażeniu (12.38) stosunek

Q



2

=

P

m



2

=

P

m

k

m

=

P

k

=A

stat

(12.39)

jest wartością (amplitudą) przemieszczenia statycznego.

Jeżeli stosunek częstości wymuszenia do częstości drgań własnych opiszemy współczynnikiem

=

p



(12.40)

to mianownik wyrażenia (12.38) można wydzielić jako:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

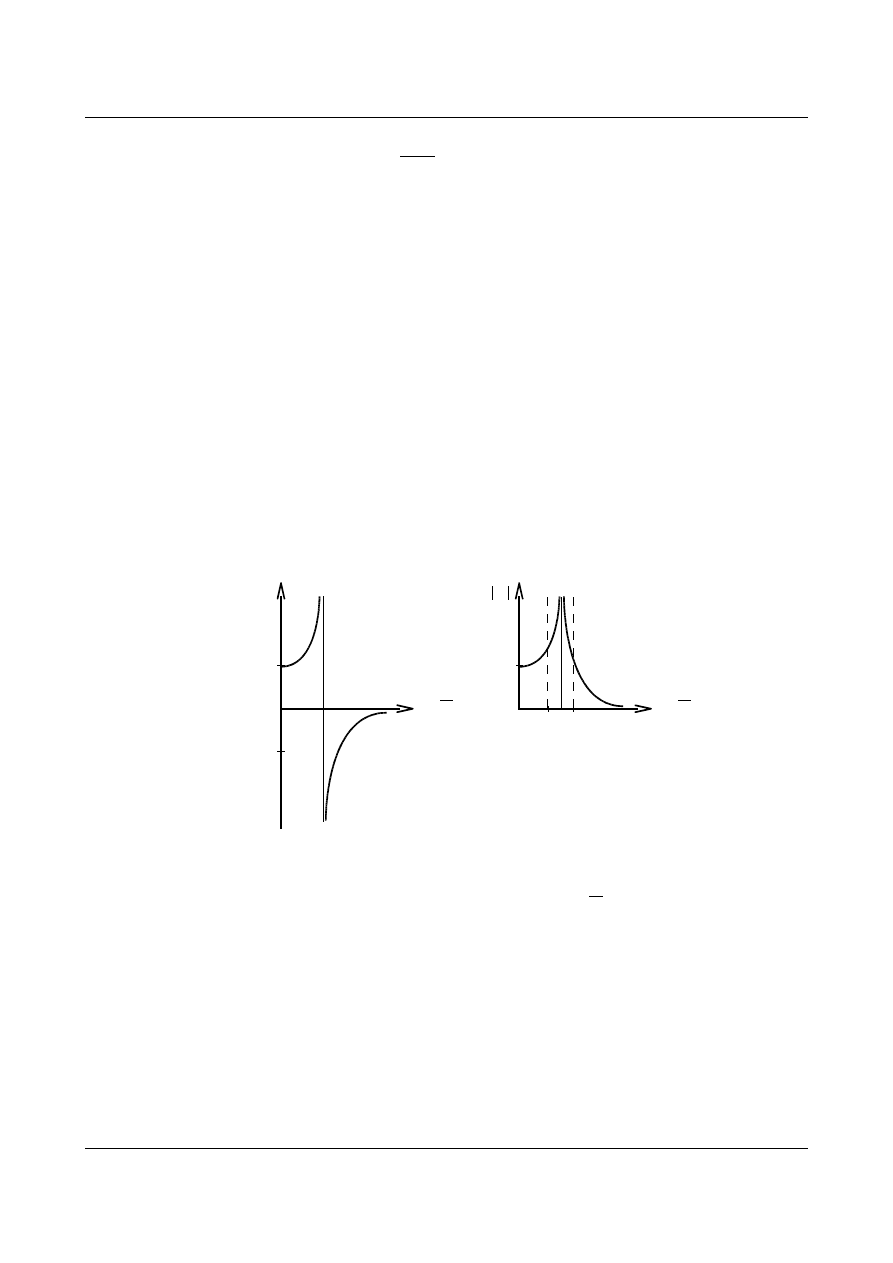
Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

16



d

=

1

1

−

2

(12.41)

Ostatecznie, więc funkcja rozwiązująca przyjmuje postać:

q



t



=A

stat



d

sin pt

(12.42)

gdzie:

A

stat

– amplituda statyczna (przemieszczenie punktu drgającego wywołane statyczną siłą P ),



d

– współczynnik dynamiczny drgań wymuszonych.

Współczynnik dynamiczny



d

zwiększa amplitudę przemieszczeń statycznych układu. Gdy częstość kołowa

drgań wymuszonych

p

jest bliska częstości drgań własnych układu

 , ugięcie (amplituda przemieszczenia)

wobec braku tłumienia wzrasta do nieskończoności przy niezmiennej wartości działającej siły.

Opisane zjawisko nazywamy rezonansem. Strefy rezonansowe (obszar wzrostu amplitudy) możemy

określić tworząc wykres wartości współczynnika dynamicznego



d

w zależności od współczynnika



(stosunek częstości wymuszenia

p do częstości drgań własnych

 ).

1

1

1

ν

d

1

1

0,75

1,25

ν

d

η

=

p

ω

η

=

p

ω

Rys. 12.14. Wykres współczynnika dynamicznego ν

d

(η)

Strefą rezonansową określa się jako przedział, w którym stosunek częstości

p



waha się w granicach od

0,75

do

1,25. Aby uchronić konstrukcję przed zniszczeniem należy unikać stosowania częstości wymuszenia w

granicach stref rezonansowych.

12.6. Drgania wymuszone tłumione

W rozważaniach zakładamy tłumienie wiskotyczne oraz harmoniczną siłę wymuszającą. Postępując

analogicznie jak w przypadku drgań własnych tłumionych (bez wymuszenia) możemy zapisać równanie
równowagi (rys. 12.10).

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

17

P



t



B



t



−Q



t



−R



t



=0

i dalej na podstawie (12.34):

m

⋅¨q



t



c⋅˙q



t



k⋅q



t



=P

1

sin pt

P

2

cos pt

=P sin



pt





(12.43)

Po przekształceniach otrzymujemy równanie różniczkowe ruchu:

¨q



t



2 ⋅˙q



t





2

⋅q



t



=

P

m

⋅sin



pt





a po uwzględnieniu (12.36):

¨q



t



2 ⋅˙q



t





2

⋅q



t



=Q⋅sin



pt





(12.44)

Rozwiązanie tego równania różniczkowego będzie składało się tak jak poprzednio z sumy dwóch całek -
ogólnej i szczególnej. Przy założeniu, że całka ogólna obrazuje drgania szybko zanikając, jest ona mało
znacząca w przypadku wystąpienia tłumienia. Zajmijmy się zatem wyłącznie rozwiązaniem szczególnym
równania różniczkowego. Rozwiązaniem szczególnym tego równania może być funkcja:

q



t



=A sin



pt





(12.45)

Różniczkując dwukrotnie powyższe rozwiązanie i podstawiając funkcje

q



t



, ˙qt  , ¨qt 

do równania (12.44)

otrzymujemy układ dwóch równań, w którym niewiadomymi są amplituda

A oraz przesunięcie fazowe φ:

¨q



t



2 ⋅˙q



t





2

⋅q



t



=Q⋅sin



pt





q



t



= A sin



pt





=A sin



pt

−



=A sin

[

 pt−

]

˙q



t



= pA cos



pt





= pA cos



pt

−



= pA cos

[

 pt−

]

¨q



t



=− p

2

A sin



pt





=− p

2

A sin



pt

−



=− p

2

A sin

[

 pt−

]

Podstawiamy

q



t



, ˙qt, ¨qt 

do równania (12.44)

− p

2

A sin

[

 pt−

]

2  pA cos

[

 pt−

]



2

A sin

[

 pt−

]

=Q sin



pt





Po rozpisaniu

− p

2

A

[

sin



pt





cos

−cos pt sin−

]

2  pA

[

cos



pt





cos

−−sin pt sin−

]





2

A

[

sin



pt





cos

−cos pt sin−

]

=Q⋅sin



pt





wyłączamy części:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

18

-dla

sin (pt+ε)

− p

2

A sin



pt





cos

−−2  pA sin pt sin−

2

A sin



pt





cos

−=Q⋅sin



pt





− p

2

A cos

−−2  pA sin−

2

A cos

−=Q

-dla

cos (pt+ε)

− p

2

A cos

 pt sin−2  pA cos



pt





cos

−

2

A cos

 pt sin−=0

− p

2

A sin

−2  pA cos−

2

A sin

−=0

Powstał układ równań:

{

− p

2

A cos

−−2  pA sin−

2

A cos

−=Q

− p

2

A sin

−2  pA cos−

2

A sin

−=0

(12.46)

Przekształcamy równanie 2

A

[



2

− p

2

 sin−2  p cos−

]

=0

Ponieważ amplituda drgań

A nie może być równa zeru, to przyrównajmy wyrażenie w nawiasie do zera:



2

− p

2

 sin−2  p cos−=0



2

− p

2

sin−=−2  p cos−

sin

−

cos

−

=−

2

 p



2

− p

2

tg

−=−

2

 p



2

− p

2

Z niego otrzymujemy zależność:

tg

−=

2

 p



2

− p

2

(12.47)

Następnie z równania 1 wyznaczamy:

A

[



2

− p

2

cos−−2  p sin−

]

=Q

A

=

Q



2

− p

2

cos−−2  p sin−

=

1

cos

−

⋅

Q



2

− p

2

−2  p

sin

−

cos

−

A

=

1

cos

−

⋅

Q



2

− p

2

−2  p tg −

Wiedząc, że

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

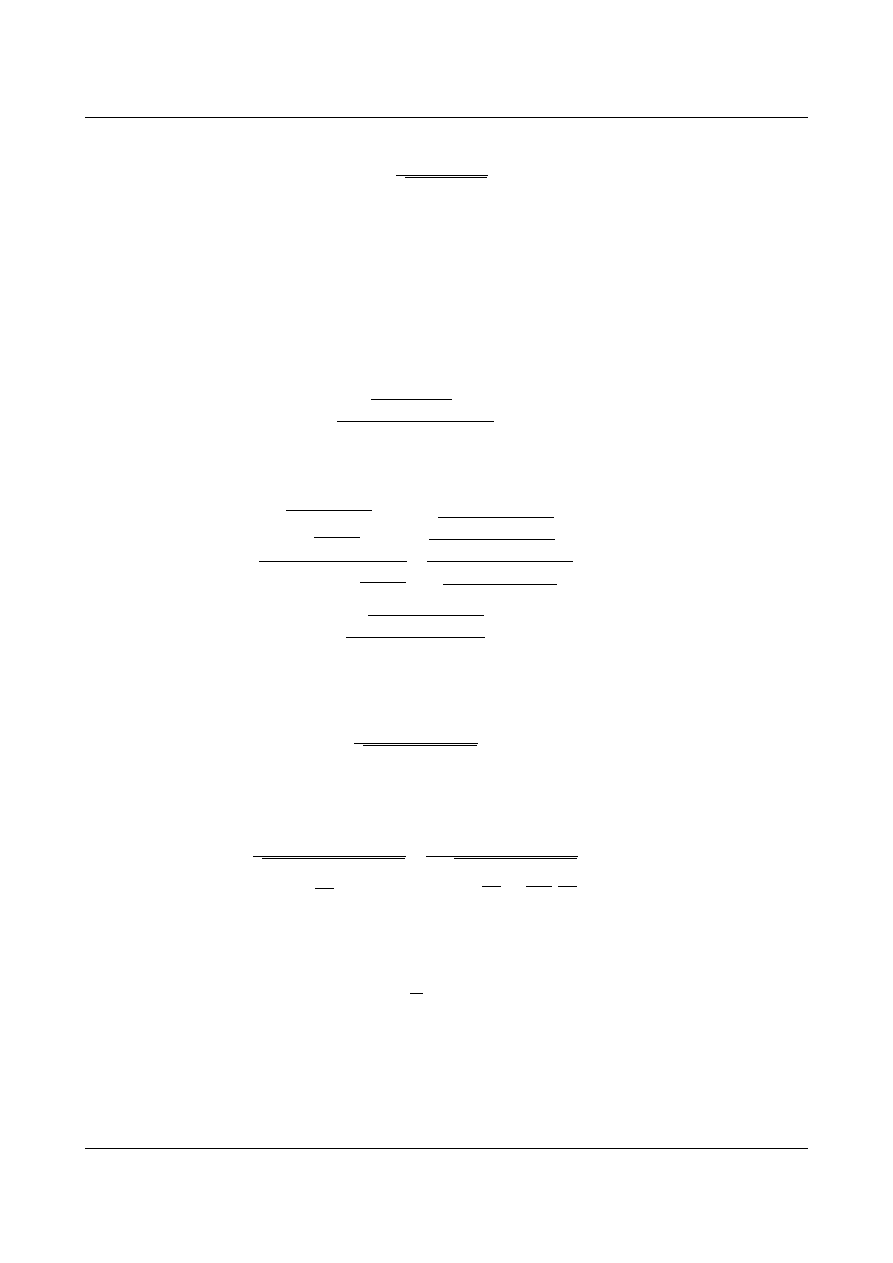
Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

19

cos

−=

1



1

tg

2

−

(12.48)

oraz

cos

−=cos−

sin

−=−sin−

tg

−=−tg −

możemy zapisać:

A

=



1

tg

2

−⋅Q



2

− p

2

2  p tg −

(12.49)

Do wzoru (12.49) opisującego amplitudę podstawiamy rozwiązanie (12.47)

A

=



1





2

 p



2

− p

2



2

⋅Q



2

− p

2

2  p

2

 p



2

− p

2

=





2

− p

2



2

4 

2

p

2



2

− p

2

⋅Q



2

− p

2



2

4 

2

p

2



2

− p

2

A

=

Q





2

− p

2



2

4 

2

p

2



2

− p

2



2

4 

2

p

2

Ostatecznie otrzymujemy:

A

=

Q







2

− p

2



2

4 

2

p

2

(12.50)

Rozwiązanie to można zapisać inaczej:

A

=

Q



[



2



1

−

p

2



2



]

2

4 

2

p

2

=

Q



2





1

−

p

2



2



2



4



2



2

⋅

p

2



2

gdzie:

Q

=

P

m

Dzieląc licznik i mianownik przez 

2

otrzymujemy wyrażenie, które można zastąpić ilorazem:

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater

Część 2

12. WPROWADZENIE DO DYNAMIKI BUDOWLI

20

Q



2

=

P

m



2

=

P

k

i dalej, amplitudę przemieszczenia dynamicznego wyrażamy przez przemieszczenie statyczne i współczynnik

dynamiczny:

A

=

P

k

⋅

1





1

−

p

2



2



2



4



2



2

⋅

p

2



2

=A

stat



d

(12.51)

Przyjęcie oznaczeń:

=

p



=





prowadzi do prostszej formy współczynnika dynamicznego.



d

=

1





1

−

2



2

4 

2

⋅

2

(12.52)

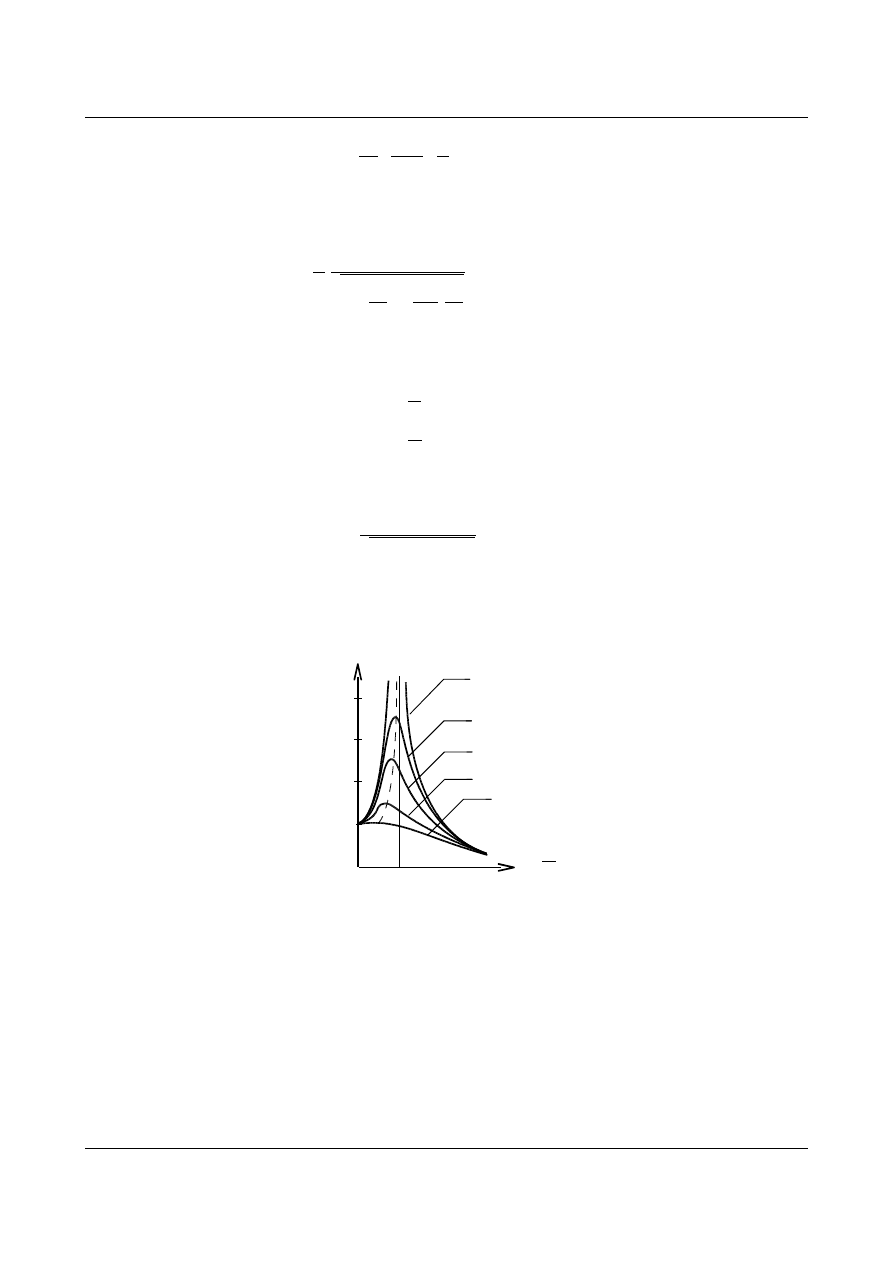
Wykresy funkcji



d

w zależności od ilorazu

 dla różnych współczynników tłumienia  przedstawiono na

rys. 12.15.

1

1

ν

d

2

3

4

ρ=0

ρ=0,15

ρ=0,25

ρ=0,5

ρ=1

η

=

p

ω

Rys. 12.15. Wykres współczynnika dynamicznego ν

d

(η) dla układów tłumionych

Wartość amplitudy przemieszczenia (12.51) jest uzależniona od współczynnika dynamicznego



d

.

Zjawisko czystego rezonansu nie zajdzie, gdyż amplituda przemieszczenia w układach z tłumieniem nie
wzrasta do nieskończoności. Jednak osiąga największe wartości dla

=1 .

Ponadto, w zależności od wartości ilorazu

 drgań mówimy o:

1 – niskim strojeniu konstrukcji,
1 – wysokim strojeniu konstrukcji.

Dobra D., Dziakiewicz Ł., Jambrożek S., Komosa M., Mikołajczak E., Przybylska P., Sysak A., Wdowska A.

AlmaMater