Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

FIZYKA

Kolokwium nr 1 (e-test)

Rozwiązał i opracował: Maciej Kujawa, SKP 2008/09

(więcej informacji na końcu dokumentu)

Zad. 1

W ruchu prostoliniowym prędkość ciała jest funkcją czasu: v=2.5t+5.5 [m/s]. Oblicz
drogę przebytą przez ciało w czasie 2s od chwili rozpoczęcia ruchu. Wynik podaj w [m]
z dokładnością do jedności. (Odp. 16)

v(0)=5.5m/s
v(2)=2.5*2+5.5=10.5m/s
a=(v2-v0)/t=5/2=2.5m/s^2

Tak naprawdę, zarówno prędkość początkową, jak i przyspieszenie można od razu zauważyć w
podanym w zadaniu wzorze, bo to nic innego jak:
v = vo + a * t
v = 5.5 + 2.5*t

s=v(0)*5+1/2*a*t^2
s=5.5*2+1/2*2.5*4
s=11+5=16m

Zad. 2

Spadające swobodnie ciało ma w punkcie A prędkość 20 cm/s, a w punkcie B prędkość
220 cm/s. Ile wynosi odległość między tymi punktami? Wynik podaj w [cm] z
dokładnością do pierwszego miejsca po przecinku. (Odp. 24,0)

h(a)-h(b)=h

v1=20cm/s=0.2m/s
v2=220cm/s=2.2m/s

mgh+1/2*m*v1^2=1/2*m*v2^2
10h+0.02=2.42
10h=2.40
h=0.24m=24cm

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 3

Ile powinien wynosić czas opóźnienia zapłonu aby wybuch granatu wyrzuconego z
prędkością 23m/s pod katem 30 stopni do poziomu, nastąpił w najwyższym punkcie
toru? (Odp. 1,1)

Zadanie polega na znalezieniu czasu, w którym granat osiągnie maksymalną wysokość. Interesuje
nas jego ruch w pionie, więc znajdujemy wartość pionowej składowej prędkości:
vy = v*sin30 = 11.5m/s

Była to początkowa prędkość, z jaką granat poruszał się w kierunku pionowym. W najwyższym
punkcie wartość tej prędkości będzie równa 0, więc wystarczy, że znajdziemy czas, w którym
granat "wytracił" całe swoje 11.5m/s, a przyspieszenie oczywiście znamy.
delta_v = at
a = g = 10m/s^2
delta_v = 11.5m/s

11.5=g*t
11.5=10t
t=1.15s

Zad. 4

Dwie cząstki zostały wysłane z początku okładu współrzędnych i po pewnym czasie ich
położenia są opisane wektorami R1=4i+3j+3k oraz R2=2i+10j-4k. Ile wynosi kwadrat
odległości pomiędzy cząstkami? (Odp. 120)

Odległość między punktami opisanymi wektorami wodzącymi jest równa długości różnicy tych
wektorów.
s=|r2-r1|

r2-r1=[-2,7,-7]
|r2-r1|^2=4+49+49=102

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 5

W rzucie poziomym zasięg równy jest wysokości początkowej. Prędkość początkowa
ciała wynosi 7 m/s. Ile wynosi prędkość końcowa ciała? Wynik podaj w [m/s] z
dokładnością do jedności. (Odp. 15,7)

h=s
1/2gt^2=vt
5t^2=7t |:t
5t=7
t=7/5

s=7*7/5=9.8m=h

I z zasady zachowania energii:
mgh+1/2mv^2=1/2mv2^2
10h+24.5=1/2v2^2
245=v2^2
v2~15.65

Zad. 6

Spadające swobodnie ciało pokonało w czasie pierwszych 1,8s 0,7 całej drogi. Ile
wynosi wysokość? (Odp. 23,1)

t=1.8s

Obliczamy drogę, jaką pokonało to ciało w ciągu 1.8s:
s=1/2*g*t^2
s=5*1.8^2=16.2

Ta droga stanowi 0.7 wysokości, więc obliczamy:
0.7h=s
h=16.2/0.7=23.142

Zad. 7

W rzucie poziomym prędkość końcowa ciała była 3,2 razy większa od jego prędkości
początkowej, która miała wartość 9m/s. Ile wynosiła wysokość początkowa rzutu?
(Odp. 37,4)

g=10m/s^2
vk=3.2*9=28.8m/s
vp=9m/s

mgh + mvp^2/2 = mvk^2/2

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

10h+40.5=414.72
h=37.4

Zad. 8

Szerokość rzeki wynosi 200m. Łódka przepłynęła rzekę z v=4m/s względem wody,
skierowaną prostopadle do jej równoległych brzegów. Jednocześnie prąd rzeki zniósł
łódkę o 110m w swoim kierunku. Ile wynosi prędkość prądu rzeki? (Odp 2,2)

Szukamy prędkości rzeki, drogę znamy (110m), więc brakuje tylko czasu. Przeanalizujmy ;)
Łódka płynie od jednego brzegu do drugiego z prędkością 4m/s, skierowaną prostopadle do
brzegów rzeki, czyli jej droga (w tym kierunku) wyniesie tyle ile szerokość rzeki, czyli 200m.
Wiedząc to, możemy bez problemu obliczyć czas, w jakim łódka dopłynie do drugiego
brzegu:
v=s/t, t=s/v
t=200/4=50sekund

Zatem 50 sekund to czas, w jakim łódka się poruszała. Czytamy dalej: prąd zniósł łódkę w
tym czasie o 110m. Nic prostszego:
v_rzeki = s/t = 110/50 = 2.2 m/s

Zad. 9

Długość pasa startowego samolotu wynosi 500m, aby oderwać się od ziemi samolot
musi osiągnąć prędkość 130m/s. Zakładając, że ruch samolotu jest jednostajnie
zmienny oblicz czas rozbiegu samolotu. (Odp. 7,7)

s=500m
v=130=at
a=130/t

s=1/2at^2
500=65t
t~7.7s

Oczywiście jest to całkowity absurd – samolot, według danych z zadania, przyspiesza do około
500km/h w niecałe 8 sekund ;)

Zad. 10

Kolarz rozpoczynając jazdę pierwsze 30s jedzie ruchem jednostajnie przyspieszonym.
Promień kół rowerowych wynosi 0,4m a przyspieszenie kątowe tych kół 0.8 rad/s^2. Jaką
prędkość osiągnie kolarz po tym czasie? (Odp. 9,6)

v = w*r, w = e*t (w – prędkość kątowa, e – przyspieszenie kątowe)
v = etr = 0.8*30*0.4 = 9.6m/s

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 11

W czasie 0.1s ręka koszykarza trzymająca nieruchomo piłkę o masie 0.36kg nadała jej
prędkość o wartości=3m/s. ile wyniosła średnia wartość siły, z jaka ręka zadziałała w
tym czasie na piłkę? (Odp. 10,8)

F = m*a
a = v/t

a = 3/0.1 = 30
F = 0.36*30 = 10.8N

Zad. 12

Punkt materialny zaczął poruszać się po okręgu o promieniu 18cm ze stałym co do
wartości przyspieszeniem stycznym 7cm/s^2. Po jakim czasie przyspieszenie
dośrodkowe będzie co do wartości dwa razy większe od przyspieszenia stycznego.
(Odp. 2,3)

ar = v^2/r = 2*a = 14 cm/s^2
14 = v^2/18
v^2= 252
v ~ 15.87cm/s

Znamy już prędkość, dla której przyspieszenie dośrodkowe będzie dwa razy większe od stycznego,
teraz tylko szukamy czasu, w jakim ciało osiągnie tą prędkość:
t = v/a = 2.26 ~ 2.3s

Zad. 13

Szerokość rzeki wynosi 200m. Łódka przepłynęła rzekę z 3,6m/s względem wody,
skierowaną prostopadle do jej równoległych brzegów. Jednocześnie prąd rzeki zniósł
łódkę o 130m w swoim kierunku. Ile wynosi prędkość prądu rzeki? (Odp. 2,3)

Obliczamy czas, w jakim odbywał się ruch łódki:
t = s/v = 200/3.6 = 55.56s

Obliczamy prędkość prądu rzeki:
v = s/t = 130/55,56 ~ 2.3 m/s

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 14

Prędkość łodzi względem wody w spoczynku wynosi 5,7m/s. Woda w rzece płynie z
jednakowa prędkością równą 3m/s. W jakim czasie łódź przepłynie rzekę o szerokości
90m w kierunku prostopadłym do brzegu? (Odp. 18,6)

v1=5.7m/s
v2=3m/s

Żeby łódź płynęła prostopadle, będzie musiała płynąć pod kątem, żeby "zniwelować" znoszenie
prądu rzeki. Narysuj sobie trójkąt z prędkościami łodzi, rzeki i prędkością wypadkową prostopadłą
do brzegu i wszystko będzie jasne.

5.7^2=3^2+v^2
v=4.85m/s
t=s/v ~ 18.6s

Zad. 15

Ciało ruszyło z miejsca ze stałym przyspieszeniem i osiągnęło prędkość 15m/s po
przebyciu drogi 25m. Oblicz przyspieszenie ciała. (Odp. 4,5)

v=at=15m/s
a=15/t

s=1/2*a*t^2
25=1/2*(15/t)*t^2
t=10/3 ~ 3.33s

a=15/3.33 ~ 4.5 m/s^2

Zad. 16

Wyznacz cosinus kąta, jaki tworzy wektor a=(-2)i+3j z dodatnim kierunkiem osi OX .
(Odp. -0,6)

a=[-2,3]
|a| ~ 3.6
cos alfa = ax/|a| = -0,(5) ~ -0.6

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 17

Wektor a tworzy z dodatnim kierunkiem osi OX kąt 45 stopni, a jego długość wynosi
6,6. W kartezjańskim układzie współrzędnych wektor ten można zapisać jako:
a=ax*i + ay*j. Ile wynosi wartość ax? (Odp. 4,7)

|a|=6.6
ax=|a|*cos45 ~ 4.7

Zad. 18

Pierwszą połowę drogi pojazd przebył z prędkością 45km/h, a drugą z prędkością
98km/h. Ile wyniosła średnia prędkość pojazdu na trasie? (Odp. 61,7)

v_śr = s/t

Droga była podzielona po połowie, więc zakładam, że:
s=2=1+1
t=s/v

I podstawiam:
v_śr = 2/ (1/45+1/90) = 2/ (143/4410) ~ 61.7km/h

Zad. 19

Samochód porusza się z prędkością 16m/s. Na drodze 15m jest hamowany i zmniejsza
swoją prędkość do 10m/s. Oblicz bezwzględną wartość przyspieszenia jeżeli ruch
samochodu jest jednostajnie zmienny. (Odp. 5,2)

v1=16m/s
v2=10m/s
delta_v = v1-v2 = 6m/s
delta_v = a*t
a = 6/t

Jak widać brakuje jeszcze jakiegoś równania żeby obliczyć przyspieszenie, więc wstawiamy
powyższą zależność do równania na drogę (wartość znana) w ruchu jednostajnie opóźnionym ;-)
s=v1*t-1/2*a*t^2
15=16t-1/2*(6/t)*t^2
t=1.154s

Znamy różnicę prędkości i czas, więc obliczamy szukane przyspieszenie:
a=6/1.154 ~ 5.2 m/s

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 20

W urządzeniu kafarowym, służącym do wbijania pali, ruchomy ciężar podnoszony jest
ruchem jednostajnym na wysokość 2.5m z prędkością 1m/s, a następnie spada
swobodnie na pal. Ile wynosi liczba uderzeń ciężaru na minutę? (Odp. 18,7)

s=h=2.5m
v=1m/s

Obliczamy, ile czasu zajmuje podniesienie ciężaru:
t1=s/v=2.5s

Z równania na drogę obliczamy ile czasu zajmuje opadanie ciężaru:
2.5=1/2 gt2^2
t2=0.71s

t=t1+t2=3.21s
60/3.21s ~ 18.7

Zad. 21

Ile powinien wynosić czas opóźnienia zapłonu aby wybuch granatu, wyrzuconego z
prędkością 23m/s pod katem 35 stopni do poziomu, nastąpił w najwyższym punkcie
toru? Wynik podaj z dokładnością do jednego miejsca po przecinku. (Odp. 1,3)

Wystarczy, że znajdziemy czas, w którym granat był w najwyższym punkcie, czyli czas w którym
w pionie jego prędkość była już równa zero:
vy - pionowa (igrekowa) składowa prędkości początkowej
vy = 23 * sin35 ~ 13.19m/s

vy = gt
13.19 = 9.81 * t
t = 1,34 ~ 1,3s

Zad. 22

Dany jest wektor a=1i+10j. Podaj wartość składowej iksowej nx wektora
jednostkowego kierunku n wyznaczonego przez wektor a.

a=[1,10]
|a|~10.05

n=[nx,ny]
|n|=1

Żeby wektor miał długość |n|=1, musimy podzielić wektor a przez 10.05:
nx = ax/10.05 = 1/10.05 = 0.0995

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 23

Punkt materialny A porusza się z V1=3i+3j [m/s], a pkt B z V2=(-5i)+3j [m/s]. W
chwili początkowej t=0 oba punkty znajdują się w tym samym miejscu. Ile wynosiła
odległość miedzy punktami po 8 sekundach? (Odp. 64)

v1 = [3,3]
v2 = [-5,3]

s=v*t
t=8s

s1 = v1*8 = [24,24]
s2 = v2*8 = [-40,24]

x = |s1-s2|
s1-s2 = [64,0]
x = |s1-s2| = 64m

Zad. 24

Ciało rzucone pionowo do góry po czasie 0,6s miało prędkość 3,2 razy mniejszą od
początkowej. Ile wynosiła maksymalna wysokość. (Odp. 3,73)

t = 0.6s
v1 = 3.2 * v2
g = 9.81m/s^2
h=?

Szukamy prędkości początkowej, znając czas i przyspieszenie:
v2 = v1 - gt = 3.2 * v2 - 5.886
v2 ~ 2.675m/s
v1 = 3.2 * v2 = 8.56m/s

Mamy prędkość początkową (v1), więc wysokość można obliczyć z zasady zachowania energii:
mgh = 1/2 * mv^2
9.81h = 1/2 * 8.56^2
h ~ 3.73m

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 25

Łódź płynie z prądem rzeki z przystani A do B w czasie 3h, a z B do A w czasie 5,4h.
Jaki czas jest potrzebny aby łódź spłynęła z przystani A do B z wyłączonym silnikiem?
(Odp. 13,5)

v1 - prędkość lodki,
v2 - prędkość prądu rzeki,
t=?

Porównujemy równania na drogę (s=v*t) dla trasy w jedną i w drugą stronę:

(v1+v2)*3 = (v1-v2)*5.4
8.4 * v2 = 2.4 * v1
v2 ~ 0.286 * v1

Znając zależność między v2 i v1, podstawiamy ją do równania i porównujemy z równaniem drogi
dla trzeciego przypadku (z wyłączonym silnikiem, czyli droga = prędkość prądu rzeki * szukany
czas):

v2*t = (v1 + v2)*3
0.286v1*t = (v1 + 0.286v1) * 3
0.286 t = 3.858
t ~ 13.5h

Zad. 26

Ile wynosi kwadrat odległości miedzy cząstkami:
a=4i+3j+5k
b=2i+10j-3k
jeśli zostały wysłane z początku układu współrzędnych? (Odp. 117)

s = |a-b|

a-b = 2i -7j +8k
|a-b|^2 = 2^2 + 7^2 + 8^2 = 117

PARĘ SŁÓW NA KONIEC

Powyższe zadania pochodzą z testu przygotowującego do pierwszego

kolokwium (e-testu) z Fizyki 1 dla SKP. Nie jestem autorem zadań, ani ilustracji do ich treści.
Moje rozwiązania nie przeszły żadnej korekty błędów (poza sprawdzeniem zgodności z
poprawnymi odpowiedziami), mają służyć celom edukacyjnym ;-) Większość wyników
została zaokrąglona, zgodnie z wymaganiami e-testu. W przypadku jakichkolwiek
uwag/pytań/sugestii pisz śmiało na:

[e-mail]

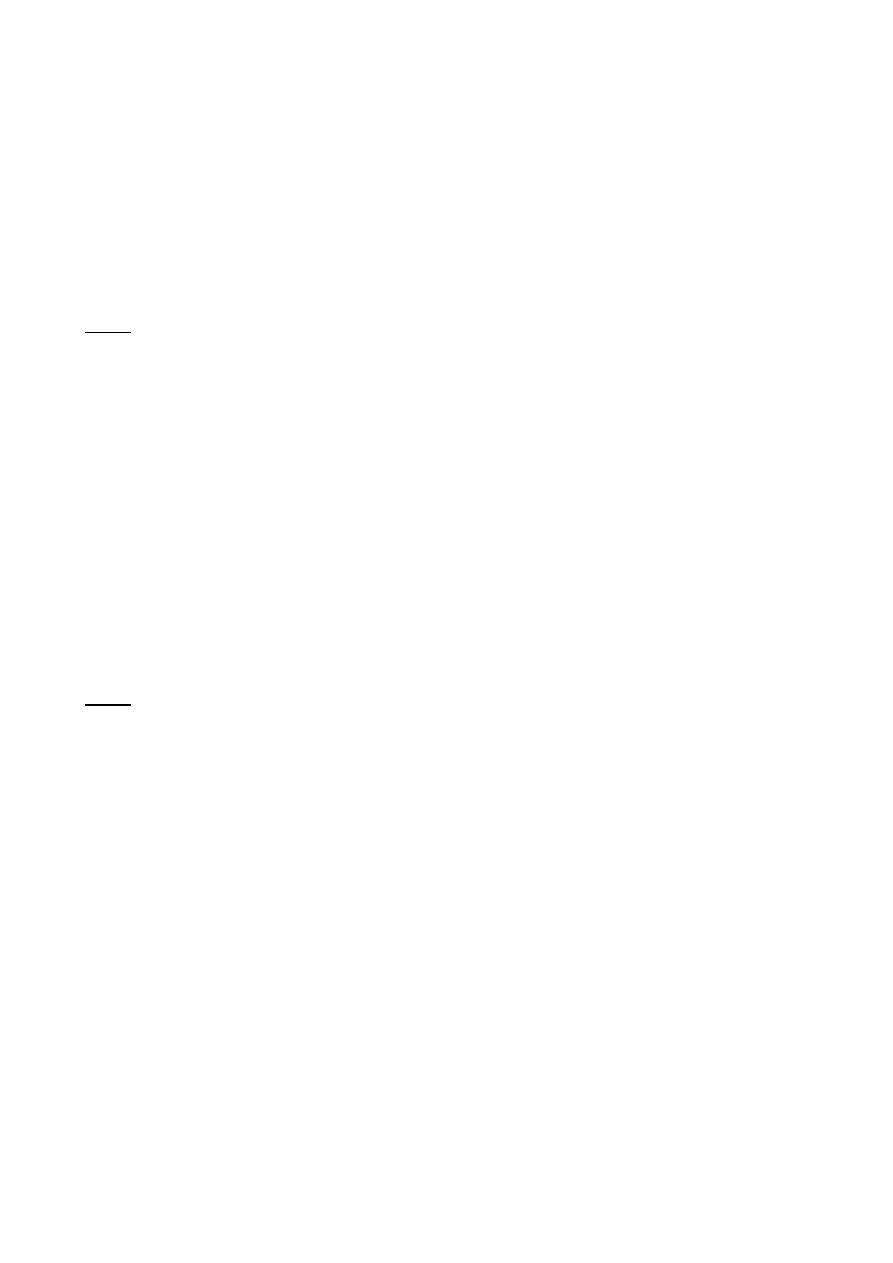
Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

FIZYKA

Kolokwium nr 2 (e-test)

Rozwiązał i opracował: Maciej Kujawa, SKP 2008/09

(więcej informacji na końcu dokumentu)

Zad. 1

Cegłę o masie 2kg położono na chropowatej desce. Następnie jeden z końców deski

zaczęto podnosić do góry, gdy tymczasem jej drugi koniec pozostawał nieruchomy. Gdy
nachylenie deski osiągnęło kąt równy 40 stopni, cegła zaczęła się zsuwać. Ile wynosi
współczynnik tarcia statycznego miedzy ciałem a deską? Wynik podaj z dokładnością do
drugiego miejsca po przecinku. (Odp. 0,84)

Deska nachylona pod kątem utworzy równię pochyłą. Sytuację, w której cegła znalazła się tuż
przed zsunięciem, możemy przedstawić tak:
Fs = T
m*g*sin40 = m*g*cos40*f
sin40 = cos40*f
0.6428 = 0.766*f
f = 0,839 ~0,84

Zad. 2

Mamy izolowany układ trzech ciał A, B i C, które działają na siebie na odległość.

Ciało A ma masę 1,8kg i działa na ciała B i C odpowiednio siłami:
Fb = (-1)*i -3*j +k [N]
Fc = i* -3*j -k [N]

Z jaką wartością przyspieszenia porusza się ciało A? Wynik podaj w [m/s^2] z

dokładnością do pierwszego miejsca po przecinku. (Odp. 3,3)

Zgodnie z trzecią zasadą dynamiki, ciała B i C działają na ciało A siłami o odpowiednich
wartościach i kierunkach, ale z przeciwnym zwrotem. Zatem na ciało A działa siła o wartości
siły wypadkowej Fb i Fc:
F = Fb + Fc = [0, -6, 0]
|F| = 6N

Właśnie ta siła wypadkowa nadaje ciału A przyspieszenie, które możemy obliczyć bez
problemu, ponieważ znamy jego masę:
F = m*a
6 = 1.8*a
a= 6/1.8 = 3.(3) ~ 3.3

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 3

Kulka o masie 0,11kg przywiązana do nici o długości 50cm obraca się w płaszczyźnie

pionowej ze stałą prędkością liniową 3m/s. Ile wynosi, w najwyższym punkcie toru siła
naprężenia nici? Wynik podaj w N z dokładnością do drugiego miejsca po przecinku. (Odp.
0,88)

Kulka porusza się po okręgu o promieniu równym długości nici. W najwyższym punkcie, na
kulkę działa siła odśrodkowa (skierowana pionowo do góry) oraz siła ciężkości (pionowo w
dół). Naprężenie nici będzie równe różnicy tych sił:
N = Fr – Fg
N = (m*v^2)/r – m*g
N = (0.11*9)/0.5 – 1.1 = 1.98 – 1.1 = 0.88N

Zad. 4

Dwa klocki, o masach m1=0,9 kg i m2=1,3kg, połączone sznurkiem są

podnoszone pionowo do góry z przyspieszeniem o wartości 5m/s^2. Ile wynosi
siła przyłożona do górnego sznurka? Wynik podaj w [N] z dokładnością do 1N.
(Odp. 33)

Siła ta będzie równa sumie wartości siły ciężkości obu klocków oraz siły nadającej im
przyspieszenie dane w zadaniu:
F = Q+F1

Q = (m1+m2)*g = 22N
F1 = (m1+m2)*5 = 11N

F = 22+11 = 33N

Zad. 5

Ciało zsuwa się bez prędkości początkowej po równi pochyłej o kącie nachylenia 60

stopni. Po czasie 1,2s prędkość ciała wynosi 11m/s. Ile wynosi współczynnik tarcia
kinetycznego ciała o równię? (Odp. -0,1)

Z danych obliczamy przyspieszenie ciała:
t = 1.2s
v = 11m/s
a = v/t = 9.167m/s^2

Po wykonaniu rysunku można wywnioskować:
F = Fs - T
a = g*sin60 - g*cos60*f
9.167 = 8.66 - 5f
0.507 = -5f
f = -0.1014 ~ -0.1

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 6

Aby ruszyć z miejsca szafę o masie 100kg, należy ją pchnąć, działając siłą o wartości

240N zwróconą poziomo. Wyznacz współczynnik tarcia statycznego szafy o podłogę. Wynik
podaj z dokładnością do drugiego miejsca po przecinku. (Odp. 0,24)

Zapisujemy równanie sił w momencie granicznym:
F = T
240 = m*g*f
240 = 1000*f
f = 0,24

Zad. 7

Na stole przymocowano jeden za drugim klocki o

masach m1=m2=1kg i m3=0,8kg. Tarcie między masami
m1, m2, m3, a podłożem możemy pominąć. Przyspieszenie
układu nadaje wisząca masa M=2,5kg. Ile wynosi naprężenie nici między ciałem m2, a m3?
Wynik podaj w [N], z dokładnością do drugiego miejsca po przecinku. (Odp. 3,77)

Na rysunku widać, że masa m3 jest na samym początku tego układu. Obliczmy wartość siły,
która nadaje przyspieszenie całemu układowi i wyznaczmy przyśpieszenie:
F = M*g = 25N
a = F/(m1+m2+m3+M) = 25/5.3 = 4.72m/s^2

Zatem naprężenie nici między m3 i m2 musi być równe sile, nadającej masie m3
przyspieszenie a:
N = m3*a = 0.8*4.72 = 3.776 ~3.77N

Zad. 8

Na poziomej desce o masie 1,2kg leży cegła o masie 2,6kg, natomiast deska spoczywa

na lodzie. Współczynnik tarcia statycznego między cegłą a deską wynosi 0,5, natomiast
między deską a lodem siła tarcia jest praktycznie równa zeru. Siłę o jakiej minimalnej
wartości należy przyłożyć do deski, aby cegła zaczęła się suwać po niej? Wynik podaj w N z
dokładnością do 1N. (Odp. 19)

Obliczmy wartość siły tarcia statycznego, jaka powstaje między deską, a cegłą:
T = m1*g*f = 26*0.5 = 13N
a = T/m1 = 13/2.6 = 5m/s^2

Aby cegła ruszyła się, musimy całemu układowi (deska + cegła) nadać przyspieszenie o
wartości co najmniej 5m/s^2:
F = (m1 + m2)*a
F = 3.8*5 = 19N

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 9

Jaka jest wartość siły wypadkowej działającej na klocek o masie 4kg, poruszający się

z przyśpieszeniem a = 3*i + 2*j? Wynik podaj w N, z dokładnością do pierwszego miejsca po
przecinku. (Odp. 14,4)

Wyznaczamy wartość przyspieszenia:
|a| = 3.6m/s^2

Obliczamy wartość siły wypadkowej działającej na klocek:
F = m*a = 4*3.6 = 14.4N

Zad. 10

Na gładkiej równi pochyłej nachylonej do poziomu pod kątem 55 stopni znajduje się

ciało o ciężarze 550N utrzymywane w równowadze przez siłę działającą w kierunku
równoległym do podstawy równi. Ile wynosi wartość siły? Wynik podaj w N z dokładnością
do 1N. (Odp. 785)

R – szukana siła, równoległa do podstawy równi
Rx – składowa szukanej siły, równoległa do równi

Polecam rysunek ;) Żeby ciało było w równowadze, składowa szukanej siły równoległa do
równi musi być równa składowej siły ciężkości równoległej do równi:
Fs = Rx
Fs = Q * sin55 = 550 * sin55 = 450.5336N = Rx

Szukana siła jest równoległa do podstawy równi. Znamy wartość składowej równoległej do
równi, więc możemy obliczyć (łatwo to zauważyć po wykonaniu rysunku):
R = Rx / cos55 = 450.5336N / 0.5736 = 785.449 ~ 785N

Zad. 11

Człowiek o masie 70kg wspina się po pionowej linie z przyspieszeniem o wartości

równej 0,8m/s^2. Ile wynosi naprężenie liny, jeżeli zaniedbamy jej masę? Wynik podaj w N, z
dokładnością do 1N. (Odp. 756)

Q – ciężar człowieka,
F – siła, z jaką człowiek musi podciągać się na linie, żeby uzyskać dane przyspieszenie,

Naprężenie liny jest równe:
N = Q + F
N = mg + ma = 700 + 56 = 756N

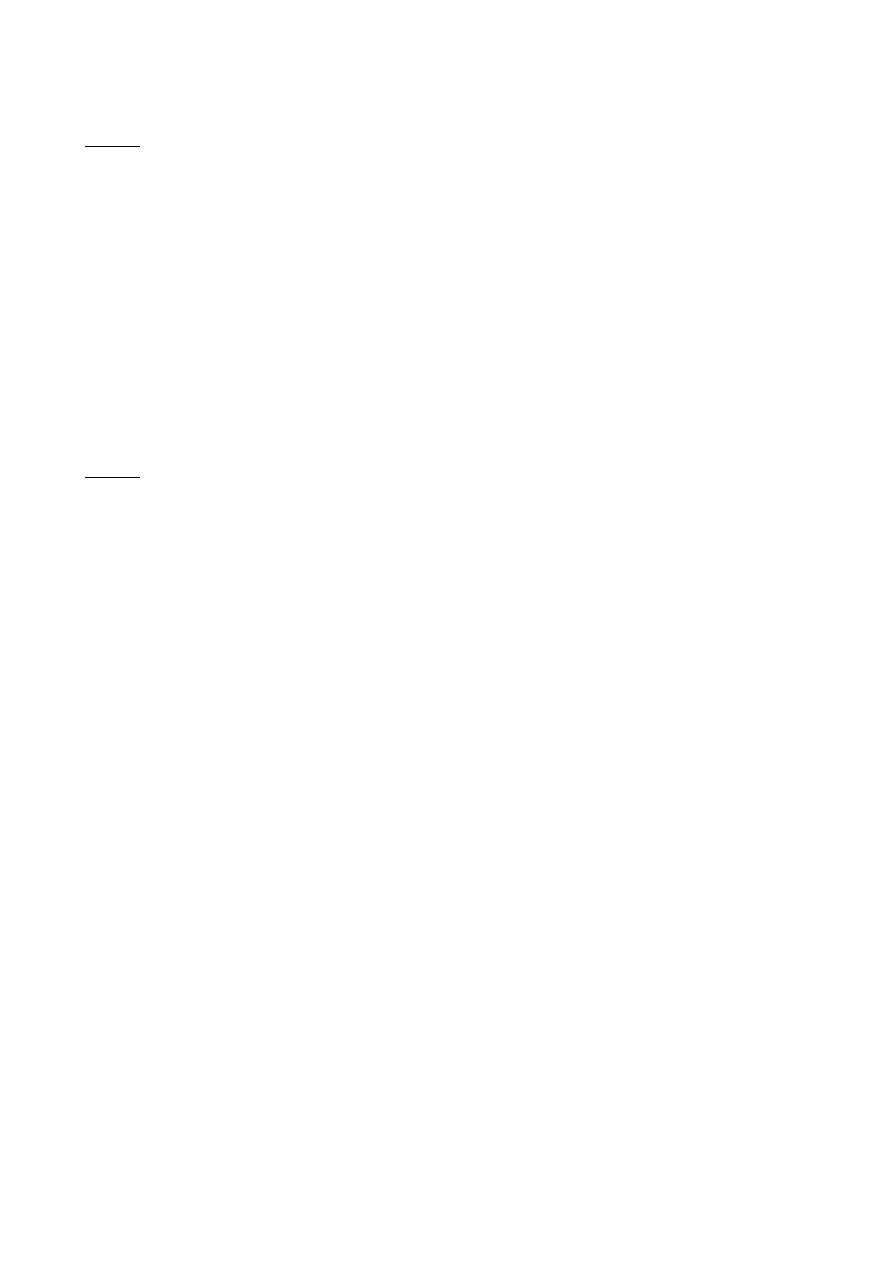
Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 12

Ciężarek o masie 165g zawieszony na nici o długości 90cm obraca się po okręgu

ruchem jednostajnym w płaszczyźnie poziomej. W czasie ruchu nić odchylona jest od pionu o
kąt 45 stopni Oblicz siłę naprężenia nici. Wynik podaj w N, z dokładnością do drugiego
miejsca po przecinku. (Odp. 2,33)

Polecam wykonać rysunek ;) Nić odchylona jest od pionu o kąt 45 stopni. To wychylenie jest
spowodowane siłą wypadkową siły ciężkości i siły odśrodkowej (między tymi siłami mamy
kąt prosty). Siły odśrodkowej nie znamy, ale możemy obliczyć wartość naprężenia w inny
sposób:
N = mg / cos45
N = 1.65 / cos45 = 2.33N

Zad. 13

Ile co najmniej powinien być równy współczynnik tarcia statycznego między oponami

samochodu a asfaltem aby samochód mógł przejechać bez poślizgu zakręt o promieniu 100m
z prędkością 76km/h, gdy jezdnia nie jest nachylona do poziomu? Wynik podaj z dokładnością
do drugiego miejsca po przecinku. (Odp. 0,45)

v = 76km/h = 21.1m/s
r = 100m

Na zakręcie w tej sytuacji na samochód działają następujące siły:
Q = mg (pionowo w dół)
Fr = m*v^2 / r (poziomo na zewnątrz zakrętu)
T = Q*f (poziomo do wewnątrz zakrętu)

Aby samochód nie wpadł w poślizg, musi zachodzić równość:
T = Fr
Q*f = m*v^2 / r
m*g*f = m*(21.1)^2 / 100
10f = 4.4521
f = 0.445 ~ 0.45

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 14

Na stole przymocowano jeden za drugim klocki o

masach m1=m2=1kg i m3=1,3kg. Tarcie między masami
m1, m2, m3, a podłożem można pominąć. Ile wynosi
przyspieszenie układu nadane przez wiszącą masę 3,5kg? Wynik
podaj z dokładnością do pierwszego miejsca po przecinku.
(Odp. 5,1)

Siła nadająca przyspieszenie temu układowi jest równa:
F = M*g = 3.5kg * 10m/s^2 = 35N

Zatem przyspieszenie całego układu będzie równe:
a = F/m

Oczywiście „m” to masa całego układu:
a = F / (m1+m2+m3+M) = 35 / 6.8 = 5.147 ~ 5.1

Zad. 15

Aby ruszyć z miejsca szafę o masie 110kg należy ją pchnąć, działając siłą o wartości

300N zwróconą poziomo. Wyznacz współczynnik tarcia statycznego szafy o podłogę. Wynik
podaj z dokładnością do drugiego miejsca po przecinku. (Odp. 0,27)

F = 300N
m = 110kg

Możemy ułożyć równanie:
F = T
300N = m*g*f
300N = 1100f
f = 0.27

Zad. 16

Do ciała o masie 4kg leżącego na równi o kącie nachylenia 30

stopni przykładano siłę o rosnącej wartości, równoległą do powierzchni
równi. Przy wartości 40N ciało zaczęło się zsuwać w dół równi. Ile
wynosi współczynnik tarcia statycznego między klockiem a równią? Wynik podaj z
dokładnością do drugiego miejsca po przecinku. (Odp. 1,73)

Standardowo układamy równanie istotnych sił działających na ciało:
Fs + F = T
sin30*mg + 40 = cos30*mgf
0.5*40 + 40 = 0.866*40f
60 = 34.64f
f = 1.73

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 17

Rakieta ma masę 8t. Jaka powinna być minimalna wartość siły ciągu silnika rakiety,

aby rakieta ta mogła wystartować z powierzchni Ziemi z przyspieszeniem o wartości 1,4g,
gdzie g jest przyspieszeniem ziemskim równym 10m/s^2? >Wynik podaj w [kN] z
dokładnością do 1kN. (Odp. 192)

m = 8t = 8000kg
a = 1.4*g = 14m/s^2

Siła ciągu silnika będzie musiała pokonać siłę ciężkości i nadać rakiecie przyspieszenie
14m/s^2:
F = mg + ma = 80000 + 112000 = 192000N = 192kN

Zad. 18

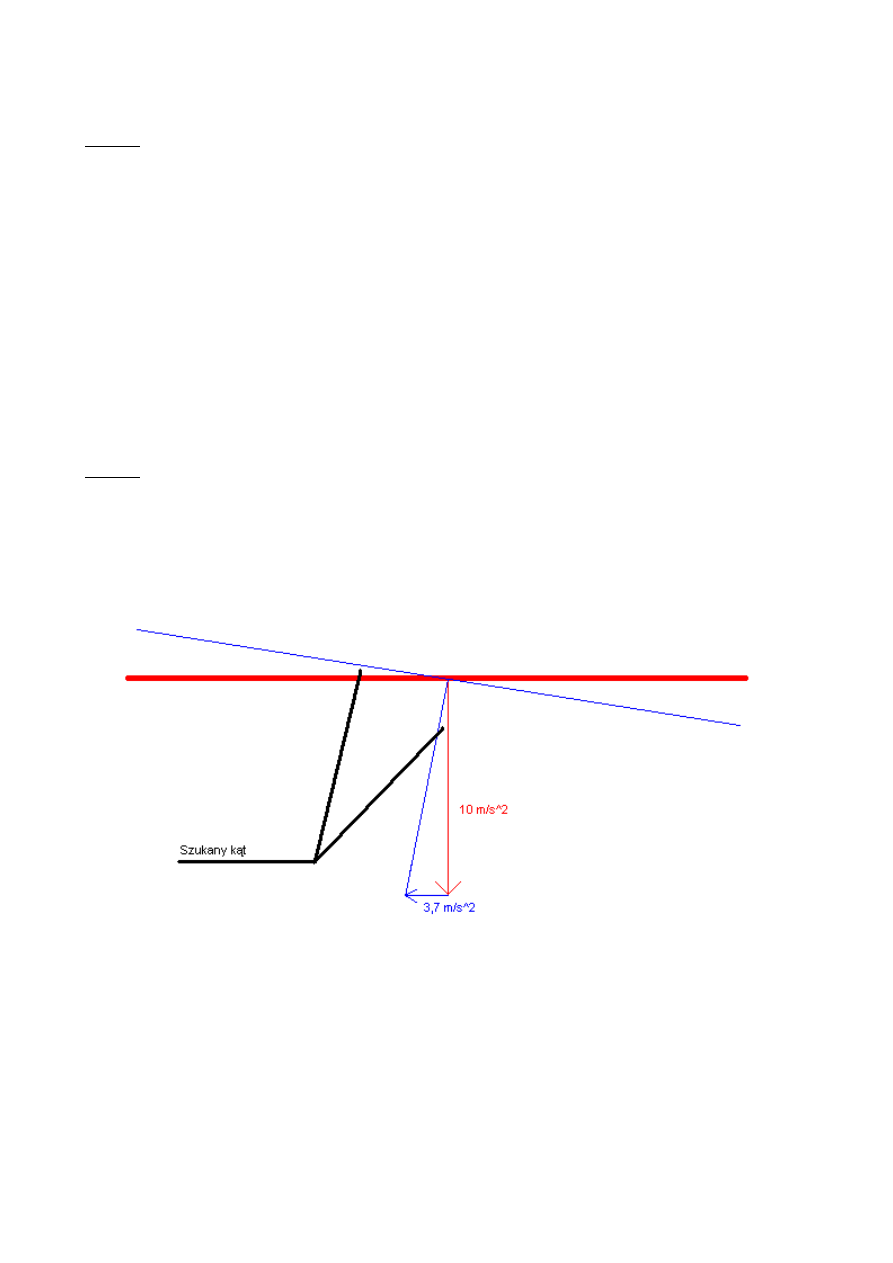
W samochodzie cysternie jest przewożona benzyna. W pewnej chwili samochód

hamuje z opóźnieniem 3,7m/s^2. Poziom cieczy odchyla się o pewien kąt. Ile wynosi tangens
tego kąta? Wynik podaj z dokładnością do drugiego miejsca po przecinku. (Odp. 0,37)

Rysunek obowiązkowy :)

Niebieska linia przedstawia poziom cieczy po rozpoczęciu hamowania. Z rysunku łatwo
wyznaczyć tangens szukanego kąta:
tgα = 3.7/10 = 0.37

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 19

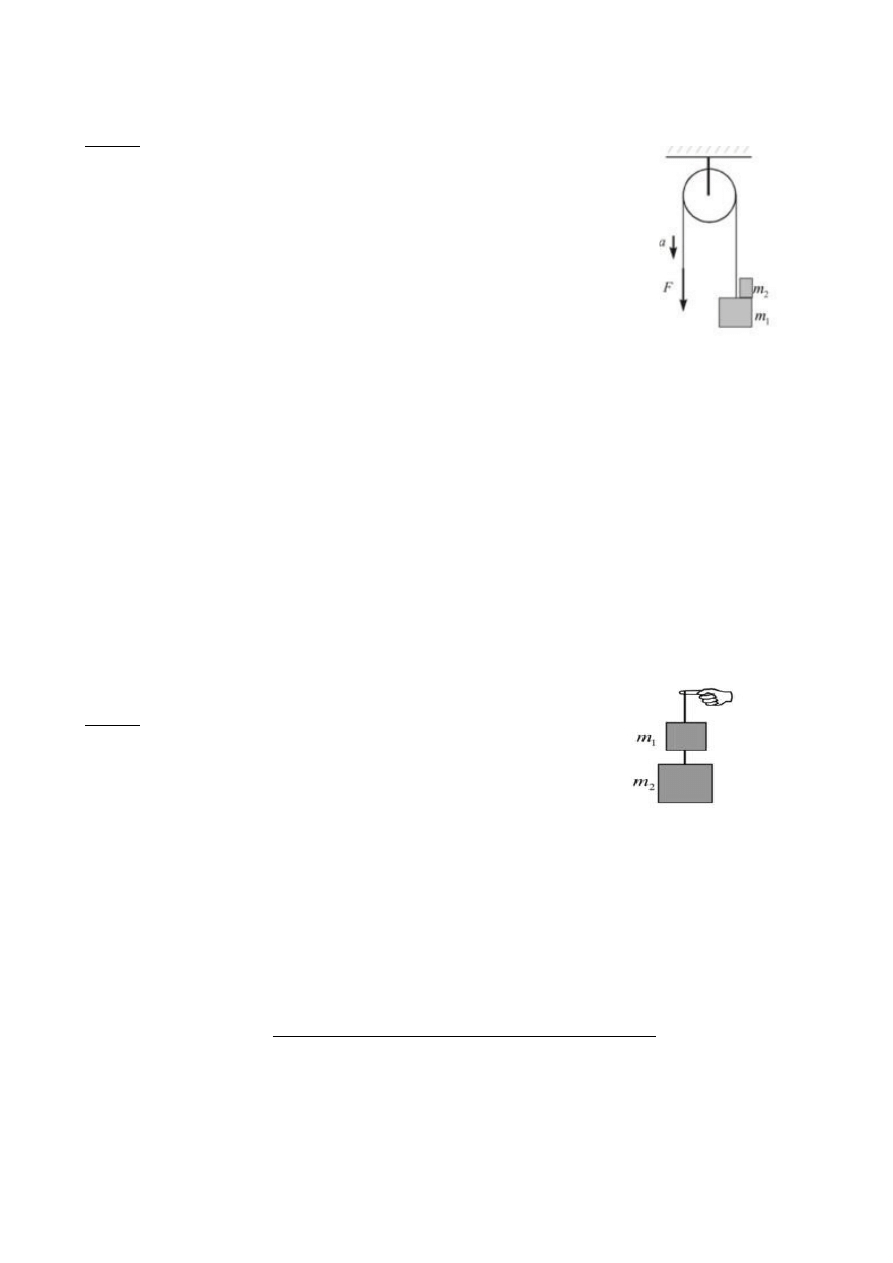
Do nieważkiej nici przerzuconej przez nieważki bloczek podwieszono

klocek o masie m1=2kg, na którym z kolei położono drugi klocek o masie
m2=0,8kg. Do drugiego końca nici przyłożono siłę skierowaną pionowo w dół
o wartości F=38N. Jaką siłą działa podczas ruchu klocek o masie m1 na
klocek o masie m2? Wynik podaj w [N] z dokładnością do pierwszego miejsca
po przecinku. (Odp. 10,9)

Wyznaczmy wartość siły nadającej przyspieszenie temu układowi ciał:
Fwyp = F – Q
Fwyp = 38 – (m1+m2)*g = 38 – 28 = 10N

Wyznaczmy przyspieszenie całego układu:
a = Fwyp / (m1+m2) = 10/2.8 = 3.57m/s^2

Klocek o masie m1 zadziała na klocek o masie m2 siłami (tak naprawdę, będą to siły
bierne – reakcje) równymi co do wartości:

1. Sile bezwładności klocka o masie m2:

Fb = m2*a = 0.8*3.57 = 2.856N

2. Ciężarowi klocka o masie m2:

Fc = m2*g = 0.8*10 = 8N

Zatem:
Fszukana = Fb+Fc = 2.856 + 8 = 10.856 ~ 10.9N

Zad. 20

Dwa klocki, o masach m1=0,5kg i m2=0,6kg połączone sznurkiem,

są podnoszone pionowo do góry ze stałą prędkością o wartości 5m/s. Ile
wynosi siła naprężenia sznurka łączącego oba klocki? Wynik podaj w [N] z
dokładnością do 1N. (Odp. 6)

Prędkość jest stała, więc a = 0. Jest to taka sama sytuacja, jakby klocki wisiały w spoczynku,
więc naprężenie sznurka łączącego oba klocki będzie równe ciężarowi klocka o masie m2:
N = Q
N = m2*g = 0.6*10 = 6N

PARĘ SŁÓW NA KONIEC

Powyższe zadania pochodzą z testu przygotowującego do drugiego kolokwium (e-

testu) z Fizyki 1 dla SKP. Nie jestem autorem zadań, ani ilustracji do ich treści. Moje
rozwiązania nie przeszły żadnej korekty błędów (poza sprawdzeniem zgodności z
poprawnymi odpowiedziami), mają służyć celom edukacyjnym ;-) Większość wyników
została zaokrąglona, zgodnie z wymaganiami e-testu. W przypadku jakichkolwiek
uwag/pytań/sugestii pisz śmiało na:

[e-mail]

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Fizyka 1 SKP – drugie kolokwium, cd. [Rozwiązał: Maciek K.]

1. Winda osobowa rusza w dół z przyspieszeniem 1m/s2. Ile wynosi siła nacisku człowieka o
masie 90 kg na podłogę windy? Wynik podaj w N z dokładnością do 1N. Odp. 810.0

Winda rusza w dół, więc siła bezwładności (Fb) działająca na człowieka będzie skierowana
do góry – nacisk na podłogę windy zmaleje:

F = Q – Fb = mg – ma = 900N – 90N = 810N

2. W czasie 0.1 s ręka koszykarza trzymającego nieruchomo piłkę o masie 0,4 kg nadała jej
prędkość o wartości 3m/s . Ile wynosiła średnia wartość siły, z jaką ręka zadziałała w tym
czasie na tę piłkę? Wynik podaj w N z dokładnością do jednego miejsca po przecinku. Odp.
12.0

F = m*(Δv/t) = 0.4*(3/0.1) = 0.4*30 = 12N

3. Dwa ciała o masach 1kg i 1,6 kg związane poziomą nicią leżą na doskonale gładkim
poziomym stole tak, że nić tworzy linię prostą równoległą do stołu. Nić może wytrzymać
natężenie nie przekraczające 30 N. Jaką maksymalną siłę poziomą można przyłożyć do
pierwszego z tych ciał, aby nić się nie zerwała. Wynik podaj w N z dokładnością do 1N. Odp.
49

Zastanówmy się, jaka siła powoduje naprężenie sznurka, gdy ciągniemy za jedno z ciał:
oczywiście siła bezwładności drugiego:

N = Fb = m2*a

F = (m1+m2)*a

30 = 1.6*a

F = 2.6*18.75

a = 18.75m/s^2

F = 49N

4. Klocek zsuwa się z równi o nachyleniu 30 stopni z przyspieszeniem 3,5 razy mniejszym od
przyspieszenia jakie miałby, gdyby między klockiem, a równią nie było tarcia. Ile wynosi
współczynnik tarcia kinetycznego między klockiem, a równią? Wynik podaj z dokładnością do
drugiego miejsca po przecinku. Odp. 0.41

Policzmy, z jakim przyspieszeniem klocek zsuwałby bez tarcia:

a1 = g*sin30 = 5m/s^2

Z tarciem przyspieszenie jest 3,5 raza mniejsze, więc:

a1/3.5 = g*sin30 – g*cos30*f

8.66*f = 5 – 1.429

1.429 = 5 – 8.66*f

f ~ 0.41

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

5. Rowerzysta o masie 80 kg jedzie ze stałą prędkością 15 m/s po torze kołowym. Kat
nachylenia płaszczyzny roweru do poziomu wynosi 45 stopni. Ile wynosi promień toru? Wynik
podaj w m z dokładnością do jednego miejsca po przecinku. Odp. 22.5

Jak zawsze – polecam rysunek ;) Z rysunku widać, że w takiej sytuacji (nachylenie roweru 45
stopni) siła odśrodkowa i siła ciężkości rowerzysty muszą być sobie równe:

Fr = Q

225/R = 10

v^2/R = g

R = 22.5

6. Ciało leżące na równi pochyłej o kącie nachylenia 50 stopni zsuwa się wzdłuż niej ze stała
prędkością 2 m/s. Ile wynosi współczynnik tarcia kinetycznego między równią, a ciałem?
Wynik podaj z dokładnością do jednego miejsca po przecinku. Odp. 1.2

Prędkość jest stała, więc przyspieszenie ciała a=0. Możemy ułożyć równanie sił działających
na to ciało, powodujących jego ruch:

Fs = T

f = sin50/cos50 = tg50

mg*sin50 = mg*cos50*f

f ~ 1.2

7. Piłka o masie 2kg uderza o doskonale gładką ścianę, ustawioną wzdłuż osi OY z
prędkością V1=((-7i+5j)m/s i odbija się od niej doskonale sprężyście w czasie 0.28 s. Oblicz
średnią wartość bezwzględną siły F z jaką ściana działa na piłkę? Wynik podaj w [N] z
dokładnością do 1N. Odp. 100 N

W tym zadaniu korzystamy ze wzoru:

F = m*(Δv/t)

Znamy masę ciała i czas, w którym nastąpiła zmiana prędkości. Musimy tylko znaleźć
wartość wektora zmiany prędkości. Można to oczywiście zrobić na kilka sposobów ;) Ten
wektor będzie równy v2-v1, a kąt odbicia jest równy kątowi padania. Z rysunku łatwo
zauważyć, że wartość tego wektora wyniesie 14.

F = 2*(14/0.28) = 100N

8. Kula o masie 16 g i prędkości 600 m/s trafia prostopadle w betonową ścianę i odbija się od
niej z prędkością 50 m/s . Oblicz wartość średniej siły działającej na ścianę, jeśli uderzenie
trwało 10^(-3)s. Wynik podaj w [N] z dokładnością do 100 N. Odp. 10400

F = m*(Δv/t)

Wszystkie dane są podane w zadaniu wprost, obliczamy jedynie wartość zmiany prędkości:

Δv = v2 – v1 = 50 – (-600) = 650m/s

F = 0.016*(650/0.001) = 10400N

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

9. Kulka o masie 0.09 kg przywiązana do nici o długości 50 cm obraca się w płaszczyźnie
pionowej ze stałą prędkością liniową 5,5 m/s. Ile wynosi, w najniższym punkcie toru siła
natężenia nici. Wynik podaj w N z dokładnością do drugiego miejsca po przecinku. Odp. 6.35

Kulka porusza się po okręgu w płaszczyźnie pionowej, więc naprężenie nici będzie
oczywiście równe:

N = Fr + Q = 0.09*(5.5^2/0.5) + 0.9 = 5.445 + 0.9 ~ 6.35N

10. Chcemy przesunąć skrzynię o masie 80 kg w dół równi pochyłej, nachylonej pod kątem 30
stopni do poziomu. Współczynnik tarcia między skrzynią a podłożem wynosi 0.15. Oblicz
wartość siły z jaką należy działać na skrzynię wzdłuż toru, aby skrzynia poruszała się ruchem
ze stałą prędkością 0.1 m/s. Wynik podaj w N z dokładnością do 1N. Odp. 296

Skrzynia ma się poruszać ze stałą prędkością, więc a = 0, czyli działające siły muszą się
równoważyć:

F + Fs = T

F = T – Fs

F = mg*cos30*f – mg*sin30 = 800*0.866*0.15 – 400 = 103.92 – 400 ~ -296N

Ujemna wartość oznacza, że siła, którą działamy będzie miała zwrot przeciwny do siły
zsuwającej. Czyli będziemy musieli tą skrzynię podpierać, żeby nam nie spadła :P

11. Dwa stykające się klocki o masach m1=5kg i m2= 4,5 kg leżą na idealnie gładkim stole.
Do pierwszego z nich przyłożono siłę F o wartości 10 N. Jaką wartość ma siła działająca na
drugi klocek. Wynik podaj w N z dokładnością do jednego miejsca po przecinku. Odp. 4.7

Trzeba to przemyśleć. Klocek pierwszy zadziała na drugi taką samą siłą, jaką drugi na niego –
zgodnie z III zasadą dynamiki. A klocek drugi zadziała na pierwszy siłą równą swojej sile
bezwładności:

Fb = m2*a

Obliczamy przyspieszenie układu, nadawane przez siłę 10N:

a = F/(m1+m2) = 10/9.5 = 1.05

Wyznaczamy siłę bezwładności drugiego klocuszka:

Fb = 4.5*1.05 ~ 4.7N

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

12. Pojazd o masie 1400 kg porusza się po poziomej jezdni z prędkością 72 km/h. Jaka musi
być wartość siły hamującej, która zatrzyma ten pojazd na drodze 10 m? Wynik podaj w kN z
dokładnością do jednego miejsca po przecinku? Odp. 28.0

Najłatwiej skorzystać z zasady zachowania energii, tzn. uwzględniając pracę siły hamującej:

Ek = W

(1400*400)/2 = F*10

(mv^2)/2 = F*s

F = 28kN

13. Samochód o masie 1400 kg porusza się z prędkością 84 km/h po wypukłym moście,
którego promień krzywizny wynosi 50 m. Jaka jest wartość siły nacisku, jaką samochód
wywiera na środek mostu? Wynik podaj w [kN] z dokładnością do jednego miejsca po
przecinku. Odp. -1.2

Samochód jadąc po moście będzie oczywiście poruszał się po okręgu w płaszczyźnie
pionowej, więc:

N = Q – Fr

N ~ 14000 – 15240 = -1240N

N = 14000 – 1400*(23.33^2/50)

N ~ -1.2kN

Nad tym minusem tutaj trzeba się chwilkę zastanowić. Jest on ważny – skoro siła odśrodkowa
jest większa od siły ciężkości, to samochód oderwie się od ziemi przejeżdżając przez ten
most. Ciężko wtedy mówić o wywieraniu jakiegoś nacisku... ;-)

14. Piłka o masie 0.24 kg uderza w ścianę, z prędkością 12m/s pod kątem 45 stopni i odbija
się od niej doskonale sprężyście. Wiedząc, że zderzenie ze ścianą trwało 0.02 s, podaj wartość
siły, którą piłka działa na ścianę. Wynik podaj w [N] z dokładnością do pierwszego miejsca
po przecinku. Odp. 203.6

Kolejne zadanko z odbiciem, znowu trzeba będzie znaleźć wartość wektora zmiany prędkości,
bo tylko tej danej brakuje, żeby obliczyć siłę:

F = m*(Δv/t)

Robimy rysuneczek z wektorkami i od razu widzimy, że wektor zmiany prędkości (v2-v1)
będzie równy 12*sqrt(2) ;-)) Jeśli ktoś nie widzi, podpowiadam: z przekątnej kwadratu.
Pewnie są inne sposoby jak to obliczyć, ale na razie ich nie znam. Zatem:

|v2-v1| = 16.97

F = 0.24*(16.97/0.02) ~ 203.6N

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

15. Ciało o masie 5,5 kg porusza się, wzdłuż osi OX, początkowo ze stała prędkością
v0=10m/s. W chwili t=0 zaczyna na nie działać, wzdłuż osi OX, zmienna siła hamująca Fx=-
pt, gdzie p=100N/s. Z opóźnieniem o jakiej wartości bezwzględnej poruszało się ciało w
chwili 4s? Wynik podaj w [m/s2] z dokładnością do 1m/s2. Odp. 73

m = 5.5kg

vO = 10m/s

Fx = -p*t, gdzie p = 100N/s

t = 4s

|a| = ?

No to raczej wszystko już mamy :P Obliczamy wartość siły działającej na ciało w 4-tej
sekundzie:

F4 = -100*4= -400N

|a| = F4/m = 400/5.5 = 72.72 ~ 73m/s^2

16. Balon o masie 300 kg opada pionowo w dół z prędkością 1,2 m/s. na balon oprócz siły
ciężkości i siły wyporu powietrza działa również siła oporu R= bv, gdzie v – wartość
prędkości, natomiast b=140Ns/m. Jaką masę balastu należy wyrzucić z balonu, aby zaczął
poruszać się z prędkością 1.2 m/s do góry. Wynik podaj z dokładnością do 1 kg. Odp. 34 kg.

W obu przypadkach przyspieszenie balonu jest równe zero, czyli siły na niego działające
muszą się równoważyć. Możemy więc zapisać równanie dla sytuacji, gdy balon opada:

Q – Foporu = Fwyporu

I dla sytuacji, w której wznosi się (Q2 to siłą ciężkości balonu po wyrzuceniu balastu):

Q2 + Foporu = Fwyporu

Mamy wszystko, przyrównujemy i obliczamy:

Q – Foporu = Q2 + Foporu

2664N = m2*10

3000N – 168N = m2*g + 168N

m2 = 266.4kg

Wiemy już, ile ważył balon po wyrzuceniu balastu. Obliczamy, ile balastu wyrzucono:

300 – 266.4 = 33.6 ~ 34kg

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

17. Spadochroniarz o masie 75 kg wyskoczył z samolotu i otworzył spadochron . W czasie
spadania na spadochron działa siła oporu o wartości F=bv^2, gdzie v-wartość prędkości,
natomiast b=48Ns^2/m^2. W wyniku działania tej siły po pewnym czasie lotu prędkość
spadania spadochroniarza ustaliła się. Z jaką prędkością wyląduje spadochroniarz? Wyniki
podaj w [m/s] z dokładnością do jednego miejsca po przecinku. Odp. 4.0.

Na spadochroniarza będą działały dwie siły. Siła ciężkości:

Q = mg = 750N

Oraz siła oporu, ze zwrotem przeciwnym do siły ciężkości:

F = b*v^2

W zadaniu mamy informację, że po pewnym czasie prędkość była stała, czyli a = 0, więc siły
działające na spadochroniarza muszą się równoważyć:

Q = F

750 = 48*v^2

15.625 = v^2

v ~ 4.0m/s

PARĘ SŁÓW NA KONIEC

Nie jestem autorem treści zadań. Moje rozwiązania nie przeszły żadnej korekty

błędów, poza sprawdzeniem poprawności z prawidłowymi odpowiedziami. Pytania, sugestie?

[e-mail]

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Fizyka 1 SKP – drugie kolokwium, cd2. [Rozwiązał: Maciek K.]

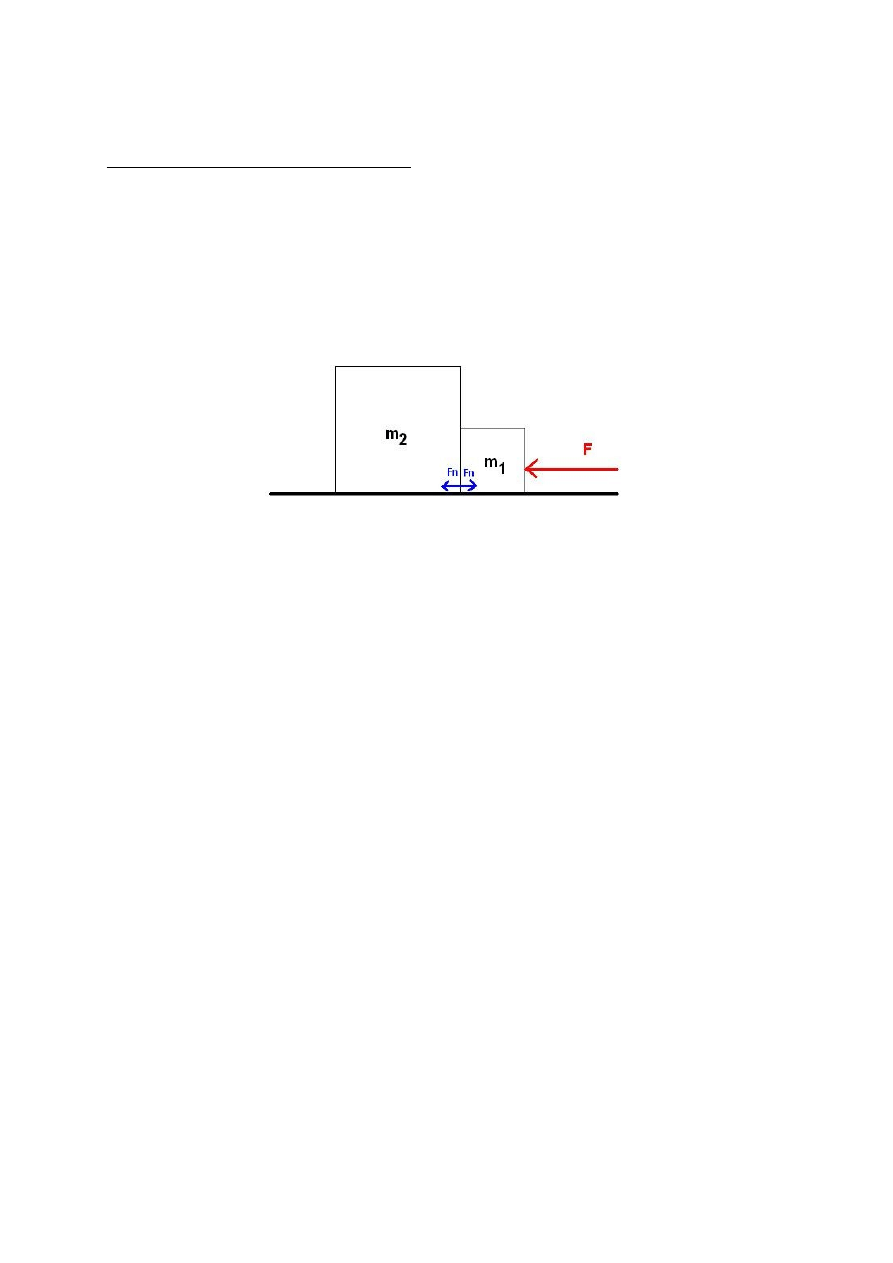
1. Dwa stykające się klocki o masach m1=2 i pewnej masie m2 (patrz rysunek) leżą na
idealnie gładkim stole. Do pierwszego z nich przyłożono siłę o wartości 35N . Na skutek
działania tej siły klocki zaczęły poruszać się z przyspieszeniem o wartości 2m/s2. Jaką
wartość Fn, mają siły wzajemnego nacisku klocków? Wynik podaj w N z dokładnością do
pierwszego miejsca po przecinku. (odp. 31.0)

Fn będzie równe sile bezwładności ciała m2. Przyspieszenie jest dane, musimy znaleźć masę
m2:

a = F / (m1+m2)

Fn = m2*a

2 = 35 / (2+m2)

Fn = 15.5*2 = 31N

m2 = 15.5kg

2. Na końcach nieważkiej nici, przerzuconej przez nieważki blok, zawieszono ciężarki o
masach 1,5kg i 3,6 kg. Lżejszy z nich znajduje się o dwa metry niżej od cięższego. Wszelkie
opory ruchu pomijamy. Z jakim przyspieszeniem ciężarki zaczną poruszać się jeśli puścimy je
swobodnie. Wynik podaj w [m/s2] z dokładnością do jednego miejsca po przecinku. odp. (4.1)

Przyspieszenie „nadaje” układowi siła wypadkowa. Na ciężarki działają siły ciężkości i to od
nich będzie pochodziła siła wypadkowa, cięższy pociągnie lżejszy:

F = Q2 – Q1 = m2*g – m1*g = 36-15 = 21N

Nie pozostaje nam nic innego, jak tylko podstawić dane do wzoru i wyznaczyć przyspieszenie
układu ;)

a = F / (m1+m2) = 21/5.1 ~ 4.1m/s^2

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

3. Pod wpływem stałej siły F ciało o masie 10g zmieniło swoją prędkość od v1=(3i+5j)m/s do
v2 ((-5)i+10j)m/s w czasie 0.02 s. Ile wynosi wartość bezwzględna siły F? Wynik podaj w N z
dokładnością do jednego miejsca po przecinku. (odp. 4.7)

F = m*(Δv/t)

Wystarczy jeden rzut oka na ten wzór i od razu każdy zauważy, że brakuje nam tylko Δv,
reszta dana jest w zdaniu. Obliczamy Δv:

Δv = v2-v1 = -8i+5j = [-8,5]
|Δv| = 9.43m/s

F = 0.01*(9.43/0.02) ~ 4.7N

4. Przy prędkości samochodu 8m/s jego droga hamowania wynosi 7m. Przyjmując, że
podczas hamowania samochód porusza się ruchem jednostajnie opóźnionym, oblicz
efektywny współczynnik tarcia kół samochodu o nawierzchnię drogi. Wynik podaj z
dokładnością do jednego miejsca po przecinku. (odp.0.5)

Najłatwiej będzie skorzystać z zasady zachowania energii (uwzględniając pracę siły tarcia).
Zapisujemy równanie:

Ek = W

1/2*64 = 10*f*7

Ek = T*s

32 = 70f

1/2*(mv^2) = m*g*f*s

f ~ 0.5

5. Ciężarek o masie 45 g zawieszony na nici o długości 85 cm obraca się po okręgu ruchem
jednostajnym w płaszczyźnie poziomej. W czasie ruchu nić odchylona jest od pionu o kąt 30
stopni. Ile wynosi prędkość liniowa ciężarka? Wynik podam w [m/s] z dokładnością do
jednego miejsca po przecinku. ?(odp.1.6)

Bez rysunku ciężko sobie to wyobrazić. Ale po narysowaniu i zaznaczeniu siły odśrodkowej i
ciężkośći od razu widać, że:

Fr / Q = tg30 = 0.577

v^2 / 4.35 = 0.577

(mv^2*1/r) / (mg) = 0.577

v ~ 1.6m/s

v^2/rg = 0.577

Promień obliczyłem w ten sposób:

r/0.85 = sin30
r = 0.425

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

6. Punkt materialny rozpoczyna ruch po okręgu o promieniu 0,5m ze stałym przyspieszeniem
kątowym 3.5s^(-2). Po jakim czasie siła dośrodkowa będzie 9 razy większa od siły stycznej?
Wynik podaj w sekundach z dokładnością do drugiego miejsca po przecinku. (odp.1.60)

Najważniejsze równanie w tym zadaniu:

Fr = 9F
(mv^2)/r = 9*ma

v = w*r

w = e*t

v = etr

(etr)^2 / r = 9*e*r
et^2 = 9
t^2 = 2.57

t ~ 1.60s

7. Jaka jest wartość siły wypadkowej działającej na klocek o masie 6 kg poruszający się z
przyspieszeniem a=5i+2j. Wynik podaj w N z dokładnością do jednego miejsca po przecinku.
(odp.32,3)

F =ma
|a| = 5.39

F = 6*5.39 ~ 32.3N

8. Na gładkiej równi pochyłej nachylonej do poziomu pod kątem 50 stopni znajduje się ciało
o ciężarze 550N utrzymywane w równowadze przez siłę R działającą w kierunku równoległym
od podstawy równi. Ile wynosi wartość siły R?Wynik podaj w N z dokładnością do 1N.
(odp.655)

Rx – składowa szukanej siły R, równoległa do równi,

Rx = Fs
Fx = mg*sin50 = 421.32N

Siła R jest równoległa do podstawy, więc możemy zapisać:

Rx / R = cos50
R = Rx / cos50 = 421.32 / 0.643 ~ 655N

PARĘ SŁÓW NA KONIEC

Nie jestem autorem treści zadań. Moje rozwiązania nie przeszły żadnej korekty

błędów, poza sprawdzeniem poprawności z prawidłowymi odpowiedziami. Pytania, sugestie?

[e-mail]

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

FIZYKA

Kolokwium nr 3 (e-test)

Rozwiązał i opracował: Maciej Kujawa, SKP 2008/09

(więcej informacji na końcu dokumentu)

Zad. 1

Z balkonu znajdującego się na wysokości 11m nad ziemią wypadła poduszka o masie

0.25kg. Na poduszkę, oprócz siły grawitacji, działa siła oporu powietrza zależna od jej
prędkości. Poduszka spadła na Ziemię z prędkością 12m/s. Ile wynosi wartość pracy jaką
wykonała nad poduszką siła oporu powietrza? Wynik podaj w [J] z dokładnością do
pierwszego miejsca po przecinku. (Odp. 9,5)

Energia potencjalna poduszki znajdującej się na balkonie będzie równa sumie energii
kinetycznej tuż przed upadkiem oraz pracy siły oporu powietrza:
Ep = Ek + W

Ep = mgh

Ek = (1/2)*m*v^2

mgh = (1/2)*m*v^2 + W
0.25*10*11 = (1/2)*0.25*144 + W
27.5 = 18 + W
W = 27.5 – 18 = 9.5J

Zad. 2

Jaką wartość pędu posiada klocek o masie 9kg poruszający się z prędkością

3i + 4j [m/s]? Wynik podaj w [kg m/s] z dokładnością do pierwszego miejsca po przecinku.
(Odp. 45)

v = [3, 4]

|v| = 5

p = m*v

= 9*5 = 45

Zad. 3

Człowiek o masie 70kg, biegnący naprzeciw wózka z prędkością 9.5km/h wskakuje na

wózek o masie 50kg, jadący z prędkością 4km/h. Ile wynosi wartość prędkości wózka z
człowiekiem bezpośrednio po tym jak człowiek wskoczył na wózek? Wynik podaj w [km/h] z
dokładnością do pierwszego miejsca po przecinku. (Odp. 3,9)

Skorzystamy z zasady zachowania pędu (

pęd przed zderzeniem = pęd po zderzeniu

). Pęd

układu przed zderzeniem (znak minus oznacza, że prędkości ciał miały przeciwne zwroty):
p = p_człowieka – p_wózka = m1*v1 – m2*v2 = 70*9.5 – 50*4 = 465

Pęd układu po zderzeniu:
p' = (m1+m2)*u = 120*u

p = p'

465 = 120u
u = 3.875 ~ 3.9km/h

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 4

Kula o masie 15.5g wyrzucona pionowo w górę z prędkością 18m/s, spadła na ziemię

z prędkością 2m/s. Ile wynosi praca sił tarcia kuli o powietrze? Wynik podaj w dżulach z
dokładnością do pierwszego miejsca po przecinku. (Odp. 2,5)

m = 0.0155kg
v1 = 18m/s
v2 = 2m/s

Zapisujemy równanie energii:
Ek1 = Ek2 + W

Ek1 = (1/2)*m*v1^2 = 2.511
Ek2 = (1/2)*m*v2^2 = 0.031

2.511 = 0.031 + W
W = 2.511 – 0.031 = 2.48 ~ 2.5J

Zad. 5

Kamień o masie 3.5kg spada swobodnie z przyspieszeniem 10 m/s^2. Ile wynosiła, po

11s lotu, wartość jego pędu wyrażona w jednostkach SI? Wynik podaj z dokładnością do
jedności. (Odp. 385)

m = 3.5kg

v = a*t

= 10*11 = 110m/s

a = 10m/s^2

p = m*v = 110*3.5 = 385

t = 11s

Zad. 6

Ciało o masie 0.2kg znajduje się na równi o kącie nachylenia 30. Jaką prędkość

należałoby nadać ciału u podnóża równi o długości 4m, aby na jej końcu ciało zatrzymało się,
jeśli współczynnik tarcia kinetycznego jest równy 0.4? Wynik podaj w [m/s] z dokładnością do
pierwszego miejsca po przecinku. (Odp. 8,2)

U podnóża równi ciało będzie „miało” tylko energię kinetyczną i ta energia zostanie
zamieniona na energię potencjalną (na szczycie równi) oraz pracę siły tarcia:
Ek = Ep + W

Nie znamy wysokości równi, a jest ona niezbędna do wyznaczenia energii potencjalnej:
h/4 = sin30

h = sin30*4 = 2m

Żeby wyznaczyć pracę siły tarcia, musimy znać siłę tarcia oraz drogę, na jakiej działała:

W = F*s

s = 4m (długość równi)

F = mg*cos30*f = 0.2*10*0.866*0.4 = 0.6928

Podstawiamy:
(1/2)*m*v^2 = mgh+ F*s
0.1*v^2 = 4 + 2.7712
v^2 = 67.712

v ~ 8.2m/s

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 7

Ciało o masie 0.8kg wyrzucono ukośnie z prędkością początkową równą 14m/s pod

kątem 60 stopni. Ile wynosiła energia kinetyczna ciała w najwyższym punkcie toru? Wynik
podaj w dżulach z dokładnością do pierwszego miejsca po przecinku. (Odp. 19,6)

Początkowa energia kinetyczna będzie równa sumie energii potencjalnej w najwyższym
punkcie oraz energii kinetycznej w tym punkcie. Musimy wyznaczyć wysokość, na jaką
wzniesie się ciało:
vy = v*sin60 = 14*sin60 = 12.124m/s
t = v/a = 12.124/10 = 1.2124s

h = vy*t – 0.5*g*t^2

= 7.35m

Ek1 = Ek2 + Ep2

Ek_szukana = 0.5*m*v2^2

0.5*m*14^2 = 0.5*m*v2^2 + mgh |:m

Ek_szukana = 0.4*49 = 19.6J

0.5*196 = 0.5*v2^2 + 73.5
98 – 73.5 = 0.5*v2^2
49 = v2^2
v = 7m/s

Zad. 8

Jaką wartość pędu posiada klocek o masie 4kg poruszający się z prędkością

7i+4j m/s? Wynik podaj w [kg m/s] z dokładnością do pierwszego miejsca po przecinku.
(Odp. 32,2)

m = 4

p = m*v = 4*8.06 ~ 32.2

|v| = 8.06m/s

Zad. 9

Stojące na łyżwach dziecko o masie 44kg trzyma w ręku pakunek o masie 1kg. Tarcie

łyżew o lód jest zaniedbywalnie małe. W pewnej chwili rzuca ono ten pakunek, poziomo przed
siebie z prędkością 30m/s. Wyznacz z jaką prędkością zacznie się poruszać dziecko w wyniku
rzucenia pakunku. Wynik podaj w [m/s] z dokładnością do drugiego miejsca po przecinku.
(Odp. 0,68)

Pęd przed „zderzeniem”:

p = p'

p = (44 + 1) * 0 = 0

0 = 44*v + 30
-30 = 44v

Pęd po „zderzeniu”:

|v| ~ 0.68

p' = m1*v1 + m2*v2 = 44*v + 30

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 10

Piłkę tenisową o masie 0,1kg upuszczono z wysokości 17m. Wiemy, że po każdym

odbiciu traci ona 15% swojej energii mechanicznej. Oblicz wartość prędkości piłki tuż po
drugim odbiciu. Wynik podaj w [m/s] z dokładnością do pierwszego miejsca po przecinku.
(Odp. 15,7)

Obliczamy początkową energię piłeczki (potencjalna):
E = mgh = 0.1*10*17 = 17J

Po pierwszym odbiciu:

Po drugim odbiciu:

E1 = E*0.85 = 14.45J

E2 = E1*0.85 = 12.28J

E2 = Ek
12.28 = 0.5*0.1*v^2
245.6 = v^2
v = 15.67 ~ 15.7

Zad. 11

Człowiek o masie 70kg, biegnący z prędkością 8,5km/h dogania i wskakuje na wózek o

masie 50kg, jadący z prędkością 4km/h. Ile wynosi wartość prędkości wózka z człowiekiem
bezpośrednio po tym jak człowiek wskoczył na wózek? Wynik podaj w [km/h] z dokładnością
do pierwszego miejsca po przecinku. (Odp. 6,6)

Zapisujemy równanie pędu:
p = p'
m1v1 + m2v2 = (m1+m2)*u
595 + 200 = 120*u
u = 6.625 ~ 6.6km/h

Zad. 12

Piłka o masie 0,9kg lecąca poziomo z prędkością 1,8m/s, uderza o pionową ścianę i

odbija się od niej z prędkością 1m/s. Czas zderzenia wynosi 0,1s. Z jaką siła piłka zadziałała
na ścianę? Wynik podaj w N z dokładnością do 1N. (Odp. 25)

F = Δp/t

p1 = 0.9*1.8 = 1.62
p2 = 0.9*(-1) = -0.9
|Δp| = |p2-p1| = 2.52

F = 2.52/0.1 ~ 25N

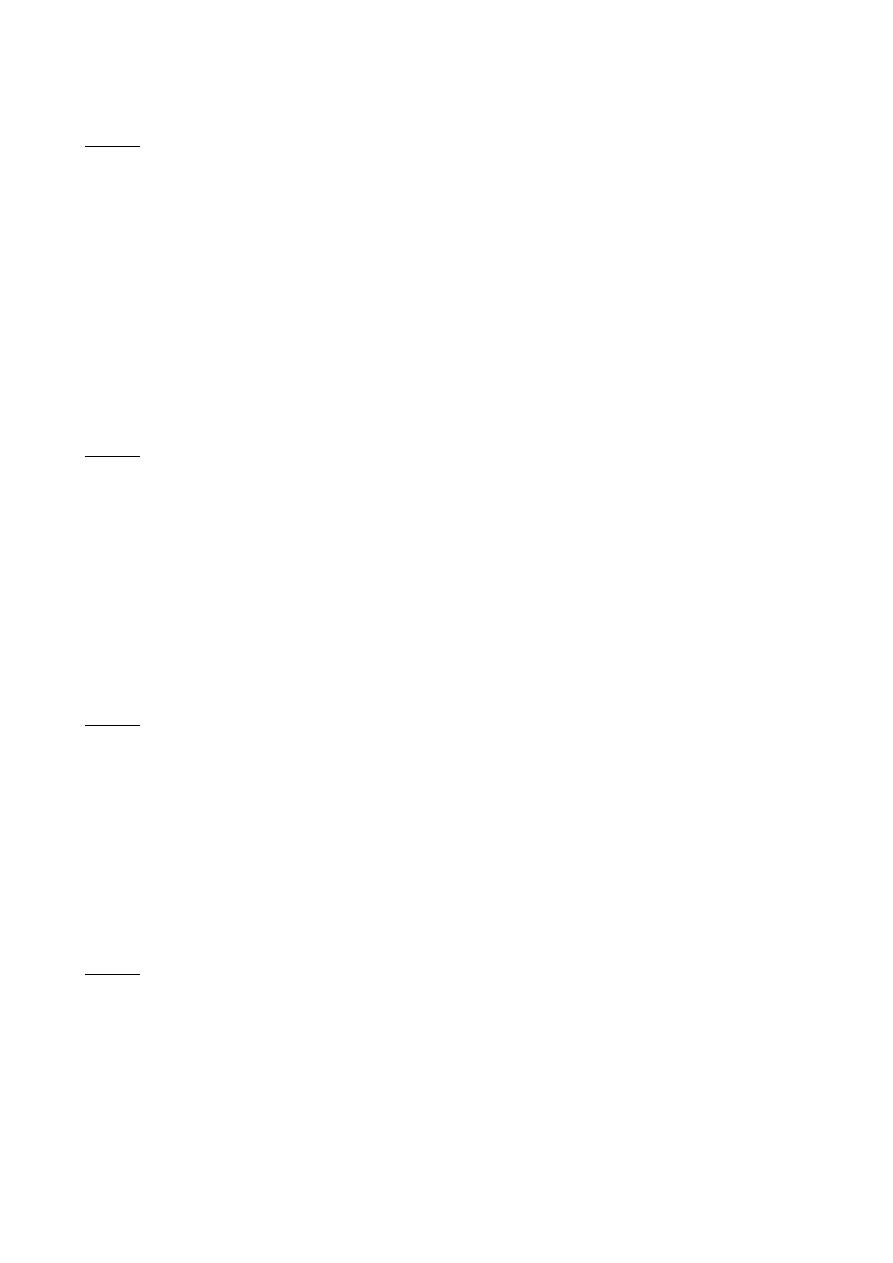
Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 13

Ze strzelby o masie 5kg oddano strzał kulą o masie 45g. Prędkość wylatującej z lufy

kuli wynosiła 950m/s. Oblicz wartość średniej siły, która działa na ramię strzelca w wyniku
strzału. Czas wzajemnego oddziaływania kuli i strzelby wynosi 0,02s. Wynik podaj w N z
dokładnością do 10N. (Odp. 2138)

p = p'

F = m*(v/t)

= 5*(8.55/0.02)

F = 2137.5 ~ 2138N

p = 0
p' = 5*v - 0.045*950 = 5*v - 42.75

0 = 5*v - 42.75
v = 8.55m/s

Zad .14

Kula lecąca poziomo z prędkością 10m/s przebija przeszkodę i dalej porusza się

poziomo. W wyniku tego zdarzenia kula zmniejsza swoją energię mechaniczną o połowę.
Wyznacz prędkość kuli po przejściu przez przeszkodę. Wynik podaj w [m/s] z dokładnością do
pierwszego miejsca po przecinku. (Odp. 7,1)

E2 = 0.5 * E1
0.5*m*v2^2 = 0.5*0.5*m*v1^2

|: (0.5*m)

v2^2 = 0.5*v1^2
v2^2 = 50
v ~ 7.1m/s

Zad. 15

Ze strzelby o masie 5kg oddano strzał kulą o masie 30g. Prędkość wylatującej z lufy

kuli wynosiła 700m/s. Z jaką prędkością, w wyniku wystrzału, którego czas wynosił 0,02 s,
strzelba została odrzucona do tyłu? Wynik podaj w [m/s] z dokładnością do pierwszego
miejsca po przecinku. (Odp. 4,2)

p = p'
0 = 5*v - 0.030*700
0 = 5*v - 21
v = 4.2m/s

Zad. 16

Obciążona kabina windy wznosi się (ruchem jednostajnym) w ciągu 1 min na

wysokość 180m. Ile wynosi moc silnika, jeżeli masa kabiny wraz z obciążeniem równa jest
7 ton? Wynik podaj w [kW] z dokładnością do 1kW. (Odp. 210)

P = W/t

P = 12600/60 = 210kW

W = ΔE = mgh = 7*10*180 = 12600kJ

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 17

Ciało o masie 2kg wyrzucone pionowo do góry posiada na wysokości 1,3m energię

kinetyczną 10J. Ile wynosiła prędkość początkowa tego ciała? Wynik w [m/s] z dokładnością
do pierwszego miejsca po przecinku. (Odp. 6,0)

Energia mechaniczna (Ep + Ek)

ciała na wysokośći h = 1.3m:

E = Ep + Ek = mgh + 10J = 2*10*1.3 + 10 = 36J

Energia kinetyczna na wysokości h = 0 (początkowa):
E = Ek0 = 0.5*2*v0^2 = 36J
v0 = 6m/s

Zad. 18

W pewnej chwili, na ciało o masie 2kg pozostające początkowo w spoczynku, zaczęła

działać siła 8,5N. Wyznacz energię kinetyczną tego ciała po 9,5s działania tej siły. Wynik
podaj w [J] z dokładnością do 1J. (Odp. 1630)

Musimy wyznaczyć prędkość ciała po 9.5s:

a = F/m

= 8.5/2 = 4.25m/s^2

v = at = 4.25 * 9.5 = 40.375m/s

Ek = 0.5*2*40.375^2 ~ 1630J

Zad. 19

Za pomocą linki przymocowanej do sufitu zawieszono sześcienny klocek o masie 12kg.

Masa linki jest zaniedbywanie mała w porównaniu do masy klocka. W klocek ten uderza
lecący poziomo na wysokości środka masy klocka, pocisk. Prędkość pocisku wynosi 200m/s, a
jego masa 0,25kg. Pocisk ten wbija się w klocek i w nim pozostaje. Na jaką wysokość
podniesie się klocek wraz z pociskiem w wyniku tego zdarzenia? Wynik podaj w [m] z
dokładnością do pierwszego miejsca po przecinku. (Odp. 0,8)

Ciekawe zadanie ;) Przeanalizujmy:
m1 = 12kg

v1 = 0

m2 = 0.25kg v2 = 200m/s

Następuje zderzenie, interesuje nas prędkość klocka (u) po zderzeniu, jest ona niezbędna do
wyznaczenia jego energii kinetycznej. Zapisujemy równanie pędu (p = p'):
12*0 + 0.25*200 = (12+0.25)*u
50 = 12.25*u
u = 4.08m/s

Wyznaczamy energię kinetyczną klocka z pociskiem po zderzeniu:
Ek = 0.5*(12+0.25)*4.08^2 = 101.96

Korzystając z zasady zachowania energii, obliczamy na jaką wysokość może wznieść się
klocek:
Ek = Ep

101.96 = 122.5*h

101.96 = mgh

h = 0.832 ~ 0.8m

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 20

Kula A o masie 1kg porusza się wzdłuż osi OX z prędkością 1,5m/s i zderza się

doskonale sprężyście i centralnie ze spoczywającą kulą B o masie 1,8 kg . W wyniku tego
zderzenia kula B zaczęła się poruszać z prędkością 0,5 m/s wzdłuż osi OX. Oblicz prędkość
kuli A. Wynik podaj w [m/s] z dokładnością do pierwszego miejsca po przecinku. (Odp. 0,6)

Zapisujemy równanie pędu:
1*1.5 + 1.8*0 = 1*v + 1.8*0.5
1.5 = v + 0.9
v = 0.6m/s

Zad. 21

Pęd kulki wzrósł o 16% względem pędu początkowego. Ile razy wzrosła w tym czasie

energia kinetyczna tej kuli? Wynik podaj z dokładnością do drugiego miejsca po przecinku.
(Odp. 1,35)

Wyznaczamy stosunek prędkości v1 i v2, a następnie wstawiamy tą zależność do wzoru na
energię kinetyczną i obliczamy iloraz:
p2 = 1.16 * p1

Ek2 : Ek1 = [1/2*m*(1.16*v1)^2] : [1/2*m*v1^2] =

m*v2 = 1.16 * m*v1

= 1.3456 ~ 1.35

v2 = 1.16*v1

Zad. 22

Pocisk o masie 13g mając początkowo prędkość 90m/s wbił się w drzewo i się w nim

zatrzymał po przebyciu drogi 5cm . Ile wynosiła średnia wartość siły oporu (hamowania
pocisku) Wynik podaj w [kN] z dokładnością do drugiego miejsca po przecinku. (Odp. 1,05)

Energia kinetyczna pocisku będzie równa pracy siły oporu:
Ek = W
0.5*0.013*90^2 = F*s
52.65 = F*0.05
F = 1053N ~ 1.05kN

Zad. 23

Na nieruchomy klocek o masie 1,5kg zaczęła działać siła wypadkowa o wartości 5N.

Jaką energię kinetyczną nadała mu ona w czasie 2s? Wynik podaj w dżulach z dokładnością
do 1J. (Odp. 33,3)

a = 5/1.5 = 3.33m/s^2
v = at = 6.66m/s
Ek = 0.5*1.5*6.66^2 = 33.2667 ~ 33.3J

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 24

Piłka o masie 1,3kg, lecąca poziomo z prędkością 2,8m/s, uderza o pionową ścianę i

odbija się od niej z prędkością 2m/s. Ile wynosi zmiana pędu piłki? Wynik podaj w [kgm/s] z
dokładnością do pierwszego miejsca po przecinku. (Odp. 6,2)

m = 1.3kg

v1=2.8m/s

v2 = -2m/s

Δp = m*Δv
|Δv| = v2-v1 = 4.8m/s

Δp = 1.3*4.8 = 6.24 ~ 6.2

Zad. 25

Ile wynosi praca jaką trzeba wykonać, aby podnieść ciało o masie 10kg na wysokość

0,7m z przyspieszeniem 1m/s^2? Wynik podaj w dżulach z dokładnością do 1J. (Odp. 77,0)

F = (g+a)*m = 11*10 = 110N
W = F*s = 110*0.7 = 77J

Drugi sposób, praca będzie równa przyrostowi energii potencjalnej oraz pracy siły, nadającej
ciału dane przyspieszenie:
W = ΔEp + Wf

ΔEp = 10*10*0.7 = 70J
Wf = F*s = m*a*s = 10*1*0.7 = 7J

W = 70 + 7 = 77J

Zad. 26

Po oblodzonym, płaskim chodniku pchnięto sanie o masie 28kg. Współczynnik tarcia

sań jest zaniedbywalnie mały. Po pchnięciu poruszają się one ze stałą prędkością 2,4m/s. W
chwili przejeżdżania spadł na sanie z drzewa, sopel lodu o masie 4kg, do tej pory wiszący
swobodnie. W chwili upadku na sanie prędkość sopla lody wynosiła 8m/s i była skierowana
prostopadle do chodnika. Oblicz prędkość sań bezpośrednio po tym zdarzeniu. Wynik podaj w
[m/s] z dokładnością do jednego miejsca po przecinku.

Niestety brakuje poprawnej odpowiedzi. Osobiście rozwiązałbym to tak – wyznaczamy pęd
saneczek:
p = M*v = 28*2.4 = 67.2

W momencie, gdy sopel spada na sanie, zwiększa się ich masa, ale prędkość działa w innym
kierunku więc nie ma (moim zdaniem :D) znaczenia:
p' = (M+m)*u

p = p'
67.2 = (28+4)*u
67.2 = 32*u
u = 2.1m/s

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 27

Piłkę tenisową o masie 0,1kg, upuszczono z wysokości 14m. Wiemy, że po każdym

odbiciu traci ona 50% swojej mechanicznej. Oblicz na jaką wysokość wzniosła się piłka tuż
po drugim odbiciu. Wynik podaj w [m] z dokładnością do pierwszego miejsca po przecinku.
(Odp. 3,5)

m = 0.1kg
h = 14m

Początkowa energia kulki:
E0 = mgh = 0.1*10*14 = 14J

Po pierwszym odbiciu:

Po drugim odbiciu:

E1 = 0.5*E0 = 7J

E2 = 0.5*E1 = 3.5J

Dysponując taką energią (E2), kulka mogła wznieść się na wysokość:
E2 = mgh
h = E2/mg = 3.5m

Zad. 28

Klocek o masie 1kg poruszał się bez tarcia po powierzchni stołu z prędkością

początkową 65m/s. Po 1s zaczęła działać na niego stała siła skierowana przeciwnie do
kierunku ruchu. W wyniku działania tej siły w ciągu kolejnych 10s pęd tego ciała zmalał do
wartości 20 kg m/s. Ile wynosiła wartość tej siły? Wynik podaj w N z dokładnością do
pierwszego miejsca po przecinku. (Odp. 4,5)

F = Δp/t

F = 45/10 = 4.5N

p1 = m * v1 = 65
p2 = 20
|Δp| = 45

PARĘ SŁÓW NA KONIEC

Powyższe zadania pochodzą z testu przygotowującego do trzeciego kolokwium

(etestu) z Fizyki 1 dla SKP. Nie jestem autorem zadań, ani ilustracji do ich treści. Moje
rozwiązania nie przeszły żadnej korekty błędów (poza sprawdzeniem zgodności z
poprawnymi odpowiedziami), mają służyć celom edukacyjnym ;-) Większość wyników
została zaokrąglona, zgodnie z wymaganiami etestu. W przypadku jakichkolwiek uwag/pytań/
sugestii pisz śmiało na:

[e-mail]

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

FIZYKA

Kolokwium nr 3 (e-test), część II

Rozwiązał i opracował: Maciej Kujawa, SKP 2008/09

(więcej informacji na końcu dokumentu)

Zad. 1

Ciało o masie 0.8kg wyrzucono ukośnie z prędkością początkową równą 14m/s pod

kątem 60 stopni. Ile wynosiła energia kinetyczna ciała w najwyższym punkcie toru? Wynik
podaj w dżulach z dokładnością do pierwszego miejsca po przecinku. (Odp. 19,6)

To drugi sposób rozwiązania tego zadania (pierwszy był tutaj: fiz1_etest3skp.pdf , zadanie
nr 7), zaproponowany przez Magdalenę :P

Prędkość początkową możemy rozłożyć na dwie składowe (vx – pozioma, vy – pionowa). W
najwyższym punkcie toru, składowa pionowa będzie równa zero, więc prędkość ciała w tym
punkcie będzie równa tylko składowej poziomej:

vo = 14m/s
v = vx = vo* cos60 = 14 * ½ = 7m/s
Ek = ½*m*v^2 = 0.5*0.8*7^2 = 0.4*49 = 19.6J

Zad. 2

Kula o masie 5kg uderza w nieruchoma kule o masie 8kg, i pozostaje w niej. dalej kule

poruszają się razem. Jaka cześć energii kinetycznej pierwszej kuli zostanie zamienna na
ciepło? (Odp. 0,6)

Musimy obliczyć zmianę energii kinetycznej pierwszej kulki i sprawdzić, jaką część
początkowej energii stanowi ta różnica.

Obliczamy początkową energię kinetyczną kulki:
Ek1 = ½ * m * v^2 = 2.5*v^2

Obliczamy energię kulki po zderzeniu i „połączeniu” z drugą:
Ek2 = ½ * (m+M) * v2^2 = ½ * 13 * v2^2 = 6.5*v2^2

Nie znamy prędkości po zderzeniu, możemy ją obliczyć z zasady zachowania pędu:
m*v + 0 = (M+m)*v2
5v = 13*v2
v2 = 5/13 * v

Podstawiamy do Ek2:
Ek2 = 6.5*(25/169)*v^2 = 0.96*v^2

E1 – E2 = 1.54*v^2

(1.54*v^2) / (2.5*v^2) = 0.616 ~ 0.6

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 3

Dwa ciała, ciało A i ciało B leżą na doskonale gładkim

(brak tarcia) płaskim stole (rysunek). Pomiędzy nimi znajduje
się nieważka sprężyna, niepołączona na trwałe z żadnym z tych
ciał. Masa ciała A jest dwa razy większa od masy ciała B. Ciała
te zbliżono do siebie, w wyniku czego sprężyna uległa ściśnięciu
i po dłuższej chwili puszczono. Po uwolnieniu ciał, ciało A miało
energię kinetyczną równą 11J. Wyznacz pracę jaką wykonano ściskając sprężynę. Wynik podaj
w [J] z dokładnością do 1J. (Odp. 33)

Nie jestem w 100% pewny, czy rozwiązanie jest poprawne. Doszedłem do wniosku, że praca
jaką wykonano ściskając sprężynę, będzie równa sumie energii kinetycznych ciał po
puszczeniu. Tyle pracy, ile wykonano, tyle energii w sumie „dostaną” ciała.

E1 – energia kinetyczna pierwszego ciała
E2 – energia kinetyczna drugiego ciała

W = E1 + E2

m1 = 2*m2

Wyznaczamy energie kinetyczne ciał po puszczeniu:
E1 = (2m2 * v1^2)/2 = m2 * v1^2 = 11J
E2 = (m2 * v2^2)/2 = ½ * m2 * v2^2

Wyznaczamy prędkość drugiego ciała (równanie pędu):
m1*v1 = m2*v2
2m2*v1 = m2*v2
v2 = 2*v1

Podstawiamy do wzoru na E2:
E2 = ½*m2*(2*v1)^2 = ½*m2*4*v1^2 = 2*m2*v1^2

Podstawiam E1 do wzoru na E2 (podkreślone wyrażenie):
E2 = 2*11J = 22J

E1 + E2 = 33J :-)

Może ktoś wpadnie na lepszy sposób ;) Jak widać, gdy ciało A miało masę dwa razy większą
od B, to jego energia kinetyczna była dwa razy mniejsza od energii ciała B...

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 4

Pod działaniem siły F ciało porusza się po osi x. Na rysunku przedstawiono wykres

zależności siły F od położenia ciała. Wyznacz pracę wykonaną przez tą siłę na drodze 1.3m?
Wynik podaj w J z dokładnością do pierwszego miejsca po przecinku. (Odp. 9,1)

Praca w tym wypadku jest równa polu powierzchni pod
wykresem, ale – uwaga: gdy siła zmienia zwrot na
przeciwny, to pracę musimy odjąć (praca to iloczyn
skalarny).

W = P1 – P2

P = (a*h)/2

Pierwszy trójkąt (nad osią x - czerwony):
P1 = (1*20)/2 = 10

Drugi trójkąt (pod osią x - niebieski):
P2 = (0,3*6)/2 = 0.9

W = 10 - 0.9 = 9.1J

Do obliczenia długości podstawy i wysokości można w takim wypadku zastosować proporcje,
na przykład:
Jeśli a=1 → h=20, więc jeśli a=1,3 → h=26 ;) Trzeba po prostu trochę pokombinować.

Zad. 5

Pociąg elektryczny o masie 80 ton przejechał drogę 130m wzdłuż wznoszącego się pod

kątem 30 stopni toru z przyspieszeniem 1.5m/s2. Efektywny współczynnik tarcia wynosi 0,05.
Ile wynosi praca jaką wykonał silnik tego pociągu? Wynik podaj w [MJ]. (Odp. 72,1)

W = F*s

Żeby wyznaczyć siłę z jaką działał silnik, zapisujemy równanie:
ma = F – T – Fs

Fs – siła zsuwająca (składowa siły ciężkości, równoległa do równi)

F = ma + T + Fs
F = 80*1.5 + mg*cos30*f + mg*sin30
F = 120 + 34.64 + 400
F = 554.64kN

W = F*s = 72103.2 kJ ~ 72.1 MJ

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 6

Pociąg elektryczny o masie 90 ton przejechał drogę 80m wzdłuż poziomego toru z

przyspieszeniem 1.5m/s2. Efektywny współczynnik tarcia wynosi 0,05. Ile wynosi praca jaką
wykonał silnik tego pociągu? Wynik podaj w [MJ]. (Odp. 14,4)

Analogicznie do poprzedniego:

ma = F – T
F = ma + T
F = 90*1.5 + m*g*f
F = 135 + 900*0.05
F = 135+45 = 180kN

W = F*s = 180*80 = 14.4MJ

Zad. 7

Pocisk o masie 15g mając początkowo prędkość 90m/s wbił się w drzewo i się w nim

zatrzymał. Ile wynosi energia cieplna wydzielana przy hamowaniu pocisku? Wynik podaj w dżulach
z dokładnością do 1J. (Odp. 60,8)

Energia cieplna będzie równa ilości energii kinetycznej, jaką stracił pocisk:
Ek = ½ * m * v^2 = 0.0075 * 8100 = 60.75 ~ 60.8J

Zad. 8

Ciało o masie 1.2kg wyrzucono ukośnie z prędkością początkową równą 15m/s pod kątem

60 stopni. Ile wynosiła energia potencjalna ciała w najwyższym punkcie toru? Wynik podaj w
dżulach z dokładnością do pierwszego miejsca po przecinku. (Odp. 101,2)

Korzystamy z zasady zachowania energii, ale Ek obliczamy dla pionowej składowej prędkości
początkowej:
Ek = Ep

Vy = Vo * sin60 = 12.99m/s

Ek = ½ * m * v^2 = 0.6 * 168.74 ~ 101.2

Zad. 9

Kula A o masie 3kg toczy się wzdłuż osi OX z prędkością 6m/s. Kula B o masie 5kg toczy się

wzdłuż osi OX z prędkością 1m/s w kierunku przeciwnym do kuli A. Po zderzeniu, które było
zderzeniem centralnym i niesprężystym obie kule poruszały się dalej razem. Wyznacz wartość
prędkości z jaką poruszały się zlepione kule. Wynik podaj w [m/s] z dokładnością do pierwszego
miejsca po przecinku. (Odp. 1,6)

Oczywiście zasada zachowania pędu:
m1*v1 – m2*v2 = (m1+m2)*u
18 – 5 = 8*u
13/8 = u
u = 1.625 ~ 1.6m/s

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 10

Człowiek o masie 85kg biegnący naprzeciw wózka z prędkością 5,5km/h wskakuje na wózek

o masie 50kg, jadący z prędkością 4km/h. Ile wynosi wartość prędkości wózka z człowiekiem
bezpośrednio po tym jak człowiek wskoczył na wózek. Wynik podaj w [km/h] z dokładnością do
pierwszego miejsca po przecinku. (Odp. 2,0)

Zapisujemy równanie pędu:
m1*v1 – m2*v2 = (m1+m2)*u
85*5.5 – 50*4 = 135*u
267.5 = 135*u
u = 1.98 ~ 2.0m/s

Zad. 11

Siatkarz o masie 60kg odbijając się od podłogi podskoczył na wysokość 1.1m. Ile wynosiła

średnia wartość siły, jaką w czasie odbicia trwającego 0.5 sekundy działał on na podłogę? Wynik
podaj w N z dokładnością do 1N. (Odp. 1163)

Siła nacisku na podłogę będzie równa sumie sił: ciężkości oraz „siły wybicia”.
N = Q + F

Q = mg = 600N
F = m*(v/t)

Musimy wyznaczyć prędkość wybicia (z zasady zachowania energii):
Ep = Ek
Ep = mgh = 600*1.1 = 660J
660 = Ek
660 = ½ * m * v^2
1320 = 60*v^2
22 = v^2
v = 4.69m/s

F = 60*(4.69/0.5) = 562.8
N = 600 + 562.8 = 1162.8 ~ 1163N

PARĘ SŁÓW NA KONIEC

Powyższe zadania pochodzą z testu przygotowującego do trzeciego kolokwium

(etestu) z Fizyki 1 dla SKP. Nie jestem autorem zadań, ani ilustracji do ich treści. Moje
rozwiązania nie przeszły żadnej korekty błędów (poza sprawdzeniem zgodności z
poprawnymi odpowiedziami), mają służyć celom edukacyjnym ;-) Większość wyników
została zaokrąglona, zgodnie z wymaganiami etestu. W przypadku jakichkolwiek uwag/pytań/
sugestii pisz śmiało na:

[e-mail]

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

FIZYKA

Kolokwium nr 4 (e-test)

Rozwiązał i opracował: Maciej Kujawa, SKP 2008/09

(więcej informacji na końcu dokumentu)

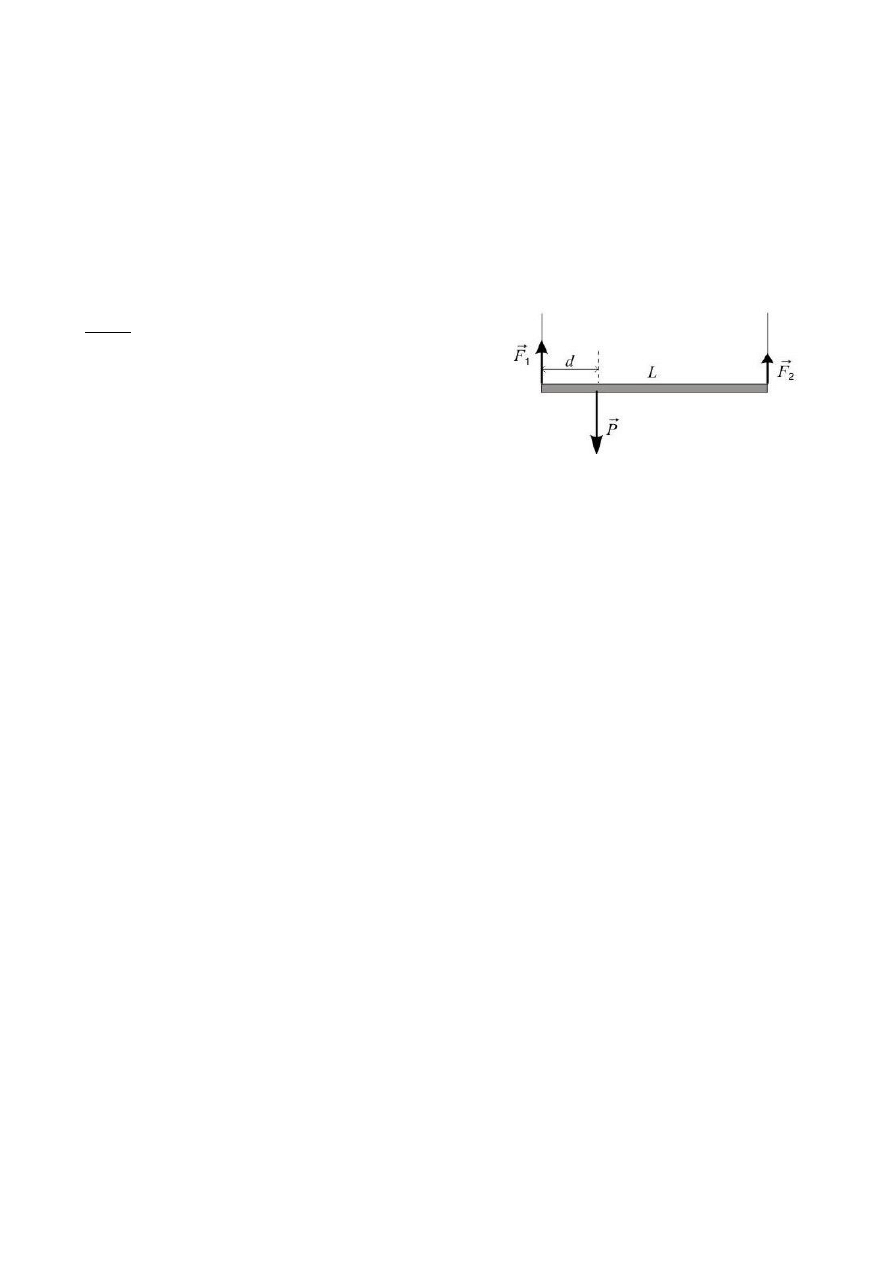
Zad. 1

Pręt jednorodny o długości 1.7m i ciężarze 100N

zawieszono poziomo na dwóch równoległych liniach o
tej samej długości. Do pręta przyczepiono ciężar
P=200N w odległości d=0.65m od jednego z jego
klocków. Ile wynosi wartość naciągu siły F

1

?

(Odp. 174N)

Żeby obliczyć wartość siły F1 skorzystamy z jednego z warunków równowagi: suma
momentów sił (M=r*F) działających na belkę musi być równa zero. Momenty liczymy
względem dowolnie wybranego punktu, ja wybrałem punkt na końcu belki, tam gdzie
zaczepiony jest wektor F2. Na rysunku nie jest zaznaczona siła ciężkości belki Q – jej
moment też musimy uwzględnić. Zapisujemy sumę momentów sił względem wybranego
punktu:

(L-d)*P + (½L)*Q – L*F1 = 0
(L-d)*P + (½L)*Q = L*F1
(1.7-0.65)*200 + 0.85*100 = 1.7*F1
210 + 85 = 1.7*F1
F1 = 173.529 ~ 174N

Uwaga 1: moment siły F2 jest równy zero, ponieważ ramię dla tej siły względem wybranego
przeze mnie punktu jest równe zero (M = r*F2 = 0*F2 = 0).

Uwaga 2: zapisując równanie momentu musimy jeden z kierunków obrotu przyjąć za dodatni.
Przyjąłem, że momenty kręcące belką przeciwnie do ruchu wskazówek zegara są dodatnie.

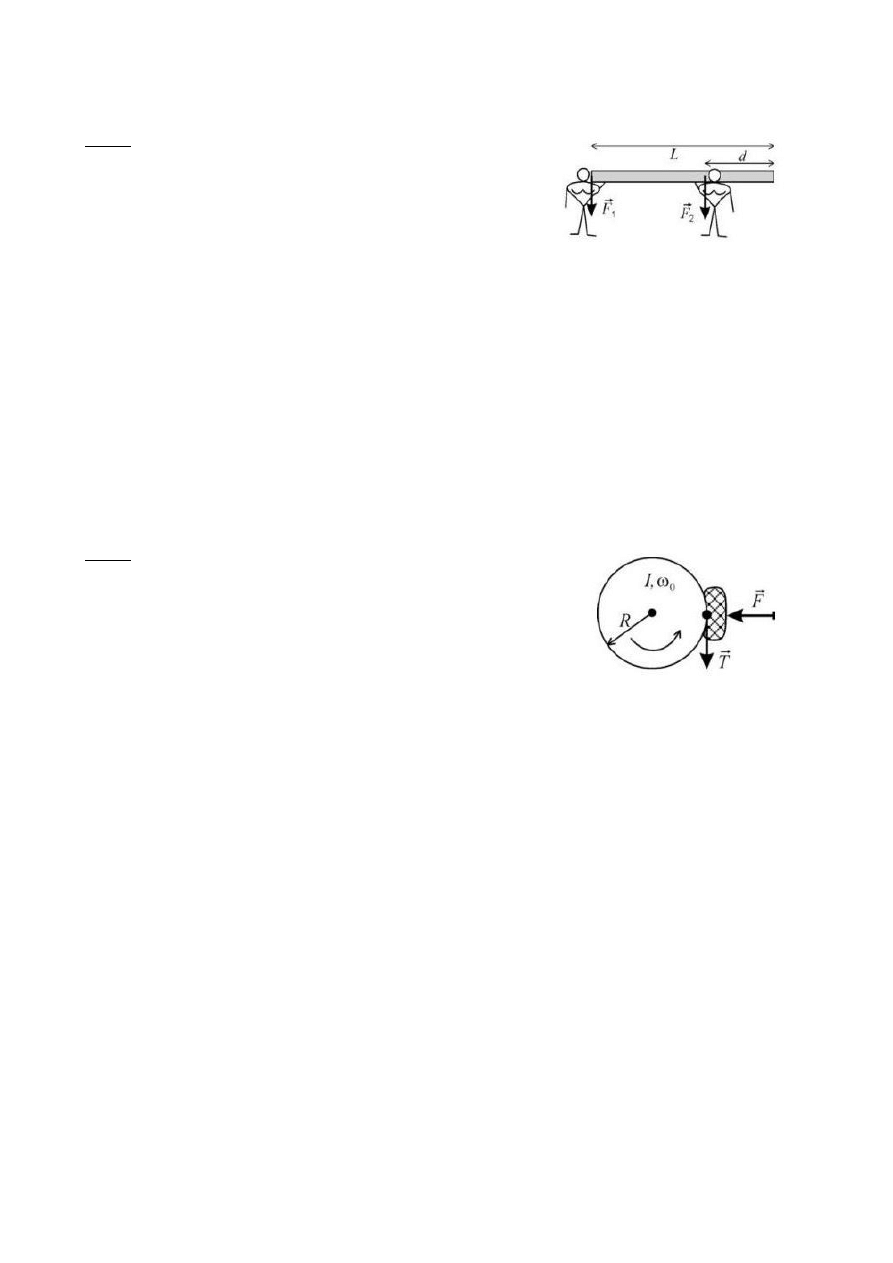
Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 2

Jednorodna metalowa belka o długości 4m i masie 80kg

spoczywa na ramionach dwóch robotników. Punkty podparcia
belki znajdują się: jeden na jednym końcu a drugi w odległości
1.6m od drugiego końca. Ile wynosi wartość siły F

2

działającej

na ramiona drugiego robotnika? (Odp. 667N)

Analogicznie do poprzedniego zadania, zapisujemy równanie momentów sił działających na
belkę, tym razem względem punktu na lewym końcu belki:

-(½L)*Q + (L-d)*R2 = 0
-2*800 + 2.4*R2 = 0
2.4*R2 = 1600
R2 = 666.67 ~ 667N = |F2|

Uwaga: siły F1 i F2 to siły działające na ramiona robotników. Gdy zapisujemy równanie,
interesują nas siły działające na belkę. W tym wypadku będą to reakcje pochodzące od tych
sił: R1 i R2, mające przeciwne zwroty do F1 i F2 (czyli R1 i R2 działają „w górę”).

Zad. 3

Koło rozpędowe o momencie bezwładności I=240kgm

2

i

promieniu R=0.5m wiruje z prędkością kątową w=100s

-1

.

Współczynnik tarcia miedzy klockiem i kołem wynosi 0,5. Ile wynosi
wartość siły

→

F

, jaką należy przycisnąć klocek hamulcowy do

powierzchni aby zatrzymać koło po upływie czasu 17s?
(Odp. 5,6kN)

Obliczamy, jakie przyspieszenie kątowe musi mieć koło, żeby zatrzymało się w 17 sekund:
w = e*t

w – prędkość kątowa, omega

100 = e*17

e – przyspieszenie kątowe, epsylion

e = 5.88

Moment siły tarcia będzie równy:
M = r*T = r*(F*f)

I – moment bezwładności

Zapisujemy też drugi wzór na moment siły tarcia, żeby wykorzystać dany moment bezwładności i
obliczone przyspieszenie kątowe:
M = I*e

Przyrównujemy oba równania i podstawiamy:
r*F*f = I*e
0.5*F*0.5 = 240*5.88
0.25F = 1411.2
F = 5644.8 ~ 5.6kN

Gra? Gra...

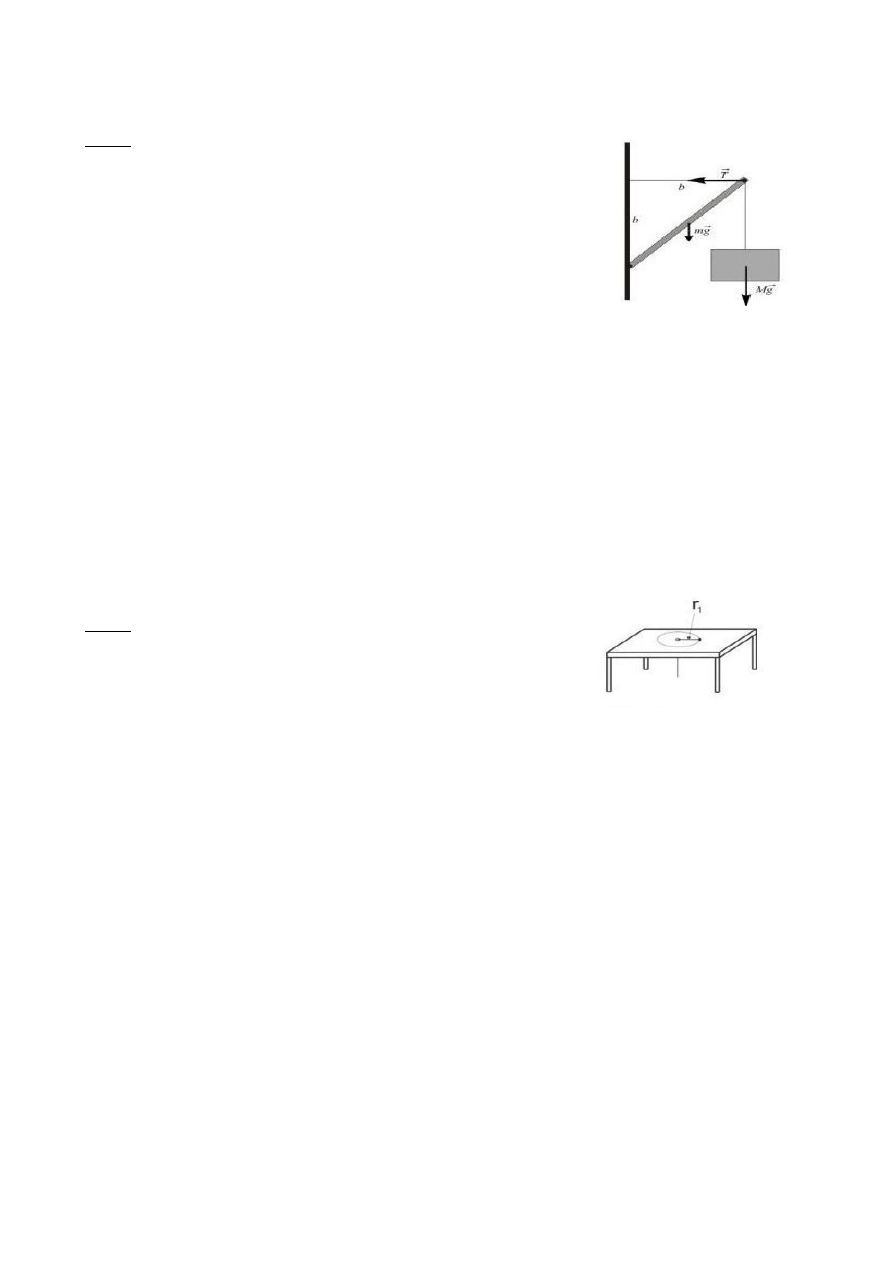
Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 4

Ciężar o masie 50kg zwisa na sznurku z wysięgnika.

Wysięgnik składa się z belki o masie 100kg na zawiasie i poziomej
liny o znikomo małej masie łączącej belkę ze ścianą. Ile wynosi
wartość siły

→

T

naprężenia liny, jeżeli długość odcinka liny b jest

równa odległości pomiędzy punktem jej zamocowania a punktem
podparcia belki. (Odp. 1,00kN)

To zadanie jest bardzo podobne to pierwszego i drugiego, tylko że
siły nie są prostopadłe do ramienia – moment siły jest iloczynem wektorowym, więc musimy
uwzględnić sinus kąta (w tym wypadku wszędzie 45 stopni) między wektorami. Zapisujemy
równanie momentów:

sin45*T – ½*sin45*mg – sin45*500 = 0
0.707*T = 0.3535*1000 + 0.707*500
0.707*T = 353.5 + 353.5
0.707*T = 707
T = 1000N = 1kN

Uwaga: w równaniu nie użyłem nigdzie długości belki, bo po pierwsze nie jest dana, a po drugie i
tak by się skróciła.

Zad. 5

Kulkę o masie 100g leżącą na gładkiej powierzchni stołu

przywiązano do sznurka, którego drugi koniec przeciągnięto przez
mały otwór znajdujący się na stole. Długość części sznurka
znajdującego się na stole wynosi r

1

=20cm. Początkowo kulka

została wprawiona w ruch po kole o promieniu r

1

z prędkością 1.5m/s. Następnie sznurem

pociągnięto w dół, w ten sposób ze na stole została część sznurka o długości r

2

=10cm. Oblicz prace

wykonana przy skracaniu sznurka. (Odp. 0,34J)

Pracę obliczymy wyznaczając zmianę energii kinetycznej kulki. Na początek skorzystamy z zasady
zachowania momentu pędu (L1 = L2), żeby wyznaczyć prędkość kulki po skróceniu sznurka:

L1 = r1*p1 = r1*m*v1 = 0.2*0.1*1.5 = 0.03
L2 = r2*p2 = r2*m*v2 = 0.1*0.1*v2 = 0.01v2
0.01v2 = 0.03

v2 = 3m/s

Zamieniamy prędkości liniowe na kątowe (są potrzebne nam do obliczenia energii kinetycznej):
w1 = v1 / r1 = 1.5/0.2 = 7.5

w2 = v2 / r2 = 3/0.1 = 30

Obliczamy energię początkową i końcową, po skróceniu sznurka:
E1 = (I*w1^2)/2 = (m * r1^2 * w1^2)/2 = (0.1 * 0.2^2 * 7.5^2)/2 = 0.1125J
E2 = (I*w2^2)/2 = (m * r2^2 * w2^2)/2 = (0.1 * 0.1^2 * 30^2)/2 = 0.45J

W = ∆E = 0.45 – 0.1125 = 0.3375 ~ 0.34J

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 6

Człowiek stoi na osi nieruchomego, obrotowego stolika trzymając

pionowo nad głową koło rowerowe o momencie bezwładności I

0

=1.4kgm

2

.

Kolo to obraca się wokół pionowej osi z prędkością kątową w

0

=10

s-1

.

Moment bezwładności człowieka wraz ze stolikiem wynosi I=4kgm

2

. Ile

wynosi prędkość kątowa ruchu obrotowego stolika wraz z człowiekiem, po
tym jak człowiek obrócił wirujące koło o kąt 180*? (Odp. 7,0)

Korzystamy z zasady zachowania momentu pędu. Na początku kręci się
tylko koło rowerowe:
L1 = I

0

*w

0

= 1.4*10 = 14

Po obróceniu koła o 180 stopni zmienia się zwrot wektora momentu pędu tego koła, zaczyna się
kręcić także stolik wraz z człowiekiem:
L2 = -(I

0

*w

0

) + I*w

Porównujemy L1 i L2:
I

0

*w

0

= -(I

0

*w

0

) + I*w

2*I

0

*w

0

= I*w

2*14 = I*w
28 = 4*w
w = 7rad/s

Zad. 7

Walec o masie 9kg i promieniu 0,1m wiruje wokół osi będącej osią symetrii walca pod

wpływem siły 36N przyłożonej do jego powierzchni bocznej. Moment bezwładności walca o masie
m i promieniu r wynosi mr

2

/2. Oblicz przyspieszenie kątowe walca. (Odp. 80)

F = 36N
r = 0.1m

Na walec działa moment siły danej w zadaniu:
M = r*F

Moment ten jest równy także:
M = I*e

e – szukane przyśpieszenie kątowe

Brakuje nam tylko momentu bezwładności:
I = mr^2/2 = 9*0.01/2 = 0.045

Mamy wszystko, przyrównujemy i podstawiamy dane do równania:
r*F = I*e
0.1*36 = 0.045*e
e = 80rad/s^2

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 8

Ile wynosi energia kinetyczna walca o masie 2kg i promieniu 30cm toczącego się bez

poślizgu po poziomej powierzchni z prędkością 3,5m/s? moment bezwładności walca można
wyznaczyć z zależności I

w

=

1

/

2

mR

2

. (Odp. 18J)

Wyraźnie napisano, że walec toczy się – zatem będzie „posiadał” zarówno energię kinetyczną ruchu
postępowego, jak i obrotowego. Musimy obliczyć najpierw moment bezwładności oraz prędkość
kątową walca:

I = ½*m*r^2 = 0.5*2*0.3^2 = 0.09
w = v/r = 3.5/0.3 = 11.67

Ek = E1 + E2 = ½*m*v^2 + ½*I*w^2 = 3.5^2 + 0.5*0.09*11.67^2 = 18.378 ~ 18J

Zad. 9

Na cząstkę działają dwa momenty siły względem początku układu współrzędnych

Nm

i

M

→

→

=

5

.

4

1

i

Nm

j

M

→

→

−

=

5

.

3

2

. Oblicz wartość wypadkowego momentu siły. (Odp. 5,7Nm)

Moment wypadkowy to oczywiście suma momentów. Dodajemy oba wektory:
M1 = [4.5, 0, 0]
M2 = [0, -3.5, 0]
M1+M2 = [4.5, -3.5, 0]

Obliczamy wartość:
|M1+M2| = sqrt(4.5^2 + 3.5^2) = 5.7Nm

Zad. 10

Jeżeli moment bezwładności względem osi obrotu koła zamachowego wykonującego

8 obrotów na sekundę wynosi 36kgm

2

, to ile wynosi energia kinetyczna koła? (Odp. 45kJ)

Obliczamy prędkość kątową:
w = (2*pi*n)/T = (2*pi*8)/1 = 50.264

Obliczamy energię kinetyczną kręcącego się koła:
Ek = ½*I*w^2 = 0.5*36*50.264^2 = 45476.45J ~ 45kJ

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 11

Jednorodny walec o masie 50kg i promieniu 0,1m stacza się z równi pochyłej nachylonej

pod kątem 30* do poziomu. Początkowo na szczycie równi – na wysokości 1.5m walec był
nieruchomy. Moment bezwładności walca względem osi symetrii można wyliczyć ze wzoru
I

w

=

1

/

2

mR

2

, m - masa walca, R – promień. Ile wynosi prędkość walca (tj. jego środka masy) na dole

równi? (Odp. 4,5m/s)

Korzystamy z zasady zachowania energii. Na szczycie równi:
E = mgh = 50*10*1.5 = 750J

Obliczamy moment bezwładności walca:
I = ½*m*r^2 = 0.25

Na dole równi walec będzie „posiadał” energię kinetyczną ruchu postępowego oraz obrotowego:
750 = ½*m*v^2 + ½*I*w^2 = ½*m*v^2 + ½*I*(v/r)^2
750 = 25*v^2 + 0.5*0.25*(v/0.1)^2
750 = 25v^2 + 0.125*(v^2/0.01)
750 = 25v^2 + 12.5v^2
750 = 37.5v^2
v = 4.47 ~ 4.5m/s

Uwaga: we wzorze na energię kinetyczną ruchu obrotowego zastąpiłem prędkość kątową („w”)
wyrażeniem v/r, ponieważ interesowała nas prędkość liniowa.

Zad. 12

Do obwodu koła rowerowego o masie 2kg przyłożono stała siłę styczną 17N i wprawiono je

w ruch obrotowy wokół nieruchomej osi. Koło rowerowe należy rozpatrywać jako cienkościenną
obręcz o momencie bezwładności mR

2

, gdzie m – masa obręczy, R – jej promień. Jaką energię

kinetyczną uzyskało koło po upływie 14s od rozpoczęcia działania siły? (Odp. 14,2kJ)

Wzór na energię kinetyczną ruchu obrotowego:
E = ½*I*w^2

Wyznaczamy moment bezwładności:
I = m*r^2 = 2*r^2

Brakuje nam prędkości/przyspieszenia kątowego. Skorzystamy ze wzoru na moment siły:
M = I*e = r*F

Obliczamy energię koła:

Podstawiamy:

Ek = ½*I*w^2

r*F = I*e

Ek = ½*(2*r^2)*(8.5/r *t)^2

r*17 = (2*r^2)*e

Ek = ½*2*r^2*(72.25/r^2)*t^2

17 = 2*r*e

Ek = 72.25*t^2

e = 8.5/r

Ek = 72.25*14^2 = 14161
Ek ~ 14.2kJ

Zatem prędkość kątowa jest równa:
w = e*t = (8.5/r)*t

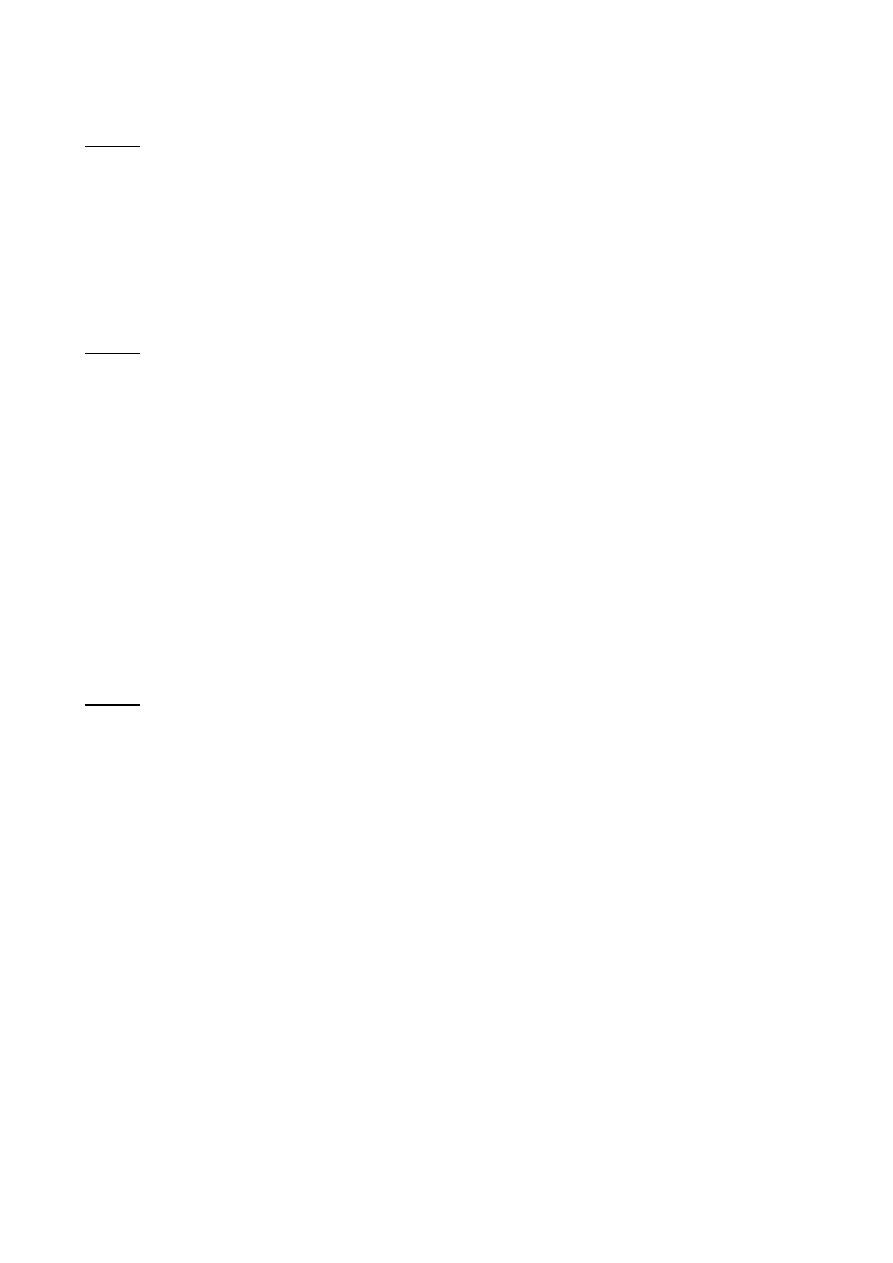
Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 14

Stosunek największej do najmniejszej odległości pewnej komety od słońca jest równy 40.

Jeżeli prędkość liniowa ruchu komety w punkcie najbardziej odległym od słońca wynosi 1,3km/s to
ile wynosi w punkcie, gdy kometa jest najbliżej słońca? (Odp. 52km/s)

Układamy proporcję:
1/40 = 1.3/x
x = 1.3*40 = 52km/s

Zad. 15

Pozioma tarcza o momencie bezwładności 20kgm

2

i promieniu 1m może obracać się

względem pionowej osi przechodzącej przez jej środek. Na brzegu tarczy stoi człowiek o masie
90kg. Ile wynosi prędkość kątowa tarczy, gdy człowiek zacznie się poruszać wzdłuż jej brzegu z
prędkością 2.2m/s względem ziemi? (Odp. 9,9)

Korzystamy z zasady zachowania momentu pędu. Początkowy pęd układu wynosi 0:
0 = I*w – r*p

L = I*w = r*p

0 = I*w – r*m*v
0 = 20*w – 1*90*2.2
90*2.2 = 20*w
w = 9.9rad/s

Uwaga: moment pędu człowieka zapisałem w równaniu z minusem, ponieważ ma on przeciwny
zwrot do momentu pędu tarczy (kręci się w drugą stronę).

Zad. 16

Cienkościenna obręcz o masie 1kg promieniu 0,5m toczy się bez poślizgu z prędkością 4m/s.

ile wynosi energia kinetyczna toczącej się obręczy? (Odp. 16,0J)

Obliczamy moment bezwładności obręczy (ten wzór wypada znać, bo wprost wynika z definicji):
I = m*r^2 = 0.25

Obliczamy prędkość kątową:
w = v/r = 4/0.5 = 8

Szukana energia będzie sumą energii kinetycznej ruchu obrotowego i postępowego:
E1 = ½*I*w^2 = 0.5*0.25*64 = 8
E2 = ½*m*v^2 = 0.5*4^2 = 8

E = 8+8 = 16J

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 17

Koło zamachowe wirujące z prędkością 220obr/min zatrzymuje się w czasie 36s.

przyjmując, ze ruch jest jednostajnie zmienny oblicz ilość obrotów do momentu zatrzymania.
(Odp. 66)

Obliczamy prędkość kątową koła:
w = (2*pi*n)/T = (2*pi*220)/60 = 23rad/s

Obliczamy przyspieszenie kątowe koła:
e = w/t = 23/36 = 0.64rad/s^2

Ilość obrotów (n) można powiązać z drogą, jaką przebędzie punkt na obwodzie tego koła:
s = 2*pi*r*n

Wyznaczamy przyspieszenie liniowe tego punktu:
a = e*r = 0.64*r

Podstawiamy do wzoru na drogę:
s = ½*a*t^2
2*pi*r*n = ½*0.64*r*36^2
2*pi*n = ½*0.64*36^2
6.283*n = 414.72
n = 66

Zad. 18

Rakieta startuje z przyspieszeniem 4razy większym niż przyspieszenie ziemskie. Ile wynosi

siła z jaka człowiek o masie 80kg działa na podłoże we wnętrzu rakiety? (Odp. 4000N)

a = 4*g = 40m/s^2

Nacisk na podłoże będzie równy sumie siły bezwładności oraz siły ciężkości człowieka:
N = F+Q = m*a + m*g = 80*40 + 80*10 = 3200 + 800 = 4000N

Zad. 19

Poziomo ułożony pręt wiruje wokół prostopadłej do ziemi osi przechodzącej przez jego

środek. Pręt jest jednorodny, a jego m=3kg. Na końcu pręta siedzi małpka o masie 2kg. Moment
bezwładności ze wzoru Ip=1/12*mL^2. Pręt ma długość 2m i wiruje z prędkością kątową 3,5rad/s.
Ile wynosi prędkość kątowa pręta po przejściu małpki z końca pręta do jego środka? (Odp. 10,5)

Ip – moment bezwładności pręta,

Im – moment bezwładności małpki,

m – masa pręta,

M – masa małpki,

Ip = 1/12*mL^2 = 1/12*12 = 1

Im = M*r^2 = 2

Zasada zachowania momentu pędu. Obliczamy początkowy oraz końcowy moment pędu:
L1 = (Ip+Im)*w1 = 3*3.5 = 10.5
L2 = Ip*w2 = w2

Uwaga: moment pędu małpki równy zero, ponieważ jej r=0!

L1 = L2
w2 = 10.5rad/s

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 20

Dwie poziome tarcze wirują wokół wspólnej, pionowej osi przechodzącej przez ich środek.

Momenty bezwładności tarcz wynoszą I

1

=1,4kgm

2

oraz I

2

=1kgm

2

a ich prędkości kątowe

odpowiednio w

1

=2rad/s oraz w

2

=4rad/s. po upadku tarczy górnej na dolną, obie tarcze (w wyniku

działania sił tarcia) obracają się dalej jak jedno ciało. Oblicz prędkość kątową tarcz po złączeniu.
(Odp. 2,8)

Zasada zachowania momentu pędu:
L1 = I1*w1 + I2*w2 = 1.4*2 + 1*4 = 6.8
L2 = (I1+I2)*w = 2.4*w
L1 = L2
6.8 = 2.4*w
w = 2.83 ~ 2.8rad/s

Zad. 21

Koło o momencie bezwładności 2,8kgm

2

obraca się z prędkością kątowa 3rad/s. Jaka pracę

wykonała siła rozpędzającą koło do prędkości 7rad/s. (Odp. 56,0J)

Wartość wykonanej pracy wyznaczymy poprzez obliczenie przyrostu energii kinetycznej:
W = E2 – E1
E1 = ½*I*w1^2 = ½*2.8*3^2 = 12.6J
E2 = ½*I*w2^2 = ½*2.8*7^2 = 68.6J
W = 68.6 – 12.6 = 56J

Zad. 22

Beton ma gęstość 1,9g/cm

3

a jego naprężenie niszczące wynosi 4*10

6

N/m

2

. Wyznacz jaka

może być maksymalna wysokość słupa o polu podstawy 0,5m

2

żeby nie zawalił się pod własnym

ciężarem. (Odp. 210,5m)

d = 1.9g/cm^3 = 0.0019kg/cm^3 = 1900kg/m^3
p = 4*10^6 = F/S

Siła, która będzie działała na słup to siła ciężkości, wykorzystujemy gęstość:
F = m*g = d*V*g = d*S*h*g

m = d*V

V = S*h

p = d*S*h*g/S = d*h*g
4*10^6 = d*h*g
4*10^5 = d*h
4*10^5 = 1900*h
h = 210.5m

Zad. 23

Ile wynosi moment bezwładności punktowego ciała o masie 4kg poruszającego się z

prędkością kątową 3rad/s po okręgu o promieniu 3,5m? (Odp. 49Kgm

2

)

I = m*r^2 = 4*3.5^2 = 49

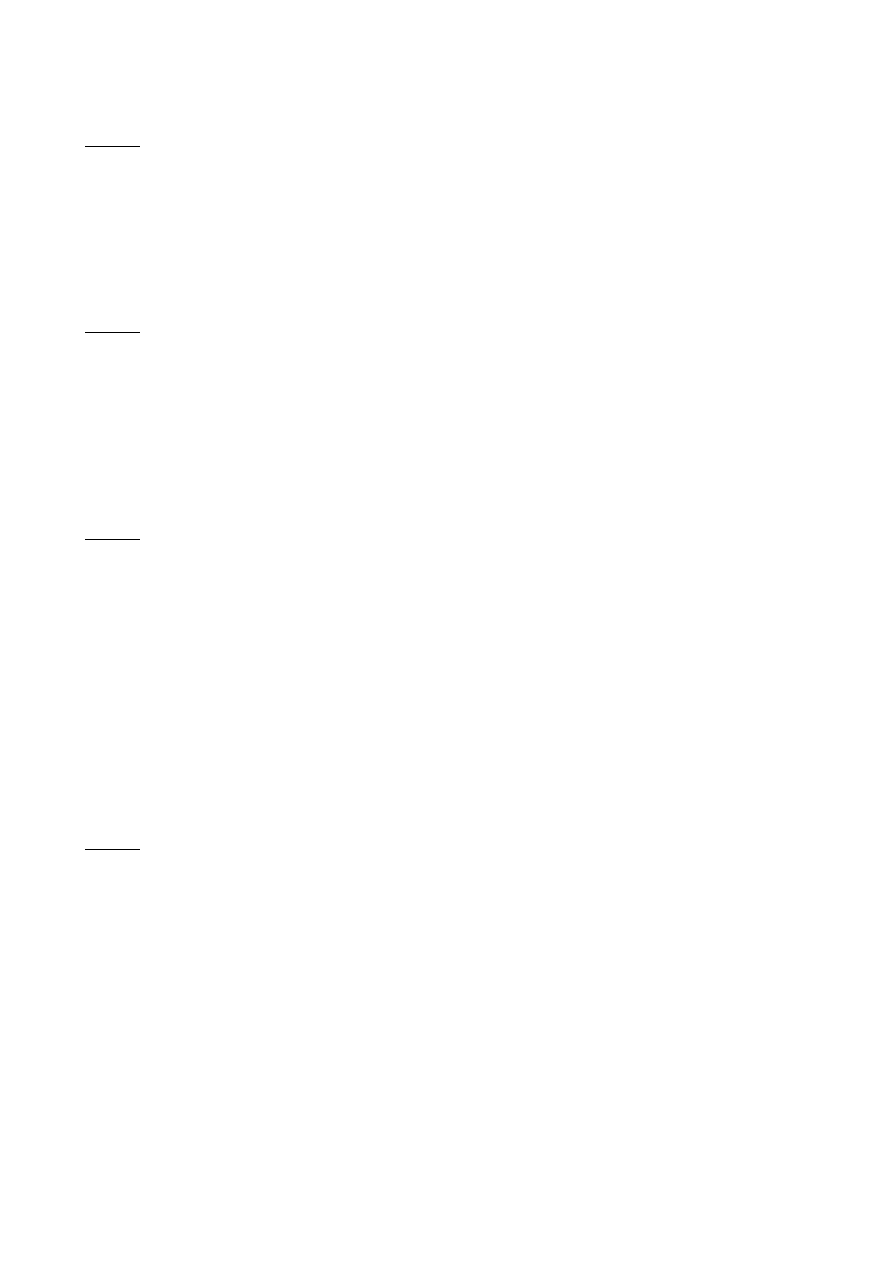
Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 24

Ciało leży na powierzchni ziemi. Oblicz ile wynosi masa ciała o ciężarze 78N. Pomiń siły

wyporu powietrza. (Odp. 7,8kg)

Q = m*g
78 = m*10
m = 7.8kg (trudne)

Zad. 25

Bęben pralki automatycznej o średnicy 0,5m osiąga maksymalna prędkość kątową

850obr/min po 30s. od rozpoczęcia obrotów. Ile wynosi w tym momencie przyspieszenie
dośrodkowe punktów znajdujących się na powierzchni bębna? (Odp. 1981m/s^2)

2r = 0.5m → r = 0.25m
w = (2*pi*n)/T = (2*pi*850)/60 = 89.009
a = w^2*r = 1980.65 ~ 1981m/s^2

Zad. 26

Bęben pralki automatycznej o średnicy 0.5m osiąga maksymalna prędkość kątową

1180obr/ min w czasie 30s. Ile wynosi okres obrotu bębna po 30s. (Odp. 0,051s)

w = (2*pi*n)/T = (2*3.1415*1180)/60 = 123.57
T = (2*pi)/w = 0.0508 ~ 0.051s

Lub inaczej. Skoro pralka ma prędkość 1180 obrotów na minutę, a nas interesuje czas jednego
obrotu, to można ułożyć proporcję:

1180 – 60
1 – T
T = 60/1180

Zad. 27

Jednorodny walec o masie 120kg i promieniu 0,2m obraca się jednostajne dookoła swej osi

symetrii z prędkością kątową 3rad/s. Moment bezwładności walca względem osi symetrii można
wyliczyć ze wzoru I

w

=

1

/

2

mR

2

, m-masa walca, R – promień. Ile wynosi energia kinetyczna

obracającego się walca? (Odp. 10,8J)

I = ½m*R^2 = 0.5*120*0.04 = 2.4
E = ½*I*w^2 = ½*2.4*9 = 10.8J

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 29

Bryła sztywna wiruje wokół stałej osi ze stała prędkością kątową. Względem tej osi moment

pędu wynosi 14kgm/s a moment bezwładności 0,36kgm

2

. Ile wynosi okres obrotu tego ruchu?

(Odp. 0,162s)

L = I*w
14 = 0.36*w
w = 38.89

w = 2*pi*1/T → T = 2*pi*1/w
T = 6.283*1/38.89 = 0.161558 ~ 0.162s

Zad. 30

Koło zamachowe wykonuje początkowo 6 obrotów na sekundę. Po przyłożeniu stałego

momentu hamującego to zatrzymuje się po 7s. Ile wynosi wartość bezwzględna opóźnienia
kątowego w tym ruchu? (Odp. 5,4)

w = 2*pi*n = 12*pi = 37.698
e = w/t = 37.698/7 = 5.385 ~ 5.4rad/s^2

Zad. 31

Jednorodny walec o masie 90kg i promieniu 0,2m obraca się jednostajne dookoła swej osi

symetrii z prędkością kątową 3.8rad/s. Moment bezwładności walca względem osi symetrii można
wyliczyć ze wzoru I

w

=

1

/

2

mR

2

, m-masa walca, R – promień. Jaką wartość ma moment stałej siły

zatrzymującej walec w czasie 5s? (Odp. 1,37Nm)

M = I*e

I = ½*m*R^2 = 45*0.04 = 1.8
e = w/t = 3.8/5 = 0.76

M = 1.8*0.76 = 1.368 ~ 1.37Nm

Zad. 32

Przyłożenie siły o wartości 10kN spowodowało wydłużenie pręta o 4,5cm. Ile wynosi

całkowite wydłużenie pręta jeżeli zwiększymy siłę o kolejne 5kN? (Odp. 6,8cm)

F1 = 10kN

ΔL1 = 4.5cm

F2 = 15kN

ΔL2 = ?

Układamy proporcję:
10/4.5 = 15/ΔL2
ΔL2 = 67.5/10 = 6.75 ~ 6.8

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 33

Metalowy pręt o przekroju kwadratu o boku 2,6cm rozciągany jest siła 35kN. Wyznacz

naprężenie pręta. (Odp. 5,2kN/cm

2

)

P = F/S
S = 2.6^2 = 6.76cm^2
P = 35/6.76 = 5.17 ~ 5.2kN/cm^2

Zad. 34

Rower o kolach o średnicy 50cm jedzie z prędkością 10m/s. Ile obrotów na sekundę

wykonują koła tego roweru? (Odp. 6,4)

r = 0.25m

w = v/r = 10/0.25 = 40rad/s
w = (2*pi*n)/T
40 = 2*pi*n
40 = 6.283*n
n = 6.366 ~ 6.4obr/s

Zad. 35

Pionowy słup o wysokości 10m i masie 120kg po podpiłowaniu przy podstawie pada na

ziemię. Wiedząc, że moment bezwładności słupa o masie m i długości L względem osi przechodzącej
przez jego koniec jest równy mL

2

/3, oblicz liniową prędkość górnego końca słupa w chwili

uderzania o ziemię. (Odp. 17,3m/s)

Obliczamy, jaką energią potencjalną ma słup: liczymy ją dla jego środka masy, czyli h = ½*L:
E = mgh = 120*10*5 = 6000J

W chwili uderzenia o ziemię, cała energia słupa będzie energią kinetyczną ruchu obrotowego.
Obliczamy moment bezwładności:

I = (mL^2)/3 = 120*100*1/3 = 12000*1/3 = 4000kgm^2
E = ½*I*w^2
6000 = ½*4000*w^2
6000 = 2000*w^2
w = 1.73

Obliczamy prędkość liniową (r = L):
v = w*r = 1.73*10 = 17.3m/s

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 36

Cząstka o masie 0,9kg porusza się po okręgu o promieniu 2,8m z prędkością kątową 2rad/s.

Do jakiej prędkości kątowej przyśpieszyła ją siła, która wykonała nad tą cząstką pracę 24J?
(Odp. 3,3rad/s)

Obliczamy energię początkową cząstki:
E1 = ½*I*w^2 = ½*0.9*2.8^2*4 = 14.112J

I = m*r^2

Nad cząstką wykonano pracę 24J, a więc jej energia zwiększy się o tą wartość:
E2 = 14.112+24 = 38.112J

Podstawiamy do równania na energię i wyznaczamy prędkość kątową:
E2 = ½*I*w^2
38.112 = ½*m*r^2*w^2
38.112 = 0.5*0.9*2.8^2*w^2
38.112 = 3.528*w^2
w = 3.2867 ~ 3.3rad/s

Zad. 37

Poziomy stolik obraca się z prędkością kątową 3,6s

-1

. Na środku stolika stoi człowiek i

trzyma w wyciągniętych rekach w odległości 0,8m od osi obrotu dwa ciężarki o masie 1,8kg każdy.
Moment bezwładności stolika wraz z człowiekiem (bez ciężarków) wynosi 4kgm

2

. Ile wynosi

prędkość kątowa obrotów stolika gdy człowiek opuścił ręce? Przyjmij, że wówczas ciężarki
znajdują się na osi obrotu. (Odp. 5,7)

Zasada zachowania momentu pędu. Zapisujemy początkowy moment pędu układu:
L1 = (Istolika_z_człowiekiem + Iciężarków)*w
L1 = (4 + 2*m*r^2)*3.6
L1 = (4 + 2*1.8*0.8^2)*3.6 = 22.6944

Gdy człowiek opuści ręce, ciężarki znajdą się na osi obrotu, czyli ich r = 0, więc ich moment pędu
również jest równy zero:
L2 = Istolika_z_człowiekiem*w2 = 22.6944
4*w2 = 22.6944
w = 5.6736 ~ 5.7rad/s

Zad. 38

Podczas obicia się skoczka od trampoliny prędkość kątowa jego obrotu wokół jego środka

masy wzrasta od 0 do 3,6rad/s w czasie 0,2s. Moment bezwładności względem jego środka masy
wynosi 9kgm

2

. Ile wynosi wartość średniego momentu siły, działającego na skoczka ze strony

trampoliny? (Odp. 162Nm)

M = I*e

← brakuje nam przyspieszenia kątowego, moment bezwładności jest dany w zadaniu

Δw = 3.6
e = Δw/t = 3.6/0.2 = 18
M = 9*18 = 162Nm

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

Zad. 39

Moment siły o wartości 36Nm nadaje kołu o średnicy 80cm obracającemu się dookoła osi

przechodzącej przez jego środek przyśpieszenie kątowe 4,4rad/s

2

. Ile wynosi moment bezwładności

koła? (Odp. 8,2kgm

2

)

M = I*e
36 = I*4.4
I = 8.18 ~ 8.2kgm^2

Zad. 40

Koło zamachowe o promieniu 0,5m i momencie bezwładności 280kgm

2

wiruje z prędkością

kątowa 24

s-1

. ile wynosi wartość bezwzględna pracy jaką należy wykonać, aby zatrzymać koło

zamachowe w czasie 10s? (Odp. 81kJ)

Wartość tej pracy będzie równa całkowitej energii koła:
E = ½*I*w^2 = 0.5*280*24^2 = 80640 ~ 81kJ

PARĘ SŁÓW NA KONIEC

Powyższe zadania pochodzą z testu przygotowującego do czwartego kolokwium

(etestu) z Fizyki 1 dla SKP. Nie jestem autorem zadań, ani ilustracji do ich treści. Moje
rozwiązania nie przeszły żadnej korekty błędów (poza sprawdzeniem zgodności z
poprawnymi odpowiedziami), mają służyć celom edukacyjnym ;-) Większość wyników
została zaokrąglona, zgodnie z wymaganiami etestu. W przypadku jakichkolwiek uwag/pytań/
sugestii pisz śmiało na:

[e-mail]

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

Zad. 1

Jakiej temperaturze w skali Celsjusza odpowiada temperatura 336.15 K? (Odp. 63)

Wzór na zamianę stopni w Celsjuszach na Kelwiny:

T = t + 273.15 K

t = T – 273.15 K

t = 336.15 – 273.15

t = 63

Zad. 2

W szklanej rurce wygiętej w kształt litery U znajdują sie dwie niemieszające sie ciecze. Gęstość cięższej z cieczy wynosi
13.6 *10^3 kg/m^3, natomiast wysokość słupa cieczy h1= 2.8 cm, natomiast wysokość słupa lżejszej cieczy z prawej
strony rurki h2= 28cm. Ile wynosi gęstość lżejszej cieczy? (Odp. 1.36)

Układamy równanie:
g1*h1= g2*h2
2.8*13.6 = 28*g2

// nie ma potrzeby mnożenia, gdyż mamy podać wynik w gramach

g2=(2.8*13.6)/28
g2=1.36

Zad. 3

Ciało o masie 7kg wykonuje drgania harmoniczne wzdłuż osi OX. Zmiana położenia odbywa sie zgodnie z równaniem
x=0.3cos(5t+pi), gdzie położenie podane jest w metrach, masa w kg zaś czas w sekundach. Ile wynosi maksymalna
siła działająca na cząstkę? Wynik podaj w N z dokładnością do pierwszego miejsca po przecinku. (Odp. 52.5)

7kg * 5^2 * 0,3 = 52.5

Zad. 4

Ogrzewając kawałek metalu o masie 0.22 *10K dostarczono ciepła w ilości 740J. Ile wynosi ciepło właściwe tego
metalu? Wynik podaj w J/kgK z dokładnością do jedności. (Odp. 336)

740/(0.22kg* 10K)=336,36

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

Zad. 5

Pręt metalowy podgrzano tak, ze jego długość zwiększyła się o 0.3%. O ile zwiększyła sie w wyniku tego podgrzania
objętość pręta? Podaj wynik w % z dokładnością do 2 miejsca po przecinku. (Odp. 0.90)

0.3^2 *10 =0,9

Zad. 6

Do menzurki nasypano pewną ilość śrutu. Tak przygotowana pływa po wodzie o gęstości 1g/cm^3 zanurzona na
głębokość 4.5 cm. Na jaką głębokość zanurzy sie tak przygotowana menzurka w cieczy o gęstości 1.15 cm/cm^3??
Podaj wynik z dokładnością do 1 miejsca po przecinku. (Odp. 3.9)

(Głębokosc1* gęstość wody)/gęstość cieczy = głębokość2, czyli:

(4.5 *1)/1.15 = 3.91

Zad. 7

Cząstka o masie 0.1 kg wykonuje drgania harmoniczne wzdłuż osi OX. Zmiana położenia odbywa sie zgodnie z
równaniem (zależnością) x=0.5 cos(7t), gdzie położenie podane jest w metrach, a czas w sekundach. Ile wynosi
maksymalna prędkość cząstki? (Odp. Nie sprawdzona)

O,5 * (7t)' =0.5*7 = 3.5

Zad. 8

Piłka plażowa ma objętość 0.055m^3, wrzucona do wody (gęstość wody wynosi 10^3kg/m^3) pływa praktycznie
całkowicie wynurzona. Jakiej wartości siłą należy zadziałać, aby zanurzyć ją do połowy? Wynik podaj w [N] z
dokładnością do jedności. (Odp. 275)

Fwyp = ro*g*V
Fwyp = 10^3 * 10 * 0.055
Fwyp = 550

Na chłopski rozum aby piłka zanurzyła się do połowy musimy zadziałać siłą która na zredukuje tą wyporu o połowę.
Czyli:
550/2 = 275

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

Zad. 9

Nurek znajduje się w zbiorniku wodnym o głębokości 7m. Gęstość wody wynosi 10^3kg/m^3 a ciśnienie
atmosferyczne 1000hPa. Ile razy ciśnienie (calkowite) działające na tego nurka jest większe od ciśnienia
atmosferycznego? (Odp. 1.7)

P = ro*g*h
P = 10*7*10^3
P = 70000

Pcałkowite = Patmosferyczne + Phydrostatyczne
Pcałkowite = 100000+70000
Pcalkowite = 170000
Pcalkowite / Patmosferyczne = 170000/100000 = 1.7

Zad. 10

Na doskonale gładkim stole leży klocek o masie masie 1.4 kg. Klocek przymocowany jest do ściany za pomocą
sprężyny o współczynniku sprężystości 500N/m i zaniedbywalnie malej masie. W klocek ten uderza lecący poziomo
pocisk i grzęźnie w nim. Prędkość pocisku przed zdarzeniem wynosi 50m/s, a jego masa 0.1 kg. Po zdarzeniu klocek
wraz z uwięzionym w nim pociskiem wykonuje drgania harmoniczne. Jaka jest energia całkowita tych drgan? Wynik
podaj w J z dokładnością do pierwszego miejsca po przecinku. (Odp. 8.3)

Dane:
m1=1.4 kg
m2=0.1 kg
v pocisku= 50 m/s
współczynnik sprężystości nie jest potrzebny do zadania.

Wzorek jest taki:
Ek = [(m1+m2)*Vx^2]/2
Vx = (m2*v) / (m1+m2)

Po podstawieniu:

Vx = (0.1*50)/1,4+0,1
Vx = 5/1.5

Podstawiamy Vx do wzorku na Ek:
Ek= [(m1+m2)*vx^2]/2
Ek= [(1.4+0.1)*(5/1.5)^2]/2

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

Ek=(1.5*11.111)/2
Ek=8.33

Zad. 11

Wewnątrz cylindra znajduje się nieściśliwa ciecz. Na tłok cylindra położono masę 80kg. Pole powierzchni tłoka wynosi
0.1 m^2, ciśnienie atmosferyczne wynosi 1000hpa. Ile wynosi ciśnienie p na głębokości 3m (patrz rysunek (tu ni ma
rysunku :P)). Gęstość cieczy 1*10^3kg/m3. Wynik podaj w hpa z dokładnością do jedności. (Odp. 1380)

Liczymy ciśnienie hydrostatyczne:
Głębokość *10^4= 3*10000= 30000

Pa = 300hPa
Ciśnienie atmosferyczne = 1000 hPa

Trzeba też dodać ciśnienie od tłoka:

p = F/S

p = 80*10 / 0.1

p = 8000 Pa

p = 80 Hpa

1000 + 300 + 80 = 1380

Zad. 12

Na sprężynie zawieszono ciężarek o masie 0.55kg. Siła, którą rozciągnięto sprężynę o 0.4m, ma wartość 10N. Ile
wynosi, po ustaleniu siły, częstotliwość drgań tego ciężarka? Podaj wynik w Hz z dokładnością do pierwszego miejsca
po przecinku. (Odp. 1.1)

m = 0.55 kg
delta l = 0.4m
Fs = 10N

f = 1/T
w = sqrt (k/m)
Fs = k*x
k = Fs/x

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

K = 10N/0.25 = 25 N/m

Podstawiamy do wzorku
w = sqrt(k/m)=2 * pi/T

Szukamy T więc:
T = w/2pi
T=[sqrt(25/0.56)] / 6.283
T = sqrt(44.642)/6.283=6.6815/6.283
T = 1.063 ~ 1.1

Zad. 13

Klocek o masie 0.7 kg przyczepiony do ściany za pomocą sprężyny (patrz rys) ślizga się po idealnie płaskim stole od
punktu x1=10cm do punktu x2=50cm wykonując drgania harmoniczne. Czas potrzebny na przemieszczenie sie klocka
pomiędzy tymi punktami wynosi 0.6 sekundy. Wyznacz stałą sprężystość sprężyny. Wynik podaj w N/m z
dokładnością do pierwszego miejsca po przecinku. (Odp. 19.2)

m=0.7 kg
deltax=50cm-10cm=40cm (jak sie okaze nie bedzie do niczego potrzebna ;P)
t=0.6s

(w jedną str. 0.6 sekundy, wiec w dwie trwa to 1.2 s, wiec okres wynosi 1.2)

T=1.2

sqrt(k/m)=2 * pi/T
k/m=4pi^2/T^2

Szukamy stałej sprężystości, czyli 'k'. Mnożymy stronami przez 'm' i mamy:
k=(4pi^2*m)/T^2
k=(4*3.1415^2*0.7)/1.2^2
K=27,633/1.44=19.189
k~19.2

Zad. 14

Do naczynia z wodą wrzucono kamień o masie 5kg i gęstości 5.4g/cm^3. Ile wynosi siła wyporu działająca na kamień
(gęstość wody jest równa 10^3kg/m^3)? Wynik podaj w N z dokładnością do pierwszego miejsca po przecinku.

(Odp. 9.3)

m = 5kg
ro = 5.4 g/cm^3

F wyporu = ro*v*g

v = m/ro
v = 5/5.4 = 0.9259

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

FW = 0.9259* 10
Fw=9.259
Fw~9.3

Zad. 15
Klocek przyczepiony do ściany za pomocą sprężyny ślizga się po idealnie gładkim stole od punktu x1=10cm do pkt
x2=42 cm wykonując drgania harmoniczne. Wyznacz amplitudę. (Odp. 16)

Klocek pokonuje = 42cm-10cm = 32 cm.
Amplituda = 32/2=16.

Zad. 16

Podnośnik hydrauliczny składa się z dwóch tłoków. Powierzchnia tłoków wynosi odpowiednio s1= 40cm^2 i
s2=180cm^2 (patrz rysunek) ;P Pomiędzy tłokami znajduje się nieściśliwa ciecz. Aby podnieść masę 100kg, która leży
na tłoku o powierzchni s2 należy do tłoka o powierzchni s1 przyłożyć siłę F o przekraczającej wartości Fkr. Ile wynosi
Fkr? Wynik podaj do 1N.

Fkr = s1/s2*(mg)
Fkr = 40/180*1000
Fkr = 222

Zad. 17
Ile wynosi ciśnienie słupa wody o gęstości 10^3 kg/m3 i wysokości 4m^2? Podaj w kpa z dokładnością do jedności.
(Odp. 40)
P = ro*h*g
P = 1000*4*10
P = 40000 Pa
P = 40Kph

Zad. 18
Jednorodne ciało wazy w powietrzu 18N. To samo ciało całkowicie zanurzone w wodzie o gęstości 10^3 cm/m3 waży
14N. Oblicz gęstość tego ciała. Wynik podaj w cm^3 z dokładnością do jedności. (Odp. 400)

Fw-sila wyporu
Fw=ro*h*g
Fw=18N-14N=4N
4=10*1000*V
V=4/(10*1000)= 0.0004 m^3=400cm^3

Zad. 20
Na sprężynie o współczynniku sprężystości 500N/m wisi szalka o masie 0.5 kg. O ile wydłuży się sprężyna po
położeniu na szalce odważnika o masie 3kg? Podaj w cm z dokładnością do jedności. (Odp. 6)

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

F=k*x, gdzie
F=30N (masa odważnika*g)
k- współczynnik sprężystości
x-wydłużenie sprężyny

Podstawiamy do wzoru i otrzymujemy:
30N=500*x
x=30/500
x=0.06m
x=6 cm.

Zad. 21
Amplituda drgań wahadła matematycznego w czasie 50s zmalała o 11 razy. Oblicz współczynnik tłumienia drgań.
Podaj wynik w 1/s z dokładnością do 3 miejsc po przecinku. (Odp. 0.048)

Współczynnik tłumienia = ln11/50 = 0.0479 ~ 0.048

gdzie ln to logarytm naturalny.

Zad. 22
Zależność prędkości szczoteczki zamontowanej w elektrycznej szczoteczce di zębów zadaje w układzie jednostek SI
funkcja v(X)=11cos(80t). Ile wynosi amplituda ruchu harmonicznego szczoteczki? Podaj z dokładnością do 2 miejsca
po przecinku. (Odp. 0.14)

w - prędkość kątowa = 80
A - amplituda
11 przy cos – kto to tam wie 

11=w*A
A=11/80
A=0.1375
A~0.14

Zad. 23

Ciało o masie 20g drga harmonicznie z okresem (pi/50)s. Amplituda tych drgań wynosi 1 cm. Ile wynosi największa
wartość siły działającej na to ciało? Wynik podaj w N z dokładnością do 1 miejsca po przecinku. (Odp. 2.0)

k - stała sprężystości
x - maksymalne wychylenie
F - siła

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

sqrt(k/m) = w = 2pi/T
sqrt(k/m) = 2pi
k/m = 4pi^2/T^2
k = (4pi^2/T^2)*m
k = (4pi^2)/(pi^2/50)- pi sie poskraca i wychodzi:
k = 4*50^2*0.02=200

F = k*x
F = 200*0.01=2.0

Zad. 24
Okres drgań pewnego wahadła matematycznego w stojącej windzie był równy 10s. Gdy winda zaczęła poruszać się
do góry z pewnym przyspieszeniem okres ten uległ skróceniu do wartości 9s. Wyznacz przyspieszenie windy. Wynik
podaj w m/s^2 z dokładnością do drugiego miejsca po przecinku.

T1 - okres w stojącej windzie
T2 - okres w poruszającej się windzie
g - przyspieszenie ziemskie
a- prędkość windy
l - długość wahadła matematycznego

T1^2/T2^2=[2pi*sqrt(l/g)]/[2pi*sqrt(l/a)]

Po przekształceniach uwierzcie na słowo, wychodzi:
T1/T2 = a/g

100/81 = a/g
a = (100/81)*10
a = 1000/81
a = 12.35

Ale działa też na windę przyspieszenie ziemskie równe 10m/s^2, więc musimy to uwzględnić i mamy
12.35 – 10 = 2.35 m/s^2

Zad. 25
W ramce z drutu rozciągnięta jest błonka z mydlin. Do ruchomej poprzeczki AB o długości 28cm podwieszono ciężar
1.6mN. Ruchoma poprzeczka przesunęła sie o a=10cm w dół i pozostała w równowadze. Ile wynosi napięcie
powierzchniowe mydlin? Wynik podaj w mN/m z dokładnością do pierwszego miejsca po przecinku. (Odp.2.9)

Fizyka I, etest nr 5. Praca wspólna, głównie: Tomek Ferenc, SKP

Σ (sigma) - napięcie powierzchniowe
F - ciężar mydlin w nM
l - długość poprzeczki
Σ = F/2l
sigma = 1.6/(2*0.28)
sigma = 2.9

Zad. 26
Nurek znajduje sie w zbiorniku wodnym na głębokości 31m. Gęstość wody wynosi 1000kg/m^3, a ciśnienie
atmosferyczne 1000hPa. Ile razy ciśnienie (całkowite) działające na tego nurka jest większe od ciśnienia
atmosferycznego? Wynik podaj z dokładnością do 1 miejsca po przecinku. (Odp.4.1)

P = ro*g*h + ciśnienie atmosferyczne
P=31*1000*10 Pa+1000hPa
P=310000 Pa+1000hPa
Teraz zamieniamy Pascale na hPa i mamy
P=3100+1000=4100 hPa.
Mamy znaleźć ile razy ciśnienie w wodzie jest większe wiec:
4100/1000= 4.1
Zad. 27
Na doskonale gładkim stole leży klocek o masie 1.8kg. Klocek przymocowany jest do ściany za pomocą sprężyny o
współczynniku sprężystości 500N i zaniedbywalnie malej masie. W klocek tan uderza lecący poziomo pocisk i grzęźnie
w nim. Prędkość pocisku przed zderzeniem wynosi 25m/s, a jego masa 0.1kg. Po zderzeniu klocek wraz z uwięzionym
poziomo w nim pociskiem wykonuje drgania harmoniczne. Jaka jest amplituda drgań? Wynik podaj w cm z
dokładnością do 1 miejsca po przecinku. (Odp. 8.1)

(k*A^2) / 2 = [(m1+m2)*Vx] / 2
A^2 = [(m1+m2)Vx^2] / k
Vx = (m2*v) / (m1+m2)
A^2 = [1.9*(2.5/1.9)^2] / 500
A^2 = 0,06579
A = 0.0811 m
Mamy podać w cm, więc:
A=8.1 cm

Plik ściągnięty ze strony: http://maciej.kujawa.org.pl/pwr

FIZYKA I, SKP & IŚ

E-test nr 5 – przydatne wzory

by MK

1. Energia całkowita w ruchu harmonicznym:

Ec = Ep + Ek = ½*k*A^2 [J]
k – współczynnik sprężyny [N/m]
A – amplituda [m]

2. Równanie położenia w ruchu harmonicznym:

x(t) = A*sin(w*t)
w (omega) – częstość kołowa [1/s]

3. Prędkość max w ruchu harmonicznym:

v = A*w [m/s]

4. Przyspieszenie max w ruchu harmonicznym:

a = A*w^2 [m/s^2]

5. Ciśnienie cieczy:

p = F/S = ro*g*h [Pa]

6. Parcie:

F = p*S [N]

7. Siła wyporu:

F = ro_cieczy * V * g [N]
V – objętość zanurzonej części ciała [m^3]

8. Ciepło właściwe:

c = Q / m*T [J / kg*K]

9. Okres drgań wahadła matematycznego:

T = 2pi* piewiastek(l/g) [s]
l – długość wahadła (np. nitki) [m]

10. Okres drgań wahadła fizycznego:

T = 2pi* pierwiastek(I/mgd) [s]
I – moment bezwładności ciała
d – odległość śrdk. ciężk. od pkt. Zawieszenia

11. Okres drgań w ruchu harmonicznym:

T = 2pi / w [s]

12. Jednostki:

1 HPa = 100 Pa = 100 N/m^2
(ciśnienie)

1 g/cm^3 = 1*10^3 kg/m^3
(gęstość)