WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

1/36

PODSTAWY

PROGRAMOWANIA

kurs I - część 3

PROWADZĄCY: dr inż. Marcin Głowacki

E-Mail:

[e-mail]

Pok.907 C-5

Wrocław 2010

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

2/36

6.

R

EKURENCJA

1

Rekurencja

polega na wywołaniu danej funkcji w jej treści. Występuje rekurencja:

-

bezpośrednia

– gdy funkcja wywołuje sama siebie;

-

pośrednia

– gdy funkcja wywołuje inną funkcję, która z kolei wywołuje tą

funkcję, z której została wywołana.

Przykład 1. Rozkład dziesiętnej liczby całkowitej na cyfry:

METODA ITERACYJNA

#include <iostream>
#include <stdlib.h>
#include <iomanip>
using namespace std;

int main() {
while(1){

//pętla główna

int i,

liczba

, cyfra[10];

cout<<"Podaj liczbe (max.10 cyfrowa) 0-konczy: ";
cin>>

liczba

;

if(!

liczba

) break;

//0 - wyjście

i

=0;

do

cyfra

[

i++

]=

liczba

%

10

;

//reszta z dzielenia przez 10

while ((

liczba

/=

10

) > 0);

//dzielenie liczby przez 10, int odcina ulamek

while (

--i

>=0)

//wydruk z tablicy cyfr w odwrotnej kolejności

cout << setw(4)<<

cyfra

[

i

];

cout<<endl;
}
system("PAUSE");
return 0;
}

Efekt:
Podaj liczbe (max.10 cyfrowa) 0-konczy: 25
2 5
Podaj liczbe (max.10 cyfrowa) 0-konczy: 230
2 3 0
Podaj liczbe (max.10 cyfrowa) 0-konczy: 299003
2 9 9 0 0 3
Podaj liczbe (max.10 cyfrowa) 0-konczy: 8903452345
3 1 3 5 1 7 7 5 3
Podaj liczbe (max.10 cyfrowa) 0-konczy: 0
Aby kontynuować, naciśnij dowolny klawisz . . .

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

3/36

R

EKURENCJA

2

METODA REKURENCYJNA

#include <iostream>
#include <stdlib.h>
#include <iomanip>
using namespace std;

void

Cyfra

(

int liczba

){

int

nowa

;

if ((

nowa

=

liczba

/10

)!=0)

//warunek zatrzymania rekurencji

Cyfra

(

nowa

);

//wywołanie rekurencyjne

cout << setw(4)<<

liczba

%10

;

}
int main(){
while(1){
int

liczba

;

cout<<"Podaj liczbe (max.10 cyfrowa) 0-konczy: ";
cin>>

liczba

;

if(!liczba) break;

//0 - wyjście

Cyfra

(

liczba

);

cout<<endl;
}
system("PAUSE");
return 0;
}

liczba = 453;

Cyfra(453){
...
...
cout<<(453%10);
}

=3

Cyfra(453/10){
...
...
cout<<(45%10);
}

=5

=45

Cyfra(45/10){
...
...
cout<<(4%10);
}

=4

=4

int main(){

Efekt:

4 5 3

Efekt:
Podaj liczbe (max.10 cyfrowa) 0-konczy: 45
4 5
Podaj liczbe (max.10 cyfrowa) 0-konczy: 788
7 8 8
Podaj liczbe (max.10 cyfrowa) 0-konczy: 59864
5 9 8 6 4
Podaj liczbe (max.10 cyfrowa) 0-konczy: 465456478
4 6 5 4 5 6 4 7 8
Podaj liczbe (max.10 cyfrowa) 0-konczy: 0
Aby kontynuować, naciśnij dowolny klawisz . . .

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

4/36

Przykład 2. Funkcja SILNIA z definicji:

n! = (n-1)!*n

, gdzie 0! = 1 i 1! = 1;

METODA ITERACYJNA

#include <iostream>
#include <stdlib.h>

using namespace std;

int main() {
while(1){

//pętla główna

unsigned int

n

;

cout<<"Podaj liczbe z zakresu od 0 do 33 (0-konczy): ";
cin>>

n

;

if(!

n

) break;

//0 - wyjście

unsigned int wynik = 1;

for

(int i=2;i<=

n

;i++) {

//pętla wykona się n-1 razy

wynik*=i;

//wynik =

1*2*3*...*n

}
cout<<"Wynik operacji "<<

n

<<"! = "<<wynik<<endl;

}
system("PAUSE");
return 0;
}

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

5/36

METODA REKURENCYJNA

#include <iostream>
#include <stdlib.h>

using namespace std;

unsigned int

fnSilnia

(unsigned int

n

) {

if (

n

==0 ||

n

==1) return 1;

// warunek zatrzymania rekurencji

return

fnSilnia

(

n

-1)*

n

;

//wywołanie rekurencyjne

}

int main() {
while(1){

//pętla główna

unsigned int

n

;

cout<<"Podaj liczbe z zakresu od 0 do 33 (0-konczy): ";
cin>>

n

;

if(!

n

) break;

//0 - wyjście

unsigned int wynik;
wynik=

fnSilnia

(

n

);

cout<<"Wynik operacji "<<

n

<<"! = "<<wynik<<endl;

}
system("PAUSE");
return 0;
}

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

6/36

int main(){

wynik=fnSilnia(3);

fnSilnia(2){
if(2==0 || 2==1) return 1;
return fnSilnia(1)*2;
}

fnSilnia(3){
if(3==0 || 3==1) return 1;
return fnSilnia(2)*3;
}

fnSilnia(1){
if(1==0 ||

1==1

) return

1

;

...
}

//warunek STOPU

wynik=

6

;

return

1*2

;

return

2*3

;

Funkcje rekurencyjne obciążają obszar stosu, ponieważ tam

przetwarzane są wszystkie wywołania funkcji, składowane adresy powrotu,
parametry wywołania oraz zmienne lokalne. Bardziej złożone algorytmy
rekurencyjne potrafią szybko zużyć całą przestrzeń pamięci stosu i zakłócić
działanie programu.

Są zadania, które są realizowane optymalnie z zastosowaniem metod
rekurencyjnych, np. kopiowanie struktury drzewa kartotek

TEN ROZUMIE REKURENCJĘ .... KTO ROZUMIE REKURENCJĘ !!!

... i tak w kółko

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

7/36

Z

ŁOśONOŚĆ

O

BLICZENIOWA

Złożoność obliczeniowa algorytmu – ilość zasobów komputera jakiej
potrzebuje dany algorytm. Pojęcie to wprowadzili J. Hartmanis i R. Stearns.
Najczęściej przez zasób rozumie się czas oraz pamięć – dlatego też używa się
określeń "

złożoność czasowa

" i "

złożoność pamięciowa

".

Za jednostkę złożoności pamięciowej przyjmuje się pojedyncze słowo maszyny
(np.

Bajt

).

W przypadku złożoności czasowej nie można podać bezpośrednio jednostki
czasu, np. milisekundy, bowiem nie wiadomo na jakiej maszynie dany
algorytm będzie wykonywany. Dlatego też wyróżnia się, charakterystyczną dla
algorytmu,

operację dominującą

.

Liczba wykonań operacji dominującej jest

proporcjonalna do wykonań wszystkich operacji.

Rozróżnia się dwa rodzaje złożoności:

1.

Złożoność pesymistyczna

określa złożoność w "najgorszym" przypadku.

2.

Złożoność oczekiwana

określa złożoność średnią czyli wartość oczekiwaną

zmiennej losowej.

Złożoność obliczeniowa nie jest wygodna w stosowaniu, bowiem operacja
dominująca na jednym komputerze może wykonywać się błyskawicznie, na
innym zaś musi być zastąpiona szeregiem instrukcji.

Dlatego też częściej stosuje się złożoność asymptotyczną, która mówi o tym jak
złożoność kształtuje się dla bardzo dużych, granicznych rozmiarów danych
wejściowych.
Do opisu złożoności asymptotycznej stosuje się trzy notacje:

1. Notacja wielkie O
2. Notacja Ω (Omega wielkie)
3. Notacja Θ (Teta)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

8/36

A

LGORYTMY

S

ORTOWANIA

Sortowaniem nazywamy proces ustawiania zbioru obiektów w określonym
porządku liniowym, w efekcie czego uzyskiwany jest liniowy ciąg elementów.
Sortowania dokonuje się w celu późniejszego łatwiejszego wyszukiwania
elementów zbioru.
Wybór algorytmu sortowania zależy od struktury przetwarzanych danych:

-

sortowanie wewnętrzne

jest to sortowanie tablic odbywające się w

pamięci operacyjnej komputera, które cechuje duża szybkość i
swobodny dostęp do danych

-

sortowanie zewnętrzne

jest to sortowanie plików w powolniejszych, lecz

pojemniejszych pamięciach zewnętrznych o ograniczonym dostępie do
danych.

Dobra metoda sortowania powinna zachować porządek względny obiektów
identycznych – nie zmieniać go w trakcie dokonywania sortowania (cecha
stabilności algorytmu sortowania).

Miarą efektywności sortowania są:

-

liczba koniecznych porównań obiektów

(czas porównania)

-

liczba koniecznych przestawień elementów

(czas przestawiania)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

9/36

K

LASYFIKACJA ALGORYTMÓW

SORTOWANIA WEDŁUG

:

*

złożoności

(

pesymistyczna

,

oczekiwana

i

obliczeniowa

) — zależność liczby

wykonanych operacji w stosunku od liczebności sortowanego zbioru (n).
Typową, dobrą złożonością jest średnia O(n log n) i pesymistyczna Ω(n

2

).

Idealną złożonością jest O(n). Algorytmy sortujące nie przyjmujące żadnych
wstępnych założeń dla danych wejściowych wykonują co najmniej O(n log n)
operacji.
*

złożoności pamięciowej

*

sposobu działania

: algorytmy sortujące za pomocą porównań to takie

algorytmy sortowania, których sposób wyznaczania porządku jest oparty
wyłącznie na wynikach porównań między elementami; dla takich algorytmów
dolne ograniczenie złożoności wynosi Ω(n log n);
*

stabilności

: stabilne algorytmy sortowania utrzymują kolejność

występowania dla elementów o tym samym kluczu. Kiedy elementy o tym
samym kluczu są nierozróżnialne, stabilność nie jest istotna.

Przykład: (para liczb całkowitych sortowana względem pierwszej wartości)

(4, 1)

(3, 7) (3, 1)

(5, 6)

W tym przypadku są możliwe dwa różne wyniki sortowania:

(3, 7) (3, 1)

(4, 1) (5, 6) (kolejność zachowana =

algorytm stabilny

)

(3, 1) (3, 7)

(4, 1) (5, 6) (kolejność zmieniona =

algorytm niestabilny

)

*

Stabilne algorytmy sortowania

gwarantują, że kolejność zostanie

zachowana.
*

Niestabilne algorytmy sortowania

mogą zmienić kolejność.

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

10/36

Z

ŁOśONOŚĆ OBLICZENIOWA

PRZYKŁADOWYCH ALGORYTMÓW

SORTOWANIA

W podanej złożoności n oznacza liczbę elementów do posortowania, k liczbę
różnych elementów.

Stabilne

* sortowanie bąbelkowe — O(n

2

); (ang. bubblesort)

* sortowanie przez wstawianie — O(n

2

); (ang. insertion sort)

* sortowanie przez scalanie — O(n log n), wymaga O(n) dodatkowej
pamięci; (ang. merge sort)
* sortowanie przez zliczanie — O(n + k), gdzie k to długość zakresu
występowania liczb n - wymaga O(n + k) dodatkowej pamięci; (ang. counting
sort)
* sortowanie kubełkowe — O(n), wymaga O(k) dodatkowej pamięci; (ang.
bucket sort)
* sortowanie pozycyjne — O(d(n + k)), gdzie k to wielkość domeny cyfr, a d
szerokość kluczy w cyfrach. Wymaga O(n + k) dodatkowej pamięci; (ang.
radix sort)
* Pbit — O(n); wymaga Θ(sizeof(n-TYPE)/(The Length of bit pattern))
dodatkowej pamięci.

Niestabilne

* sortowanie przez wybieranie — O(n

2

); (ang. selection sort)

* sortowanie Shella — złożoność nieznana; (ang. Shellsort)
* sortowanie grzebieniowe — złożoność nieznana; (ang. combsort)
* sortowanie szybkie — O(n log n), pesymistyczny Θ(n

2

); (ang. quicksort)

* sortowanie introspektywne — O(n log n); (ang. introsort)
* sortowanie przez kopcowanie — O(n log n); (ang. heapsort)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

11/36

K

LASYFIKACJA METOD PRZYKŁADOWYCH

ALGORYTMÓW SORTOWANIA

Sortowanie proste

(O(n

2

)):

- przez wstawianie - InsertionSort
- przez wybieranie - SelectionSort
- przez zamianę- BubbleSort

Szybkie sortowanie przez porównania

– metody oparte na

szybkich porównaniach obiektów (O(n log n)):

- przez podział i połączenie – MergeSort
- sortowanie szybkie QuickSort
- sortowanie prze kopcowanie HeapSort

Sortowanie pozycyjne

– wykorzystujące informację o strukturze

porównywanych elementów (zapis w systemie pozycyjnym, słowo
nad skończonym alfabetem) O(m):

- sortowanie kubełkowe – BucketSort
- sortowanie leksykograficzne - RadixSort

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

12/36

7.

P

RZYKŁADOWE ALGORYTMY

SORTOWANIA

SORTOWANIE BĄBELKOWE (ang. BUBBLESORT)

Algorytm sortowania bąbelkowego(ang. Bubblesort) jest najprostszą
koncepcyjnie (oraz w implementacji) metodą sortowania wewnętrznego.
Polega ona na kolejnym przechodzeniu sekwencyjnym przez sortowaną tablicę
i przestawianiu sąsiednich elementów, naruszających wymagane
uporządkowanie. Brak przestawień przy kolejnym przejściu oznacza, że dane
zostały posortowane.

Charakterystyka metody

•

w kolejnych przejściach mniejsze elementy systematycznie przesuwają
się ku początkowi tablicy, podobnie jak bąbelki powietrza podążają ku
górze

•

po każdym cyklu przejścia przez tablicę jeden z elementów umieszczany
jest na swoim miejscu docelowym na końcu – element ten można już
pominąć w kolejnych cyklach.

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

13/36

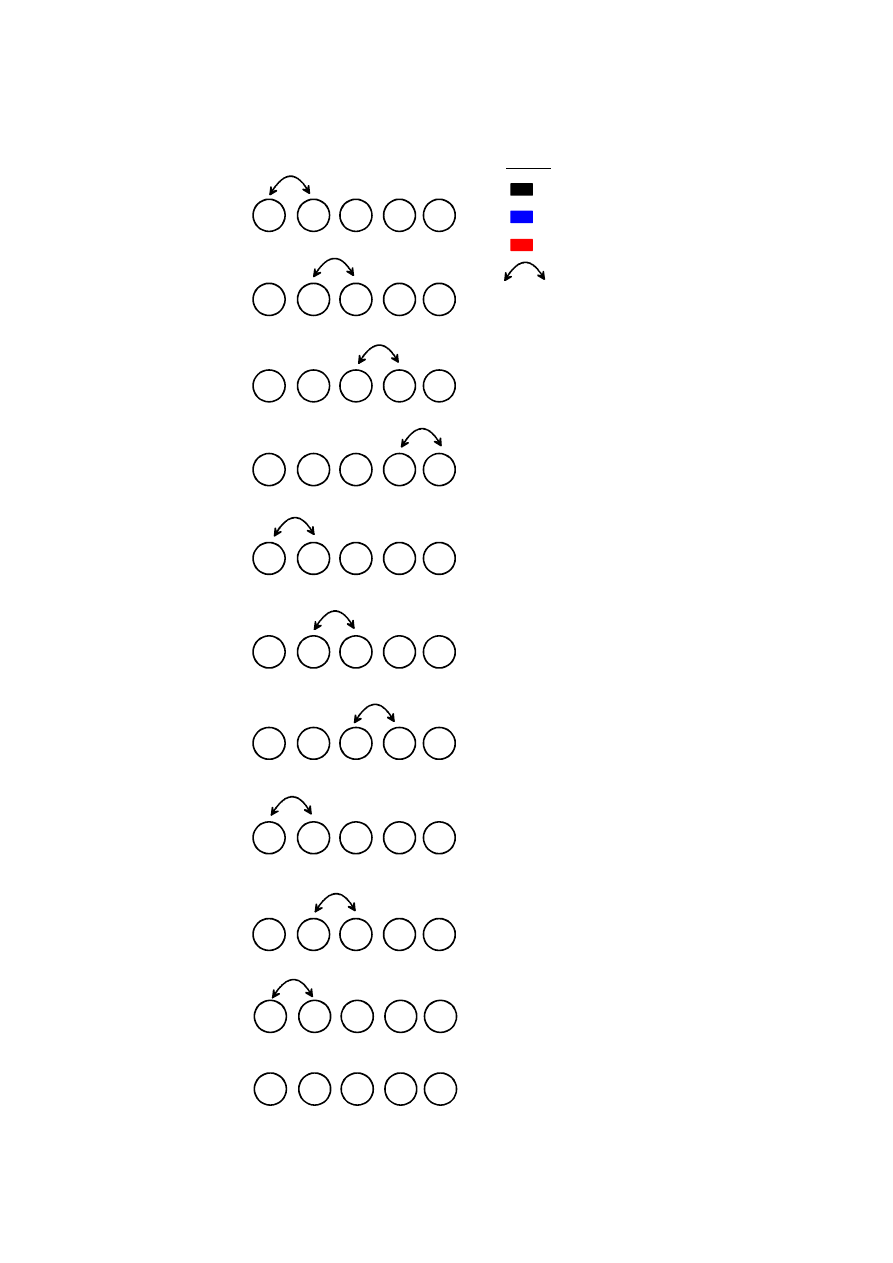
Przykład sortowania bąbelkowego ciągu liczb: 3,9,4,2,6

#include <iostream>
using namespace std;

void

BubbleSort

(int tab[], int n){

int i,j;

for

(i = 0; i< n-1;i++)

for

(j = n-1; j > i; --j)

//

wszystkie cykle

if

(

tab[j] < tab[j-1]

)

swap

(tab[j],tab[j-1]); //

zamiana miejscami

}
void Wyswietl(int tab[], int n, char *komentarz){
int i;
cout<<komentarz<<"\t";
for (i=0; i<n; i++) cout<<tab[i]<<" ";
cout<<endl;
}
int main(){
int tablica[]={3,9,4,2,6};
Wyswietl(tablica,5,"Przed sortowaniem:");
BubbleSort(tablica,5);
Wyswietl(tablica,5,"Po sortowaniu:");
system("PAUSE");
return 0;
}

Powyższa implementacja jest dość nieefektywna, ponieważ porównania
wykonuje się nawet wówczas, gdy tablica jest już uporządkowana. Procedurę
tę można ulepszyć, zabezpieczając się przed taką sytuacją. Aby to osiągnąć, do
zewnętrznej pętli for należy dołożyć flagę informującą o wykonywanej
zamianie. W przypadku wykonania cyklu bez przestawień algorytm może się
zakończyć. Zaletą tego rozwiązania jest fakt, że gdy ciąg wejściowy będzie
posortowany, to algorytm wykona

tylko jeden przebieg.

Jest to duża zaleta biorąc pod uwagę, że niektóre metody będą sortowały ciąg
nawet jeśli będzie on już posortowany. Z kolei najgorszym zestawem danych
dla tego algorytmu jest ciąg posortowany nierosnąco.

Animacja tej metody sortowania można znaleźć pod adresami:

http://www.cs.pitt.edu/~kirk/cs1501/animations/Sort1.html

http://www.ship.edu/~cawell/Sorting/applet.htm

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

14/36

3

3

4

4

6

zamiana

9

2

3

3

4

6

9

2

4

zamiana

3

3

4

6

4

zamiana

9

2

3

3

4

6

4

zamiana

9

2

3

3

4

4

2

3

3

4

4

zamiana

2

6

9

6

9

nie posortowane

Legenda:

zamiana miejscami

posortowane

3

3

4

4

2

6

9

3

3

4

4

2

6

9

Algorytm stop

3

3

4

4

6

bez zamiany

9

2

porównanie

3

3

4

6

4

9

2

bez zamiany

bez zamiany

bez zamiany

3

3

4

4

2

6

9

bez zamiany

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

15/36

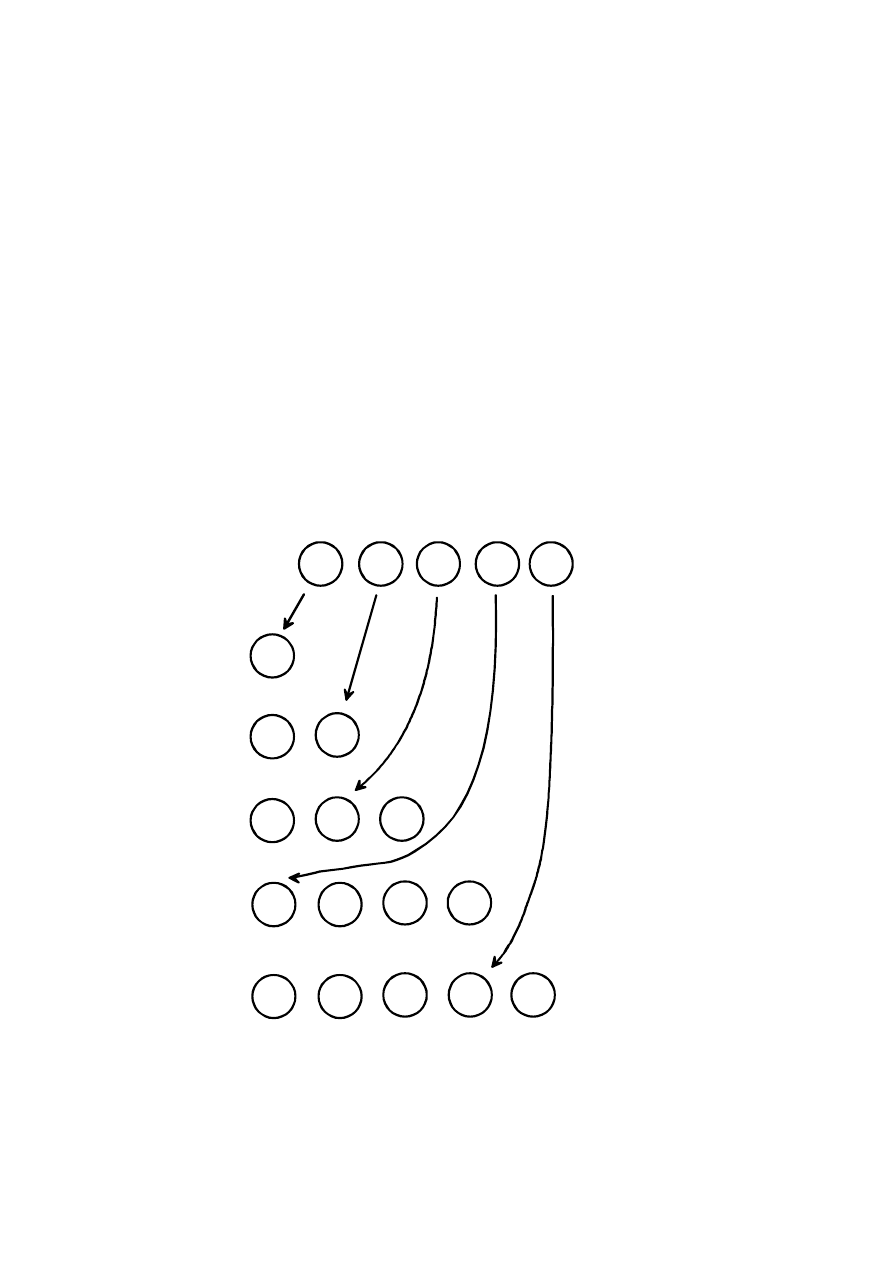
Przykład innego sortowania bąbelkowego ciągu liczb: 3,9,4,2,6

#include <iostream>
using namespace std;
void

NewBubbleSort

(int tab[], int n){

int i,sorted=0,pass=1; //

zgodna z animacją ze strony http

while

(!sorted && pass<n) {

sorted = 1;

for

(i=0;i<=n-pass-1;i++) //pass ogranicza zasieg sortowania

if

(

tab[i] > tab[i+1]

) { //od końca tablicy

swap

(tab[i],tab[i+1]);

sorted=0;
}
pass++;
}
}

void Wyswietl(int tab[], int n, char *komentarz){
int i;
cout<<komentarz<<"\t";
for (i=0; i<n; i++) cout<<tab[i]<<" ";
cout<<endl;
}
int main(){
int tablica[]={3,9,4,2,6};
Wyswietl(tablica,5,"Przed sortowaniem:");
NewBubbleSort(tablica,5);
Wyswietl(tablica,5,"Po sortowaniu:");
system("PAUSE");
return 0;
}

Analiza złożoności obliczeniowej:

Pesymistyczna

Średnia

Optymistyczna

O(n

2

)

O(n

2

)

O(n)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

16/36

SORTOWANIE PRZEZ WSTAWIANIE (ang. INSERTIONSORT )

Proste metody stosuje się w sytuacjach gdy należy wielokrotnie sortować
krótkie tablice, unikające rekurencji – oszczędność na czasie.

Sortowanie polega na pobieraniu kolejnych elementów ze zbioru i wstawiania
go we właściwe miejsce w już posortowanym ciągu - wcześniej wstawionych
elementów.

Zasada działania tego algorytmu jest często porównywana do porządkowania
kart w wachlarzu w czasie gry. Każdą kartę wstawiamy w odpowiednie
miejsce, tzn. po młodszej, ale przed starszą.

Sortowanie może odbywać się w miejscu, czyli nie wymaga dodatkowej
pamięci, za wyjątkiem kilku zmiennych pomocniczych.

3

3

4

4

6

wstawianie

9

2

3

3

3

9

3

3

4

3

9

3

3

4

3

9

2

3

3

4

3

9

2

3

6

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

17/36

Przykład sortowania przez wstawianie dla ciągu <

3,9,4,2,6

>

#include <iostream>
using namespace std;
void

Insertion

(int tab[], int n){

int i,k,x,found;

//zgodna z animacja ze strony http

for

(k=1;k<n;k++){

x=tab[k];
i=k-1;
found=0;

while

(!found && i>=0) {

if

(

tab[i]>x

) {

swap

(tab[i+1],tab[i]);

i=i-1;
} else found = 1;
}
}
}

void Wyswietl(int tab[], int n, char *komentarz){
int i;
cout<<komentarz<<"\t";
for (i=0; i<n; i++) cout<<tab[i]<<" ";
cout<<endl;
}
int main(){
int tablica[]={3,9,4,2,6};
Wyswietl(tablica,5,"Przed sortowaniem:");
Insertion(tablica,5);
Wyswietl(tablica,5,"Po sortowaniu:");
system("PAUSE");
return 0;
}

Analiza złożoności obliczeniowej:

Pesymistyczna

Średnia

Optymistyczna

O(n

2

)

O(n

2

)

O(n)

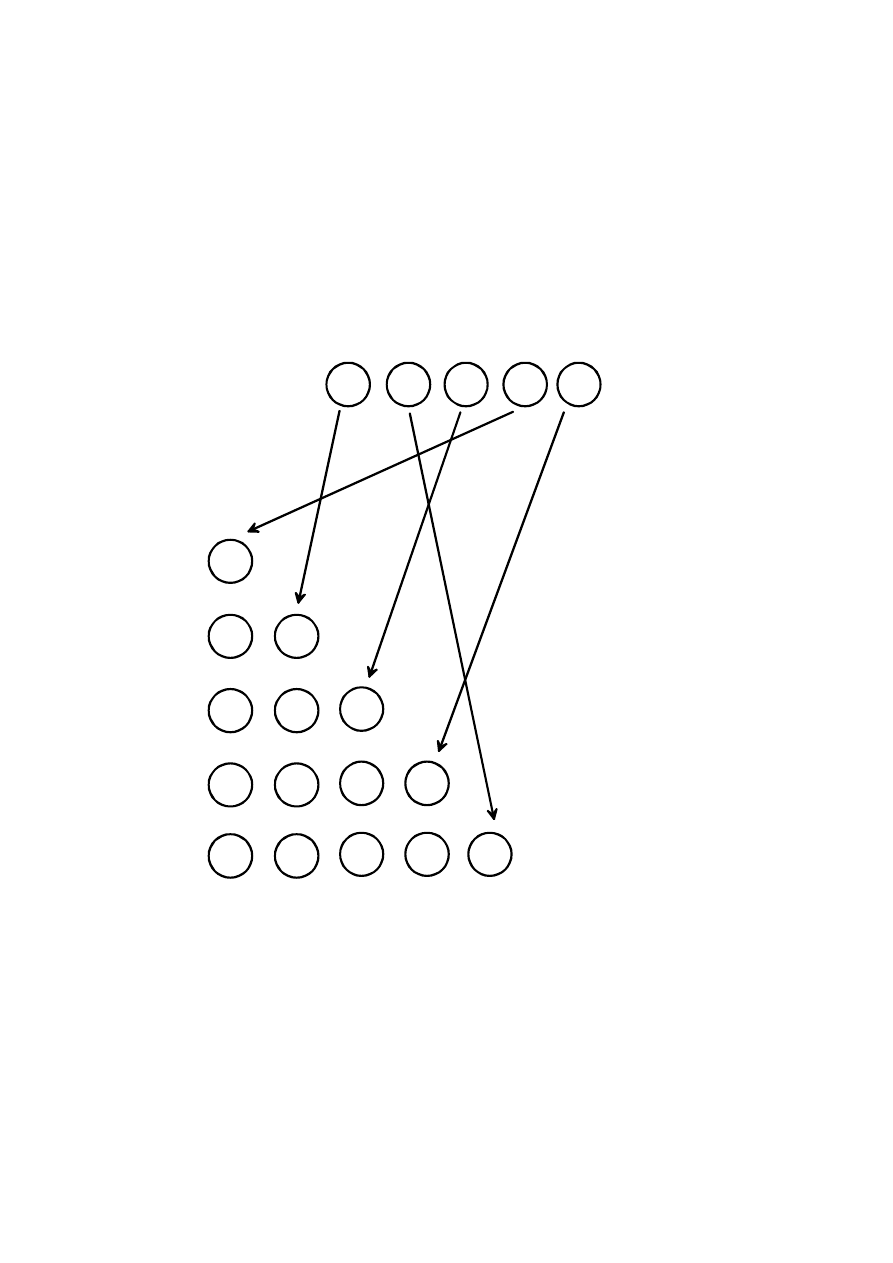
WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

18/36

SORTOWANIE PRZEZ WYBIERANIE (ang. SELECTIONSORT)

Metoda ta nazywana jest sortowaniem przez wybieranie gdyż na początku
szukany jest najmniejszy element, który następnie zamieniany jest z
pierwszym elementem tablicy. Wśród pozostałych elementów szukany jest
kolejny najmniejszy element i zamieniany z drugim elementem tablicy itd.
Czynność ta powtarzana jest aż do końca tablicy.

3

3

4

4

6

selekcja kolejnych
najmniejszych elementów

9

2

2

3

2

3

3

4

2

3

3

4

2

3

6

3

3

4

3

9

2

3

6

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

19/36

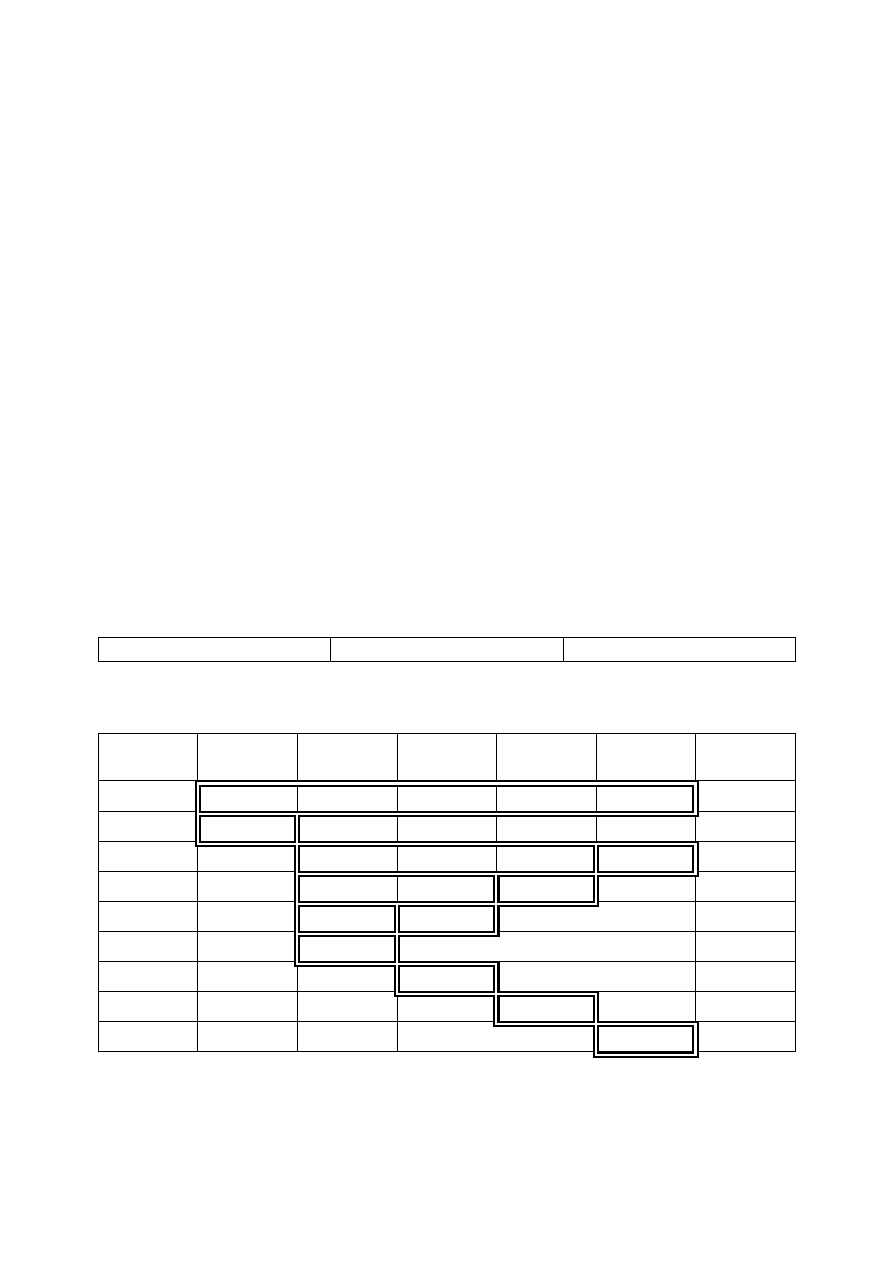
Przykład sortowania przez wybieranie dla ciągu <

3,9,4,2,6

>

#include <iostream>
using namespace std;
void

Selection

(int tab[], int n){

int i,k,current;

//zgodna z animacja ze strony http

for

(i=0;i<=n-2;i++){

current=i;

for

(k=i+1;k<=n-1;k++){ //szuka najmniejszego elementu w tab[]

if

(

tab[current]>tab[k]

) //- trzyma indeks aktualnie

current=k; // najmniejszego w current
}

swap

(tab[i],tab[current]); //zamienia kolejny w tablicy

} //z najmniejszym znalezionym
}

void Wyswietl(int tab[], int n, char *komentarz){
int i;
cout<<komentarz<<"\t";
for (i=0; i<n; i++) cout<<tab[i]<<" ";
cout<<endl;
}
int main(){
int tablica[]={3,9,4,2,6};
Wyswietl(tablica,5,"Przed sortowaniem:");
Selection(tablica,5);
Wyswietl(tablica,5,"Po sortowaniu:");
system("PAUSE");
return 0;
}

Analiza złożoności obliczeniowej:

Pesymistyczna

Średnia

Optymistyczna

O(n

2

)

O(n

2

)

O(n

2

)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

20/36

8.

SORTOWANIE SZYBKIE (ang. QUICKSORT)

Algorytm sortowania szybkiego jest uważany za najszybszy algorytm dla
danych losowych – bardzo praktyczny i szeroko stosowany.
Sortowanie może odbywać się w miejscu, czyli nie wymaga dodatkowej
pamięci, za wyjątkiem kilku zmiennych pomocniczych.

Algorytm rekurencyjny oparty o zasadę

dziel i rządź:

-

Dziel

polega na dokonaniu podziału tablicy na dwie podtablice w taki

sposób, że elementy w pierwszej części są mniejsze – równe (<=) wartości
elementów w drugiej części.

-

Rządź

polega na rekurencyjnym sortowaniu dwóch podtablic.

Rekurencja umożliwia wtórne podziały i sortowanie coraz to mniejszych
fragmentów tablicy.

-

Nie wymaga łączenia.

Do podziału można wykorzystać specjalizowaną funkcję, np. partition(...).
Funkcja ta dokonuje porównań i zamiany miejscami elementów na drodze
ustalenia miejsca podziału. Funkcja zwraca indeks miejsca podziału, np. q

W tablicy tab[]:

elementy <=

tab[q]

elementy >=

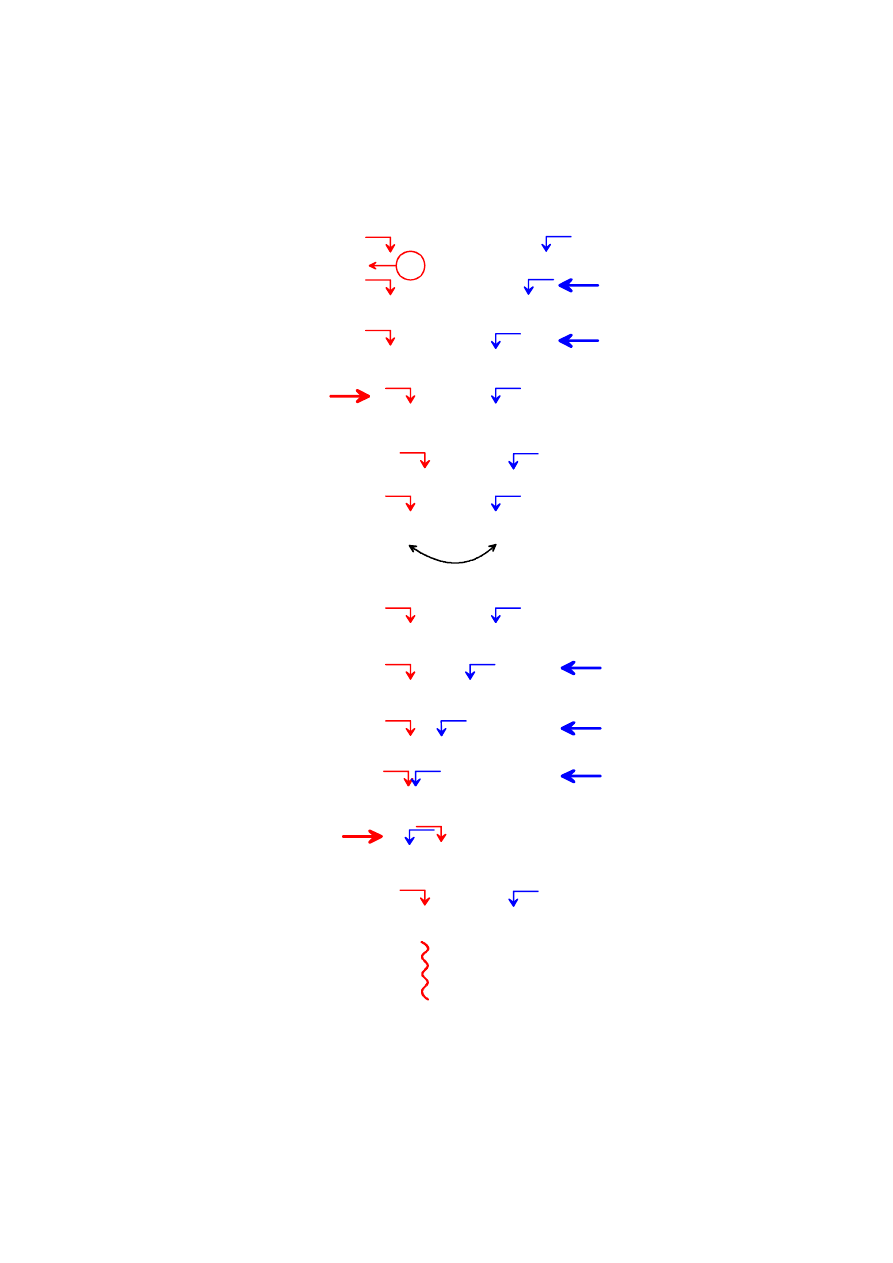
Dla ciągu tab[]={

3,9,4,2,6

}; funkcja QuickSort sortuje podtablicę od

p

do

r

- na niebiesko zamiana miejscami elementów.

p

...

r

tab[0]

tab[1]

tab[2]

tab[3]

tab[4]

partition

zwraca

q

0 ... 4

3

9

4

2

6

0

0 ... 0

2

1 ... 4

9

4

3

6

3

1 ... 3

6

4

3

2

1 ... 2

3

4

1

1 ... 1

3

2 ... 2

4

3 ... 3

6

4 ... 4

9

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

21/36

3 9 4 2 6

piv=3

3 9 4 2 6

3 9 4 2 6

if (6 <=piv) ... (FALSE)

3 9 4 2 6

if (2 <=piv) ... (TRUE)

3 9 4 2 6

if (3 >=piv) ... (TRUE)

if ( przed ) (TRUE)

3 9 4 2 6

zamiana

2 9 4 3 6

if (4 <=piv) ... (FALSE)

2 9 4 3 6

if (9 <=piv) ... (FALSE)

2 9 4 3 6

if (2 <=piv) ... (TRUE)

2 9 4 3 6

2 9 4 3 6

if (9 >=piv) ... (TRUE)

if ( przed ) (FALSE)

return (granica podzialu)

2 9 4 3 6

KROK

(1)

(1)

(2)

(3)

(4)

(5)

(7)

(8)

(9)

(10)

(11)

(12)

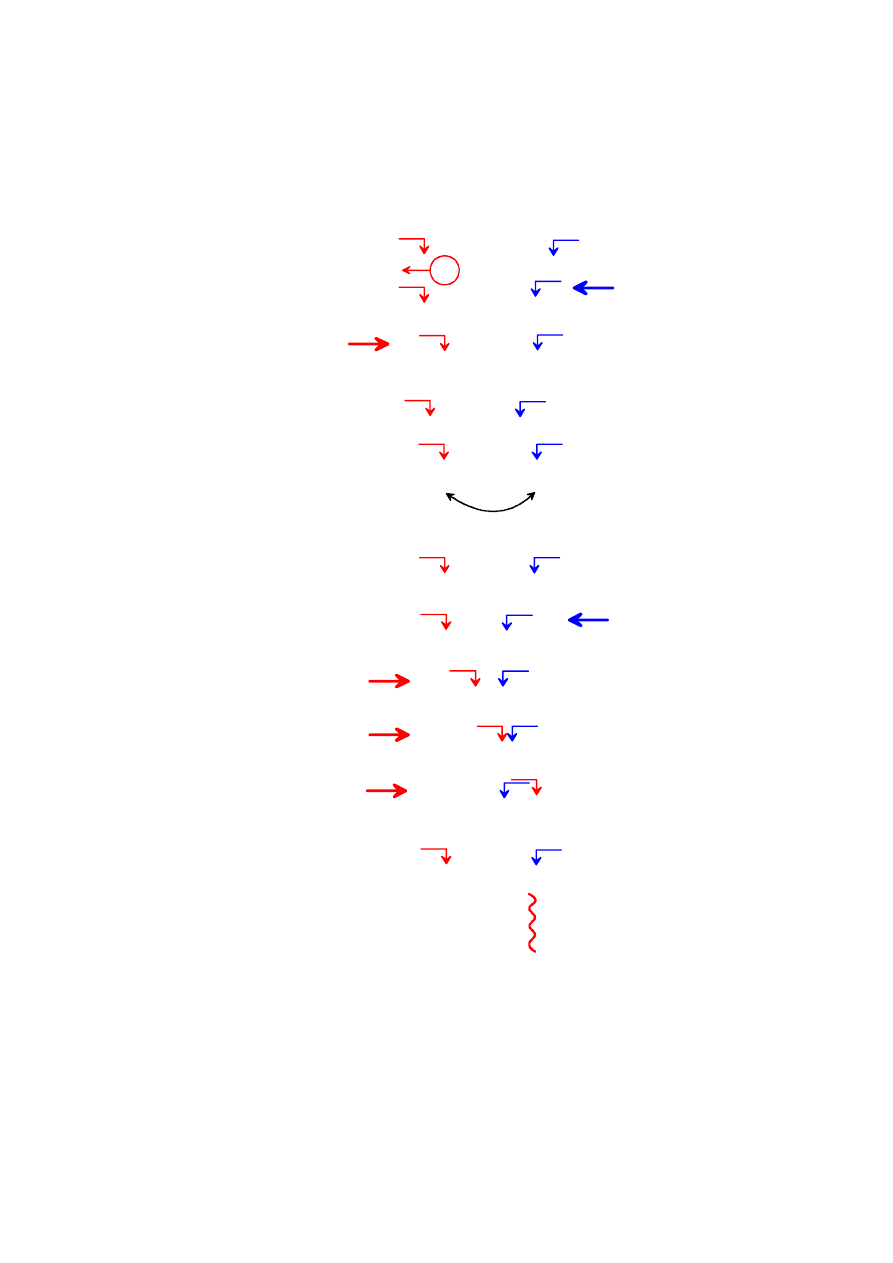
FUNKCJA PARTITION

(6)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

22/36

9 4

6

piv=9

3

9 4 3 6

9 4

6

if (6 <=piv) ... (TRUE)

9 4 3 6

if (9 >=piv) ... (TRUE)

if ( przed ) (TRUE)

9 4 3 6

zamiana

6 4 3 9

if (4 >=piv) ... (FALSE)

if ( przed ) (FALSE)

return (granica podzialu)

KROK

(1)

(1)

(2)

(3)

(4)

(6)

(7)

(8)

(9)

(10)

FUNKCJA PARTITION

(5)

3

6 4 3 9

6 4 3 9

if (3 <=piv) ... (TRUE)

if (3 >=piv) ... (FALSE)

6 4 3 9

if (9 >=piv) ... (TRUE)

6 4 3 9

(11)

6 4 3 9

ZADANIE: Wykonaj samodzielnie symulację pierwszego wywołania funkcji

partition dla ciągu: 3 9 1 2 6 (dalej rysunek z odpowiedzią).

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

23/36

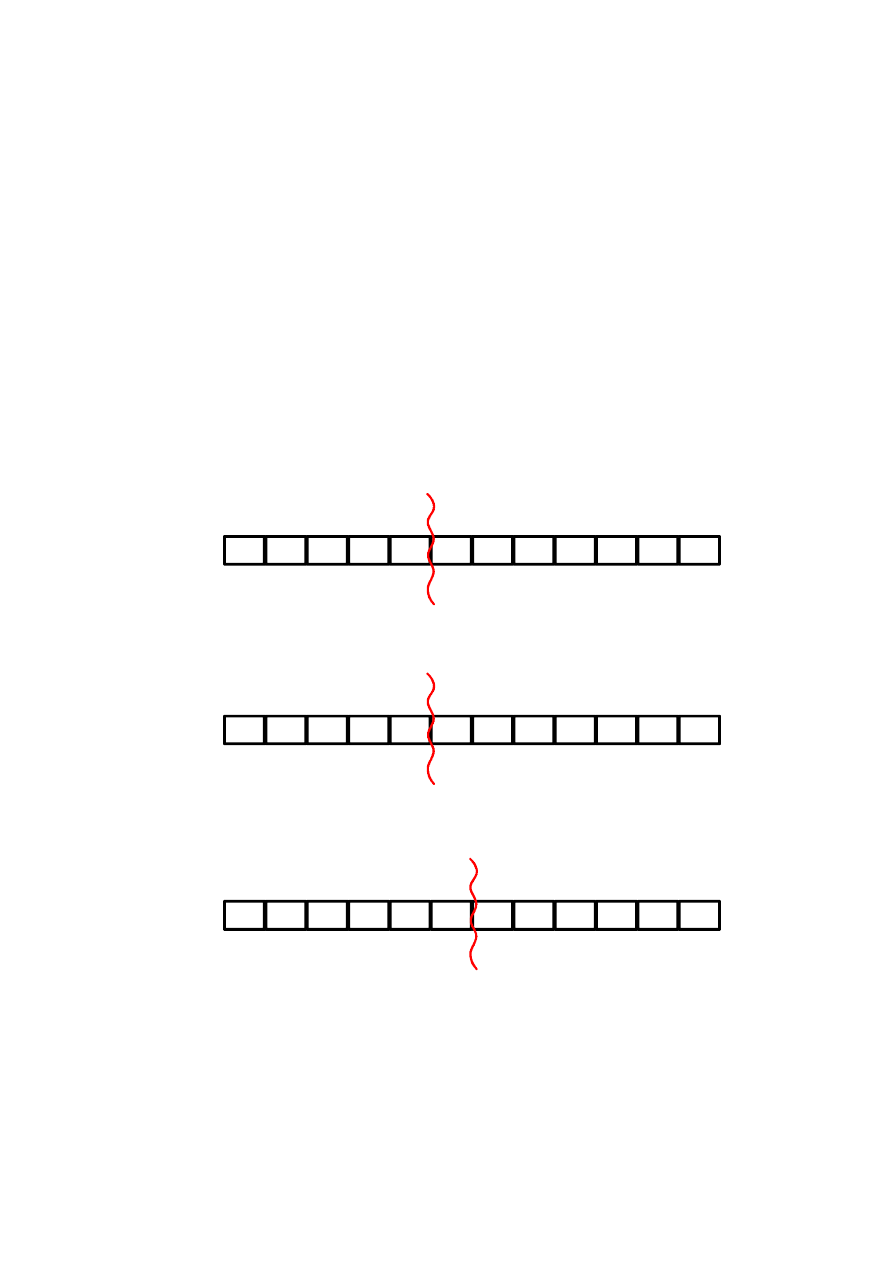
Kluczowe w metodzie Quicksort jest dokonanie podziału tablicy, który

ma spełniać kryterium z zachowaniem odpowiedniej wydajności całego
algorytmu. W przedstawionym przykładzie funkcja partition szuka granicy
podziału na dwie podtabele rozpoczynając od przyjęcia wartości początkowej
zmiennej piv, np. jako skrajnego lewego elementu tablicy. Zmienna piv nie
będzie zmieniać wartości dla danego wywołania funkcji partition. Podział
tablicy zostanie dokonany według granicznej wartości zmiennej piv – granica
będzie przebiegać z lewej lub prawej strony elementu o wartości piv, przy
czym sam element o wartości piv może ale nie musi być tuż przy samej granicy
podziału. Zatem nastąpi podział odpowiednio na elementy mniejsze od piv
oraz elementy większe lub równe piv albo na elementy mniejsze lub równe piv
i większe od piv.

piv

elementy >= piv

elementy < piv

elementy > piv

elementy <= piv

piv

LUB

piv

elementy >= piv

elementy < piv

LUB

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

24/36

Nie można zapominać, że do wykonania sortowania potrzebne będą

przestawienia wartości. Funkcja partition rozpoczyna porównania elementów
z wartością piv od prawej strony tabeli w poszukiwaniu elementu o wartości
mniejszej lub równej piv - jako kandydata do przeniesienia do lewej podtabeli.
Jeśli go znajdzie poszukuje następnie począwszy od lewej strony i przesuwając
się w prawo elementu, który jest większy lub równy piv. Jeśli funkcja znajdzie
dwóch kandydatów – lewy i prawy warunek spełniony (TRUE) może dojść do
zamiany miejscami pod warunkiem, że granice poszukiwań jeszcze się
wzajemnie nie wyminęły. W przypadku wyminięcia granic poszukiwań
funkcja partition ma pewność właściwego ułożenia elementów i zwraca
granicę podziału w miejscu wyminięcia granic – z lewej lub prawej strony
elementu posiadającego wartość pierwotną piv. Podziały następują
rekurencyjnie, aż do rozdrobnienia tabeli na podtablice jednoelementowe,
których nie da się już dalej dzielić. W tym przypadku następuje powrót z
wywołań funkcji rekurencyjnych. W konsekwencji pojedyncze elementy są już
na swoich właściwych miejscach i nie jest wymagane scalanie.

Istotne w procesie sortowania jest znalezienie granicy podziału na

podtablice, co jest bezpośrednio związane z doborem wartości stojącej na
granicy podziału, np. zmiennej piv. W niektórych odmianach algorytmów
Quicksort próbowano wprowadzić pewien element losowy, np. zmierzając do
zjawiska doboru liczby średniej (mediany) w tabeli jako wartości granicznej
do podziału. Obliczanie wartości średniej może jednak przysporzyć zbyt dużo
operacji podnosząc złożoność obliczeniową. Pojawiły się też pomysły, aby
wybierać losowo trzy dowolne liczby z tablicy i dla nich liczyć wartość średnią
uzyskując w ten sposób wynik przybliżony.

Istnieją przypadki takiego rozkładu liczb na wejściu do algorytmu, które

mogą powodować wzrost złożoności obliczeniowej aż do wartości
pesymistycznej złożoności obliczeniowej

O(n

O(n

O(n

O(n

2222

).).).).

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

25/36

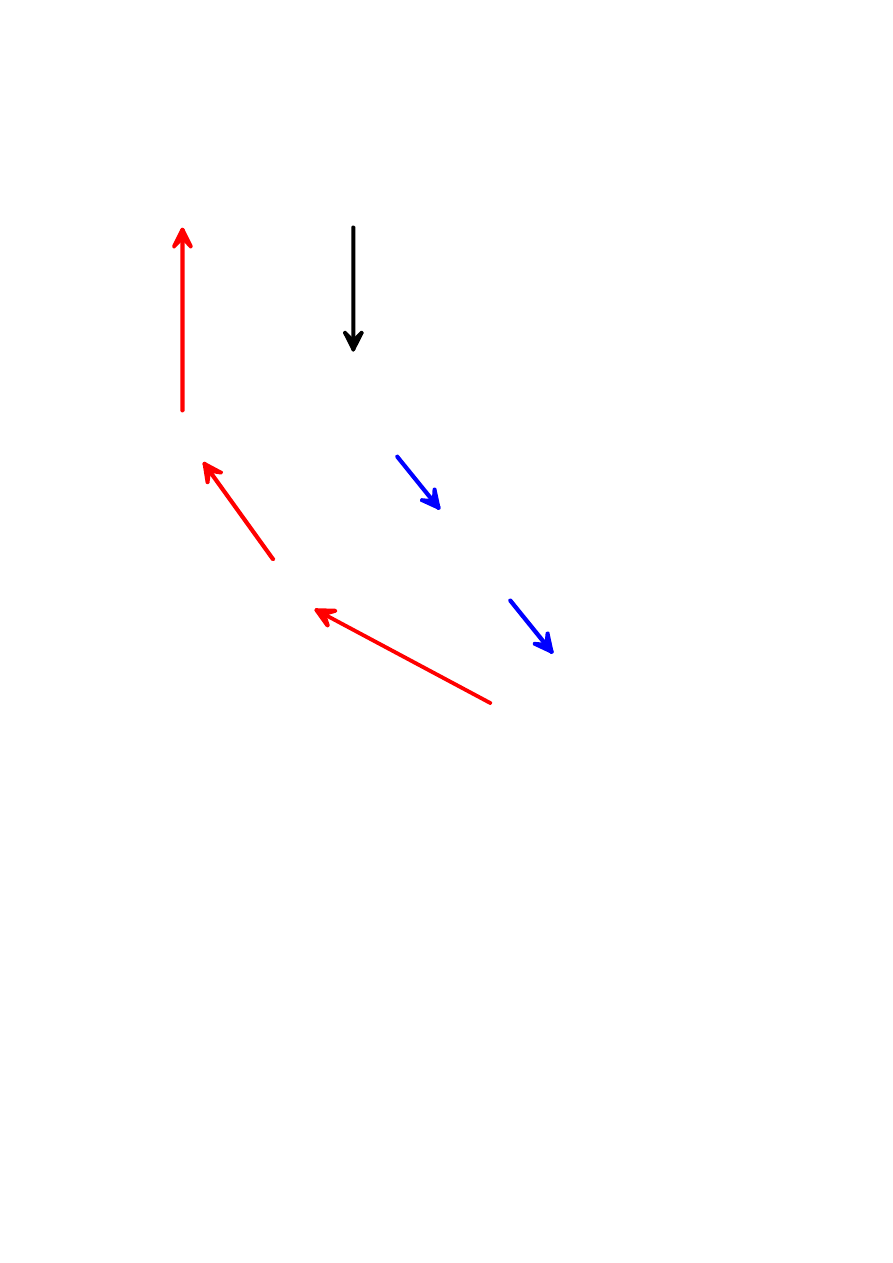
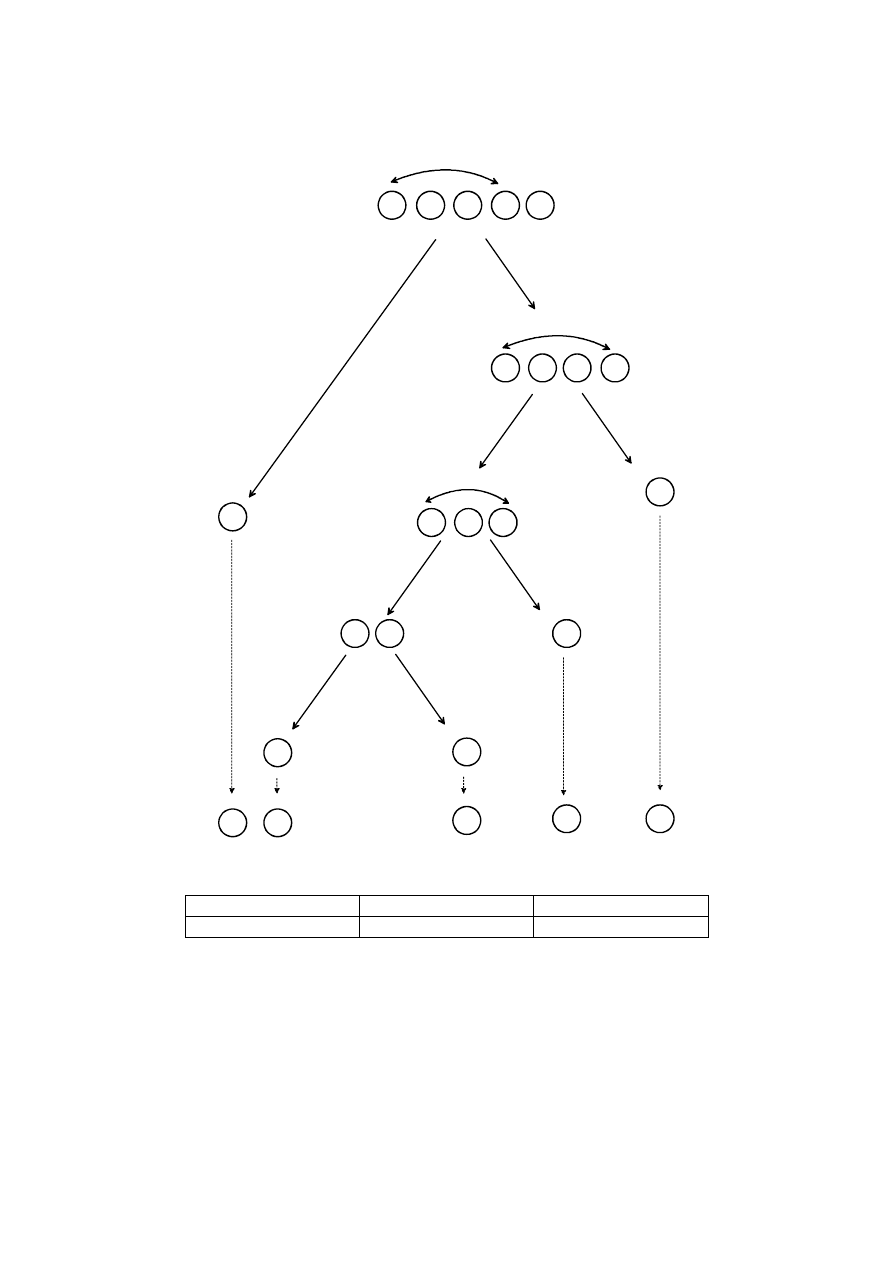
3

9

4

2

6

2

zamiana

9

4

6

3

zamiana

6

4

3

9

zamiana

3

4

6

3

4

2

3

4

6

9

Podziały na podtablice

Analiza złożoności obliczeniowej:

Pesymistyczna

Średnia

Optymistyczna

O(n

2

)

O(n

log n)

O(n log n)

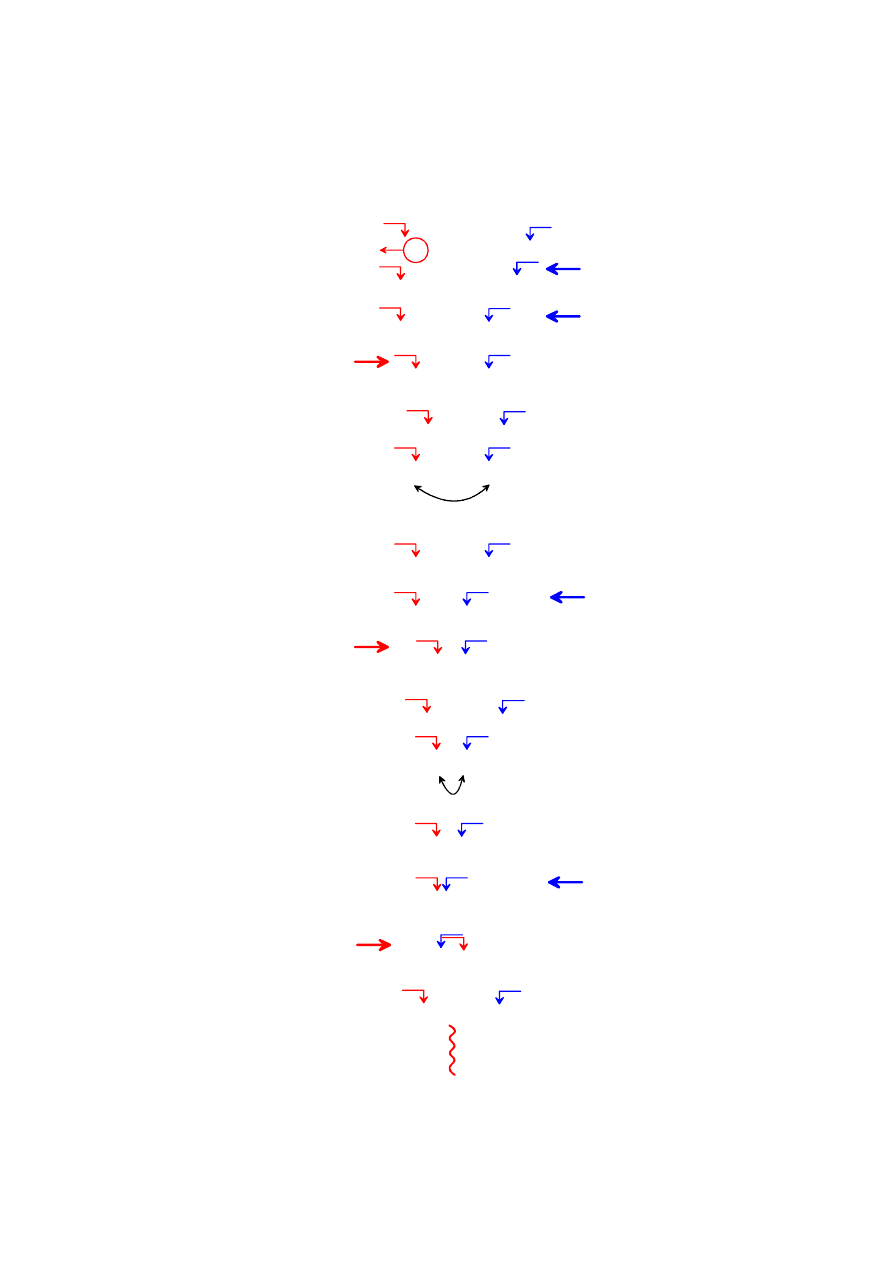
WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

26/36

3 9 1 2 6

piv=3

3 9 1 2 6

3 9 1 2 6

if (6 <=piv) ... (FALSE)

3 9 1 2 6

if (2 <=piv) ... (TRUE)

3 9 1 2 6

if (3 >=piv) ... (TRUE)

if ( przed ) (TRUE)

3 9 1 2 6

zamiana

2 9 1 3 6

if (1 <=piv) ... (TRUE)

2 9 1 3 6

2 9 1 3 6

if (9 >=piv) ... (TRUE)

if ( przed ) (FALSE)

return (granica podzialu)

KROK

(1)

(1)

(2)

(3)

(4)

(5)

(7)

(8)

(9)

(10)

(11)

(12)

FUNKCJA PARTITION

(6)

if (9 >=piv) ... (TRUE)

if ( przed ) (TRUE)

2 9 1 3 6

zamiana

2 1 9 3 6

2 1 9 3 6

if (1 <=piv) ... (TRUE)

2 1 9 3 6

2 1 9 3 6

(13)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

27/36

Efekt:
Przed sortowaniem: 3 9 4 2 6
..... Wejscie do quicksort: 0 4 -----> Partition zwraca: 0
..... Wejscie do quicksort: 0 0
...................Wyjscie z quicksort : 0 0
..... Wejscie do quicksort: 1 4 -----> Partition zwraca: 3
..... Wejscie do quicksort: 1 3 -----> Partition zwraca: 2
..... Wejscie do quicksort: 1 2 -----> Partition zwraca: 1
..... Wejscie do quicksort: 1 1
...................Wyjscie z quicksort : 1 1
..... Wejscie do quicksort: 2 2
...................Wyjscie z quicksort : 2 2
...................Wyjscie z quicksort : 1 2
..... Wejscie do quicksort: 3 3
...................Wyjscie z quicksort : 3 3
...................Wyjscie z quicksort : 1 3
..... Wejscie do quicksort: 4 4
...................Wyjscie z quicksort : 4 4
...................Wyjscie z quicksort : 1 4
...................Wyjscie z quicksort : 0 4
Po sortowaniu: 2 3 4 6 9

Przykład sortowania szybkiego dla ciągu <

3,9,4,2,6

>

#include <iostream>
using namespace std;

int

partition

(int tab[], int p, int r){

//zgodna z animacja ze strony http

int piv = tab[p];
int i = p-1;
int j = r+1;
while (1) {
do {
j--;

//przesuwa wskazanie

j

w lewo

}

while

(

tab[j] > piv

);

do {
i++;

//przesuwa wskazanie

i

w prawo

}

while

(

tab[i] < piv

);

if

(

i<j

)

swap

(tab[i],tab[j]);

//gdy się wskazania i oraz j zrównają lub wyminą

else

return j;

}
}
void

quicksort

(int tab[], int p, int r){

cout << "..... Wejscie do quicksort: " << p << ' ' << r;

if (p < r) {
int q =

partition

(tab, p, r);

//zwraca miejsce podziału tablicy

cout << " -----> Partition zwraca: "<<q<<endl;

quicksort

( tab, p, q );

//sortowanie lewej części

quicksort

( tab, q+1, r );

//sortowanie prawej części

} else cout << endl;
cout << "...................Wyjscie z quicksort : " << p
<< ' ' << r << endl;
}void Wyswietl(int tab[], int n, char *komentarz){
int i;
cout<<komentarz<<"\t";
for (i=0; i<n; i++) cout<<tab[i]<<" ";
cout<<endl;
}
int main(){
int tablica[]={3,9,4,2,6};
Wyswietl(tablica,5,"Przed sortowaniem:");
quicksort(tablica,0,4);
Wyswietl(tablica,5,"Po sortowaniu:");
system("PAUSE");
return 0;
}

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

28/36

SORTOWANIE STOGOWE (ang. HEAPSORT)

Jest to metoda bardziej skomplikowana niż sortowanie bąbelkowe czy przez
wstawianie, ale za to działa w krótszym czasie.

KOPIEC / STÓG

Kopiec inaczej zwany stogiem jest szczególnym przypadkiem drzewa
binarnego, które spełnia tzw. warunek kopca tzn.

każdy następnik jest

niewiększy od swego poprzednika.

Z warunku tego wynikają szczególne

własności kopca:

•

w korzeniu kopca znajduje się największy element

•

na ścieżkach (połączeniach między węzłami), od korzenia do liścia,
elementy są posortowane nierosnąco (max-heap) lub niemalejąco (min-
heap)

•

drzewo jest wypełniane od strony lewej do prawej i pełne na wszystkich
poziomach, być może za wyjątkiem najniższego poziomu, który może
być napełniony od lewej strony, ale niedopełniony od prawej strony,

•

tablica posortowana w porządku

nierosnącym

jest kopcem max-heap.

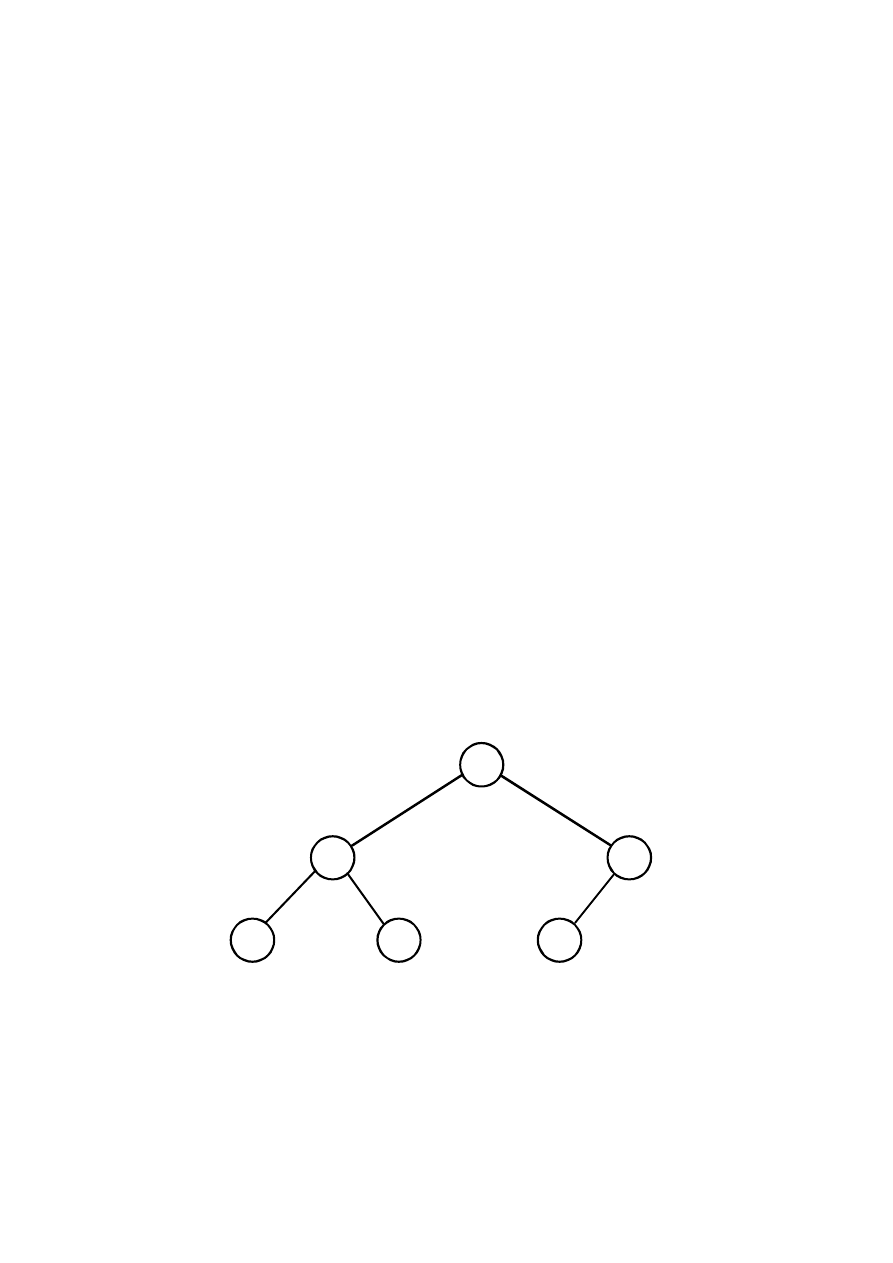
Przykładowy kopiec (max-heap):

16

8

4

10

8

12

korze

ń

w

ę

zeł

w

ę

zeł

li

ść

li

ść

li

ść

Tablica[] = {16,12,8,8,10,4}

1.

2.

3.

4.

5.

6.

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

29/36

Zakładając, że w tablicy znajdują się elementy do sortowania to z elementów
tablicy należy zbudować drzewo binarne:

•

Pierwszy element tablicy będzie korzeniem drzewa

•

Kolejne elementy będą stanowiły kolejne węzły od lewej do prawej.
Stąd, każdy następny i-ty element będzie miał co najwyżej dwa
następniki o numerach: 2*i +1 oraz 2*i+2

•

Łatwo stwierdzić, że dla każdego i-tego elementu (oprócz korzenia)
numer elementu w tablicy, będącego jego poprzednikiem określa się
wzorem: i / 2

Po zbudowaniu drzewa należy wykonać odpowiednie kroki, które zapewnią
mu cechy stogu:

•

Należy sprawdzać (poczynając od poprzednika ostatniego liścia idąc w
górę do korzenia) czy poprzednik jest mniejszy od następnika i jeżeli tak
to zamienić je miejscami.

Po wykonaniu tych czynności drzewo binarne staje się stogiem. Z jego
własności wynika, że

w korzeniu znajduje się największy element

. Zatem

można go zapisać na koniec tablicy, a na jego miejsce wstawić ostatni liść. Po
zabraniu korzenia tablica z drzewem zmniejsza się o 1 element, a porządek
kopca zostaje zaburzony, ponieważ nie jest wiadome, czy ostatni liść będący
teraz korzeniem jest największym elementem. By przywrócić cechy stogu
należy ponownie uporządkować drzewo. Po przywróceniu porządku w stogu
można znowu pobrać korzeń i wstawić go do tablicy wynikowej, a na jego
miejsce wstawić ostatni liść, co zmniejsza rozmiar tablicy źródłowej o 1.
Czynność jest powtarzana aż pozostanie tylko korzeń, który jest w danym
momencie najmniejszym, czyli pierwszym elementem w tablicy posortowanej.
W ten sposób tablica wynikowa zawiera posortowane elementy z tablicy
wejściowej.
Możliwe jest użycie pojedynczej tablicy, w ten sposób, że końcowy element
tablicy – jako ostatni liść będzie zamieniany z korzeniem w kolejnych cyklach
tworzenia stogów. Tym bardziej jest to możliwe, ponieważ liczba elementów w
kolejnych stogach będzie malała.

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

30/36

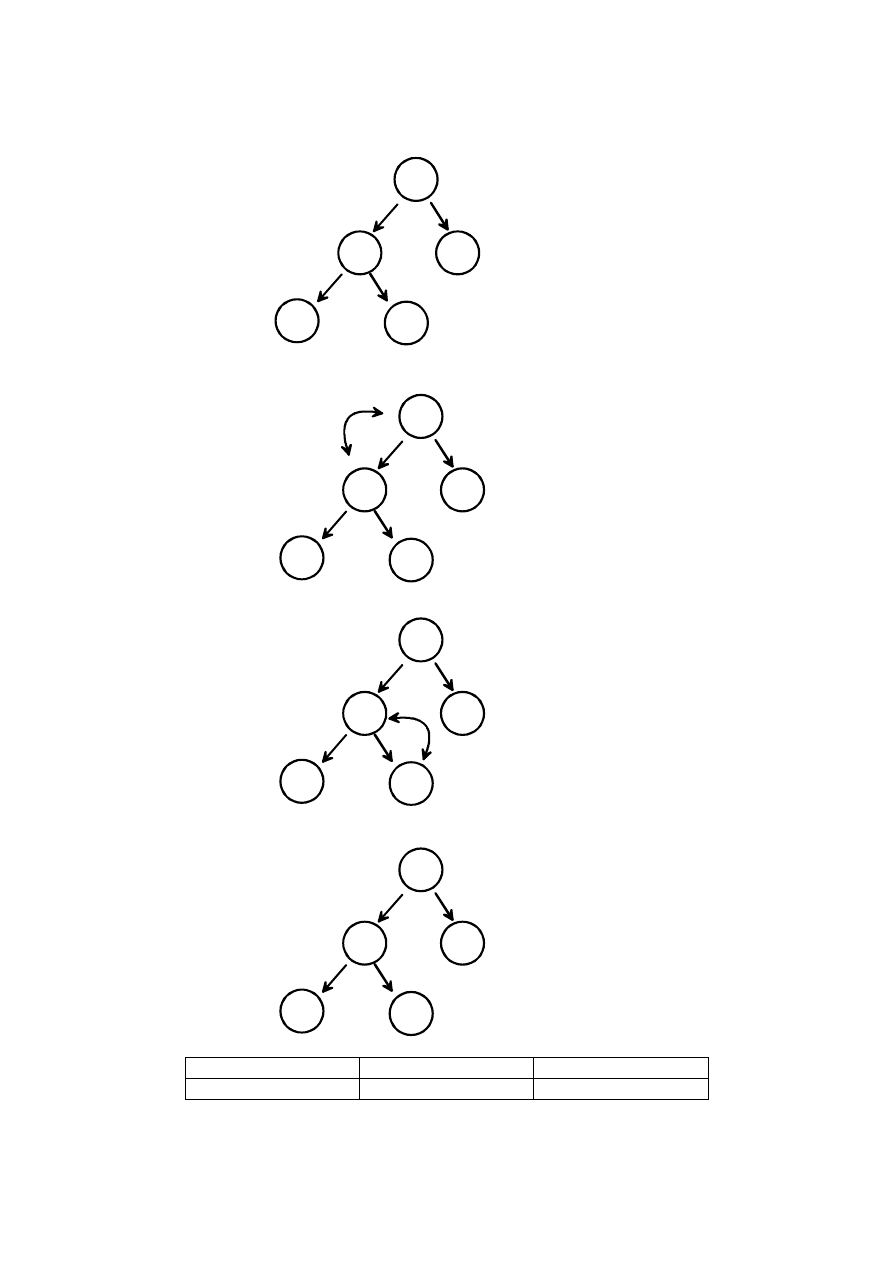
TABLICA: tab[] = {3,9,4,2,6}

3

3

4

4

6

9

2

DRZEWO BINARNE

3

3

4

4

6

9

2

Funkcja HEAPIFY

zamiana

3

4

4

9

6

2

Funkcja HEAPIFY

zamiana

3

4

4

9

2

STÓG

3

6

TABLICA: tab[] = {9,3,4,2,6}

TABLICA: tab[] = {9,6,4,2,3}

3

TABLICA: tab[] = {3,9,4,2,6}

Pesymistyczna

Średnia

Optymistyczna

O(n

log n)

O(n

log n)

O(n log n)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

31/36

Efekt:
Przed sortowaniem: 3 9 4 2 6
Pierwszy stog: 9 6 4 2 3
Kolejny stog: 6 3 4 2 Posortowane: 9
Kolejny stog: 4 3 2 Posortowane: 6 9
Kolejny stog: 3 2 Posortowane: 4 6 9
Kolejny stog: 2 Posortowane: 3 4 6 9
Po sortowaniu: 2 3 4 6 9

Przykład sortowania stogowego dla ciągu <

3,9,4,2,6

>

#include <iostream>
using namespace std;
void Wyswietl(int tab[], int n, char *komentarz, char koniec='\n'){
int i;
cout<<komentarz<<"\t";
for (i=0; i<n; i++) cout<<tab[i]<<" ";
cout<<koniec;
}
void

Heapify

(int tab[],int i,int HeapSize){

int

left

=2*i+1,

right

=2*i+2, max;

if

((left < HeapSize) && (tab[left] > tab[i]))

max = left;

else

max = i;

//zgodna z animacja ze strony http

if

((right < HeapSize) && (tab[right] > tab[max]))

max = right;

if

(max != i) {

swap

(tab[i],tab[max]);

Heapify

(tab,max,HeapSize);

//wywołanie rekurencyjne dla kolejnej

}

//gałęzi stogi – dwóch węzłów poniżej

}
void

HeapSort

(int tab[], int n){

int j,k,HeapSize=n;
for (j= HeapSize/2-1; j >= 0; j--)

//zbudowanie stogu po raz pierwszy

Heapify

(tab,j,HeapSize);

Wyswietl(tab,HeapSize,"Pierwszy stog:");
for (k= n-1; k>=1; k--) {

//przekładanie korzenia na koniec tabeli

swap

(tab[0],tab[k]);

HeapSize--;

//jako element ciągu posortowanego

Heapify

(tab,0,HeapSize);

//budowa kolejnych stogów

Wyswietl(tab,HeapSize,"Kolejny stog:",'\t');
Wyswietl(tab+HeapSize,n-HeapSize,"Posortowane:");
}
}
int main(){
int tablica[]={3,9,4,2,6};
Wyswietl(tablica,5,"Przed sortowaniem:");

HeapSort

(tablica,5); Wyswietl(tablica,5,"Po sortowaniu:");

system("PAUSE"); return 0;
}

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

32/36

SORTOWANIE PRZEZ SCALANIE (ang. MERGESORT)

Algorytm polega na

podziale

tablicy na dwie połowy tworzące od tej pory parę

i sortowaniu ich niezależnie.

Scalanie

jest procesem odwrotnym, który łączy

tablice należące do pary w ten sposób, że wybierane są kolejno mniejsze
elementy z najmniejszych elementów z obu tablic. W scalonej tablicy elementy
są posortowane.
Jeśli zjawisko dzielenia tablic będzie dokonywane wielokrotnie w sposób
rekurencyjny, to możliwy jest taki podział tablic aż do uzyskania

podtablic

jednoelementowych

. Wtedy w procesie scalania pary takich tablic

dokonywany jest wybór mniejszego elementu i powstaje posortowana tablica
dwuelementowa. Na drodze scalania par coraz liczniejszych tablic
dokonywane jest posortowanie całej tablicy.

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

33/36

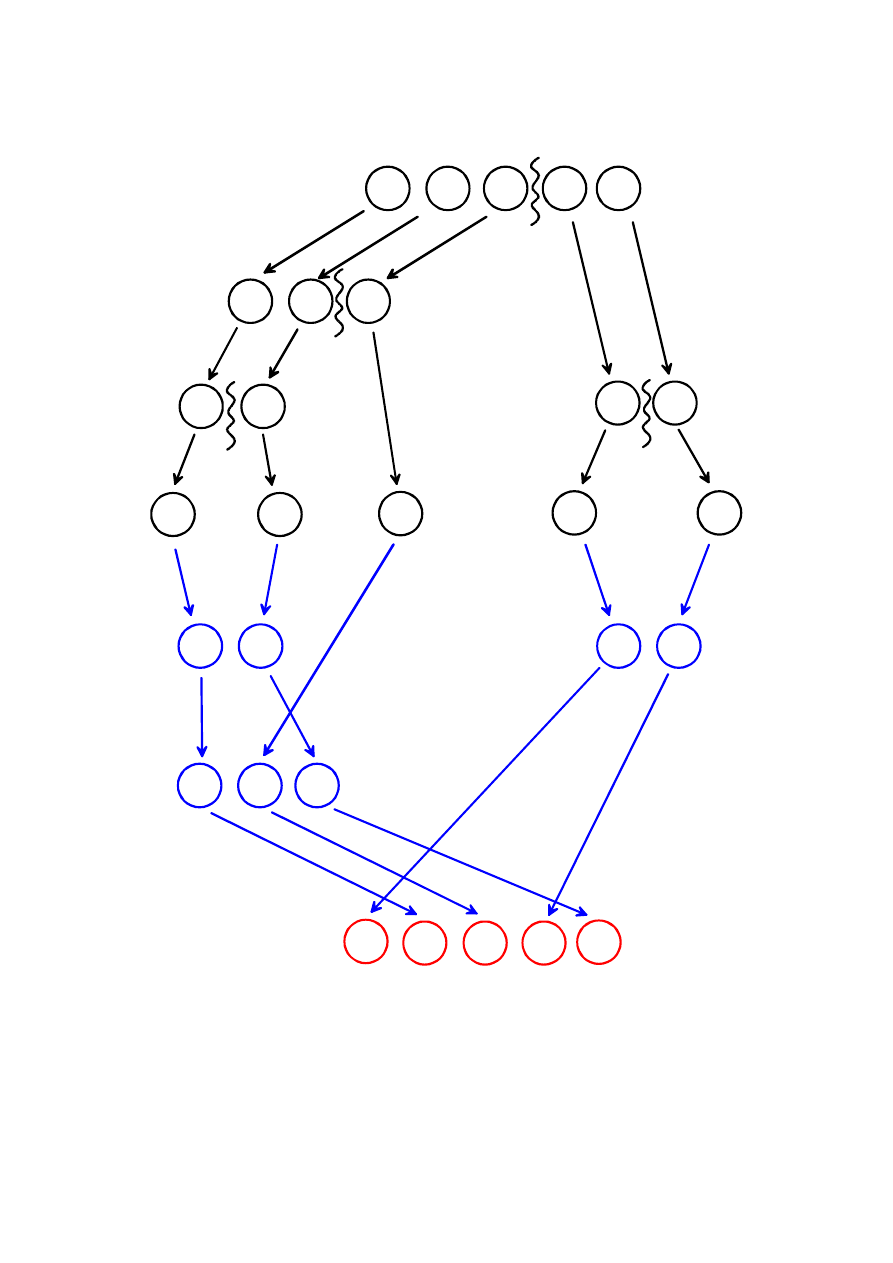
Podział

ciągu tab[]={

3,9,4,2,6

} w funkcji MergeSort na podtablice od

lo

do

hi

oraz

scalanie

(w tym sortowanie) podtablic podczas powrotów z wywołań

rekurencyjnych.

lo

...

hi

tab[0]

tab[1]

tab[2]

tab[3]

tab[4]

mid

0 ... 4

3

9

4

2

6

2

0 ... 2

3

9

4

1

0 ... 1

3

9

0

0 ... 0

3

0

Powrót z 0 ... 0

3

1 ... 1

9

1

Powrót z 1 ... 1

9

Powrót z 0 ... 1

3

9

2 ... 2

4

2

Powrót z 2 ... 2

4

Powrót z 0 ... 2

3

4

9

3 ... 4

2

6

3

3 ... 3

2

3

Powrót z 3 ... 3

2

4 ... 4

6

4

Powrót z 4 ... 4

6

Powrót z 3 ... 4

2

6

Powrót z 0 ... 4

3

4

9

2

6

Podczas powrotów z wywołań rekurencyjnych następuje scalanie podtablic z
jednoczesnym sortowaniem elementów tych podtablic (

na niebiesko

)

W konsekwencji cała tablica zostaje posortowania podczas ostatniego scalenia
(

na czerwono

).

Analiza złożoności obliczeniowej:

Pesymistyczna

Średnia

Optymistyczna

O(n

log n)

O(n

log n)

O(n log n)

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

34/36

3

3

4

4

6

9

2

3

3

4

4

6

9

2

4

3

3

9

4

6

2

3

3

9

9

3

3

4

9

6

2

3

2

4

6

9

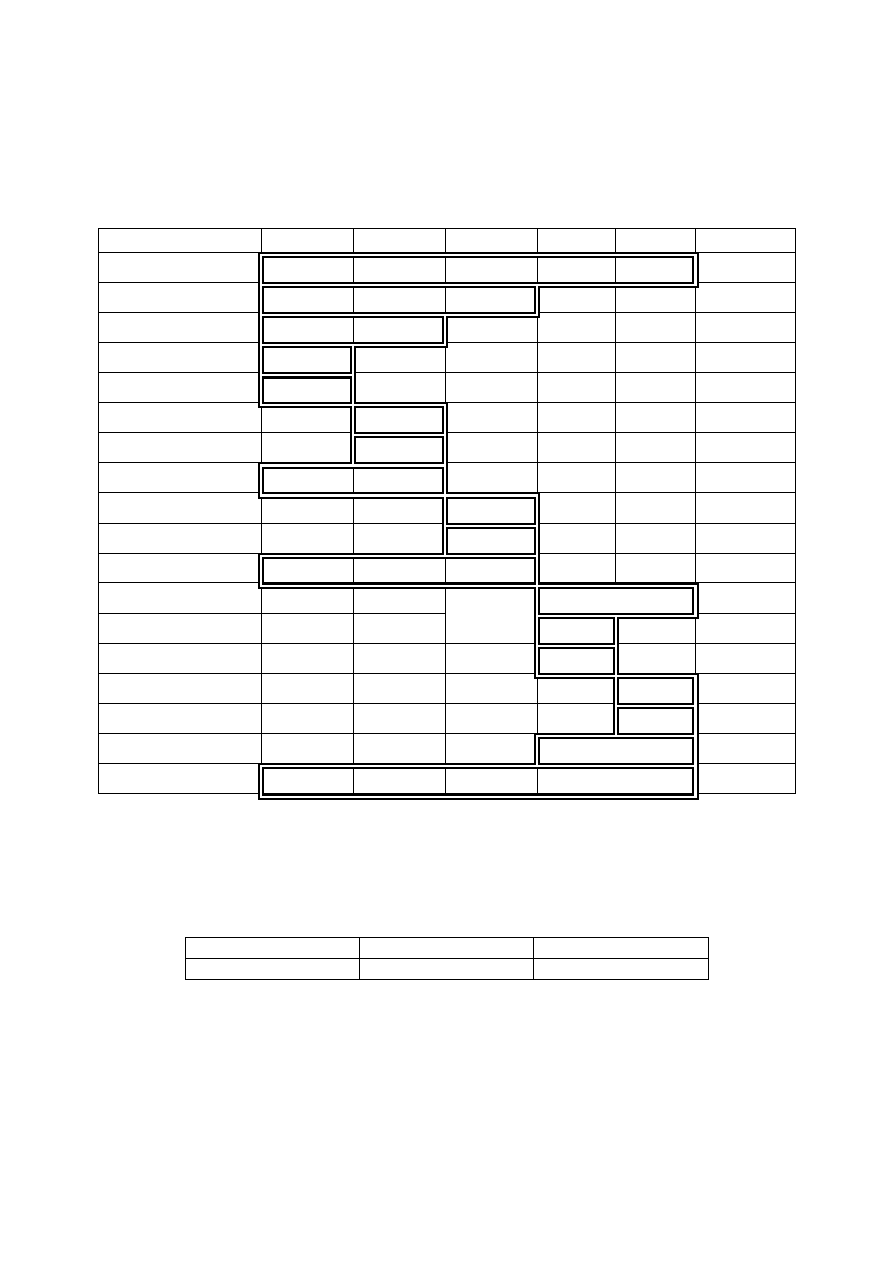
PODZIAŁ

SCALANIE

POSORTOWANE

WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

35/36

Efekt:
Przed sortowaniem: 3 9 4 2 6
..... Wejscie do mergesort: 0 4
..... Wejscie do mergesort: 0 2
..... Wejscie do mergesort: 0 1
..... Wejscie do mergesort: 0 0
...................Wyjscie z mergesort : 0 0
..... Wejscie do mergesort: 1 1
...................Wyjscie z mergesort : 1 1
...................Wyjscie z mergesort : 0 1
..... Wejscie do mergesort: 2 2
...................Wyjscie z mergesort : 2 2
...................Wyjscie z mergesort : 0 2
..... Wejscie do mergesort: 3 4
..... Wejscie do mergesort: 3 3
...................Wyjscie z mergesort : 3 3
..... Wejscie do mergesort: 4 4
...................Wyjscie z mergesort : 4 4
...................Wyjscie z mergesort : 3 4
...................Wyjscie z mergesort : 0 4
Po sortowaniu: 2 3 4 6 9

Przykład sortowania przez scalanie dla ciągu <

3,9,4,2,6

>

#include <iostream>
using namespace std;
void

mergesort

(int tab[], int lo, int hi){

//zgodna z animacja ze strony http

cout << "..... Wejscie do mergesort: " << lo << ' ' << hi<< endl;
int mid,L,H,k,buf[hi-lo+1];
if (lo < hi) {
mid = (lo+hi)/2;

//podział tablicy na pół

mergesort

( tab, lo, mid );

//rekurencyjne sortowanie niższej połowy

mergesort

( tab, mid+1, hi );

//rekurencyjne sortowanie wyższej połowy

L=lo; //początek niższej połowy
H=mid+1; //początek wyższej połowy

for

(k=lo;k<=hi;k++)

if

((L<=mid)&&((H>hi)||(tab[L]<tab[H]))) {

buf[k]=tab[L];

//zapisz posortowane do bufora

L++;
}

else

{

buf[k]=tab[H];

//zapisz posortowane do bufora

H++;
}

for

(k=lo;k<=hi;k++)

tab[k]=buf[k]; //przepisz z bufora do tab
}
cout << "...................Wyjscie z mergesort : " << lo
<< ' ' << hi << endl;
}
void Wyswietl(int tab[], int n, char *komentarz){
int i;
cout<<komentarz<<"\t";
for (i=0; i<n; i++) cout<<tab[i]<<" ";
cout<<endl;
}
int main(){
int tablica[]={3,9,4,2,6};
Wyswietl(tablica,5,"Przed sortowaniem:");

mergesort

(tablica,0,4);

Wyswietl(tablica,5,"Po sortowaniu:");
system("PAUSE"); return 0;
}

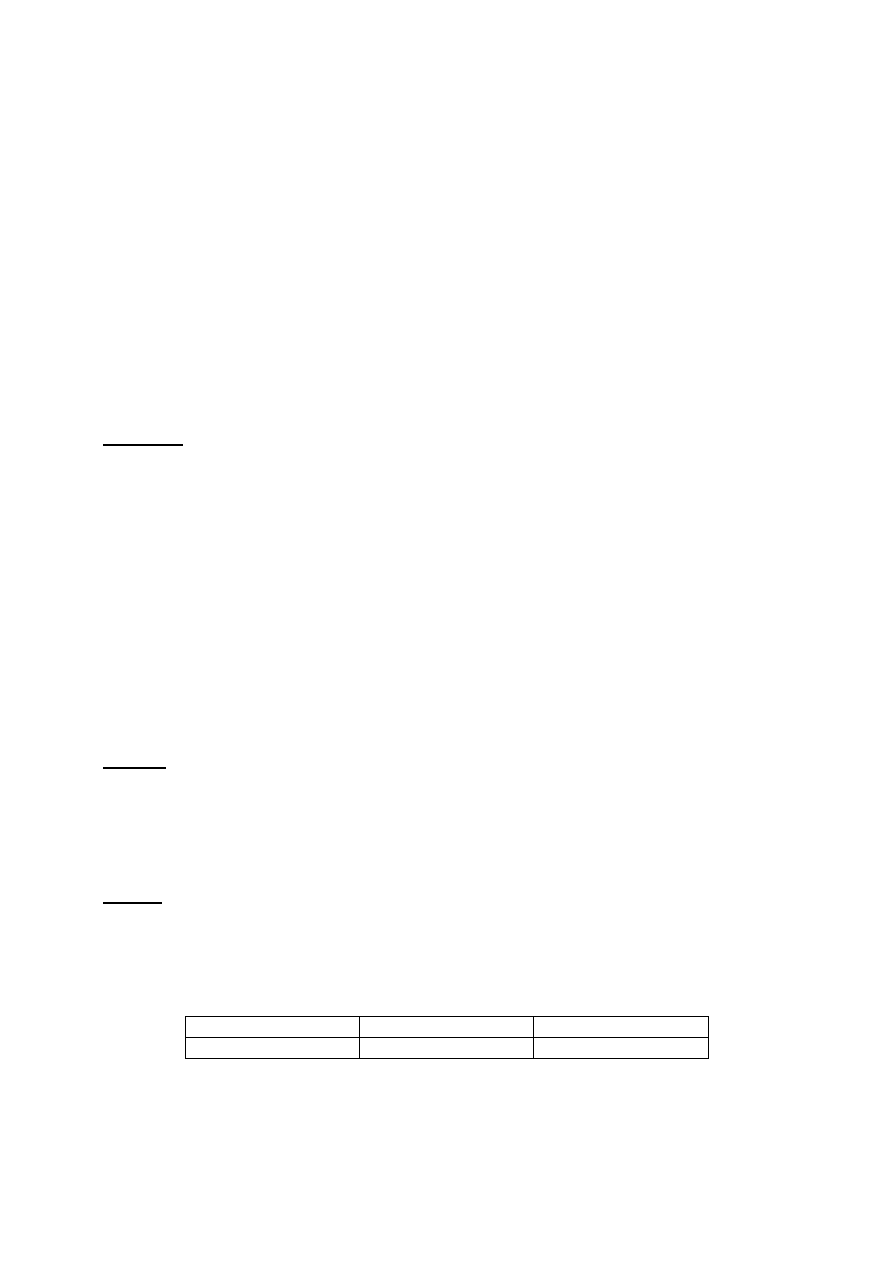
WYKŁADY cz.3 v.5 (2010) Podstawy programowania

(dr.inż Marcin Głowacki)

36/36

SORTOWANIE PRZEZ ZLICZANIE (ang. COUNTINGSORT)

Sortowanie przez zliczanie ma jedną

WIELKĄ

zaletę

i jedną równie

WIELKĄ

wadę

:

•

Zaleta

: działa w czasie liniowym (jest szybki)

•

Wada

: może sortować wyłącznie liczby całkowite

Obydwie te cechy wynikają ze sposobu sortowania. Polega ono na liczeniu, ile
razy dana liczba występuje w ciągu, który mamy posortować. Następnie
wystarczy utworzyć nowy ciąg, wykorzystując dane zebrane wcześniej.

Przykład – sortowanie przez zliczanie ciągu: 3,6,3,2,7,1,7,1.
Po zliczeniu (w jednym kroku) operujemy danymi na temat liczebności
wystąpień:

•

Liczba 1 występuje 2 razy

•

Liczba 2 występuje 1 raz

•

Liczba 3 występuje 2 razy

•

Liczba 4 występuje 0 razy

•

Liczba 5 występuje 0 razy

•

Liczba 6 występuje 1 raz

•

Liczba 7 występuje 2 razy

Na podstawie tych danych tworzymy ciąg: 1,1,2,3,3,6,7,7. Jest to ciąg
wejściowy, ale posortowany.
Zalety:

1. Proces zliczania odbył się w jednym kroku
2. Nie doszło do ani jednej zamiany elementów
3. Proces tworzenia tablicy wynikowej odbył się w jednym kroku

Wady:

1. Do przechowywania liczby wyrazów ciągu musimy użyć tablicy, o liczbie

elementów równej największemu elementowi ciągu

2. Sortować można jedynie liczby całkowite

Pesymistyczna

Średnia

Optymistyczna

O(n

+ k)

O(n

+ k)

O(n

+ k)

Gdzie k to długość przedziału, do którego należą liczby n.