PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 86 NR 12/2010                                                     319 

Jiefeng XIONG

1,2

,Bolin WANG

1

  

Hohai University (1), Nanjing University of Information Science and Technology (2) 

 
 

Measuring power system harmonics and interharmonics by 

envelope spectrum analysis 

 
 

Abstract. An envelope spectrum analysis-based algorithm for harmonics and interharmonics estimation is proposed. First the envelope is extracted 
with narrow band Hilbert transform. Then the spectrum of the envelope and the harmonic components are calculated with windowing and 
interpolation method. Finally the interharmonic parameters are restored according to amplitude modulation equation. The proposed method has two 
distinguish features, first, it is able to confirm if the calculated interharmonic components do exist, and second, it is not affected by the spectral 
leakage caused from the harmonics. Several simulation examples are given to demonstrate the precision, effectiveness, and feasibility. 
 
Abstract. Zaproponowano algorytm analizy widmowej umożliwiający określanie składowych harmonicznych. Najpierw wydzielana jest obwiednia 
przy wykorzystaniu wąskopasmowej transformaty Hilberta. Następnie obliczane jest widomo obwiedni i składowych harmonicznych metodami 
interpolacyjnymi. Wreszcie parametry interharmonicznych są odtwarzane na podstawie równania modulacji amplitudowej. Zaproponowana metoda 
ma dwie istotne zalety – umożliwia obliczanie składowych interharmonicznych i nie jest obciążona wpływem przecieku od harmonicznych. 
Zaprezentowano kilka przykładów symulacji potwierdzających skuteczność metody. (Pomiary harmonicznych i interharmonicznych w 
systemach mocy metodą analizy spektralnej obwiedni).  
 
Keywords: harmonic analysis, interharmonic, envelope extraction, discrete Fourier transforms, spectral leakage. 
Słowa kluczowe: analiza widmowa, wydzielanie obwiedni, Dyskretna Transformata Fouriera. 
 
 

Introduction 

 

Accurate harmonic/interharmoincs analysis and 

measurement in electrical power systems are of particular 
importance, since a true and exact spectrum of a waveform 
provides a clear understanding of the causes and effects of 
waveform distortion.  

The most popular and effective algorithm for harmonics 

and interharmonics measurement is windowed discrete 
Fourier transform (DFT). When interharmonics are present, 
the direct application of the DFT with a constant sampling 
rate may lead to inaccurate measurement results due to the 
spectral leakage and picket fence effects[1-3]. These 
effects strongly increase difficulties in measuring 
interharmonics, which can even ‘create’ new interharmonic 
components (fake interharmonics) in the spectrum that do 
not exist at all[4].  

Various methods have been proposed to overcome these 

effects, especially the spectral leakage effect to obtain 
better estimates of the power harmonics or interharmonics. 
References [5-8] put forward methods based on windowing 
and interpolation in the frequency domain, in which the 
errors created by leakage are eliminated by windowing 
technique, and the errors by picket effects are reduced by 
the interpolation algorithm. A desynchronized processing 
technique was employed for harmonic and interharmonic 
analysis, in which harmonics are filtered out from the signal 
to obtain better estimates of the interharmonics [9]. An 
adaptive window width method based on correlation 
calculation can be found in [10], and claimed suffering no 
leakage effect. In [11], the time-domain averaging was used 
for harmonic processing, and then a difference filter for the 
improved detection of interharmonics was proposed. 
Interharmonic-subgroups were recommend by the IEC 
group to reduce the spectral leakage problem, which aims 
at standardization, simplification and unification, more 
details can be found in [12-13]. 

Anyway, it is well known that a through solution for the 

problems due to the DFT spectral leakage is to select 
window width as an exact multiple of all signal periods, 
which is called the synchronization of the sampling 
procedure. However synchronizing to interharmoics is 
practically infeasible because their frequencies are usually 
unpredictable or the necessary window width is too large. 

Reference [14] uses wavelets for spectral estimation to 

reduce the spectral leakage problem. Modern signal 

processing technique based on advanced spectrum 
estimation were also used for harmonic and interharmonic 
analysis, which theoretically has an infinitely frequency 
resolution, and their improvements can be found in [15-17]. 
Whereas, spectrum estimation methods operate effectively 
only on the narrow-band signal in frequency domain which 
has limited components. Moreover, the computational 
burden may result sensibly increased when high accuracy 
is required.  

In this paper an envelope spectrum analysis-based 

method is proposed for interharmonics estimation of 
signals. The proposed method focuses on the point that the 
envelope of the power system signal contains information 
for interharmonic estimation. The method extracts the 
envelope of the signal, calculates its spectrum, and then 
restores the interharmonic parameters according to 
amplitude modulation equation. It is shown that the effects 
(or fake interharmonics), caused by the spectral leakage 
from harmonics, can be avoided with the proposed method. 
The new method benefits higher computing speed and 
more stable than advanced spectrum estimation-based 
method, and more accurate than traditional DFT-based 
method. 

The organization of this paper is as follows. The 

relationship between interharmonics, voltage fluctuation and 
voltage flicker are recalled in section II. The interharmonics 
measurement method based on envelope spectrum 
analysis is proposed in section III. Then, simulation results 
to demonstrate the precision, feasibility and robustness of 
the algorithm are presented in section IV. At last the 
conclusions are given in section V. 

 

Interharmonics, voltage fluctuation and voltage flicker 

Interharmonics, voltage fluctuation and voltage flicker 

have an inherent relationship. At steady state without any 
disturbance, the voltage waveform in a power system is 
sinusoidal with constant amplitude. When a voltage 
waveform contains interharmonics (generated from the 
operation of fluctuating loads), the peak and RMS 
magnitudes of the waveform will fluctuate. This is because 
the periods of the interharmonics components are not 
synchronous with the fundamental frequency cycle. Figure 
1 shows the waveform of 

320                                                    PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 86 NR 12/2010 

(1) 

 













( ) sin 2 50

0.05sin 2 45

/ 2

         0.05sin 2 55

/ 2

y t

t

t

t





















  

  It contains a fundamental component (50Hz) and two 
interharmonics (45Hz and 55Hz), and its envelope appears 
with a noticeable 5Hz fluctuation. 

 

Fig. 1. Amplitude modulation voltage waveform caused by 
interharmonics  
 

If the fluctuation magnitude is sufficiently large and the 

fluctuation frequency is in a range perceptible by human 
eyes (0.5 to 30Hz), a light flicker will occur. Consequently, a 
conclusion can be drawn that if there are interharmincs in 
the signal, a voltage flicker or a modulation of the voltage 
waveform will occur, and vice versa. 

It should be mentioned that the summations of one or 

more small interharmonics to fundmental frequency can 
always be interpreted in terms of amplitude modulation and 
phase modulation [18]. However, the most traditional 
approach to study the voltage flicker (voltage fluctuation) is 
based on amplitude modulation [19] and a voltage with an 
amplitude modulation can be described as 
 (2) 









1

1

1

( )

1

( )

sin 2

y t

d t A

f t





 



   

 where d(t) is the ‘envelope’(modulating signal), A

1

, f

1

,and 

Φ

1

 are the fundamental amplitude, frequency, and phase of 

the system individually. 
 

Due to the load characteristics, d(t) can be cyclic, such 

as operation of a reciprocation pump. And it also can be 
stochastic, such as operating electric arc furnaces [20]. 
With no additional explanation, only periodic modulating 
signal is considered in this paper, and d(t)  can be 
expressed as 

(3) 





1

( )

sin 2

L

l

l

l

d t

D

l

t













   

 

where  D

l

  and  θ

l

  are amplitude and phase of the  lth 

harmonic component of d(t), η is the fundamental frequency 
of d(t). It should be noted that although the flicker model (2) 
is still needs to be improved, many field measurement 
results demonstrate its effectiveness in calculating voltage 
flicker and identifying the interharmonic polluters [20-23]. 
  When harmonics are considered, a more complex 
model can be expressed as: 

 (4)   









1

1

( )

1

( )

sin 2

M

m

m

m

y t

d t

A

m f t







 





 

If we substitute (3) into (4), this will yield 

 

 

(5) 













1

1

1

1

1

( )

sin 2

sin 2

sin 2

M

m

m

m

L

M

l

l

m

m

l

m

y t

A

m f t

D

l

t

A

m f t





 



























 

 













1

1

1

1

1

1

sin 2

sin 2

sin 2

M

m

m

m

M

m

m

m

A

m f t

D

t

A

m f t





 























 

 









2

2

1

1

sin 4

sin 2

M

m

m

m

D

t

A

m f t

 

















 

 









1

1

sin 2

sin 2

M

L

L

m

m

m

D

L

t

A

m f t

 

















 

 





























1

1

1 1

1

1

1

1 1

1

1

1

2 1

1

1

2

2 1

1

1

2

1

1

1

1

1

sin 2

1

cos 2

2

1

cos 2

2

1

cos 2

2

2

1

cos 2

2

2

1

cos 2

2

1

cos 2

2

M

m

m

m

L

L

L

L

L

A

m f t

D A

f

t

D A

f

t

D A

f

t

D A

f

t

D A

f

L t

D A

f

L t









 





 





 





 





 





 













 













 















 













 



















 































    

























1

1

1

1

1

1

2

1

2

2

1

2

1

1

1

cos2

2
1

cos2

2
1

cos2

2

2
1

cos2

2

2

1

cos2

2

1

cos2

2

M

M

M

M

M

M

M

M

L M

M

L

L M

M

L

D A

Mf

t

D A

Mf

t

D A

Mf

t

D A

Mf

t

D A

Mf

L t

D A

Mf

L t































































































































































 

 From (5), it can be known that if η is not integral multiple 

of  f

1

, components with frequency  (f

1

±η),  (f

1

±2η),…, (f

1

±Lη), 

(2f

1

±η), (2f

1

±2η),…(2f

1

±Lη),…(Mf

1

±η) (Mf

1

±2η), … (Mf

1

±Lη) 

are all interharmonics. We can also find that the envelope 
signal  d(t)  never changes the amplitude and phase of 
harmonic components’, and it only ‘produces’ 
interharmonics. Note that if  Lη< f

1

/2  is also satisfied, each 

interharmoic component will appear once in (5), and great 
simplification of interharmonic measurement can be 
achieved. 

 

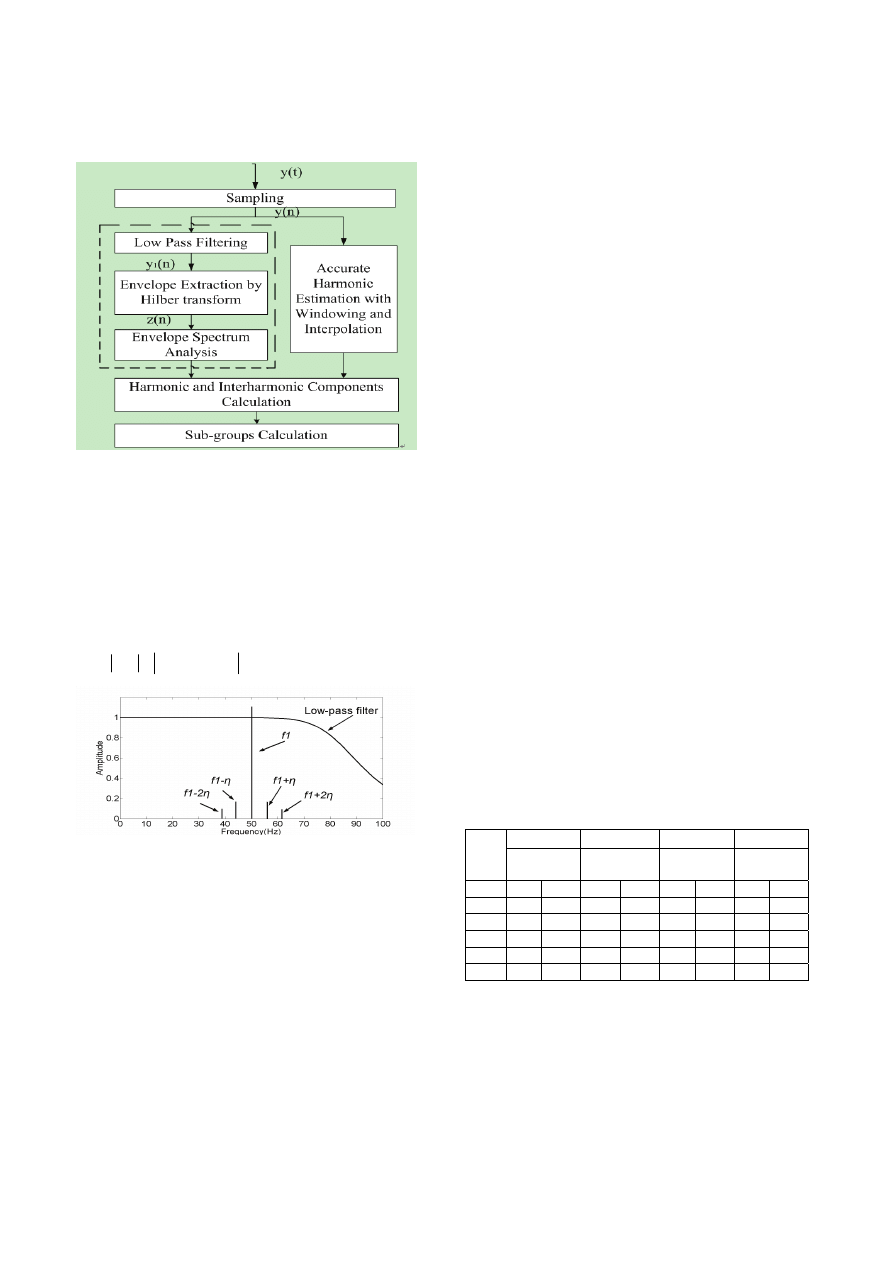
Envelope spectrum analysis-based method 

Based on the above discussion, the new measurement 

algorithm for power system harmonics and interharmonics 
is completely presented with the help of the flowchart 
(Figure 2) in this section. The phases of θ

l

  and  Φ

1

  are 

assumed to be zero, and this will simplify the calculations 
without affecting the interpretation of the algorithm. 

The signal y(t) is digitized with equally sampling space T

s

 

in the sampling block, thus the output of this block is 

(6)   









1

1

1

( )

1

sin 2

sin 2

L

M

l

s

m

s

l

m

y n

D

l

nT

A

m f nT













 













 

The low pass filtering block is composed of a sixth order 

Butterworth low-pass filter with an 85Hz cut-off frequency. 
The amplitude response of this filter is shown in Figure 3. 

 

PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 86 NR 12/2010                                                     321 

This low-pass filter gives a strong attenuation at frequencies 
higher than 85Hz. Consequently, the terms of (5) that 
include frequencies of  (2f

1

±η), (2f

1

±2η),…(2f

1

±Lη),…(Mf

1

±η) 

(Mf

1

±2η), … (Mf

1

±Lη)  are suppressed. The elimination in (5) 

of all these components leads to the following expression: 

 

 
 
 

 

 
 

Fig. 2. Flowchart of the envelope spectrum analysis-based method 

(7) 









1

1

1

1

( )

1

sin 2

sin 2

L

l

s

s

l

y n

D

l

nT

A

f nT

























 

If Hilbert transform is applied to (7), it yields 

(8) 









1

1

1

1

ˆ ( )

1

sin 2

cos 2

L

l

s

s

l

y n

D

l

nT

A

f nT

























 

The analytic signal constructed by (7) and (8) is 

expressed as 
(9) 

1

1

ˆ

( )

( )

( )

z n

y n

jy n





 

And its amplitude takes the following form 

(10)  





1/ 2

2

2

1

1

1

1

ˆ

( )

( )

( )

1

sin 2

L

l

s

l

z n

y n

y n

A

D

l

nT



























 

 
 
 
 
 
 
 
 
 
 

Fig. 3. Amplitude response of the low-pass filter 
 

It is important to note that (10) only contains the dc 

component and periodic envelope d(n).  With DFT based 
method, the spectrum of (10) can be obtained, and then the 
spectrum of   y(t)  can be calculated according to (5) if the 
parameters of harmonics have been obtained. 

The following summarizes major steps of the solution for 

harmonic and interharmonics measurement. 
1.  digitize the estimated signal  y(t)  with equally sampling 

space for nearly S periods, note that window width 
should cover at least one period of the envelope and 
the synchronous error should be as little as possible. 

2.  calculate the spectrum of integral harmonics of y(n) with 

DFT based algorithm, windowing and interpolation 
techniques are recommended in order to improve the 
measurement precision. In this paper, Hanning window 
is selected because it is characterized by a relatively 
narrow main lobe and fast-decaying side lobes.  

3.  extract modulating signal d(n) from  y(n), this can be 

accomplished by filter, Wavelet transform and Hilbert-
Huang Transaction, and the narrow band Hilbert 
transform is employed in the paper.  

4.  calculate the spectrum of d(t) with DFT based algorithm 

when  d(t)  is periodic, and  Hanning window and 
interpolation are recommended again to obtain better 
results.  

5.  calculate the frequencies and amplitudes of each 

interharmonic using (5). 

6.  calculate the harmonic and interharmonic sub-groups 

according to IEC standards. 

 
Simulation results 

According to IEC standard, instrument precision for 

interharmonic analysis is tested with the input signal which 
contains fundamental component and only one 
interharmonic component.  It should be mentioned that, if 
this interharmonic locates far from the fundamental 
component in the spectrum, spectral leakage effect from the 
fundamental component can always be negligible for 
interharmonic measurement. Whereas, this tested signal is 
quite different from the practical waveform in power system, 
in which multiple harmonic and interharmonic components 
always exist. 

The proposed algorithm based on envelope spectrum 

analysis extracts the envelope (modulating) signal, 
calculates the spectrum of modulating signal, and then 
interharmonic parameters can be restored according to (5). 
In this way the effects (or fake interharmonics), caused by 
the spectral leakage from harmonics, can be eliminated, it is 
more accurate for interharmonic analysis than traditional 
methods in the real world. 

Four simulations are performed in Matlab6.5 to 

demonstrate the effectiveness of the proposed algorithm. 
The sampling frequency for all the experiments is 10KHz. 
 
A) Waveforms with only Harmonics 

Synchronization characteristics of both the proposed 

method and the IEC technique are studied in this section. 
The signal x(t)=220×√2sin(2πft)+220×√2sin(6πft) is 
considered in the case, which consists of the fundamental 
component and the 3rd harmonic. The ideal fundamental 
frequency f is assumed to be 50 Hz and it is assumed to be 
varying from 49.5Hz to 50.5Hz. The harmonic and 
interharmonic subgroup evaluated with both the new 
method and the IEC technique are given in Table 1.  

 

Table 1. Absolute errors in calculating harmonic-subgroup and 
interharmonic-subgroup 

f(Hz) 

Gsg,1（V） 

Gisg,1（V） 

Gsg,3（V） 

Gisg,3（V） 

True value 

(220V) 

True value 

(0V) 

True value 

(35V) 

True value 

(0V) 

 

IEC 

NEW  I E C NEW 

IEC 

NEW 

IEC 

NEW 

50.00 

0 0  0  0 0 0 0 0 

50.05 

0.11 0 1.73 0 0.20 0 1.13 0 

50.50 

2.61 0 17.57 0 2.36 0 9.16 0 

49.95 

0.06 0 1.71 0 0.15 0 1.13 0 

49.5 

1.85 0 16.00 0 2.30 0 8.99 0 

 
With IEC technique, errors can always be observed on 

the harmonic/interharmonic sub-groups estimation in the 
case of loss of synchronization, and accurate results can 
only be obtained under synchronous sampling(f=50Hz). 
Special notice should be taken that, under asynchronous 
sampling,  Gisg,1 and Gisg,3 are ‘fake’ interharmonic 
components caused by spectral leakage effect from the 
harmonics. 

Whereas, the proposed method based on demodulation 

spectrum analysis is not affected by asynchronous 

322                                                    PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 86 NR 12/2010 

sampling, and so no fake interharmonics are found. For 
simplicity, the calculation procedures with only f=50.5Hz is 
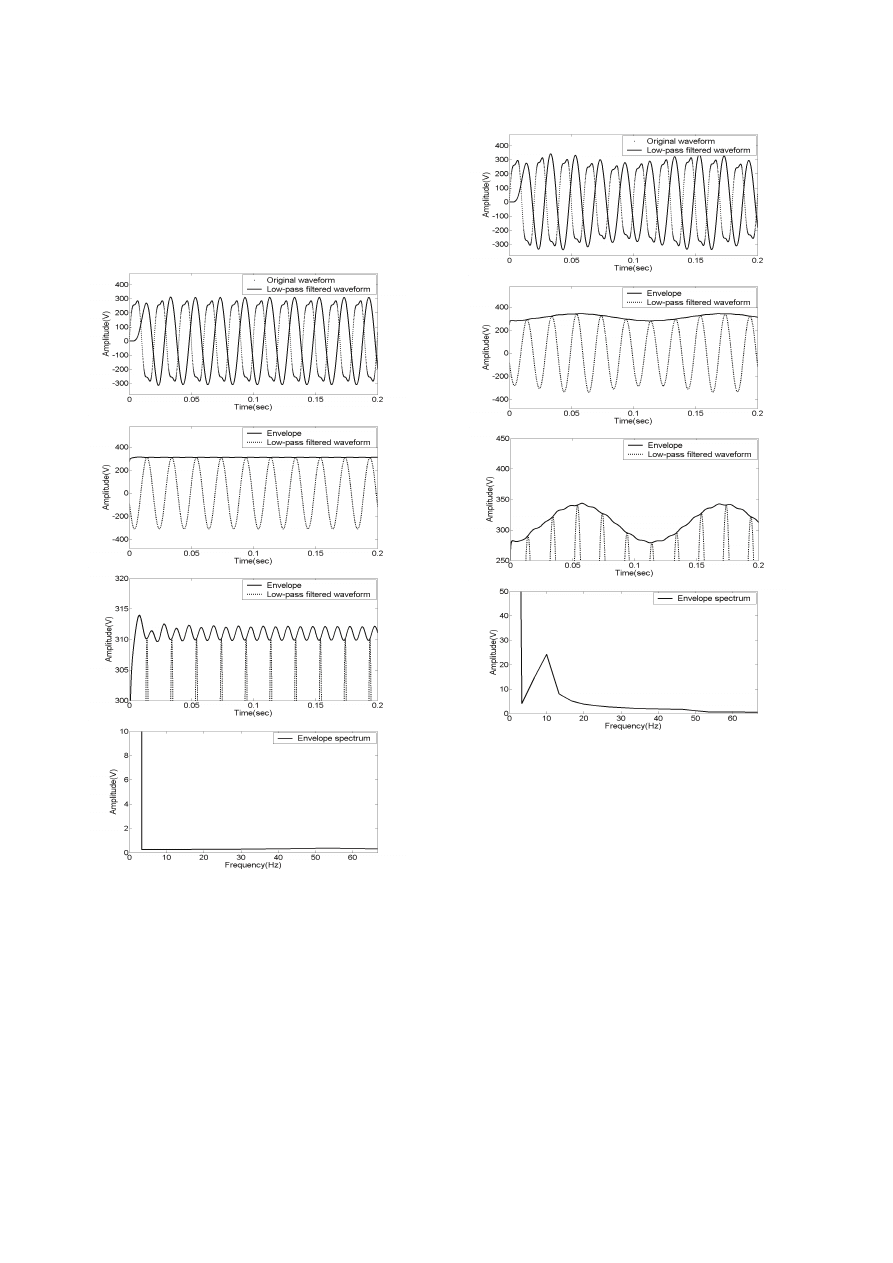
shown in Figure 4. From figure 4.a, we can find that the 
original waveform and low-pass filtered waveform are not 
amplitude modulated due to containing no interharmoinc 
component, thus the amplitude of the demodulated signal 
(envelope) is almost constant as shown in figure 4.b.  And 
its detailed waveform is reported in figure 4.c. No frequency 
component (0.5 to 30Hz) can be found in the spectrum of 
the demodulated signal as shown in figure 4.d, which 
demonstrates no interharmonic component existing in the 
original signal. 

(a) 

(b) 

(c) 

(d) 

Fig. 4. Calculation procedures of envelope spectrum analysis-
based method for x(t).(a) original waveform and low-pass filtered 
waveform. (b)envelope of low-pass filtered waveform. (c) detailed 
waveform of (b). (d) amplitude spectrum of demodulated signal. 
 

As the harmonics components can be obtained 

accurately with windowing and interpolation technique, the 
new method leads to a considerable precision improvement 
compared with IEC method. 

 

B) Waveforms with harmonics and interharmonics 

The aim of this case is to test the accuracy of the 

proposed method compared with the IEC technique when 
signal containing both harmonics and interharmonics, which 
is expressed as x

1

(t)=[1+0.1×sin(2π×8.6t)] x(t). Figure 5 

shows the calculation procedures in the case of f=50.5Hz 
with the new method. It can be seen that the waveform is 
modulated by a low frequency component (8.6Hz), and so a 

nearly 10Hz component can be found in the spectrum of 
demodulated signal. This is helpful to confirm the existence 
of the interharmonic.  

(a) 

(b) 

(c) 

(d) 

Fig. 5. Calculation procedures of envelope spectrum analysis-
based method for x1(t).(a) original waveform and low-pass filtered 
waveform. (b)envelope of low-pass filtered waveform. (c) detailed 
waveform of (b). (d) amplitude spectrum of demodulated signal. 
 

With windowing and interpolation technique, modulation 

frequency and amplitude are, respectively, equal to 8.59Hz 
and 0.0999 and the parameters of harmonics and 
interharmonics can be obtained according to (5), and then 
the harmonic and interharmonic subgroups evaluated with 
both the proposed method and the IEC technique are given 
in Table 2. It is observed that the proposed method enjoys 
much more accuracy than the IEC technique as expected.

  

 

C) Waveforms with multiple Harmonics and 
Interharmonics 

Practically, waveforms in the power system always 

contain multiple harmonics and interharmonics 
components. The case in this simulation is to test the 
precision and stability of the new proposed method for 
complex signals. The signal model expressed as (3) and (4) 
is considered, in which M=21, A

m

=1/m（m is odd）, A

m

=1/40

（

m is even）, f=50.05Hz,  Φ

m

＝

0, L=1, D

l

＝

0.1/l, η=8.6 Hz,  

θ

l

 =0。 

 
 
 

 

PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 86 NR 12/2010                                                     323 

Table 2.

 

Absolute errors in calculating harmonic-subgroup and 

interharmonic-subgroup 

f(Hz) 

Gsg,1（V） 

Gisg,1（V） 

Gsg,3（V） 

Gisg,3（V） 

True value 

(220V) 

True value 

(11V) 

True value 

(35V) 

True value 

(1.75V) 

 IEC 

NEW IEC NEW IEC NEW IEC NEW 

50.00 

2.68 

-0.18 

-1.32 

-0.04 

0.39 

-0.03 

-0.08 

0.00 

50.05 

2.51 

-0.17 

-0.20 

-0.04 

0.17 

-0.02 

0.66 

0.00 

50.50 

-0.52 

-0.06 

12.90 

-0.04 

-2.25 

0.00 

7.92 

0.00 

49.95 

0.80 

-0.17 

-2.27 

-0.04 

0.56 

-0.02 

-0.31 

0.00 

49.5 

-0.49 

-0.06 

0.63 

-0.03 

-1.62 

0.00 

6.18 

0.00 

 
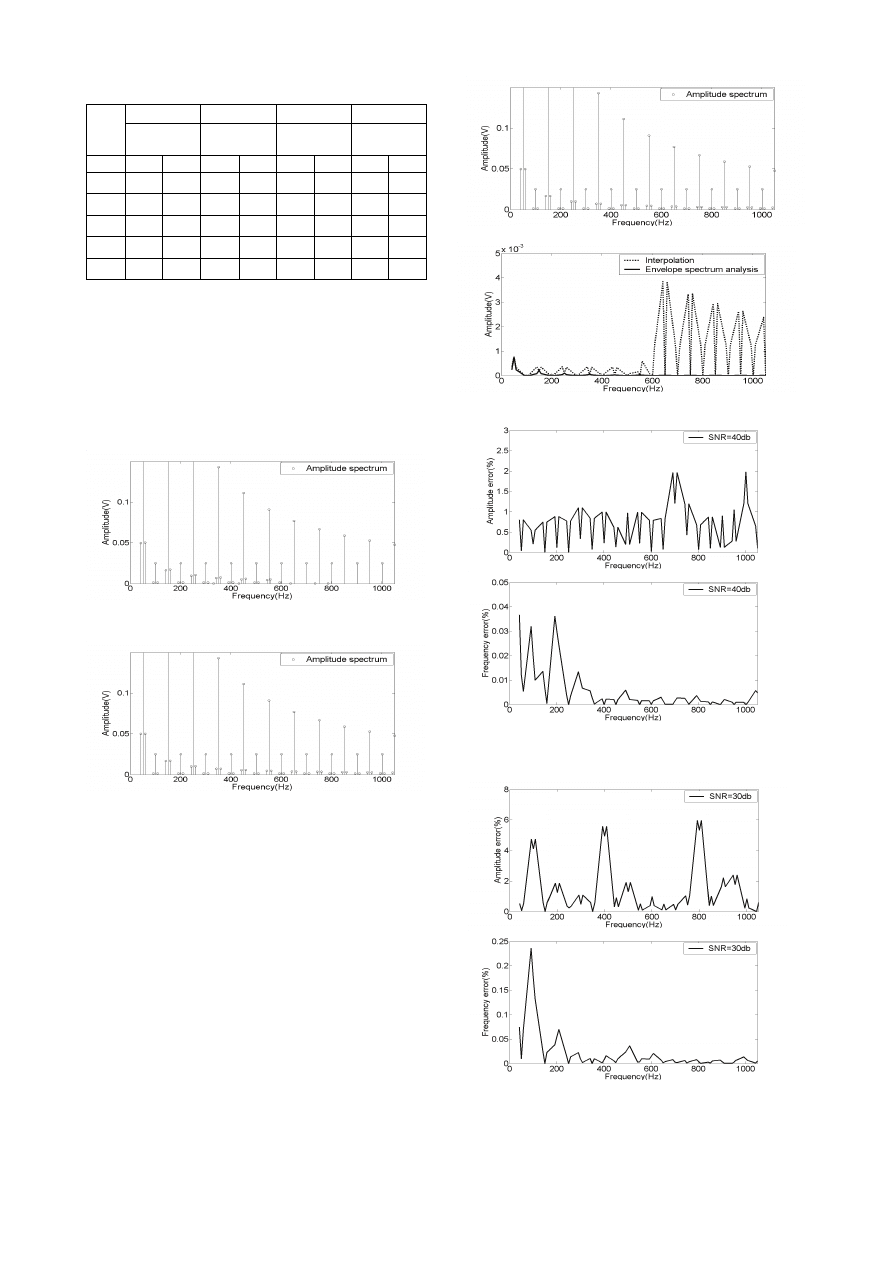
Figure 6 displays the amplitudes spectrums with Hanning 

windowing and interpolation technique when the window 
width is 0.4s, and the results for 0.6s are reported in figure 
7. By comparing the results in these two figures, we can 
find that the precision and stability of windowing and 
interpolation technique are affected by the sampling window 
width. Interharmoinics around high order harmonics can not 
be estimated due to their relatively small amplitude in the 
0.4s case. 

 

 

Fig. 6. Amplitude spectrum with interpolation technique for 0.4s. 

 

 

Fig. 7. Amplitude spectrum with interpolation technique for 0.6s. 

 

Modulation frequency of 8.5907Hz and amplitude of 

0.0999 can be obtained by the proposed method when the 
window width is 0.4s. Then the interharmonic components 
can be calculated according to (5), and the results are 
shown in figure 8. Absolute error with these two methods for 
0.4s are compared in figure 9, it can be clear seen that new 
method leads to more accurate results. 

 

D) Waveforms with added white Noise 

Noise characteristics of the proposed algorithm are 

studied in this section through simulation. The signal in the 
previous simulation is corrupted with an added zero-mean 
Gaussian white noise, and three cases are discussed in 
which their SNR values are 20dB, 30dB and 40dB 
individually based on the rms value of the signal. As the 
results may change in each simulation, only one test results 
for each case are reported in figure 10, figure 11, and figure 
12.  From the figures, we can find that the new method 
exhibits desirable performance to the noise. 

 

Fig. 8. Amplitude spectrum with proposed method for 0.4s.

 

 

Fig. 9. Absolute amplitude errors with interpolation and proposed 
method for 0.4s. 

(a) 

(b) 

 Fig. 10. Performance of the proposed algorithm when the input 
signal is corrupted with a white Gaussian noise of zero mean and 
its SNR value is 40dB. (a) relative amplitude errors. (b) relative 
frequency errors. 

(a) 

(b) 

Fig. 11. Performance of the proposed algorithm when the input 
signal is corrupted with a white Gaussian noise of zero mean and 
its SNR value is 30dB. (a) relative amplitude errors. (b) relative 
frequency errors.

 

324                                                    PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), ISSN 0033-2097, R. 86 NR 12/2010 

(a) 

(b) 

Fig. 12. Performance of the proposed algorithm when the input 
signal is corrupted with a white Gaussian noise of zero mean and 
its SNR value is 20dB. (a) relative amplitude errors. (b) relative 
frequency errors 

 
Conclusions

 

An envelope spectrum analysis-based algorithm for 

interharmonics measurement is proposed in this paper. The 
proposed method restores the interharmonic parameters 
with the envelope and harmonic spectrum according to 
amplitude modulation equation. The effects (or fake 
interharmonics), caused by the spectral leakage from 
harmonics, can be eliminated with the new method. In 
addition, the new method exhibits desirable performance to 
the noise. All of these features make the proposed 
algorithm precise, effective and feasible.

 

 

REFERENCES 

[1]  Harris F.J., On the use of windows for harmonic analysis with 

the discrete Fourier transform, Proceedings of the IEEE 66 (1) 
(1978) 51–83. 

[2]  Nuttal A.H., Some windows with very good sidelobe behavior,  

IEEE Trans. Acoustic, Speech, and Signal Processing., vol. 
29, no. 1, pp. 84–91 , Apr 1981. 

[3]  Tseng F. I., Sarkar T. K., Weiner D. D., A novel window for 

harmonic analysis, IEEE Trans. Acoustic, Speech, and Signal 
Processing.,  vol. 29, no. 2, pp. 177－188,  Apr 1981. 

[4]  Li C., Xu W., Tayjasanant T., Interharmonics: Basic concepts 

and techniques for their detection and measurement, Elect. 
Power Syst. Res., vol. 66, pp. 39–48, 2003. 

[5]  Jain H. Collins W. L., Davis D. C., High-accuracy analog 

measurements via interpolated FFT, IEEE Transactions on. 
Instrurn. Meus.,vol. 1M-28, pp. 113-122, June 1979. 

[6]  Grandke T., Interpolation algorithms for discrete Fourier 

transforms of weighted signals, IEEE Trans. on Instrum. 
Meas., vol. IM-32, pp.350-355, June 1983. 

[7]  Zhang F. S., Geng Z.X.,Yuan W, , The algorithm of 

interpolating windowed FFT for farmonic analysis of electric 
power system, IEEE Trans. Power Del.,  vol. 16, pp.160-164, 
Apr 2001 

[8]  Hao Q.  , Z. Rongxiang，C. Tong, “Interharmonics analysis 

based on interpolating windowed FFT algorithm”, IEEE Trans. 
Power Del., vol. 22, no. 2, pp. 1064-1069,  Apr 2007. 

[9]  Gallo D., Langella R., Testa A.,Desynchronized processing 

technique for harmonic and interharmonic analysis, IEEE 
Trans. Power Del., vol. 19, no. 3, pp. 993-1001, Jul 2004. 

[10]  Zhu T. X., Exact Harmonics/Interharmonics Calculation Using 

Adaptive Window Width, IEEE Trans. Power Del., vol. 22, no. 
3, pp. 2279-2288, Oct 2007. 

[11] Liu Z., Himmel J., Bong K.W.,Improved processing of 

harmonics and interharmonics by time-domain averaging, 
IEEE Trans. Power Del., vol. 20, no. 4, pp. 2370-2380, Oct 
2005. 

[12] 

General Guide on Harmonics and Interharmonics 
Measurements， for Power Supply Systems and Equipment 
Connected Thereto， IEC Std. 61000-4-7，2002. 

[13] Power Quality Measurements Methods ，  Testing and 

Measurement Techniques， IEC Std. 61000-4-30，2002. 

[14] 

Keaochantranond T., Boonseng C., Harmonics and 
interharmonics estimation using wavelet transform, 
Transmission and Distribution Conference and Exhibition., pp. 
6-10, 2002. 

[15] Bracale A. , Caramia P. , Carpinelli G., Adaptive Prony 

method for waveform distortion detection in power systems, 
Electrical Power and Energy System, vol. 29, pp. 371-379, 
2007. 

[16]  Bracale A., Carpinelli G., Leonowicz Z., Measurement of IEC 

groups and subgroups using advanced spectrum estimation 
methods,  IEEE Trans. on Instrum. Meas., vol. 57, no. 1, pp. 
672-681, Apr 2008. 

[17] Lobos T., Leonowicz Z., and Rezmer J., High-resolution 

spectrum estimationmethods for signal analysis in power 
systems, IEEE Transactions on Instrum. Meas., vol. 55, no. 1, 
pp. 219-225, Feb 2006. 

[18]  R. Langella and A. Testa． “Amplitude and phase modulation 

effects of waveform distortion in power systems”. Electrical 
Power quality and utilization, no.1, pp.25-32, 2007.. 

[19]  Girgis A. A., Stephens J. W., E. B. Makram, Measurement and 

Prediction of Voltage Flicker Magnitude and Frequency, IEEE 
Trans. Power Del., vol. 10, no. 3, pp. 1600-1605,Jul 1995. 

[20]  Chang W. N., Wu C. J., Yen S. S., “A flexible voltage flicker 

teaching facility for electrical power quality education”, IEEE 
Trans. on  Power System., vol. 13, no. 1, pp. 27-33, Feb 1998.  

[21] Wu C. J., Fu T. H., “Effective voltage flicker calculation 

algorithm using indirect demodulation method,” Proc. Inst. 
Elect. Eng., Gen., Transm. Distrib., vol. 150, no. 4, pp. 493–
500, Jul. 2003. 

[22]  Axelberg P. G. V., Bllen M. H. J., An algorithm for determining 

the direction to a flicker source, IEEE Trans. Power Del., vol. 
21, no.2, pp. 755–760, Apr. 2006. 

[23]  Axelberg P. G. V., Bollen M. H. J., and Gu.I, Y. H., Trace of 

Flicker Sources by Using the Quantity of Flicker Power , IEEE 
Trans. Power Del., vol. 23, no.1, pp. 465–471, Jan. 2008. 

 

 

Authors: Jiefeng Xiong,Hohai University, Nanjin 210098, China ,E-
mail: jiefengxiong@163.com; prof. Bolin Wang, Hohai University, 
Nanjin 210098, China ,E-mail: phdwbl@163.com.