Podstawy teorii informacji
- teoria informacji
- teoria kodowania (kody optymalne, korekcyjne)
- podstawy kryptografii
Teoria informacji
Co jest nośnikiem, co zawartością (dane, informacja, wiadomości)
⇒ pojęcia podstawowe
należy wyróżnić.
• wiadomość //nośnik//
syntaktyka
słowo, zdanie
dane
nazwa
• informacja //zawartość//
semantyka
treść słowa, zdania
interpretacja danych
pojęcia
Przetwarzanie wiadomości:
α - przekształcenie
2
1
1
1
W
W
⎯
⎯ ⎯
←
⎯
⎯ →
⎯
−
α
α
o
- odwracalne, bez straty informacji
2
1
2
W
W
⎯
⎯ →
⎯
α
o
- ze stratą informacji
Elementy teorii grafów
Euler chciał przejść przez każdy most w Kaliningradzie dokładnie raz.
Grafem nazywamy trójkę
Γ=(E, K, r), gdzie:
E - niepusty zbiór, którego elementy nazywamy wierzchołkami (węzłami) grafu
K - zbiór, którego elementy nazywamy krawędziami grafu
r - relacja incydencji przypisująca każdej krawędzi co najmniej jeden i co najwyżej
dwa wierzchołki
Przedstawienia grafu:
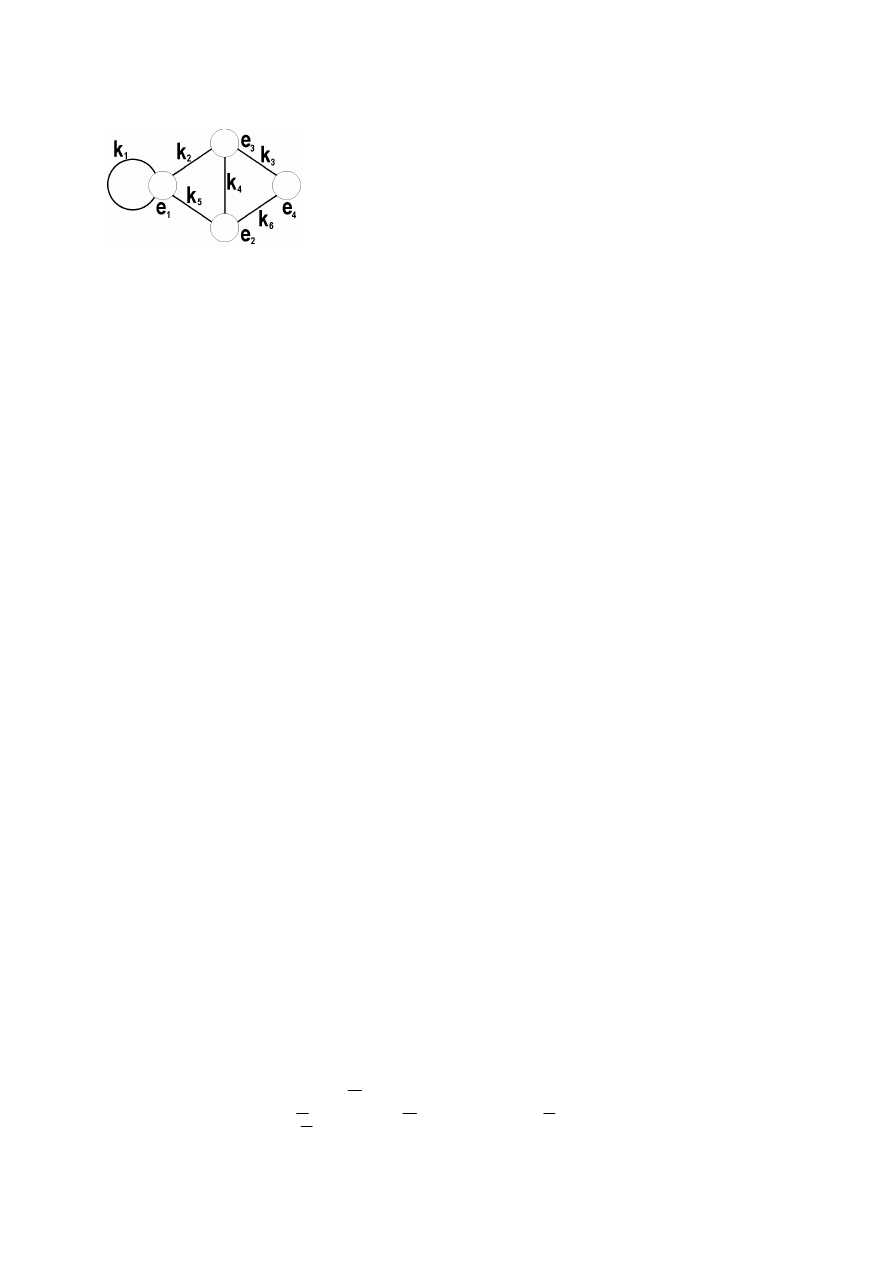
• graficzne
• zbiór par
(
) (
) (
)
{
}
k e
k e
k e
1
1
2
1
2
3
,
;
,
;
,
;... , gdzie k
i
oznacza i-tą krawędź a e
j
j-ty wierzchołek
• macierz incydencji
e
e
e
e
e e e e
1
2
3
4
1
2
3
4
1 1 1 0
1 0 1 1
1 1 0 1
0 1 1 0
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
- tu nie rozróżniamy krawędzi
k
k
k
e e e e
1
2
3
1
2
3
4
1 0 0 0
1 0 1 0
M
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
Krawędź, z którą jest incydentny dokładnie jeden wierzchołek nazywamy pętlą.
Rzędem (stopniem) wierzchołka
nazywamy liczbę incydentnych z nim krawędzi, przy
czym pętle liczymy dwukrotnie.
Drogą
w grafie nazywamy ciąg, w którym występują na przemian wierzchołki i krawędzie;
wierzchołki i krawędzie sąsiadujące są incydentne. Drogą zamkniętą nazywamy drogę, w
której pierwszy wierzchołek jest też ostatnim. Rozróżniamy również drogę otwartą. Droga
prosta
to taka na której wierzchołki nie powtarzają się. Długością drogi nazywamy liczbę
krawędzi do niej należących.
Drogę, w której wszystkie krawędzie są różne nazywamy łańcuchem. Łańcuch, który jest
drogą zamkniętą to cykl.
Drogą Eulera
nazywamy cykl zawierający wszystkie krawędzie grafu. W grafie istnieje taka
droga, gdy wszystkie wierzchołki mają parzysty stopień. Drogą jednobieżną lub otwartą
drogą Eulera
nazywamy łańcuch, który nie jest cyklem, zawierający wszystkie krawędzie
grafu. W grafie istnieje taka droga, gdy dokładnie dwa wierzchołki mają nieparzysty stopień.
Łańcuch Hamiltona to
droga prosta zawierająca wszystkie wierzchołki grafu.
Graf jest spójny wtedy gdy dla dowolnych dwóch wierzchołków istnieje droga, w której
wierzchołki te są wierzchołkami początkowym i końcowym.
Graf nazywamy zorientowanym lub skierowanym jeżeli każdej krawędzi
przyporządkujemy wierzchołek początkowy i końcowy.
• relacje incydencji
( )
(
)
( )
{
}
k e
k e
k e
1
1
1
2
2
2
,
;
,
;
,
;... , przy czym e
i
oznacza, że wierzchołek jest
początkowy, natomiast e
i
że jest końcowy
• macierz:
k
k
k
a
b
a
b
b
a
e e e
1
2
3
1
2
3
0
0
0
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
i a oznacza wierzchołek początkowy, b oznacza końcowy, p.
oznacza początkowy i końcowy jednocześnie, a 0 oznacza, że jest nieincydentny
Grafy ważone
to grafy, w których krawędziom przyporządkowane są liczby rzeczywiste
(wagi).
Grafy spójne zawierające co najmniej jedną krawędź i nie zawierające cykli nazywamy
drzewem
.
Graf zorientowany nazywamy drzewem zorientowanym gdy zawiera on dokładnie jeden
węzeł, który nie jest węzłem końcowym żadnej krawędzi (korzeń), a każdy z pozostałych
węzłów jest węzłem końcowym dokładnie jednej krawędzi. Poziomem węzła nazywamy
długość drogi od korzenia do tego węzła.
Jeżeli liczba krawędzi wychodzących z każdego węzła jest ograniczona z góry liczbą r to
drzewo nazywamy r-narnym. Jeżeli poziomy wszystkich węzłów końcowych są jednakowe i
równe h to drzewo nazywamy drzewem h-poziomowym. Jeżeli w drzewie r-narnym z
każdego węzła nie będącego liściem wychodzi dokładnie r krawędzi to drzewo nazywamy
drzewem pełnym
.
Nierówność Krafta
: Liczby naturalne m
1
, m
2
, ..., m
n
, są poziomami końcowymi drzewa r-
narnego gdy:
r
m
i
n
i
−
=
∑
≤
1
1
Zbiory wiadomości
Rodzaje zbiorów:
• prosty:
{
}
W
w w
w
n
=
1
2
,
,...,
, gdzie w
i
- wiadomość elementarna
• złożony: zbiór wiadomości zawiera ciągi
{
}
w w
w
i
i
ik
1
2
,
,...,
, gdzie w
W
ij
∈
Przykład
{
}
W
= 01
9
, ,..., , k = 4,
(
) (
)
0000
9999
−
• wielowymiarowy: A A
A
m
1
2
,
,...,
- zbiory proste, m wymiarowym zbiorem wiadomości
określonym na zbiorach prostych A A
A
m
1
2
,
,...,
nazywamy iloczyn kartezjański
A
A
A
m
1
2
×
× ×
...
Przykład
{
}
D
= 1 2
31
, ,...,
{
}
M
I II
XII
= , ,...,
{
}
L
= 0000 0001
9999
,
,...,
np. 12 X 1995, UWAGA! D M L
L
M
D
×
× ≠ ×
×
Ilość informacji. Źródło wiadomości.
Ilość informacji to wielkość związana z prawdopodobieństwem pojawienia się,
wygenerowania tej informacji. Im większe prawdopodobieństwo, tym mniejszą ilość
informacji niesie wiadomość.
{
}
W
w w
w
n
=
1
2
,
,...,
Def.
( )
( )
I w
p w
r
i
r
i
= log
1
.
Ilość informacji wyrażamy w jednostkach r-narnych. Np. gdy r = 2 to jednostką jest bit, a gdy
r = e to jednostką jest nat.
Jeżeli dane są zbiór wiadomości
{
}
W
w w
w
n
=
1
2
,
,...,
i prawdopodobieństwa wygenerowania
tych wiadomości
( ) ( )
( )
p w
p w
p w
n
1
2
,
,...,
to mamy określone źródło wiadomości.
Def. Źródło nazywamy źródłem bezpamięciowym jeżeli prawdopodobieństwo
(
)
( )
( )
p w w
p w
p w
i
j
i
j
,
=
⋅
.
Inaczej:
(
) ( )
p w
w
p w
j
i
j
/
=
dla i,j = 1,2,...,n
Umowa: co wcześniej, co później
(
)
w w
i
j
,
- to oznacza, że pojawiła się wiadomość w
i
przed
w
j
.
Def. Średnią ilość informacji przypadającą na wiadomość generowaną przez źródło
nazywamy entropią źródła.
( )
( ) ( )
( )
( )
H W
p w
I w
p w
p w
r
i
r
i
i
n
i
r
i
i
n
=
⋅
=
⋅
=
=
∑
∑
1
1
1
log
( )
p w
p
i
i
=
, r
= 2
( )
H W
p
p
r
i
i
i
n
=
⋅
=
∑
log
1
1
Tw.
Entropia przyjmuje wartość maksymalną, gdy p
p
p
n
n
1
2
1
=
= =
=
...
i równa jest
log
r
n
Identyfikacja źródła wiadomości.
W={ w
1
, w
2
, ..., w
n
}, p
1
, p
2
, ..., p
n
Aby wiedzieć jaką wiadomość wysyła to źródło to mamy zestaw pytań r-narnych. Nazywa się
to systemem identyfikacji źródła wiadomości.
Każdej wiadomości w systemie identyfikacji odpowiada pewna liczba zapytań, oznaczamy ją
przez
i
l , dla wiadomości
i
w . Jakość systemu identyfikacji określa wtedy średnia liczba
pytań przypadająca na wiadomość.
( )
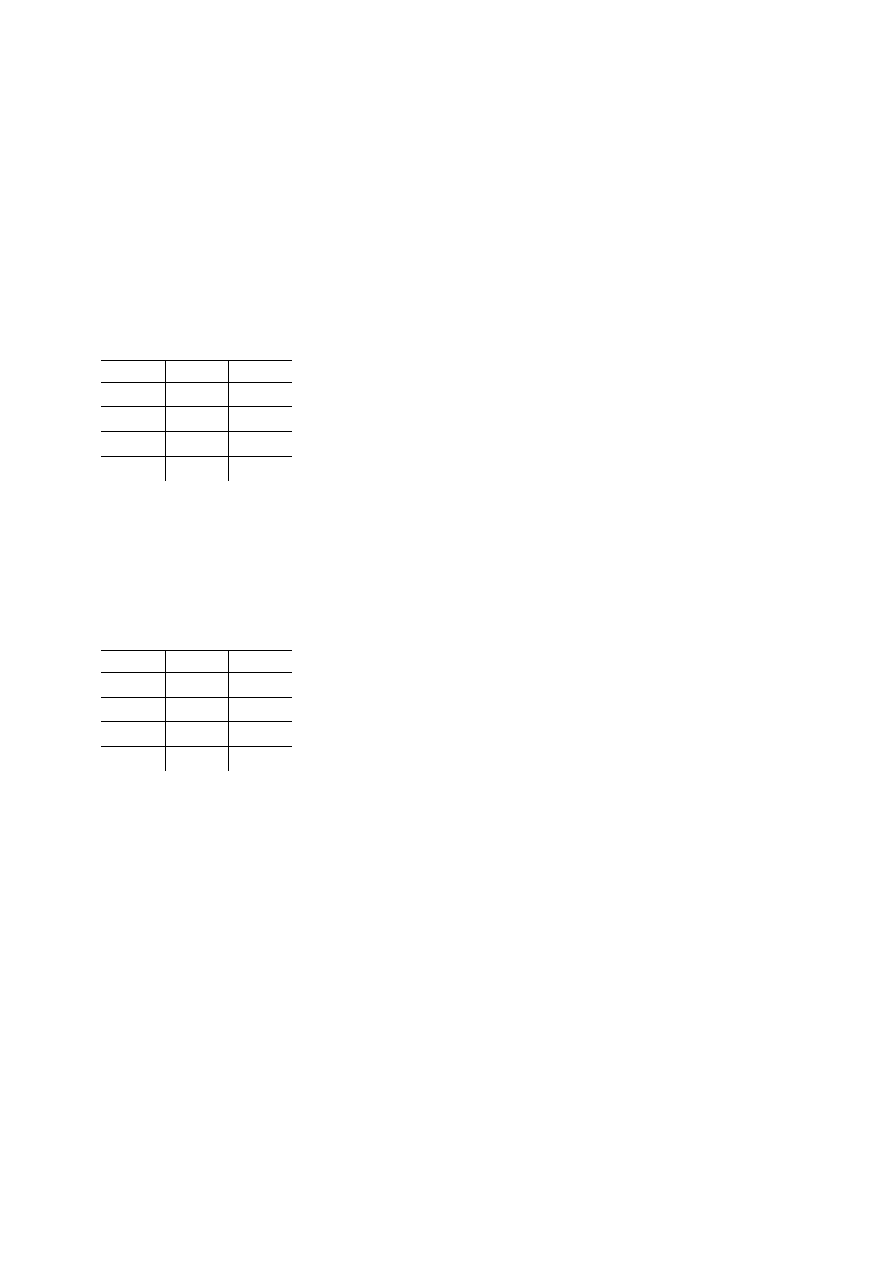
E s
p l
r
i
i
i
n
=
⋅
=
∑
1
Kody - podstawowe pojęcia.
Zbiór wiadomości - W, alfabet, zbiór liter alfabetu - X.
Def. Kodem nazywamy dowolne przyporządkowanie, w którym każdemu ciągowi
wiadomości ze zbioru W odpowiada ciąg liter alfabetu ze zbioru X.
Przykład.
{
}
W
w w w w
=
1
2
3
4
,
,
,
{ }
X
= 01
,
albo
w
1
0 0
w
2
1 00
w
3
0 11
w
4
1 00
Kod nazywamy blokowym jeśli każdej wiadomości w
i
ze zbioru W odpowiada ciąg x
i
(ciąg
kodowy
, słowo kodowe) ze zbioru X.
Def. Kod blokowy nazywamy kodem nieosobliwym jeżeli słowa kodowe są parami różne.
Przykład.
albo
w
1
00 0
w
2
01 00
w
3
11 1
w
4
10 11
Def. K-krotnym rozszerzeniem kodu blokowego nazywamy kod, w którym każdemu
ciągowi wiadomości (w
i1
, w
i2
, ..., w
ik
) ze zbioru W odpowiada ciąg liter alfabetu (x
i1
, x
i2
, ...,
x
ik
) gdzie x
ij
- słowo kodowe odpowiadające wiadomości w
ij
.
Przykład.
(
)
( )
w w
1 1
00
→
(
)
(
)
w w
1
2
000
→
(
)
( )
w w
1
3
01
→
..................
(
)
(
)
w w
4
4
1111
→
Def. Kod blokowy nazywamy kodem jednoznacznie dekodowalnym wtedy, gdy k-krotne
rozszerzenie tego kodu jest kodem nieosobliwym dla dowolnego k.
Przykład.
{
}
W
w w w w
=
1
2
3
4
,
,
,
K
1
K
2
w
1
00 0
w
2
01 01
w
3
10 011
w
4
11 0111
Def. Kod blokowy nazywamy kodem jednoznacznie dekodowalnym bez opóźnienia,
wtedy, gdy żadne słowo kodowe nie jest przedrostkiem żadnego innego słowa kodowego.
Kod jest kodem równomiernym, gdy słowa kodowe są równej długości.
Konstrukcja kodów jednoznacznie dekodowalnych bez opóźnienia
Źródło
{
}
W
w w
w
n
=
1
2
,
,...,
i p p
p
n
1
2
, ,...,
System identyfikacji, r = 3
Znając r-narny system identyfikacji źródła wiadomości kodujemy r-narny kod jednoznacznie
dekodowalny bez opóźnienia za pomocą następującej procedury:
1. Krawędzie wychodzące z każdego węzła drzewa oznaczamy różnymi literami alfabetu.
2. Spisujemy litery oznaczające krawędzie należące do drogi od korzenia do każdego węzła
końcowego. Ciągi liter odpowiadające poszczególnym węzłom końcowym są słowami
kodowymi wiadomości przyporządkowanych tym węzłom.
Def. Kod
r-narny zbudowany zgodnie z podaną procedurą jest kodem jednoznacznie
dekodowalnym bez opóźnienia.
Znając kod r-narny jednoznacznie dekodowalny bez opóźnienia można zbudować r-narny
system identyfikacji źródła wiadomości stosując następującą procedurę:
1. Budujemy h-poziomowe r-narne drzewo pełne, w którym h równe jest maksymalnej
długości słowa kodowego danego kodu.
2. Krawędzie wychodzące z każdego węzła oznaczamy różnymi literami alfabetu.
3. Redukujemy drzewo pozostawiając wyłącznie krawędzie, które tworza drogi od korzenia
do węzłów końcowych oznaczone literami zgodnymi ze słowami kodowymi kodu.
4. Węzły końcowe zredukowanego drzewa oznaczamy odpowiednimi wiadomościami a
pozostałym węzłom przyporządkowujemy odpowiednie pytania r-narne
1.
( ) ( )
l w
d w
i
i
=
dla i = 1,2,...,k
( )
E s
p l
r
i
i
i
n
=
⋅
=
∑
1
; średnia liczba pytań r-narnych
( )
E k
d l
r
i
i
i
n
=
⋅
=
∑
1
; średnia długość słowa kodowego
2.
( )
( )
E s
E k
r
r
=
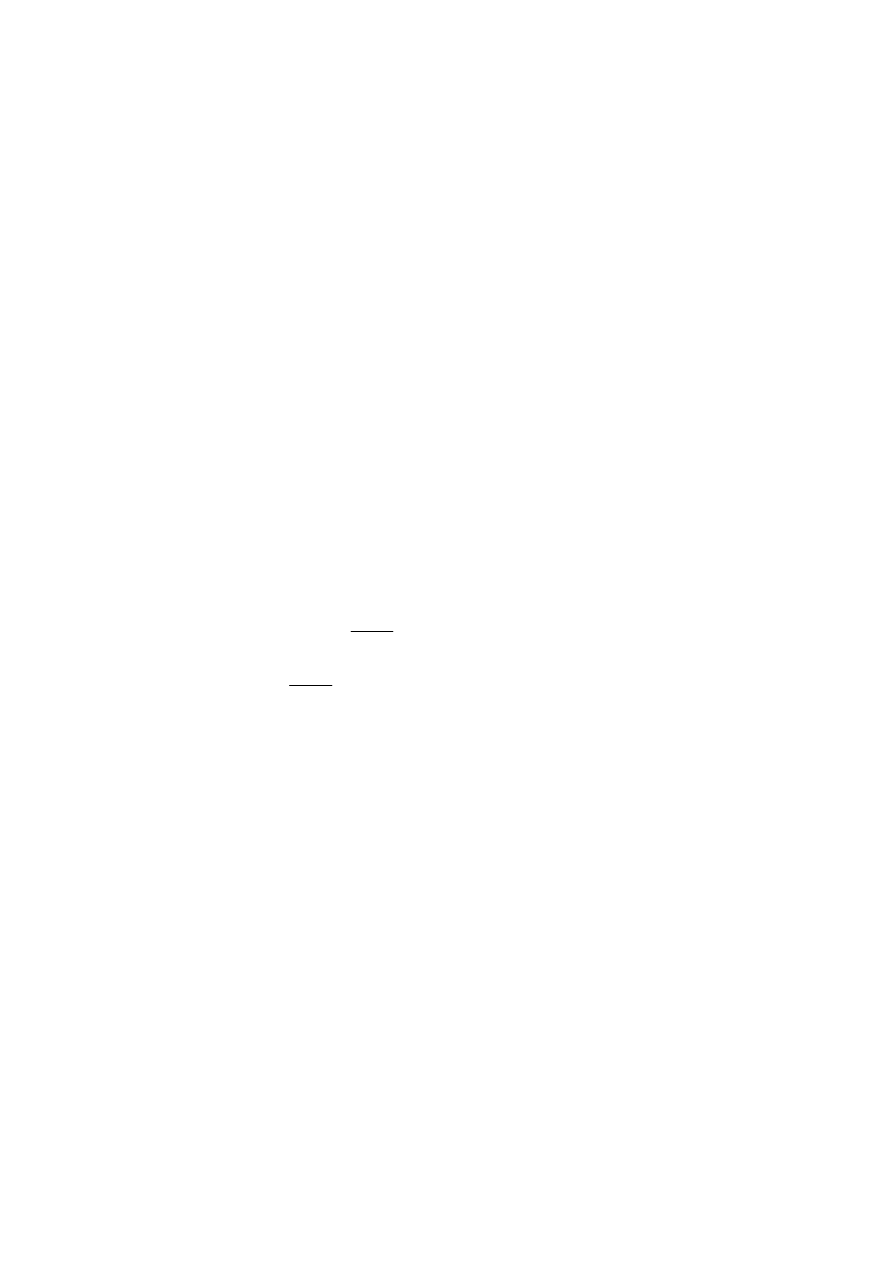
Dane jest źródło
2
1
2
W
W
⎯
⎯ →
⎯
α
o
i p p
p
n
1
2
, ,...,
Mówimy, że kod K
1
jest lepszy od kodu K
2
jeżeli średnia długość słowa kodowego
( )
( )
E K
E K
r
r
1
1
<
Kod K nazywamy kodem optymalnym, jeżeli dla każdego kodu K'
( )
( )
E K
E K
r
r
≤
'
Używana jest również nazwa kod zwięzły.
Źródło rozszerzone
- zbiór złożony
- kod rozszerzony (k - krotne rozszerzenie kodu)
{
}
W
w w
w
n
=
1
2
,
,...,
i p p
p
n
1
2
, ,...,
- źródło bezpamięciowe
k - krotnie rozszerzone
{
}
W
w w
w
k
k n
=
⋅
1
2
,
,...,
, gdzie
(
)
w
w w
w
i
i
i
ik
=
1
2
,
,...,
, w
W
ij
∈ , dla j = 1,...,k
( ) ( ) ( ) ( )
p w
p w
p w
p w
i
i
i
ik
=
⋅
⋅ ⋅
1
2
...
Entropia tego źródła:
( )
( )
( )
H W
p w
p w
r
k
i
r
i
i
n
i
n
i
n
k
=
⋅
=
=
=
∑
∑
∑
L
log
1
1
1
1
2
1
( )
( )
( )
H W
p w
p w
r
k
i
r
i
W
k
=
⋅
∑
log
1
Można wykazać, że
( )
( )
H W
k H W
r
k
r
= ⋅
Źródło ciągów Markowa
{
}
W
w w
w
n
=
1
2
,
,...,
Mówimy, że źródło W jest źródłem ciągów Markowa m - tego rzędu, jeżeli znane są
prawdopodobieństwa warunkowe:
(
)
P w
w
w
w
i
j
j
jm
/
,
,...,
1
2
(
) (
)
(
)
(
) (
)
(
)
(
) (
)
(
)
P
w
w
w
p w
w
p w
w
p w
w
p w
w
p w
w
p w
w
p w
w
p w
w
p w
w
w
w
w
n
n
n
n
n
n
n
n
=
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
1
2
1
1
2
1
1
1
2
2
2
2
1
2
1
2
M
L
L
M
M
O
M
L
L
/
/
/
/
/
/
/
/
/
( ) (
) (
)
(
)
p w
p w w
p w w
p w w
n
1
1
1
2
1
1
=
+
+ +
,
,
...
,
( ) (
) ( ) (
) ( )
(
) ( )
p w
p w
w
p w
p w
w
p w
p w
w
p w
n
n
1
1
1
1
1
2
2
1
=
⋅
+
⋅
+ +
⋅
/
/
...
/
(
)
( )
w w
1
3
01
→
Ilość informacji pod warunkiem, że źródło w określonym stanie:
(
)
(
)
I w
w
w
w
p w
w
w
w
r
i
j
j
jm
r
i
j
j
jm
/
,
,...,
log
/
,
,...,
1
2
1
2
1
=
Średnia ilość informacji zawartej w wiadomości wygenerowanej w określonym stanie:
(
)
(
) (
)
∑
=
⋅
=
n
i
jm
j
j
i
r
jm
j
j
i
jm
j
j
r
w
w
w
w
I
w
w
w
w
p
w
w
w
w
H
1
2
1
2
1
2
1
,...,
,
/
,...,
,
/
,...,
,
/
A ogólnie , w dowolnym stanie:
( )
(
) (
)
∑
⋅
=
m
W
jm
j
j
r
jm
j
j
r
w
w
w
w
H
w
w
w
p
w
H
,...,
,
/
,...,
,
2
1
2
1
( )
(
)
(
) (
)
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
∑
∑
=
=
jm
j
j
i
r
n
i
jm
j
j
i
n
i
jm
j
j
r
w
w
w
w
I
w
w
w
w
p
w
w
w
p
w
H
,...,
,
/
,...,
,
/
,...,
,
2
1
1
2
1
1
2
1
( )
(
) (
)
(
)
H w
p w
w
w
p w
w
w
w
p w
w
w
w
r
j
j
jm
i
j
j
jm
W
r
i
j
j
jm
m
=
⋅
⋅
+
∑
1
2
1
2
1
2
1
1
,
,...,
/
,
,...,
log
/
,
,...,
{
}
W
w w
w
n
=
1
2
,
,...,
- źródło bezpamięciowe generujące wiadomości z
prawdopodobieństwami równymi prawdopodobieństwom ergodycznym źródła Markowa m -
tego rzędu. Nazywamy je źródłem stowarzyszonym.
( )
( )
H w
H w
r
r
≥
równość ta ma miejsce wtedy i tylko wtedy gdy prawdopodobieństwa:
(
)
( )
p w
w
w
w
p w
i
j
j
jm
i
/
,
,...,
1
2
=
dla wszystkich stanów.
Kody optymalne
{
}
W
w w
w
n
=
1
2
,
,...,
; p p
p
n
1
2
, ,...,
;
( )
k
E k
r
−
Tw.
( )
( )
E k
H w
r
r
≥
- żeby zapisać wiadomość ze źródła W potrzeba zorganizować
przynajmniej tyle ile wynosi średnia ilość informacji
Tw. Dla dowolnego źródła wiadomości
{
}
W
w w
w
n
=
1
2
,
,...,
; p p
p
n
1
2
, ,...,
można zbudować
kod jednoznacznie dekodowalny bez opóźnienia taki, że:
( )
( )
( )
H w
E k
H w
r
r
r
≤
<
+1
(jedna jednostka r-narna)
• Algorytm wyznaczania r-narnego kodu dla źródła
{
}
W
w w
w
n
=
1
2
,
,...,
;
p p
p
n
1
2
, ,...,
;
1. Rozszerzać źródło wiadomości dodając wiadomości z prawdopodobieństwami
równymi 0, aż liczba wiadomości będzie równa
(
)
r
k
r
+ ⋅ −1
, k N
∈ .
2. Uporządkować wiadomości wg niemalejących wartości prawdopodobieństw.
3. Zastąpić r wiadomości z najmniejszymi prawdopodobieństwami jedną wiadomością z
prawdopodobieństwem równym sumie prawdopodobieństw wiadomości
zastępowanych.
4. Sprawdzić czy liczba wiadomości jest równa 1. Jeśli nie, to wykonać czynność 2.
Jeżeli tak to czynność 5.
5. Zbudować r-narne drzewo, w którym węzły odpowiadają wiadomościom, a krawędzie
łączą węzły (wiadomości) za zastępujące z wiadomościami zastępowanymi.
6. Zbudować r-narny kod zgodny z drzewem otrzymanym (r-narnym) tj.
b)
oznaczyć krawędzie literami alfabetu
c)
ustalić ciągi liter na drogach od korzenia do liści
Tw. Kod wyznaczony zgodnie z powyższym algorytmem jest kodem optymalnym
Tw. (Shannona) Dla kodu
K
k
(źródła k-krotnie rozszerzonego) spełniającego warunek
( )
( )
( )
H W
E K
H W
r
k
r
k
r
k
≤
<
+1
zachodzi zależność:
( )
( )
lim
k
r
k
r
E K
k
H W
→∞
=
Jeżeli zbudujemy taki kod to dla kolejnych rozszerzeń źródła wiadomości mamy ciąg, którego
granicą jest średnia entropia źródła wiadomości.
Metody kompresji
Jak przedstawić krócej wiadomości niż zostały przedstawione?
Jeśli
( )
( )
E K
H W
r
r
=
, to nie da się krócej zapisać ciągu.
Jeśli
( )
( )
E K
H W
r
r
≠
, to ciąg z nadmiarem.
( )
( )
µ
=
H W
E K
r
r
- sprawność kodu,
0
1
< ≤
µ
( )
( )
( )
λ
µ
= − =
−
1
E K
H W
E K
r
r
r
- rozwlekłość (redundancja) kodu
l
wej
- długość ciągu początkowego
l
wyj
- długość ciągu po zastosowaniu kompresji
k
l
l
wej
wyj
=
- jakość kompresji (współczynnik)
Metody kompresji dzielimy na:
a) bez straty informacji (odwracalne)
b) ze stratą informacji (nieodwracalne)
• Kompresja ciągów binarnych
1. Bezpośrednie kodowanie runów
Runem nazywamy dowolny skończony podciąg binarny. Będziemy wyróżniać runy tzw.
zerowe i jedynkowe. Runy zerowe to ciąg złożone z zer i zakończonych jedynką, a
jedynkowe na odwrót.
Runy zerowe
(1)
(01) (001) (00...001)
Runy jedynkowe (0)
(10) (110) (11...110)
Ciąg zerowy
(00...00)
Ciąg jedynkowy (11...11)
Podany ciąg binarny dzielimy na runy; wyznaczamy prawdopodobieństwa występowania
tych runów; wtórnie kodujemy;
Przykład.
01 001 1 001 01 01 1 01 000 01 000 01 1
n - maksymalna długość runu i również długość ciągu zerowego
3
=
n
1 - 3
( )
13
3
1
=
p
1
w
01 - 6
( )
13
6
01
=
p
2
w
001 - 2
( )
13
2
001
=
p
3
w
000 - 2
( )
13
2
000
=
p
4
w
2. Metoda Golomba
n - parametr
n
k
= 2
, czyli n = 2,4,8,...
Każdemu runowi przyporządkowany jest ciąg binarny złożony z rdzenia, separatora i
końcówki.
• rdzeń - ciąg złożony wyłącznie z liter 1, których liczba jest równa części całkowitej
l
n
−1
, gdzie l - długość runu
• separator - zawsze litera 0
• końcówka - ciąg będący resztą z dzielenia
l
n
−1
zapisany na
log n
pozycjach
3. Rozrzedzanie ciągów
Dzieli się ciąg binarny na podciągi o określonej długości i ponownie koduje dając temu,
który występuje najczęściej same zera.
• Kompresja obrazów
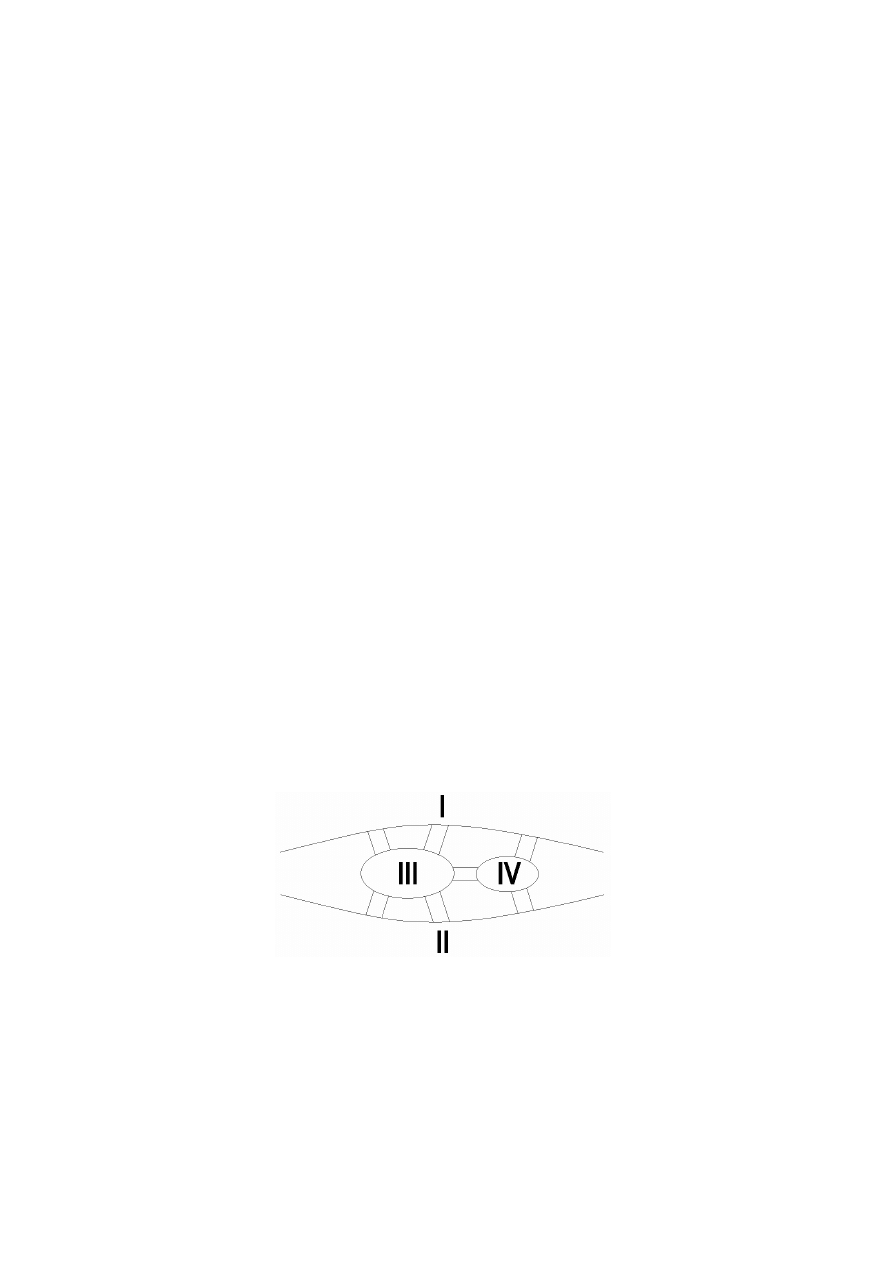
1. Kompresja obrazów czarno-białych
Przedstawienie za pomocą wyrażenia z nawiasami
k
k
2
2
×
k
2
k
2
(O) = ((I)(II)(III)(IV)) = (0(101(0(0101)01))(0(1100)0(1011))1)
1 - pole czarne
0 - pole białe
{
}
1
,
0
),
(,
=
W
( 00
) 01
0 10
1 11
przedstawienie za pomocą drzewa czwórkowego
2. obrazy z gradacją kontrastu
k
k
2
2
×
p - pole
x
- piksel
( )
x
s
- stopień szarości
k
- liczba pikseli należących do p
( )
p
s
- średni stopień szarości pola p
( )
( )
∑
∈
=
p
x
x
s
k
p
s
1
( )
p
δ
- odchylenie standardowe stopnia szarości pikseli w polu p
( )
( ) ( )
(
)
k
x
s
p
s
p
p
x
∑
∈
−
=
2
δ
δ - wartość progowa odchylenia standardowego stopnia szarości pikseli
Kanały informacyjne
Nadawca:
- generowanie wiadomości
- kodowanie
- modulacja
NADAWCA
KANAŁ
ODBIORCA
Kanał
- przesyłanie
Odbiorca
- odbiór
- demodulacja
- dekodowanie
Kanał informacji to:
1. Źródło wiadomości
{
}
W
w w
w
n
=
1
2
,
,...,
;
p p
p
n
1
2
,
,...,
2. Macierz kanału (kanał)
3. Zbiór informacji odebranych:
{
}
Z
z z
z
m
=
1
2
, ,...,
;
( ) ( )
( )
p z
p z
p z
m
1
2
,
,...,
Macierz kanału P jest macierzą prawdopodobieństw warunkowych
(
)
p z
w
j
i
/
, gdzie
i =1,2,...,n, j = 1,2,..,m
P
w
w
w
p
p
p
p
p
p
p
p
p
z
z
z
n
m
m
n
n
nm
m
=
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
1
2
11
12
1
21
22
2
1
2
1
2
M
L
L
M
M
O
M
L
L
,
(
)
p
p z
w
ij
j
i
=
/
Kanał definiujemy też jako macierz P. Musi ona spełniać warunki:
(
)
p z
w
p
j
i
j
n
ij
j
m
/
= ⇔
=
=
=
∑
∑
1
1
1
1
Przykład.
P
=
⎡
⎣
⎢
⎤
⎦
⎥
1
2
1
4
1
8
1
8
1
3
1
3
1
3
0
0
0
, to może być macierz kanału
Interpretacja: jeżeli była nadana jakaś wiadomość, to musi być odebrana jako jakaś
wiadomość ze zbioru Z.
Typy kanałów:
1. Kanał idealny
(W i Z równoliczne)
( )
( )
card W
card Z
=
oraz
(
)
p z
w
j
i
/
= ∨
0 1
2. Kanał odwracalny
(ogólniejszy)
( )
( )
card W
card Z
≤
; Na podstawie odebranej wiadomości jednoznacznie
wiemy, co nadano.
3. Kanał deterministyczny
( )
( )
card W
card Z
≥
; Wiemy jaka wiadomość będzie odebrana, jeśli wiemy jaką
nadaliśmy.
1. Kanał binarny (symetryczny)
P
p
p
p
p
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
1
1
Parametry kanału informacyjnego
(
)
[
]
P
p z
w
j
i
=
/
;
(
)
p w
z
i
j
/
?
=
Mamy źródło wiadomości
{
}
W
w w
w
n
=
1
2
,
,...,
; p p
p
n
1
2
,
,...,
(
) ( ) ( )
p w
z
p z
p w z
i
j
j
i
j
/
,
⋅
=
(
)
( )
(
)
p z
w
p w
p w z
j
i
i
i
j
/
,
⋅
=
← kolejność nie jest istotna
⇓
(
) ( ) (
)
( )
p w
z
p z
p z
w
p w
i
j
j
j
i
i
/
/
⋅
=
⋅
(
) (
)
( )
( )
p w
z
p z
w
p w
p z
i
j
j
i
i
j
/
/
=
⋅
( ) (
)
( )
(
)
( )
(
)
( )
p z
p z
w
p w
p z
w
p w
p z
w
p w
j
j
j
j
n
n
=
⋅
+
⋅
+ +
⋅
/
/
...
/
1
1
2
2
⇓
( )
(
)
( )
p z
p z
w
p w
j
j
i
i
i
n
=
⋅
=
∑
/
1
( )
(
)
[
]
P
p w
z
i
j
−
=
1
/
- macierz kanału odwróconego, macierz prawdopodobieństw odwrotnych
•
(
)
(
)
I w
z
p w
z
r
i
j
r
i
j
/
log
/
=
1
; w idealnym
I
r
= 0
, jak różne to warto się zapytać o średnią
•
(
)
(
) (
)
(
)
(
)
H w z
p w
z
I w
z
p w
z
p w
z
r
j
i
j
r
i
j
i
n
i
j
r
i
j
i
n
/
/
/
/
log
/
=
⋅
=
⋅
=
=
∑
∑
1
1
1
(
)
( ) (
)
H W Z
p z
H W z
r
j
r
j
j
m
/
/
=
⋅
=
∑
1
(
)
( )
(
)
(
)
( ) (
)
(
)
H W Z
p z
p w
z
p w
z
p z
p w
z
p w
z
r
j
i
j
r
i
j
i
n
j
m
j
i
j
r
i
j
j
m
i
n
/
/
log
/
/
log
/
=
⋅
⋅
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟ =
⋅
⋅
=
=
=
=
∑
∑
∑
∑
1
1
1
1
1
1
(
)
(
)
(
)
H W Z
p w z
p w
z
r
i
j
r
i
j
j
m
i
n
/
,
log
/
=
⋅
=
=
∑
∑
1
1
1
i to się nazywa stratą informacji w kanale
•
(
)
I W Z
r
,
- średnia ilość informacji przekazywanych przez kanał informacyjny
•
( )
H W
r
- średnia po stronie nadawcy
( )
(
)
(
)
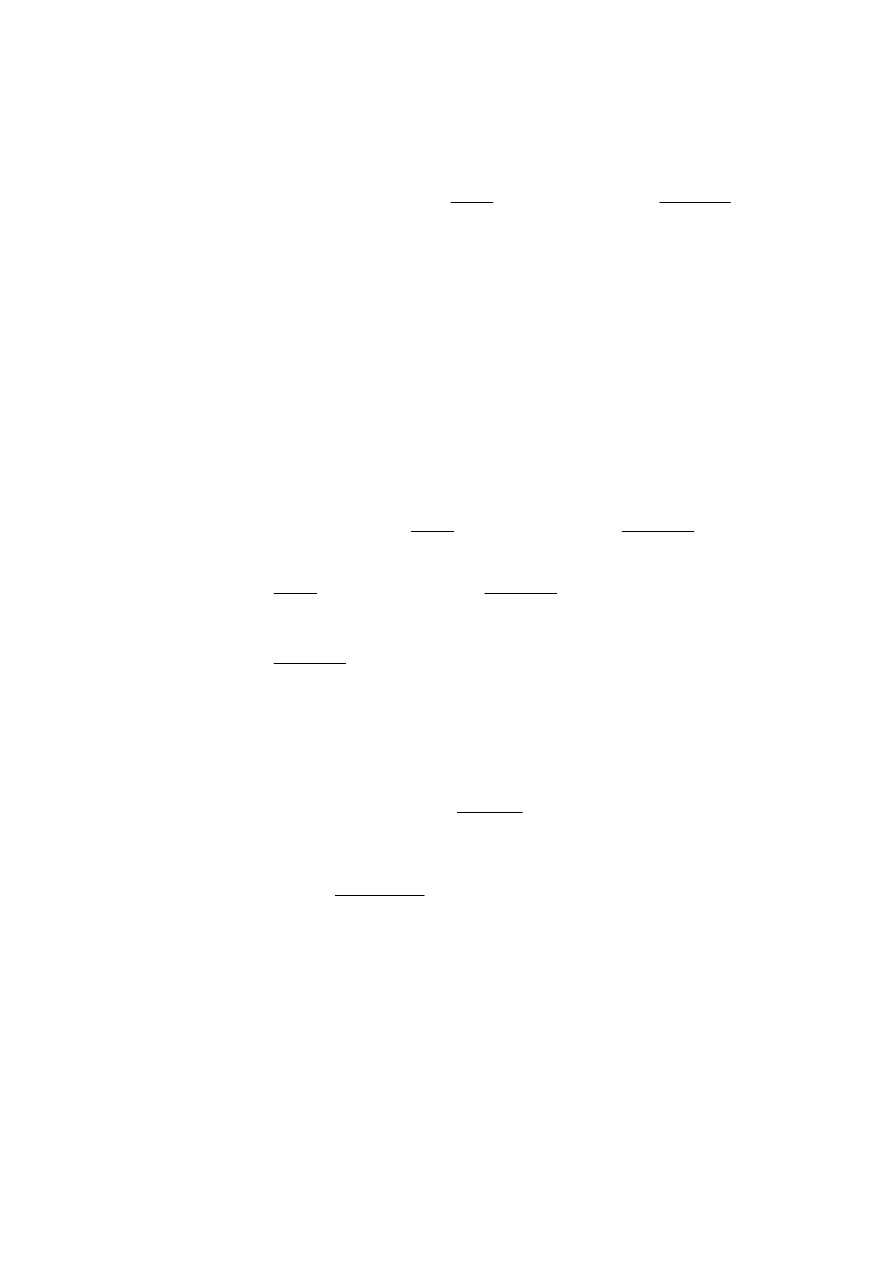
H W
H W Z
I W Z
r
r
r
−
=
/
,
⇓
(
)
( )
(
)
( )
( )
(
)
(
)
I W Z
H W
H W Z
p w
p w
p w z
p w
z
r
r
r
i
r
i
i
n
i
j
r
j
m
i
j
i
n
,
/
log
,
log
/
=
−
=
⋅
−
⋅
=
=
=
∑
∑
∑
1
1
1
1
1
a ponieważ:
( )
(
)
( )
p z
p z
w
p w
j
j
i
i
j
n
=
⋅
=
∑
/
1
( )
(
) ( )
p w
p w
z
p z
i
i
j
j
j
n
=
⋅
=
∑
/
1
||
(
)
p w z
i
j
i
n
,
=
∑
1
mamy więc:
(
)
(
) ( )
( )
(
)
(
)
(
)
( )
(
)
(
)
(
)
(
)
( )
I W Z
p w
z
p z
p w
p w z
p w
z
p w z
p w
p w z
p w
z
p w z
p w
z
p w
r
i
j
j
j
m
r
i
i
n
i
j
r
j
m
i
j
i
n
i
j
r
i
j
m
i
n
i
j
r
j
m
i
j
i
n
i
j
r
i
j
i
j
m
i
n
,
/
log
,
log
/
,
log
,
log
/
,
log
/
=
⋅
⎛
⎝
⎜
⎞
⎠
⎟ ⋅
−
⋅
=
=
⋅
−
⋅
=
=
⋅
=
=
=
=
=
=
=
=
=
=
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
1
1
1
1
1
1
1
1
1
1
1
1
1
1
ale zauważmy:
(
) ( ) ( )
p w
z
p z
p w z
i
j
j
i
j
/
,
⋅
=
, a stąd
(
) (
)
( )
p w
z
p w z
p z
i
j
i
j
j
/
,
=
⇓
(
)
(
)
(
)
( )
( )
∑∑
=
=
⋅
⋅
=
n
i
m
j
j
i
j
i
r
j
i
r
z
p
w
p
z
w
p
z
w
p
Z
W
I
1
1
,
log
,
,
I tu symetria, przestawiamy w
i
z z
j
i to ma praktyczną INTERPRETACJĘ:
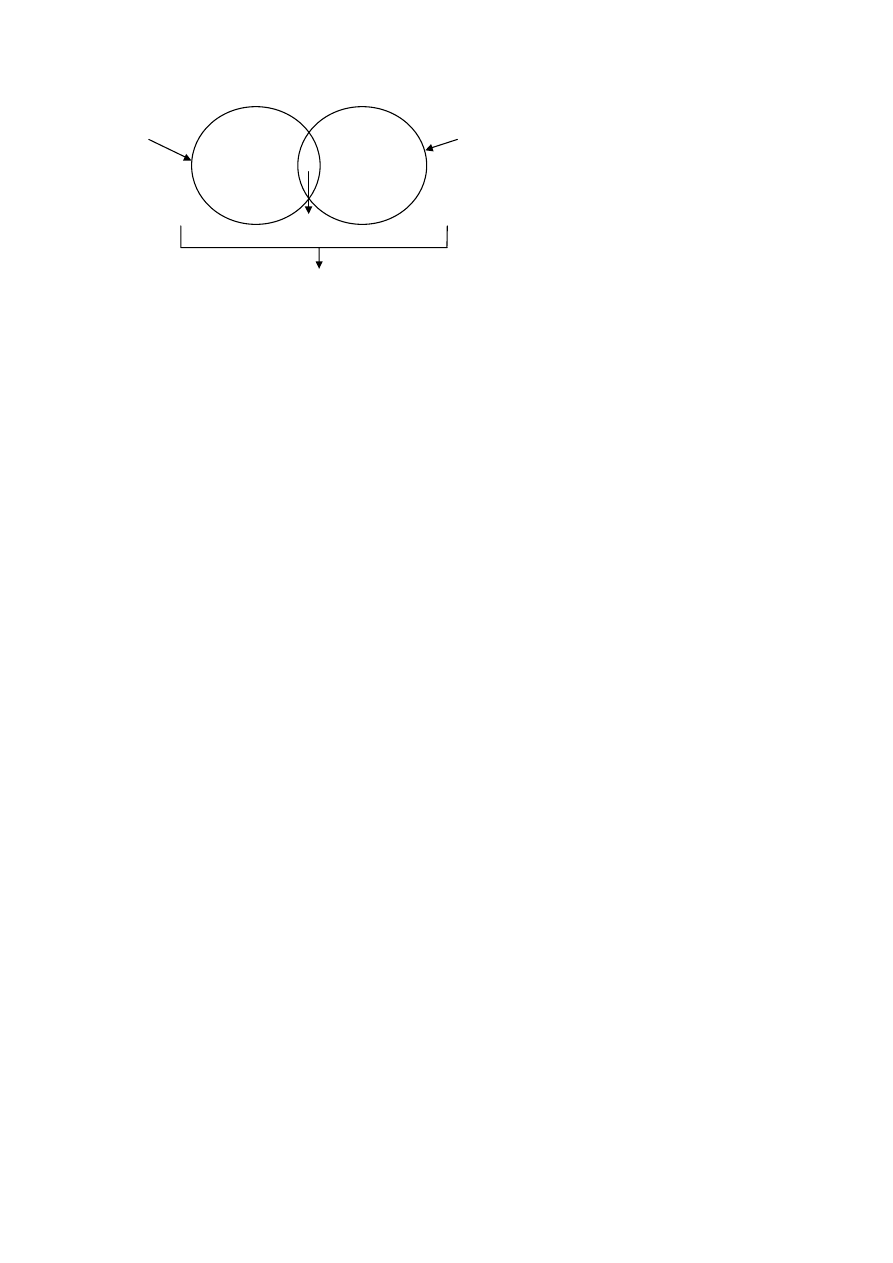
H
r
(W|Z)
H
r
(Z|W)
H
r
(W)
H
r
(Z)
I
r
(W,Z)
H
r
(W,Z)
Def. Przepustowość kanału
( )
(
)
(
)
C
I W Z
W
r
= max
,
Π
//ustalona poprzez dobieranie prawdopodobieństw wiadomości generowanych przez źródło//
( )
(
)
Π W
p p
p
p
n
i
i
n
=
=
⎧
⎨
⎩
⎫
⎬
⎭
=
∑
1
2
1
1
,
,...,
:
,
( )
p
p w
i
i
=
//bardzo złożony algorytm wyznaczania tego//
Interpretacja:
[
]
(
)
(
)
[
]
[
]
P
p z
w
n m
j
i
n m
×
×
=
/
n - wierszy, m - kolumn
Reguły decyzyjne
Pozwalają określić jaka wiadomość została nadana
z
j
- wiadomość odebrana
w * - wiadomość przyjęta z a nadaną (ustalona jako nadana)
Miara błędu, jaki popełniamy:
( )
(
)
p e z
p w
z
j
j
/
* /
= −
1
Średni błąd decyzji:
( )
( )
( )
p e
p e z
p zj
j
j
m
=
⋅
=
∑
/
1
Dobre decyzje - gdy minimalizujemy tę sumę, czyli gdy przyjmiemy taką wiadomość w
każdym przypadku, aby błąd konkretnej decyzji wiadomości był minimalny:
(1.)
(
) (
)
p w
z
p w
z
j
i
j
* /
/
≥
, gdzie i = 1,2,...,n
Czyli bierzemy teraz macierz kanału odwróconego
( )
P
−1
. Sposób wyboru decyzji nazywamy
regułą decyzyjną
. (1.) nazywana jest regułą największego prawdopodobieństwa.
Przykład.
{
}
W
w w w
=
1
2
3
,
,
,
{
}
Z
z z z
=
1
2
3
, ,
, p
1
0
= ,2 , p
2
0
= ,7 , p
3
0 1
= ,
P
w
w
w
z z z
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
2
3
1
2
3
0 1 0
0
0 8 0 1 0 1
0 1 0
0 5
,
,2
,7
,
,
,
,
,4
,
i na tej podstawie, na podstawie macierzy kanału nie da się tego
określić!!
Napiszmy tę samą regułę inaczej:
(2.)
(
)
( )
( )
(
)
( )
( )
p z
w
p w
p z
p z
w
p w
p z
j
j
j
i
i
j
/ *
*
/
⋅
≥
⋅
i tu widzimy jak obliczać ale jeszcze inaczej:
(3.)
(
)
( )
(
)
( )
p z
w
p w
p z
w
p w
j
j
i
i
/ *
*
/
⋅
≥
⋅
Jeśli nie znamy prawdopodobieństw p p
p
n
1
2
,
,...,
i nie mamy żadnych innych przesłanek to
przyjmuje się, że:
p
p
p
n
1
2
=
= =
...
(Największej wiarygodności)
⇓
(4.)
(
) (
)
p z
w
p z
w
j
j
i
/ *
/
≥
, dla i = 1,2,...,n
Mówimy, że określona jest reguła decyzyjna jeżeli wiemy jaką wiadomość przyjąć za
nadaną, gdy znamy wiadomość odebraną.
Przykład.
{
}
Z
z z
z
=
1
2
5
, ,...,
,
{
}
W
w w w
=
1
2
3
,
,
Z
z
1
z
2
z
3
z
4
z
5
W
w
2
w
3
w
1
w
2
w
3
Z
{ }
z
3
{
}
z z
1
4
,
{
}
z z
2
5
,
W
w
1
w
2
w
3
Reguła decyzyjna jest określona przez funkcję:
f
W
:Z
→
, gdzie Z jest podziałem zbioru wiadomości odebranych Z, czyli
{
}
Z
= z z
z
k
1
2
, ,...,
,
gdzie z
Z
i
⊆ dla i = 1,2,...,k; z
z
i
j
∩
= 0 dla i
j
≠ ;
z
Z
i
i
k
=
=
1
U
Strata i ryzyko
Przykład.
(
)
R w w
i
*,
- funkcja strat, gdzie:
w
i
-wiadomość rzeczywiście nadana
w * - wiadopmość ustalona jako nadana
• ogólny przykład definiowania:
{
}
W
w w
=
1
2
,
, R - w dowolnych jednostkach
1)
(
)
(
)
R w w
R w w
1
1
1
1
2
2
0
,
,
=
=
(
)
(
)
R w w
R w w
1
1
2
1
2
1
1
,
,
=
=
2)
R
c w
w
i
2
=
−
*
, gdzie w
w
w
w
w
w
i
j
i
j
i
j
−
=
=
≠
⎧
⎨
⎩⎪
0
1
gdy
gdy
3)
{
}
W
w w
w
n
=
1
2
,
,...,
( )
R
c w
w
i
3
=
−
*
• Ustalona jest reguła decyzyjna r i funkcja strat
(
)
R w w
i
*,
Średnia strata przy stosowaniu reguły r określa wówczas funkcja:
(
)
(
)
r
R w w
p w z
i
i
j
j
m
i
n
=
⋅
=
=
∑
∑
*,
,
1
1
Kody korekcyjne
Przestrzeń wektorowa
( )
r
GF
n
W przestrzeni wektorowej
( )
2
n
GF
elementami są ciągi (wektory) binarne.
Należy określić operacje dodawania wektorów i mnożenia wektora przez skalar.
Oznaczenia: a, b, c - skalary, u, v, w - wektory
Dodawanie:
(
)
n
u
u
u
u
,...,
,
2
1
=
,
(
)
n
v
v
v
v
,...,
,
2
1
=
(
)
n
n
v
u
v
u
v
u
v
u
⊕
⊕
⊕
=
⊕
,...,
,
2
2
1
1
,
gdzie
⎩
⎨
⎧
≠
=
=
⊕
i
i
i
i
i
i
v
u
v
u
v
u
gdy
1
gdy
0
, czyli
(
)
2
mod
i
i
i
i
v
u
v
u
+
=
⊕
Kody liniowe - struktura i własności
Def. Zbiór
słów kodowych oznaczać będziemy przez
( )
K n k
, - kod liniowy, w którym n -
długość słowa kodowego, k - liczba pozycji informacyjnych niezbędnych do rozróżnienia 2
k
kodowanych wiadomości
Def. Odległością
( )
d u v
, słów kodowych u i v kodu
( )
K n j
,
nazywamy liczbę pozycji, na
których wartości w ciągach u i v są różne.
Def. Wagą słowa
( )
w v
słowa kodowego v nazywamy liczbę jedynek występujących w tym
słowie.
Def. Minimalną odległością słów kodowych kodu K nazywamy liczbę
( )
d
d u v
u v K
u v
=
∈
≠
,
min
,
,
liczba d nazywana jest również minimalną odległością kodu K
Tw. Minimalna odległość kodu K jest równa minimalnej wadze słowa kodowego v, gdzie
v
K
∈ i v ≠ 0
( )
d
w v
v K
v
=
∈
≠
min
0
Tw.
W kodzie liniowym spełniona jest nierówność d
n
k
≤ − +1
Przykład.
(
)
v
= 10111
(
)
v'
= 11101
(
) (
) (
)
v
v
e
v
'
'
=
+
=
10111
01010
11101
Tw. Jeżeli znamy wektor błędów e to możemy ustalić wektor v na podstawie odebranego
wektora v’, a mianowicie: v v e
= +
'
Przykład.
(
)
v'
= 11101
(
)
e
= 01010
(
)
v
= 10111
• Opis kodu za pomocą macierzy
Zauważmy, że kod liniowy (podprzestrzeń
( )
GF
n
2 ) jest jednoznacznie określony przez
macierz złożoną z wektorów tworzących podprzestrzeń. Macierz tę nazywamy macierzą
generującą kod liniowy, oznaczoną literą G.
Przykład. n
= 5 , k = 5 ,
( )
GF
5
2 zawiera 2
5
wektorów
G
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
0
0
0
1
0
0
0
1
1
0
1
1
1
0
Macierz generującą można przekształcić zamieniając kolumny i zastępując niektóre wiersze
kombinacjami liniowymi.
Przykład.
G'
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
1
0
0
1
0
0
0
1
1
0
1
1
0
0
G''
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
0
1
0
1
1
0
0
0
1
1
0
1
1
0
0
Kody generowane przez tak przekształcone macierze nazywamy kodami równoważnymi.
Mówimy, że macierz G generująca kod K jest macierzą w postaci kanonicznej jeżeli:
[
]
(
)
[
]
[
]
G
I
P
k k
k
n k
=
×
× −
M
i macierz z przykładu jest w postaci kanonicznej.
Skoro kod K jest podprzestrzenią przestrzeni
( )
GF
n
2 zatem istnieje podprzestrzeń, która jest
ortogonalnym dopełnieniem przestrzeni K. Oznaczamy ją przez K
⊥
. K
⊥
jest kodem liniowym
(bo każda podprzestrzeń
( )
GF
n
2 jest kodem liniowym)
Kody K i K
⊥
nazywamy kodami dualnymi
Niech H będzie macierzą generującą kod K
⊥
.
Zauważmy, że jeżeli K jest kodem (n, k) to K
⊥
jest kodem (n, n-k). Zatem macierz H ma
rozmiar
(
)
[
]
n
k
n
−
× . Wynika stąd, że:
v H
T
⋅
= 0 (wektor zerowy o długości n-k) Á v ∈K
i G H
T
⋅
= 0 (macierz zerowa)
Tw. Macierz
H generującą kod dualny K
⊥
nazywamy macierzą kontrolną kodu K i
odwrotnie: macierz G nazywać będziemy macierzą kontrolną kodu K
⊥
.
Tw. Jeżeli macierz G jest w postaci kanonicznej, to
(
)
[
]
(
) (
)
[
]
[
]
H
P
I
n k
k
n k
n k
=
− ×
− × −
M
Dowód:
G H
T
⋅
= 0,
[ ]
G H
I P
P
I
P
P
T
⋅
=
×
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
= + =
M
L
0
Przykład.
G
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
1
0
0
0
1
0
0
0
1
1
0
1
1
1
0
M
M
M
H
=
⎡
⎣
⎢
⎤
⎦
⎥
1
1
0
1
1
0
1
0
0
1
M
M
H
T
=
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
1
1
0
1
1
0
1
0
0
1
L L
G H
T
⋅
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
+
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
+
+
+
+
+
+
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
1 1
0 1
1 0
1 1
0 1
1 0
1 1 1 1
0 0 1 1
1 1 0 0
0
Kodowanie i dekodowanie
G
, H ,
( )
n k
,
2
k
- wiadomość
v
K
∈ , v
i
- część informacyjna
Elegancka metoda kodowania
v
v G
i
= ⋅
( )
w
GF
n
∈
2
i sprawdzanie:
w H
T
⋅
= 0 to w K
∈ , w v
=
w H
T
⋅
≠ 0 to
przyjmujermy,
że nadane zostało słowo kodowe najblizsze odebranemu
ciągowi w (czyli v, jak dobrze przygotowany ciąg liczy się odległość i trzeba policzyć do
każdego ale w praktyce: )
Przykład.
(
) (
)
w k
,
,
= 100 50
słów
( )
2
2
10
10
50
10 5
35
15
⋅
≈
=
, czyli po stwierdzeniu, że to nie jest słowo kodowe to
porównanie jest potężnie złożone, ale jest bardziej racjonalna metoda (UNIWERSALNA)
Niech v
v v
v
k
1
2
3
2
0
= , , ,...,
będą słowami kodowymi kodu
( )
n k
,
( )
GF
n
2 2
n
wektorów i to
możemy rozwiązać, bo może się pojawić któryś z nich:
// l
n
- wektor o długości l zawierający jedynkę na n-tej pozycji
1 warstwa
v
1
0
=
v
2
v
3
...
v
k
2
2 warstwa
0
1
+ l
v
2
+ l
1
v
3
+ l
1
v
k
2
+ l
1
3 warstwa
0
2
+ l
v
2
+ l
2
v
3
+ l
2
v
k
2
+ l
2
//żaden z tych ciągów nie jest równy poprzedniemu, bo jedynka na innej pozycji, jak się
skończy to 2 jedynki i znów na innej pozycji i tych warstw będzie: //
2
n k
−
warstwa
0
2
1
+
−
−
l
n k
v
2
+
−
−
l
n k
2
1
v
3
+
−
−
l
n k
2
1
v
k
2
+
−
−
l
n k
2
1
//nowa warstwa będzie już powtórzeniem, ta tablica 2
n k
−
warst zawiera wszystkie wektory
przestrzeni
( )
GF
n
2 //
Iloczyn s v H
T
= ⋅
, gdzie
( )
v
GF
n
∈
2 nazywamy syndromem błędów (wskaźnikiem błędów)
Zauważmy, że jeżeli ciągi v i v' należą do tej samej warstwy to syndromy błędów dla tych
ciągów są sobie równe
Wprowadzenie do kryptografii
M - tekst jawny
C
- tekst niejawny
E - algorytm szyfrowania
D - klucz szyfrowania
k
E - przekształcenie szyfrujące
k
D przekształcenie deszyfrujące
( )
M
E
C
k
=
( )
( )
(
)
M
E
D
C
D
M
k
k
k
=
=
M
C
M
k
E
k
D
M
C
M
k
E
k
D
1.
- poufność danych
2.
- autentyczność danych
( )
(
)
( )
(
)
M
D
E
M
E
D
M
k
k
k
k
=
=
Szyfr - sposób zapisania danych taki, aby był on utajniony
Szyfry dzielimy na:
• przestawieniowe
• podstawieniowe
Przestawieniowe (zmiany pozycji poszczególnych znaków)
• sztachetowe
• macierzowe albo tablicowe, kolumnowe
Przykład: KRYPTOGRAFIA
1) zapisujemy w postaci tablicy
[
]
2
3
×
←
parametr
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
A
I
F
A
R
G
O
T
P
Y
R
K
2) odczytujemy kolumnami KYTRPOGAIRFA
Klucz może być w postaci
[
]
1
,
2
,
2
3
×
, gdzie cyfry następujące po wymiarze tablicy są
kolejnością czytania kolumn
• permutacyjne
f: X
→
X
i = (123)
f(i) = (231)
KRY PTO GRA FIA
→
RYK TOP RAG IAF
Podstawieniowe
• 1 - 1 monoalfabetyczne
• 1 - n
• m - n poligramowe
a) ABCDEFGHIJKLMNOPQRSTUWXYZ //Cezara k=2
np. BAL
⇒
DCN
//zmodyfikowany Cezar
SZYFRABCDEG...
SZYFR to klucz, musi być jednoznaczny
//uogólniony i trudniejszy
1.
( ) (
)
n
k
a
a
f
mod
+
=
, gdzie a - numer litery, n - liczba liter
wyrażenie deszyfrujące ma postać:
( )
( ) (
)
n
k
c
c
f
mod
1
−
=
−
2.
( ) (
)
n
k
a
a
f
mod
⋅
=
, gdy
( )
1
,
=
n
k
NWD
wtedy jednoznacznie
wyrażenie deszyfrujące ma postać:
( )
( )
(
)
n
k
c
c
f
mod
1
1
−
−
⋅
=
Arytmetyka modularna (resztowa)
Liczby całkowite a i b nazywamy liczbami kongruentnymi (przystającymi) według modulo n
(całkowite)
⇔
n jest dzielnikiem (a - b)
Zapisujemy to: a
b
n
≡
lub
(
)
a
b
m
≡ mod
Liczbę b nazywamy residium liczby a mod n i odwrotnie.
Zbiór liczb całkowitych
{
}
r r
r
n
1
2
, ,...,
nazywamy zupełnym zbiorem residiów modulo n
(względem modulo n)
⇔
dla dowolnej liczby całkowitej a istnieje w tym zbiorze dokładnie
jedna liczba r
i
, taka, że a
r
n
i
≡
.
W szczególności zbiór
{
}
01
1
, ,..., n
− jest zbiorem zupełnym residiów modulo n.
Jeśli przyjmiemy przedział [0, n-1] jako zbiór zupełny residów to piszemy:
r
a
n
i
= mod .
Jeżeli ograniczymy się do zbioru liczb całkowitych dodatnich, to residium liczby a jest reszta
z dzielenia tej liczby przez moduł n.
Dane są liczby a i n.
Operację wyznaczania residium modulo n liczby a nazywamy redukcją liczby a modulo n
Operacja redukcji liczb (ze zbioru) z pierścienia liczb całkowitych (można wykazać, że zbiór
liczb zredukowanych z operacjami
+ − ⋅
, , jest pierścieniem przemiennym) w pierścień liczb
całkowitych modulo n jest przekształceniem homomorficznym, czyli dla dowolnych liczb
całkowitych a i b i dowolnej operacji
{
}
⊗ ∈ + − ⋅
, , mamy równość:
(
)
(
) (
)
[
]
a
b
n
a
n
b
n
n
⊗
=
⊗
mod
mod
mod
mod
Przykład:
n = 9
356947 7
-154715 -5
2 2
Zredukowanym zbiorem rezidiów modulo n nazywamy podzbiór zbioru {0,1,..., n-1}
zawierający liczby względnie pierwsze z n.
Przykład:
n = 10 {1,3,7,9} - residium zredukowane, {0,...,9} - rezydium zupełne
n = 12 {1,5,7,11}
Liczbę elementów zredukowanych zbiorów rezidiów modulo n określa tzw. Funkcja Eulera
Φ(n).
Jeżeli n
p
p
p
e
e
k
e
k
=
⋅
⋅ ⋅
1
2
1
2
...
, to
( )
(
)
Φ n
p
p
i
e
i
i
k
i
=
⋅
−
−
=
∏
1
1
1 .
Operacja odwrotna do mnożenia istnieje wtedy i tylko wtedy, gdy dla kazdej liczby a istnieje
liczba a
−1
taka, że:
a a
n
⋅
=
−1
1
mod
Twierdzenie Fermata. Jeżeli
( )
NWD ,
a p
= 1
, gdzie p - liczba pierwsza to a
p
p
mod
= 1.
Twierdzenie Eulera. Jeżeli
( )
NWD ,
a n
= 1, to
( )
a
n
n
Φ
mod
= 1
Wynika stad, że:
( )
a a
n
n
⋅
=
−
Φ
1
1
mod
, a więc
( )
a
a
n
n
−
−
=
1
1
Φ
mod
Czyli jak mamy pierścień, gdzie wszystkie wzajemnie pierwsze to każda ma odwrotną i staje
się ten zbiór ciałem.
Liczby naturalne m m
m
n
1
2
,
,...
są względnie pierwsze, jeżeli
(
)
NWD
,
,...,
m m
m
n
1
2
1
=
. Sa one
parami względne jeżeli
(
)
NWD
,
m m
i
j
= 1 dla każdej pary liczb i, j spełniającej
1
≤ < ≤
i
j
n .
Algorytm Euklidesa:
Dane są dwie liczby m m
N
1
2
,
∈ , gdzie m
m
1
2
≥
. Jeżeli m
2
jest dzielnikiem m
1
, to
(
)
NWD
,
m m
m
1
2
2
=
. Jeżeli m
2
nie jest dzielnikiem m
1
, to wykonujemy dzielenie z resztą m
1
przez m
2
. Niech q
2
będzie ilorazem, a m
3
- resztą z tego dzielenia. Mamy więc
m
q m
m
1
2
2
3
=
+
, gdzie m
m
3
2
<
. Jeżeli
m m
3
2
( m
3
jest dzielnikiem m
2
), to
(
)
NWD
,
m m
m
1
2
3
=
.
Jeżeli m
3
nie jest dzielnikiem m
2
, to wykonujemy dzielenie z resztą m
2
przez m
3
. Niech
q
3
będzie ilorazem, a m
4
- resztą z tego dzielenia, tzn m
q m
m
2
3
3
4
=
+
, gdzie m
m
4
3
<
.
Postępując analogicznie w dalszym ciągu otrzymujemy ciąg skończony m m m
m
m
n
n
1
2
3
1
,
,
,...,
,
−
,
w którym m
m
m
m
n
n
1
2
1
>
> >
>
−
...
, m m
2
1
/| , m m
3
2
/|
, ..., m
m
n
n
−
−
/
1
2
|
oraz m m
n
n
|
−1
. Wtedy
(
)
NWD
,
m m
m
n
1
2
=
.
Algorytm szybkiego potęgowania modularnego
Algorytm ten pozwala na obliczenie działania: a
n
b
mod , gdzie wszystkie liczby są liczbami
całkowitymi (a oraz b nieujemne a n dodatnie).
1. d
← 1
2. niech
b b
b
k
k
,
,...,
−1
0
będzie binarną reprezentacją b
3. for i
← k downto 0
4. do d
← (d·d) mod n
5.
if
b
i
= 1
6.
then d
← (a·d) mod n
7. return d
Algorytm RSA (Rivesta, Shamira i Adelmana)
Klucze jawny i tajny szyfru RSA są funkcjami pary dużych liczb pierwszych. W celu
wygenerowania kluczy odbiorca kryptogramu losuje dwie liczby pierwsze p i q oraz liczbę e.
Iloczyn n = pq oraz e stanowią publiczny klucz szyfrujący. Liczba e musi być względnie
pierwsza z funkcją Eulera
( )
ϕ
n
. Spełnione są więc zależności:
n
p q
= ⋅
( )
(
)(
)
ϕ
n
p
q
=
−
−
1
1
( )
(
)
NWD ,
e
n
ϕ
= 1
Do przeprowadzenia szyfrowania i deszyfrowania potrzebne są dwie takie pary:
( )
e d
,
oraz
(
)
e d
', ' , gdzie e wybieramy losowo (pamiętając o tym, że ma być względnie
pierwsza z
( )
ϕ
n
), natomiast d liczymy ze wzorów:
( )
(
)
( )
d
e
n
n
=
−
ϕ ϕ
ϕ
1
mod
(
)( )
(
)
(
)(
)
d
e
p
q
p
q
=
−
−
−
− −
ϕ
1
1
1
1
1
mod
Wiadomość zaszyfrowaną liczy się następująco:
(
)
C
M
n
n
d
e
=
mod
mod
'
Proces deszyfrowania przebiega bardzo podobnie:
(
)
M
C
n
n
d
e
=
'
mod
mod
Algorytm Pohliga-Hellmana
[
]
M
p
∈
−
0
1
,
C
M
p
e
=
mod M
C
p
d
=
mod
n
p
p
p
a
a
k
a
k
=
⋅
⋅ ⋅
1
2
1
2
...
( )
(
)
Φ n
p
p
i
a
i
k
i
i
=
−
−
=
∏
1
1
1
( )
Φ p
p
= −1
( )
e d
n
⋅
=
mod
Φ
1
( )
(
)
( )
d
e
n
n
=
−
ϕ ϕ
ϕ
1
mod
Algorytm Merklego-Hellmana
Klucz tajny jest generowany za pomocą generatora liczb losowych i zawiera ciąg
superrosnący (tzn. elementy tego ciągu są tak wybrane aby każdy element był większy od
sumy poprzedzajacych go elementów) oraz liczbę pierwszą u i liczbę losową w .
Klucz tajny: A
a
a
a
n
' ( ', ',..., ' )
=
1
2
Liczby u i w spełniają zależności:
u
a
i
i
n
>
=
∑
'
1
,
1
< <
w
u .
Dla liczby w liczbę odwrotną w
−1
oblicza się z zależności:
w w
u
⋅
=
−1
1
mod
Elementy klucza jawnego obliczane są z zależności:
a
a w
u
i
i
= ' mod
Szyfr Merklego - Hellmana jest szyfrem blokowym, szyfrującym ciągi binarne. Ciag
informacyjny m m
1
2
,
,... dzieli się na bloki
(
)
M
m m
m
n
=
1
2
,
,...,
, zawierajace po n bitów.
Szyfrowanie bloku odbywa się z udziałem klucza jawnego A według wzoru: C
a m
i
i
i
=
∑
.
W procesie deszyfrowania wykorzystuje się klucz tajny. Podczas deszyfracji najpierw oblicza
się C'
C
Cw
u
'
mod
=
−1
1)
Przygotowanie do szyfrowania
• Ustalamy ciąg superrosnący A
a
a
a
n
' ( ', ',..., ' )
=
1
2
• Ustalamy liczbę u
a
i
i
n
>
=
∑
'
1
• Wybieramy liczbę w względnie pierwszą z u
• Obliczamy w
u
−1
mod
• Przekształcamy wektor A' w wektor A : A w A
= ⋅ ' , czyli a
w a
u
i
i
= ⋅ ' mod
2)
Szyfrowanie
• C A M
= ⋅
, czyli C
a m
i
i
i
n
=
=
∑
1
3)
Deszyfrowanie
• A w A
u
'
mod
=
−1
• C w C
u
'
mod
=
−1
, gdzie C
A M
'
'
= ⋅
• Wyznaczamy M znajac A' i C'