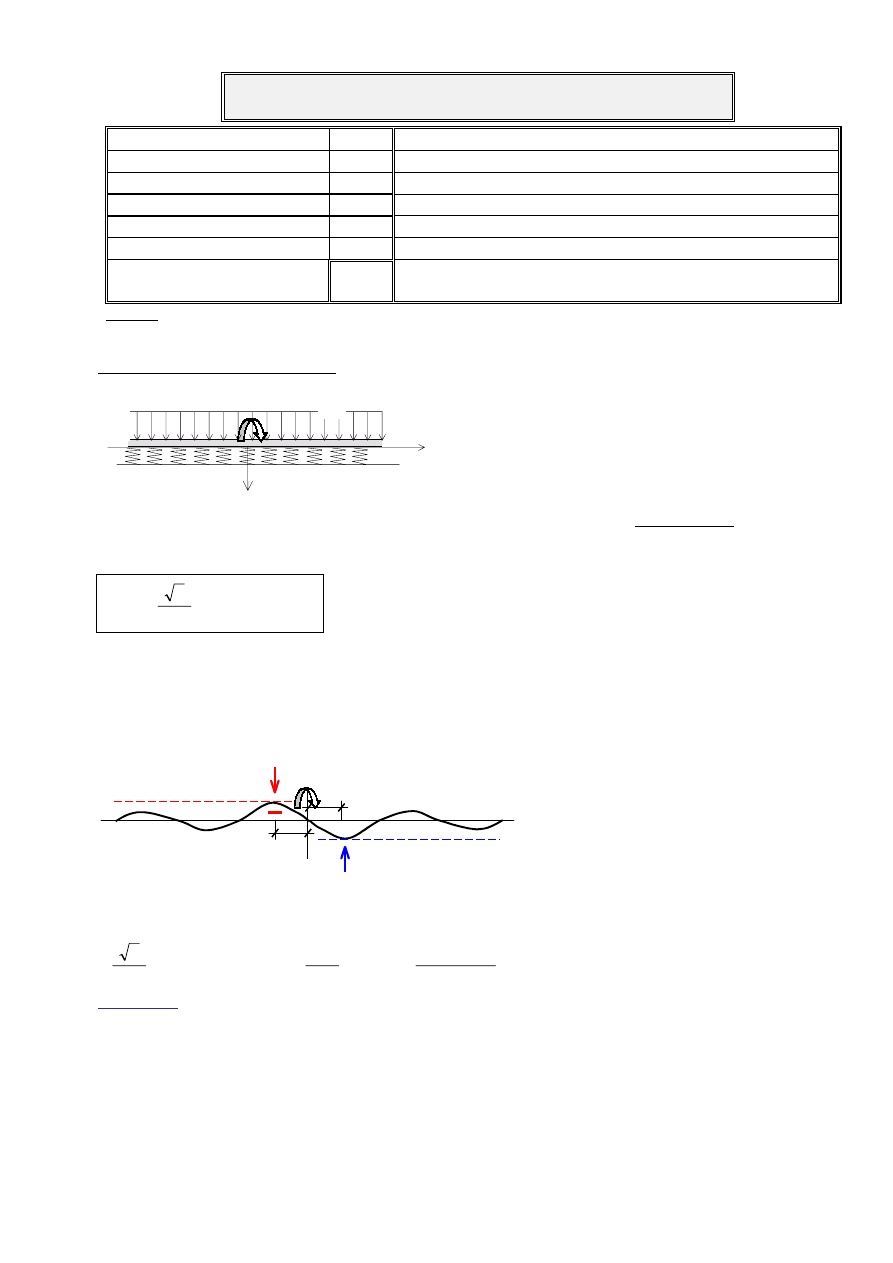
Zadanie 1 (za 8 punktów, ok. 15min)

Nieskończenie długa belka o szerokości B = 0,75m spoczy-
wa na podłożu Winklera o stałej C = 44MN/m

3

i jest obcią-

żona momentem skupionym w przekroju

ξ

o

= 0.

Wystąpiłyby wówczas ujemne reakcje na pewnych
odcinkach belki i przemieszczeń skierowanych do góry.
Aby tego uniknąć belkę obciążono dodatkowo w sposób
równomierny q

o

= const na całej długości, co powoduje jej

równomierne osiadania. Obliczyć minimalną wartość q

o

[kN/m], która zapewnia niewystąpienie rozciągania na

styku belki z podłożem, tj. sumaryczne osiadania mają być wszędzie nieujemne.
Przyjąć, że obciążenie M

o

powoduje następujące osiadania y [m] dla

ξ

≥

0:

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

Rozwiązanie na całej osi jest funkcją nieparzystą (antysymetria) w postaci „zanikającej fali”.
Największe rozciąganie wystąpiłoby w odległości

ξξξξ

e

na lewo od przyłożonego momentu. Jest to liczba

przeciwna do największego ściskania w odległości

ξξξξ

e

na prawo od przyłożonego momentu.

Ma być dy/d

ξξξξ

= 0 w punkcie

ξξξξ

e

.

0

],

sin

[

=

⋅

−

ξ

ξ

e

+

−

⋅

−

ξ

ξ

sin

[

e

0

]

cos

=

⋅

−

ξ

ξ

e

+

−

ξ

sin

[

0

]

cos

=

ξ

,

czyli

ξξξξ

e

=

ππππ

/4 + k

⋅⋅⋅⋅ππππ

(tutaj k = 0).

Równomierne obciążenie spowoduje równomierne osiadanie: y

q

= q

o

⋅⋅⋅⋅

(C

⋅⋅⋅⋅

B)

-1

[m].

Z warunku y + y

q

≥≥≥≥

0 (zasada superpozycji!) otrzymuje się:

0

44000

75

,

0

001

,

0

45

sin

1000

2

4

/

4

/

≥

⋅

+

−

=

⋅

+

⋅

⋅

−

⋅

−

+

o

o

o

q

C

B

q

e

e

π

π

Odpowiedź: q

o

≥≥≥≥

33 kN/m .

(Prawie to samo zadanie rozwiązałem na tablicy pod koniec drugiego wykładu).

KOLOKWIUM Z FUNDAMENTOWANIA II (KB)

Zad. 1 (15 minut, max 8p.)

Zad. 2 (10 minut, max 3p.)

DATA KOLOKWIUM:

22.01.2003r.

Pyt. 1 (5 minut, max 3p.)

Pyt. 2 (5 minut, max 3p.)

imię i nazwisko:

Włodzimierz Brząkała

Pyt. 3 (5 minut, max 3p.)

numer albumu:

35705

RAZEM (40 minut, max 20p.)

KOŃCOWY WYNIK KOLOKWIUM:

Uwaga:

ewentualna odpowiedź wykazująca zupełną nieznajomość zagadnienia

może zostać oceniona punktami ujemnymi !

M

o

y

ξ

+

∞

-

∞

q

o

+

ξ

e

ξ

e

ξ

ξ

ξ

π

sin

1000

2

)

(

4

/

⋅

−

+

⋅

⋅

=

e

e

y

Zadanie 2 (za 3 punkty, ok. 10min)
Fundament o całkowitej długości 13m składa się ze stopy 3x5m oraz
dwóch ław po 1x4m każda.
Ile wynosi maksymalna siła rozciągająca N

max

w fundamencie,

jeśli zasięg strefy przedgranicznej x

Θ

= 2m,

a graniczne tarcie jednostkowe pod fundamentem

Θ

= 20 kPa.

Pominąć działanie wszelkich sił na bocznych powierzchniach ławy

.

•

Siła ze strefy przedgranicznej (x

Θ

Θ

Θ

Θ

= 2m < 5/2m !):

N

1

= 3m x 2m x ½ x

Θ

Θ

Θ

Θ

= 60kN

•

Siła ze strefy granicznej (reszta stopy+jedna ława):

N

2

= 3m x (5/2-2)m x

Θ

Θ

Θ

Θ

+ 1m x 4m x

Θ

Θ

Θ

Θ

= 110kN.

•

Odpowiedź: 60 + 110 = 170kN.

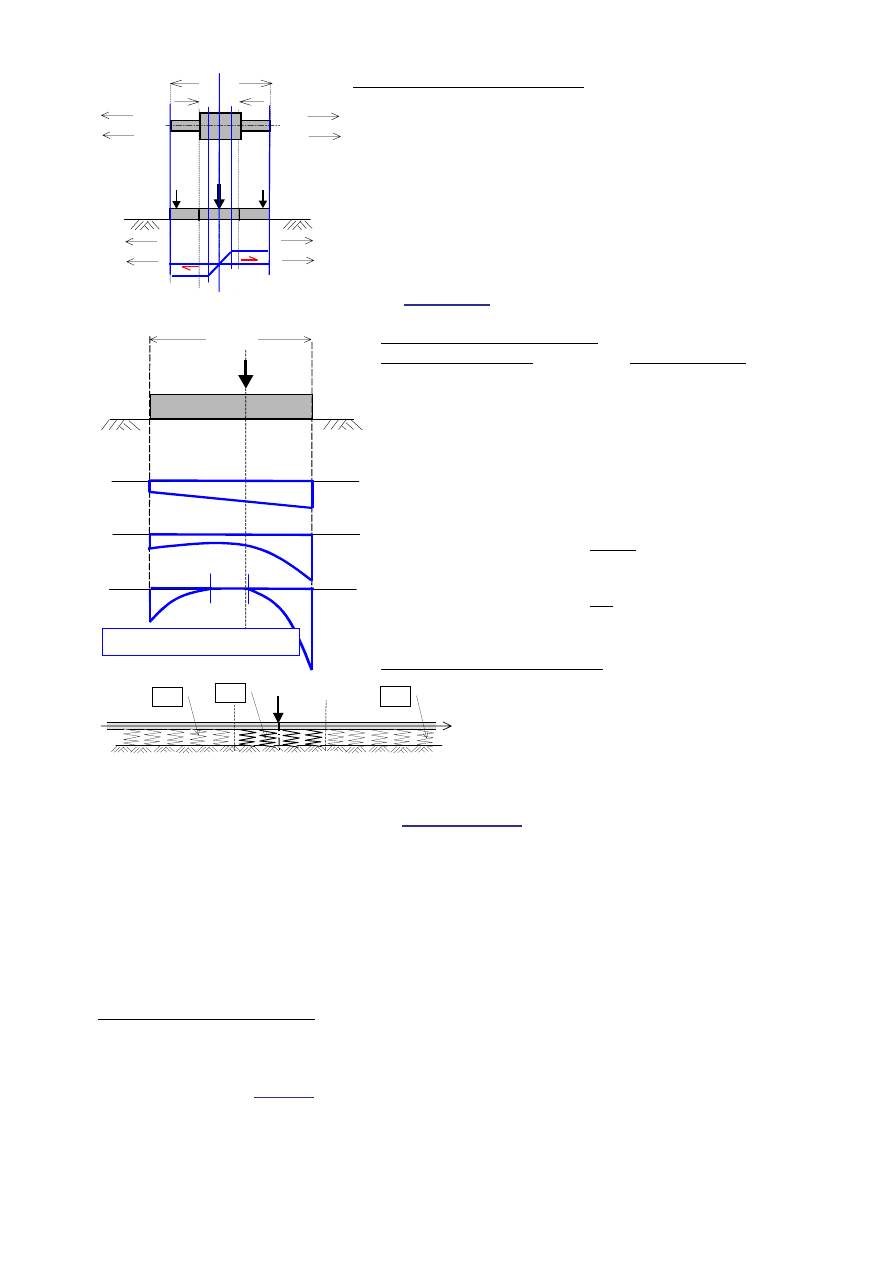
Pytanie 1. (za 3 punkty, ok. 5min)
Nieskończenie sztywny fundament na podłożu Winklera jest obciążony
siłą pionową na niewielkim mimośrodzie e < L/6.
Na rysunku obok naszkicować typowy wykres reakcji podłoża,
tj. pionowe naprężenia pod fundamentem r(x).

A)

przed wystąpieniem deformacji górniczej

B) po wystąpieniu wklęsłej w dół krzywizny terenu górniczego
o R < 0, gdy promień graniczny nie jest przekroczony (R < R

gr

< 0)

C) po wystąpieniu wklęsłej w dół krzywizny terenu górniczego
o R < 0, gdy promień graniczny jest przekroczony (R

gr

< R < 0).

Pytanie 2. (za 3 punkty, ok. 5min):

Modelem ławy fundamentowej jest nieskończenie
długa belka o sztywności EI = const na podłożu
Winklera. Na odcinku –1 < x < +1 stała podłoża wy-
nosi C

1

, a poza tym C

2

≠

C

1

. Siła skupiona P działa w

przekroju x

o

= 0. Zaproponować koncepcję rozwiąza-

nia belki (wystarczy na półosi x > 0 – dlaczego?).

* * * * * * * * * * * * * * * * * *

1. Wystarczy dla x > 0, bo y(x) będzie funkcją parzystą, a z tej funkcji wynikają wszystkie pozostałe

rozwiązania statyczne r(x), M(x), Q(x).

2. Najlepiej jest podzielić belkę na odcinki gdzie C

i

= const, tutaj wystarczy (0,+1)

∪

∪

∪

∪

(+1,+

∞

∞

∞

∞

).

3. Dla x > +1 rozwiązaniem we współrzędnych bezwymiar. jest y(

ξξξξ

) = exp{-

ξξξξ

}

⋅⋅⋅⋅

[S

1

⋅⋅⋅⋅

sin

ξξξξ

+ S

2

⋅⋅⋅⋅

cos

ξξξξ

]

4. Dla 0 < x < +1 rozwiązaniem jest y(

ξξξξ

) = exp{-

ξξξξ

}

⋅⋅⋅⋅

[S

3

⋅⋅⋅⋅

sin

ξξξξ

+ S

4

⋅⋅⋅⋅

cos

ξξξξ

] + exp{+

ξξξξ

}

⋅⋅⋅⋅

[S

5

⋅⋅⋅⋅

sin

ξξξξ

+ S

6

⋅⋅⋅⋅

cos

ξξξξ

]

5. Sześć stałych S

i

należy obliczyć z 2 warunków brzegowych (dla

ξξξξ

=0 jest dy/d

ξξξξ

=0 oraz Q=-P/2)

i z 4 warunków ciągłości rozwiązania w x = +1. Są to warunki ciągłości dla y, dy/dx, Q oraz M.

(Za 1. dawałem 1pkt., a za warunki typu 5. dawałem dodatkowo 1pkt. lub nawet 1½pkt. - na trzy możliwe.
Podobne zadanie jest od trzech miesięcy na stronie WWW i kilka osób o nie pytało na konsultacjach).

Pytanie 3. (za 3 punkty, ok. 5min)
Parcie czynne i parcie bierne gruntu oblicza się w normie PN-83/B-03010 generalnie za pomocą metody Ponceleta.
Wprowadza się tam jednak pewien współczynnik korygujący

η

.

Jest to współczynnik dla parcia czynnego, biernego, czy dla obu parć? . . .

tylko dla parcia biernego, czyli odporu gruntu

Dlaczego wprowadza się ten współczynnik

η

? . . . . .

w celu skorygowania zbyt upraszczającego założenia Ponceleta, że klin odporu jest trójkątem

Od czego zależy wartość tego współczynnika? . . . . .

od kątów

ββββ

,

δδδδ

2

,

εεεε

,

ϕϕϕϕ

Podać przykład sytuacji, w której

η

→

1 . . . . .

w warunkach Coulomba (

ββββ

=0,

δδδδ

2

=0,

εεεε

=0) jest wręcz

ηηηη

= 1.

ε

ε

ε

ε

13m

5m

x

θ

<

2,5m

A

B

C

L

0

w szystkie łuki są parabolam i

P

x

-1

+1

0

-

∞

+

∞

C

2

C

1

C

2