1
Algorytmy ewolucyjne
Wprowadzenie
Inspiracją do podjęcia badań dotyczących algorytmów
ewolucyjnych było naśladowanie natury w zakresie zjawisk
na gruncie genetyki (przekazywanie korzystnych cech
potomstwu poprzez krzyżowanie i mutacje).
Idea ta została wykorzystana do rozwiązywania zagadnień
optymalizacyjnych. Mówiąc najprościej – poszukiwanie
takich rozwiązań oparte jest o zasadę, że spośród rozwiązań,
które dziedziczą pewne cechy po swoich rodzicach,
„przeżywają” tylko te rozwiązania, które są najlepiej
przystosowane.
Klasyczne metody optymalizacji
Klasyczne metody poszukiwania optymalnych rozwiązań
dzielą się na: metody analityczne, przeglądowe, oraz losowe.
W
metodach
analitycznych
poszukujemy
lokalnych
ekstremów funkcji rozwiązując układy równań (zwykle
nieliniowych). Metody te maja liczne wady – są złożone, nie
zawsze dadzą się zastosować, często „utykają” w lokalnych
ekstermach funkcji.
Metody przeglądowe polegają, mówiąc w uproszczeniu, na
obliczaniu wartości funkcji celu w całej przestrzeni
poszukiwań po kolei. Oczywiście dla dużych przestrzeni jest
to bardzo nieefektywne i często po prostu niemożliwe.
Metody losowe polegają na losowym przeszukiwaniu
przestrzeni
rozwiązań
i
zapamiętywaniu
otrzymanych
wyników, z których potem wybiera się najlepsze. Są one
również mało efektywne.
2
Idea algorytmów ewolucyjnych
Są to algorytmy oparte na mechanizmach doboru
naturalnego i dziedziczenia. Korzystają z ewolucyjnej zasady
przeżycia osobników najlepiej dostosowanych.
Główne cechy algorytmów ewolucyjnych, to:
Wyjście do przeszukiwania nie z pojedynczego punktu
przestrzeni poszukiwań, lecz z pewnej ich populacji,
Przetwarzanie nie bezpośrednio parametrów zadania,
lecz pewnej zakodowanej postaci tych parametrów,
Losowy wybór jest tu tylko pewnym narzędziem, a nie
zasadniczą ideą przeszukiwania, jak w klasycznych
metodach losowych.
Podstawowe pojęcia:
Populacja jest określonym zbiorem osobników,
Osobnikiem jest zakodowany w postaci chromosomu
zbiór parametrów zadania,
Chromosom to uporządkowany ciąg genów,
Gen jest cechą, pojedynczym elementem genotypu,
Genotyp to zespół chromosomów danego osobnika
(chociaż często jest to po prostu pojedynczy
chromosom),
Fenotyp to zdekodowana struktura, czyli po prostu
zbiór parametrów zadania.
Bardzo ważnym pojęciem jest funkcja przystosowania,
zwana również funkcją dopasowania, lub funkcją oceny.
Pozwala ona ocenić stopień dopasowania danego osobnika w
populacji i w ten sposób wybrać osobniki najlepiej
przystosowane ( o największej wartości funkcji dopasowania)
zgodnie z ewolucyjną zasadą przetrwania „najsilniejszych”. W
teorii sterowania funkcją przystosowania może być funkcja
3
błędu, którą się minimalizuje. W teorii gier – funkcja kosztu,
podlegająca również minimalizacji.
W algorytmie ewolucyjnym w każdej jego iteracji, ocenia się
przystosowanie każdego osobnika danej populacji za pomocą
funkcji przystosowania i na tej podstawie tworzy nową
populację osobników, stanowiących zbiór potencjalnych
rozwiązań problemu.
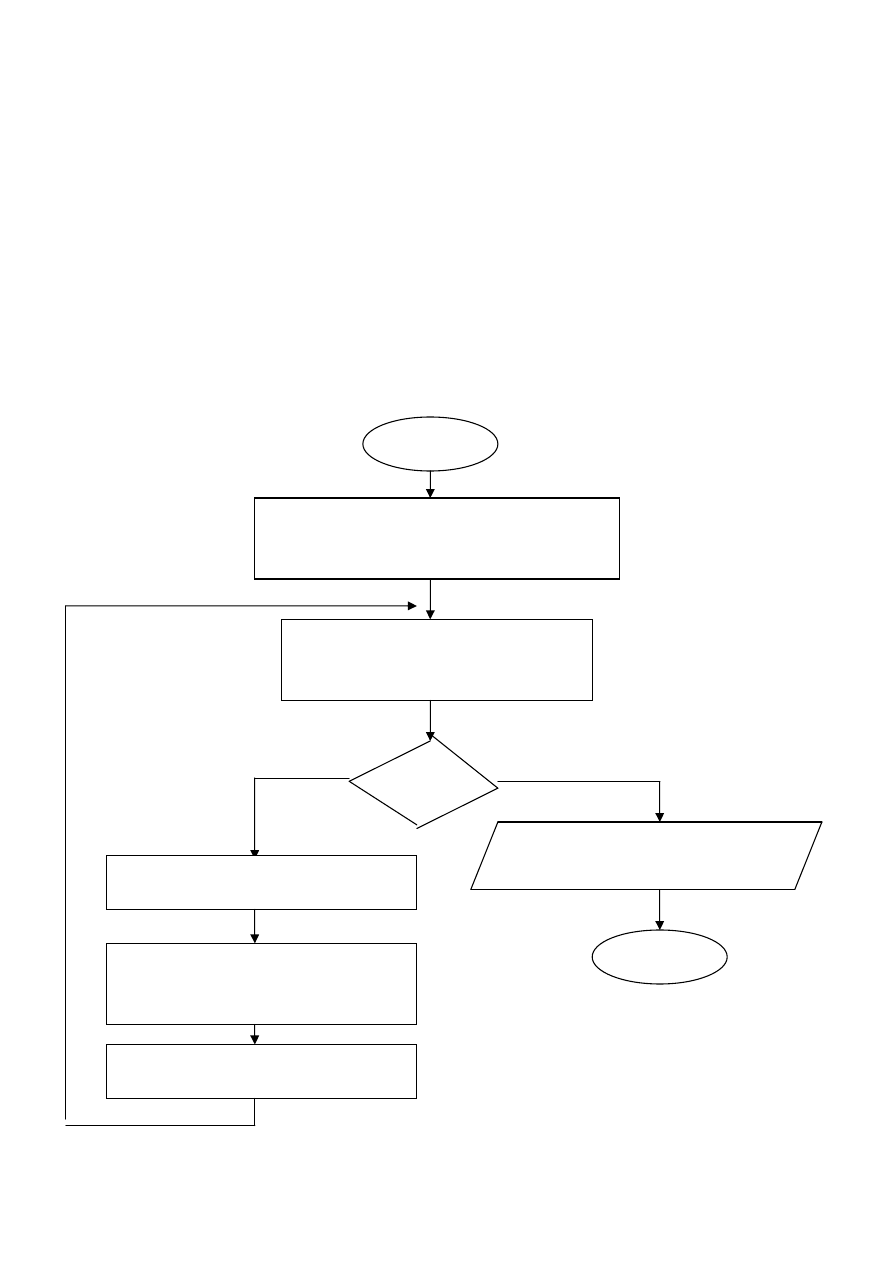
Klasyczny algorytm genetyczny
Nie Tak
warunek
Wyprowadzenie „najlepszego
chromosomu
START
INICJACJA – wybór początkowej
populacji chromosomów
OCENA przystosowania
chromosomów w populacji
SELEKCJA chromosomów
Zastosowanie operatorów
genetycznych
Utworzenie nowej populacji
STOP
4
Rys. 16. Schemat blokowy klasycznego algorytmu
genetycznego
Inicjacja (utworzenie populacji początkowej) polega na
losowym wyborze żądanej liczby chromosomów (osobników)
reprezentowanych przez ciągi binarne o określonej długości.
Ocena przystosowania osobników z populacji polega na
obliczeniu wartości funkcji przystosowania dla każdego
chromosomu z populacji.
Sprawdzenie warunków zatrzymania. Zależą one od
konkretnego zadania. Najczęściej jest to:
- osiągnięcie żądanej wartości optymalnej,
- osiągnięcie wartości optymalnej z określoną
dokładnością,
- przekroczenie
ustalonego
czasu
działania
algorytmu,
- wykonanie obliczeń dla żądanej liczby generacji.
Selekcja chromosomów polega na wybraniu na podstawie
wartości funkcji przystosowania, tych chromosomów, które
będą brały udział w tworzeniu następnego pokolenia.
Najbardziej popularną metodą selekcji jest metoda ruletki.
W wyniku procesu selekcji zostaje utworzona populacja
(pula) rodzicielska o liczebności zazwyczaj takiej, jak
liczebność bieżącej populacji.
Operatory genetyczne
Zastosowanie operatorów genetycznych do chromosomów
wybranych metodą selekcji prowadzi do utworzenia nowej
5
populacji, która jest populacją potomków, otrzymanej z
populacji rodziców.
W klasycznym algorytmie genetycznym stosuje się dwa
podstawowe operatory genetyczne: operator krzyżowania i
operator mutacji. W klasycznym algorytmie genetycznym
krzyżowanie występuje prawie zawsze (z prawdopodo-
bieństwem p
k
,które zwykle zawiera się w przedziale [0.5,1]),
podczas, gdy mutacja zachodzi dość rzadko (z prawdo-
podobieństwem p
m
zwykle nie większym niż 0.1 ). Wynika to
także z analogii do świata organizmów żywych, gdzie mutacje
zachodzą niezwykle rzadko.
W algorytmach genetycznych mutacje stosuje się zarówno na
populacji rodziców przed operacją krzyżowania, jak i na
populacji potomków, utworzonych w wyniku krzyżowania.
Przykład operacji krzyżowania i mutacji
Weźmy dwa chromosomy ch
1
i ch
2
majce po 10 genów.
Stanowić one będą parę rodzicielską. W celu przeprowadzenia
krzyżowania
wylosujmy
liczbę
z
przedziału
[1,9].
Wylosowano 5.
para rodziców krzyżowanie para potomków
ch
1
=[10010
|
01100] Ch
1
=[10010
|
11110]
ch
2
=[10011
|
11110] Ch
2
=[10011
|
01100]
Omówmy teraz przykład rozwiązania problemu mutacji.
W tym celu losujmy liczbę rzeczywistą z przedziału [0,1] dla
każdego z dziesięciu genów. Wylosowano:
0.23 0.76 0.54 0.10 0.28 0.68
0.01
0.30 0.95 0.12
Przyjmijmy, że p
m
=0.02. Do mutacji zostaną wybrane tylko
te geny, dla których wylosowana liczba jest <= p
m
– u nas gen
siódmy.
6
mutacja
ch
1
=[100100
1
100] Ch
1
=[100100
0
100]
Przykład wykorzystania algorytmu genetycznego
Zadanie 1:
Znaleźć maksimum funkcji y=2*x+1 w przedziale liczb
całkowitych [0,31]. Zbiorem potencjalnych rozwiązań (czyli
przestrzenią poszukiwań) jest więc zbiór {0,1,2,…,32}. Każdy
z elementów tego zbioru jest fenotypem. Fenotypy
zakodujemy przy pomocy chromosomów 5-bitowych (bo
wartości 32) odpowiada chromosom [11111].
1.
Losowanie populacji początkowej
Ustalono liczność populacji początkowej na N=8.
Chromosom fenotyp funkcja dostosowania
F(ch
i
)=2* ch
i
+1
ch
1
=[00110] ch
1
*
= 6
13
ch
2
=[00101] ch
2
*
= 5
11
ch
3
=[01101] ch
3
*
=13
27
ch
4
=[10101] ch
4
*
=21
43
ch
5
=[11010] ch
5
*
=26
53
ch
6
=[10010] ch
6
*
=18
37
ch
7
=[01000] ch
7
*
= 8
17
ch
8
=[00101] ch
8
*
= 5
11
2. Ocena funkcji dostosowania
Wartości funkcji dostosowania obliczono wg. wzoru
F(ch
i
)=2* ch
i
+1
3. Selekcja chromosomów
Selekcji dokonano metoda koła ruletki.
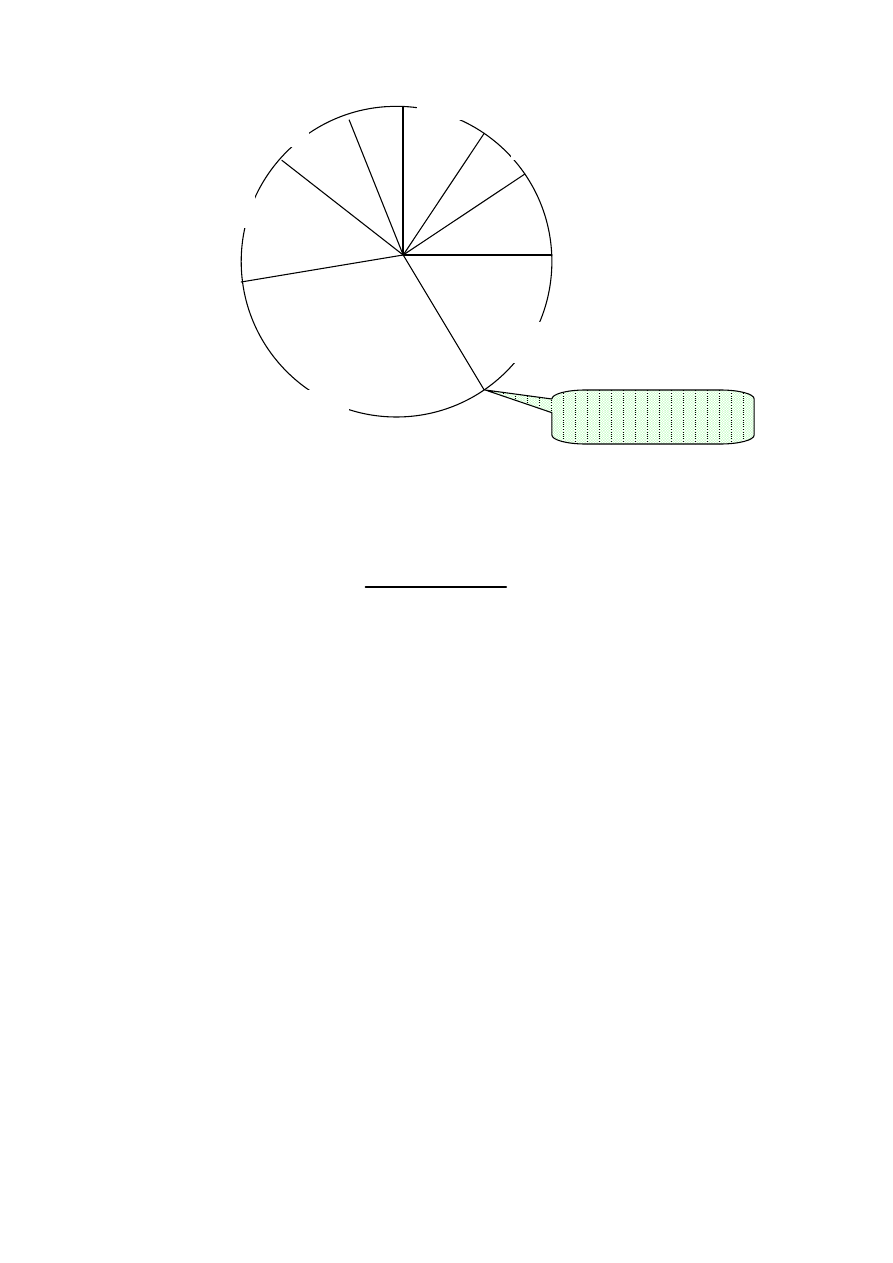
7
Pola wycinków koła ruletki obliczono wg wzoru
N
j
j
i
i
ch
F
ch
F
ch
1
)
(
)
(
)
(
Selekcja chromosomów za pomocą koła ruletki sprowadza
się do losowego wyboru poprzez zakręcenie kołem ruletki ( w
tym przypadku ośmiu) liczb z przedziału [0,100]. Suma
wszystkich wartości
( ch
i
) jest równa 100%.
Wylosowano następujące liczby:
79 44 9 74
45
86 48 23
co odpowiada następującym wylosowanym chromosomom
ch
6
ch
4
ch
2
ch
6
ch
5
ch
6
ch
5
ch
3
Dla przykładu piąty z wylosowanych chromosomów jest
chromosomem
ch
5
ponieważ jako piątą wylosowano liczbę
45
a jest to liczba większa od sumy granicznej 44,34.
Selekcja metodą koła ruletki pozwoliła wzmocnić „garnitur
chromosomowy”. Dla przykładu: najlepiej dostosowany
chromosom ch
6
wylosowano dwukrotnie, słabo dostosowane
6,13%
5,19%
25%
12,74%
20,28%
17,45%
8,02%
5,19%
suma=44,34%
8
ch
1
, ch
7
i ch
8
ani razu. Wylosowano też chromosom ch
2
o
najniższym dostosowaniu.
Zadanie 2:
Zadaniem będzie rozwiązanie tzw. problemu plecakowego.
Dane jest n przedmiotów, każdy o wadze w
i
i ważności p
i
.
Zadanie polega na takim załadowaniu plecaka, aby znalazły
się w nim przedmioty, z których mielibyśmy jak największą
korzyść. Założymy, że największej korzyści odpowiada
maksymalna możliwa wartość sumy ważności przedmiotów,
które da się zabrać przy ograniczeniu wagowym W.
W
x
w
n
i
i
i
1
Tutaj n jest ilością zabranych przedmiotów, x
i
przyjmuje dla
danego przedmiotu wartość 0, lub 1, ( zależności od tego, czy
i-ty przedmiot występuje, czy nie występuje w plecaku), W
jest dopuszczalną wagą plecaka.
Funkcja dostosowania może mieć postać
n
i
i
i
j
x
p
ch
F
1
)
(
gdzie ch
j
jest zakodowanym binarnie chromosomem o
długości n genów.
Problem plecakowy jest problemem o wykładniczej
złożoności
obliczeniowej.
Zastosowanie
algorytmu
genetycznego
pozwala
rozwiązać
go
w
czasie
wielomianowym.
Przeprowadzono eksperyment, w którym:
- liczba przedmiotów n=10,
- ważności każdego przedmiotu była taka sama p
i
=1
9
- wagi
przedmiotów
były
równe
numerowi
przedmiotu w
j
=i i=1, 2,…,10
- nośność plecaka była w przybliżeniu równa
połowie sumy wszystkich wag W=27,
Zastosowano klasyczny algorytm genetyczny z selekcją
proporcjonalną (koło ruletki) z prawdopodobieństwem
krzyżowania p
k
=0,7 i prawdopodobieństwem mutacji p
m
=0,01
Liczba osobników w populacji wynosiła 10.
F(ch
j
)
6
5
4
3
2
1
0
1 11 21 31 41 51 61 71 81 91
generacje
Rys. Wykres maksymalnej w populacji funkcji dostosowania
(najlepszego chromosomu) w 100 kolejnych generacjach
Dopiero w 43 populacji algorytm znalazł najlepsze
rozwiązanie z wartością funkcji dostosowania równą 6.
Algorytm został uruchomiony 100 razy. Znaleziono:
- 2 rozwiązania z 4 przedmiotami,
- 24 rozwiązania z 5 przedmiotami,
- 74 rozwiązania z 6 przedmiotami.
100 rozwiązań
Przykładowe rozwiązanie z 6 przedmiotami: 1,2,4,5,7,8.
W kolejnym eksperymencie założono: n=50, W=318. Ze
względu na skomplikowanie zadania ustalono wielkość
populacji na 100 osobników. Pozostałe parametry – bez zmian
10
Eksperyment przeprowadzono dla 200 generacji.
F(ch
j
)
30
25
20
15
10
5
0
1 21 41 61 81 101 121 141 161 181
generacje
Rys. Wykres maksymalnej w populacji funkcji dostosowania
(najlepszego chromosomu) w 200 kolejnych generacjach
Jak wynika z wykresu, już po dwudziestu kilku generacjach,
w populacji występowały chromosomy (rozwiązania) o
wysokiej, zbliżonej do maksymalnej, wartości funkcji
dostosowania. W dalszych generacjach zdarzały się jeszcze
lepsze rozwiązania, ale bywało, że w kolejnych generacjach
znikały. Na przykład, znaleziono tylko 2 rozwiązania z 33
przedmiotami, ale aż 38 rozwiązań z 31 przedmiotami.
Strategie ewolucyjne
Strategie ewolucyjne są algorytmami ewolucyjnymi, w
których w odróżnieniu od algorytmów genetycznych:
Działania odbywają się na wektorach liczb zmienno-
przecinkowych,
W procesie selekcji tworzona jest tymczasowa
populacja, a jej wielkość różni się od wielkości
populacji rodzicielskiej. Kolejna generacja osobników
powstaje przez wybór najlepszych, co zapobiega
przypadkowemu wyborowi osobników bardzo słabych.
11
Osobniki nowej populacji wybierane są bez powtórzeń.
Ten sam osobnik nie może wystąpić w nowej populacji
wielokrotnie.
Najpierw następuje proces rekombinacji (krzyżowania
i/lub mutacji) a dopiero potem selekcji, czyli odwrotnie
niż w algorytmach genetycznych.
Prawdopodobieństwo krzyżowania i prawdopodobień-
stwo mutacji nie są stałe w procesie ewolucji, lecz
podlegają ciągłej zmianie (samoadaptacji).
Istnieje wiele różnych strategii ewolucyjnych. Pozwalają one
przybliżyć sztucznie symulowany proces ewolucji do procesu
naturalnego.
Eksploracja i eksploatacja
Każdy algorytm ewolucyjny ma tendencję podążania w
kierunku lepszych rozwiązań. Proces ten nazywamy
naciskiem selektywnym. Z dużym naciskiem selektywnym
mamy do czynienia, gdy większa jest średnia wartość liczby
kopii lepszych osobników, niż średnia liczba kopii gorszych
osobników. Nacisk ten jest ściśle powiązany z zależnością
między eksploracją i eksploatacją.
Eksploracja
pozwala
przeszukiwać
całą
przestrzeń
rozwiązań w celu znalezienia rozwiązania globalnego.
Eksplorację
osiągamy
poprzez
zmniejszenie
nacisku
selektywnego.
Wybierane
są
osobniki
nie
najlepiej
przystosowane, ale mogące w przyszłości zbliżyć nas do
rozwiązania globalnego.
Eksploatacja natomiast jest poruszaniem się po fragmencie
przestrzeni rozwiązań, dobrze jeśli w pobliżu rozwiązania
globalnego. Eksploatacje uzyskujemy poprzez zwiększenie
nacisku selektywnego, co powoduje że osobniki przechodzące
do następnej populacji szybko uzyskują wartości coraz bliższe
12
oczekiwanym, i tu należy zadbać aby odbywało się to w
pobliżu rozwiązania globalnego.
Algorytm ewolucyjny może balansować między tymi dwoma
mechanizmami, co można osiągnąć poprzez zmianę jego
parametrów. Na przykład zwiększenie prawdopodobieństwa
krzyżowania i mutacji powoduje większą różnorodność
osobników, co w konsekwencji prowadzi do poszerzenia
obszaru poszukiwań i zapobiega przedwczesnej zbieżności (na
przykład do minimum lokalnego, które nie jest globalnym).
Natomiast zmniejszenie tych prawdopodobieństw prowadzi do
tworzenia osobników podobnych do siebie i zawęża obszar
poszukiwań.
Porównanie metod selekcji
Jak to już zostało powiedziane, metody selekcji polegają na
wyborze najlepiej dostosowanych osobników (populacji
rodzicielskiej) w celu dalszego przetwarzania za pomocą
operatorów
genetycznych.
W
klasycznym
algorytmie
genetycznym używa się proporcjonalnej metody selekcji,
zwanej kołem ruletki. Jej niewątpliwe słabości to:
- możliwość
używania
tylko
w
zadaniach
maksymalizacji (a nie minimalizacji) funkcji
dostosowania,
- osobniki o zbyt małej funkcji dostosowania są zbyt
wcześnie eliminowane (metoda ma zbyt dużą
wartość nacisku selektywnego, bez możliwości
sterowania tym naciskiem).
W celu eliminacji wyżej wymienionych wad metody koła
ruletki, stosuje się różne metody skalowania funkcji
dostosowania (będą omówione w dalszej części wykładu).
Omówione teraz zostaną inne metody selekcji.
13
Selekcja rankingowa
liczba
kopii
ranga
W selekcji rankingowej liczba kopii osobników wybrana do
puli rodzicielskiej jest tym większa, im wyższa jest ich ranga
(wartość funkcji dostosowania). Metoda może być używana
zarówno w zadaniach maksymalizacji, jak i minimalizacji
funkcji dostosowania. Nie ma też potrzeby odrębnego
skalowania tej funkcji, gdyż skalowanie można osiągnąć
poprzez
odpowiednie
nachylenie
funkcji
określającej
zależność liczby kopii od rangi osobnika (jak na rysunku
wyżej).
Selekcja turniejowa
l
K osobników
populacji
2-3 osobniki
2-3 osobniki
1 „najlepszy”
osobnik
1 „najlepszy”
osobnik
pula
rodzicielska
14
W selekcji turniejowej dzieli się całą pulę osobników na 2-3
elementowe podgrupy, a następnie biorąc po dwie podgrupy,
wydziela się w każdej z podgrup po jednym „najlepszym”
osobniku. Wchodzą one jako para do puli rodzicielskiej (patrz
rysunek wyżej).
Metoda turniejowa nadaje się zarówno do maksymalizacji,
jak i minimalizacji funkcji, ponadto – można łatwo zmieniać
rozmiar podgrup, na jakie dzielona jest populacja. Badania
wykazują, że działa ona lepiej od metody ruletki.
Selekcja progowa
Selekcja progowa jest szczególnym przypadkiem selekcji
rankingowej. Tutaj zależność liczy kopii osobników od rangi
ma postać progu, którego przekroczenie daje pewność wejścia
do puli rodzicielskiej. Umożliwia to sterowanie naciskiem
selektywnym poprzez odpowiedni dobór wartości progu.
Selekcja stłoczenia
Jest to ciekawa metoda selekcji. Przeprowadza się ją w ten
sposób, że tworzy się pewną pulę nowych osobników, a
następnie zastępuje się nimi, najbardziej podobne do nich
osobniki populacji poprzedniej niezależnie od wartości ich
funkcji dostosowania.
Postępuje się w ten sposób, aby zachować jak największą
różnorodność populacji. Jest to metoda o słabym nacisku
selektywnym. Wprowadzony parametr CF (ang. crowding
factor) określa liczbę rodziców podobnych do nowo
powstałego osobnika, spośród których wyznaczony zostanie
osobnik do usunięcia. Podobieństwo między nowymi i starymi
osobnikami wyznacza tzw. miara Hamminga.
15
Skalowanie funkcji dostosowania
Proporcjonalna metoda koła ruletki umożliwia wybór
osobników rodzicielskich proporcjonalnie do wartości ich
funkcji dostosowania. Z metody koła ruletki można korzystać,
gdy wartości funkcji dostosowania są dodatnie.
Drugą słabą stroną tej metody jest to, że osobniki o bardzo
małej wartości funkcji dostosowania są dość wcześnie
eliminowane z populacji, co doprowadza do ogólnie
przedwczesnej zbieżności algorytmu genetycznego.
Kolejną słabą stroną jest fakt, że nawet po wielu generacjach,
populacja będzie zawierała kopie najlepszych chromosomów,
ale zbudowanych w oparciu o określoną populację
początkową. Jest mało prawdopodobne, aby najlepszy
chromosom reprezentował optymalne rozwiązanie globalne,
skoro populacja początkowa była małą próbką losową z całej
przestrzeni poszukiwań. Skuteczną ochroną przed dominacją
nie całkiem optymalnych chromosomów okazały się metody
skalowania funkcji przystosowania. Jest ich kilka.
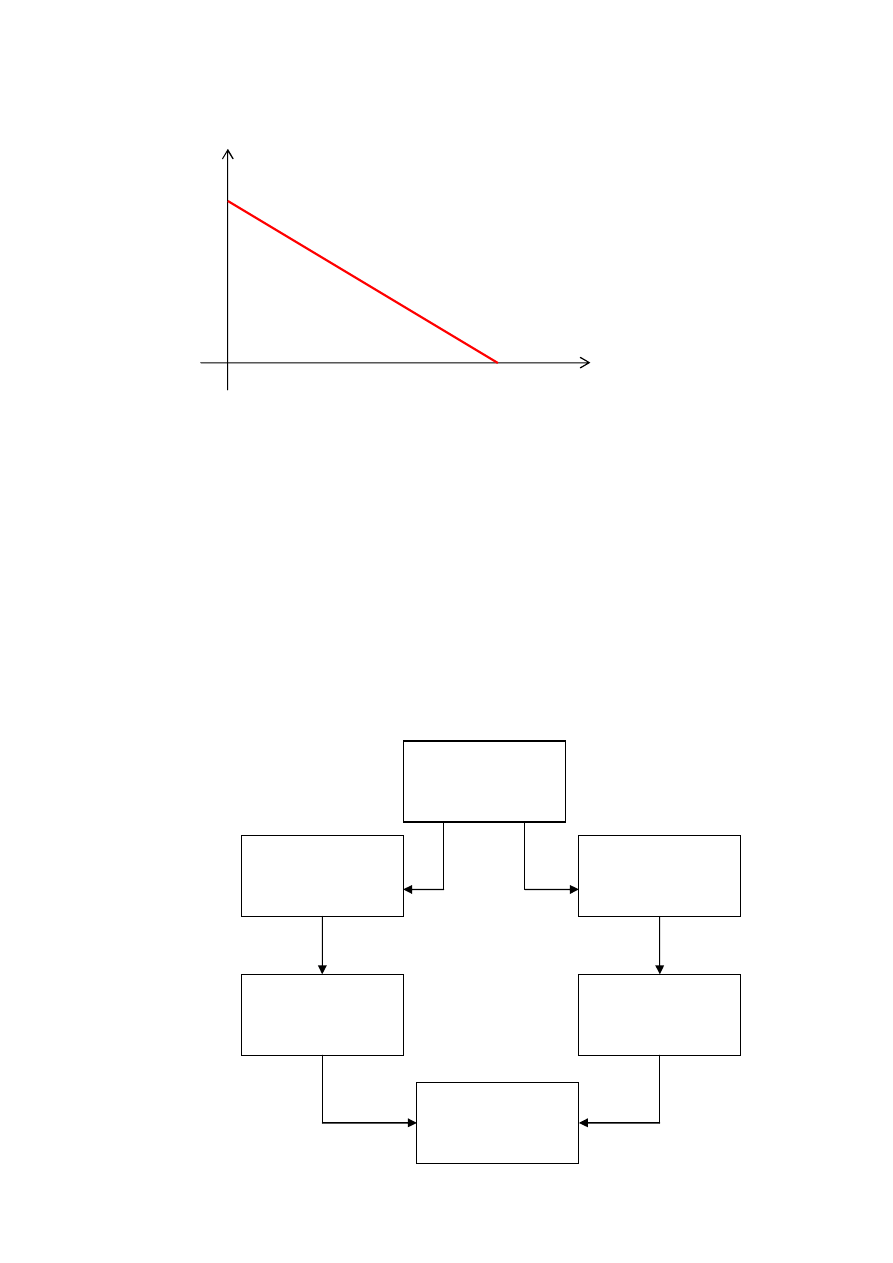
Skalowanie liniowe
wartości F
’
funkcji F
dostosow.
_ _ przestrzeń poszukiwań
F= F
’
Rys. Skalowanie liniowe dla przykładowej liniowej funkcji
dostosowania F
16
Skalowanie liniowe odbywa się wg. wzoru F
’
= a * F + b.
gdzie:
F jest wartością funkcji przystosowania,
F
’
jest jej przeskalowaną wartością,
a i b są stałymi dobranymi tak, aby średnia wartość funkcji
przystosowania
była
równa
średniej
wartości
przed
skalowaniem, natomiast wartość maksymalna po skalowaniu
była kilkakrotnie większa od wartości średniej i aby funkcja
F
’
nie przyjmowała wartości ujemnych. Zwykle przyjmuje się
wartość a między 1,2 a 2,0.
Skalowanie liniowe pozwala proporcjonalnie zwiększać, lub
zmniejszać nacisk selektywny.
Obcinanie typu sigma
Skalowanie odbywa się tu wg. wzoru F
’
= (F
S
– c*
)
gdzie:
F
S
jest wartością średnią funkcji przystosowania w populacji,
F
’
jest jej przeskalowaną wartością,
c jest mała liczbą naturalną (zwykle od 1 do 5),
jest odchyleniem standardowym średniej w populacji.
Wartości ujemne funkcji F
’
są obcinane do zera.
W tej metodzie stopień zwiększenia nacisku zależy od kształtu
funkcji obrazującej rozkład normalny wartości funkcji
dostosowania. Im odchylenie wartości średniej funkcji
dostosowania
większe, tym stopień zmniejszenia siły
nacisku mniejszy.
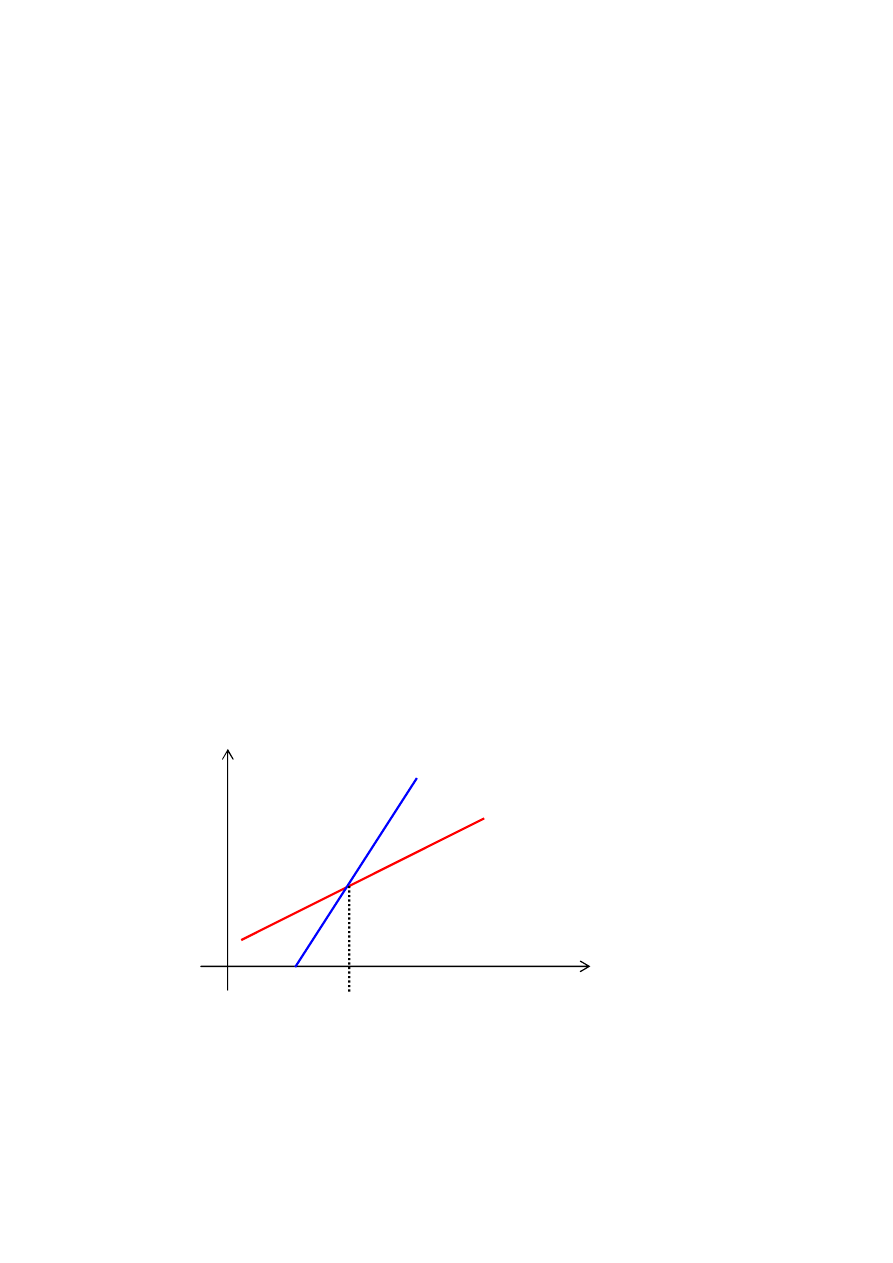
Skalowanie potęgą
Skalowanie odbywa się wg. wzoru F
’
= F
k
.
Wybór wartości stałej k zależy zwykle od rodzaju
rozwiązywanego problemu. Można przyjąć na przykład
k=1.005.
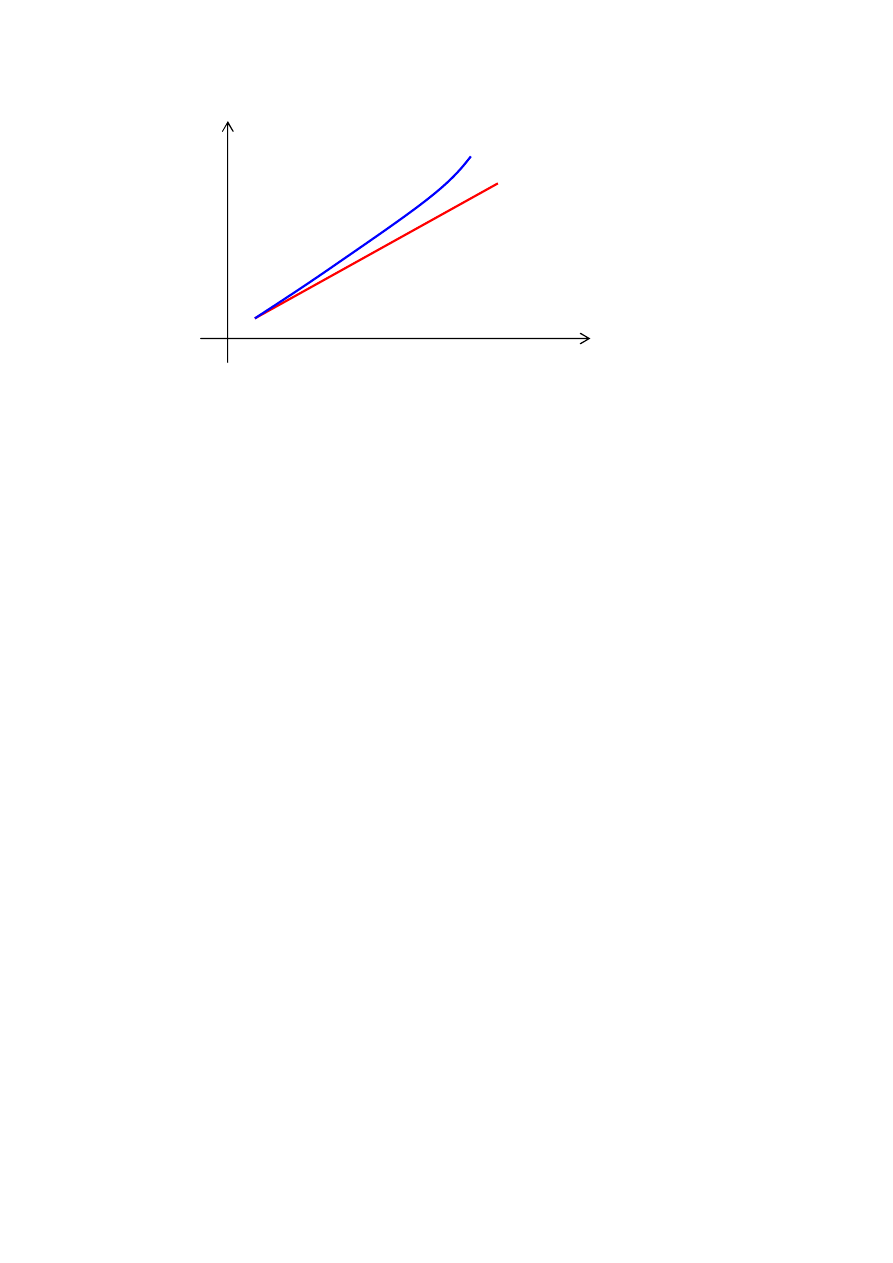
17
wartości F
’
funkcji F
dostosow.
przestrzeń poszukiwań
Rys. Skalowanie potęgą dla przykładowej liniowej funkcji
dostosowania F
Z innych, spotykanych w literaturze metod skalowania, można
wymienić: skalowanie logarytmiczne, skalowanie „metodą
okna”, metodę Boltzmana, oraz rankingowanie liniowe i
rankingowanie wykładnicze.
Specjalne procedury reprodukcji
Oprócz wyżej wymienionych metod selekcji stosuje się
jeszcze specjalne procedury reprodukcji, z których dwie
zostaną omówione.
Strategia elitarna
Strategia
elitarna
polega
na
ochronie
najlepszych
chromosomów w kolejnych generacjach. W klasycznym
algorytmie genetycznym nie zawsze najlepszy chromosom
przechodzi do następnej generacji. Strategia elitarna
zabezpiecza przed utratą takiego osobnika, bowiem zawsze
przechodzi on do następnej generacji.
18
Algorytm genetyczny z częściową wymianą populacji
Strategia ta charakteryzuje się tym, że część populacji
przechodzi do następnej generacji bez jakichkolwiek zmian
(nie podlegając mutacji i krzyżowaniom).
Przykład:
Metodę koła ruletki oraz strategię elitarną zastosowano do
rozwiązania omawianego wcześniej problemu plecakowego.
Strategia elitarna polegała na automatycznym przechodzeniu
do następnej populacji 2 osobników najlepiej przystosowa-
nych. Pozostałe parametry pozostawiono bez zmian.
F(ch
j
)
30
25
20
15
10
5
0
1 21 41 61 81 101 121 141 161 181
generacje
Rys. Wykres maksymalnej w populacji funkcji dostosowania
(najlepszego chromosomu) w 200 kolejnych generacjach z
zastosowaniem strategii elitarnej
Łatwo zauważyć, że zmiany wartości funkcji przystosowania
najlepszego osobnika nie zachodzą już tak nieregularnie,
bowiem w kolejnych generacjach najlepsze rozwiązania nie są
już tracone.
Najciekawszym jednak jest fakt, że znaleziono nowe
rozwiązania, które w poprzednich (bez strategii elitarnej) 100
19
kolejnych uruchomieniach algorytmu genetycznego nie
zostały znalezione.
Teraz znaleziono:
- 1 rozwiązanie z 33 przedmiotami
(poprzednio 2 rozwiązania),
- 57 rozwiązań z 34 przedmiotami,
- 42 rozwiązania z 35 przedmiotami.
100 rozwiązań
Poprzednio w ogóle nie znaleziono rozwiązań z 34 i 35
przedmiotami. Dominowały gorsze rozwiązania z 30 i 31
przedmiotami.
Metody hybrydowe
Metody hybrydowe są to metody, które łączą w sobie
(najczęściej dwie) różne metody sztucznej inteligencji.
Algorytmy ewolucyjne w projektowaniu sieci
neuronowych
Algorytmy ewolucyjne znalazły zastosowanie w celu
wspomagania niżej wymienionych problemów z zakresu sieci
neuronowych:
do poszukiwania optymalnej architektury sieci,
do uczenia wag sieci neuronowych,
jednocześnie do uczenia wag i określania topologii sieci
neuronowych.
Architektura sieci (liczba warstw, liczba neuronów w
warstwie, sposób połączenia neuronów) jest zwykle tworzona
metodą prób i błędów.
20
Optymalne projektowanie architektury sieci neuronowych z
wykorzystaniem algorytmów ewolucyjnych traktować można
jako poszukiwanie takiej struktury sieci, która działa najlepiej
dla określonego zadania, rozwiązywanego przez sieć. Oznacza
to przeszukiwanie przestrzeni architektur i wybór najlepszej
przestrzeni.
Etapy przykładowego projektowania architektury sieci
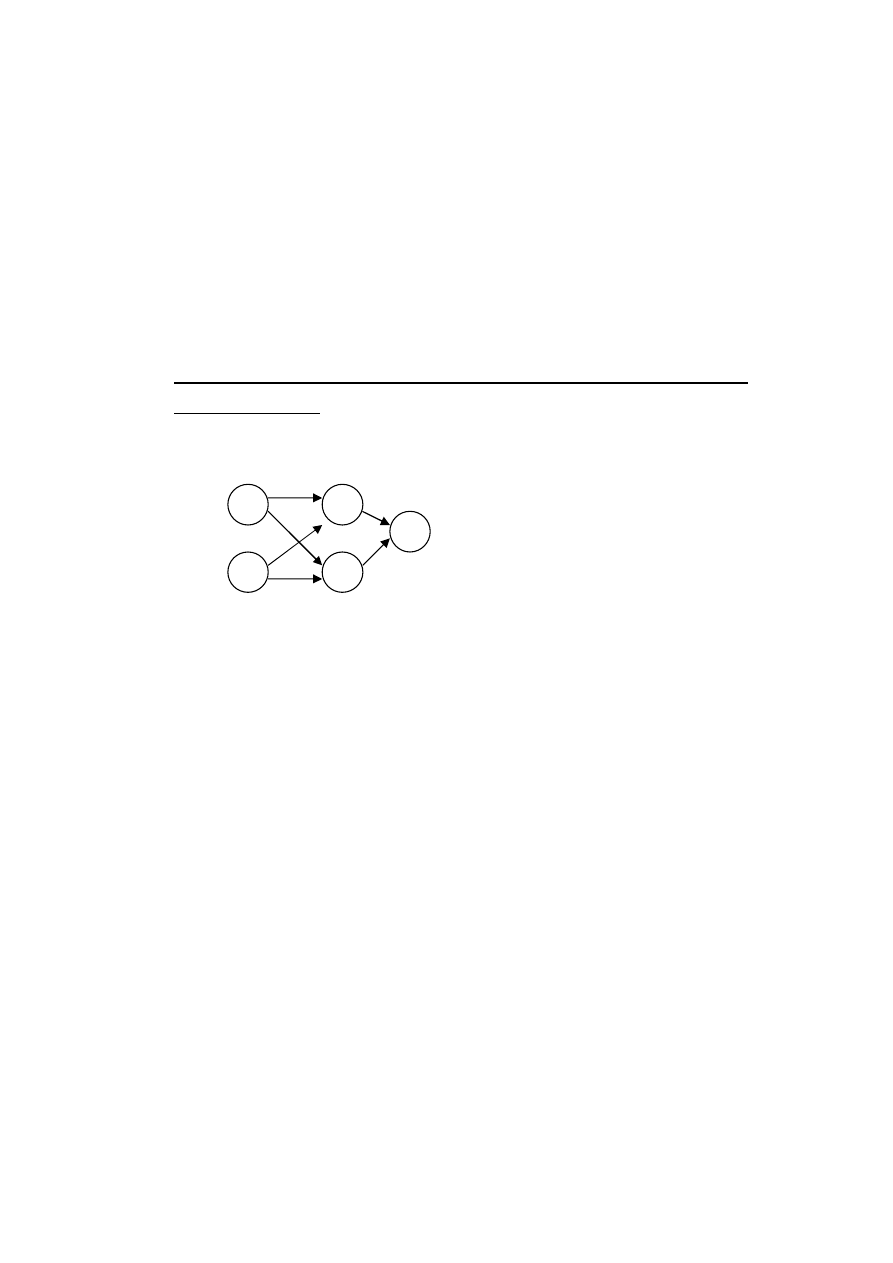
neuronowej z wykorzystaniem algorytmów genetycznych:
1. Wybór sposobu reprezentowania architektury sieci w
chromosomie. Jedną z wielu, najprostszą, metodą jest tu
kodowanie bazujące na połączeniach.
[0110110011]
Rys. Przykład reprezentacji chromosomowej dla sieci z
połączeniami „do przodu”
2. Dekodowanie każdego osobnika bieżącej generacji
(chromosomu) do architektury wynikającej z przyjętego
schematu kodowania.
3. Uczenie każdej sieci neuronowej.
4. Ocena dostosowania każdego osobnika (zakodowanej
architektury) na podstawie rezultatów uczenia, np.
najmniejszego średniego kwadratowego błędu uczenia.
5. Reprodukcja osobników z prawdopodobieństwem
odpowiednim do ich dostosowania.
6. Zastosowanie operatorów genetycznych i otrzymanie
nowej generacji.
1
2
3
4
5
21
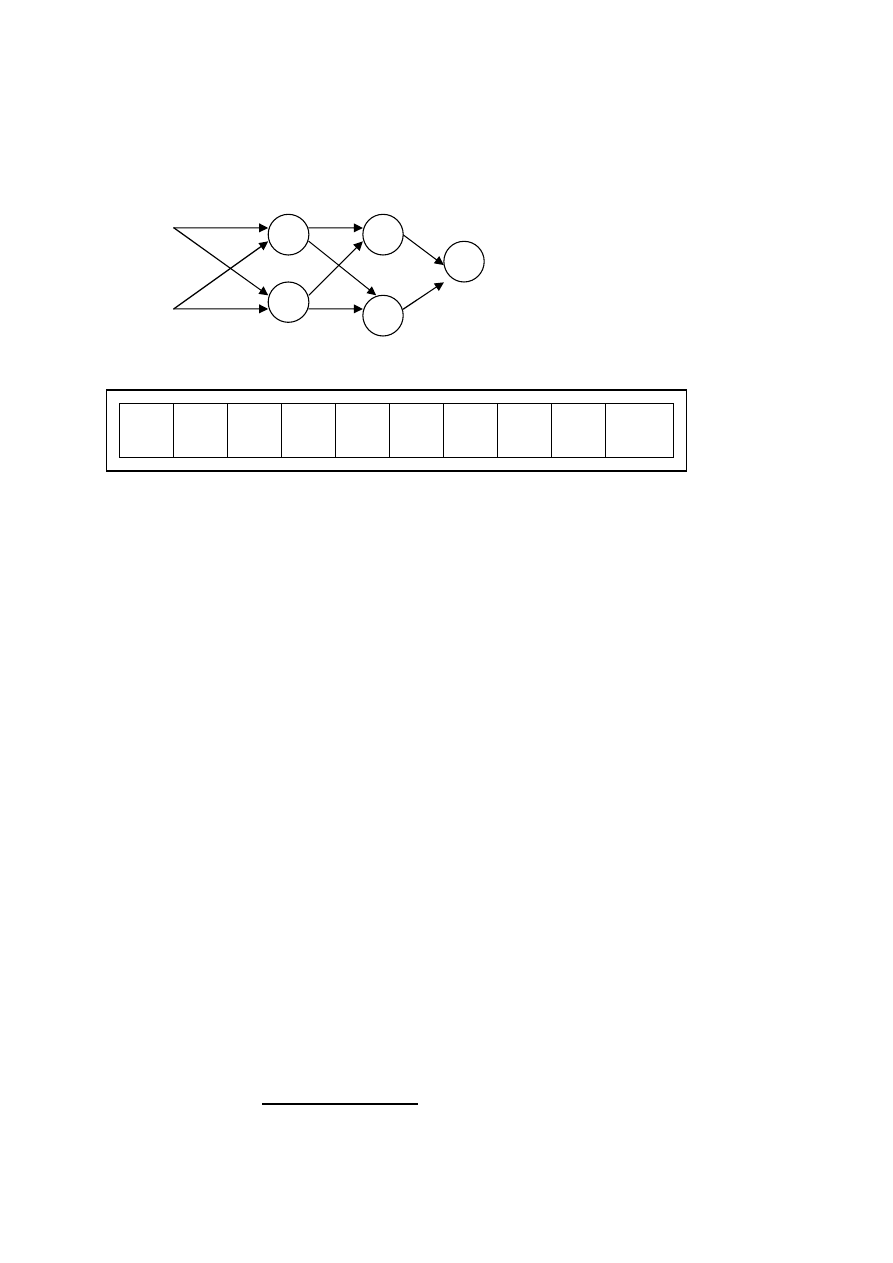
Algorytmy ewolucyjne w uczeniu wag sieci neuronowych
w
1
w
5
x
1
w
2
w
6
w
9
w
3
w
7
w
10
x
2
w
4
w
8
Rys. Odwzorowanie wag sieci neuronowej w chromosomie
dla przykładowej sieci
Uczenie sieci neuronowej polega na wyznaczeniu wartości
wag sieci, której architektura została wcześniej ustalona. Wagi
mogą być kodowane w chromosomie za pomocą wektora liczb
rzeczywistych. Każdy osobnik populacji jest określony przez
całkowity wektor wag. Kolejność umieszczenia wag w
chromosomie jest dowolna, ale nie może być zmieniana w
trakcie uczenia.
Ocena przystosowania osobników dokonywana jest na
podstawie funkcji przystosowania zdefiniowanej jako suma
kwadratów błędów, będących różnicami między sygnałem
wzorcowym a sygnałem wyjściowym sieci dla różnych
danych wejściowych.
Po wybraniu schematu chromosomowej reprezentacji, np. tak
jak pokazano na rys. powyżej, algorytm działa na populacji
osobników (chromosomów reprezentujących sieci neuronowe
o tej samej architekturze i metodzie uczenia, ale różnych
wartościach początkowych wag) wg. typowego cyklu
ewolucji, przedstawionego powyżej.
5
4
1
2
3
w
1
w
2
w
3
w
4
w
10
w
9
w
8
w
7
w
6
w
5
22
Algorytmy ewolucyjne do uczenia wag i określania
architektury sieci neuronowych jednocześnie
Opisany proces ewolucji architektur ma wiele wad. Uczenie
dla dużej populacji chromosomów wymaga bardzo dużo
czasu, a jego wynik zależy od początkowego zainicjowania
wag połączeń. Podobnie dobieranie wag za pomocą
algorytmów genetycznych może odbywać się tylko dla jednej,
określonej architektury. Wady te można wyeliminować łącząc
metody kodowania wag i struktur (opartych na kodowaniu
połączeń) jednocześnie.
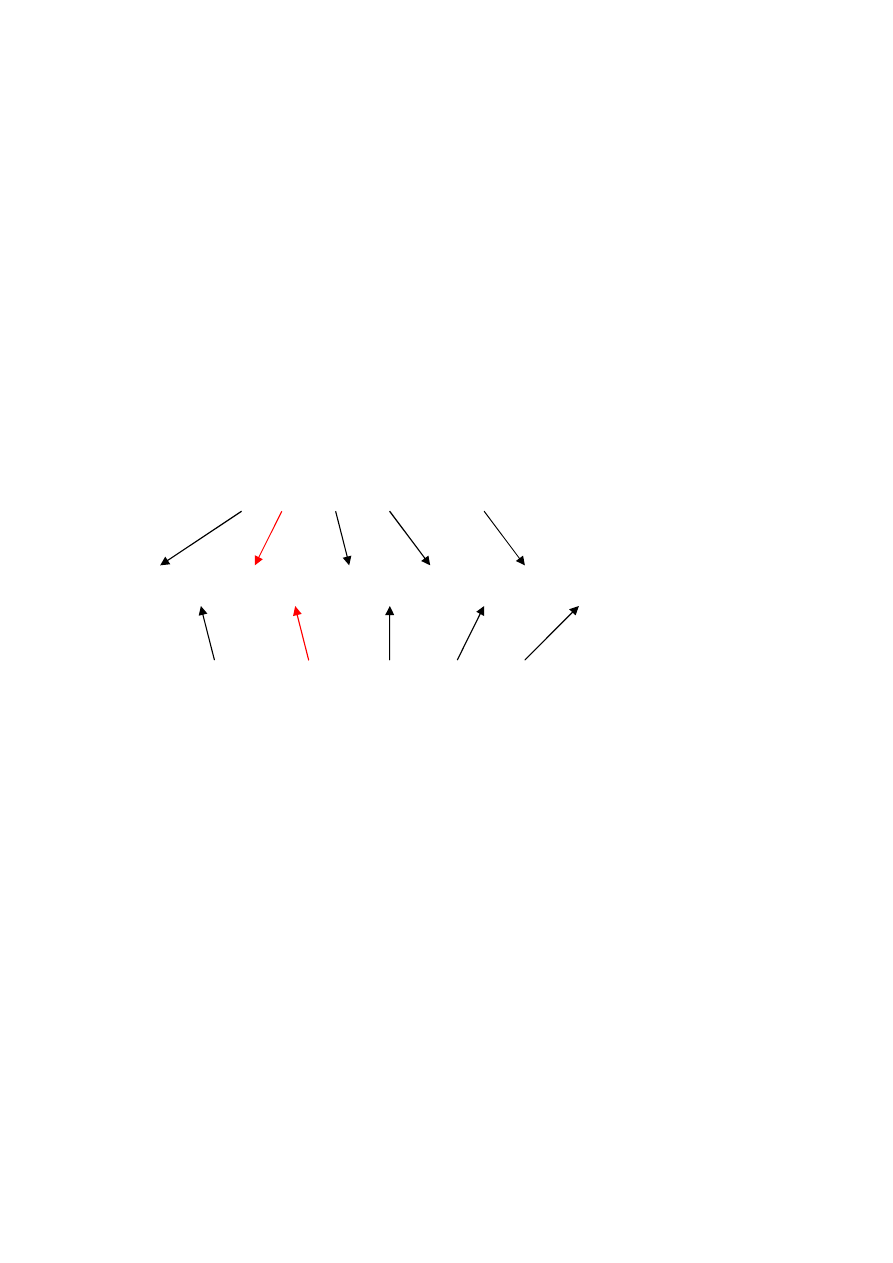
Bity wystąpienia połączenia
1 111
0 110
1 010 1 000 0 100
Bity zakodowanych wag połączeń
Rys. Przykład jednoczesnego kodowania struktury i wag sieci
neuronowej
Rysunek
przedstawia
najprostszy
sposób.
Połączenie
neuronów w sieci jest określone za pomocą jednego bitu.
Dodatkowo wprowadzono zakodowane binarnie wartości wag
połączeń. Jeżeli jednak gen odpowiadający za połączenie jest
nieaktywny (przyjmuje wartość zero), zakodowane wartości
wag tego połączenia nie są brane pod uwagę przy
dekodowaniu struktury.
Inny sposób kodowania informacji o wagach i połączeniach
sieci jednocześnie wykorzystuje fakt, że informacja o
połączeniu zawarta jest w samej wartości wagi – jeśli waga
23
wynosi zero, to połączenie nie jest brane pod uwagę przy
dekodowaniu struktury chromosomu. Metoda ta wymaga
dodatkowego operatora genetycznego, który z pewnym
prawdopodobieństwem usuwa, bądź tworzy nowe połączenia,
zerując, bądź losując wartości wag połączeń.
Adaptacyjne rozmyte algorytmy ewolucyjne
Jednym z najpoważniejszych problemów w trakcie pracy
algorytmu
jest
dobór
właściwych
proporcji
między
eksploatacją, a eksploracją. Jak to już zostało powiedziane,
równowagę osiągać można poprzez zwiększanie, lub
zmniejszanie nacisku selektywnego.
Spośród metod zmiany nacisku selektywnego wymienić
należy:
zmianę prawdopodobieństwa krzyżowania i mutacji,
zmianę rozmiarów populacji,
skalowanie funkcji przystosowania.
Wszystkie te metody zostały już omówione w rozdziałach
poprzednich. Potraktujmy je jako parametry sterujące pracą
algorytmu genetycznego.
Adaptacyjne algorytmy ewolucyjne same mogą nastawiać te
parametry w celu osiągnięcia jak najlepszych rezultatów. Do
modyfikacji parametrów używa się rozmytych systemów
wnioskujących.
Podczas pracy algorytmu ewolucyjnego (patrz rys. poniżej)
generowane są różne statystyki. Na podstawie ich wartości
rozmyty system wnioskujący analizuje pracę algorytmu i
dynamicznie dobiera wartości wybranych parametrów.
Rozmyty system wnioskujący ma, odpowiednio przygotowaną
przez eksperta, bazę wiedzy w formie reguł lingwistycznych.
Na ich podstawie dobiera parametry algorytmu. Proces ten
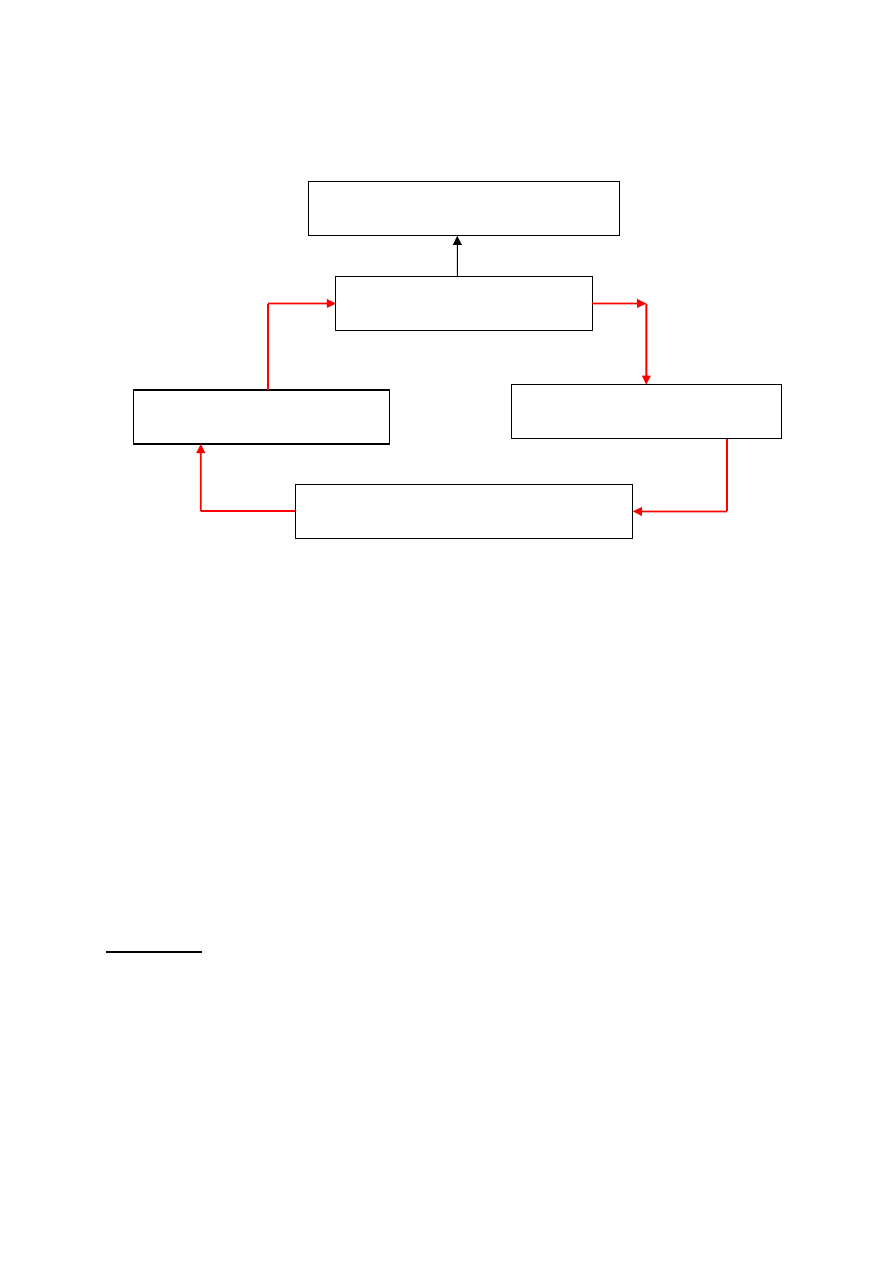
24
odbywa się w sposób ciągły sterując pracą algorytmu
ewolucyjnego.
Rys. Schemat ogólny adaptacyjnego algorytmu ewolucyjnego
Statystyki, na podstawie których sterownik rozmyty
podejmuje decyzje o zmianie parametrów, można podzielić na
kilka grup:
- ocena różnorodności osobników za pomocą pewnej
funkcji miary,
- badanie przystosowania fenotypów,
- ocena
liczby
mutacji,
które
poprawiły
dostosowanie do wszystkich mutacji.
Można stosować inne jeszcze statystyki.
Przykład:
Niech danymi wejściowymi do sterownika rozmytego będą
cztery parametry:
- statystyka
= średnie przystosowanie / najlepsze przystosowanie
- statystyka
= najgorsze przystosowanie / średnie przystosowanie
Optymalizowany problem
Algorytm ewolucyjny
Statystyki działania
Parametry algorytmu
Rozmyty system wnioskujący
25
- prawdopodobieństwo krzyżowania p
k
,
- wielkość populacji.
Załóżmy, że wyżej wymienione cztery parametry opisane
zostały za pomocą zbiorów rozmytych: duże, średnie, małe.
Przykładowy fragment bazy reguł, sterujących doborem
parametrów algorytmu, może wyglądać jak poniżej.
W tym przykładzie parametrem sterującym jest wielkość
populacji, za pomocą której możemy bezpośrednio wpływać
na stopień różnorodności osobników, czyli zwiększać, lub
zmniejszać nacisk selektywny.
Algorytmy ewolucyjne w projektowaniu systemów
rozmytych
Projektowanie systemów rozmytych, podobnie jak w innych
metodach
sztucznej
inteligencji,
wymaga
czasu,
doświadczenia i wiedzy eksperta. Proces ten można znacznie
wspomóc
dzięki
algorytmom
ewolucyjnym,
których
elastyczność
i
niezależność,
można
wykorzystać
w
rozwiązywaniu takich problemów, jak:
dopasowanie (ang: tuning) funkcji przynależności do
zbioru rozmytego, poprzez zmianę położenia, lub kształtu
tej funkcji,
generowanie odpowiednio dopasowanej bazy reguł
lingwistycznych.
JEŻELI
jest duże
TO
zwiększ populację
JEŻELI
jest małe
TO
zmniejsz populację
JEŻELI
p
k
jest małe
I
populacja jest mała
TO
zwiększ
populację
26
Interesujące jest zwłaszcza drugie rozwiązanie. Stosuje się tu
trzy podejścia:
Podejście Michigan – wykorzystywany jest tu pomysł
reprezentacji
jednej
reguły
w
chromosomie
i
poszukiwania w pewnej populacji pożądanego zbioru
reguł,
Podejście Pittsburgh jest metodą bardziej odpowiadającą
działaniu algorytmu ewolucyjnego. Cała baza reguł
zakodowana jest w jednym chromosomie. Poszukiwane
rozwiązanie znajdujemy w najlepiej przystosowanym
osobniku,
Uczenie iteracyjne łączy najlepsze cechy podejścia
Michigan i Pittsburgh. Wykorzystano pomysł kodowania
jednej reguły w chromosomie, ale utworzenie całej bazy
odbywa się stopniowo. Ostateczną bazę reguł tworzą
najlepsze
osobniki,
będące
rezultatem
działania
kolejnych uruchomień algorytmu ewolucyjnego.
Dopasowanie funkcji przynależności za pomocą algorytmu
genetycznego
Mając wybraną bazę reguł decyzyjnych systemu rozmytego
można
jeszcze
zwiększyć
ich
skuteczność
poprzez
odpowiednie dopasowanie funkcji przynależności użytych
zbiorów
rozmytych.
Algorytm
ewolucyjny
może
modyfikować
funkcje
przynależności
poprzez
zmianę
położenia punktów charakterystycznych tych funkcji. Są to
najczęściej współrzędne wierzchołków figur, które te funkcje
opisują. Informacje o wierzchołkach kodowane są w
chromosomach.
Podejście to pozwala modyfikować często używane kształty
funkcji
przynależności:
trójkątne,
trapezowe,
funkcje
gaussowską, sigmoidalną.
27
W zależności od zastosowanego algorytmu ewolucyjnego,
punkty charakterystyczne koduje się w chromosomie w
postaci binarnej, lub za pomocą liczb rzeczywistych.