Algorytm genetyczny

1

Algorytm genetyczny

Algorytm genetyczny - rodzaj algorytmu przeszukującego przestrzeń alternatywnych rozwiązań problemu w celu

wyszukania rozwiązań najlepszych.

Sposób działania algorytmów genetycznych nieprzypadkowo przypomina zjawisko ewolucji biologicznej, ponieważ

ich twórca John Henry Holland właśnie z biologii czerpał inspiracje do swoich prac. Obecnie zalicza się go do grupy

algorytmów ewolucyjnych.

Wstęp

Problem definiuje środowisko, w którym istnieje pewna populacja osobników. Każdy z osobników ma przypisany

pewien zbiór informacji stanowiących jego genotyp, a będących podstawą do utworzenia fenotypu. Fenotyp to zbiór

cech podlegających ocenie funkcji przystosowania modelującej środowisko. Innymi słowy - genotyp opisuje

proponowane rozwiązanie problemu, a funkcja przystosowania ocenia, jak dobre jest to rozwiązanie.

Genotyp składa się z chromosomów, gdzie zakodowany jest fenotyp i ewentualnie pewne informacje pomocnicze

dla algorytmu genetycznego. Chromosom składa się z genów.

Wspólnymi cechami algorytmów ewolucyjnych, odróżniającymi je od innych, tradycyjnych metod optymalizacji, są:

1. stosowanie operatorów genetycznych, które dostosowane są do postaci rozwiązań,

2. przetwarzanie populacji rozwiązań, prowadzące do równoległego przeszukiwania przestrzeni rozwiązań z

różnych punktów,

3. w celu ukierunkowania procesu przeszukiwania wystarczającą informacją jest jakość aktualnych rozwiązań,

4. celowe wprowadzenie elementów losowych.

Zapis algorytmu

Najczęściej działanie algorytmu przebiega następująco:

1. Losowana jest pewna populacja początkowa.

2. Populacja poddawana jest ocenie (selekcja). Najlepiej przystosowane osobniki biorą udział w procesie

reprodukcji.

3. Genotypy wybranych osobników poddawane są operatorom ewolucyjnym:

1. są ze sobą kojarzone poprzez złączanie genotypów rodziców (krzyżowanie),

2. przeprowadzana jest mutacja, czyli wprowadzenie drobnych losowych zmian.

4. Rodzi się drugie (kolejne) pokolenie i algorytm powraca do kroku drugiego, jeżeli nie znaleziono dostatecznie

dobrego rozwiązania. W przeciwnym wypadku uzyskujemy wynik.

Działanie algorytmu genetycznego obejmuje kilka zagadnień potrzebnych do ustalenia:

1. ustalenie genomu jako reprezentanta wyniku

2. ustalenie funkcji przystosowania/dopasowania

3. ustalenie operatorów przeszukiwania

Algorytm genetyczny

2

Kodowanie

Kodowanie jest bardzo istotnym etapem projektowania algorytmu. Sposób zakodowania w chromosomie informacji

o proponowanym rozwiązaniu wydatnie wpływa na szybkość i jakość znajdowanych wyników. Przyczyną takiego

zjawiska jest wpływ kodowania na sposób w jaki przeszukiwana jest przestrzeń rozwiązań. Złe kodowanie może

spowodować, że nigdy nie zostanie przeszukany fragment przestrzeni, w którym znajdują się najlepsze rozwiązania!

Najczęściej stosowane kodowania chromosomu:

• wektorem genów, z których każdy z nich może być jedno- lub wielobitową liczbą całkowitą, bądź też liczbą

rzeczywistą.

• za pomocą drzewiastych struktur danych.

Funkcja przystosowania

Proces wyboru osobników poddanych ocenie według określonych kryteriów. Kryteria te zapisuje się w postaci

funkcji oceny albo inaczej funkcji przystosowania. Algorytm genetyczny dąży zwykle do jej minimalizacji

(maksymalizacji). Jako kryterium często przyjmowana jest funkcja celu rozważanego problemu optymalizacji.

Funkcja oceny

Funkcja oceny to miara jakości dowolnego osobnika (fenotypu, rozwiązania) w populacji. Dla każdego osobnika jest

ona obliczana na podstawie pewnego modelu rozwiązywanego problemu. Załóżmy dla przykładu, że chcemy

zaprojektować obwód elektryczny o pewnej charakterystyce. Funkcja oceny będzie premiowała rozwiązania

najbardziej zbliżonej do tej charakterystyki, zbudowane z najmniejszej liczby elementów. W procesie selekcji

faworyzowane będą najlepiej przystosowane osobniki. One staną się "rodzicami" dla populacji.

Metody selekcji

Istnieje wiele metod selekcji. Dla przykładu można przedstawić tzw. metodę ruletki. Budujemy wirtualnie koło,

którego wycinki odpowiadają poszczególnym osobnikom. Im lepszy osobnik, tym większy wycinek koła zajmuje.

Rozmiar wycinków może zależeć od wartości funkcji oceny, jeśli wysoka wartość oceny oznacza wysokie

przystosowanie. W takim układzie prawdopodobieństwo, że lepszy osobnik zostanie wybrany jako rodzic, jest

większe. Niestety ewolucja przy takim algorytmie z każdym krokiem zwalnia. Jeżeli osobniki są podobne, to każdy

dostaje równy wycinek koła fortuny i presja selekcyjna spada. Algorytm słabiej rozróżnia osobniki dobre od

słabszych.

Pozbawiona tej wady jest metoda rankingowa. Obliczamy dla każdego osobnika funkcję oceny i ustawiamy je w

szeregu najlepszy-najgorszy. Pierwsi na liście dostają prawo do rozmnażania, a reszta trafia do historii. Wadą

metody jest niewrażliwość na różnice pomiędzy kolejnymi osobnikami w kolejce. Może się okazać, że sąsiadujące

na liście rozwiązania mają różne wartości funkcji oceny, ale dostają prawie taką samą ilość potomstwa.

Istnieją także metody selekcji wielokryterialnej. Tworzymy kilka różnych funkcji oceny (oceniających pewne

wybrane cechy osobników osobno). Dla przykładu osobniki mogą być ułożone nie w jednym, ale w kilku szeregach

najlepszy-najgorszy, a proces selekcji jest bardziej złożony.

Jak widać, selekcja daje większe prawdopodobieństwo reprodukcji osobnikom o dużym przystosowaniu, więc

kolejne pokolenia są coraz lepiej przystosowane. Spada jednak różnorodność genotypu populacji - populacja z

czasem zostaje zmonopolizowana przez nieznacznie różniące się (lub wręcz identyczne) odmiany tego samego

osobnika. Objawia się to zbieżnością kolejnych, najlepszych rozwiązań do pewnej granicy. Czasami zbieżność jest

przedwczesna, a ewolucja utyka i uzyskane rozwiązania przedstawiają pewne ekstrema lokalne. Mogą być one

dalekie od oczekiwanych rozwiązań globalnych, czyli tych najlepszych w całej przeszukiwanej przestrzeni.

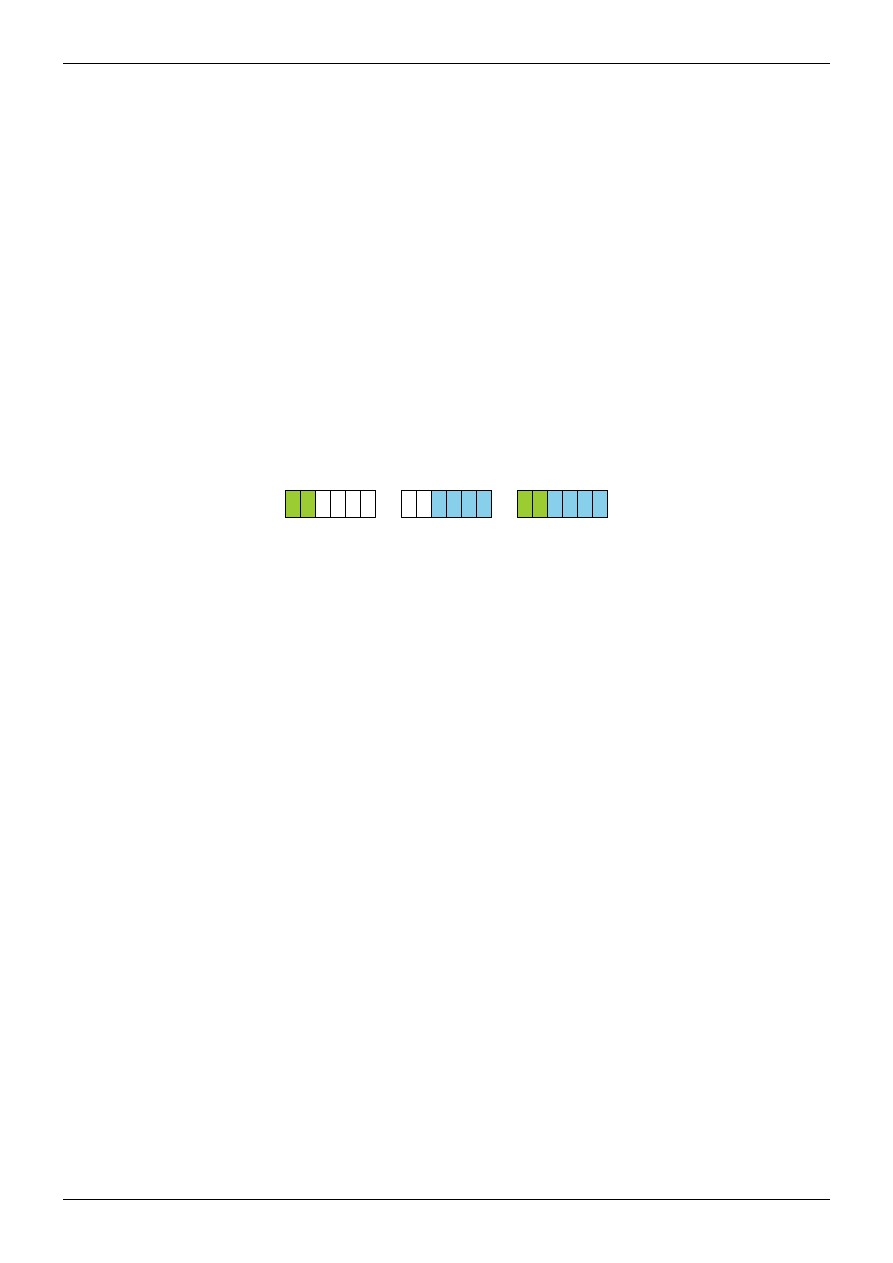
Algorytm genetyczny

3

Operatory przeszukiwania

W każdym cyklu (każde pokolenie) poddawane są "obróbce" za pomocą operatorów ewolucyjnych. Celem tego

etapu jest wygenerowanie nowego pokolenia, na podstawie poprzedniego, które być może będzie lepiej dopasowane

do założonego środowiska.

Operator krzyżowania ma za zadanie łączyć w różnych kombinacjach cechy pochodzące z różnych osobników

populacji, zaś operator mutacji ma za zadanie zwiększać różnorodność tych osobników. O przynależności

dowolnego algorytmu do klasy algorytmów genetycznych decyduje głównie zastosowanie operatora krzyżowania i

praca z całymi populacjami osobników (idea łączenia w przypadkowy sposób genotypów nieprzypadkowo

wybranych osobników). Równie ważny jest operator mutacji. Jeśli krzyżowanie traktować jako sposób eksploatacji

przestrzeni rozwiązań, to mutacja jest sposobem na jej eksplorację. Może się jednak zdarzyć, że dla niektórych

zagadnień jej zastosowanie nie jest krytyczne.

Krzyżowanie

Przykładowe krzyżowanie chromosomów zakodowanych binarnie w algorytmach

genetycznych

0 1

1 0 1 0

+

1 1

0 1 1 1

=

0 1 0 1 1 1

Krzyżowanie polega na połączeniu niektórych (wybierane losowo) genotypów w jeden. Kojarzenie ma sprawić, że

potomek dwóch osobników rodzicielskich ma zespół cech, który jest kombinacją ich cech (może się zdarzyć, że tych

najlepszych).

Sposób krzyżowania jest zależny od kodowania chromosomów i specyfiki problemu. Jednak można wskazać kilka

standardowych metod krzyżowania:

• rozcięcie dwóch chromosomów i stworzenie nowego poprzez sklejenie lewej części jednego rodzica z prawą

częścią drugiego rodzica (dla chromosomów z kodowaniem binarnym i całkowitoliczbowym),

• stosowanie operacji logicznych (kodowanie binarne),

• obliczenie wartości średniej genów (kodowanie liczbami rzeczywistymi).

Mutacja

Mutacja wprowadza do genotypu losowe zmiany. Jej zadaniem jest wprowadzanie różnorodności w populacji, czyli

zapobieganie (przynajmniej częściowe) przedwczesnej zbieżności algorytmu. Mutacja zachodzi z pewnym

przyjętym prawdopodobieństwem - zazwyczaj rzędu 1%. Jest ono niskie, ponieważ zbyt silna mutacja przynosi efekt

odwrotny do zamierzonego: zamiast subtelnie różnicować dobre rozwiązania - niszczy je. Stąd w procesie ewolucji

mutacja ma znaczenie drugorzędne, szczególnie w przypadku długich chromosomów.

W przypadku chromosomów kodowanych binarnie losuje się zazwyczaj dwa geny i zamienia się je miejscami bądź

np. neguje pewien wylosowany gen.

W przypadku genotypów zakodowanych liczbami całkowitymi stosuje się permutacje.

W przypadku genotypów zakodowanych liczbami rzeczywistymi wprowadza się do przypadkowych genów losowe

zmiany o danym rozkładzie - najczęściej normalnym.

Algorytm genetyczny

4

Zastosowania algorytmów genetycznych

Rozwiązywanie problemów NP

Algorytmy genetyczne znajdują zastosowanie tam, gdzie nie jest dobrze określony lub poznany sposób rozwiązania

problemu, ale znany jest sposób oceny jakości rozwiązania. Przykładem jest np. problem komiwojażera, gdzie

należy znaleźć najkrótszą drogę łączącą wszystkie miasta, tak by przez każde miasto przejść tylko raz. Ocena jakości

proponowanej trasy jest błyskawiczna, natomiast znalezienie optymalnej trasy kwalifikuje się do klasy problemów

NP-trudnych. Przy zastosowaniu podejścia ewolucyjnego dobre rozwiązanie można znaleźć bardzo szybko, ale

oczywiście pewni możemy być jedynie uzyskania rozwiązań sub-optymalnych, co wynika z formalnie opisanej

trudności problemów klasy NP. Algorytmy genetyczne równie dobrze radzą sobie w znajdowaniu przybliżeń

ekstremów funkcji, których nie da się obliczyć analitycznie.

Projektowanie genetyczne

Algorytmy genetyczne wykorzystywane są również do zarządzania populacją sieci neuronowych. Projektowanie

maszyn bądź obwodów elektrycznych jest doskonałym polem dla wykazania się algorytmów genetycznych.

Inżynierowi podczas tworzenia nowych pomysłów nie chodzi o znalezienie najlepszego możliwego rozwiązania.

Wystarczy tylko przybliżone spełnienie granicznych warunków oraz optymalizacja projektu. Algorytmy genetyczne

w odróżnieniu od człowieka nie działają schematycznie. Program nie zna wcześniejszych projektów i dlatego

czasami wykazuje się pewną inwencją. Co więcej człowiek często opiera się na bardzo przybliżonych modelach,

które dają fałszywy obraz problemu. Algorytm genetyczny może przeanalizować złożony model / zagadnienie i

znaleźć rozwiązanie, na które człowiek by nie wpadł.

Projektowanie obwodów elektrycznych

Algorytmy genetyczne można wykorzystać do projektowania obwodów elektrycznych. Ocena każdego osobnika

opiera się na ilości elementów oraz własnościach elektrycznych, które łatwo jest obliczyć. Główna różnica tkwi w

algorytmie budowy osobnika na podstawie genomu. Ma on postać instrukcji dla programu, który na jego podstawie

buduje obwód elektryczny. Najpierw mamy proste połączenie wejścia z wyjściem. Następnie program dodaje i

usuwa połączenia i elementy. Zbudowany tak obwód jest oceniany na podstawie prostych zależności fizycznych.

Podobny algorytm genetyczny zbudował samodzielnie filtr drabinkowy. Analogiczne podejście można zastosować

przy projektowaniu anten. Różnica tkwi w tym, że wirtualny budowniczy porusza się w trójwymiarowej przestrzeni i

ustawia metalowe elementy odbijające fale.

Jednym z nowszych pomysłów jest wykorzystanie algorytmów genetycznych w połączeniu z układami FPGA

(field-programmable gate arrays). Mają one postać chipów, które można błyskawicznie zaprogramować, aby zmienić

strukturę zawartego w nich obwodu elektrycznego. Algorytmy genetyczne badają zwykle zachowanie

symulowanych pokoleń. Dzięki układom FPGA możliwe jest ewoluowanie prawdziwych obwodów elektrycznych.

Są one wpisywane do chipa, a następnie ich właściwości elektryczne są mierzone rzeczywistym obwodem

testowym. W ten sposób ewolucja może wykorzystać wszystkie fizyczne własności rzeczywistego układu

elektrycznego.

Okazało się, że regulatory stosowane w automatyce również można udoskonalić dzięki zastosowaniu algorytmów

genetycznych. Najpopularniejszy algorytm sterowania czyli PID, można wyobrazić sobie jako pewien zestaw

połączonych ze sobą członów różniczkujących i całkujących. Odpowiedni algorytm genetyczny może zbudować taki

układ analogicznie do obwodu elektrycznego. Korzystając z tej metody John R. Koza opracował nowe wersje PID-a

[1].

Stworzono ponadto eksperymentalny system, zbudowany na bazie algorytmów genetycznych, który sam produkuje

roboty, poddaje ocenie fizycznego środowiska i optymalizuje pod kątem jak najlepszego poruszania się w tym

środowisku. Projekt nosi nazwę Golem.

Algorytm genetyczny

5

Niestety, aby ewolucja mogła zajść potrzeba bardzo dużo czasu. W praktyce oznacza to, konieczność badania

populacji tysięcy układów, na przestrzeni setek pokoleń. Moc obliczeniowa dzisiejszych komputerów jest zbyt mała,

aby sprostać takiemu zdaniu w rozsądnym czasie. Z tego powodu wykorzystuje się klastry komputerów. Na każdym

przebywa pewna populacja układów. Co pewien czas, część z nich migruje do innego komputera, aby polepszyć

uzyskiwane wyniki. Jednak rozwój techniki komputerowej spowoduje, że za kilka lat algorytmy genetyczne będą

mogły trafić pod strzechy.

Przeszukiwanie

Algorytmy genetyczne zapewniają skuteczne mechanizmy przeszukiwania dużych przestrzeni rozwiązań. Ponieważ

grupowanie należy do tej kategorii zadań to oczywiste jest, że algorytmy genetyczne stosowane są w grupowaniu.

Algorytmy genetyczne są bardziej niezależne od wstępnej inicjalizacji oraz mniej skłonne do znajdowania lokalnych

rozwiązań w miejsce optymalnych. Przykładem może być zagadnienie grupowania w którym w miejsce klasycznych

algorytmów z powodzeniem stosuje się algorytmy genetyczne.

Linki zewnętrzne

Polskie

• O algorytmach genetycznych

[2]

Angielskie

• Golem Project, automatyczne projektowanie i wytwarzanie robotów - http:/

/

demo.

cs.

brandeis.

edu/

golem/

• Wstęp do algorytmów genetycznych, bardzo dobrze opracowana strona z appletami Javy - http:/

/

cs.

felk.

cvut.

cz/

~xobitko/

ga/

• Genetic Programming - http:/

/

www.

genetic-programming.

com

• Genetic Programming Conference - http:/

/

www.

genetic-programming.

org

• Michalewicz's Evolution System - http:/

/

www.

cs.

adelaide.

edu.

au/

~zbyszek/

evol-systems.

html

Bibliografia

Polska

• John R. Koza, A. Keane, Mattethew J. Streeter: O dokonywaniu wynalazków drogą ewolucji.

• „Świat nauki”. Nr 4 (140), kwiecień 2003, s. 40-47.

• D. E. Goldberg: Algorytmy genetyczne i ich zastosowania. Warszawa: WNT, 1998.

• Z. Michalewicz: Algorytmy genetyczne + struktury danych = programy ewolucyjne. Warszawa: WNT, 1996.

• J. Arabas: Wykłady z algorytmów ewolucyjnych. Warszawa: WNT, 2001.

Angielska

• R. Poli, W.B. Langdon, N.F. McPhee: A Field Guide to Genetic Programming.  (O książce

[3]

)

• Alan M. Turing: Computing Machinery and Intelligence.
• „Mind”. Tom 59, nr 236, s. 433-460; X/1950. (dostępny tekst

[4]

)

• John R. Koza: Genetic Programming: On The Programming of Computers by Means of Natural Selection. MIT

Press, 1992.

• John R. Koza, James P. Rice: Genetic Programming: The Movie. MIT Press, 1992.

• Randy L. Haupt, Sue Ellen Haupt: Practical Genetic Algorithms. John Wiley & Sons, 1998.

• John R. Koza, Forest H. BennetII, David Andre, Martin A. Keane, Scott Brave: Genetic Programming III:

Darwinian Invention and Problem. Solving. Morgan Kaufmann, 1999.

Algorytm genetyczny

6

• John R. Koza, Martin A. Keane, Matthew J. Streeter, William Mydlowec, Jessen Yu: Genetic Programming III:

Videotape: Human-Competitive Machine Intelligence. Kluwer Academic Publishers, 2003.

Zobacz też

• przegląd zagadnień z zakresu matematyki

• sztuczna inteligencja

• sztuczne życie

Przypisy

[1] http:/

/

www.

genetic-programming.

com/

hc/

pid.

html

[2] http:/

/

www.

k0pper.

republika.

pl/

geny.

htm

[3] http:/

/

www.

gp-field-guide.

org.

uk/

[4] http:/

/

www.

abelard.

org/

turpap/

turpap.

htm

Źródła i autorzy artykułu

7

Źródła i autorzy artykułu

Algorytm genetyczny  Źródło: http://pl.wikipedia.org/w/index.php?oldid=21914059  Autorzy: A., ABX, Borkowsk, CiaPan, Crematory, Darekm, Dome, Ert, Ignasiak, JaBoJa, Jersz, Klejas,
Kocio, KoziK, Kpjas, Kyokpae, LeonardoRob0t, Masur, Miczek, Miggawka, Morte, Nameless, Olaf, Palladinus, Pawelgx, Rfl, Rogra, Rz, Selena von Eichendorf, Sielim, Stepa, Stok, Stotr,
Superborsuk, Taw, Test30, Thin, Tsca, Zolv, 49 anonimowych edycji

Licencja

Creative Commons Attribution-Share Alike 3.0 Unported
http:/

/

creativecommons.

org/

licenses/

by-sa/

3.

0/