Algorytmy przeszukiwania grafów i drzew

dla gier i łamigłówek

Przemysław Kl ˛esk

[e-mail]

Katedra Metod Sztucznej Inteligencji i Matematyki Stosowanej

Zagadnienia i algorytmy

1

Algorytm Breadth-First-Search

2

Algorytm Best-First-Search

3

Algorytm A

∗

4

Algorytm MIN-MAX

5

Algorytm przycinanie α-β

Przemysław Kl ˛esk (KMSIiMS, ZUT)

2 / 48

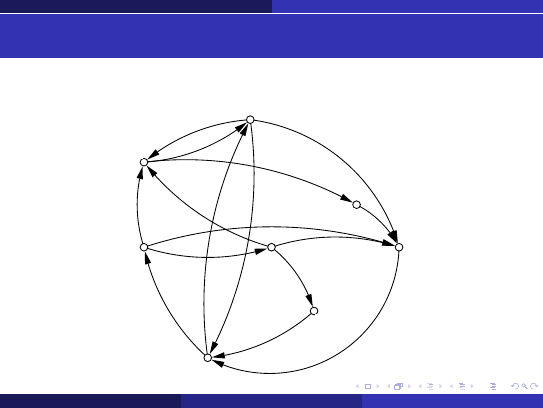
Algorytm Breadth-First-Search

Czy istnieje ´scie ˙zka do celu?

v

1

v

2

v

3

v

4

v

5

v

6

v

7

v

8

Przemysław Kl ˛esk (KMSIiMS, ZUT)

3 / 48

Algorytm Breadth-First-Search

Własno´sci algorytmu

Breadth First Search

Wykonuje zachłanne (w skrajnym przypadku wyczerpuj ˛ace)
przeszukiwanie całego grafu

wszerz

, a ˙z do natrafienia na w ˛ezeł

docelowy.

Algorytm ten mo ˙zna traktowa´c, jako ogólny schemat, którego
szczególne (usprawnione) przypadki to algorytmy: Best First
Search, A

∗

, algorytm Dijkstry, i inne.

Breadth First Search operuje na dwóch zbiorach:

Open

(zawiera

w ˛ezły, które maj ˛a by´c jeszcze rozpatrzone) i

Closed

(zawiera

w ˛ezły, które ju ˙z rozpatrzono).

Ka ˙zdy z w ˛ezłów ma mo ˙zliwo´s´c zapami ˛etania jednego swojego
poprzednika, tak aby po znalezieniu rozwi ˛azania mo ˙zna było

prze´sledzi´c ´scie ˙zk ˛e

.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

4 / 48

Algorytm Breadth-First-Search

Breadth First Search

Algorytm

1

Ustaw w w ˛e´zle pocz ˛atkowym pustego poprzednika i dodaj ten
w ˛ezeł do zbioru Open.

2

Dopóki zbiór Open pozostaje niepusty powtarzaj:

1

Pobierz (i usu ´n) jeden w ˛ezeł ze zbioru Open. Nazwijmy ten
w ˛ezeł v.

2

Je ˙zeli v jest w ˛ezłem docelowym (spełnia warunek stopu), to
przerwij cały algorytm i zwró´c v jako wynik.

3

Włó ˙z do zbioru Open tych wszystkich potomków w ˛ezła v,
którzy nie wyst ˛epuj ˛a w zbiorze Closed. Zapami ˛etaj w nich v
jako ich poprzednika.

4

Włó ˙z v do zbioru Closed.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

5 / 48

Algorytm Breadth-First-Search

Breadth First Search

´Sledzenie ´scie ˙zki

1

Przypisz do roboczego w ˛ezła o nazwie v, w ˛ezeł b ˛ed ˛acy
rozwi ˛azaniem.

2

Zainicjalizuj ci ˛ag reprezentuj ˛acy ´scie ˙zk ˛e zawarto´sci ˛a v:
Path = (v).

3

Dopóki v ma niepustego poprzednika, powtarzaj:

1

Przypisz w miejsce v jego poprzednika (v ← v.parent).

2

Dopisz z przodu ´scie ˙zki Path zawarto´s´c v.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

6 / 48

Algorytm Breadth-First-Search

Przykładowe działanie

(dla grafu ze str. 3)

1

Open = {v

1

}, Closed = {}.

2

Open = {v

1

} , ∅ wi ˛ec wykonujemy ciało p ˛etli:

2.1

v = v

1

, Open = {}.

2.2

v = v

1

,

v

8

(warunek stopu niespełniony).

2.3

Open = {v

2

, v

3

, v

6

}.

2.4

Closed = {v

1

}.

2

Open = {v

2

, v

3

, v

6

} , ∅ wi ˛ec wykonujemy ciało p ˛etli:

2.1

v = v

2

, Open = {v

3

, v

6

}.

2.2

v = v

2

,

v

8

(warunek stopu niespełniony).

2.3

Open = {v

3

, v

6

} (uwaga: v

3

jako potomek v

2

nie jest po raz drugi dodawany do

Open).

2.4

Closed = {v

1

, v

2

}.

2

Open = {v

3

, v

6

} , ∅ wi ˛ec wykonujemy ciało p ˛etli:

2.1

v = v

3

, Open = {v

6

}.

2.2

v = v

3

,

v

8

(warunek stopu niespełniony).

2.3

Open = {v

6

, v

4

} (uwaga: v

1

jako potomek v

3

nie jest dodawany do Open, bo jest ju ˙z

w Closed.)

2.4

Closed = {v

1

, v

2

, v

3

}.

2

. . .

Przemysław Kl ˛esk (KMSIiMS, ZUT)

7 / 48

Algorytm Breadth-First-Search

Uwagi o Breadth First Search

Zbiory Open i Closed w przypadku Breadth First Search
zazwyczaj implementuje si ˛e jako zwykłe kolejki FIFO. Dopiero w
specjalizowanych wersjach algorytmu tj. w algorytmach
BestFirstSearch i A

∗

, zbiory te implementuje si ˛e odpowiednio jako:

kolejk ˛e priorytetow ˛a

i

hashmap ˛e

.

Je ˙zeli przeszukiwanie dotyczy drzewa (grafu bez cykli), to zbiór
Closed mo ˙zna pomin ˛a´c.

Breadth First Search nie jest w ˙zaden sposób ukierunkowany na
szybsze dotarcie do rozwi ˛azania (przeszukuje wszerz): nie
minimalizuje długo´sci ´scie ˙zki, nie wykorzystuje ˙zadnej
heurystyki.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

8 / 48

Algorytm Best-First-Search

Własno´sci algorytmu

Best First Search

(Judea Pearl)

Ka ˙zdemu przeszukiwanemu stanowi (w ˛ezłowi) v nadawana jest

heurystyczna ocena liczbowa

f (v) , szacuj ˛aca, na ile daleko dany stan

jest od docelowego.

Algorytm przeszukuje w pierwszej kolejno´sci stany o najni ˙zszej
warto´sci funkcji heurystycznej.

Zbiór Open implementowany jest przez

kolejk ˛e priorytetow ˛a

(ang. PriorityQueue)

porz ˛adkuj ˛ac ˛a stany wg heurystyki. Wstawienie

nowego elementu do kolejki z zachowaniem porz ˛adku ma zło ˙zono´s´c

O(log n)

. Wyci ˛agni ˛ecie elementu z kolejki ma zło ˙zono´s´c

O(1)

.

Zbiór Closed implementowany jest przez

hashmap ˛e

. Sprawdzenie, czy

pewien stan ju ˙z był rozpatrzony i jest w zbiorze Closed, ma zło ˙zono´s´c

O(1)

.

Ka ˙zdy stan przechowuje dotychczas najkorzystniejszego dla niego
poprzednika.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

9 / 48

Algorytm Best-First-Search

Sudoku

Maj ˛ac dany pewien stan pocz ˛atkowy planszy 9 × 9, podzielonej
dodatkowo na 9 podkwadratów o wymiarach 3 × 3 ka ˙zdy, nale ˙zy
napełni´c plansz ˛e tak, aby w ka ˙zdym wierszu, w ka ˙zdej kolumnie i w
ka ˙zdym podkwadracie były wykorzystane wszystkie liczby ze zbioru
{1, 2, . . . , 9}.

1*5

*37

**8

*7*

***

***

**8

1**

***

**3

*7*

**1

74*

*1*

*63

2**

*4*

9**

***

**5

1**

***

***

*8*

4**

62*

5*7

−→

195

237

648

674

859

312

328

164

759

853

976

421

749

512

863

216

348

975

962

785

134

537

491

286

481

623

597

(Best First Search w Javie: czas = 1607 ms (procesor 2 GHz), odwiedzonych stanów = 3168.)

Przemysław Kl ˛esk (KMSIiMS, ZUT)

10 / 48

Algorytm Best-First-Search

Sudoku

Ogólne sudoku n

2

Maj ˛ac dany pewien stan pocz ˛atkowy planszy n

2

× n

2

, podzielonej

dodatkowo na n

2

podkwadratów o wymiarach n × n ka ˙zdy, nale ˙zy

napełni´c plansz ˛e tak, aby w ka ˙zdym wierszu, w ka ˙zdej kolumnie i w
ka ˙zdym podkwadracie były wykorzystane wszystkie liczby ze zbioru
{1, 2, . . . , n

2

}.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

11 / 48

Algorytm Best-First-Search

Problem n-hetmanów

Na szachownicy n × n nale ˙zy ustawi´c n hetmanów, w taki sposób, aby

˙zaden przez ˙zadnego „nie był szachowany”.

Dla n = 2, 3 rozwi ˛azanie nie istnieje. Przykład rozwi ˛azania dla n = 4:

Q

Q

Q

Q

Przemysław Kl ˛esk (KMSIiMS, ZUT)

12 / 48

Algorytm Best-First-Search

Best First Search

Algorytm

1

Ustaw w stanie pocz ˛atkowym pustego poprzednika i dodaj ten stan do
zbioru Open.

2

Dopóki zbiór Open pozostaje niepusty powtarzaj:

1

Pobierz (i usu ´n) jeden stan v ze zbioru Open (jest to stan najlepszy w sensie zadanej
heurystyki).

2

Je ˙zeli v jest stanem docelowym (spełnia warunek stopu), to przerwij cały algorytm
i zwró´c v jako wynik.

3

Wygeneruj wszystkie stany potomne dla v i dla ka ˙zdego z nich wykonaj:

1

Je ˙zeli stan wyst ˛epuje w Closed, to nie badaj go dalej.

2

Policz warto´s´c heurystyki dla tego stanu.

3

Je ˙zeli stan nie wyst ˛epuje w Open, to dodaj go ustawiaj ˛ac v jako jego
poprzednik.

4

Je ˙zeli stan wyst ˛epuje w Open, to podmie ´n w nim warto´s´c heurystyki i
poprzednika, o ile nowo obliczona warto´s´c jest korzystniejsza, i uaktualnij
jego pozycj ˛e w Open.

4

Włó ˙z v do zbioru Closed.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

13 / 48

Algorytm Best-First-Search

Przykładowe heurystyki

Sudoku (heurystyka naiwna)

Rozpoczynamy od zadanej planszy (stan pocz ˛atkowy) i dostawiamy
w puste pola (dowolne) dopuszczalne liczby (maks. 9 potomków na
ka ˙zdym poziomie drzewa). Mówimy, ˙ze stan jest tym bli ˙zszy
rozwi ˛azaniu, im mniej ma pustych pól.

f (v) =















∞,

je ˙zeli stan jest niepoprawny

;

liczba pustych pól w v.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

14 / 48

Algorytm Best-First-Search

Przykładowe proste heurystyki

Sudoku (heurystyka wg minimum pozostałych mo ˙zliwo´sci)

Uto ˙zsamijmy v z tablic ˛a sudoku. Niech R

v

(i, j) oznacza pozostałe mo˙zliwo´sci

dla komórki (i, j) tablicy v — pozostałe poprzez wyeliminowanie liczb
obecnych w wierszu i, kolumnie j i podkwadracie, do którego nale ˙zy (i, j).

Mówimy, ˙ze stan jest tym bli ˙zszy rozwi ˛azaniu, im ma mniej pozostałych

mo ˙zliwo´sci dla pewnej komórki. Dzieci podpinamy w tej wła´snie komórce.

f (v) = min

i,j

#R

v

(i, j).

Przemysław Kl ˛esk (KMSIiMS, ZUT)

15 / 48

Algorytm Best-First-Search

Przykładowe proste heurystyki

Sudoku (heurystyka wg sumy pozostałych mo ˙zliwo´sci)

Mówimy, ˙ze stan jest tym bli ˙zszy rozwi ˛azaniu, im ma mniejsz ˛a sum ˛e
pozostałych mo ˙zliwo´sci wzi ˛et ˛a po wszystkich komórkach. Dzieci
podpinamy w komórce: arg min

i,j

#R

v

(i, j).

f (v) =

X

i,j

#R

v

(i, j).

Przemysław Kl ˛esk (KMSIiMS, ZUT)

16 / 48

Algorytm Best-First-Search

Przykładowe proste heurystyki

n-hetmanów (heurystyka naiwna)

Rozpoczynamy od pustej szachownicy i dostawiamy w kolejnych wierszach
hetmany.

Mówimy, ˙ze stan jest bli ˙zszy rozwi ˛azaniu im ma mniej pustych wierszy.

f (v) =















∞,

je ˙zeli hetmany szachuj ˛a si ˛e

;

liczba pustych wierszy w v.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

17 / 48

Algorytm Best-First-Search

Przykładowe proste heurystyki

n-hetmanów (heurystyka wg minimum pozostałych mo ˙zliwo´sci)

Niech R

v

oznacza liczb ˛e pozostałych nieszachowanych pól w v. Mówimy, ˙ze

stan jest bli ˙zszy rozwi ˛azaniu im ma mniej nieszachowanych pól.

f (v) =















∞,

je ˙zeli hetmany szachuj ˛a si ˛e

;

R

v

.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

18 / 48

Algorytm Best-First-Search

Minimalne sudoku

Problem (w ogólno´sci dla sudoku n

2

)

Znale´z´c wszystkie pocz ˛atkowe układy sudoku, dla których istnieje
dokładnie jedno rozwi ˛azanie i które maj ˛a minimaln ˛a liczb ˛e ustalonych pól w
stanie pocz ˛atkowym.

Dowód, ˙ze takie stany istniej ˛a

Poczynaj ˛ac od dowolnej rozwi ˛azanej planszy (całkowicie wypełnionej)
odbieramy kolejno po jednej liczbie i sprawdzamy, czy nadal mo ˙zna b ˛edzie
rozwi ˛aza´c sudoku jednoznacznie. Przerywamy, gdy b ˛edzie istniało wi ˛ecej
ni ˙z jedno rozwi ˛azanie. Zwa ˙zywszy na fakt, ˙ze całkowicie pusta plansza nie
jest jednoznacznie rozwi ˛azywalna, wida´c ˙ze takie post ˛epowanie b ˛edzie
miało punkt stopu przy pewnym cz ˛e´sciowym zapełnieniu planszy. ¥

Przemysław Kl ˛esk (KMSIiMS, ZUT)

19 / 48

Algorytm Best-First-Search

Poszukiwanie minimalnych sudoku

Zarys algorytmu zachłannego

Rozpoczynamy od pełnej (rozwi ˛azanej) planszy.

Potomkami danego stanu s ˛a stany powstałe przez odebranie jednej
liczby z rodzica. Zatem mo ˙zemy utworzy´c n

2

potomków — tyle, ile jest

pól.

Dla ka ˙zdego potomka sprawdzamy, wykonuj ˛ac algorytm Best First
Search dla zwykłego problemu sudoku, czy istniej ˛a co najmniej 2
rozwi ˛azania.

Je ˙zeli pewien stan ma jedno rozwi ˛azanie, a wszystkie jego potomki
maj ˛a wi ˛ecej ni ˙z jedno, to nale ˙zy go zapami ˛eta´c jako kandydata na
minimalne sudoku.

Algorytm musimy jednak wykona´c, a ˙z do przejrzenia pełnego grafu.
Nie mo ˙zna zatrzyma´c si ˛e na pierwszym rozwi ˛azaniu, jako ˙ze w innych
„rejonach” grafu, mog ˛a istnie´c rozwi ˛azania o mniejszej liczbie
elementów na planszy pocz ˛atkowej.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

20 / 48

Algorytm Best-First-Search

Poszukiwanie minimalnych sudoku

Dla n = 2 rozpoczynaj ˛ac od poni ˙zszej planszy znaleziono 128 minimalnych sudoku (maj ˛acych 4
pozycje ustalone).

12

34

34

12

23

41

41

23

→

∗∗

∗∗

∗∗

12

∗∗

∗∗

4∗

∗3

,

∗∗

∗∗

∗∗

12

∗∗

∗∗

41

∗∗

,

∗∗

∗∗

∗∗

12

∗∗

∗1

4∗

∗∗

,

. . .

Oczywi´scie, aby pozna´c prawdziw ˛a liczb ˛e wszystkich rozwi ˛aza ´n „bazowych” nale ˙załoby: (1)
uto ˙zsami´c wszystkie układy równowa ˙zne sobie ze wzgl ˛edu na jedn ˛a z osi symetrii planszy, (2)
uto ˙zsami´c wszystkie stany równowa ˙zne sobie ze wzgl ˛edu na permutacj ˛e symboli, (3) uruchomi´c
przeszukiwanie dla wszystkich nieto ˙zsamych układów pocz ˛atkowych.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

21 / 48

Algorytm Best-First-Search

Poszukiwanie minimalnych sudoku

Dla n = 3

Nie udało si ˛e wykona´c programu do ko ´nca przy 2GB pami ˛eci
RAM, a swap’owanie bardzo istotnie spowalnia prac ˛e programu.
Sugestia: mo ˙zna próbowa´c zadanie obliczy´c w sposób
rozproszony (na wielu maszynach).

Udało si ˛e na pewno wykry´c, ˙ze minimalne sudoku 3

2

s ˛a o

liczno´sci pocz ˛atkowej 6 18.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

22 / 48

Algorytm Best-First-Search

Uwagi o Best First Search

Best First Search przeszukuje w gł ˛ab (a nie wszerz) coraz bardziej
oddalaj ˛ac si ˛e od stanu pocz ˛atkowego.

Przy natkni ˛eciu si ˛e na stan niepoprawny (w szczególno´sci, gdy
wszyscy potomkowie s ˛a niepoprawni), algorytm wycofuje si ˛e do
stanów o gorszej warto´sci heurystyki.

Liczba takich wycofa ´n zale ˙zy od: jako´sci podanej heurystyki i od
sposobu budowania stanów potomnych (pewn ˛a wiedz ˛e o
problemie mo ˙zna zawrze´c ju ˙z tu, aby nie dopuszcza´c do stanów
bezpo´srednio niepoprawnych).

Przemysław Kl ˛esk (KMSIiMS, ZUT)

23 / 48

Algorytm A

∗

Własno´sci algorytmu

A

∗

(Hart, Nilsson, Raphael, 1968)

Funkcja decyduj ˛aca o porz ˛adku wyci ˛agania stanów ze zbioru Open jest
sum ˛a dwóch funkcji:

f (v) = g(v) + h(v),

gdzie g(v) wyra ˙za faktyczny koszt (odległo´s´c) przebyty od stanu

pocz ˛atkowego do v, natomiast h(v) jest heurystyk ˛a szacuj ˛ac ˛a koszt
(odległo´s´c) od stanu v do stanu docelowego.

Funkcja h musi by´c tzw.

dopuszczaln ˛a heurystyk ˛a

, tzn. nie wolno jej

przeszacowywa´c kosztu (odległo´sci) do stanu docelowego (o tym
dokładniej jeszcze pó´zniej. . . ).

W zastosowaniach path-finding czy routing (gdzie mamy
fizyczny/geograficzny graf) cz ˛estym i poprawnym wyborem dla h, jest
zwykła odległo´s´c w linii prostej od v do stanu docelowego (na pewno
nie przeszacowujemy).

Przemysław Kl ˛esk (KMSIiMS, ZUT)

24 / 48

Algorytm A

∗

Własno´sci algorytmu

A

∗

(Hart, Nilsson, Raphael, 1968)

W odró ˙znieniu od Best First Search, A

∗

bierze pod uwag ˛e tak ˙ze

g(v), a nie tylko heurystyk ˛e zorientowan ˛a na cel. A zatem w
budowanej ´scie ˙zce z jednej strony preferowane s ˛a stany bliskie
pocz ˛atkowemu, a z drugiej jednocze´snie bliskie ko ´ncowemu (w
sensie minimalizacji tej sumy).

W algorytmie, ka ˙zdy stan v musi mie´c mo ˙zliwo´s´c zapami ˛etania
swoich trzech warto´sci: g(v), h(v), f (v).

Przechodz ˛ac od pewnego stanu v do pewnego stanu w, warto´s´c
funkcji g wyznaczamy jako:

g(w) = g(v) + d(v, w)

, gdzie d(v, w)

oznacza koszt przej´scia z v do w.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

25 / 48

Algorytm A

∗

A

∗

Algorytm

1

Dla stanu pocz ˛atkowego wyznacz warto´s´c h, a nast ˛epnie ustaw:
g = 0, f = 0 + h. Ustaw tak ˙ze pustego poprzednika i wstaw stan
pocz ˛atkowy do zbioru Open.

2

Dopóki zbiór Open pozostaje niepusty powtarzaj:

1

Pobierz (i usu ´n) jeden stan v ze zbioru Open (jest to stan najlepszy w sensie
warto´sci f ).

2

Je ˙zeli v jest stanem docelowym (spełnia warunek stopu), to przerwij cały algorytm
i zwró´c v jako wynik.

3

Wygeneruj wszystkie stany w potomne dla v i dla ka ˙zdego z nich wykonaj:

1

Je ˙zeli stan w wyst ˛epuje w Closed, to nie badaj go dalej.

2

Policz: g(w) = g(v) + d(v, w) i f (w) = g(w) + h(w).

3

Je ˙zeli stan nie wyst ˛epuje w Open, to dodaj go ustawiaj ˛ac v jako jego
poprzednik.

4

Je ˙zeli stan wyst ˛epuje w Open, to podmie ´n w nim warto´sci g i f (oraz
poprzednika), o ile f korzystniejsze, i uaktualnij jego pozycj ˛e w Open.

4

Włó ˙z v do zbioru Closed.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

26 / 48

Algorytm A

∗

Zastosowania

A

∗

Ogólnie: poszukiwanie najkrótszej ´scie ˙zki w grafie. . .

poruszanie si ˛e postaci (boot’ów) w grach komputerowych,

przechodzenie labiryntów,

routing problems,

układanki, łamigłówki, gdzie nale ˙zy dodatkowo zminimalizowa´c
liczb ˛e ruchów (np. puzzle n

2

− 1),

. . .

Przemysław Kl ˛esk (KMSIiMS, ZUT)

27 / 48

Algorytm A

∗

Labirynty — wyniki

A

∗

Rozmiary siatki: 30 × 30, odwiedzonych stanów do momentu rozwi ˛azania: 258.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

28 / 48

Algorytm A

∗

Labirynty — wyniki

A

∗

Rozmiary siatki: 30 × 30, odwiedzonych stanów do momentu rozwi ˛azania: 331.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

29 / 48

Algorytm A

∗

Labirynty — wyniki

A

∗

Rozmiary siatki: 50 × 50, odwiedzonych stanów do momentu rozwi ˛azania: 1441.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

30 / 48

Algorytm A

∗

Dobra i zła (przeszacowuj ˛aca) heurystyka

h(v) =

q

(v

x

− goal

x

)

2

+

(v

y

− goal

y

)

2

lub h(v) = |v

x

− goal

x

| + |(v

y

− goal

y

)|

h(v) =

4

q

(v

x

− goal

x

)

2

+

(v

y

− goal

y

)

2

Przemysław Kl ˛esk (KMSIiMS, ZUT)

31 / 48

Algorytm A

∗

Puzzle n

2

− 1

Dla n = 3

Wychodz ˛ac od stanu pocz ˛atkowego i przesuwaj ˛ac pola z liczbami w
miejsce puste ’9’ (w ogólno´sci niech pole puste równe jest ’n

2

’), nale ˙zy

w jak najmniejszej liczbie ruchów doj´s´c do stanu docelowego:

1

2

3

4

5

6

7

8

9

Przemysław Kl ˛esk (KMSIiMS, ZUT)

32 / 48

Algorytm A

∗

Puzzle n

2

− 1

Przykładowa heurystyka

Dla danego w ˛ezła v niech v

i

x

oraz v

i

y

oznaczaj ˛a

odpowiednio współrz ˛edne x i y, na których poło ˙zona jest
liczba i w układance.
Niech lewe górne pole ma współrz ˛edne (0, 0) a prawe dolne
(n − 1, n − 1).
Przykładowa funkcja heurystyczna mo ˙ze mie´c wówczas

posta´c:

h(v) =

1
2

X

i∈{1,2,...,n

2

}

³

|v

i

x

− ((i − 1) mod n)| + |v

i

y

− ⌊(i − 1)/n⌋|

´

.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

33 / 48

Algorytm A

∗

Przykładowa ´scie ˙zka A

∗

dla puzzle 2

2

− 1

Odwiedzonych stanów: 15.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

34 / 48

Algorytm A

∗

Przykładowa ´scie ˙zka

A

∗

dla puzzle 3

2

− 1

Odwiedzonych stanów: 19.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

35 / 48

Algorytm A

∗

Własno´sci A

∗

i monotoniczno´s´c heurystyki

Heurystyka jest na pewno dopuszczalna, je ˙zeli jest monotoniczna, tzn.:

∀v, w h(v) 6 d(v, w) + h(w).

(1)

Innymi słowy, dodanie do jakiejkolwiek ´scie ˙zki dodatkowego w ˛ezła
powoduje, ˙ze nowa ´scie ˙zka jest niekrótsza od poprzedniej. A równo´s´c
mo ˙ze mie´c miejsce tylko, gdy dodamy w ˛ezeł poruszaj ˛ac si ˛e po prostej
do celu.

Je ˙zeli heurystyka h spełnia w/w warunek to algorytm A

∗

gwarantuje, ˙ze:

(1) znalezione rozwi ˛azanie jest optymalne (´scie ˙zka najkrótsza), (2) sam
algorytm jest optymalny w ramach h, tj. ˙zaden inny algorytm u ˙zywaj ˛acy
h jako heurystyki nie odwiedzi mniejszej liczby stanów ni ˙z A

∗

.

Niech h

∗

oznacza doskonał ˛a heurystyk ˛e tj. tak ˛a, która ani nie

przeszacowuje, ani nie niedoszacowuje. Algorytm pracuj ˛acy na
podstawie h

∗

jest tak ˙ze doskonały — odwiedza mo ˙zliwie najmniej

w ˛ezłów. St ˛ad te ˙z oryginalnie rozró ˙zniano dwie nazwy tego algorytmu
A i A

∗

.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

36 / 48

Algorytm A

∗

Jak

A

∗

ma si ˛e do algorytmu Dijkstry i Best

First Search?

Przy ustawieniu ∀v h(v) = 0 algorytm A

∗

staje si ˛e klasycznym

algorytmem Dijkstry do poszukiwania najkrótszej ´scie ˙zki w
grafie z punktu do punktu.

Przy ustawieniu ∀v g(v) = 0 algorytm A

∗

staje si ˛e algorytmem

Best First Search. Nieistotna jest długo´s´c ´scie ˙zki, liczy si ˛e tylko
osi ˛agni ˛ecie/odkrycie rozwi ˛azania/rozwi ˛aza ´n (np. sudoku,
problem n hetmanów).

Przemysław Kl ˛esk (KMSIiMS, ZUT)

37 / 48

Algorytm MIN-MAX

Algorytm

MIN-MAX

(lub MINIMAX)

Stosuje si ˛e do gier dwuosobowych jak np. szachy, warcaby, GO, itp..

Algorytm w wersji niezmodyfikowanej składa si ˛e z dwóch cz ˛e´sci:

(1)

buduj ˛acej drzewo gry do zadanej gł ˛eboko´sci

(np. poprzez Breadth First

Search),

(2) przechodz ˛acej drzewo od dołu w gór ˛e i nadaj ˛acej oceny

poszczególnym stanom gry

, tak ˙ze w efekcie ocenione zostaj ˛a mo ˙zliwe

ruchy pochodz ˛ace od stanu podstawowego.

Przechodzenie drzewa w gór ˛e rozpoczyna si ˛e od wystawienia ocen
stanom ko ´ncowym (li´sciom). Zwykle jest to heurystyka np. ró ˙znica
pomi ˛edzy liczb ˛a bierek białych i czarnych.

Nast ˛epnie drzewo przechodzone jest poziomami w gór ˛e. Ka ˙zdy
poziom jest skojarzony z ruchami jednego z graczy.

Jeden z graczy

nazywany jest minimalizuj ˛acym, drugi maksymalizuj ˛acym

.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

38 / 48

Algorytm MIN-MAX

Algorytm

MIN-MAX

(lub MINIMAX)

Zwyci ˛estwo gracza maksymalizuj ˛acego reprezentowane jest przez ∞
(w szachach: białe matuj ˛a czarne), a minimalizuj ˛acego −∞ (czarne
matuj ˛a białe).

Pozycje inne ni ˙z zwyci ˛eskie musimy ocenia´c heurystycznie. Np. jedna z
najprostszych heurystyk dla szachów mierzy ró ˙znic ˛e pomi ˛edzy
„materiałem” białych a czarnych, licz ˛ac piony za 1 pkt., skoczki za 3
pkt., go ´nce za 3.5 pkt, wie ˙ze za 5 pkt., hetmana za 9 pkt.

Tylko poziom najni ˙zszy (stany li´scie) jest oceniany heurystycznie.
Oceny dla wy ˙zszych poziomów wynikaj ˛a z minimaksowej procedury
przechodzenia drzewa w gór ˛e.

Uwaga: w literaturze ruch jednego z graczy nazywany jest cz ˛esto

półruchem (ang. ply)

, a przesuwanie si ˛e o jeden poziom w drzewie

liczone jest jako ±

1
2

. Dopiero 2 ruchy obu graczy traktowane s ˛a jako całe

posuni ˛ecie.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

39 / 48

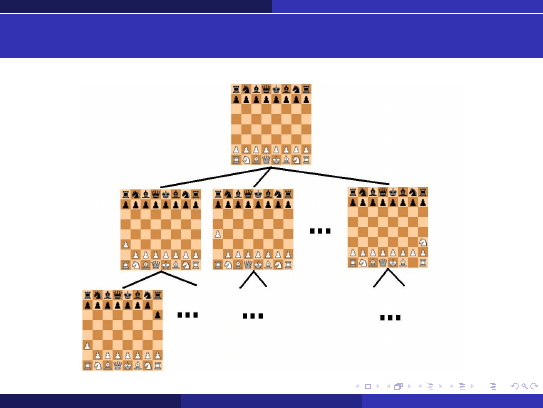
Algorytm MIN-MAX

Ilustracja fragmentu drzewa gry dla szachów

Przemysław Kl ˛esk (KMSIiMS, ZUT)

40 / 48

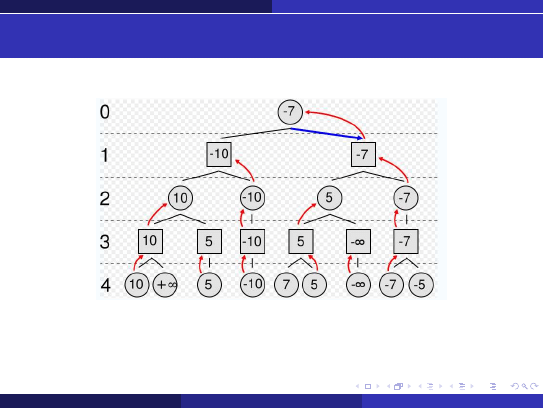
Algorytm MIN-MAX

Algorytm

MIN-MAX

(lub MINIMAX)

Rysunek:

´

Zródło: http://en.wikipedia.org/wiki/Image:Minimax.svg

Przemysław Kl ˛esk (KMSIiMS, ZUT)

41 / 48

Algorytm MIN-MAX

Algorytm MIN-MAX rekurencyjnie

Procedura mmEvaluateMax(s, d, D)

1

Je ˙zeli s jest terminalem, to zwró´c h(s).

2

Przypisz v = −∞.

3

Dla wszystkich stanów t b ˛ed ˛acych potomkami s wykonuj:

1

v := max{v, mmEvaluateMin(t, d +

1

2

, D)

}.

4

Zwró´c v.

Procedura mmEvaluateMin(s, d, D)

1

Je ˙zeli s jest terminalem, to zwró´c h(s).

2

Przypisz v = ∞.

3

Dla wszystkich stanów t b ˛ed ˛acych potomkami s wykonuj:

1

v := min{v, mmEvaluateMax(t, d +

1

2

, D)

}.

4

Zwró´c v.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

42 / 48

Algorytm MIN-MAX

Algorytm

MIN-MAX

(lub MINIMAX)

Podstawowym problemem algorytmu w wersji niezmodyfikowanej jest
du ˙za zło ˙zono´s´c pami ˛eciowa. Niech dla uproszczenia b oznacza ´sredni ˛a
lub stał ˛a liczb ˛e ruchów dost ˛epn ˛a na ka ˙zdym poziomie dla ka ˙zdego z
graczy (dla szachów b ≈ 40). Wówczas przejrzenie D poziomów
gł ˛eboko´sci wymaga O(b · b · · · b

|ÃÃÃ{zÃÃÃ}

D

) =

O(b

D

)

pami ˛eci.

Najbardziej znan ˛a modyfikacj ˛a algorytmu, która redukuje w pewnym
stopniu zło ˙zono´s´c pami ˛eciow ˛a, jest

przycinanie α-β (ang. α-β cutoffs)

.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

43 / 48

Algorytm MIN-MAX

Algorytm

MIN-MAX

(lub MINIMAX)

Efekt horyzontu

Z uwagi na ograniczon ˛a gł ˛eboko´s´c przeszukiwania, algorytm mo ˙ze
cierpie´c na tzw.

efekt horyzontu

— nast ˛epny ruch poza najgł ˛ebszym

przejrzanym poziomem mo ˙ze okaza´c si ˛e katastrofalny dla jednego z
graczy, mimo ˙ze poziom wy ˙zej oceny s ˛a dla niego korzystne (np. w
szachach nie rozpatrzenie a ˙z do tzw. pozycji martwej kombinacji zbi´c).

Przemysław Kl ˛esk (KMSIiMS, ZUT)

44 / 48

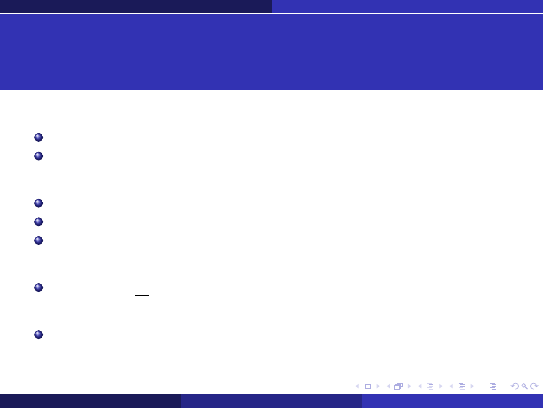
Algorytm przycinanie α-β

Algorytm

przycinanie α-β

(ang. α-β cut-offs lub α-β pruning)

Wielu niezale ˙znych odkrywców: Samuel (1952), McCarthy (1956), Newell i Simon (1958).

W trakcie analizy drzewa propagowane s ˛a w dół i gór ˛e drzewa warto´sci:
α — gwarantowana dotychczas wypłata gracza maksymalizuj ˛

acego

,

β — gwarantowana dotychczas wypłata gracza minimalizuj ˛

acego

.

W wywołaniu dla korzenia zadaje si ˛e α = −∞, β = ∞.
Dzieci (i ich poddrzewa) s ˛a analizowane dopóki α < β.

W momencie gdy α > β, przestajemy rozpatrywa´c kolejne dzieci (i ich poddrzewa) — nie
b ˛ed ˛a one miały wpływu na wynik całego drzewa, s ˛a wynikiem nieoptymalnego
post ˛epowania graczy.

W optymistycznym przypadku zysk w zło˙zono´sci wzgl ˛edem MIN-MAX’a z O(b

D

) na

O

³

b

D/2

´

=

O

³

√

b

D

´

, gdzie b — branching factor (stały lub ´sredni współczynnik

rozgał ˛eziania). Np. dla szachów b ≈ 40.
Dzi ˛eki zyskowi w zło ˙zono´sci mo ˙zna szuka´c gł ˛ebiej.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

45 / 48

Algorytm przycinanie α-β

Algorytm

przycinanie α-β

Procedura fsAlphaBetaEvaluateMax(s, d, D, α, β)

1

Je ˙zeli s jest terminalem, to zwró´c h(s).

2

Dla wszystkich stanów t b ˛ed ˛acych potomkami s wykonuj:

1

v := fsAlphaBetaEvaluateMin(t, d +

1

2

, D, α, β).

2

α := max

{α, v}.

3

Je ˙zeli α > β, to zwró´c α.

(przyci ˛ecie)

3

Zwró´c α.

Procedura fsAlphaBetaEvaluateMin(s, d, D, α, β)

1

Je ˙zeli s jest terminalem, to zwró´c h(s).

2

Dla wszystkich stanów t b ˛ed ˛acych potomkami s wykonuj:

1

v := fsAlphaBetaEvaluateMax(t, d +

1

2

, D, α, β).

2

β := min

{β, v}.

3

Je ˙zeli α > β, to zwró´c β.

(przyci ˛ecie)

3

Zwró´c β.

Przemysław Kl ˛esk (KMSIiMS, ZUT)

46 / 48

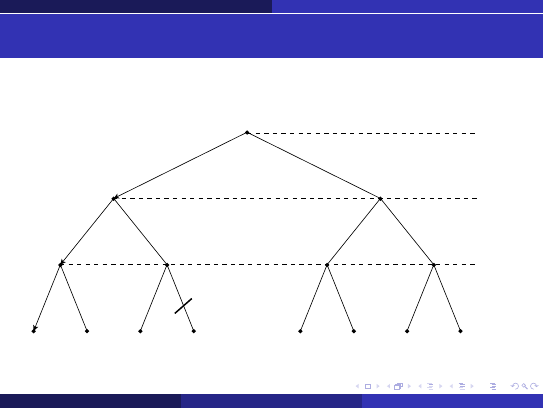
Algorytm przycinanie α-β

Ilustracja przycinania α-β — przykład 1

MAX

MIN

MAX

α =

−∞

β =

∞, 5

α =

−∞, 5

β =

∞

α =

−∞, 5

β =

∞

5

4

α =

−∞, 6

β = 5

α = 5, 7, 10

β =

∞

α = 5

β =

∞, 10, 5

α = 5

β = 10

6

∗

7

10

4

4

Przemysław Kl ˛esk (KMSIiMS, ZUT)

47 / 48

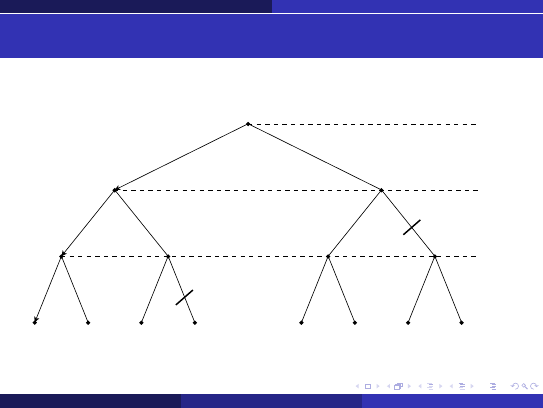
Algorytm przycinanie α-β

Ilustracja przycinania α-β — przykład 2

MAX

MIN

MAX

α =

−∞

β =

∞, 5

α =

−∞, 5

β =

∞

α =

−∞, 5

β =

∞

5

4

α =

−∞, 6

β = 5

α = 5

β =

∞

α = 5

β =

∞, 5

6

∗

3

2

*

*

Przemysław Kl ˛esk (KMSIiMS, ZUT)

48 / 48