Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

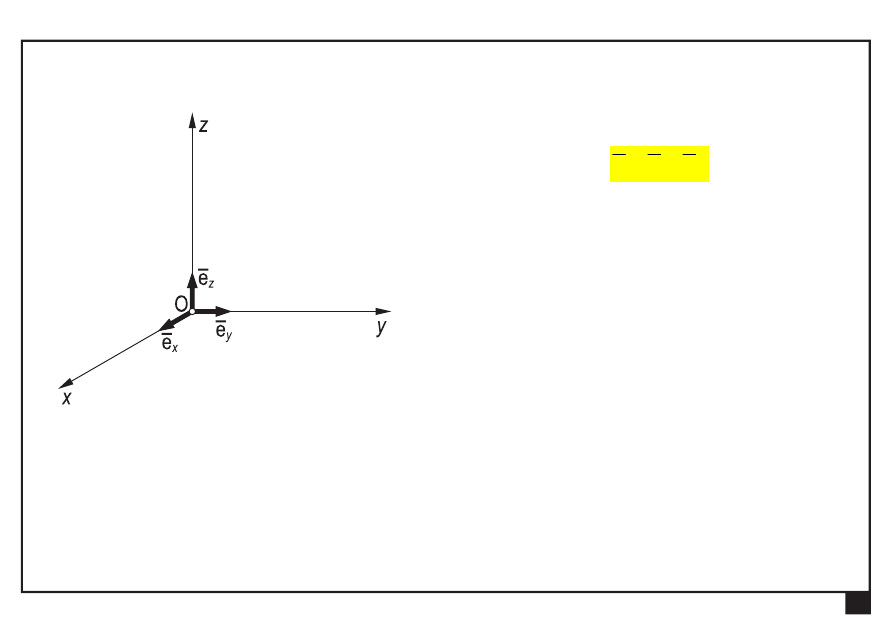
Przestrzenny kartezjański układ współrzędnych

wersory

z

y

x

e

,

e

,

e

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

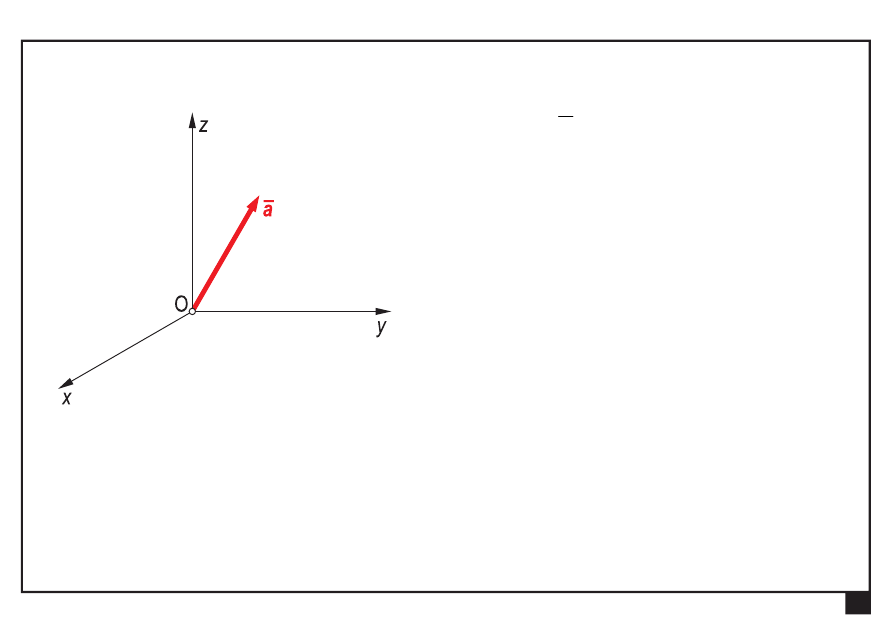
Przestrzenny kartezjański układ współrzędnych

wektor

a

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

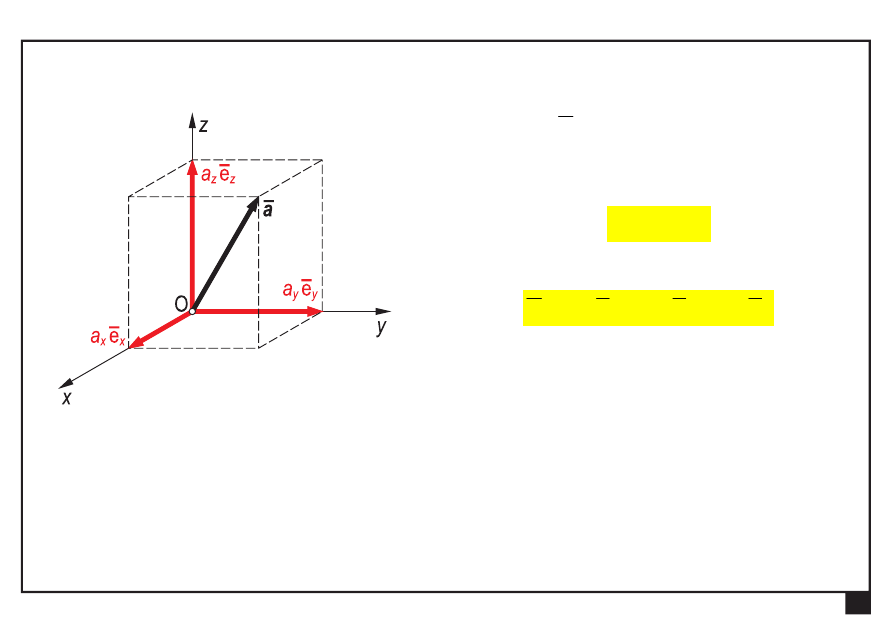
Przestrzenny kartezjański układ współrzędnych

wektor

a

— składowe wektora

z

y

x

a

a

a

,

,

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

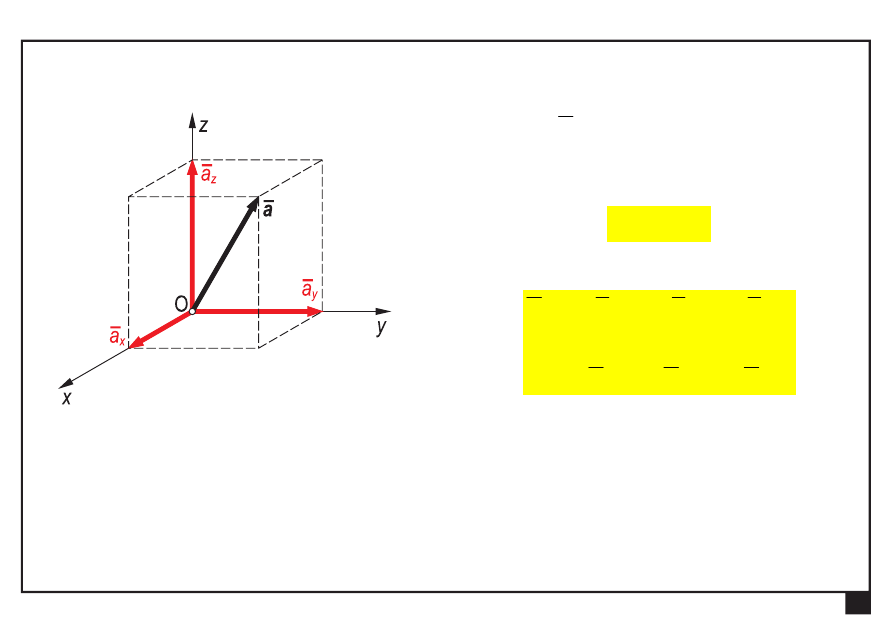
Przestrzenny kartezjański układ współrzędnych

wektor

a

— składowe wektora

z

y

x

a

a

a

,

,

— zapis analityczny

z

z

y

y

x

x

a

a

a

a

e

e

e







Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Przestrzenny kartezjański układ współrzędnych

wektor

a

— składowe wektora

z

y

x

a

a

a

,

,

— zapis analityczny

z

y

x

z

z

y

y

x

x

a

a

a

a

a

a

a







































e

e

e

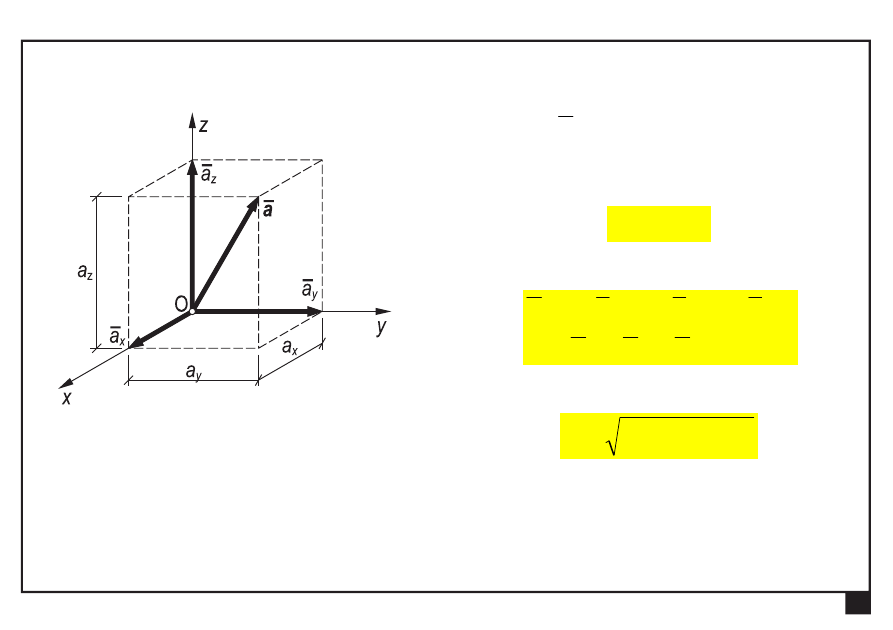
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Przestrzenny kartezjański układ współrzędnych

wektor a

— składowe wektora

z

y

x

a

a

a

,

,

— zapis analityczny

z

y

x

z

z

y

y

x

x

a

a

a

a

a

a

a















e

e

e

— moduł (wartość) wektora

2

2

2

z

y

x

a

a

a

a







Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Przestrzenny kartezjański układ współrzędnych

wektor

a

— kosinusy kierunkowe

wektora

a

a

x

x





cos

a

a

y

y





cos

a

a

z

z





cos

1

cos

cos

cos

2

2

2







z

y

x







Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Wektory swobodne, liniowe i zaczepione

wektor swobodny
— wartość
— zwrot
— kierunek

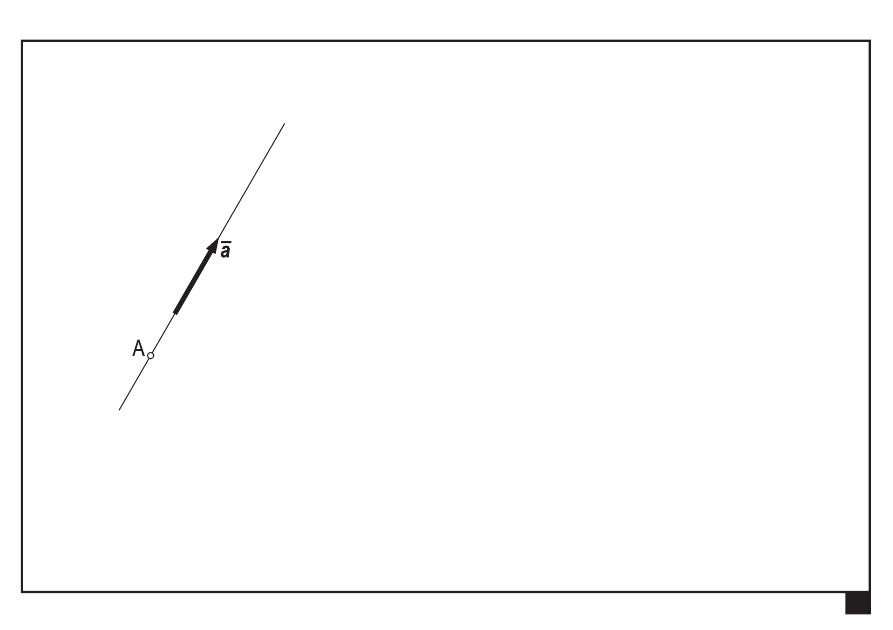
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Wektory swobodne, liniowe i zaczepione

wektor liniowy
— wartość
— zwrot
— prosta działania

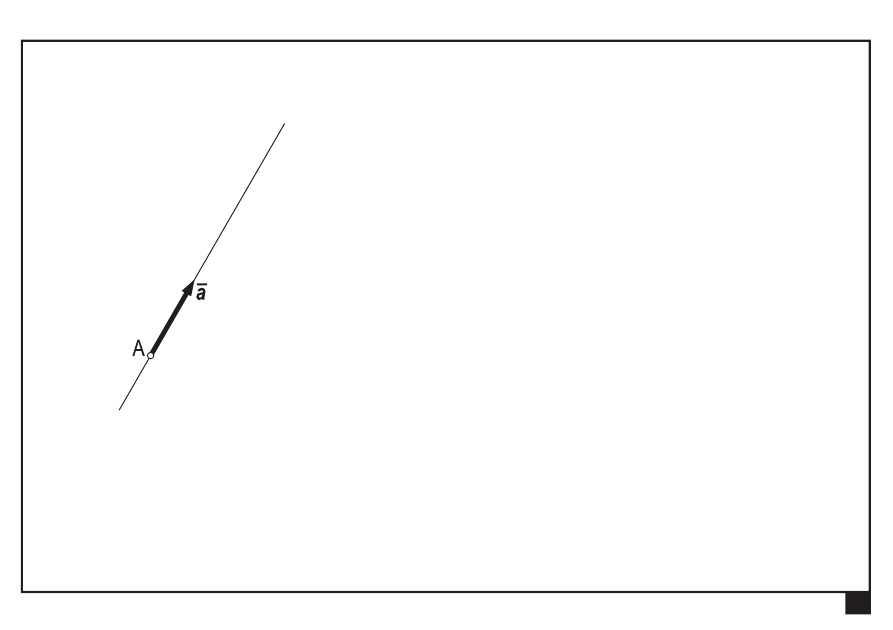
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Wektory swobodne, liniowe i zaczepione

wektor zaczepiony
— wartość
— zwrot
— prosta działania
— punkt zaczepienia

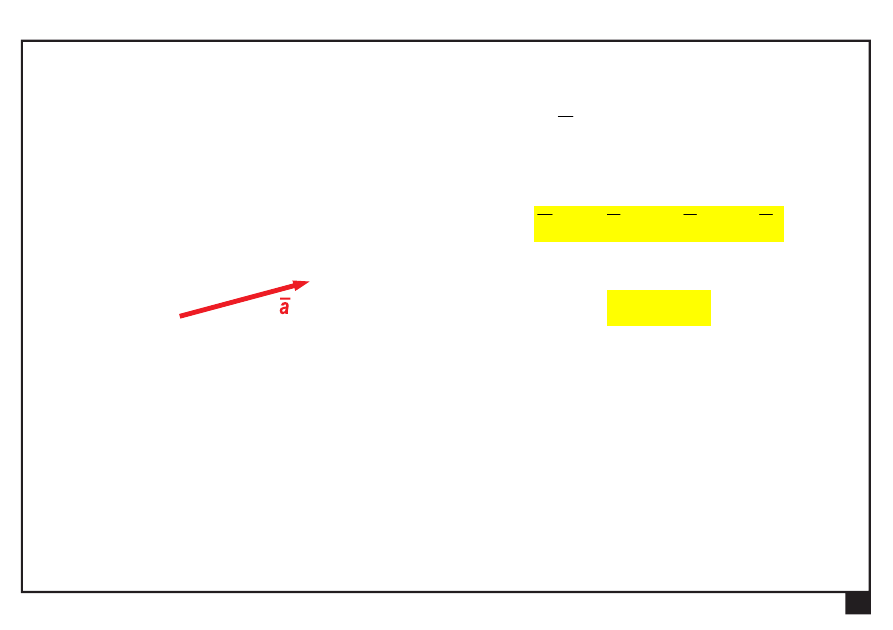
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Zmiana zwrotu wektora

wektor a

— zapis analityczny

z

z

y

y

x

x

a

a

a

a

e

e

e







— składowe

z

y

x

a

a

a

,

,

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Zmiana zwrotu wektora

wektor b o zwrocie przeciwnym

a

b





z

z

y

y

x

x

a

a

a

b

e

e

e









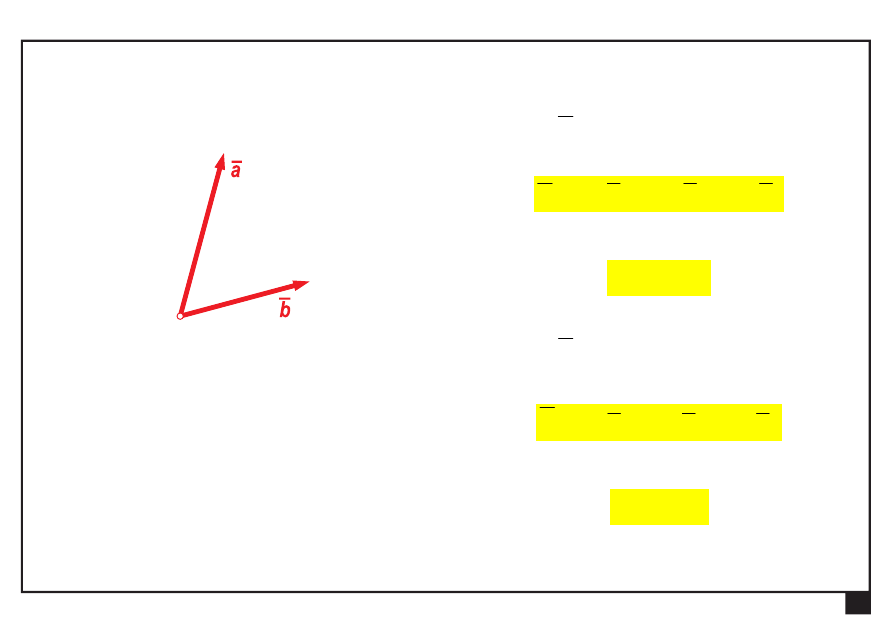
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Suma dwóch wektorów

wektor

a

— zapis analityczny

z

z

y

y

x

x

a

a

a

a

e

e

e







— składowe

z

y

x

a

a

a

,

,

wektor

b

— zapis analityczny

z

z

y

y

x

x

b

b

b

b

e

e

e







— składowe

z

y

x

b

b

b

,

,

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Suma dwóch wektorów

wektor

c

będący sumą

wektorów

a

i

b

b

a

c





— zapis analityczny

z

z

y

y

x

x

c

c

c

c

e

e

e







— składowe

x

x

x

b

a

c





y

y

y

b

a

c





z

z

z

b

a

c





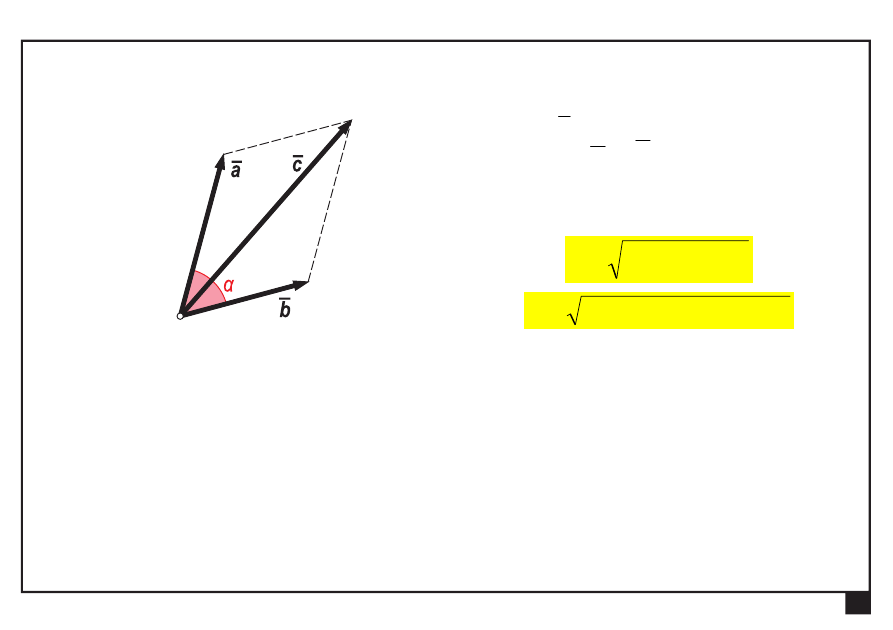
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Suma dwóch wektorów

wektor

c

będący sumą

wektorów

a

i

b

— wartość (moduł)

2

2

2

z

y

x

c

c

c

c









cos

2

2

2

ab

b

a

c







Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

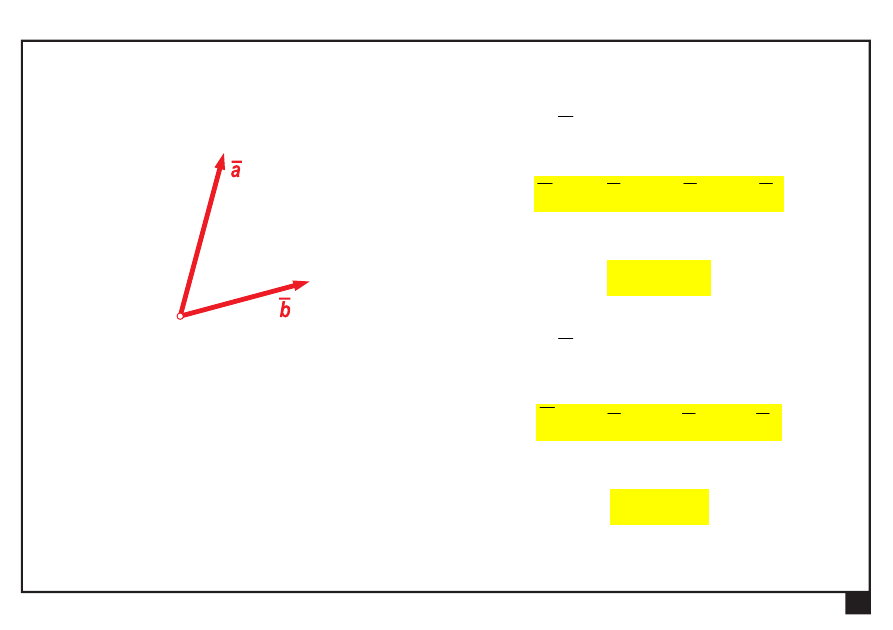
Różnica dwóch wektorów

wektor

a

— zapis analityczny

z

z

y

y

x

x

a

a

a

a

e

e

e







— składowe

z

y

x

a

a

a

,

,

wektor

b

— zapis analityczny

z

z

y

y

x

x

b

b

b

b

e

e

e







— składowe

z

y

x

b

b

b

,

,

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Różnica dwóch wektorów

wektor

b



— zapis analityczny

z

z

y

y

x

x

b

b

b

b

e

e

e











— składowe

z

y

x

b

b

b

,

,

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Różnica dwóch wektorów

wektor

c

będący różnicą

wektorów

a

i

b

)

(

b

a

b

a

c











— zapis analityczny

z

z

y

y

x

x

c

c

c

c

e

e

e







— składowe

x

x

x

b

a

c





y

y

y

b

a

c





z

z

z

b

a

c





Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Mnożenie wektora przez skalar

wektor

b

będący wynikiem mnożenia wektora

a

przez skalar

s

a

s

b





— zapis analityczny

z

z

y

y

x

x

b

b

b

b

e

e

e







— składowe

x

x

a

s

b 

y

y

a

s

b 

z

z

a

s

b 

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn skalarny dwóch wektorów

wynik iloczynu skalarnego

skalar (liczba)

z

z

y

y

x

x

b

a

b

a

b

a

b

a

s











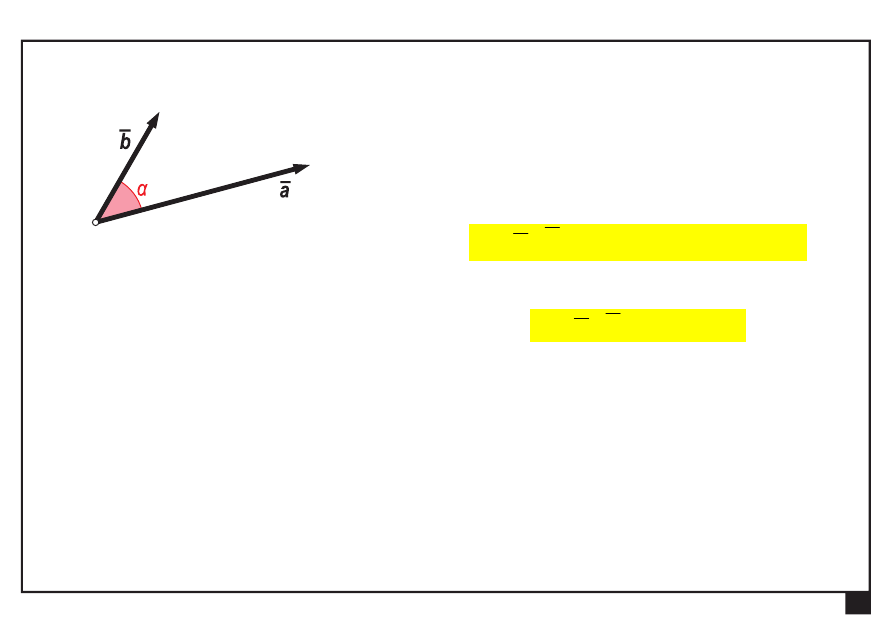
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn skalarny dwóch wektorów

wynik iloczynu skalarnego

skalar (liczba)

z

z

y

y

x

x

b

a

b

a

b

a

b

a

s













cos

b

a

b

a

s







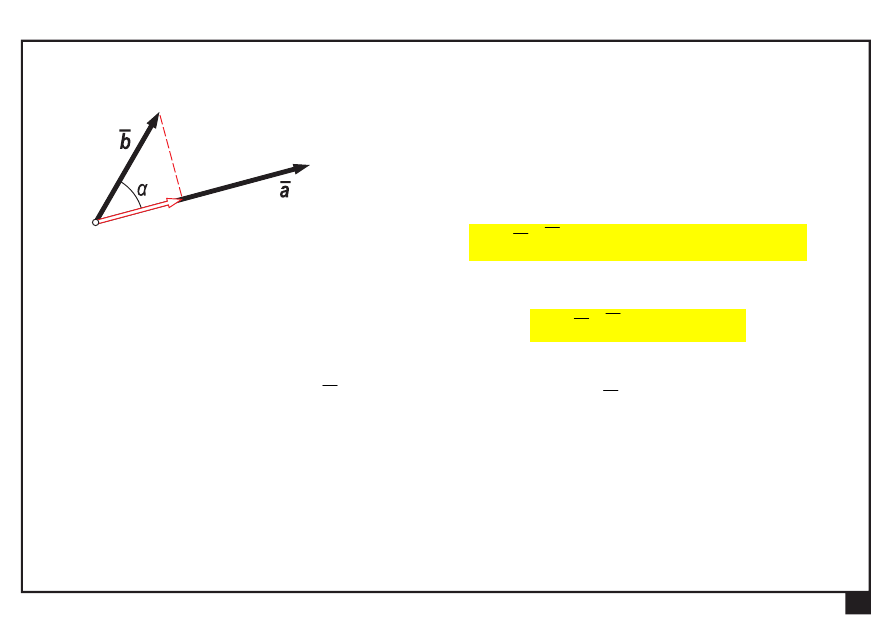
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn skalarny dwóch wektorów

wynik iloczynu skalarnego

skalar (liczba)

z

z

y

y

x

x

b

a

b

a

b

a

b

a

s













cos

b

a

b

a

s









cos

b

— rzut wektora

b

na kierunek wektora

a

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

wynik iloczynu wektorowego

wektor

zapis wyznacznikowy

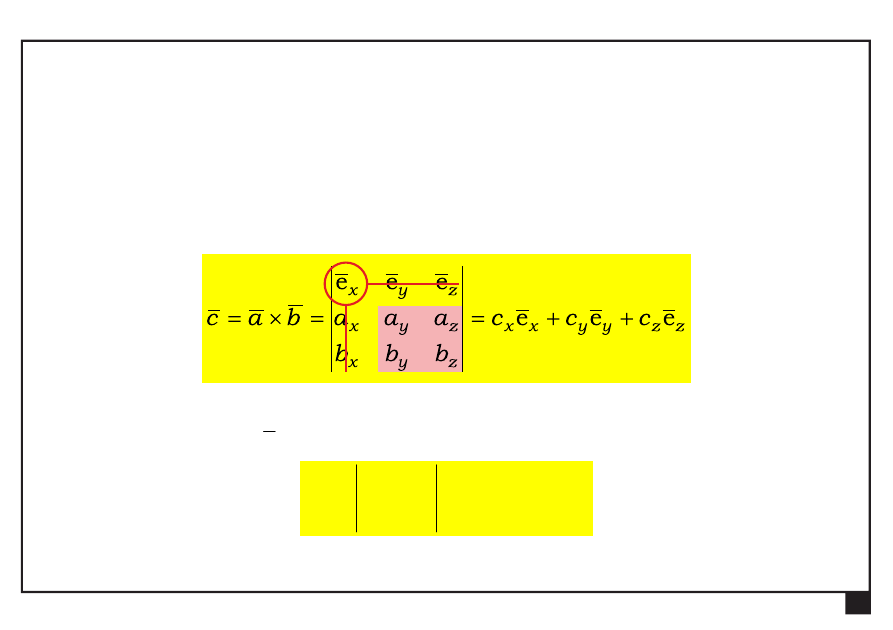
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

wynik iloczynu wektorowego

wektor

zapis wyznacznikowy

składowe wektora

c

*

)

y

z

z

y

z

y

z

y

x

b

a

b

a

b

b

a

a

c







*

)

rozwinięcie Laplace’a według elementów pierwszego wiersza

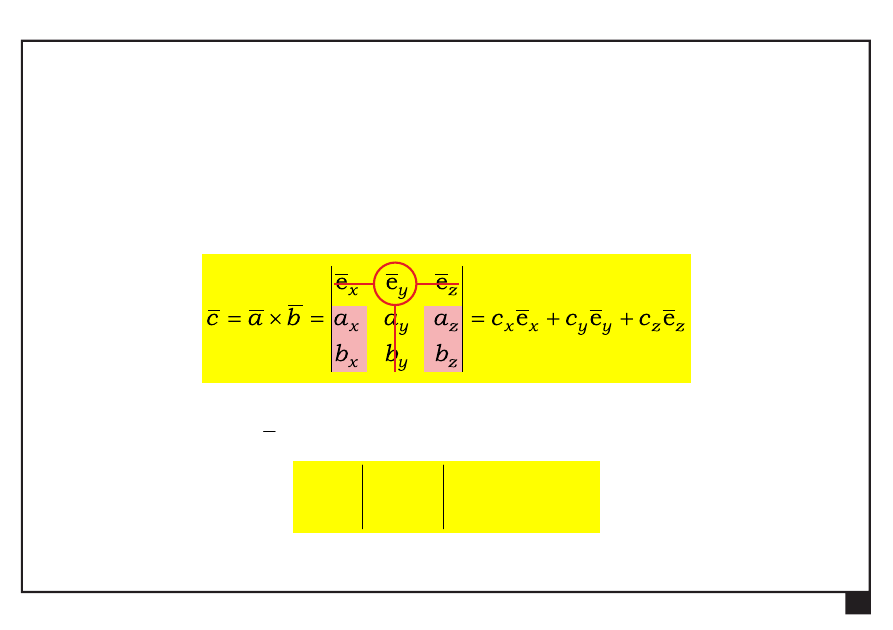
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

wynik iloczynu wektorowego

wektor

zapis wyznacznikowy

składowe wektora

c

z

x

x

z

z

x

z

x

y

b

a

b

a

b

b

a

a

c









Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

wynik iloczynu wektorowego

wektor

zapis wyznacznikowy

składowe wektora

c

x

y

y

x

y

x

y

x

z

b

a

b

a

b

b

a

a

c







Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

wynik iloczynu wektorowego —

wektor

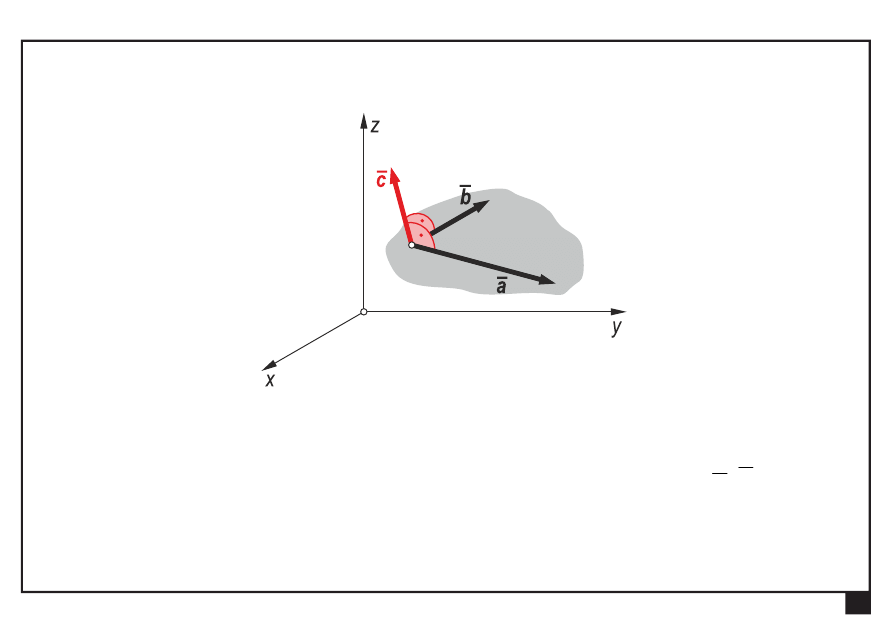
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

wynik iloczynu wektorowego —

wektor

— prostopadły do płaszczyzny utworzonej przez wektory

b

a,

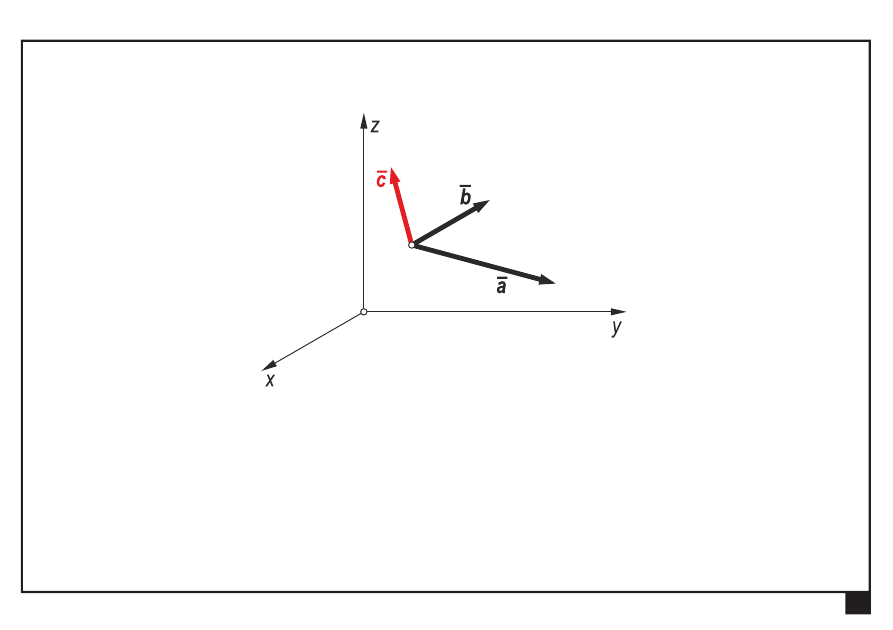
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

wynik iloczynu wektorowego —

wektor

— o zwrocie zgodnym z regułą prawej dłoni

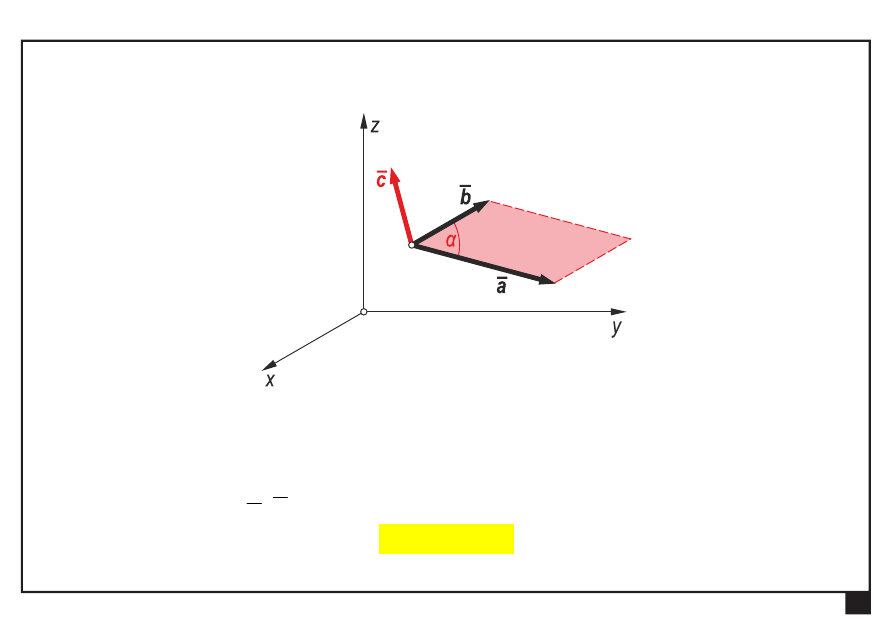
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

wynik iloczynu wektorowego —

wektor

— o wartości równej polu równoległoboku rozpiętego

na wektorach

b

a,



sin

b

a

c 

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Iloczyn wektorowy dwóch wektorów

mnożenie wektorowe nie jest przemienne

b

a

a

b









Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Wektory na płaszczyźnie

y

y

x

x

a

a

a

e

e 



y

y

x

x

b

b

b

e

e 











90

0

cos

z

z





— dodawanie

y

y

x

x

c

c

b

a

c

e

e 







x

x

x

b

a

c





,

y

y

y

b

a

c





— odejmowanie

y

y

x

x

c

c

b

a

c

e

e 







x

x

x

b

a

c





,

y

y

y

b

a

c





Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Wektory na płaszczyźnie

y

y

x

x

a

a

a

e

e 



y

y

x

x

b

b

b

e

e 











90

0

cos

z

z





— iloczyn skalarny

y

y

x

x

b

b

a

s

b

e

e 







x

x

a

s

b 

,

y

y

a

s

b 

— iloczyn wektorowy

z

z

y

x

y

x

z

y

x

c

b

b

a

a

b

a

c

e

0

0

e

e

e









x

y

y

x

z

b

a

b

a

c





Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Punkt materialny

— obiekt o zerowych wymiarach i skończonej

masie. Punkt materialny jest pojęciem abstrakcyjnym.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Punkt materialny

— obiekt o zerowych wymiarach i skończonej

masie. Punkt materialny jest pojęciem abstrakcyjnym.

Ciało sztywne

— zbiór punktów materialnych

o stałych odległościach między nimi.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Punkt materialny

— obiekt o zerowych wymiarach i skończonej

masie. Punkt materialny jest pojęciem abstrakcyjnym.

Ciało sztywne

— zbiór punktów materialnych

o stałych odległościach między nimi.

Bryła

— ciało sztywne (nieodkształcalne) 3D.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Punkt materialny

— obiekt o zerowych wymiarach i skończonej

masie. Punkt materialny jest pojęciem abstrakcyjnym.

Ciało sztywne

— zbiór punktów materialnych

o stałych odległościach między nimi.

Bryła

— ciało sztywne (nieodkształcalne) 3D.

Tarcza

— bryła, której grubość

h jest o rząd mniejsza od dwóch

pozostałych wymiarów gabarytowych.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

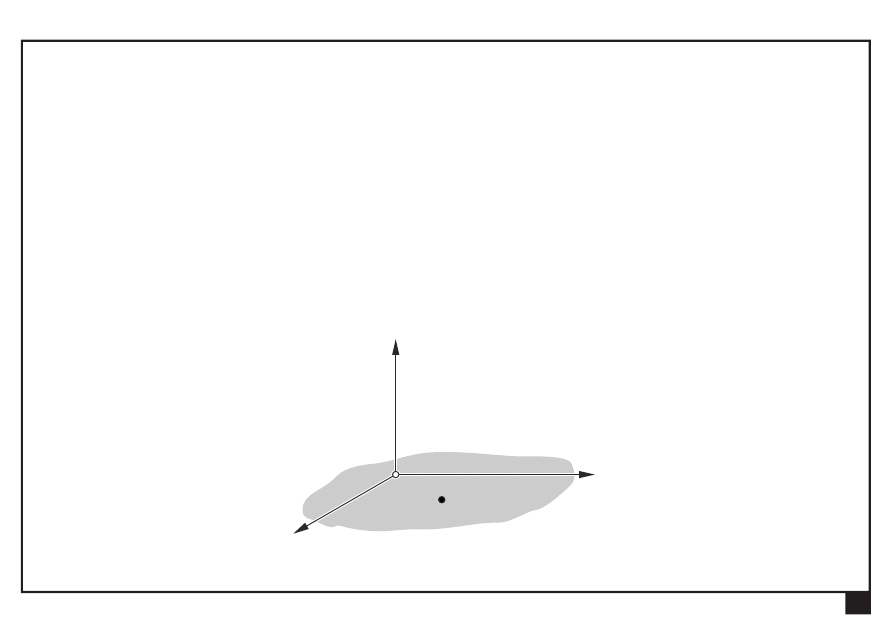
Liczba stopni swobody

punktu materialnego lub ciała sztywnego

nazywamy liczbę

n niezależnych przemieszczeń opisujących ruch

punktu lub ciała:
— punkt na płaszczyźnie:

x

z

y

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Liczba stopni swobody

punktu materialnego lub ciała sztywnego

nazywamy liczbę

n niezależnych przemieszczeń opisujących ruch

punktu lub ciała:
— punkt na płaszczyźnie:

n = 2

x

z

y

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Liczba stopni swobody

punktu materialnego lub ciała sztywnego

nazywamy liczbę

n niezależnych przemieszczeń opisujących ruch

punktu lub ciała:
— punkt na płaszczyźnie:

n = 2

— punkt w przestrzeni:

x

z

y

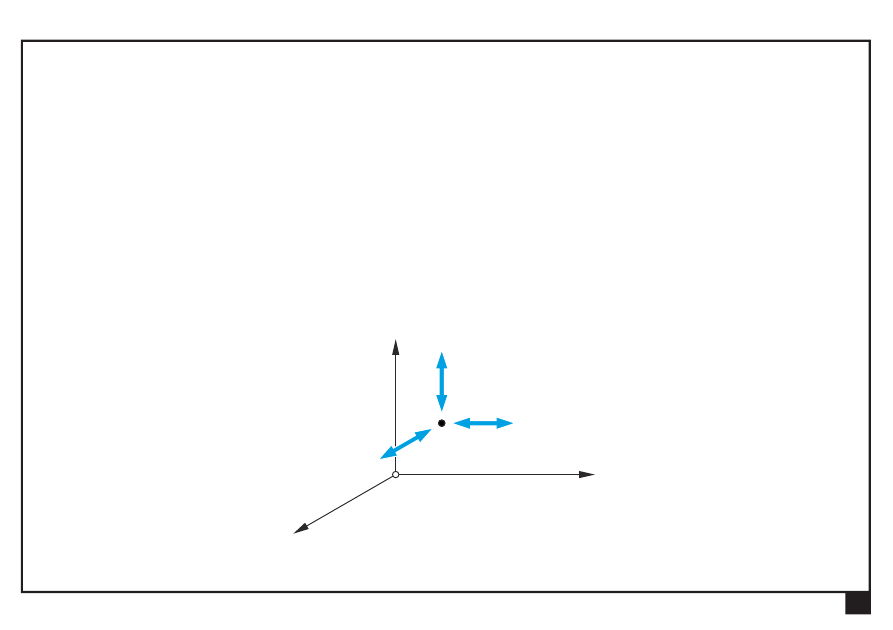
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Liczba stopni swobody

punktu materialnego lub ciała sztywnego

nazywamy liczbę

n niezależnych przemieszczeń opisujących ruch

punktu lub ciała:
— punkt na płaszczyźnie:

n = 2

— punkt w przestrzeni:

n = 3

x

z

y

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Liczba stopni swobody

punktu materialnego lub ciała sztywnego

nazywamy liczbę

n niezależnych przemieszczeń opisujących ruch

punktu lub ciała:
— punkt na płaszczyźnie:

n = 2

— punkt w przestrzeni:

n = 3

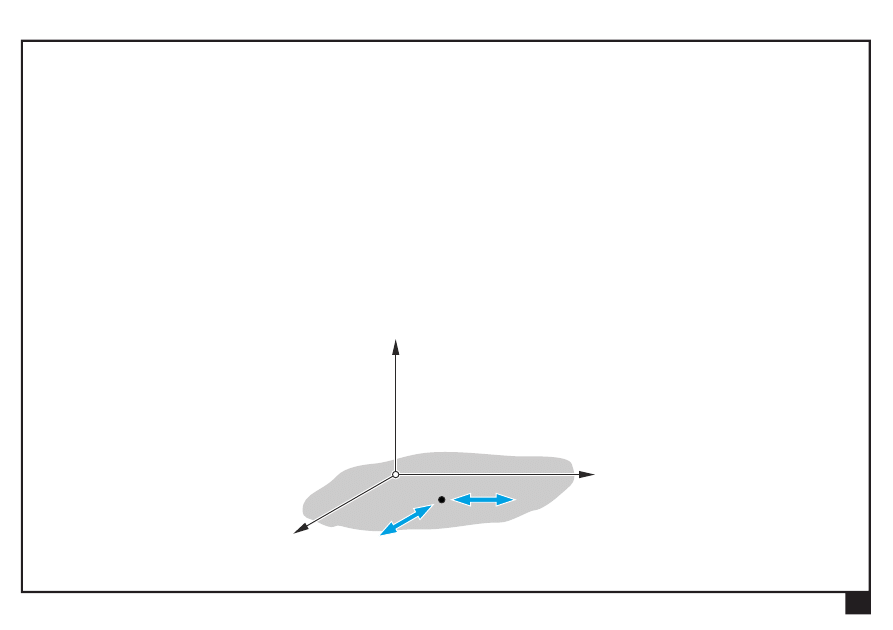
— tarcza lub pręt na płaszczyźnie:

x

z

y

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Liczba stopni swobody

punktu materialnego lub ciała sztywnego

nazywamy liczbę

n niezależnych przemieszczeń opisujących ruch

punktu lub ciała:
— punkt na płaszczyźnie:

n = 2

— punkt w przestrzeni:

n = 3

— tarcza lub pręt na płaszczyźnie:

n = 3

x

z

y

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Liczba stopni swobody

punktu materialnego lub ciała sztywnego

nazywamy liczbę

n niezależnych przemieszczeń opisujących ruch

punktu lub ciała:
— punkt na płaszczyźnie:

n = 2

— punkt w przestrzeni:

n = 3

— tarcza lub pręt na płaszczyźnie:

n = 3

— bryła w przestrzeni:

x

z

y

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Liczba stopni swobody

punktu materialnego lub ciała sztywnego

nazywamy liczbę

n niezależnych przemieszczeń opisujących ruch

punktu lub ciała:
— punkt na płaszczyźnie:

n = 2

— punkt w przestrzeni:

n = 3

— tarcza lub pręt na płaszczyźnie:

n = 3

— bryła w przestrzeni:

n = 6

x

z

y

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Więzy

— ograniczenia nałożone na ruch punktu

lub ciała sztywnego:
— więzy idealne (bez tarcia) lub nieidealne (z tarciem)
— więzy nieodkształcalne lub odkształcalne
—

więzy dwustronne lub jednostronne

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— pojęcie abstrakcyjne

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

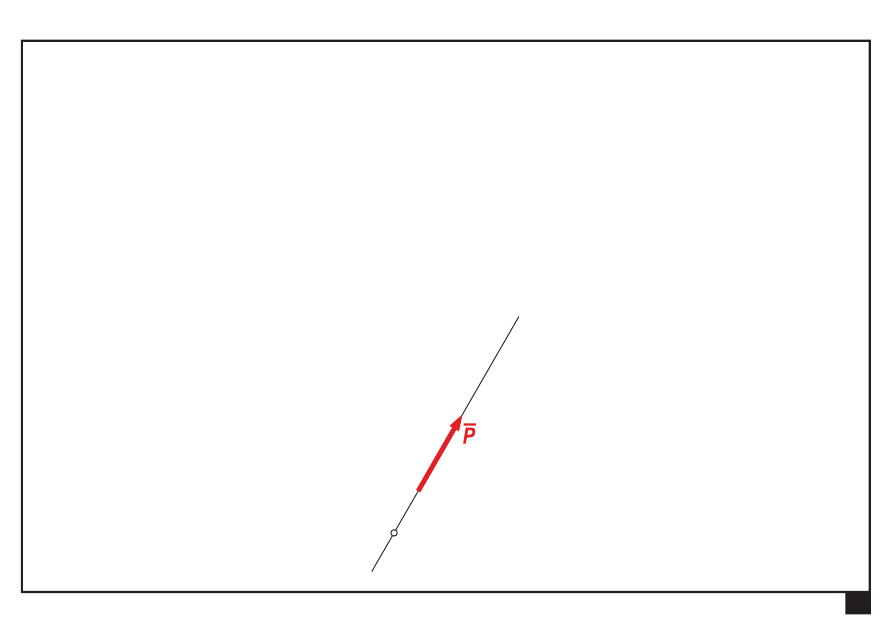
Pojęcia podstawowe

Siła

— pojęcie abstrakcyjne
— poznawalna po skutkach swego działania

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— pojęcie abstrakcyjne
— poznawalna po skutkach swego działania
— wektor liniowy (wartość, zwrot i prosta działania)

u

A

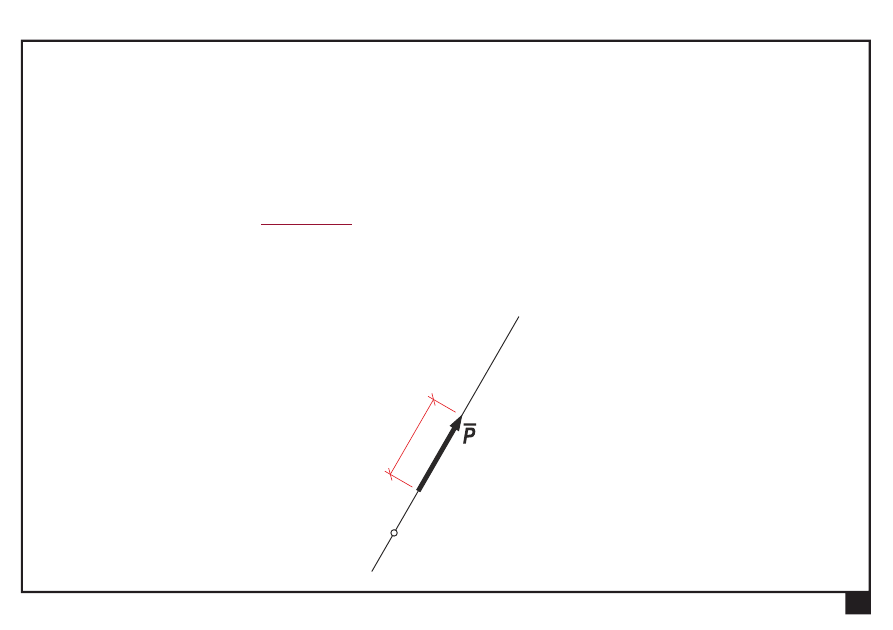
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— pojęcie abstrakcyjne
— poznawalna po skutkach swego działania
— wektor liniowy (

wartość

, zwrot i prosta działania)

u

P

A

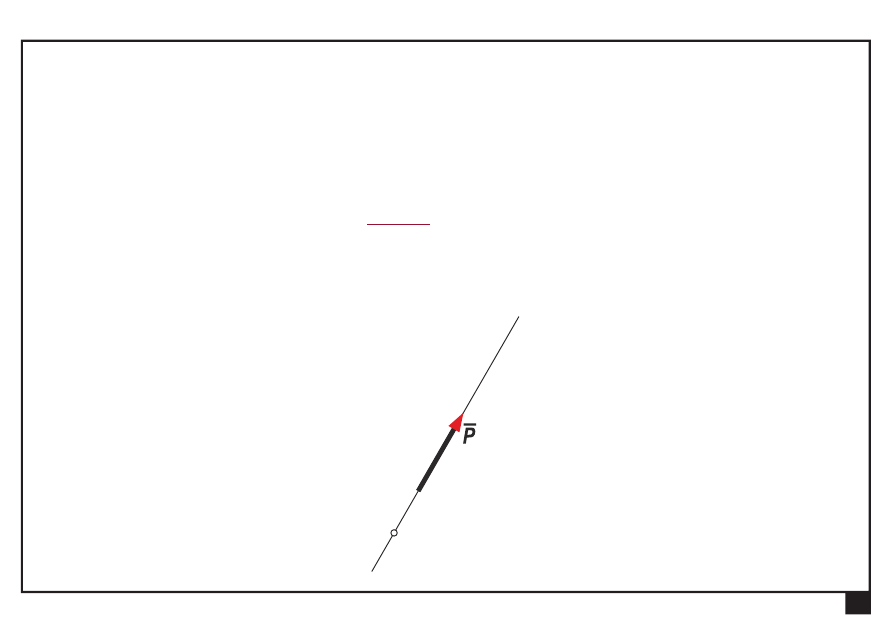
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— pojęcie abstrakcyjne
— poznawalna po skutkach swego działania
— wektor liniowy (wartość,

zwrot

i prosta działania)

u

A

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— pojęcie abstrakcyjne
— poznawalna po skutkach swego działania
— wektor liniowy (wartość, zwrot i

prosta działania

)

u

A

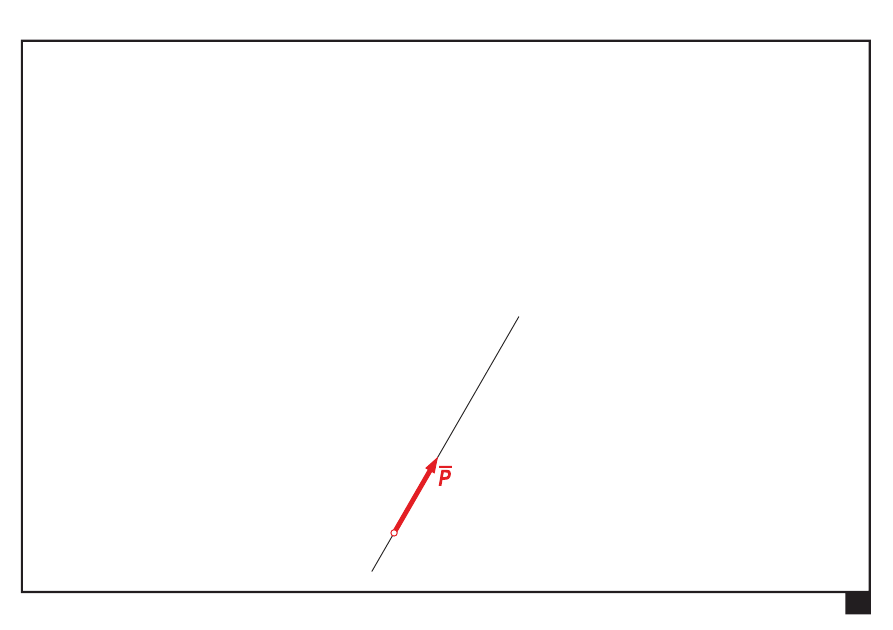
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— pojęcie abstrakcyjne
— poznawalna po skutkach swego działania
— wektor liniowy (wartość, zwrot i prosta działania)

Siłę można przesunąć do punktu lokacyjnego prostej działania siły.

u

A

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

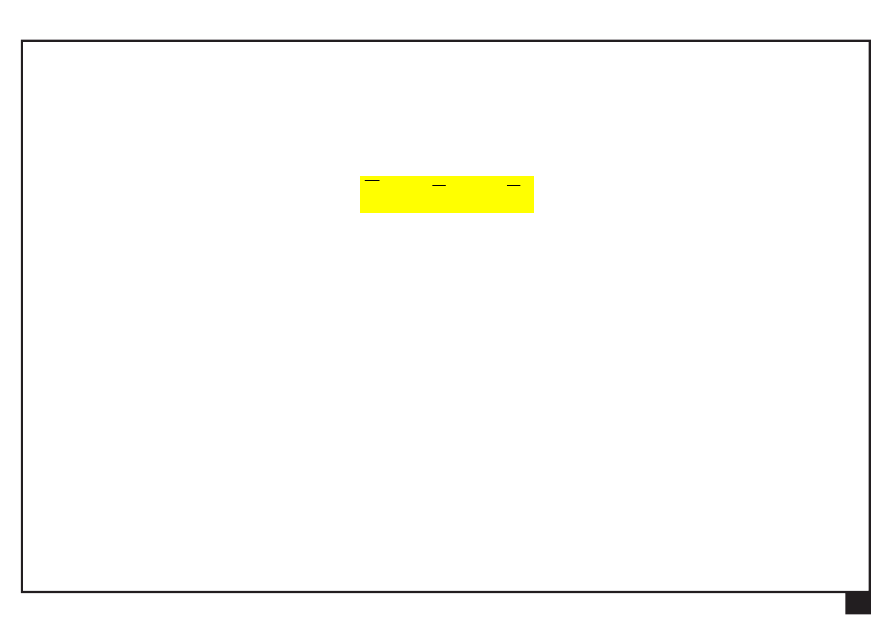
Pojęcia podstawowe

Siła

— zapis analityczny siły na płaszczyźnie:

y

y

x

x

P

P

P

e

e 



Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

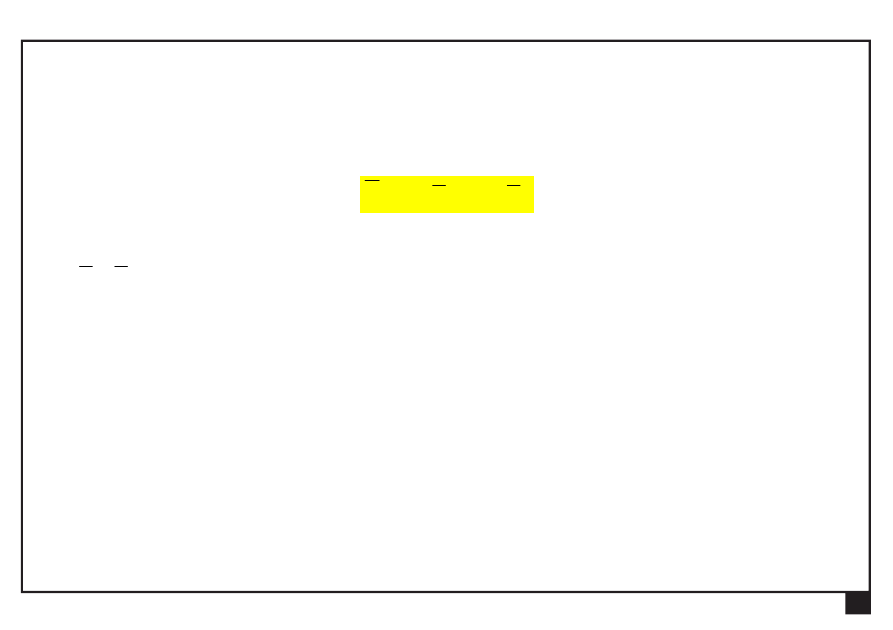
— zapis analityczny siły na płaszczyźnie:

y

y

x

x

P

P

P

e

e 



y

x

P

P ,

— składowe siły

y

x

e

,

e

— wersory osi

x i y

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

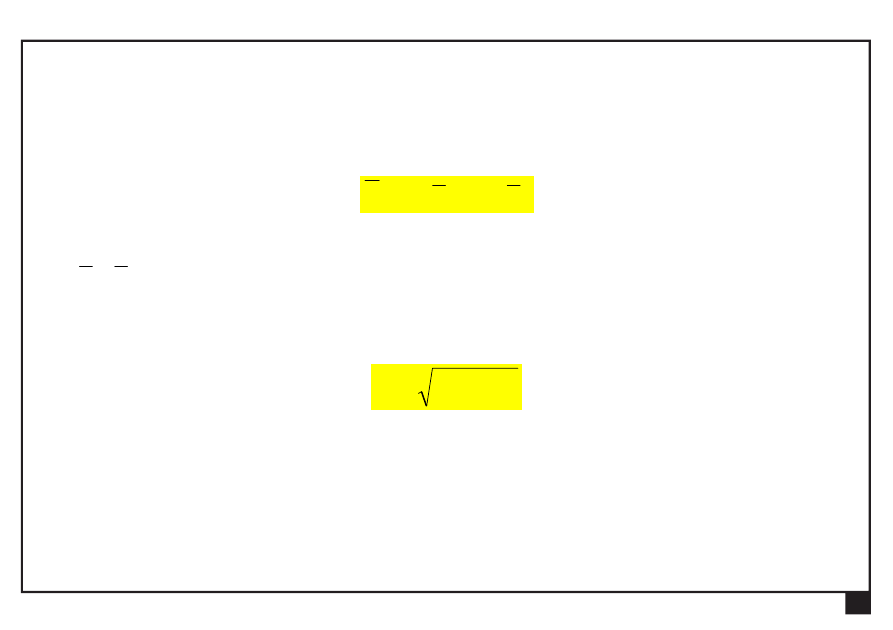
— zapis analityczny siły na płaszczyźnie:

y

y

x

x

P

P

P

e

e 



y

x

P

P ,

— składowe siły

y

x

e

,

e

— wersory osi

x i y

— wartość siły:

2

2

y

x

P

P

P





Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— zapis analityczny siły w przestrzeni:

z

z

y

y

x

x

P

P

P

P

e

e

e







Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— zapis analityczny siły w przestrzeni:

z

z

y

y

x

x

P

P

P

P

e

e

e







z

y

x

P

P

P

,

,

— składowe siły

z

y

x

e

,

e

,

e

— wersory osi

x, y i z

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— zapis analityczny siły w przestrzeni:

z

z

y

y

x

x

P

P

P

P

e

e

e







z

y

x

P

P

P

,

,

— składowe siły

z

y

x

e

,

e

,

e

— wersory osi

x, y i z

— wartość siły:

2

2

2

z

y

x

P

P

P

P







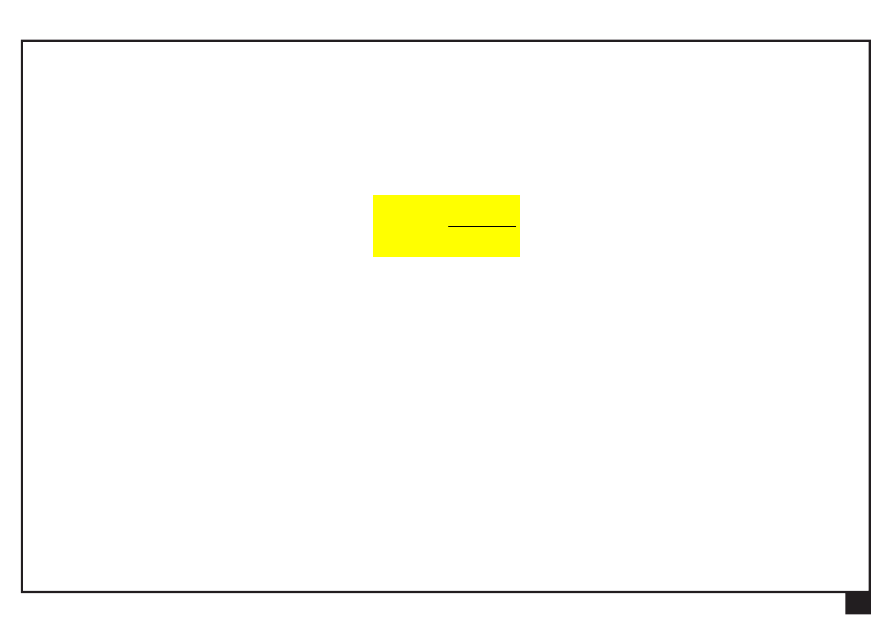
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Siła

— jednostki składowych siły

z

y

x

P

P

P

,

,

oraz modułu P :

2

s

m

kg

1

N

1





N

10

N

000

1

kN

1

3





N

10

N

000

000

1

MN

1

6





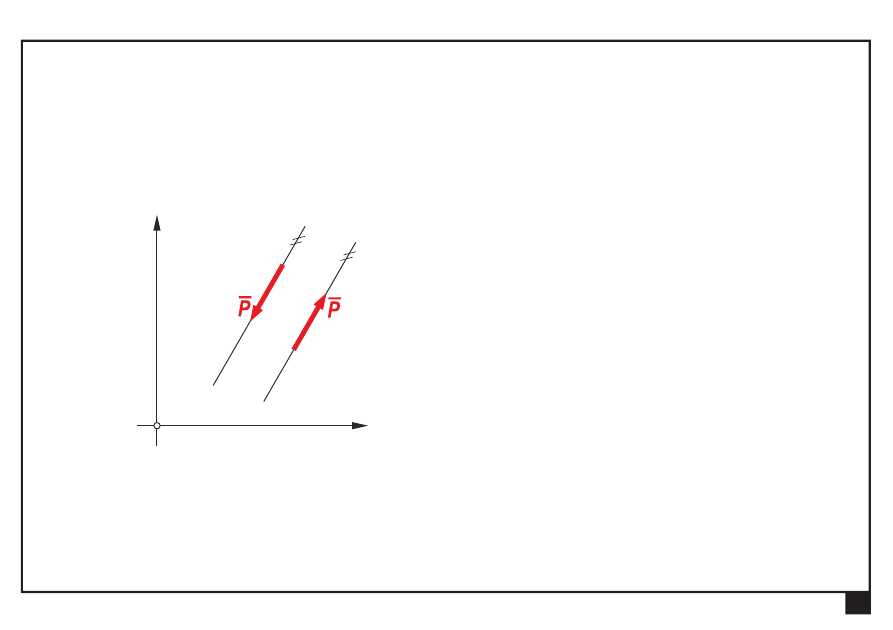
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Para sił

— dwie siły leżące na prostych równoległych, mające

tę samą wartość i przeciwne zwroty

y

x

( )

z

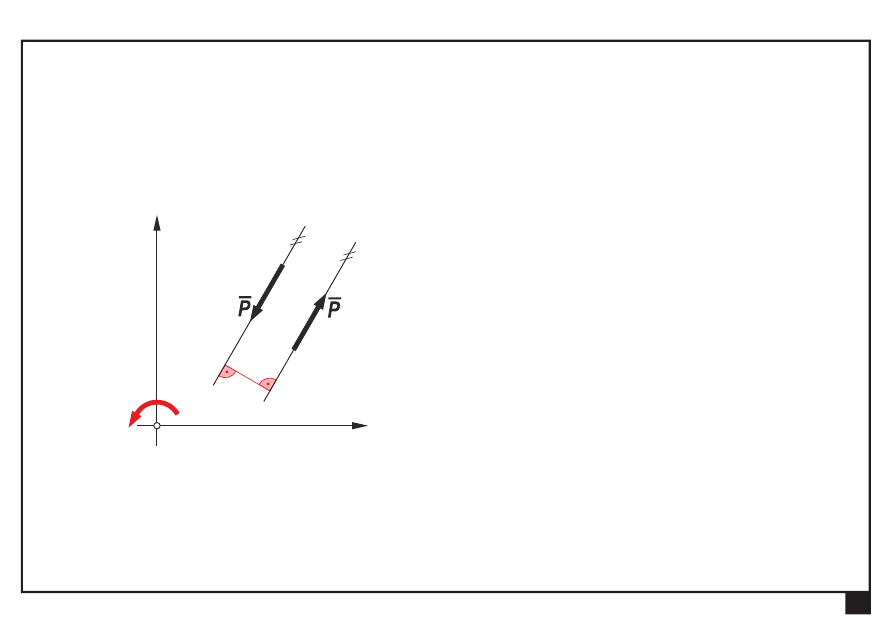
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Para sił

— dwie siły leżące na prostych równoległych, mające

tę samą wartość i przeciwne zwroty

a

y

x

( )

z

M

— parę sił można zastąpić momentem

M, działającym

w płaszczyźnie pary sił

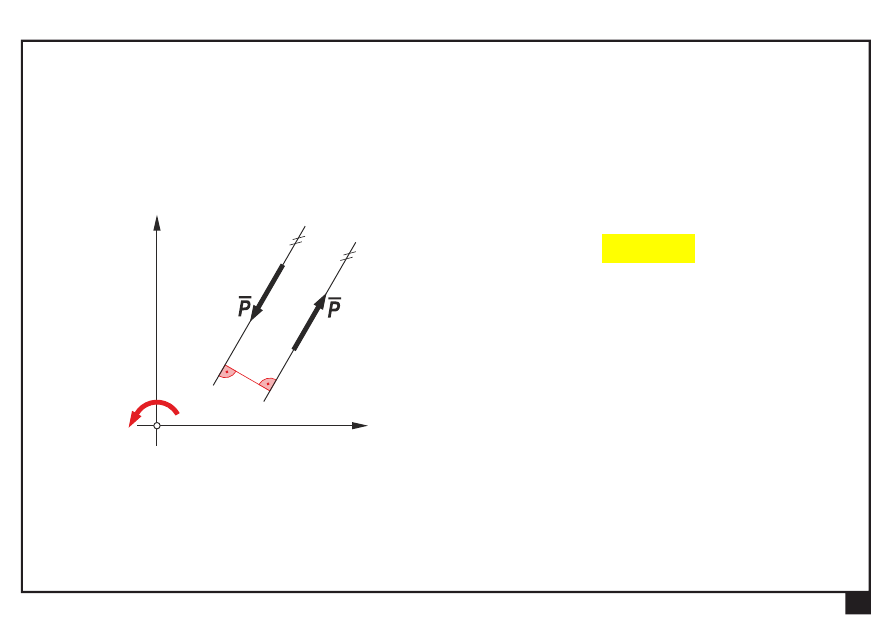
Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Para sił

— dwie siły leżące na prostych równoległych, mające

tę samą wartość i przeciwne zwroty

a

y

x

( )

z

M

a

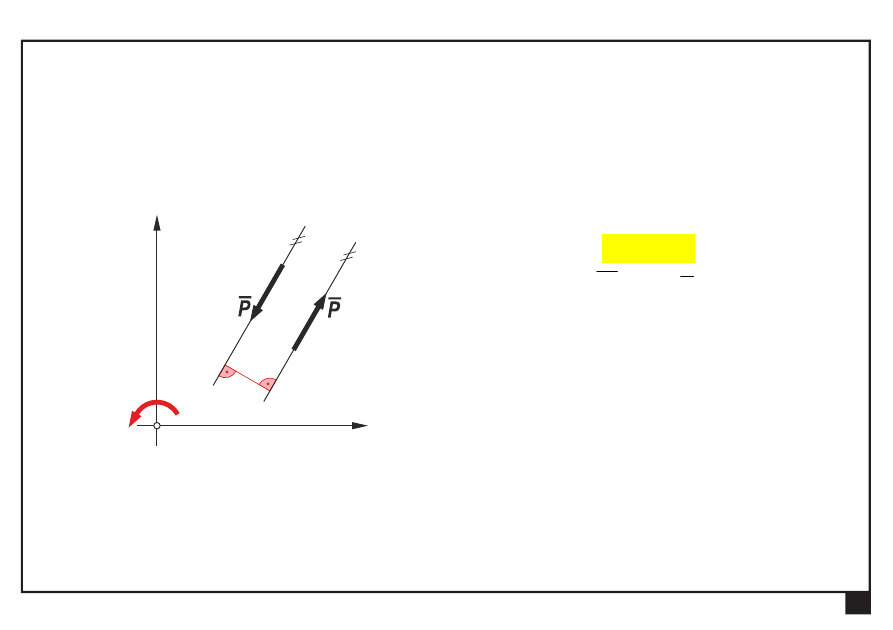
P

M 

— parę sił można zastąpić momentem

M, działającym

w płaszczyźnie pary sił
a — ramię pary sił

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Para sił

— dwie siły leżące na prostych równoległych, mające

tę samą wartość i przeciwne zwroty

a

y

x

( )

z

M

a

P

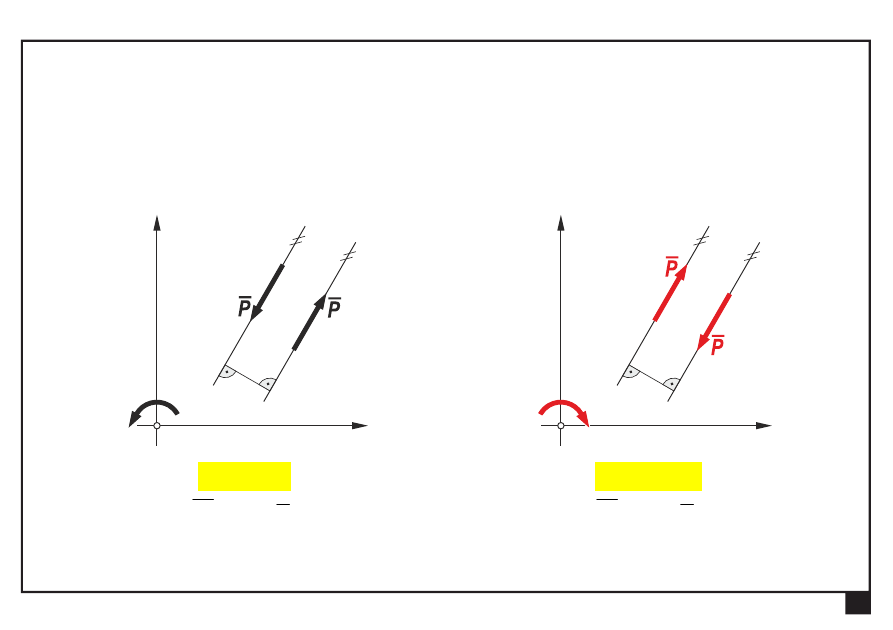
M 

z

z

M

M

e



a

P

M

z



— parę sił można zastąpić momentem, działającym

w płaszczyźnie pary sił

— zwrot momentu

M wynika z reguły prawej dłoni

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Para sił

— dwie siły leżące na prostych równoległych, mające

tę samą wartość i przeciwne zwroty

a

y

x

( )

z

M

a

P

M 

z

z

M

M

e



a

P

M

z



a

y

x

( )

z

M

a

P

M





z

z

M

M

e



a

P

M

z





Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

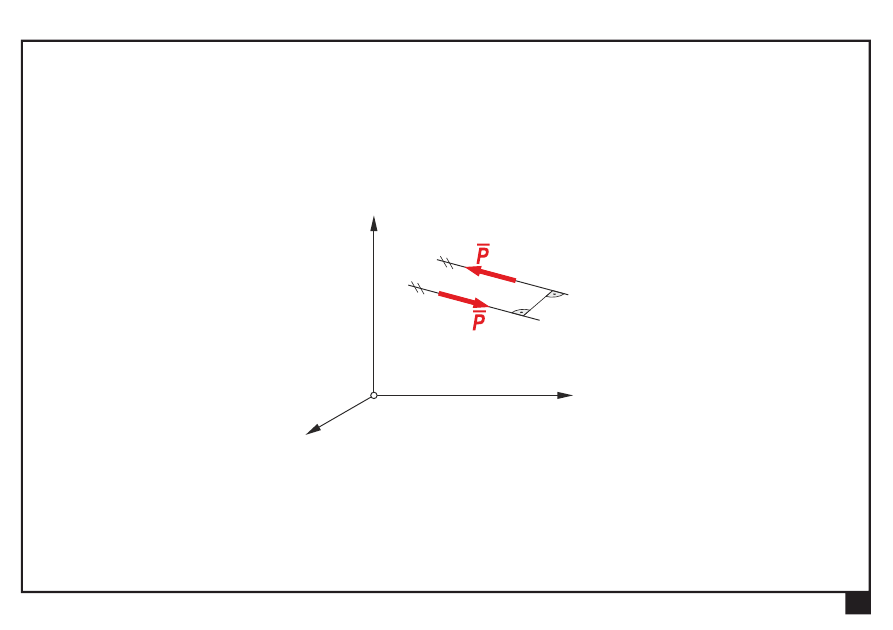
Pojęcia podstawowe

Para sił

— dwie siły leżące na prostych równoległych, mające

tę samą wartość i przeciwne zwroty

z

y

x

a

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

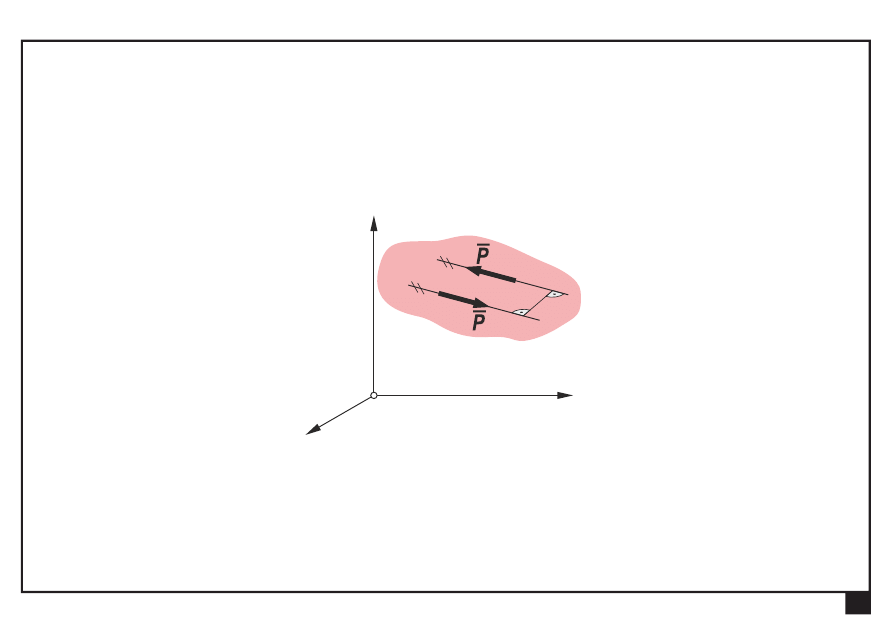
Pojęcia podstawowe

Para sił

— dwie siły leżące na prostych równoległych, mające

tę samą wartość i przeciwne zwroty

z

y

x

a

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Para sił

— dwie siły leżące na prostych równoległych, mające

tę samą wartość i przeciwne zwroty

z

y

x

a

a

P

M



z

z

y

y

x

x

M

M

M

M

e

e

e







Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Moment pary sił

— wektor swobodny, prostopadły do płaszczyzny działania

pary sił, o zwrocie zgodnym z regułą prawej dłoni

z

y

x

a

o wartości

a

P

M



Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Pojęcia podstawowe

Moment pary sił

— jednostki składowych momentu

z

y

x

M

M

M

,

,

oraz modułu M :

m

N

1 

m

N

10

m

N

000

1

m

kN

1

3











m

N

10

m

N

000

000

1

m

MN

1

6











Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Definicje

Obciążenie dowolne

— układ sił i/lub momentów działających

na ciało sztywne.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Definicje

Obciążenie dowolne

— układ sił i/lub momentów działających

na ciało sztywne.

Dwa układy obciążeń są sobie równoważne, jeśli zastąpienie jednego
układu obciążeń układem drugim wywołuje takie same skutki.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Definicje

Obciążenie dowolne

— układ sił i/lub momentów działających

na ciało sztywne.

Dwa układy obciążeń są sobie równoważne, jeśli zastąpienie jednego
układu obciążeń układem drugim wywołuje takie same skutki.

Redukcja układu obciążeń

— zastąpienie tego układu

najprostszym układem równoważnym.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Definicje

Obciążenie dowolne

— układ sił i/lub momentów działających

na ciało sztywne.

Dwa układy obciążeń są sobie równoważne, jeśli zastąpienie jednego
układu obciążeń układem drugim wywołuje takie same skutki.

Redukcja układu obciążeń

— zastąpienie tego układu

najprostszym układem równoważnym.

Układ obciążeń działających na ciało sztywne jest w równowadze
statycznej, jeśli redukuje się do zera.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Definicje

Obciążenie dowolne

— układ sił i/lub momentów działających

na ciało sztywne.

Dwa układy obciążeń są sobie równoważne, jeśli zastąpienie jednego
układu obciążeń układem drugim wywołuje takie same skutki.

Redukcja układu obciążeń

— zastąpienie tego układu

najprostszym układem równoważnym.

Układ obciążeń działających na ciało sztywne jest w równowadze
statycznej, jeśli redukuje się do zera.

Statyka

— dział mechaniki ogólnej zajmujący się badaniem

równowagi statycznej układów obciążeń i przekształcaniem
tych układów.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Prawa Newtona — zasady dynamiki Newtona

I prawo Newtona — I zasada dynamiki
(zasada bezwładności)

Jeśli układ sił działających na punkt materialny
jest w równowadze statycznej, to punkt ten jest nieruchomy
lub jest w ruchu prostoliniowym jednostajnym.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Prawa Newtona — zasady dynamiki Newtona

II prawo Newtona — II zasada dynamiki

Pochodna pędu punktu materialnego jest równa
sile działającej na ten punkt.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Prawa Newtona — zasady dynamiki Newtona

III prawo Newtona — III zasada dynamiki
(zasada akcji i reakcji)

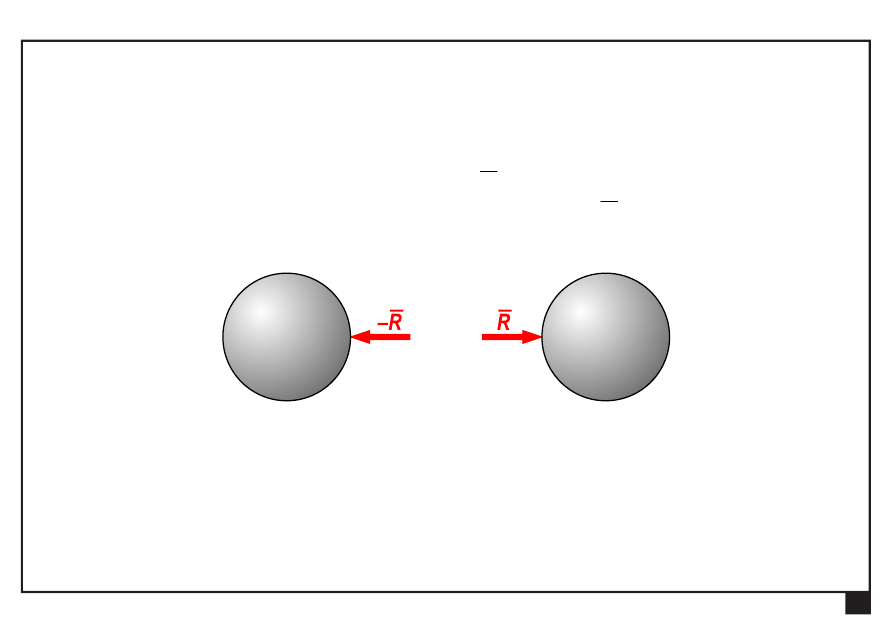
Jeśli ciało A działa na ciało B siłą R ,
to ciało B działa na ciało A siłą kolinearną R



.

A

B

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Prawa Newtona — zasady dynamiki Newtona

III prawo Newtona — III zasada dynamiki
(zasada akcji i reakcji)

Jeśli ciało A działa na ciało B siłą R ,
to ciało B działa na ciało A siłą kolinearną R



.

A

B

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Prawa Newtona — zasady dynamiki Newtona

III prawo Newtona — III zasada dynamiki
(zasada akcji i reakcji)

Jeśli ciało A działa na ciało B siłą R ,
to ciało B działa na ciało A siłą kolinearną R



.

A

B

Siły R i R



mają jednakową wartość, wspólną prostą działania

i przeciwne zwroty.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Prawa Newtona — zasady dynamiki Newtona

Prawo powszechnego ciążenia (prawo grawitacji)

Dwa punkty materialne przyciągają się
poprzez siłę grawitacji równą

2

2

1

r

m

m

k

P 

m

1

,

m

2

— masy punktów materialnych,

r —

odległość punktów materialnych,

k —

stała grawitacji,

2

3

11

s

kg

m

10

67

,

6









k

.

m

1

m

2

r

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Prawa Newtona — zasady dynamiki Newtona

Prawo powszechnego ciążenia (prawo grawitacji)

W warunkach ziemskich prawo grawitacji objawia się
siłą ciężkości

G punktu materialnego

g

m

G 

g — przyspieszenie ziemskie,

2

s

m

81

,

9



g

m

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

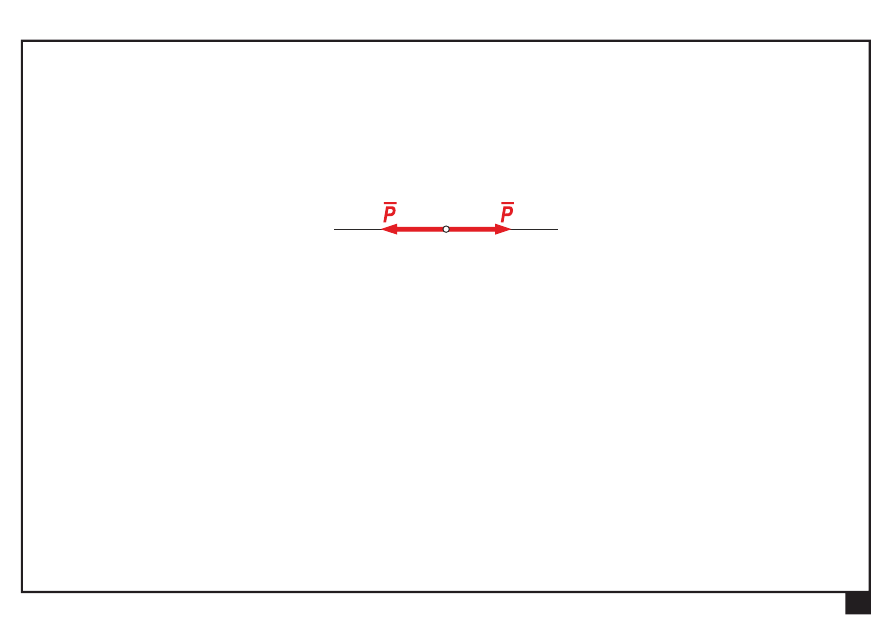
Aksjomaty statyki

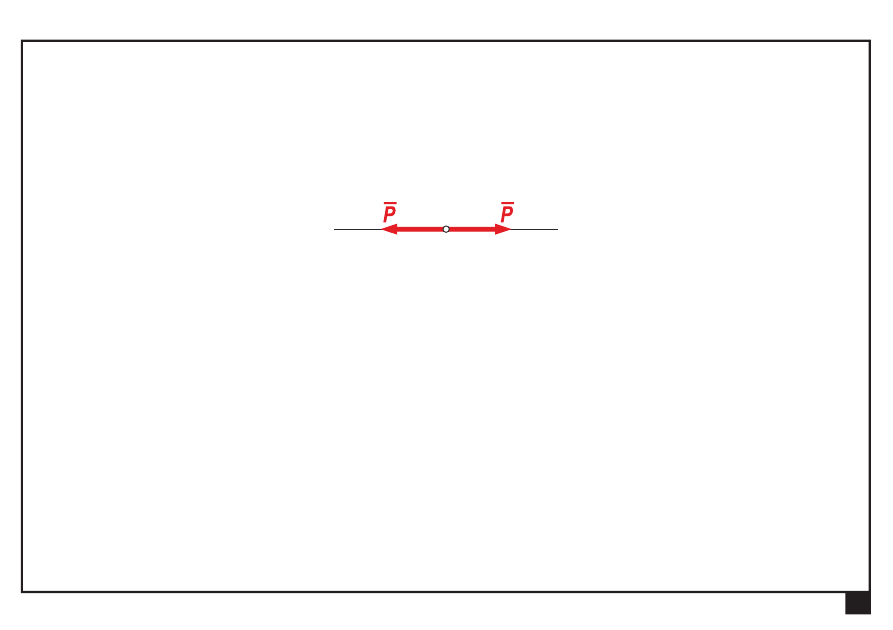
Dwie siły kolinearne, o tej samej wartości i przeciwnych zwrotach
są w równowadze statycznej.

A

u

Układ taki nazywamy

układem zerowym sił

.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Aksjomaty statyki

Dwie siły kolinearne, o tej samej wartości i przeciwnych zwrotach
są w równowadze statycznej.

A

u

Układ taki nazywamy

układem zerowym sił

.

Jeśli do układu obciążeń działających na ciało sztywne
dodamy układ zerowy sił, to skutek działania układu obciążeń
nie zmieni się

.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

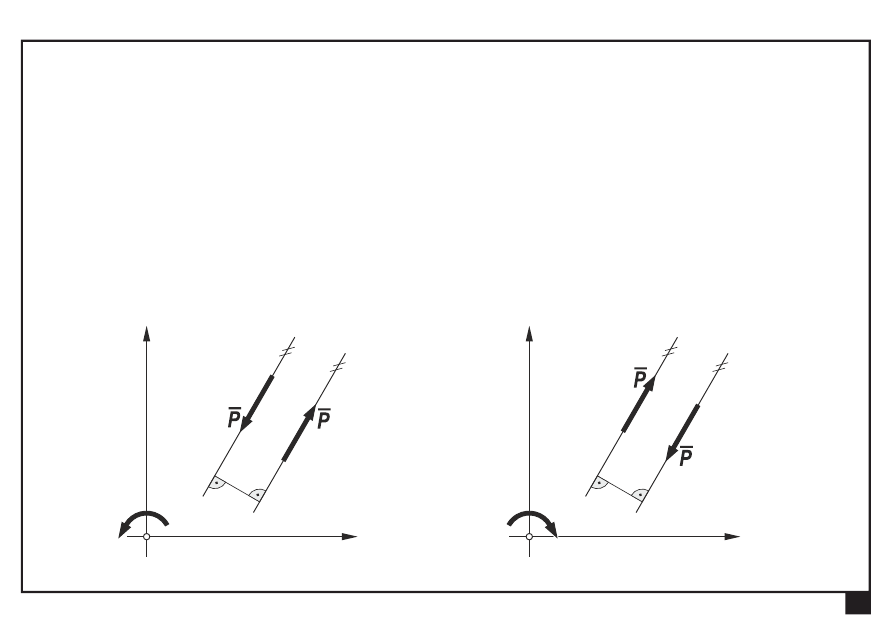
Aksjomaty statyki

Parę sił działającą w płaszczyźnie

xy można zastąpić

momentem

M, który jest wektorem swobodnym,

o zwrocie zgodnym z regułą prawej dłoni,
prostopadłym do płaszczyzny

xy.

Moment ten nazywamy

momentem pary sił

.

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Aksjomaty statyki

Parę sił działającą w płaszczyźnie

xy można zastąpić

momentem

M, który jest wektorem swobodnym,

o zwrocie zgodnym z regułą prawej dłoni,
prostopadłym do płaszczyzny

xy.

Moment ten nazywamy

momentem pary sił

.

a

y

x

( )

z

M

a

y

x

( )

z

M

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

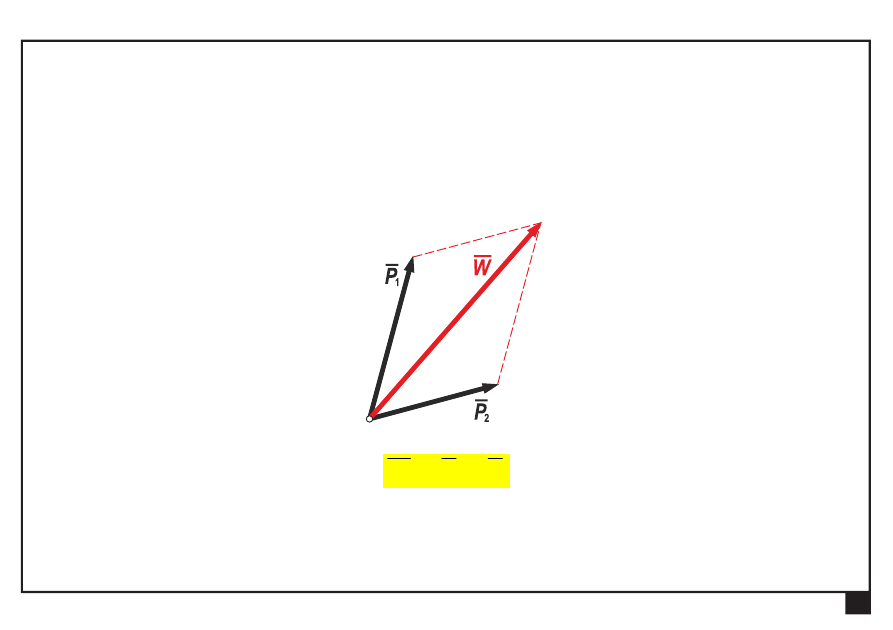
Aksjomaty statyki

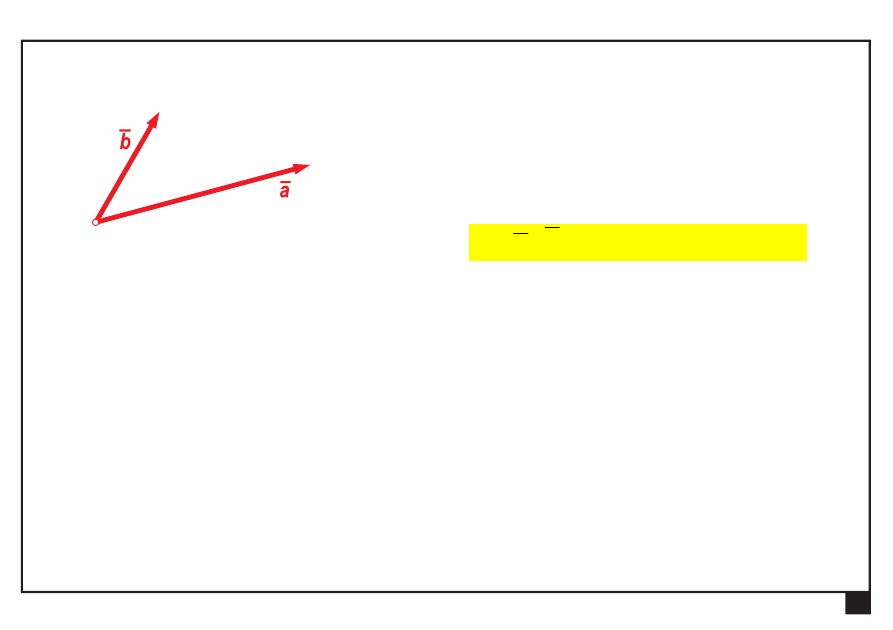
Dwie siły zbieżne

P

1

i

P

2

działające na punkt A można zastąpić

ich wypadkową

W, będącą przekątną równoległoboku

rozpiętego na tych siłach.

A

2

1

P

P

W





Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Aksjomaty statyki

Układ momentów par sił działających w płaszczyźnie

xy

można zastąpić jednym momentem o wartości















m

j

jz

m

j

jz

z

M

M

M

1

1

)

(

y

x

( )

z

M

1

M

2

M

j

M

m

y

x

( )

z

M

z

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

1

Bibliografia

Klasztorny M., Niezgoda T.,

Mechanika ogólna. Podstawy teoretyczne,

zadania z rozwiązaniami, OW PW, Warszawa 2006.
Klasztorny M.,

Mechanika ogólna, DWE, Wrocław 2005.