1

Kodowanie liczb

Kodowanie stałopozycyjne liczb całkowitych

Niech liczba całkowita a ma w systemie dwójkowym postać:





.

...

2

0

1

1

a

a

a

a

a

n

n







Wtedy może być ona przedstawiona w postaci (n+2)-bitowej przy pomocy trzech niżej

zdefiniowanych kodów.

Kod prosty

















jest

liczby

znakiem

gdy

,

....

1

jest

liczby

znakiem

gdy

,

....

0

]

[

0

1

1

0

1

1

a

a

a

a

a

a

a

a

a

n

n

n

n

pr

Kod odwrotny, 1-kod, kod uzupełniony do 1

















,

jest

liczby

znakiem

gdy

,

....

1

jest

liczby

znakiem

gdy

,

....

0

]

[

0

1

1

0

1

1

a

a

a

a

a

a

a

a

a

n

n

n

n

pr

gdzie

i

i

a

a





1

dla

.

,

...

,

1

,

0

n

i



Kod dopełnieniowy, 2-kod, kod uzupełniony do 2























,

jest

liczby

znakiem

gdy

,

01

...

0

....

1

jest

liczby

znakiem

gdy

,

....

0

]

[

razy

1

0

1

1

0

1

1

n

n

n

n

n

odw

a

a

a

a

a

a

a

a

a

gdzie

i

i

a

a





1

dla

.

,

...

,

1

,

0

n

i



Uwaga.

Liczba 0 w kodzie prostym i kodzie odwrotnym jest kodowana jako

0



lub

;

0



w systemie

dopełnieniowym jest ona kodowana tylko jako

.

0



Przykłady.

Zakodujemy podane liczby całkowite przy pomocy 7 bitów.

a)

.

11001

2





a

Mamy

,

011001

2





a

skąd

 

 

 

0011001







dop

odw

pr

a

a

a

b)

.

11001

2





a

Mamy

,

011001

2





a

skąd

 

 

1100111

0000001

1100110

]

[

;

1100110

;

1011001











dop

odw

pr

a

a

a

c)

.

111111

2





a

Wtedy

;

1111111

]

[



pr

a

;

1000000

]

[



odw

a

.

1000001

0000001

1000000

]

[







dop

a

2

d)

.

0

2



a

Jeżeli przyjmiemy, że

,

000000

2





a

to

 

 

 

.

0000000







dop

odw

pr

a

a

a

W kodzie prostym i w kodzie odwrotnym można założyć, że

,

000000

2





a

i wtedy

 

;

1000000



pr

a

 

.

1111111



odw

a

Przykłady

Rozkodujemy przykładowe liczby, tzn. znajdziemy ich reprezentacje dwójkowe na podstawie wartości

ich kodów 7-bitowych.

a)

 

.

1101

001101

0001101

2

2





















a

dop

odw

pr

kod

a

kod

b)

 

.

1

|

110111



kod

a

;

101111

2









a

pr

kod

;

10000

010000

2













a

odw

kod

 

.

10001

010001

1101110

0000001

1101111

2

2





















a

a

dop

kod

odw

c)

 

100

|

1010



kod

a

;

10100

2









a

pr

kod

;

101011

0101011

2

2













a

odw

kod

 

.

101100

1010011

0000001

1010100

2

















a

a

dop

kod

odw

d)

 

1000000



kod

a

;

0

00000

2

2











a

pr

kod

;

111111

2









a

odw

kod

 



















2

111111

0111111

0000001

1000000

a

a

dop

kod

odw

sprzeczność, bo





.

0111111

111111





dop

A więc zgodnie z przyjętym określeniem kodu dopełnieniowego równość nie jest możliwa!. Dlatego

na podstawie dodatkowej umowy przyjmuje się, że





.

1000000

1000000

2





dop

Kodowanie stałopozycyjne a dodawanie i odejmowanie liczb

całkowitych

Dodawanie

Przypadek kodu odwrotnego

Prześledzimy zagadnienie na reprezentatywnych przykładach liczb kodowanych przy pomocy

8 bitów.

Przykłady

a)





1

0

1

1

0

0

1

0

1

0

1

1

0

0

1

0

0

0

0

0

1

0

1

0

1

1

0

1

0

2

2

2



















odw

b

a

b

a

b

a

 

 

 

 

1

0

1

1

0

0

1

0

0

0

0

0

0

1

0

0

1

0

1

1

0

1

0

0









odw

odw

odw

odw

b

a

b

a

3

b)





1

1

0

0

1

0

0

0

1

1

0

0

1

0

0

0

1

0

1

1

0

1

1

0

1

1

0

1

1

2

2

2



















odw

b

a

b

a

b

a

 

 

1

1

0

0

1

0

0

0

1

0

1

0

0

1

0

0

0

1

1

0

1

0

0

1

0

1

1

0

1

1

0

1

1

0





odw

odw

b

a

c)





0

0

1

1

0

1

1

1

1

1

0

0

1

0

0

1

0

1

1

0

1

1

0

1

0

1

1

0

1

2

2

2



















odw

b

a

b

a

b

a

 

 

 

 

0

0

1

1

0

1

1

1

0

1

0

0

1

0

0

1

0

1

0

1

1

0

1

0









odw

odw

odw

odw

b

a

b

a

d)





0

1

0

0

1

1

0

1

1

0

1

1

0

0

1

0

0

0

0

0

1

0

1

0

1

1

0

1

0

2

2

2



















odw

b

a

b

a

b

a

 

 

0

1

0

0

1

1

0

1

1

1

0

0

0

1

1

0

1

1

1

1

1

1

1

0

1

1

0

1

0

0

1

0

1

1





odw

odw

b

a

Wniosek.

Aby otrzymać kod odwrotny sumy dwóch liczb, należy dodać ich kody odwrotne i w

przypadku powstania bitu przepełnienia sumę tę powiększyć o 1.

Przypadek kodu dopełnieniowego

Prześledzimy zagadnienie na reprezentatywnych przykładach liczb kodowanych przy pomocy

8 bitów.

Przykłady

a)





1

0

1

1

0

0

1

0

1

0

1

1

0

0

1

0

0

0

0

0

1

0

1

0

1

1

0

1

0

2

2

2



















dop

b

a

b

a

b

a

 

 

 

 

1

0

1

1

0

0

1

0

0

0

0

0

0

1

0

0

1

0

1

1

0

1

0

0









dop

dop

dop

dop

b

a

b

a

b)





1

1

0

0

1

0

0

0

1

1

0

0

1

0

0

0

1

0

1

1

0

1

1

0

1

1

0

1

1

2

2

2



















dop

b

a

b

a

b

a

 

 

1

1

0

0

1

0

0

0

1

1

0

0

1

0

0

0

1

0

1

1

0

0

1

0

1

1

0

1

1

0

1

1

0





dop

dop

b

a

+

+

odrzucić!

4

c)





1

0

1

1

0

1

1

1

1

1

0

0

1

0

0

1

0

1

1

0

1

1

0

1

0

1

1

0

1

2

2

2



















dop

b

a

b

a

b

a

 

 

 

 

1

0

1

1

0

1

1

1

1

1

0

0

1

0

0

1

0

1

0

1

1

0

1

0









dop

dop

dop

dop

b

a

b

a

d)





1

1

0

0

1

1

0

1

1

0

1

1

0

0

1

0

0

0

0

0

1

0

1

0

1

1

0

1

0

2

2

2



















dop

b

a

b

a

b

a

 

 

1

1

0

0

1

1

0

1

1

1

0

0

1

1

0

1

1

0

0

0

0

0

1

1

1

1

1

0

0

1

0

1

1





dop

dop

b

a

Wniosek.

Aby otrzymać kod dopełnieniowy sumy dwóch liczb, należy dodać ich kody dopełnieniowe

i ewentualny bit przepełnienia odrzucić.

Odejmowanie

Z uwagi na równość

)

( b

a

b

a









odejmowanie może być zastąpione dodawaniem liczby a i liczby przeciwnej do liczby b.

Dlatego powstaje problem uzyskiwania kodu liczby przeciwnej z kodu liczby danej. Prześle-

dzimy zagadnienie na reprezentatywnych przykładach liczb kodowanych przy pomocy 8

bitów.

Przypadek kodu odwrotnego

Przykłady

a)

 

 





1

2

2

0101101

1010010

101101

0101101

101101

dop

odw

odw

a

a

a

a





















b)

 

 





1

2

2

0010010

1101101

010010

0010010

010010

dop

odw

odw

a

a

a

a





















c)

 

 





1

2

2

1011000

0100111

100111

1011000

100111

dop

odw

odw

a

a

a

a





















d)

 

 





1

2

2

1100111

0011000

011000

1100111

011000

dop

odw

odw

a

a

a

a





















odrzucić!

5

Wniosek.

Aby otrzymać kod odwrotny liczby przeciwnej należy obliczyć tzw. dopełnienie do 1 kodu liczby

danej.

Przykłady

Oto przykłady operacji, o której mowa w ostatnim wniosku.

a)





;

1100111

0011000

1



dop

b)





.

0111111

1000000

1



dop

Przypadek kodu dopełnieniowego

Przykłady

a)

 

 





2

2

2

1

|

010110

1010011

101101

0101101

101101

dop

dop

dop

a

a

a

a





















b)

 

 





2

2

2

10

|

00100

1101110

010010

0010010

010010

dop

dop

dop

a

a

a

a





















c)

 

 





2

2

2

1

|

101100

0100111

100111

1011001

100111

dop

dop

dop

a

a

a

a





















d)

 

 





2

2

2

1000

|

110

0011000

011000

1101000

011000

dop

dop

dop

a

a

a

a





















Wniosek.

Aby otrzymać kod dopełnieniowy liczby przeciwnej należy obliczyć tzw. dopełnienie do 2 kodu

liczby danej.

Przykłady

Oto przykłady operacji, o której mowa w ostatnim wniosku.

a)





1101000

1000

|

001

1



dop

Inna metoda:

0

0

0

1

0

1

1

1

1

1

1

0

0

1

1



6

b)





0101001

1

|

101011

2



dop

Inna metoda:

1

0

0

1

0

1

0

1

0

0

0

1

0

1

0



c)





1000000

1000000

|

2



dop

Inna metoda:

0

0

0

0

0

0

1

1

1

1

1

1

1

1

0



Otrzymaliśmy sprzeczność, bo liczba przeciwna do liczby o rozważanym kodzie jest poza zakresem!

Ćwiczenie.

Wykonać poniższe dodawanie i odejmowanie przy pomocy kodu odwrotnego i kodu

dopełnieniowego argumentów tych operacji. Sprawdzić otrzymane wyniki przy pomocy tradycyjnego

dodawania i tradycyjnego odejmowania.

a)



 



.

0101011

1001110

2

2









s

Kod odwrotny





10110001

1001110

2





odw





11010100

0101011

2





odw

.

1111001

0

1

1

0

0

0

0

1

1

1

0

1

0

0

0

0

1

0

0

1

0

1

0

1

1

1

0

0

0

1

1

0

1

2





























s

1

Kod dopełnieniowy





10110010

1001110

2





dop





11010101

0101011

2





dop

.

1111001

1

1

1

0

0

0

0

1

1

1

1

0

0

0

0

1

1

0

1

0

1

0

1

1

0

1

0

0

1

1

0

1

2























s

1

Sprawdzenie

2

2

2

1

0

0

1

1

1

1

1

1

0

1

0

1

0

0

1

1

1

0

0

1







Odrzucić!

+

7

b)



 



.

0101100

1110001

2

2









r

Kod odwrotny





10001110

1110001

2





odw









00101100

11010011

11010011

0101100

1

2









dop

odw

.

1000101

0

1

0

1

1

1

0

1

0

0

1

1

0

1

0

0

0

1

1

1

0

0

0

1

2





















r

Kod dopełnieniowy





10001111

1110001

2





dop









00101100

11010100

11010100

0101100

2

2









dop

dop

.

1000101

1

1

0

1

1

1

0

1

0

0

1

1

0

1

0

0

1

1

1

1

0

0

0

1

2





















r

Sprawdzenie

2

2

2

1

0

1

0

0

0

1

0

0

1

1

0

1

0

1

0

0

0

1

1

1







Kodowanie dwójkowo-dziesiętne

Istota tego systemu polega na kodowaniu przy pomocy 4 bitów każdej cyfry zapisu dziesięt-

nego liczby. Można stworzyć wiele systemów tego typu, ale w praktyce stosuje się kod BCD (Binary

Coded Decimal) zwany także kodem 8-4-2-1, kod Aikena zwany także kodem 2-4-2-1 i kod z nad-

miarem 3, oznaczany dalej symbolem +3.

Oto definicja tych systemów:

Cyfra

dziesiętna

Kod 8-4-2-1

Kod 2-4-2-1

Kod +3

0

0000

0000

0011

1

0001

0001

0100

2

0010

0010

0101

3

0011

0011

0110

4

0100

0100

0111

5

0101

1011

1000

6

0110

1100

1001

7

0111

1101

1010

8

1000

1110

1011

9

1001

1111

1100

Przykład





;

0000

|

0111

|

1001

|

1000

|

0001

18970

1

2

4

8













;

0000

|

1101

|

1111

|

1110

|

0001

18970

1

2

4

2













.

0011

|

1010

|

1100

|

1011

|

0100

18970

3





8

Ćwiczenie

Zakodować przy pomocy 16 bitów poniższe liczby dziesiętne:

a)

.

7925

Rozwiązanie.





;

0101

|

0010

|

1001

|

0111

7925

1

2

4

8













;

1011

|

0010

|

1111

|

1101

7925

1

2

4

2













.

1000

|

0101

|

1100

|

1010

7925

3





b)

.

0348

348



Rozwiązanie.





;

1000

|

0100

|

0011

|

0000

0348

1

2

4

8













;

1110

|

0100

|

0011

|

0000

0348

1

2

4

2













.

1011

|

0111

|

0110

|

0011

0348

3





Ćwiczenie

Rozkodować liczby dziesiętne zakodowane przy pomocy 16 bitów:

a)

 

.

1011

|

1100

|

0100

|

0011



kod

x

Rozwiązanie.

ć!

sprzecznoś

)

11

)(

12

(

34

"

1

2

4

8

"















x

kod

3465

"

1

2

4

2

"













x

kod

.

0198

"

3

"









x

kod

b)

 

.

0011

|

1000

|

0111

|

1001



kod

x

Rozwiązanie.

9783

"

1

2

4

8

"













x

kod

ć!

sprzecznoś

3723

"

1

2

4

2

"















x

kod

.

6450

"

3

"









x

kod

Kodowanie zmiennopozycyjne liczb rzeczywistych

Jeżeli ustalona jest podstawa systemu liczbowego

,

2



p

to każda liczba rzeczywista a może

być zapisana przy pomocy tzw. notacji naukowej w postaci:

,

c

p

m

a







gdzie współczynnik m nazywa się mantysą, a wykładnik c będący liczbą całkowitą – cechą liczby a.

Zakładać będziemy, że część ułamkowa mantysy ma rozwinięcie skończone, co oznacza, że opisana

reprezentacja niekiedy przedstawia liczbą a w sposób przybliżony.

Ponieważ notacja naukowa nie jest jednoznaczna, więc w przypadku, gdy

,

0



a

częstą

stosuje się tzw. notację znormalizowaną polegającą na tym, że m oraz c są tak dobrane,

aby





,

..

.

0

2

1

p

k

m

m

m

m



przy czym

.

0

1



m

Gwarantuje to zachodzenie nierówności

.

1

1





m

p

Innym stosowanym warunkiem normalizacyjnym jest przedstawianie m w postaci





,

..

.

1

2

1

p

k

m

m

m

m



tak, aby zachodziła nierówność

.

1

p

m





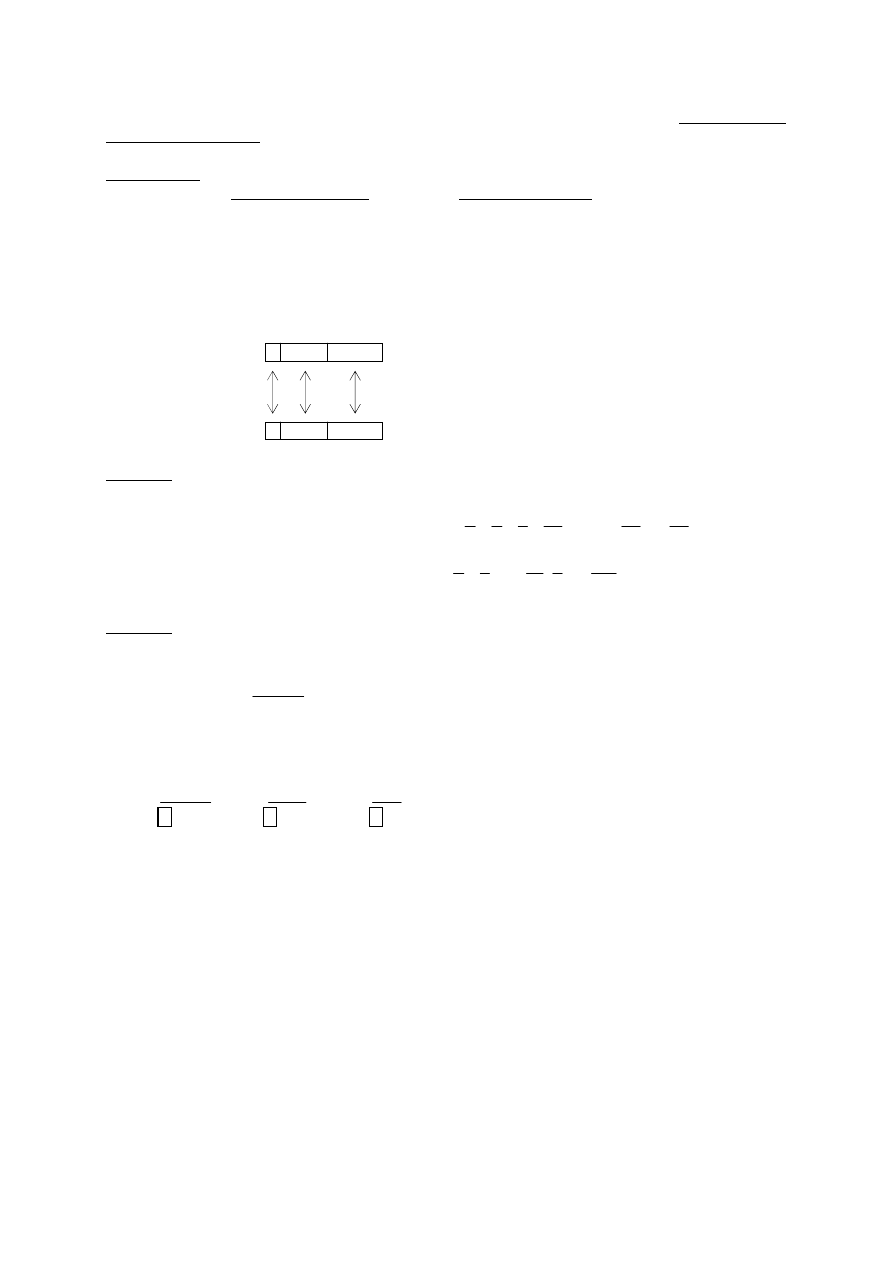
9

Opisane niżej systemy kodowania liczb rzeczywistych zwane reprezentacjami

zmiennoprzecinkowymi w sposób istotny wykorzystują opisane notacje naukowe.

Standard IBM.

Występuje tu tzw. reprezentacja krótka 32-bitowa i reprezentacja długa 64-bitowa. Jeżeli kodowana

liczba rzeczywista a nie jest zerem, to daje się ona przedstawić w postaci

,

)

.

0

(

16

)

1

(

2

64

M

a

C

S











gdzie parametr S równy 0 lub 1 określa znak liczby a, parametr C nazywa się charakterystyką a

parametr M jest częścią ułamkową wyrażonej w systemie dwójkowym mantysy liczby a. Jeżeli C

zostanie przedstawione w systemie dwójkowym przy pomocy 7 bitów, to liczba a jest kodowana w na-

stępujący sposób:

Reprezentacja krótka:

31

8

7

1

0





Reprezentacja długa:

63

8

7

1

0





Przykłady

Rozkodujemy liczby zmiennoprzecinkowe zakodowane w standardzie IBM.
a)

 

.

5

.

15

2

29

32

29

16

32

1

8

1

4

1

2

1

16

)

1

(

0

...

111010

|

1000001

|

0

64

65

0













































IBM

a

b)

 

.

0390625

.

0

128

5

8

5

16

1

8

1

2

1

16

)

1

(

0

...

10100

|

0111111

|

1

64

63

1

























 













IBM

a

Przykłady

Zakodujemy liczbę w standardzie IBM.

a)

,

111

.

0

16

)

1

(

875

.

0

16

16

917504

16

917504

2

64

69

1

5

5

5



























a

gdyż

0

5

7

.

1

2

5

7

8

.

0



0

5

.

1

2

5

7

.

0



0

.

1

2

5

.

0



Ponadto

2

0

1

2

3

4

5

6

1000101

2

1

2

0

2

1

2

0

2

0

2

0

2

1

1

4

64

69





































i dlatego

 

0

...

1110

|

1000101

|

1



IBM

a

b)

2

64

0

0

...

0

.

0

16

0











a

i dlatego

 

0

...

00

|

000000

|

0



IBM

a

S

C

M

10

Standard IEEE

Tu również występuje reprezentacja krótka 32-bitowa i reprezentacja długa 64-bitowa. Na potrzeby

tej pierwszej przedstawiamy liczbę

0



a

w postaci

 

2

127

.

1

2

)

1

(

F

a

E

S











(symbole E oraz F oznaczają pewne liczby naturalne a nie cyfry sytemu pozycyjnego) i definiujemy

reprezentację w następujący sposób zakładając, że E jest wyrażone w systemie dwójkowym:

31

9

8

1

0





W przypadku reprezentacji długiej punktem wyjścia jest przedstawienie

 

2

1023

.

1

2

)

1

(

F

a

E

S











a kod ma postać

63

12

11

1

0





Przykłady. Rozkodujemy liczby zmiennoprzecinkowe zakodowane w systemie krótkim IEEE.

a)

 

.

1

0

.

1

2

)

1

(

0000

0000

0000

0000

0000

000

|

1

1111

011

|

0

800000

3

2

127

127

0

16



















F

a

IEEE

b)

 

.

1

0

.

1

2

)

1

(

0000

0000

0000

0000

0000

000

|

1

1111

011

|

1

800000

127

127

1

16



















BF

a

IEEE

c)

 

















2

127

128

0

16

1001

.

1

2

)

1

(

0000

0000

0000

0000

1000

100

|

0

0000

100

|

0

40480000

IEEE

a

.

125

.

3

8

1

3

001

.

11

2







Przykład. Zakodujemy liczbę

25

.

30





a

w krótkim systemie IEEE. Mamy

















































2

2

1

0

1

2

3

4

01

.

11110

2

1

2

0

2

0

2

1

2

1

2

1

2

1

25

.

30

a

,

111001

.

1

2

)

1

(

111001

.

1

2

2

127

131

1

4















oraz

.

10000011

2

1

2

1

2

0

2

0

2

0

2

0

2

0

2

1

1

2

128

131

2

0

1

2

3

4

5

6

7









































Stąd

 

.

20000

1

0

...

00

|

0010

|

1111

|

0001

|

1100

16

F

C

a

IEEE





Przykład. Rozkodujemy liczbę zmiennoprzecinkową a zakodowaną w systemie długim IEEE.

Niech

 

.

0

...

0000

1110

|

0011

0000

100

|

1

0

...

0

03

16

12











razy

IEEE

E

C

a

Stąd

.

30

)

2

4

8

16

(

11110

111

.

1

2

111

.

1

2

)

1

(

2

2

4

2

1023

1027

1



































a

S

E

F

S

S

E

F

S

11

Przykład. Zakodujemy liczbę

625

.

7



a

w długim kodzie IEEE.

Mamy







































2

101

.

111

8

1

2

1

1

2

4

8

1

4

8

16

32

8

61

8

5

7

40

25

7

1000

625

7

a

,

2

1023

1025

0

2

2

11101

.

1

2

)

1

(

11101

.

1

2













przy czym

.

0001

0000

100

1

1024

1025

2







Stąd

 

.

0000

0000

8000

401

0

...

0

|

1000

|

1110

|

0001

|

0000

|

0100

16

E

a

IEEE





Uwaga. W przypadku standardu IEEE, zarówno krótkiego jak i długiego, następujące przypadki

szczególne wymagają wyjaśnienia.

a) Jeżeli

0

...

0



E

oraz

,

0

...

0



F

to a jest najmniejszą liczbą, co do wartości bezwzględnej, którą

można w danym systemie zakodować i dlatego przyjmuje się w zależności od tego, czy bit S jest

zerem, czy jedynką, że jest to reprezentacja 0



albo 0



.

b) Jeżeli

1

...

1



E

oraz

,

0

...

0



F

to czynnik

127

2



E

albo

1023

2



E

osiąga największą możliwą

wartość i dlatego przyjmuje się w zależności od tego, czy bit S jest zerem, czy jedynką, że jest to

reprezentacja





albo





.