
Instytut Badań Systemowych Polskiej Akademii Nauk
mgr inż. Marcin Jaruszewicz
Neuro-genetyczny system komputerowy
do prognozowania zmiany indeksu giełdowego
Rozprawa Doktorska
promotor: dr hab. inż. Jacek Mańdziuk, prof. PW
Wydział Matematyki i Nauk Informacyjnych
Politechniki Warszawskiej
Warszawa, 2007 r.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
2
Spis treści
1.
Wprowadzenie .................................................................................................................................... 3
1.1.
Cel i zakres badań .......................................................................................................................... 3
1.2.
Hipotezy badawcze ....................................................................................................................... 4
1.3.
Treść rozprawy ............................................................................................................................... 5
2.
Wprowadzenie do giełdy .................................................................................................................. 7
2.1.
Giełda i jej podstawowe zasady ................................................................................................... 7
2.2.
Zachowanie inwestorów ............................................................................................................. 10
2.3.
Analiza fundamentalna ............................................................................................................... 11
2.4.
Analiza techniczna ....................................................................................................................... 12
3.
Metody numeryczne oraz metody inteligencji obliczeniowej w prognozie giełdy .............. 20
3.1.
Zastosowanie sieci neuronowych w prognozie ....................................................................... 20
3.2.
Algorytm genetyczny i jego wybrane zastosowania ............................................................... 22
3.3.
Prognoza wskaźników giełdowych w literaturze ................................................................... 23
4.
Wstępny opis proponowanego systemu ....................................................................................... 29
4.1.
Dane wejściowe ............................................................................................................................ 29
4.2.
Algorytm genetyczny .................................................................................................................. 32
4.3.
Sieć neuronowa ............................................................................................................................ 35
4.4.
Cel prognozy i miara sukcesu .................................................................................................... 40
5.
Przekształcenia danych .................................................................................................................... 41
5.1.
Przekształcenia danych źródłowych ......................................................................................... 41
5.2.
Oscylatory ..................................................................................................................................... 42
5.3.
Kodowanie sygnałów kupna i sprzedaży ................................................................................. 46
5.4.
Algorytm wyznaczania formacji ................................................................................................ 47
5.5.
Kodowanie informacji o formacji ............................................................................................... 50
6.
Wybór danych wejściowych ........................................................................................................... 52
6.1.
Dziedzina zmiennych wejściowych........................................................................................... 52
6.2.
Korelacja miedzy zmiennymi ..................................................................................................... 55
6.3.
Wybór zmiennych do nauki i prognozy ................................................................................... 58
7.
Implementacja systemu ................................................................................................................... 60
7.1.
Implementacja algorytmu genetycznego .................................................................................. 60
7.2.
Implementacja sieci neuronowej ................................................................................................ 69
8.
Definicja eksperymentu .................................................................................................................. 71
8.1.
Mierniki jakości prognozy .......................................................................................................... 71
8.2.
Scenariusz eksperymentu ........................................................................................................... 73
8.3.
Ustawienia parametrów systemu .............................................................................................. 74
8.4.
Algorytmy testowe ...................................................................................................................... 76
9.
Charakterystyka działania systemu............................................................................................... 79
9.1.
Rozwój populacji .......................................................................................................................... 79
9.2.
Charakterystyka preferowanych zmiennych ........................................................................... 91
9.3.
Możliwość nauki sieci neuronowej ............................................................................................ 95
10.
Wyniki eksperymentów .................................................................................................................. 97
10.1.
Wyniki jakościowe .................................................................................................................. 97
10.2.
Wyniki finansowe – podstawowy eksperyment ................................................................. 98
10.3.
Analiza liczby realizowanych transakcji ............................................................................ 102
10.4.
Analiza statystyczna działania algorytmu opartego o losowe sygnały ......................... 103
10.5.
Weryfikacja wpływu zmienności zależności ..................................................................... 104
10.6.
Weryfikacja powtarzalności wyników ............................................................................... 107
10.7.
Weryfikacja stabilności wyników ....................................................................................... 109
10.8.
Analiza uwzględnienia kosztów transakcji ....................................................................... 110
11.
Podsumowanie i wnioski .............................................................................................................. 112

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
3
1.
Wprowadzenie
1.1.
Cel i zakres badań
Przedmiotem przedstawionych badań jest prognoza szeregu czasowego
skonstruowanego z kolejnych procentowych zmian wartości indeksu DAX niemieckiej
giełdy GSE. Zmiany wartości indeksu zależą od wielu czynników, zarówno
mierzalnych jak i niemierzalnych. Zastosowane metody inteligencji obliczeniowej
pozwalają na odkrycie i uwzględnienie zależności między poszczególnymi zmiennymi
opisującymi sytuację na giełdzie. Zależności te nie mają charakteru stałego. Wpływ
poszczególnych zmiennych na prognozowaną wartość indeksu giełdowego zmienia się
w czasie. Zaproponowany system neuro-genetyczny dokonuje ponownego, w
kolejnych okresach, dopasowania parametrów wejściowych w celu uzyskania
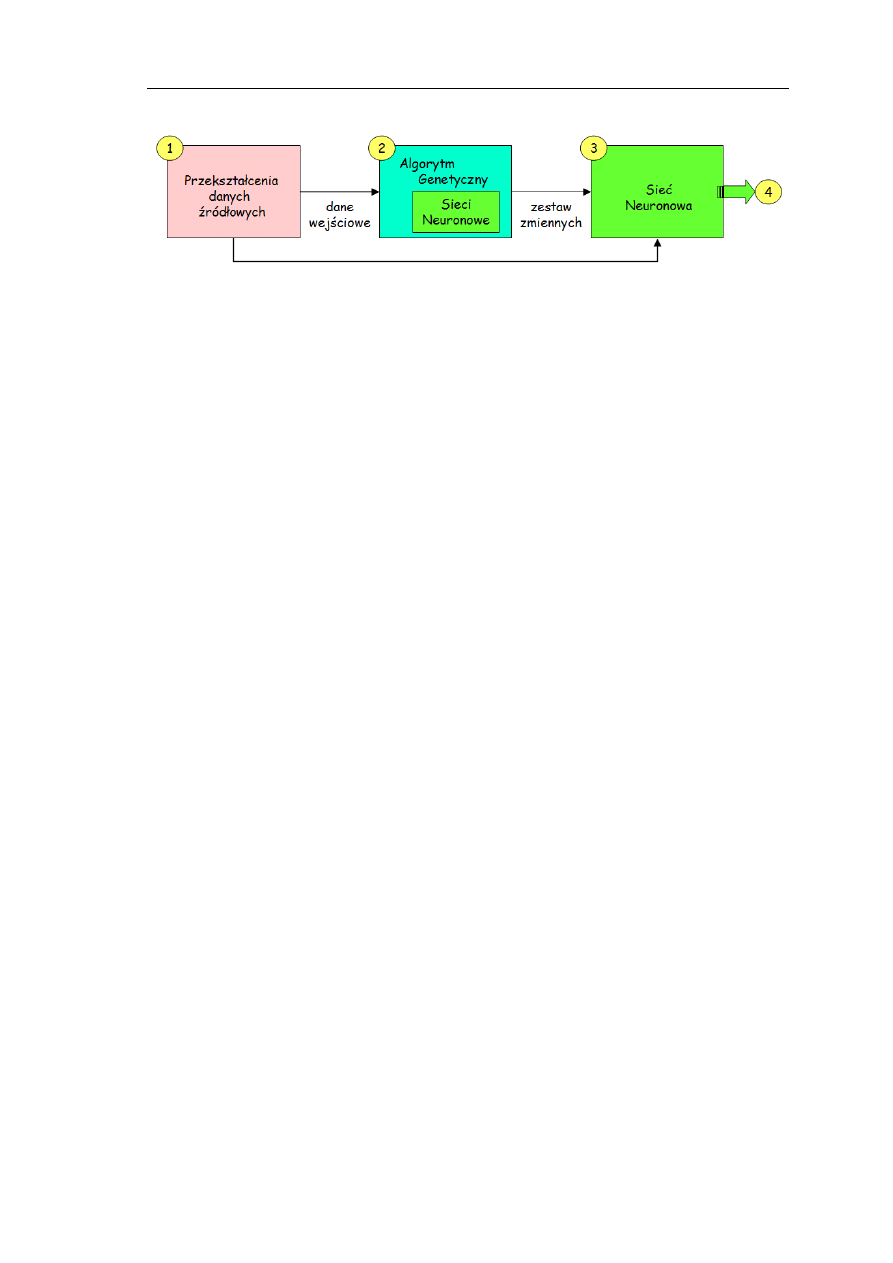
możliwie najlepszej prognozy. Schemat przedstawiający podstawowe kroki działania
systemu prezentuje Diagram 1.
Pierwszym krokiem jest skonstruowanie zbioru parametrów opisujących
aktualną sytuację na giełdzie. Do tego celu wykorzystywane są przekształcenia
zdefiniowane w analizie technicznej, jednej z dwóch podstawowych teorii
uzasadniających wartość i opisujących zachowanie indeksu giełdowego oraz cen akcji.
W drugim etapie eksperymentu spośród dostępnych zmiennych, ograniczonych
wstępną preselekcją, wybierane są te, dla których skuteczność nauki jest największa w
zadanym horyzoncie czasu. Wyboru zmiennych dokonuje algorytm genetyczny.
Operatory genetyczne modyfikują populację chromosomów, z których każdy definiuje
zbiór zmiennych wejściowych dla sieci neuronowej. W kolejnym, trzecim etapie sieć
neuronowa wybrana w wyniku działania algorytmu genetycznego uczona jest metodą
propagacji wstecznej z momentem. Nauczona sieć neuronowa wykorzystywana jest do
prognozy indeksu giełdowego (krok 4). Przedstawiony schemat powtarza się wraz z
kolejnymi 5-dniowymi okresami czasu, w których konstruowana jest nowa sieć
neuronowa.
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
4
Diagram 1.
Schemat działania systemu neuro-genetycznego
Do weryfikacji skuteczności prognozy zaproponowany został uproszczony
model inwestycyjny. Hipotetyczne zyski osiągane przez opisywany system
porównywane są z wynikami uzyskanymi w oparciu o wybrane heurystyki. W
zdefiniowanym modelu osiągnięty został wynik od 9% do 15% wyższy od uzyskanego
przy pomocy strategii „kupuj i trzymaj”, której to wynik jest proporcjonalny do
zmiany indeksu w zadanym okresie testu. W wybieranych zmiennych widoczny jest
udział oscylatorów znanych z analizy technicznej w preferowanych przez algorytm
zmiennych. Oscylatory są stosowane w codziennej pracy analityków giełdowych.
Postulowana zmienność zależności między parametrami jest również widoczna w
doborze oscylatorów. Potwierdzona została istotność zmiennych opisujących inne od
prognozowanej giełdy (japoński indeks NIKKEI oraz amerykański indeks Dow Jones -
DJIA) oraz wskaźniki kursów walut (EUR/USD oraz USD/JPY).
1.2.
Hipotezy badawcze
Poza głównym celem badań jakim jest zbadanie skuteczności metody neuro-
genetycznej w prognozowaniu zmiany wartości indeksu giełdowego w ciągu jednego
dnia sformułowane zostały dodatkowe hipotezy badawcze.
Hipoteza 1:
Pierwsza hipoteza mówi o niestałości w czasie zależności
między zmiennymi opisującymi prognozowaną giełdę. Przesłanką do tej hipotezy jest
praktyka, z której wynika, że nawet najlepszy w danej chwili wskaźnik stosowany w
prognozie stosunkowo szybko przestaje generować poprawne sygnały. Konieczne jest
wtedy znalezienie innego wskaźnika, który będzie wykorzystywany do momentu
wyczerpania swojej skuteczności. Drugą przesłanką jest złożoność problemu prognozy

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
5
wartości indeksu giełdowego oraz trudność w uzyskaniu pozytywnych wyników przy
wykorzystaniu statycznych reguł. Hipoteza została zweryfikowana eksperymentalnie
poprzez wykonanie prognoz na podstawie zmiennych wybranych dla wcześniejszego
okresu czasu niż najbliższy prognozie. Pokazana została różnica w wyniku uzyskanym
przez tak zmodyfikowany system w stosunku do jego podstawowej wersji.
Hipoteza 2:
W komentarzach analityków dotyczących zachowania indeksów
na giełdach widoczne są wzajemne zależności pomiędzy rynkami. Informacje o
istotnych zmianach na głównych giełdach powodują analogiczny ruch cen na
pozostałych parkietach. Wobec łatwości przepływu informacji pomiędzy maklerami
oraz międzygiełdowych transakcji giełdy stanowią system naczyń połączonych.
Uwzględniając wskazane obserwacje postawiona została druga hipoteza badawcza.
Zakłada ona, że uzasadnione jest wykorzystanie informacji pochodzących spoza giełdy
prognozowanej. Hipoteza ta została potwierdzona poprzez analizę proponowanych
przez algorytm genetyczny zmiennych. Pokazane zostały istotne preferencje
zmiennych spoza prognozowanej giełdy.
1.3.
Treść rozprawy
Treść dokumentu ukierunkowana została na przedstawienie wyników
eksperymentów stanowiących podsumowanie badań objętych zakresem rozprawy
doktorskiej. W pierwszej kolejności przedstawiony został kontekst badań. Poświęcony
temu jest Dział A. W pierwszych rozdziałach opisane są podstawowe pojęcia związane
z giełdami kapitałowymi i towarowymi. Wskazane zostały odniesienia do bieżących
publikacji bezpośrednio związanych z tematem pracy. Przedstawione zostały
podstawowe założenia działania algorytmu genetycznego oraz sieci neuronowej.
Kolejny dział poświęcony został opisowi zrealizowanej implementacji
przedstawionych
wcześniej
przekształceń
danych
oraz
metod
inteligencji
obliczeniowej. Główny nacisk został położony na opis algorytmu genetycznego oraz na
sposób jego zastosowania do doboru zestawu zmiennych. Optymalny zestaw
zmiennych, który wykorzystuje sieć neuronowa jest kluczowym elementem
proponowanego systemu neuro-genetycznego.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
6
Po wprowadzeniu w kontekst badań oraz opisie realizacji systemu,
przedstawione zostały wyniki eksperymentów potwierdzających skuteczność neuro-
genetycznego podejścia do prognozy oraz weryfikujących postawione hipotezy.
Definicje eksperymentów oraz analiza wyników znajdują się w ostatnim, trzecim
dziale rozprawy.
Istotne informacje natury technicznej zostały umieszczone w załącznikach. Jest to
lista zmiennych wykorzystywanych w systemie, zestawy zmiennych wybierane przez
algorytm genetyczny oraz podstawowy opis techniczny systemu.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
7
Teoria i zastosowania
Implementacja
Wyniki badań
Dział A.
Teoria i zastosowania
W poniższych rozdziałach przedstawiony został
kontekst badań będących tematem rozprawy.
Opisane zostały pojęcia oraz mechanizmy
rynków finansowych. Zaprezentowany został
również cel oraz ogólny zakres badań.
2.
Wprowadzenie do giełdy
2.1.
Giełda i jej podstawowe zasady
„Giełdą papierów wartościowych są regularne, odbywające się w określonym
czasie i miejscu, podporządkowane określonym normom i zasadom, spotkania osób
pragnących zawrzeć umowę kupna-sprzedaży oraz osób pośredniczących w
zawieraniu transakcji, których przedmiot stanowią zamienne papiery wartościowe,
przy czym ceny owych transakcji ustalone są na podstawie układu podaży i popytu, a
następnie podawane do wiadomości publicznej”.
Powyższa definicja podana przez A. Dorosza i M. Puławskiego (Dorosz,
Puławski 1991) opisuje dzisiejszy wizerunek giełdy. Początki tej instytucji sięgają
jednak czasów starożytnych. Pierwowzorem giełdy były jarmarki, gdzie handlowano
różnego rodzaju towarami. Z czasem okazało się korzystne dokonywanie transakcji
bez przywożenia na targowisko sprzedawanych artykułów. Wymagało to budowania
zaufania pomiędzy stronami. Był to zalążek giełdy towarowej. Giełdy kapitałowe mają
swój rodowód w handlu wekslami, w późniejszym czasie udziałami w firmach. Od
roku 1667 rozpoczął się proces regulowania handlu na giełdzie. Kupieckie
Dyrektorium w Zurychu ustaliło regulamin oraz obowiązek rejestracji dla
pośredników, tzw. brokerów. Dalsze działania wzmacniające bezpieczeństwo oraz
swobodę transakcji doprowadziły do dzisiejszego obrazu giełdy.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
8
Teoria i zastosowania
Implementacja
Wyniki badań
Oprócz organizacji giełda charakteryzuje się wyraźnie zdefiniowanymi grupami
uczestników (Dębski 2005). Są to przede wszystkim maklerzy. Maklerem jest osoba
zawodowo zajmująca się pośredniczeniem w zawieranych transakcjach, działająca w
imieniu dużych podmiotów występujących na parkiecie. Specyficznym typem w
obrębie tej grupy są maklerzy kursowi. Nie działają oni w imieniu konkretnego
podmiotu ani własnym. Zajmują się ustaleniem optymalnego dla wszystkich kursu
walut lub walorów, a tym samym pracują w interesie ogólnym uczestników giełdy.
Odrębną grupę graczy stanowią maklerzy samodzielni. Są to osoby dopuszczone do
obrotu giełdowego, działające we własnym imieniu.
Transakcje na giełdzie (Dębski 2005) mogą dotyczyć obrotu towarami (giełdy
towarowe) lub papierami udziałowymi i wierzytelnościowymi (giełdy papierów
wartościowych). Towarem najczęściej są płody rolne, surowce mineralne i metale
szlachetne. Papierem udziałowym są akcje. Potwierdzają one prawo współwłasności w
spółce akcyjnej. Akcje posiadają trzy, najczęściej różne ceny. Cena nominalna wynika z
równego podziału części majątku spółki na wszystkie emitowane akcje. Jest to wartość
wyjściowa akcji. Cena, po jakiej akcje są wprowadzane do obiegu to cena emisyjna.
Może być ona wyższa od ceny nominalnej. W trakcie obrotu akcjami na giełdzie
wartość akcji jest reprezentowana przez cenę rynkową. Wynika ona wprost z prawa
popytu i sprzedaży. Papierami wartościowymi wierzytelnościowymi są obligacje.
Poświadczają one zobowiązanie dłużne podmiotu wobec posiadacza dokumentu
obligacji. Obligacje posiadają cenę nominalną oraz aktualną cenę rynkową w obrocie
giełdowym. Dodatkowym atrybutem obligacji, który nie występuje w akcjach jest
termin wykupu. Jest to określona przyszła data, w której obligacja powinna być
wykupiona po cenie nominalnej przez podmiot, który ją wyemitował.
Na giełdzie wyróżnione zostały dwa rodzaje transakcji. Charakteryzuje je
długość czasu realizacji liczonego od momentu zawarcia transakcji. Są to transakcje
natychmiastowe oraz terminowe. Pierwszy typ transakcji opisuje zawarcie umowy
kupna-sprzedaży z równoczesnym przekazaniem nabywanych praw. Drugi typ, to
transakcje terminowe, które wiążą się z opóźnieniem realizacji w stosunku do
momentu zawarcia transakcji. Transakcje te dotyczą dostarczenia w konkretnym czasie

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
9
Teoria i zastosowania
Implementacja
Wyniki badań
w przyszłości określonej ilości dobra o znanej jakości. Transakcje terminowe dzielą się
na dwie grupy: bezwarunkowe i warunkowe. Pierwsza z nich nakłada na strony
obowiązek zrealizowania zawartej transakcji. W skład tej grupy wchodzą kontrakty
forward i futures. Reprezentantem drugiej grupy są opcje, które dają nabywcy prawo
wyboru zrealizowania transakcji lub wycofania się z niej.
Kontrakty forward i futures zobowiązują obie strony do wykonania
zobowiązania kupna-sprzedaży w określonym czasie. W przypadku kontraktów
futures istnieje możliwość rozliczenia na zasadzie zawarcia transakcji przeciwstawnej
bez konieczności dostarczania zakupionego dobra. Kontrakty forward najczęściej
dotyczą handlu towarami. Kontrakty futures są z reguły kontraktami finansowymi.
Opcje różnią się od kontraktów bezwarunkowych możliwością nieskorzystania z
realizacji transakcji. Decyzję podejmuje nabywca na podstawie aktualnej ceny oraz
własnej kalkulacji opłacalności. Opcja może być zrealizowana w dowolnym momencie
od zawarcia transakcji (typ amerykański) lub w zdefiniowanym terminie wygaśnięcia
(typ europejski). Za możliwość podjęcia tej decyzji nabywca płaci sprzedającemu
premię, która nie podlega zwrotowi. Opcje dotyczą wyłącznie rynku finansowego.
Transakcje są dokonywane na papierach wartościowych lub wcześniej zdefiniowanych
kontraktach terminowych.
Wyznaczanie bieżących cen walorów oraz dokonywanie transakcji odbywa się w
trakcie sesji. Sesja giełdowa w większości przypadków dzieli się na pięć faz
(Sopoćko 2005). W pierwszej fazie, jeszcze przed rozpoczęciem właściwej sesji,
zbierane są zlecenia od inwestorów. Obecnie zlecenia najczęściej są zapisywane w
formie elektronicznej. Otwarcie sesji rozpoczyna się od tzw. pierwszego fixingu, czyli
wyliczenia na podstawie złożonych zleceń cen otwarcia walorów. W trakcie trwania
sesji, w fazie obrotów ciągłych zlecenia są realizowane tak szybko, jak to jest możliwe.
Jeżeli natychmiastowa realizacja zlecenia nie jest możliwa, zapisywane są one w
specjalnym arkuszu zleceń. Realizacja oczekujących zleceń ma miejsce w kolejności
zależnej od ceny. Zlecenia z korzystną ceną (niższą przy sprzedaży, wyższą przy
zakupie) są realizowane w pierwszej kolejności. Na zakończenie sesji wyliczane są
ceny zamknięcia walorów. Jest to tzw. drugi fixing. W ostatniej fazie, już po

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
10
Teoria i zastosowania
Implementacja
Wyniki badań
faktycznym zamknięciu sesji przyjmowane są zlecenia na dzień następny.
Wykonywane są też szczegółowe czynności kontrolne.
Złożenie zlecenia kupna-sprzedaży może występować w różnych wariantach
zależnych od oczekiwanej przez zlecającego ceny. Podstawowy typ zlecenia, to kupno
lub sprzedaż „po każdej cenie”. Oznacza ono chęć realizacji transakcji po cenie bieżącej
lub wyliczonej w czasie fixingu. Jest to najbardziej popularny typ zleceń. Kolejny typ,
to „zlecenia z limitem ceny”. Pozwala on na określenie przez inwestora brzegowej
ceny, na którą może się zgodzić. Zlecenie oczekuje na realizację do momentu
osiągnięcia przez walor tej ceny. Z kolei typ zlecenia stop-loss pozwala na wycofanie
się z transakcji w przypadku niekorzystnej dla inwestora zmiany ceny. W
przeciwieństwie do zlecenia z limitem ceny transakcja powinna być zrealizowana jak
najszybciej, zanim warunki nie zmienią się na niekorzystne dla inwestora. Połączeniem
obu opisanych wcześniej zleceń jest zlecenie typu stop-limit. Pozwala ono na
zdefiniowanie obu granic ceny waloru, przez co inwestor ma pewność realizacji
transakcji w ściśle przez niego zdefiniowanym przedziale. Wśród mniej popularnych
typów zleceń znajdują się między innymi transakcje z zapewnieniem jej
niepodzielności w przypadku braku możliwości realizacji całego zlecenia oraz zlecenia
do realizacji w pierwszym lub ostatnim fixingu.
2.2.
Zachowanie inwestorów
Inwestorzy giełdowi działają w celu uzyskania zysku z zawieranych transakcji,
dbając jednocześnie o zachowanie akceptowalnego poziomu ryzyka. Cel ten jest
możliwy do realizacji na różne sposoby. Wyróżnione zostały trzy główne strategie
inwestorów (Dębski 2005). Największy zysk przynosi spekulacja wykorzystywana w
operacjach na kontraktach terminowych. Inwestor wykorzystuje zmianę ceny w
okresie od zawarcia kontraktu do jego realizacji. Powodzenie tej strategii zależy od
skuteczności przewidywania kierunku zmiany ceny waloru. Charakteryzuje się
znacznym poziomem ryzyka, ale jednocześnie nie wymaga zaangażowania dużego
kapitału. Konieczne jest jedynie wpłacenie depozytu zabezpieczającego, który
najczęściej wynosi kilka procent wartości transakcji. Odmienną strategią jest arbitraż.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
11
Teoria i zastosowania
Implementacja
Wyniki badań
Inwestor stosujący tę strategię stara się wykorzystać różnice w cenie tego samego
waloru na różnych giełdach lub w obrębie różnych kontraktów terminowych.
Możliwość wykorzystania arbitrażu jest w dzisiejszych czasach rzadka z powodu
sprawnego przepływu informacji. Również mechanizmy giełdy dążą do minimalizacji
sytuacji pozwalających na arbitraż. Strategia ta jest związana z niewielkim ryzykiem.
Jednocześnie w przypadku zainwestowania znaczących środków możliwy jest do
osiągnięcia duży zysk. Uzupełnieniem powyższych dwóch strategii osiągania zysku
jest hedging, czyli transakcje zabezpieczające. Ich celem jest zmniejszenie ryzyka
wynikającego z nieprzewidzialnych zmian cen. W tej strategii stosuje się kontrakty
terminowe futures do zapewnienia realizacji zleceń po ustalonej cenie. Opisane
powyżej strategie pozwalają na operowanie na giełdzie z uwzględnieniem własnych
możliwości finansowych i przy oczekiwanym poziomie ryzyka. Należy jednak
zaznaczyć, że rentowność inwestycji jest proporcjonalna do ponoszonego ryzyka. W
przypadku spekulacji, która daje potencjalnie najwyższy zysk z inwestycji, szczególnie
duże znaczenie ma umiejętność właściwego doboru portfela inwestycyjnego, a przede
wszystkim skutecznego przewidywania zmiany cen. Powyższa analiza przedstawia
podstawowe mechanizmy zachowania inwestorów. Aspekty psychologiczne zostały
umieszczone w książce autorstwa Martina Pringa (Pring 2001).
W kolejnych dwóch rozdziałach opisane zostały dwie podstawowe metodyki
pozwalające na prognozowanie przyszłych cen na giełdzie. Są nimi analiza
fundamentalna i analiza techniczna.
2.3.
Analiza fundamentalna
Analiza fundamentalna opiera się na założeniu, że ceny walorów wprost
wynikają z wartości dobra, jakie za nimi stoi. Teoria ta ma zastosowanie przede
wszystkim do oceny wartości akcji. Skupia się więc na odzwierciedleniu oceny
kondycji przedsiębiorstwa w cenie jego akcji i porównania jej oczekiwanej wartości z
bieżącą wartością na giełdzie. Zmiany cen zależą zarówno od zmian w kondycji firmy
jak i zmian w jej otoczeniu polityczno-gospodarczym. Analiza fundamentalna opiera
się na analizie przyczyn zmiany wartości. Wykorzystuje szerokie spektrum narzędzi

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
12
Teoria i zastosowania
Implementacja
Wyniki badań
oraz informacji. Informacje pochodzą przede wszystkim spoza samej giełdy. W
pierwszym kroku są to raporty z działalności spółki. Zawierają one mierzalne
wskaźniki takie, jak: płynność, aktywność, zadłużenie, rentowność oraz wartość
rynkowa. Jednocześnie ważne są dane niemierzalne. Są to między innymi relacje z
kontrahentami, relacje współwłasności, wiarygodność na rynku oraz ewentualne
problemy natury prawnej. Na kondycję przedsiębiorstwa i co za tym idzie wycenę jego
akcji wpływ mają również czynniki makroekonomiczne takie, jak koniunktura
gospodarcza, sytuacja polityczna w regionie oraz wszelkiego rodzaju potencjalne
konflikty zbrojne.
Warto odnotować istnienie modeli matematycznych zbudowanych na podstawie
wskaźników analizy fundamentalnej (Chung, Kim 2001; LeBaron 2001). Celem
konstruowania takich modeli jest próba opisania zmian w czasie ryzyka i zysku z
inwestycji. Do podstawowych modeli tego typu zalicza się model jednowskaźnikowy
oraz model arbitrażu cenowego (Sopoćko 2005).
2.4.
Analiza techniczna
„Analiza techniczna to badanie zachowań rynku, przede wszystkim przy użyciu
wykresów, którego celem jest przewidywanie przyszłych trendów cenowych”
(Murphy 1999). Analiza techniczna w swojej istocie różni się od analizy
fundamentalnej. Bada ona wyłącznie skutki wpływu pewnych czynników na giełdę w
odróżnieniu od przyczyn, co jest domeną analizy fundamentalnej. Zachowanie rynku
w tym przypadku jest rozumiane zarówno jako zmienność cen walorów, jak również
wolumenu transakcji oraz liczby otwartych kontraktów terminowych. Analiza
techniczna opiera się na trzech założeniach: rynek wszystko dyskontuje, ceny
podlegają trendom, historia się powtarza. Najważniejsze jest pierwsze założenie.
Wszystko co ma wpływ na cenę akcji, zdaniem zwolenników analizy technicznej ma
swoje odbicie w jej historycznych wartościach. Co więcej, ich wpływ na
charakterystykę zmienności cen ma miejsce wcześniej niż możliwość ich
bezpośredniego zaobserwowania chociażby metodami analizy fundamentalnej
(Murphy 1999). Są to zarówno czynniki zdefiniowane przez analizę fundamentalną jak

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
13
Teoria i zastosowania
Implementacja
Wyniki badań
i elementy psychologii zachowania inwestorów. Większość z nich ma charakter
niemierzalny. Jednak ich odbicie w wartościach walorów ma charakter liczbowy. Daje
to możliwość zdefiniowania jednoznacznych, co nie znaczy nieomylnych, wskaźników
prognozujących zmiany wartości ceny. Zostaną one przedstawione w następnym
akapicie. Analiza techniczna opiera się w gruncie rzeczy na analizie trendów. Ich
istnienie jest widoczne na wykresach wartości w czasie. Pomimo chaotycznych zmian
w krótkim okresie czasu, możliwe jest wyznaczenie trendu w dłuższym horyzoncie.
Mechanizmy zachowania inwestorów powodują, że większe jest prawdopodobieństwo
zachowania trendu niż jego zmiany. Trend trwa do momentu jego zmiany. Wydaje się
to być truizmem bez znaczenia. Jednak celem analizy technicznej jest odnalezienie
przesłanek ku tej zmianie. Obserwowane powtarzające się w czasie kształty wykresu
wartości pozwalają założyć, że istnieją określone warunki, przy których giełda
zachowuje się typowo. Założenie o powtarzalności historii jest kluczowe dla
stosowania analizy technicznej, która opiera się wyłącznie na przeszłych wartościach.
Jednym z aspektów analizy technicznej jest analiza wykresów. Stosowane są dwa
główne typy wykresów: liniowe i słupkowe. Pierwszy z nich powstaje poprzez
połączenie linią kolejnych punktów wartości ceny przy ustalonej jednostce czasu.
Natomiast wykres słupkowy zawiera więcej informacji niż wykres liniowy. Dla każdej
jednostki czasu pokazane są: cena otwarcia i zamknięcia oraz cena minimalna i
maksymalna w danej jednostce. Popularnym wykresem tego typu są świece japońskie
(Diagram 2). Cechą charakterystyczną jest kolor korpusu świecy. Kolor czarny oznacza
spadek kursu w ciągu jednostki czasu. Kolor biały oznacza, że kurs zamknięcia był
wyższy niż kurs otwarcia.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
14
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 2.
Świece japońskie – znaczenie poszczególnych elementów
Oprócz wykresu wartości wykorzystywany jest również wykres wielkości
wolumenu transakcji oraz liczby otwartych kontraktów terminowych. Dodatkowe
wykresy są prezentowane równocześnie z podstawowym wykresem cen. Pozwala to
na precyzyjne obserwowanie sytuacji na giełdzie, której pełny obraz daje połączenie
wszystkich opisanych informacji. Dla wszystkich rodzajów wykresów jednostką czasu
najczęściej są dni, tygodnie lub miesiące, zależnie od przyjętego horyzontu analizy.
Istotnym elementem analizy wykresów jest wskazanie linii trendu oraz
poziomów wsparcia i oporu. Są to abstrakcyjne linie, z których pierwsze wykreślają
granice cen będących w trendzie, drugie zaś wyznaczają psychologiczne bariery
utrzymania bieżącego trendu. Przykładowe linie zostały pokazane na poniższym
diagramie (Diagram 3).
Maksimum
Kurs zamknięcia
Kurs otwarcia
Minimum
Maksimum
Kurs otwarcia
Kurs zamknięcia
Minimum
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
15
Teoria i zastosowania
Implementacja
Wyniki badań
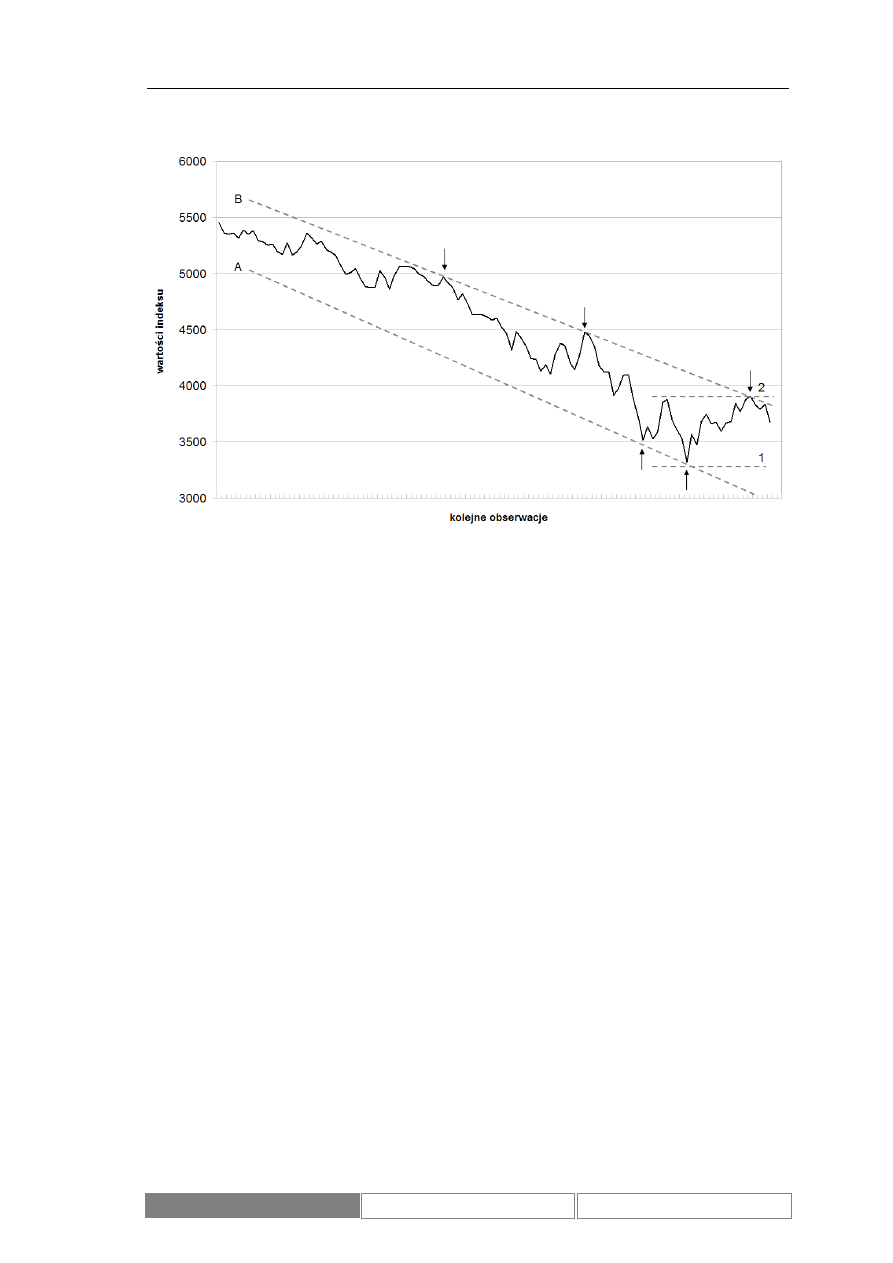
Diagram 3.
Wykresy liniowe – linie trendu (A, B), linie wsparcia (1) i oporu (2)
Poziom wsparcia jest zdefiniowany jako dno ostatniej zniżki cen (linia 1), poziom
oporu natomiast jako szczyt ostatniego wzrostu (linia 2). Coraz niższe linie wsparcia
oznaczają kontynuowanie trendu spadkowego (analogicznie coraz wyższe linie oporu
przy trendzie wzrostowym). Osiągnięcie przez wartość indeksu poziomu wsparcia lub
oporu jest pierwszym sygnałem zmiany trendu.
Linie trendu wyznacza się na podstawie kolejnych znaczących punktów
ekstremalnych wykresu. Za potwierdzoną linię trendu uznaje się taką linię, od której
wykres ceny „odbił” się przynajmniej trzy razy. Punkty takie zostały oznaczone na
wykresie strzałką. Linię B można zatem uznać za potwierdzoną, podczas gdy linia A
wymaga jeszcze jednego dojścia do niej wartości ceny, aby osiągnąć tę cechę. Zakłada
się, że wszelkie korekty ceny w najbliższej przyszłości będą miały miejsce w granicach
wyznaczonych przez potwierdzone linie trendu. Podobnie jak w przypadku linii
oporu, przebicia linii trendu są sygnałami do jego zmiany. Wymagają również
ponownego wykreślenia linii trendu z uwagi na możliwość zmiany jego
charakterystyki.
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
16
Teoria i zastosowania
Implementacja
Wyniki badań
Powtarzalność historii postulowana w analizie technicznej szczególnie jest
widoczna w wyznaczaniu formacji (Murphy 1999). Są to określone schematy kształtu
wykresu wartości ceny. Określają one powtarzalne zachowanie się rynku, w efekcie
prognozując zmianę lub utrzymanie dotychczasowego trendu. Należy pamiętać, że nie
tylko kształt wykresu wyznacza daną formację, ale znaczenie ma również właściwe
zachowanie wartości wolumenu transakcji, który potwierdza charakterystyczne
punkty formacji.
Formacje zapowiadające zmianę trendu to przede wszystkim: głowa i ramiona,
podwójny szczyt/dno, spodek oraz formacja V. Do najważniejszych formacji
podtrzymujących bieżący trend zaliczane są: trójkąt, flaga, chorągiewka, klin oraz
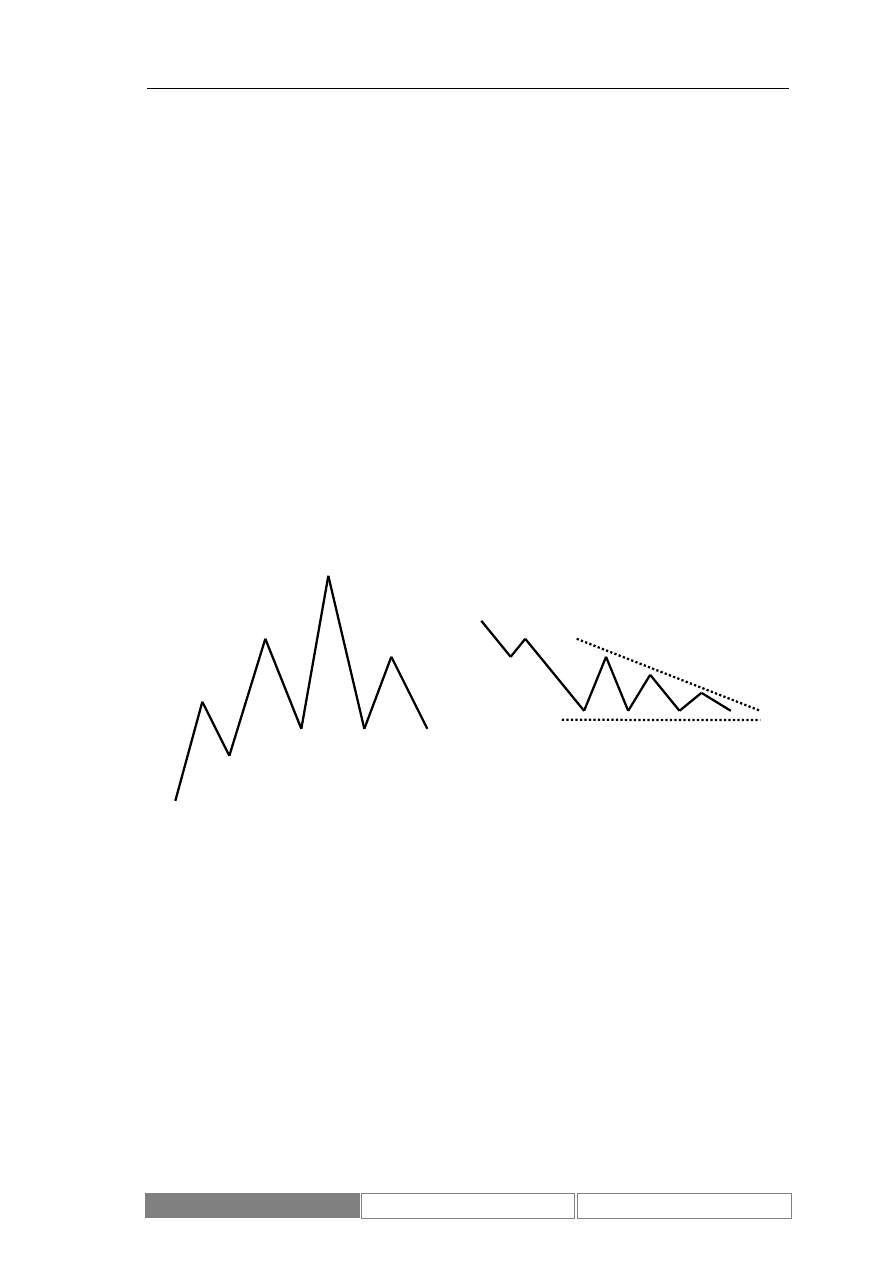
prostokąt. Wybrane formacje zostały zaprezentowane na poniższym diagramie.
Diagram 4.
Formacje: głowa i ramiona, trójkąt
Analogicznie do formacji odnajdywanych na liniowych wykresach wartości cen
wyróżnione są również charakterystyczne układy świec japońskich (Murphy 1999).
Podobnie zapowiadają one zmianę trendu lub go potwierdzają. Do pierwszej grupy
zaliczane są między innymi formacje „zasłona ciemnej chmury” oraz „gwiazda
wieczorna/poranna” (Diagram 5). Najważniejszymi formacjami zaliczanymi do
Głowa i ramiona
zapowiedź odwrócenia trendu rosnącego
Głowa
Ramię
prawe
Ramię
lewe
Trójkąt
zapowiedź zachowania trendu
spadkowego
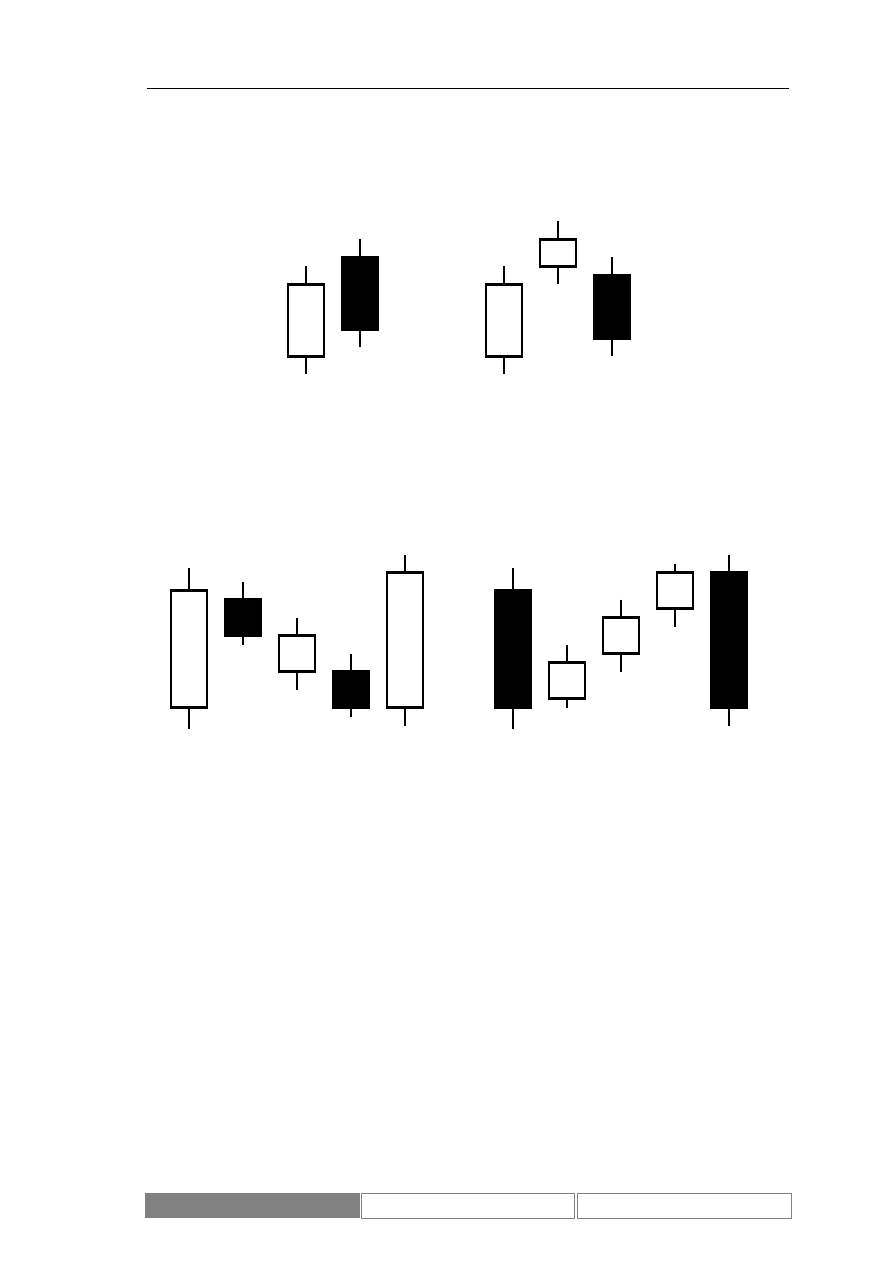
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
17
Teoria i zastosowania
Implementacja
Wyniki badań
drugiej, potwierdzającej trend grupy są „naszyjnik rozpięty” oraz „trójki hossy i bessy”
(Diagram 6).
Diagram 5.
Formacje świecowe: zasłona ciemnej chmury (a), gwiazda wieczorna (b)
Diagram 6.
Formacje świecowe: trójka hossy (a), trójka bessy (b)
Każda z formacji odzwierciedla zachowania inwestorów w konkretnych
sytuacjach na rynku. Część z nich jest uważana za szczególnie wiarygodne. Są to
przede wszystkim formacje głowy i ramion oraz gwiazda wieczorna/poranna. Sygnały
generowane przez formacje powinny być jednak zawsze potwierdzane wynikami z
innych narzędzi pokazujących zachowanie rynku.
Występowanie formacji nie jest częstym zjawiskiem, zatem nie jest też najczęściej
stosowanym wskaźnikiem zachowania rynku. Znacznie częściej wykorzystywane są
wszelkiego rodzaju wskaźniki numeryczne. Są to jednoznacznie zdefiniowane
(a) Trójka hossy
(b) Trójka bessy
(a) Zasłona ciemnej
chmury
(b) Gwiazda
wieczorna

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
18
Teoria i zastosowania
Implementacja
Wyniki badań
przekształcenia historycznych wartości cen oraz wolumenu. Najprostsze z nich to
średnie kroczące. Ponieważ znaczenie wartości późniejszych jest większe niż wartości
wcześniejszych, stosuje się średnią ważoną lub częściej średnią wykładniczą. Średnia
ważona uwzględnia wartości z zadanego przedziału czasu, przykładając wagę równą
kolejnemu numerowi obserwacji. W efekcie największą wagę ma ostatnia obserwacja.
Średnia wykładnicza uwzględnia wartości historyczne, przykładając wykładniczo
rosnące wagi. W zależności od oczekiwanej czułości średniej, stosuje się 5, 10, 20, 40 -
dniowe średnie kroczące. Uznaje się, że przebicie linii cen przez linię średniej jest
sygnałem zbliżającej się zmiany trendu. Pomimo, że sygnały generowane przez tak
proste zastosowanie średnich nie mają dużej wiarygodności, stanowią popularne
narzędzie zwracające uwagę inwestora na zmianę sytuacji na giełdzie.
Alternatywą dla średnich kroczących są bardziej złożone przekształcenia –
oscylatory (Murphy 1999). Ich konstrukcja opiera się na pomiarze różnych aspektów
zmian cen. Wykorzystuje się proste różnice lub iloczyny wartości cen (oscylatory:
Impet, Wskaźnik Zmian, Oscylator Stochastyczny, Williams) albo funkcje średnich
kroczących (oscylatory: Wskaźnik Siły Względnej, MACD). Sygnały zmian trendu
odczytywane są na podstawie wartości ekstremów osiąganych przez oscylator lub
alternatywnie osiągnięcia określonego poziomu wartości. Wyjątkiem jest oscylator
MACD, który zbudowany jest z dwóch przekształceń. W tym przypadku sygnały są
generowane w punktach przecięć obu linii oscylatora. Skuteczność oscylatorów nie jest
stała. Po pewnym czasie relatywnie skutecznego działania konkretnego oscylatora jego
skuteczność spada. Konieczne jest wtedy odnalezienie innego oscylatora, który będzie
właściwie przewidywał sytuację na giełdzie przez kolejny okres czasu. Z uwagi na
ryzyko fałszywych sygnałów wykorzystuje się kilka oscylatorów jednocześnie,
szukając wzajemnego ich potwierdzenia. Są jednak stany rynku, np. wczesna faza
trendu, w których skuteczność oscylatorów jest ogólnie niska. Uzasadnione jest wtedy
wykorzystanie innych niż oscylatory wskaźników.
Opisane powyżej techniki są głównymi ze stosowanych w analizie technicznej.
Istnieje szereg dalszych, które rozwijają podstawowe lub bazują na całkowicie
odmiennych założeniach dotykając na przykład numerologii. Niezależnie od

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
19
Teoria i zastosowania
Implementacja
Wyniki badań
przywiązania do wybranych narzędzi analizy technicznej konieczne jest jednoczesne
stosowanie szerokiego ich spektrum dla zmniejszenia ryzyka fałszywych sygnałów.
Wykorzystanie analizy technicznej jest obecnie znacznie ułatwione dzięki rozwojowi
systemów informatycznych. Wskaźniki są wyznaczane bez opóźnień, dostarczając
bogatej informacji o stanie rynku. Jednak nadal najważniejszym i decydującym
czynnikiem pozostaje wiedza oraz intuicja człowieka podejmującego decyzje.
Przy omawianiu podstaw analizy technicznej warto odnotować istnienie tzw.
Hipotezy Rynku Efektywnego. Według niej, przy uwzględnieniu szczególnych
warunków, wartość ceny na giełdzie odzwierciedla historyczne parametry związane z
giełdą (w wersji „słabej” hipoteza obejmuje jedynie przeszłe wartości obserwowanej
ceny). Jednak uwzględnienie tych parametrów następuje w czasie tak krótkim, że nie
jest możliwe wykonanie na ich podstawie prognozy wartości ceny. W myśl tej hipotezy
zmiana ceny na giełdzie ma charakter błądzenia przypadkowego (ang. random walk)
o zerowej korelacji kolejnych zmian. Prawdziwość tej hipotezy zamknęłaby możliwość
skuteczniej prognozy wartości indeksu giełdowego. Istnieją jednak badania
podważające jej słuszność. Ciekawy sposób na jej zaprzeczenie został zaprezentowany
w artykule (Shmilovici i in. 2003). Zdefiniowany został problem równoważny badanej
hipotezie. Według autorów publikacji zmiany cen na giełdzie mają charakter losowy,
jeśli nie istnieje metoda kompresji ciągu wartości cen. Opierając się na powyższych
założeniach zdefiniowany został skuteczny algorytm realizujący takie przekształcenie.
Przedstawione przez autorów wyniki zaprzeczają Hipotezie Rynku Efektywnego,
dając nadzieję na możliwość skutecznej predykcji kolejnej wartości ceny na giełdzie.
Analiza techniczna jest przedmiotem wielu publikacji opisujących badania nad
skutecznością prognozy zachowania giełdy, np. w pracach (Chung i in. 2004; Dempster
i in. 2001; Podding, Rehkegler 1996).

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
20
Teoria i zastosowania
Implementacja
Wyniki badań
3.
Metody numeryczne oraz metody inteligencji obliczeniowej w prognozie
giełdy
3.1.
Zastosowanie sieci neuronowych w prognozie
Sieci neuronowe w swojej idei opierają się na analogii do działania komórek
neuronowych tworzących struktury mózgu żywych organizmów (Osowski 2000).
Podstawowa struktura to neuron. Sygnały docierające do neuronu sumują się i po
przekroczeniu zdefiniowanego progu są przekazywane do kolejnych neuronów.
Przekroczenie progu, nazywane aktywacją, może mieć charakter skokowy lub ciągły.
W modelu ciągłym generowany sygnał jest najczęściej nieliniowym przekształceniem
sumy sygnałów wejściowych. Neurony są połączone ze sobą tworząc sieć. Najczęściej
stosowany jest model sieci jednokierunkowej, w której sygnały rozprzestrzeniają się od
neuronów wejściowych do ostatnich na ścieżce neuronów wyjściowych. Najczęściej
stosowane sieci neuronowe mają ściśle strukturalną architekturę, w której sygnał
przepływa przez sieć w jednym kierunku, dając wartości wyjściowe. Możliwe jest
także stosowanie połączeń powodujących krążenie sygnałów w sieci w celu
wprowadzenia historycznych danych, jednak w złożoności architektury daleko im do
biologicznego mózgu. Nieporównywalna z biologicznym odpowiednikiem jest
również liczba neuronów oraz połączeń między nimi. Naturalnym ograniczeniem dla
sztucznych sieci neuronowych jest zarówno wydajność komputerów jak i specyficzne,
ograniczone możliwości ich stosowania.
Wprawdzie podobieństwo modelu matematycznego sztucznej sieci neuronowej
do jej odpowiednika biologicznego nie jest duże, to pewne cechy działania są wspólne.
Dobór parametrów sieci neuronowej dokonuje się w procesie nauki, który
wykorzystuje specyficzne do tego celu algorytmy. Identyfikowane są oraz podlegają
zapamiętaniu zależności definiujące przekształcenia sygnałów wejściowych w
odpowiedź sieci. Ostatecznie, z matematycznego punktu widzenia sieć neuronowa
stanowi nieliniowe przekształcenie przestrzeni wejściowych rekordów na wynikową
przestrzeń, odwzorowując nieznaną funkcję. Teoria Kołmogorowa (Osowski 2000)

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
21
Teoria i zastosowania
Implementacja
Wyniki badań
opisuje maksymalną, w rozumieniu wielkości, architekturę jednokierunkowych,
wielowarstwowych sieci typu perceptron, wystarczającą (teoretycznie) do realizacji
problemu aproksymacji przekształceń. Dla aproksymacji ciągłego przekształcenia
przestrzeni N wymiarowej w przestrzeń M wymiarową wystarczająca jest sieć
neuronowa posiadająca jedną warstwę ukrytą o rozmiarze (2N+1) zbudowaną z
neuronów sigmoidalnych. Dla przekształcenia nieliniowego konieczne może być
dodanie drugiej warstwy ukrytej.
Siła sieci neuronowej jest ukryta w równolegle przetwarzanych przez nieliniowe
funkcje sygnałach oraz sposobie dostosowania wag w procesie uczenia. W procesach
tych niejednokrotnie stosowane są analogie z nauk biologicznych (Nałęcz i in. 2000)
czy fizyki (Kosiński 2002).
Sieć neuronowa posiada własność uogólnienia informacji pozyskanych w
procesie nauki. Oznacza to zachowanie określonej poprawności wyliczania wartości
wynikowej dla nieznanych w czasie nauki rekordów wejściowych. Cecha ta pozwala
na stosowanie tej metody aproksymacji do przetwarzania danych zaburzonych oraz
niepełnych. Sieć neuronowa może być wykorzystana zarówno do odtworzenia
brakujących danych jak i prognozy kolejnych wartości w ciągu. Dla skuteczności
działania sieci nie stanowi zasadniczej różnicy znaczenie danych, które są
przetwarzane. Ważna jest jednak możliwość pozyskania z nich wystarczająco dużej
ilości informacji. Podstawowe obszary zastosowań sztucznych sieci neuronowych to
klasyfikacja (np. w diagnostyce medycznej (Nałęcz i in. 2000)) oraz predykcja wartości
(np. danych pogodowych (Jaruszewicz, Mańdziuk 2002a; Jaruszewicz, Mańdziuk
2002b) lub zużycia surowców (Grzenda, Macukow 2002)). Sieci neuronowe
wykorzystuje się również do rozwiązywania problemów optymalizacyjnych – sieci
Hopfielda (Mańdziuk 2000), kompresji danych czy redukcji szumu np. zapisu
dźwiękowego.
Odrębnym kierunkiem rozwoju sieci neuronowych jest przetwarzanie informacji
niepewnej oraz niezdefiniowanej numerycznie. Rozszerzenie działania sieci
neuronowych na liczby i zbiory rozmyte (Łachwa 2001; Rutkowska 1997) pozwoliło na
modelowanie przekształceń o atrybutach takich jak „duży”, „ciepły”, itp. W ramach

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
22
Teoria i zastosowania
Implementacja
Wyniki badań
logiki rozmytej sieci neuronowe są wykorzystywane do tworzenia zbioru reguł
opisujących oczekiwane wartości wyjściowe w zależności od warunków, jakie
spełniają zmienne wejściowe.
3.2.
Algorytm genetyczny i jego wybrane zastosowania
Zgodnie z wcześniejszym opisem, sztuczne sieci neuronowe są uniwersalnymi
narzędziami do aproksymacji. Wymagają jednak określenia szeregu parametrów
definiujących ich działanie. Jednocześnie często spotykana w praktyce duża liczba
danych uczących wymaga preselekcji w celu podania do procesu nauki najbardziej
wartościowych danych. Doboru parametrów oraz danych uczących można dokonywać
w sposób analityczny, wykorzystując własną intuicję lub stosując modele
matematyczne oraz algorytmy oparte na analizie statystycznej. Możliwy jest również
dobór parametrów i danych na zasadzie prób i błędów.
W zagadnieniach wyboru architektury sieci neuronowych lub doboru danych
uczących stosowane są także algorytmy genetyczne (Nałęcz i in. 2000; Rutkowska i in.
1997; Rutkowska 1997). Powstanie tej metody, podobnie jak powstanie sieci
neuronowych, było zainspirowane obserwacją natury. Jej pierwowzorem jest ewolucja
żywych organizmów, która z prostych form, zgodnie z prawami selekcji naturalnej
tworzyła coraz bardziej złożone i wyspecjalizowane jednostki.
Podstawowymi elementami algorytmu genetycznego są osobniki zdefiniowane
poprzez chromosom lub zestaw chromosomów zawierający definicję ich zachowania.
Wszystkie osobniki tworzą populację, która podlega zasadom ewolucji. W kolejnych
generacjach powstają osobniki o coraz lepszym przystosowaniu. Osobnik o
maksymalnym przystosowaniu w populacji jednocześnie koduje najlepsze rozwiązanie
problemu.
Modyfikacje populacji odbywają się przy pomocy dwóch operatorów:
krzyżowania i mutacji. Pierwszy z nich generuje nowe osobniki, które powstają przez
połączenie, wybranych spośród osobników populacji, rodziców. Wymianie podlega
materiał genetyczny rodziców, tworząc dzieci o cechach wspólnych i jednocześnie

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
23
Teoria i zastosowania
Implementacja
Wyniki badań
innych od każdego z rodziców. Każdy z osobników może podlegać mutacji, czyli
losowym zmianom genów w swoim chromosomie. Zmiany te mają na celu zaburzenie
genotypu i umożliwienie odkrywania nowych cech, które mogły wcześniej nie być
kodowane w genach rodziców. Zarówno krzyżowanie jak i mutacja sterowane są
określonymi prawdopodobieństwami zdarzenia. Krzyżowanie jest procesem
powszechnym, podczas gdy mutacja ma charakter akcydentalny.
Algorytm genetyczny poszukuje coraz lepszych rozwiązań, eksplorując
przestrzeń możliwych kombinacji parametrów. Poprawne zdefiniowanie zawartości
chromosomów oraz funkcji oceniającej osobniki pozwala na rozwiązywanie
problemów optymalizacyjnych o bardzo zróżnicowanym charakterze.
W przypadku problemu zdefiniowania efektywnej architektury sieci neuronowej
lub doboru sekwencji danych wejściowych takiej sieci możliwe jest zapisanie ich
reprezentacji w chromosomie oraz wykorzystanie algorytmu genetycznego z funkcją
oceny określoną jako skuteczność nauki. Po określonej liczbie generacji populacji
wskazane zostanie najbardziej wartościowe rozwiązanie, często bliskie optymalnemu.
3.3.
Prognoza wskaźników giełdowych w literaturze
Narzędzia matematyczne
Dotychczasowe badania w dziedzinie modelowania zachowania giełdy obejmują
zarówno wykorzystanie analizy fundamentalnej jak i technicznej do konstrukcji
matematycznego opisu zachowań wartości walorów. Ważnym elementem większości
badań jest aspekt przekształcenia danych wejściowych do procesu doboru parametrów
modelu.
Założenia analizy fundamentalnej są wykorzystywane do konstrukcji modeli
matematycznych, które przekształcają parametry wpływające na wyliczaną wartość
spółki. Celem jest oszacowanie aktualnej rzeczywistej wartości spółki (Chung, Kim
2001), co powinno mieć wpływ na przyszłe zmiany jej wartości na giełdzie. Należy
oczekiwać, że cena na giełdzie zmieni się w kierunku rzeczywistej wyceny danego
przedsiębiorstwa. Stosowane są również metody eksploracji danych (ang. data

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
24
Teoria i zastosowania
Implementacja
Wyniki badań
mining) w celu identyfikacji reguł umożliwiających opis zależności parametrów i na
ich podstawie prognozę ich przyszłych wartości (John i in. 1996; Last i in. 2001).
Odmienny cel jest stawiany modelom matematycznym, które odzwierciedlają
działanie giełdy (O’Neil 1995). Stworzenie modelu giełdy, który prawidłowo oddaje
zachowanie giełdy rzeczywistej pozwala na rozwój badań zmierzających do poznania
jej mechanizmów oraz zbudowania narzędzi do skutecznej prognozy (Hann, Steurer
1996). W oparciu o modele matematyczne rozpatrywane są również algorytmy doboru
optymalnych portfeli inwestycyjnych (Bauerle, Riedel 2004; Moody, Staffell 2001;
Walk, Yakowitz 2002). Jednym z pierwszych i jednocześnie najczęściej stosowanym do
porównania efektywności pozostałych modeli jest model Black & Scholes (Lai, Wong
2004; Malliaris, Salchenberger 1996; Shepp 2002). Pierwsza definicja modelu Black &
Scholes została zaproponowana w publikacji (Black, Scholes 1973). Bardziej złożony
model rynku został zaprezentowany w pracy (LeBaron 2001). Zbudowany został
model giełdy zawierający analogiczne do rzeczywistych zasady inwestowania oraz
uwzględniający zachowanie inwestorów. Opiera się on na populacji agentów
podejmujących decyzje na podstawie własnej oceny bieżącej sytuacji. W czasie
działania modelu, ewolucji podlega populacja złożona z inwestorów – agentów
stosujących specyficzne reguły decyzyjne oparte o sieci neuronowe. Tak
skonstruowany model w wielu aspektach zachowuje się w sposób statystycznie
podobny do zachowania się rzeczywistego rynku papierów wartościowych.
Sieci neuronowe
Jako narzędzie do prognozowania parametrów giełdy szeroko stosowane są sieci
neuronowe. Właściwości sieci neuronowych opisane w Rozdziale 3.1 pozwalają na
obiecujące badania w tym obszarze zastosowań. Wykorzystywane są zarówno sieci o
sigmoidalnej postaci funkcji aktywacji neuronu (Chenoweth, Obradovic 1996; Gencay,
Qi 2001; Yao, Tan 2000; Jaruszewicz, Mańdziuk 2004; Jaruszewicz, Mańdziuk 2006), jak
również specyficznych funkcjach radialnych (Cao, Tay 2003; Hansen, Nelson 2002; Xu
1998; Kodogiannis, Lolis 2002; Lee 2004). Zastosowanie rekurencyjnych sieci
neuronowych, których model zakłada wsteczne połączenia między neuronami
pozwala na uchwycenie dynamiki zmian wartości parametrów giełdy (Saad i in. 1998;

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
25
Teoria i zastosowania
Implementacja
Wyniki badań
Tino i in. 2001; Lee 2004; Kim 1998). Inną metodę bazującą na koncepcji sieci
neuronowych zaprezentowali autorzy prac (Vapnik 1995; Vapnik 1998). Jest to metoda
wektorów wspomagających (ang. Support Vector Machines). Jest ona często
stosowana do predykcji zmiennych obserwowanych na giełdzie (Cao i in. 2003;
Gavrishchaka, Ganguli 2003; Cao, Tay 2003; Tay, Cao 2002; Gestel i in. 2001).
Przetwarzanie danych
Stosowanie sieci neuronowych do zagadnienia predykcji wartości indeksu
giełdowego wymaga odpowiedniego przetworzenia danych wejściowych w celu
wydobycia najbardziej wartościowych dla nauki cech. Metody przetwarzania danych
wejściowych obejmują zarówno wydzielenie okresów o charakterystycznych trendach
(Chenoweth, Obradovic 1996) jak i danych o istotnym statystycznie rozkładzie
zmienności (Kohara i in. 1996; Deco i in. 1997). Metody klasyfikacji i segmentacji
przestrzeni danych wejściowych znajdują zastosowanie również do bezpośredniej
prognozy zmiany wartości indeksu giełdowego (Baram 1998). Odmienne metody
wstępnego przygotowania danych wejściowych opierają się na przekształceniu
przestrzeni wektorów wejściowych do przestrzeni, w której zmienne są statystycznie
niezależne. Są to przekształcenia PCA (analiza składników głównych) (Cao i in. 2003)
oraz ICA (analiza składników niezależnych) (Cao i in. 2003; Capobianco 2002; Cheung,
Xu 2001).
Modele statystyczne
Alternatywą dla metod inteligencji są modele statystyczne. Stanowią one
znaczący odsetek prac w obszarze metod prognozowania wartości parametrów giełdy.
Obejmują one stosunkowo proste Modele Markowa (Bengio i in. 2001; Bengio, Frasconi
1996; Kim i in. 2002; Shepp 2002; Tino i in. 2001) oraz bardziej złożone modele oparte
na analizie średnich i wariancji - ARIMA i GARCH (Mantegna, Stanley 2000;
Kamitsuji, Shibata 2003; Erkip, Cover 1998). Badania pokazują jednak, że skuteczność
modeli ARIMA i GARCH nie jest zadowalająca w porównaniu z sieciami
neuronowymi lub SVM (Kohzadi i in. 1996). Z tego powodu zarówno sieci neuronowe
jak i metoda wektorów wspomagających cieszą się większą popularnością. Szczególnie

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
26
Teoria i zastosowania
Implementacja
Wyniki badań
interesujące porównania skuteczności modeli zostały zawarte w pracach (Hansen,
Nelson 2002; Tino, Schittenkopf 2001).
Narzędzia interdyscyplinarne
Ciekawą grupę zaawansowanych metod opisujących zachowanie giełdy
stanowią narzędzia pierwotnie skonstruowane do opisu zjawisk fizycznych. W
publikacji (Vandewalle i in. 1998) autorzy zadają pytanie czy spektakularne załamania
rynku finansowego mogły być przewidziane. Pokazana została zgodność obserwacji
zachowania giełdy z modelem Isinga wykorzystywanym w mechanice kwantowej.
Inny ciekawy przykład wykorzystania teorii fizycznych stanowią funkcje falkowe (ang.
wavelets). Pierwotnie stosowane są one do opisu Wszechświata (Coveney, Highfield
1996; Heller 2002). Wykorzystanie falek w przekształceniach sygnałów i w
konsekwencji identyfikacji ukrytych zależności między danymi giełdowymi zostało
przedstawione w artykule (Capobianco 2002).
Algorytm genetyczny
Opisane powyżej metody wymagają określenia szeregu parametrów oraz
optymalnego doboru danych wejściowych dla optymalnej pracy. Jedną z metod
wykorzystywanych do przeszukania przestrzeni różnorodnych parametrów oraz
możliwych układów zmiennych wejściowych są algorytmy genetyczne. W pracy
(Thawornwong, Enke 2004) autorzy zaprezentowali system oparty na sieci neuronowej
do podejmowania decyzji w grze na giełdzie. Danymi wejściowymi były zmienne z
zakresu analizy fundamentalnej (por. Rozdział 2.3). Dobór optymalnego ich zbioru jest
realizowany przez algorytm genetyczny.
Inne obszary zastosowań algorytmów genetycznych związane z giełdą to
konstrukcja optymalnych reguł (Dempster i in. 2001; Kaboudan 2000) oraz wybór
architektury sieci neuronowej do prognozy wskaźników finansowych (Fieldsend,
Singh 2005; Kim, Lee 2004; Hayward 2002). Identyfikacja w ciągu wartości indeksu
typowych formacji zdefiniowanych w analizie technicznej została opisana w artykule
(Chung i in. 2004). Cechą wyróżniającą przedstawionego przez autorów algorytmu jest
zastosowanie algorytmu genetycznego do elastycznego dopasowania dowolnej

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
27
Teoria i zastosowania
Implementacja
Wyniki badań
długości wykresu wartości indeksu do zdefiniowanych schematów formacji.
Podstawowe możliwości algorytmu pokrywają się z możliwościami algorytmu
wyszukiwania
formacji,
będącego
elementem
systemu
neuro-genetycznego
zaproponowanego w rozprawie.
Portfel inwestycyjny
O skuteczności gry na giełdzie w kategoriach zysku decydują nie tylko właściwe
decyzje oparte na skutecznej prognozie, ale również właściwy dobór walorów, którymi
inwestor obraca. Zestaw taki nazwany jest portfelem inwestycyjnym. Wybór portfela
jest zarówno związany z oczekiwanym zyskiem z inwestycji jak i utrzymaniem
akceptowanego poziomu ryzyka.
Optymalny portfel może być konstruowany za pomocą technik eksploracji
danych przy jednoczesnym tworzeniu reguł predykcyjnych (John i in. 2006). Inne
metody opierają się na wykorzystaniu łańcuchów Markowa (Bauerle, Riedel 2004),
aproksymacji stochastycznej (Walk, Yakowitz 2002) oraz metodach statystycznych
(Cover 1994; Erkip, Cover 1998).
Przetwarzanie informacji w naturalnym języku
Wszystkie opisane powyżej metody opierają się na przetwarzaniu danych
wyłącznie numerycznych. Pozostaje znaczący obszar informacji dostępnych
inwestorom, których nie da się wyrazić wartościami liczbowymi. Co więcej, ich
charakter jest rozproszony, niejednorodny i często niepewny. Do grupy takich
informacji zaliczyć można biuletyny giełdowe, specjalistyczne teksty o charakterze
analitycznym, publikacje w czasopismach ekonomicznych oraz strony informacyjne w
Internecie. Próba uwzględnienia informacji formułowanych w naturalnym języku
została podjęta w pracach (Constantino i in. 1996; Constantino i in. 1997). Identyfikacja
informacji opiera się na zdefiniowanych wzorcach typów. Przykładowo wzorzec
„przejęcie spółki” może posiadać atrybuty: firma przejmowana, firma przejmująca,
rodzaj przejęcia, wartość kontraktu. Wartości atrybutów są ekstrahowane z artykułów
o tematyce finansowej i treści zgodnej z danym wzorcem. Niestety autorzy nie
prezentują konkretnej realizacji systemu pozyskującego opisaną powyżej wiedzę. Nie

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
28
Teoria i zastosowania
Implementacja
Wyniki badań
ulega jednak wątpliwości przydatność informacji o charakterze subiektywnym w
prognozowaniu
zachowania
giełdy.
Informacje
tego rodzaju
są
szeroko
wykorzystywane przez maklerów giełdowych. Uwzględnienie ich w systemie
informatycznym może być przykładowo oparte na prostych regułach zamieniających
wyekstrahowane informacje na sygnał do możliwej zmiany ceny.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
29
Teoria i zastosowania
Implementacja
Wyniki badań
4.
Wstępny opis proponowanego systemu
4.1.
Dane wejściowe
Źródłowe dane giełdowe (www.parkiet.com.pl) zostały ograniczone do wartości
indeksów najważniejszych giełd papierów wartościowych. Wybrane zostały indeksy
trzech giełd światowych: DAX, NIKKEI oraz DJIA. Wykorzystane zostały również
wartości walut: stosunek kursu dolara amerykańskiego do japońskiego jena oraz euro
do dolara amerykańskiego.
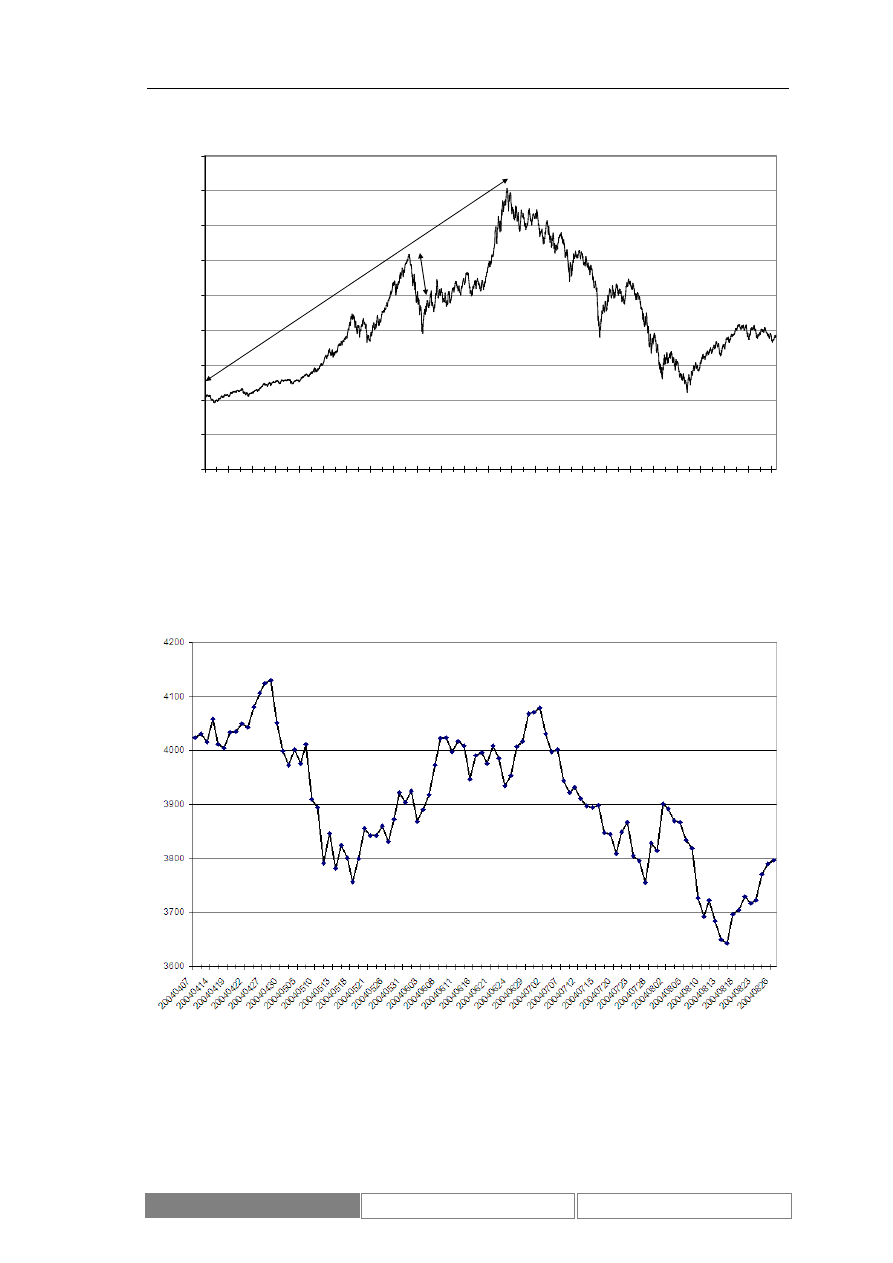
Poniżej przedstawione zostały wykresy wartości indeksu DAX. Diagram 7
przedstawia wartości w przedziale czasu od 1995/01/30 do 2004/08/26. Na potrzeby
testów wybrany został ciągły okres 100 dni roboczych od 2004/04/07 do 2004/08/26
(Diagram 8). Zaprezentowany został również wykres zmian wartości indeksu w
testowym okresie czasu (Diagram 9). Podstawowe parametry statystyczne
rozważanego zbioru danych zawiera Tabela I. Średnia dzienna zmienność wartości
indeksu giełdowego DAX w okresie testów wynosi 0.04%, przy maksymalnej zmianie
w wysokości 2.85%.
Zmiany wartości indeksu podlegają trendom. Są to zarówno trendy o
charakterze długotrwałym, trwające kilka lat, jak i krótkoterminowe. W czasie, kiedy
kurs jest w długoterminowym trendzie może lokalnie znajdować się w trendzie
przeciwnym. Przykładowe trendy przedstawia Diagram 7. Zaznaczony został
długoterminowy trend rosnący oraz lokalny trend malejący.
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
30
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 7.
Wartości indeksu DAX w okresie od 1995/01/30 do 2004/09/01
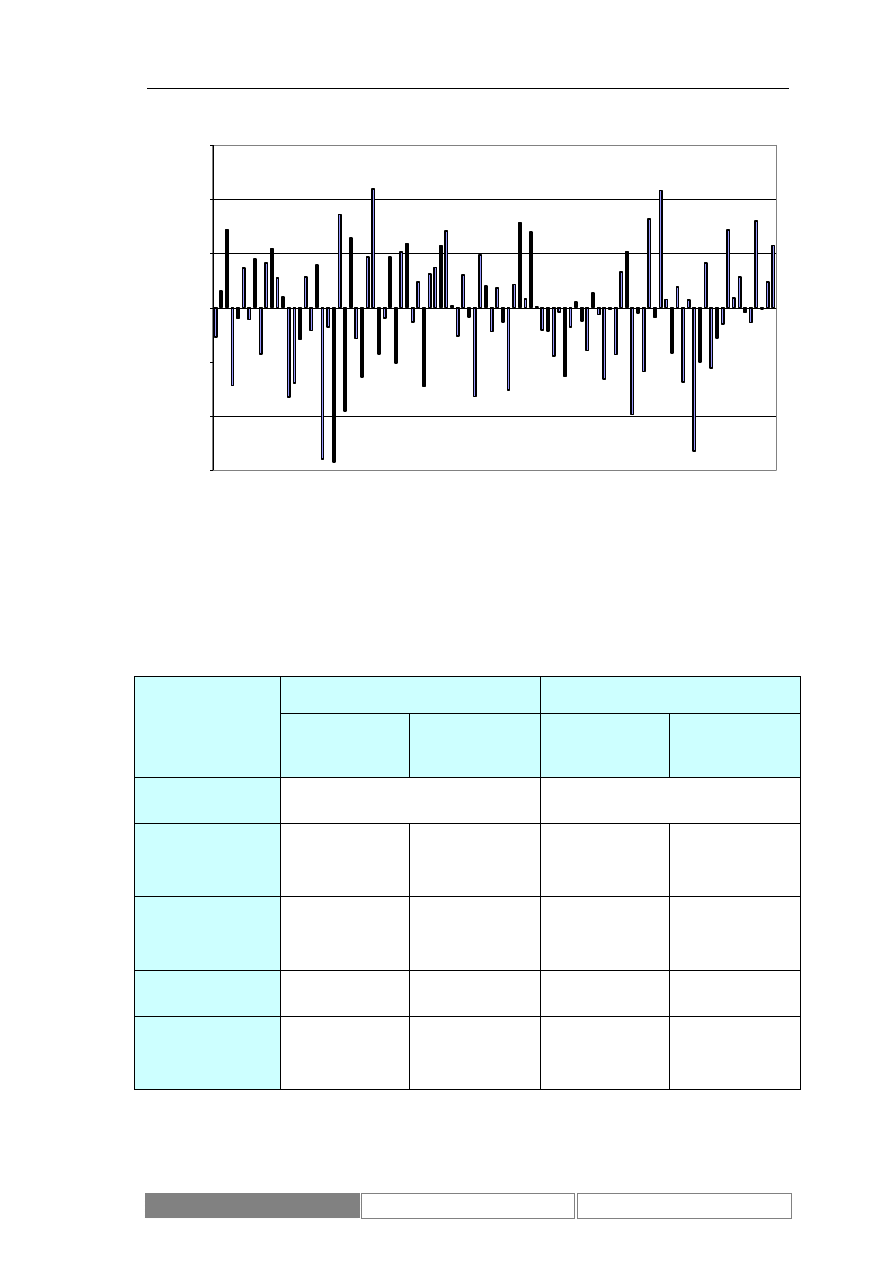
Diagram 8.
Wartości indeksu w okresie testowym od 2004/04/07 do 2004/08/26
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
19
95
01
30
19
95
06
27
19
95
11
15
19
96
04
10
19
96
09
03
19
97
01
29
19
97
06
25
19
97
11
13
19
98
04
09
19
98
09
04
19
99
01
28
19
99
06
24
19
99
11
11
20
00
04
03
20
00
08
24
20
01
01
17
20
01
06
11
20
01
10
29
20
02
03
25
20
02
08
15
20
03
01
09
20
03
06
03
20
03
10
21
20
04
03
16
20
04
08
05
trend rosn
ą
cy
trend malej
ą
cy
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
31
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 9.
Dzienne zmiany wartości zamknięcia indeksu w okresie testowym od
2004/04/07 do 2004/08/26
wszystkie dane
dane testowe
wartości indeksu
wartości zmian
indeksu
wartości indeksu
wartości zmian
indeksu
liczba rekordów
2420
100
dolne ograniczenie
zbioru
1911
−
8.4922%
3643.08
−
2.8501%
górne ograniczenie
zbioru
8064
7.8452%
4130.49
2.1909%
wartość średnia
4319.44
0.0393%
3906.47
0.0429%
odchylenie
standardowe
1533.63
1.6269%
116.58
1.0523%
Tabela I.
Charakterystyka zbioru wartości indeksu DAX
-3,00%
-2,00%
-1,00%
0,00%
1,00%
2,00%
3,00%
20
04
04
07
20
04
04
14
20
04
04
19
20
04
04
22
20
04
04
27
20
04
04
30
20
04
05
05
20
04
05
10
20
04
05
13
20
04
05
18
20
04
05
21
20
04
05
26
20
04
05
31
20
04
06
03
20
04
06
08
20
04
06
11
20
04
06
16
20
04
06
21
20
04
06
24
20
04
06
29
20
04
07
02
20
04
07
07
20
04
07
12
20
04
07
15
20
04
07
20
20
04
07
23
20
04
07
28
20
04
08
02
20
04
08
05
20
04
08
10
20
04
08
13
20
04
08
18
20
04
08
23
20
04
08
26
P
ro
c
e
n
to
w
a
z
m
ia
n
a
w
a
rt
o
ś
c
i

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
32
Teoria i zastosowania
Implementacja
Wyniki badań
Wykorzystując podstawy analizy technicznej, których opis zawiera Rozdział 2.4,
zostały wygenerowane dodatkowe zmienne potencjalnie pomocne w prognozie.
Przede wszystkim są to ważone średnie kroczące o różnym horyzoncie czasu.
Wyliczone zostały również podstawowe oscylatory. Na podstawie kształtu wykresu
wartości indeksu wyznaczone zostały formacje. W tym celu opracowany został
autorski algorytm analizujący przebieg wartości indeksu. Wszystkie przekształcenia
tworzące początkowy zbiór zmiennych wejściowych zostały opisane w Rozdziale 5.
Celem zastosowania tych przekształceń jest pokazanie z różnych perspektyw
historycznych zmian wartości indeksu. Powiększa to możliwości odnalezienia
zależności między danymi historycznymi a prognozowaną przyszłą wartością
indeksu.
4.2.
Algorytm genetyczny
Działanie
algorytmu
genetycznego
bazuje
na
swoim
biologicznym
odpowiedniku – ewolucji. Zdefiniowana jest populacja osobników, która podlega
zmianom w kolejnych generacjach. Każdy osobnik charakteryzuje się zestawem cech,
który stanowi o wartości jego przystosowania. Cechy osobnika zapisane są w jego
chromosomie. Konstrukcja chromosomu oraz możliwe wartości cech pozwalają na
zakodowanie możliwych rozwiązań danego problemu. W przyrodzie najczęściej
chodzi o przeżycie osobnika i gatunku. W zastosowaniach informatycznych może to
być przykładowo problem znalezienia najkrótszej drogi w grafie. W takim przypadku
chromosom mógłby zawierać listę krawędzi. Każdy osobnik podlega ocenie, czyli
wyznaczeniu wartości przystosowania. Jest to przypisanie wartości kodowanego przez
niego rozwiązania postawionego zadania. Od sposobu kodowania w dużej mierze
zależy skuteczność działania operatorów krzyżowania i mutacji. Funkcja oceny
rozwiązania może być wprost wynikiem weryfikacji na podstawie danych testowych
lub funkcją heurystyczną odzwierciedlającą warunki oczekiwanego rozwiązania.
Wybór funkcji oceny najczęściej jest kompromisem pomiędzy jakością testu a
szybkością wyliczenia jej wartości. Przy dużej populacji lub częstych zmianach w

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
33
Teoria i zastosowania
Implementacja
Wyniki badań
chromosomach w czasie działania algorytmu genetycznego funkcja przystosowania
jest wyliczana stosunkowo często.
Algorytm genetyczny iteracyjnie modyfikuje populację chromosomów
opisujących rozwiązanie problemu. Zmiany w populacji preferują chromosomy lepiej
przystosowane, czyli opisujące lepsze rozwiązanie. Jednocześnie zapewnione jest
przeszukiwanie wielu obszarów przestrzeni rozwiązań. Po inicjalizacji pierwszej
generacji populacji cykl życia zamyka się w następujących działaniach: określenie
przystosowania chromosomów, wybór chromosomów do krzyżowania, powstanie
nowych osobników w wyniku krzyżowania, ewentualne zastąpienie wybranych
osobników z poprzedniej generacji nowymi osobnikami, mutacja wylosowanych
chromosomów. Szczegółowy opis implementacji algorytmu zawiera Rozdział 7.1.
Poniżej zostały opisane wszystkie operacje wchodzące w skład cyklu życia populacji.
Istnieje wiele wariantów ich realizacji, jednak przedstawione zostały tylko te, które
zostały wykorzystane w badaniach.
W pierwszym kroku tworzona jest wyjściowa populacja chromosomów.
Inicjalizacja ma charakter losowy przy zapewnieniu warunków równomiernego
pokrycia przestrzeni rozwiązań. Skuteczność działania algorytmu zależy od rozmiaru
populacji. Duży rozmiar znacząco zwiększa czas trwania obliczeń, zbyt mały
uniemożliwia odpowiednio szerokie eksplorowanie przestrzeni rozwiązań. W
zależności od sposobu realizacji wymiany osobników po krzyżowaniu, populacja w
kolejnych generacjach może mieć stałą lub zmienną liczebność.
W każdej kolejnej generacji wyliczana jest funkcja przystosowania dla nowych
chromosomów. W zależności od przyjętego sposobu kodowania chromosomu może
istnieć konieczność oznaczenia chromosomów, które kodują rozwiązanie niezgodne z
narzuconymi warunkami. Chromosomy takie mogą być zmodyfikowane tak, żeby
spełniać warunki rozwiązania, mogą zostać usunięte z populacji lub pozostać z
odpowiednio niekorzystną wartością oceny.
W kolejnym kroku wybierane są chromosomy, które będą rodzicami dla nowych
osobników powstałych w czasie krzyżowania. Ze względu na swoją skuteczność,
najczęściej stosowana jest selekcja turniejowa. Populacja jest dzielona na grupy
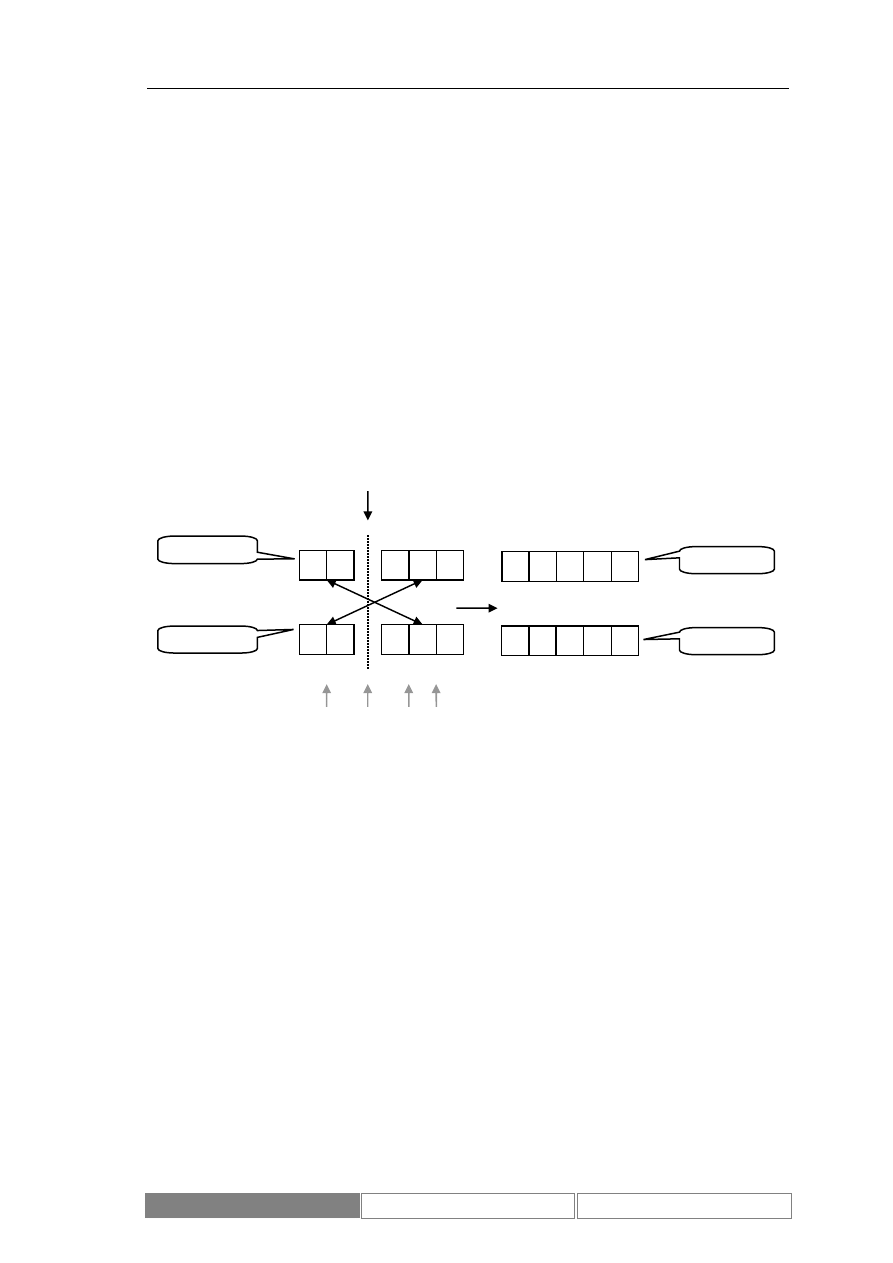
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
34
Teoria i zastosowania
Implementacja
Wyniki badań
osobników, spośród których na podstawie funkcji oceny znajdowani są zwycięzcy.
Zwycięzcy grup stają się rodzicami dla nowych osobników.
Po wskazaniu chromosomów rodziców następuje krzyżowanie zgodnie ze
zdefiniowanym
prawdopodobieństwem.
Najczęściej
wykorzystywane
jest
krzyżowanie jednopunktowe. Polega ono na podziale w określonym miejscu
wektorów opisujących kod chromosomów i utworzeniu nowych osobników poprzez
połączenie różnych odcinków chromosomów rodziców. Diagram 10 prezentuje
opisany sposób powstawania nowych osobników. Nowe osobniki powstałe w czasie
krzyżowania zastępują swoich rodziców.
Diagram 10.
Schemat krzyżowania jednopunktowego
Osobniki w populacji podlegają również losowym zaburzeniom – mutacji.
Mutacja polega na zmianie losowo wybranej wartości z kodu chromosomu na inną
dozwoloną wartość. Mutacje mają miejsce w każdej kolejnej generacji, a ich działanie
jest ograniczone przez zdefiniowane prawdopodobieństwo. W czasie jednej mutacji
zmianie podlega określona liczba cech kodowanych przez chromosom. Parametry
mutacji decydują o możliwości rozszerzenia przez populację obszaru opisywanych
rozwiązań. Ponieważ mutacja ma charakter obligatoryjny, czyli z określonym
prawdopodobieństwem modyfikuje chromosom niezależnie od jego oceny, może
modyfikować populację w potencjalnie niekorzystnym kierunku przystosowania.
X
1
X
2
X
3
Y
1
Y
2
Y
3
Y
4
Y
5
X
2
Y
3
Y
4
Y
5
Y
1
Y
2
X
3
X
1
Rodzic 1
Rodzic 2
Dziecko 1
Dziecko 2
Wybrany podział
Możliwe podziały

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
35
Teoria i zastosowania
Implementacja
Wyniki badań
Pozwala to jednak na eksplorację przestrzeni rozwiązań, której algorytm mógłby nie
osiągnąć za pomocą operatora krzyżowania.
Algorytm genetyczny działa iteracyjnie aż do osiągnięcia zdefiniowanej liczby
generacji lub spełnienia dodatkowych warunków zatrzymania. Oprócz zadanej liczby
iteracji warunkiem zatrzymania może być nieduża zmienność przeciętnego
przystosowania populacji, brak poprawy najlepszego chromosomu w określonym
czasie lub zbyt duża jednorodność populacji zdefiniowana jako bliskość wszystkich
chromosomów do średniej wartości przystosowania. Po zakończeniu ostatniej iteracji
ze wszystkich generacji wybierany jest chromosom o najlepszym przystosowaniu.
Definiuje on rozwiązanie zadania postawionego algorytmowi genetycznemu.
4.3.
Sieć neuronowa
W omawianym systemie predykcyjnym wykorzystane zostały sieci typu
perceptron. Perceptrony to sieci neuronowe zbudowane z neuronów pogrupowanych
w warstwy. Neurony połączone są ze sobą jedynie pomiędzy sąsiednimi warstwami.
Ustalony jest kierunek przepływu sygnału od pierwszej warstwy (wejściowej) do
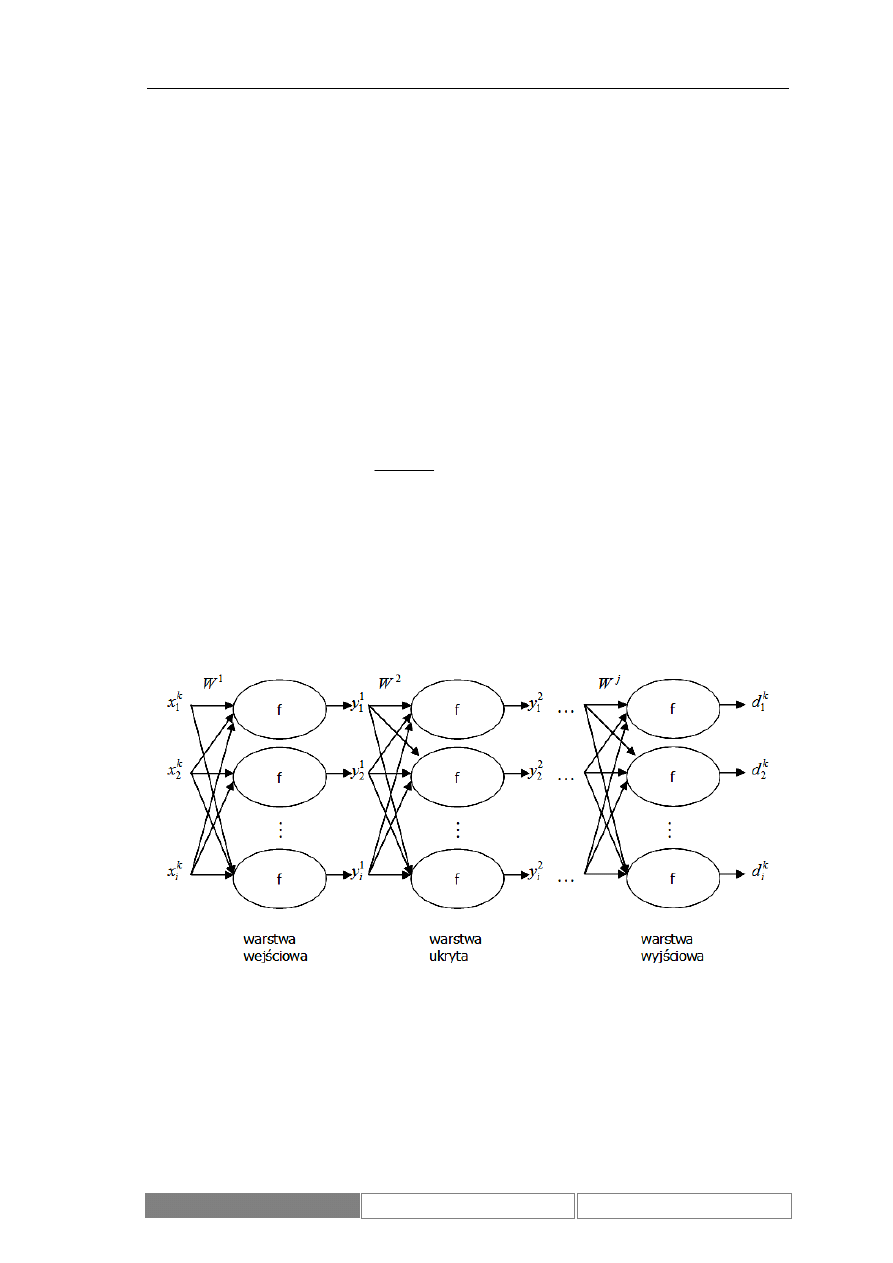
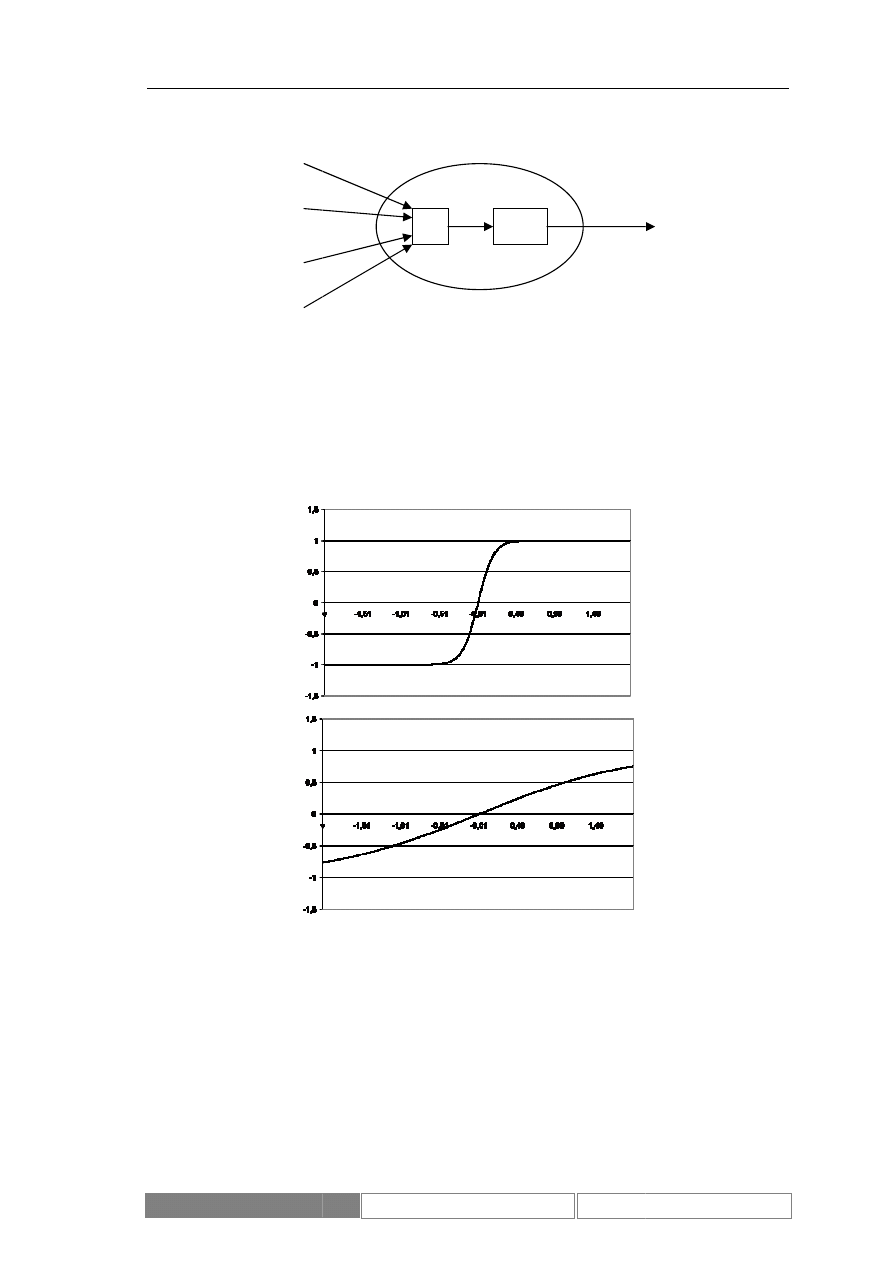
warstwy ostatniej (wyjściowej). Ogólny schemat sieci neuronowych rozważanego typu
z oznaczeniami parametrów i sygnałów zawiera Diagram 11. Dla każdej sieci rozmiary
poszczególnych warstw (indeks i) oraz ich liczba (indeks j) mogą być różne. Przyjęte
zostały następujące oznaczenia:
k
i
x
– wartość i-tego sygnału wejściowego dla k-tej
próbki uczącej,
k
i
d
– wartość i-tego sygnału wejściowego sieci dla k-tej próbki uczącej,
j
i
y
– wartość sygnału wyjściowego i-tego neuronu w j-tej warstwie,
j
W
– wektor wag
j-tej warstwy, f – funkcja aktywacji neuronu [1]. Oznaczenie numeru próbki uczącej jest
obecne jedynie w symbolach sygnałów wejściowych i wyjściowych z sieci. Dla
zachowania czytelności wzorów pozostałe symbole nie zostały oznaczone numerem
próbki.
Każdy neuron w sieci odbiera i przetwarza sygnały liczbowe dochodzące do
niego z poprzedniej warstwy. Do pierwszej warstwy neuronów sygnały są
wprowadzane bez dodatkowego przetworzenia jako zewnętrzne dane wejściowe. Do
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
36
Teoria i zastosowania
Implementacja
Wyniki badań
pozostałych warstw docierają one do neuronu po wzmocnieniu lub osłabieniu
określonym przez wagę, jako iloczyn sygnału oraz wagi połączenia. Po zsumowaniu
sygnał wejściowy jest przetwarzany przez przekształcenie definiujące wartość
przekazaną przez neuron jako jego sygnał wyjściowy. Przekształcenie to zostało
nazwane funkcją aktywacji neuronu. Decyduje ono o charakterystyce jego działania.
Diagram 12 przedstawia model neuronu, gdzie y jest sygnałem wyjściowym neuronu,
i
w
jest wartością wagi połączenia z i-tym neuronem poprzedniej warstwy.
Realizowane przez neuron przekształcenie nieliniowe f w prezentowanych badaniach
jest funkcją sigmoidalną opisaną wzorem [1].
1
1
2
)
(
*
−
+
=
−
v
e
v
f
β
,
[1]
gdzie β jest współczynnikiem definiującym nachylenie wykresu funkcji,
natomiast v jest sygnałem wejściowym. Sterując parametrem β możemy zapewnić, że
w pobliżu punktu 0 funkcja będzie zbliżona np. do funkcji binarnej lub liniowej
(Diagram 13).
Diagram 11.
Model sieci neuronowej
Neuro-genetyczny system komputerowy do prognozowa
Teoria i zastosowania
Diagram 12.
Model neuronu
Diagram 13.
Sigmoidalna funkcja aktywacja dla współczynnika
Metoda nauki sieci neuronowej stosowana w opisywanych badaniach to
propagacja wsteczna z momentem.
kroku modyfikowane są wagi na podstawie informacji o różnicy między uzyskanym
sygnałem wyjściowym a oczekiwaną jego wa
x
1
x
2
x
3
x
i
sygnał wejściowy
genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
Implementacja
Model neuronu
Sigmoidalna funkcja aktywacja dla współczynnika
β=10 i
Metoda nauki sieci neuronowej stosowana w opisywanych badaniach to
propagacja wsteczna z momentem. Jest to algorytm iteracyjny, w którego każdym
kroku modyfikowane są wagi na podstawie informacji o różnicy między uzyskanym
sygnałem wyjściowym a oczekiwaną jego wartością. W każdej iteracji prezentowany
w
1
v
w
2
w
3
w
i
∑
f(v)
wagi połączeń
sumator sygnałów
funkcja aktywacji
sygnał wyjściowy
37
Wyniki badań
=10 i
β=1
Metoda nauki sieci neuronowej stosowana w opisywanych badaniach to
Jest to algorytm iteracyjny, w którego każdym
kroku modyfikowane są wagi na podstawie informacji o różnicy między uzyskanym
W każdej iteracji prezentowany
y
sygnał wyjściowy

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
38
Teoria i zastosowania
Implementacja
Wyniki badań
jest jeden rekord uczący. Po zakończeniu prezentacji wszystkich rekordów uczących
nauka jest powtarzana aż do momentu uzyskania zadowalającego błędu lub
przekroczenia zadanej liczby powtórzeń. Dodatkowy współczynnik (współczynnik
momentu) pozwala na uwzględnienie ostatniej zmiany wag w wyznaczeniu aktualnej
w danym kroku zmiany. Zwiększa to szanse algorytmu na uniknięcie lokalnego
minimum. Opisany powyżej sposób zmiany wag można przedstawić ogólnym
wzorem:
1
)
(
−
∆
+
=
∆
k
k
k
k
k
w
w
p
w
γ
α
,
[2]
gdzie k jest bieżącym krokiem nauki,
α
jest współczynnikiem nauki,
γ
jest
współczynnikiem momentu a p(·) oznacza zmianę wag wynikającą z optymalizacji
działania sieci. Najczęściej przyjmuje się, że współczynnik nauki maleje wraz z
kolejnymi iteracjami. Pozwala to na szybkie znalezienie lokalnego rozwiązania i
dalsze, stopniowe zbliżanie się do niego. Współczynnik momentu ustala wpływ
składnika równego zmianie w poprzedniej iteracji na aktualną zmianę wag. Jego
wielkość także maleje w czasie działania algorytmu. Metoda wyznaczania wartości
p(·) została opisana w kolejnych akapitach.
Istota algorytmu propagacji wstecznej zawiera się w sposobie wyliczenia
aktualnej zmiany wag p(·). Zmiana następuje w kierunku minimum funkcji błędu [3].
∑∑
=
=
=
=
−
=
M
k
k
N
i
i
k
i
k
i
d
r
w
E
1
1
2
)
(
2
1
)
(
,
[3]
gdzie w oznacza wektor wag sieci, i=1..N określa neuron wyjściowy, k=1..M jest
numerem próbki uczącej,
k
i
d
oraz
k
i
r
to odpowiednio sygnał wyjściowy oraz
oczekiwana wartość wyjściowa dla i-tego neuronu, dla k-tej próbki uczącej.
Działanie algorytmu opiera się na wyliczeniu sygnałów generowanych przez sieć
neuronową przy przejściu sygnałów od jej wejścia do wyjścia, z uwzględnieniem
bieżących wartości wag oraz funkcji aktywacji [1]. W drugiej części algorytmu nauki
metodą propagacji wstecznej wykorzystywana jest sieć neuronowa powstała z
wyjściowej sieci poprzez odwrócenie kierunku przepływu sygnałów oraz zamianę
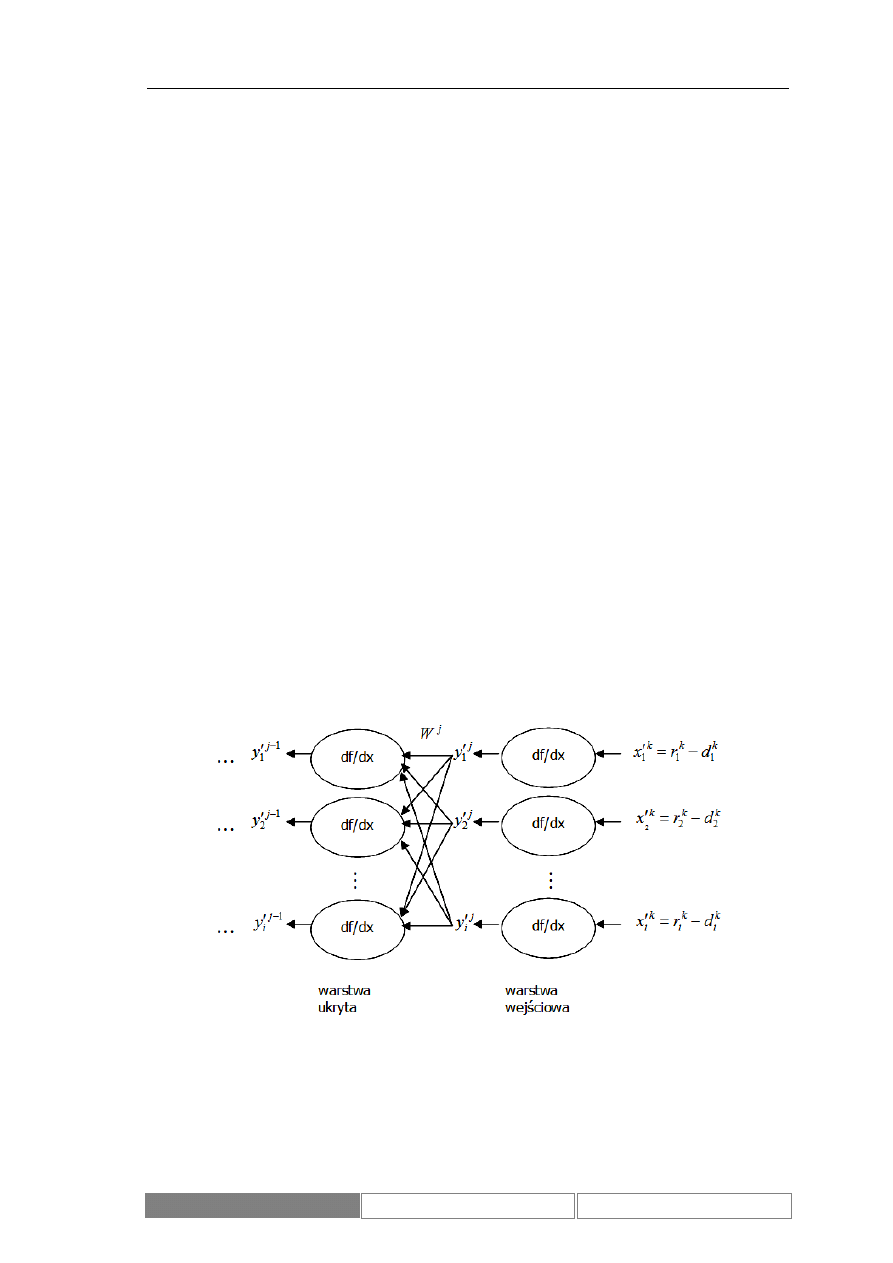
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
39
Teoria i zastosowania
Implementacja
Wyniki badań
funkcji aktywacji na jej pochodną (Diagram 14). Symbole stosowane w opisie
odwróconej sieci neuronowej oznaczone zostały znakiem prim dla swoich
odpowiedników w pierwotnej sieci neuronowej. Jako sygnał wejściowy, do
odwróconej sieci neuronowej, podawana jest wartość błędu zdefiniowana wzorem [4].
k
i
k
i
k
i
d
r
x
−
=
′
[4]
Sygnał wyjściowy i-tego neuronu uwzględnia wartość pochodnej funkcji
aktywacji w punkcie
i
v
sygnału dla pierwotnej sieci, zgodnie ze wzorem [5].
)
(
i
k
i
j
i
v
f
x
y
′
′
=
′
[5]
Przy tak zdefiniowanych oznaczeniach wartość zmiany wagi jest opisana
wzorem [6].
j
n
j
m
k
j
n
m
y
y
w
p
′
=
−
1
,
,
)
(
,
[6]
gdzie
k
j
n
m
w
,
,
oznacza wagę połączenia od m-tego neuronu warstwy j-1 do n-tego
neuronu warstwy j w kroku k (pozostałe oznaczenia są zgodne z dotychczasowymi).
Wyznaczona wartość p(·) ma wpływ na ostateczną zmianę wag zgodnie ze wzorem [2].
Diagram 14.
Model odwróconej sieci neuronowej w nauce metodą propagacji wstecznej

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
40
Teoria i zastosowania
Implementacja
Wyniki badań
Zmiana wag jest wyliczana i uwzględniana dla każdego rekordu ze zbioru
rekordów uczących. Algorytm działa przez zdefiniowaną liczbę iteracji. Dodatkowo
stosowany jest warunek zatrzymania nauki na podstawie aktualnego błędu działania
sieci. Wyliczany jest on w każdej iteracji dla wybranych rekordów (rekordy
walidacyjne), które nie są bezpośrednio wykorzystywane do wyliczania zmian
wartości wag. W procesie nauki błąd sieci dla rekordów walidacyjnych maleje w
kolejnych iteracjach. Istnieje jednak zjawisko przeuczenia sieci neuronowej, czyli
moment, w którym błędy te zaczynają rosnąć. Wystąpienie przeuczenia stanowi
podstawę do zatrzymania dalszej nauki. Nauczona sieć neuronowa jest testowana na
wartościach trzeciej grupy rekordów – rekordach testowych. Rekordy te nie są
wykorzystywane w procesie nauki, ani do wyliczania wag, ani do zatrzymania tego
procesu.
4.4.
Cel prognozy i miara sukcesu
Celem badań jest skonstruowanie systemu pozwalającego na prognozę zmiany
wartości indeksu giełdowego w kolejnym dniu. System wykorzystuje spektrum
danych zdefiniowanych w analizie technicznej. Pochodzą one nie tylko z giełdy
prognozowanej, ale również z wybranych innych giełd światowych oraz sytuacji na
rynku walut. Badania obejmują zachowanie algorytmu, szczególnie modułu algorytmu
genetycznego oraz analizę uzyskanych wyników prognozy. Wyniki przedstawione są
jako średni błąd prognozy oraz zysk w czasie hipotetycznego inwestowania na giełdzie
w oparciu o dane generowane przez system. Do porównania zostało zbudowanych
pięć alternatywnych algorytmów inwestycyjnych – algorytm losowy, model oparty na
metodzie "kupuj i trzymaj", heurystyka oparta na zachowaniu trendu, heurystyka
oparta na wartościach oscylatora MACD oraz inwestowanie z uwzględnieniem
znajomości przyszłości.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
41
Teoria i zastosowania
Implementacja
Wyniki badań
Dział B.
Implementacja
Poniższe
rozdziały
zawierają
definicje
przekształceń tworzących zbiór zmiennych oraz
sposób
ich
zastosowania.
Zaprezentowane
zostały
również
szczegóły
implementacji
zaproponowanego systemu neuro-genetycznego.
5.
Przekształcenia danych
Jeśli nie zostało podane inaczej, w dalszych wzorach występujących w tym
rozdziale stosuje się następujące oznaczenia: k jest długością okresu, dla którego
liczone jest przekształcenie, V
i
oznacza wartości indeksu lub oscylatora w dniu i, gdzie
V=O dla wartości otwarcia, V=C dla wartości zamknięcia, V=H dla największej wartości
w ciągu dnia, V=L dla najmniejszej wartości w ciągu dnia. W przypadku opisu
oscylatora, V przyjmuje jego nazwę (np. V=MACD). Dla i=0 V
i
jest wartością z
bieżącego (względem obliczeń) dnia.
5.1.
Przekształcenia danych źródłowych
Na
podstawie
wartości
indeksu
zostały
wyznaczone
podstawowe
przekształcenia: wartości ważonych średnich kroczących [7] dla okresów 5-, 10-, 20-
dniowych dla V=O oraz względne zmiany wartości indeksu [8] w okresie 1, 5, 10, 20
dni.
∑
∑
+
−
=
+
−
=
+
−
+
−
=
t
k
t
i
t
k
t
i
i
V
k
k
t
i
V
k
t
i
t
avg
1
1
)
(
*
)
(
)
(
[7]

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
42
Teoria i zastosowania
Implementacja
Wyniki badań
k
t
k
t
t
k
O
O
O
t
pc
−
−
−
=
)
(
[8]
Dane wykorzystane do nauki prognozy zostały przeskalowane do przedziału
[
−
1,1] za pomocą przekształcenia [9]:
)
max( A
A
A
i
i
→
,
[9]
gdzie A jest zbiorem wartości danej zmiennej, max(
|
A
|
) wartością największą
zbioru modułów wartości A zaobserwowanych do danej chwili. Dane podlegające
skalowaniu podaje Tabela XV (Załącznik A).
5.2.
Oscylatory
Oscylatory (Murphy 1999) zgodnie z analizą techniczną definiują przekształcenia
pomagające w analizie zachowania rynku, w szczególności sygnałów potencjalnej
zmiany trendu. Jako dane, na podstawie których wykonywana była prognoza
wykorzystane zostały zarówno wartości oscylatorów jak i sygnały kupna lub
sprzedaży generowane przez wybrane oscylatory. Sygnały te mają zastosowanie
pomocnicze i odzwierciedlają jedynie podstawowe własności oscylatorów. Inwestorzy
giełdowi
wykorzystują
sygnały
uwzględniając
szereg
innych
czynników,
nieuwzględnionych w niniejszych badaniach. Poniżej zdefiniowane zostały wszystkie
wykorzystywane oscylatory.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
43
Teoria i zastosowania
Implementacja
Wyniki badań
MACD
)
(
)
(
)
(
20
10
t
avg
t
avg
t
MACD
O
O
−
=
[10]
)
(
)
(
)
(
20
5
t
avg
t
avg
t
MACD
MACD
MACD
LS
−
=
[11]
Wykorzystanie oscylatora MACD opiera się na analizie zachowania linii MACD
[10] oraz linii sygnału MACD
LS
[11]. Oscylator ten generuje sygnały kupna i sprzedaży
w punktach przecięcia obu linii zgodnie z poniższymi warunkami.
)
1
(
)
1
(
)
(
)
(
:
)
1
(
)
1
(
)
(
)
(
:
−
>
−
=
−
<
−
=
t
MACD
t
MACD
i
t
MACD
t
MACD
t
dniu
w
sprzedaj
t
MACD
t
MACD
i
t
MACD
t
MACD
t
dniu
w
kupuj
LS
LS
LS
LS
[12]
Dwie Średnie
)
(
)
(
)
(
2
20
5
t
avg
t
avg
t
avgs
O
O
−
=
[13]
Na podstawie aktualnych wartości średnich kroczących określany jest sygnał
kupna lub sprzedaży zgodnie z poniższymi zależnościami.
0
)
1
(
2
0
)
(
2
:
0
)
1
(
2
0
)
(
2
:
>
−
≤
<
−
≥
t
avgs
i
t
avgs
t
dniu
w
sprzedaj
t
avgs
i
t
avgs
t
dniu
w
kupuj
[14]
Williams
)
(
min
)
(
max
)
(
max
100
)
(
t
t
C
t
t
WILLIAMS
L
k
H
k
t
H
k
k
−
−
=
[15]
dla k=10, gdzie
H
k
max
oznacza największą wartość indeksu spośród k ostatnich
dni,
L
k
min
oznacza najmniejszą wartość spośród k ostatnich dni.
Sygnały kupna lub sprzedaży oscylatora Williams są generowane odpowiednio
przy przekraczaniu przez wartości oscylatora progów 20 i 80 punktów, zgodnie z
poniższymi warunkami.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
44
Teoria i zastosowania
Implementacja
Wyniki badań
20
)
1
(
20
)
(
:
80
)
1
(
80
)
(
:
≤
−
>
≥
−
<
t
WILLIAMS
i
t
WILLIAMS
t
dniu
w
sprzedaj
t
WILLIAMS
i
t
WILLIAMS
t
dniu
w
kupuj
[16]
gdzie WILLIAMS(t) oznacza wartość oscylatora WILLIAMS w dniu t.
Impet
k
t
k
C
C
t
IMPET
−
=
)
(
[17]
dla k=5, 10, 20.
Wartość parametru k określa czułość oscylatora na zmiany wartości. Często
przecięcia wartości oscylatora oraz linii 0 są odczytywane jako sygnały kupna lub
sprzedaży, jednak najczęściej analizie podlega zachowanie oscylatora w celu określenia
siły trendu na giełdzie.
ROC (Wskaźnik zmian)
k
t
k
C
C
t
ROC
100
)
(
=
[18]
dla k=5, 10, 20.
Oscylator ROC jest uzupełnieniem oscylatora IMPET, prezentując tempo zmian
opisywanej wartości. Oscylator ten nie generuje sygnałów.
RSI (Wskaźnik siły względnej)
}
0
,
max{
)
(
i
t
i
C
C
t
pos
−
=
[19]
}
0
,
max{
)
(
t
i
i
C
C
t
neg
−
=
[20]

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
45
Teoria i zastosowania
Implementacja
Wyniki badań
∑
∑
=
=
=
k
i
i
k
i
i
k
t
neg
t
pos
t
RS
1
1
)
(
)
(
)
(
[21]
)
(
1
100
100
)
(
t
RS
t
RSI
k
k
+
−
=
[22]
dla k=5.
Sygnały kupna lub sprzedaży generowane są przez oscylator RSI przy
przekraczaniu wartości progów 30 i 70 punktów, zgodnie z poniższymi warunkami.
70
)
1
(
70
)
(
:
30
)
1
(
30
)
(
:
>
−
<
<
−
>
t
RSI
i
t
RSI
t
dniu
w
sprzedaj
t
RSI
i
t
RSI
t
dniu
w
kupuj
[23]
Oscylator RSI powstał jako ulepszenie oscylatora IMPET, uniezależniając go od
gwałtownych, ale chwilowych zmian, jednocześnie ograniczając jego wartości do
stałego przedziału [0,100]. Analogicznie do oscylatora IMPET, wartość parametru k
określa czułość oscylatora na zmiany wartości.
SO (Oscylator stochastyczny), FSO (Szybki oscylator stochastyczny)
)
(
min
)
(
max
)
(
min
100
)
(
t
t
t
C
t
SO
L
k
H
k
L
k
t
k
−
−
=
[24]
)
(
)
(
t
avg
t
FSO
SO
k
=
,
[25]
gdzie
SO
k
avg
jest średnią wartością oscylatora SO dla k dni (dla oscylatora SO
k=14, dla FSO k=3).
Oscylatory stochastyczne SO i FSO określają relacje pomiędzy ostatnią ceną
zamknięcia a wahaniami cen w okresie zdefiniowanym przez parametr k. Inwestorzy
wykorzystują większe wartości tego parametru, jednak na potrzeby jednodniowej
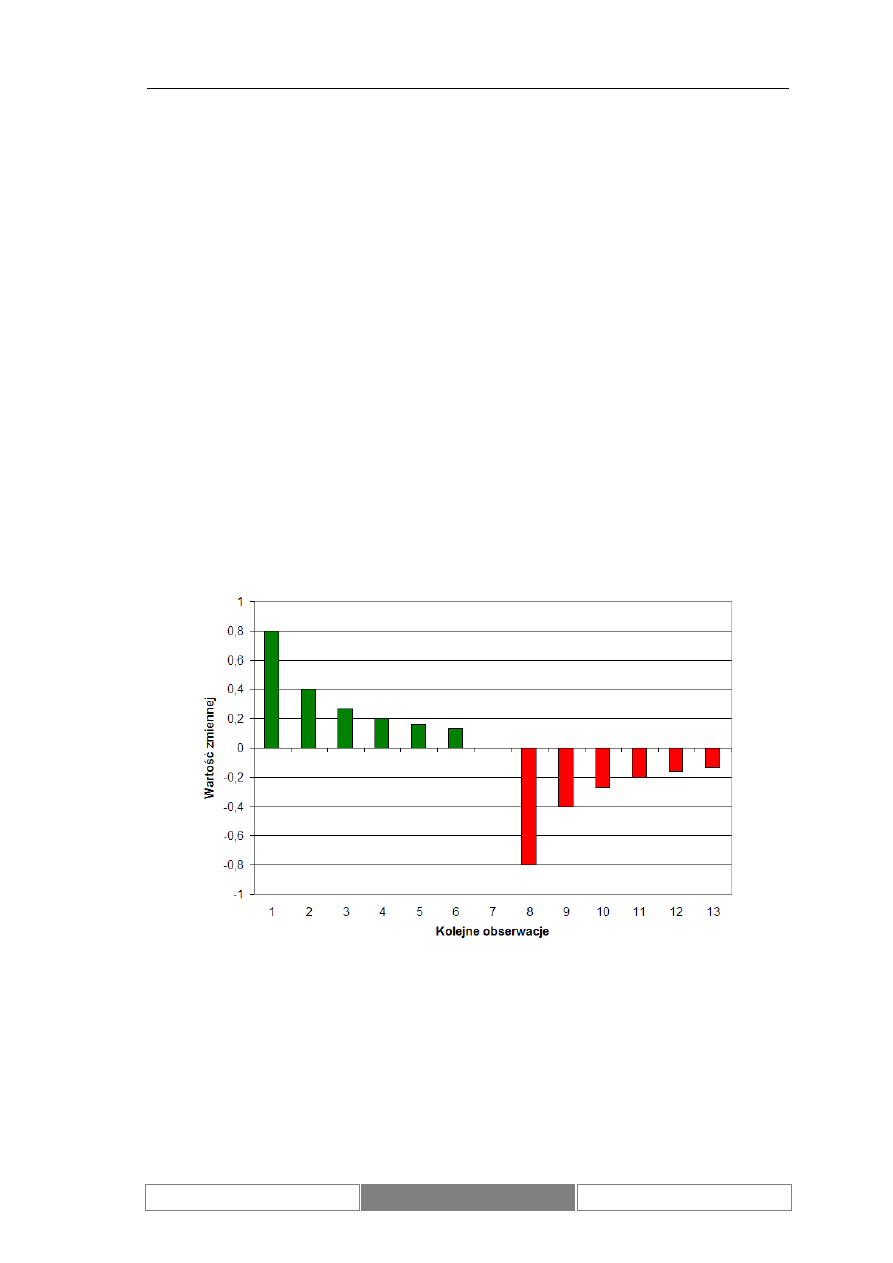
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
46
Teoria i zastosowania
Implementacja
Wyniki badań
prognozy w niniejszych badaniach przyjęte zostały wartości minimalne. W rozprawie
wykorzystane są jedynie numeryczne wartości oscylatora Impet oraz pozostałych
oscylatorów ROC, RSI, SO i FSO, bez sygnałów przez nie generowanych.
5.3.
Kodowanie sygnałów kupna i sprzedaży
W poprzednim rozdziale podane zostały warunki, przy których uznaje się, że
dany oscylator generuje sygnały kupna lub sprzedaży. Informacja ta (dla oscylatorów
MACD, Dwie Średnie oraz Williams) jest zapisana w danych w sposób numeryczny.
Wartości przypisane poszczególnym sygnałom to: kupuj = 0.8, sprzedaj =
−
0.8. Sygnały
zostały zapisane nie tylko dla dni, w których zostały wygenerowane, ale również dla
pięciu kolejnych dni, zmniejszając swoją wartość (Diagram 15). Ma to swoje
uzasadnienie w tym, że sygnał najczęściej jest prawdziwy również w ciągu kilku
kolejnych dni.
Diagram 15.
Kodowanie sygnałów kupna (wartości dodatnie) i sprzedaży (wartości ujemne)

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
47
Teoria i zastosowania
Implementacja
Wyniki badań
5.4.
Algorytm wyznaczania formacji
Rozdział 2.4 opisuje podstawowe własności oraz wykorzystanie formacji w
analizie technicznej. W niniejszym rozdziale przedstawiony został autorski algorytm
wyznaczania formacji oraz przykładowy wynik jego działania.
W pierwszym kroku wyznaczane są wszystkie lokalne minima (dna) i maksima
(szczyty) wykresu wartości indeksu giełdowego. Najczęściej jednak zidentyfikowane
wierzchołki wykresu znajdują się jednak w zbyt bliskiej odległości od siebie by
umożliwić oczekiwaną identyfikację formacji. Konieczne jest wybranie optimów
istotnych dla identyfikacji formacji.
Wybór lokalnych optimów dla właściwej identyfikacji formacji ma miejsce w
drugim kroku algorytmu. Z listy wszystkich lokalnych optimów usuwane są
wierzchołki, dla których procentowa różnica wartości indeksu w stosunku do
poprzedniego wierzchołka odmiennego typu nie przekracza progu
ε
=0.01. Parametr
ten pozwala na sterowanie „długością” formacji, czyli liczbą dni jakie może obejmować
swoim zasięgiem. Im większa wartość parametru, tym więcej wierzchołków jest
eliminowanych. Ponieważ formacja rozpinana jest na stałej liczbie wierzchołków,
oznacza to ich większą „długość”. Dla
ε
=0 żaden z wierzchołków nie zostanie
usunięty w drugim kroku algorytmu. W efekcie potencjalne formacje będą miały
„długość” rzędu tygodnia. Diagram 16 prezentuje wykres wartości indeksu z
zaznaczonymi wierzchołkami wybranymi w pierwszych dwóch krokach algorytmu.
Widoczna jest również formacja głowy i ramion, zidentyfikowana w ostatnim, trzecim
kroku algorytmu.
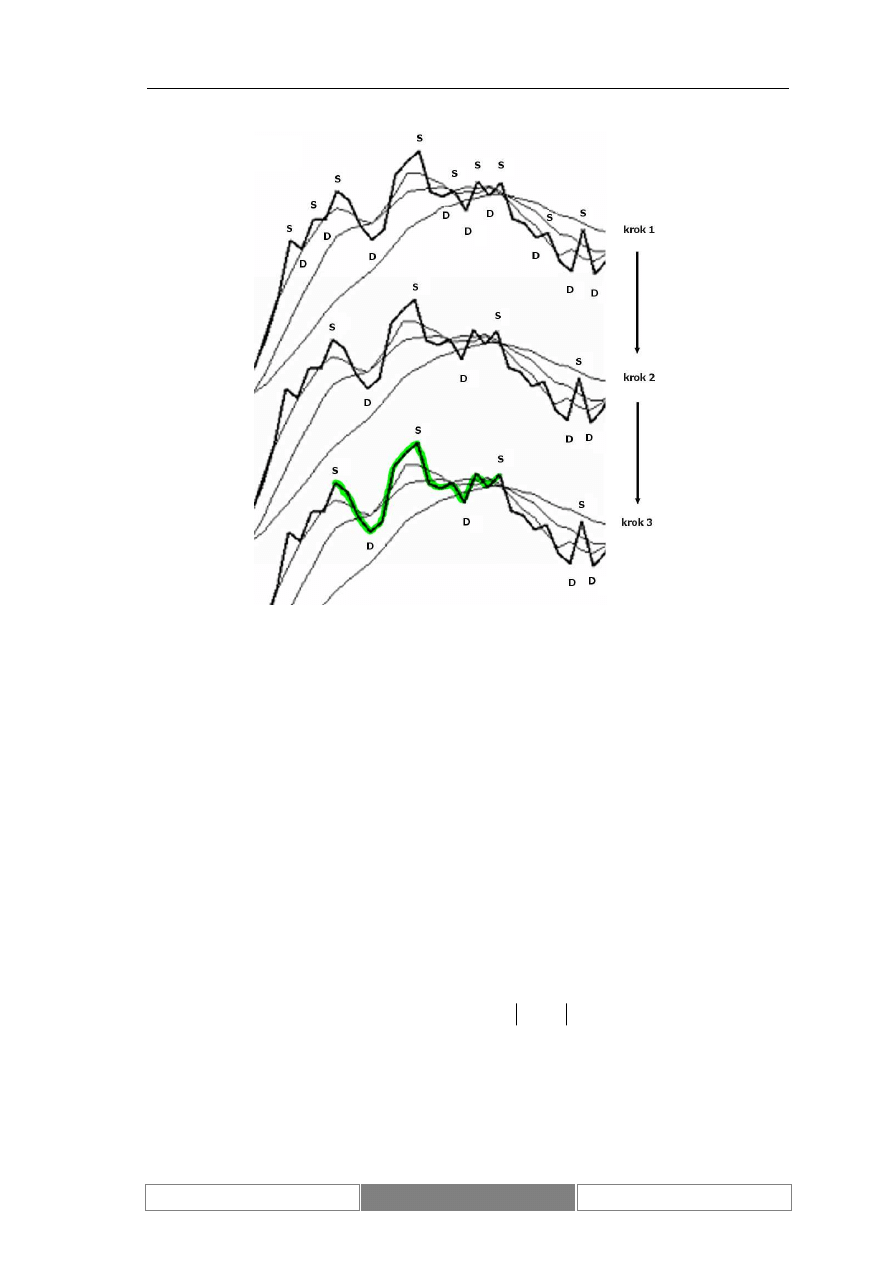
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
48
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 16.
Działanie algorytmu wyznaczania formacji (S-szczyt, D-dno)
W kroku trzecim na bazie oznaczonych wierzchołków dokonuje się właściwa
identyfikacja formacji. Na potrzeby porównywania charakterystycznych punktów
wykresu wprowadzone zostały pojęcia „podobieństwa” oraz „różnicy” punktów,
zdefiniowane zależnościami [26], [27]. Uznaje się, że dwa punkty mają podobne
wartości, jeśli różnica między nimi nie przekracza zdefiniowanego progu
p
ε
.
Analogicznie, uznaje się, że dwa punkty mają różne wartości, jeśli różnica między nimi
jest większa niż zdefiniowany próg
r
ε
.
≤
−
=
.
.
)
,
(
2
1
2
1
p
p
w
z
s
ł
a
f
x
x
dla
a
d
w
a
r
p
x
x
e
n
b
o
d
o
p
p
ε
[26]

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
49
Teoria i zastosowania
Implementacja
Wyniki badań
>
−
=
.
.
)
,
(
2
1
2
1
p
p
w
z
s
ł
a
f
x
x
dla
a
d
w
a
r
p
x
x
e
n
ż
ó
r
r
ε
[27]
dla
p
ε
=100,
r
ε
=10.
Na podstawie definicji „podobieństwa” oraz „różnicy” zdefiniowane zostały
następujące operatory:
)
,
(
2
,
1
2
1
x
x
e
n
b
o
d
o
p
x
x
⇔
=′
[28]
)
,
(
2
,
1
2
1
2
1
x
x
e
n
ż
ó
r
i
x
x
x
x
>
⇔
>′
[29]
)
,
(
2
,
1
2
1
2
1
x
x
e
n
ż
ó
r
i
x
x
x
x
<
⇔
<′
[30]
Każda z formacji opisana jest poprzez wzorzec stworzony z kolejnych 5
wierzchołków. Przykładowo, wzorzec formacji głowy i ramion został zdefiniowany w
następujący sposób:
)
B
(B
)
S
(S
)
S
(S
)
S
(B
)
S
(S
)
B
(S
4
2
5
1
5
3
5
4
1
3
2
1
=′
∧
=′
∧
>′
∧
<′
∧
>′
∧
>′
,
[31]
gdzie S
i
oznacza i-ty wierzchołek będący lokalnym maksimum, B
i
oznacza i-ty
wierzchołek będący lokalnym minimum, a
∧
jest iloczynem logicznym. Powyższy
wzorzec został zidentyfikowany na przykładowym fragmencie wykresu (Diagram 16).
Liczbę znalezionych formacji w rozważanych danych giełdowych zawiera
Tabela II.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
50
Teoria i zastosowania
Implementacja
Wyniki badań
Formacja
Prognoza
Liczba wystąpień
podwójne dno
zmiana trendu
157
podwójny szczyt
zmiana trendu
184
pojedyncze dno
zmiana trendu
54
pojedynczy szczyt
zmiana trendu
54
potrójne dno
zmiana trendu
95
potrójny szczyt
zmiana trendu
239
trójkąt rosnący
zachowanie trendu
0
trójkąt malejący
zachowanie trendu
24
prostokąt rosnący
zachowanie trendu
119
prostokąt malejący
zachowanie trendu
95
głowa i ramiona
zmiana trendu
156
odwrócona głowa i ramiona
zmiana trendu
112
łącznie
1289
Tabela II.
Formacje zidentyfikowane w danych w okresie od 1995/01/30 do 2004/09/01
5.5.
Kodowanie informacji o formacji
Jako dane uczące dla sieci neuronowej podawane są zarówno informacje o
konkretnej formacji, jak również prognoza zmiany lub zachowania trendu, wynikająca
z typu formacji. Prognozy zmiany lub zachowania trendu dla poszczególnych dni
zapisywane są jako wartości
−
1 oraz 1. Konstrukcja algorytmu wyznaczającego
formacje pozwala na pokrywanie się formacji w pewnych przedziałach czasu. W takim
przypadku wartości opisujące typ formacji są sumowane uwzględniając ich znak.
Identyfikacja w tym samym czasie formacji o różnym typie spowoduje wyzerowanie
informacji o prognozie zmiany lub zachowania trendu. Analogicznie jak dla sygnałów
generowanych przez oscylatory, informacja o formacji jest zapisywana przez kolejnych
5 dni od wystąpienia formacji (por. Rozdział 5.3). Dane te podlegają w późniejszym
etapie skalowaniu zgodnie z przekształceniem [9]. Wszystkie dane wynikające z
identyfikacji formacji zapisywane są w rekordach występujących bezpośrednio po
rekordach faktycznie zawierających daną formację. W przeciwnym przypadku
oznaczenie tych punktów wynikiem identyfikacji formacji byłoby wykorzystaniem

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
51
Teoria i zastosowania
Implementacja
Wyniki badań
informacji z przyszłych obserwacji ponieważ identyfikacja formacji wymaga
znajomości wszystkich punktów ją opisujących.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
52
Teoria i zastosowania
Implementacja
Wyniki badań
6.
Wybór danych wejściowych
6.1.
Dziedzina zmiennych wejściowych
W Rozdziale 5 przedstawione zostały przekształcenia wykorzystane do
uzyskania zmiennych opisujących sytuację na giełdzie. Podsumowanie dostępnych dla
prognozy zmiennych zawiera Tabela XV (Załącznik A). Zmienne te można podzielić
na trzy grupy ze względu na ich pochodzenie. Pierwsza grupa, to bezpośrednie
wartości indeksu będące jednocześnie danymi źródłowymi pochodzącymi z
obserwacji. Druga grupa, to statystyczne przekształcenia wartości indeksu: procentowe
zmiany oraz średnie kroczące. Ostatni rodzaj zmiennych jest związany z analizą
techniczną giełdy. Do tej grupy należą informacje o formacjach oraz wartości
oscylatorów wraz z generowanymi przez nie sygnałami kupna i sprzedaży. Wykresy
wartości wybranych zmiennych zostały przedstawione na poniższych diagramach
(Diagram 17 - Diagram 21). Zaprezentowane wartości nie zostały przeskalowane i są
ograniczone do wybranych 50 dni obserwacji. Skalowanie jest stosowane jako ostatni
krok przekształceń danych wejściowych do nauki i prognozy. Na diagramach
opisujących oscylatory Impet i ROC widoczne są różnice wykresów oscylatorów tego
samego typu, ale dla różnych wartości parametrów sterujących k (zgodnie ze wzorami
[17][18]). Dla k=5 wartości oscylatorów Impet i ROC charakteryzują się większą
zmiennością niż analogiczne wykresy dla parametru k=10 oraz k=20. Wynika to wprost
z konstrukcji oscylatorów.
Niezależnie od zakresu informacyjnego zawartego w zmiennych opisujących
daną giełdę istnieją zależności pomiędzy zachowaniem inwestorów a sytuacją na
innych rynkach oraz informacjami pozagiełdowymi. Przykładowe wykorzystanie
informacji z wielu światowych giełd zostało opisane w publikacji (Podding, Rehkegler
1996). W niniejszych badaniach położono akcent na pokazanie i wykorzystanie
zależności między zmiennymi prognozowanej giełdy niemieckiej (GSE, indeks DAX)
oraz dwóch wybranych rynków z innych części świata (japońska giełda TSE, indeks
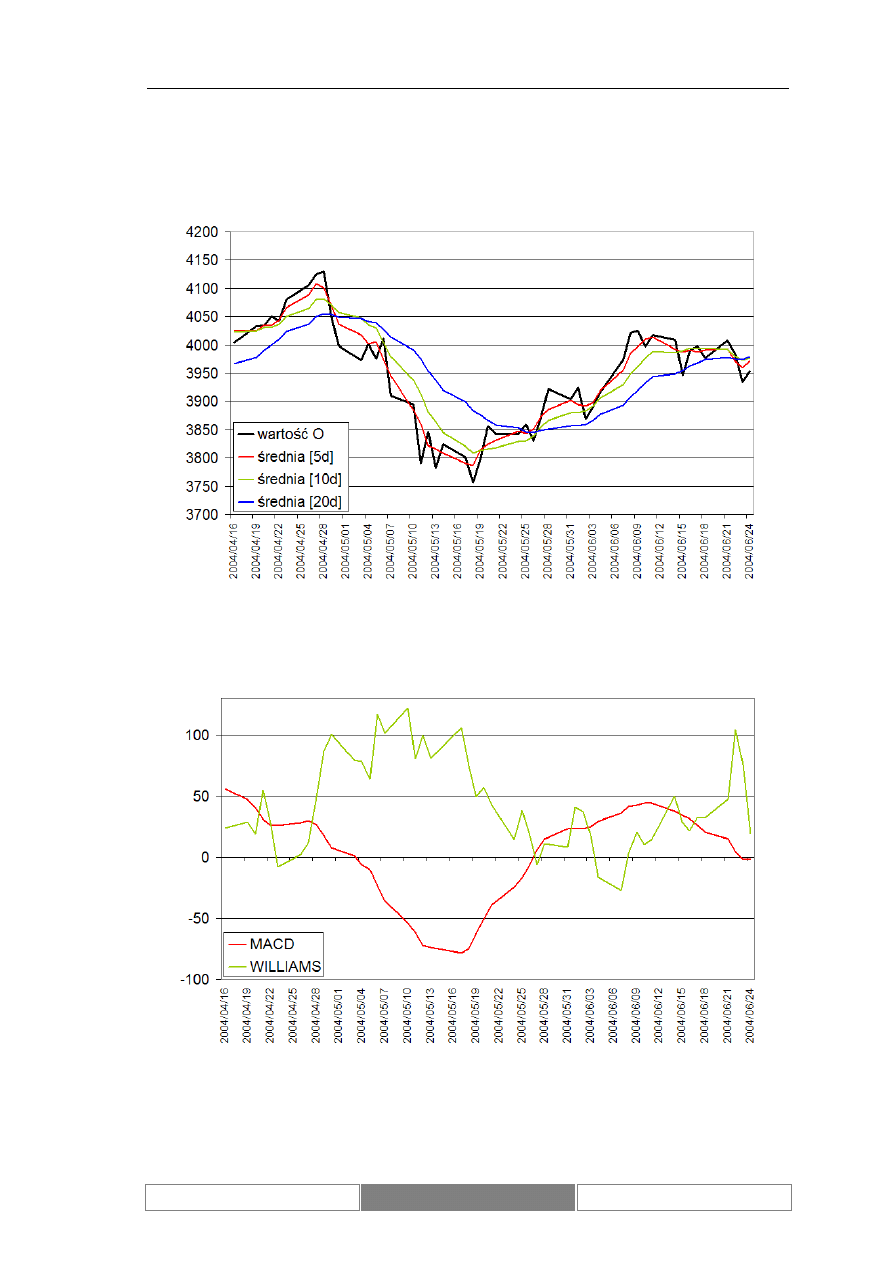
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
53
Teoria i zastosowania
Implementacja
Wyniki badań
NIKKEI; amerykańska giełda NYSE, indeks DJIA). Wyniki analizy korelacji pomiędzy
zmiennymi zostały zaprezentowane w Rozdziale 6.2.
Diagram 17.
Wartości indeksu oraz średnie 5-, 10-, 20-dniowe
Diagram 18.
Wartości oscylatorów MACD i Williams
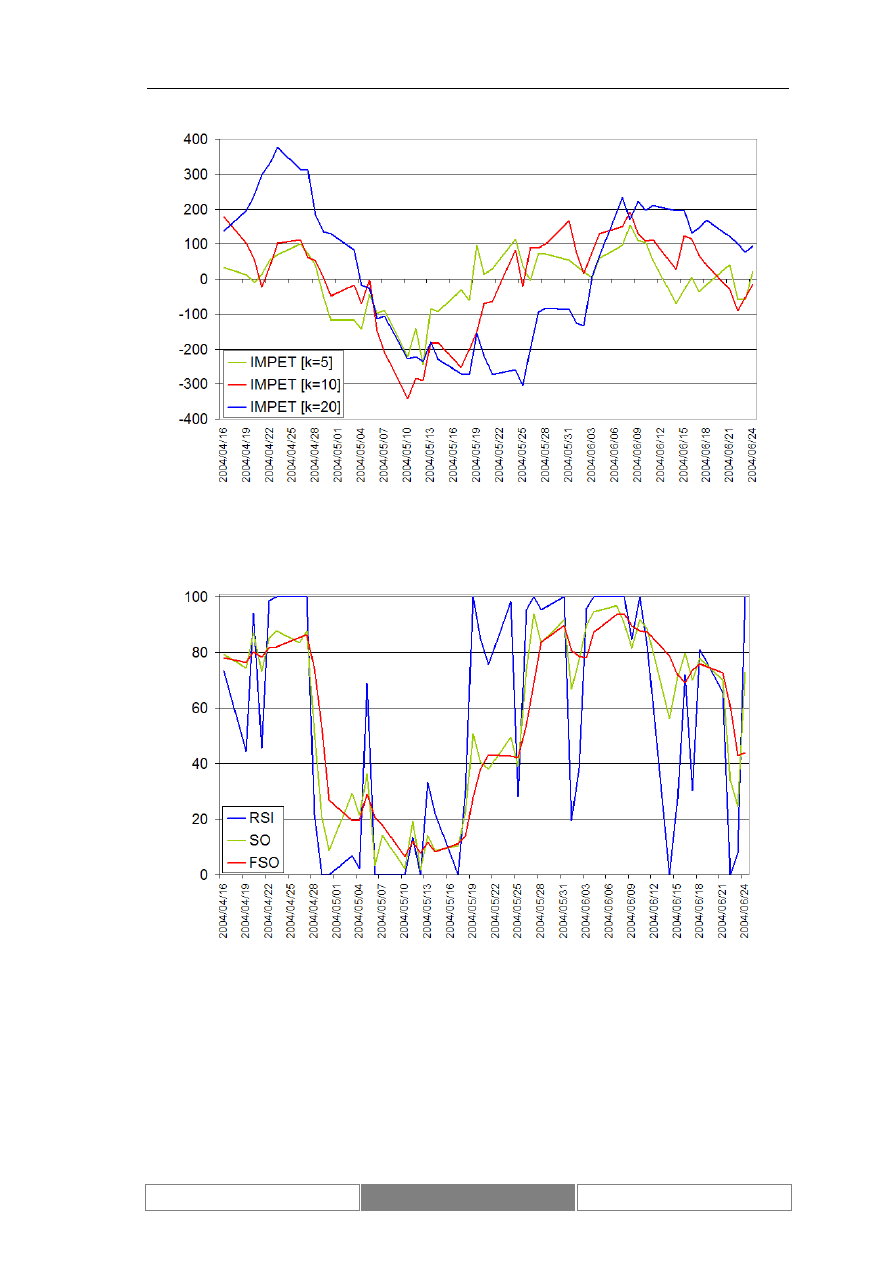
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
54
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 19.
Wartości oscylatora Impet dla k=5, 10, 20
Diagram 20.
Wartości oscylatorów RSI, Stochastycznego (SO), Szybkiego Stochastycznego
(FSO)
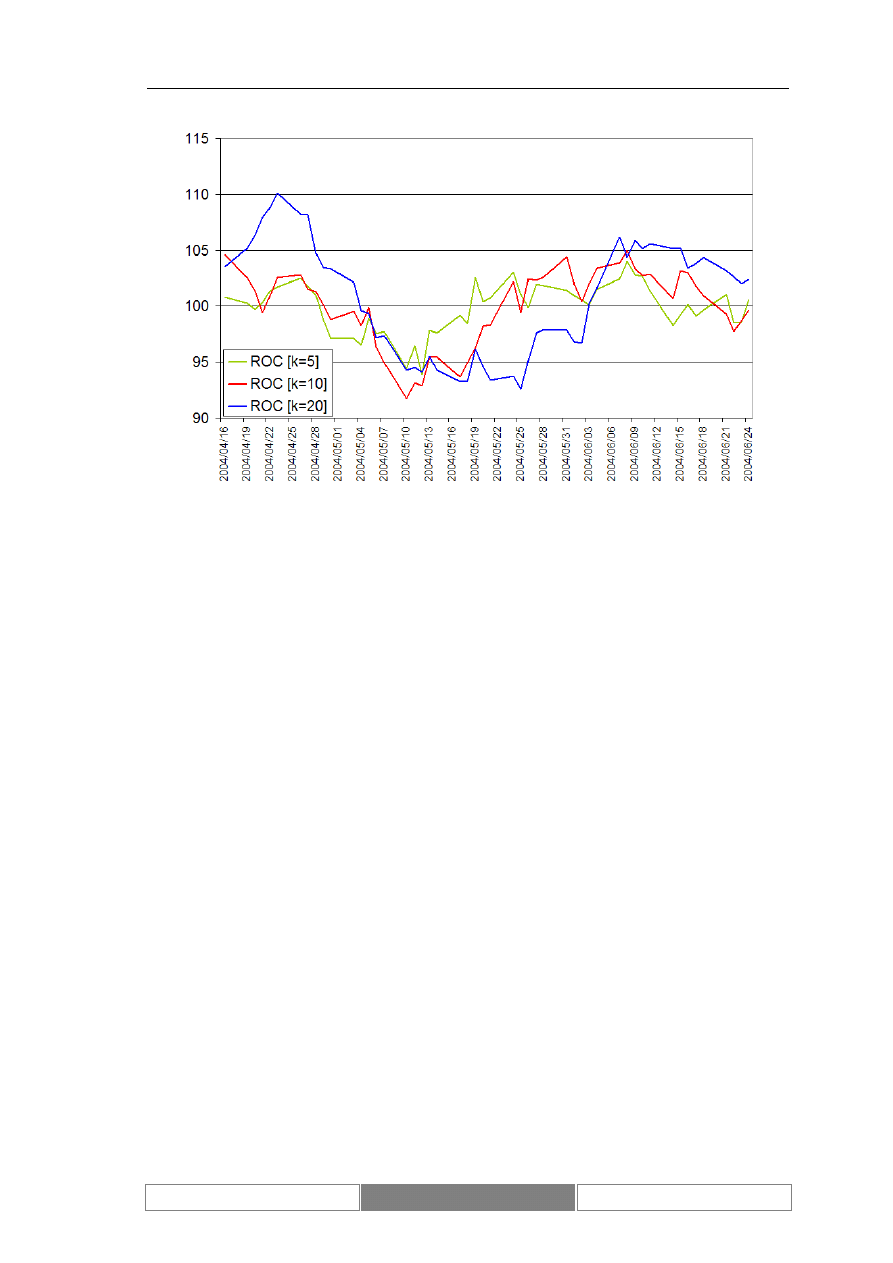
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
55
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 21.
Wartości oscylatora ROC dla k=5, 10, 20 (horyzont 50 dni)
6.2.
Korelacja miedzy zmiennymi
Rynki papierów wartościowych, przy dzisiejszej skuteczności przepływu
informacji, wykazują zachowania analogiczne do zmian w systemie naczyń
połączonych. Sytuacja na dużych rynkach międzynarodowych ma wpływ na pozostałe
rynki. Analiza zależności między zmiennymi opisującymi zachowanie giełdy oraz
wykorzystanie tych zależności zostały przedstawione w pracach (Ormoneit 1999;
Thawornwong, Enke 2004). Zależności między zmiennymi wykorzystanymi w
niniejszych badaniach zostały zdefiniowane na podstawie korelacji liniowej
wyznaczonej przez współczynnik Pearson’a (LC
Pearson
). Wzór [32] definiuje korelację
zmiennych x i y. Wartości współczynnika LC
Pearson
bliskie
−
1 lub 1 oznaczają wysoką
korelację zmiennych.
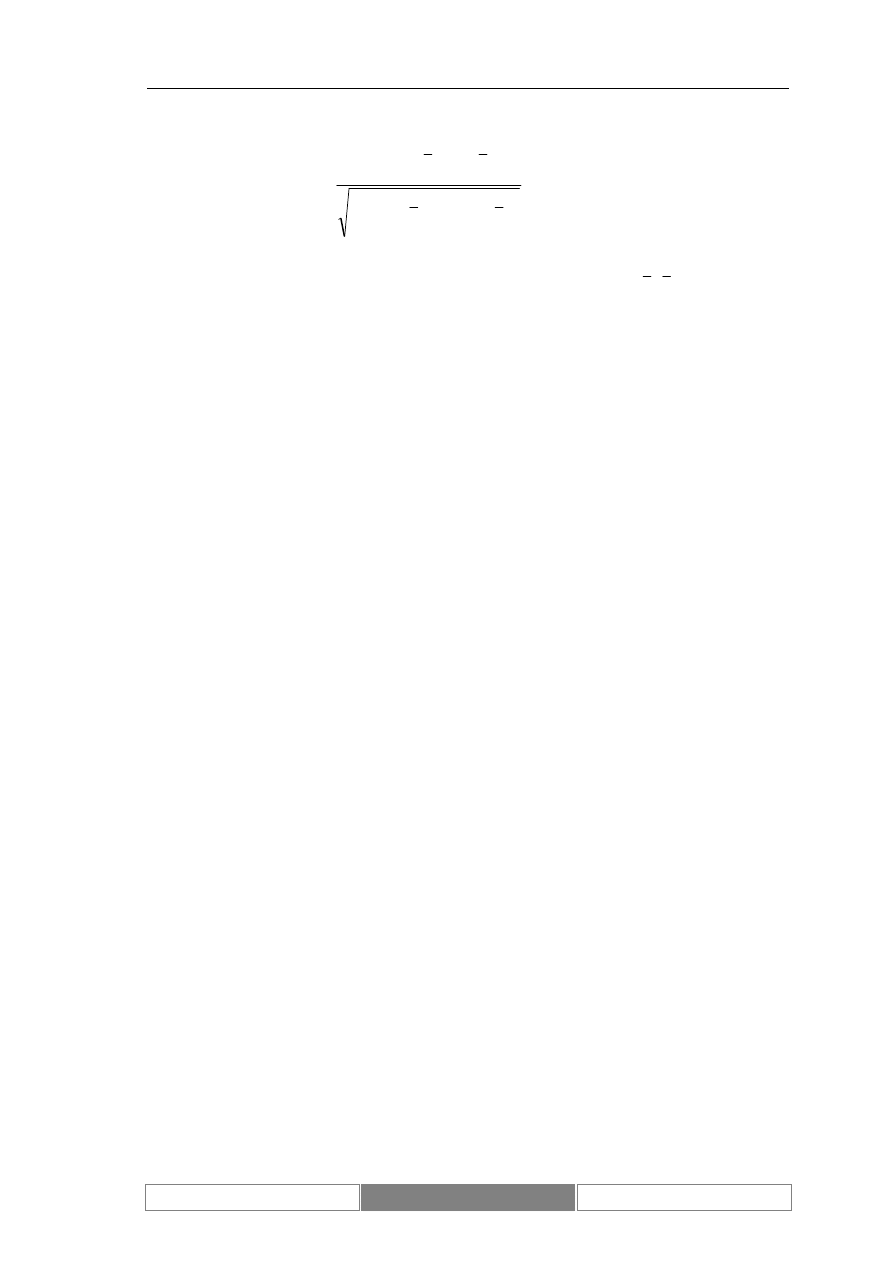
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
56
Teoria i zastosowania
Implementacja
Wyniki badań
∑
∑
∑
=
=
=
=
=
=
−
−
−
−
=
n
i
i
i
n
i
i
i
n
i
i
i
i
Pearson
y
y
x
x
y
y
x
x
LC
1
2
1
2
1
)
(
)
(
)
)(
(
,
[32]
gdzie n jest liczbą elementów w zbiorze zmiennych x i y,
y
i
x
są wartościami
średnimi odpowiednio zmiennych x i y.
Korelacje między prognozowaną zmienną, którą jest wartość ceny zamknięcia
indeksu, a wszystkimi zmiennymi z trzech giełd przedstawia Diagram 22. Korelacja
została policzona dla wszystkich rekordów z dostępnego przedziału czasu. Wskazane
zostały
najbardziej
charakterystyczne
zależności.
Największa
korelacja
z
prognozowaną zmienną występuje dla zmiennych pochodzących z tej samej giełdy.
Wyraźna jest również korelacja pomiędzy giełdą niemiecką (GSE) i amerykańską
(NYSE). Znacząca jest zależność między wartościami ceny zamknięcia indeksu. Dużo
mniejsze zależności widoczne są dla giełdy japońskiej (TSE).
Na omawianym diagramie widoczne są powtarzające się schematy rozkładu
korelacji dla określonych grup zmiennych. Największe korelacje prognozowanej
zmiennej występują z wartościami zmian cen zamknięcia indeksu. Inna,
charakterystyczna ze względu na silną korelację, grupa zmiennych widocznych na
wykresie na prawo od zmiany ceny indeksu to wartości oscylatorów.
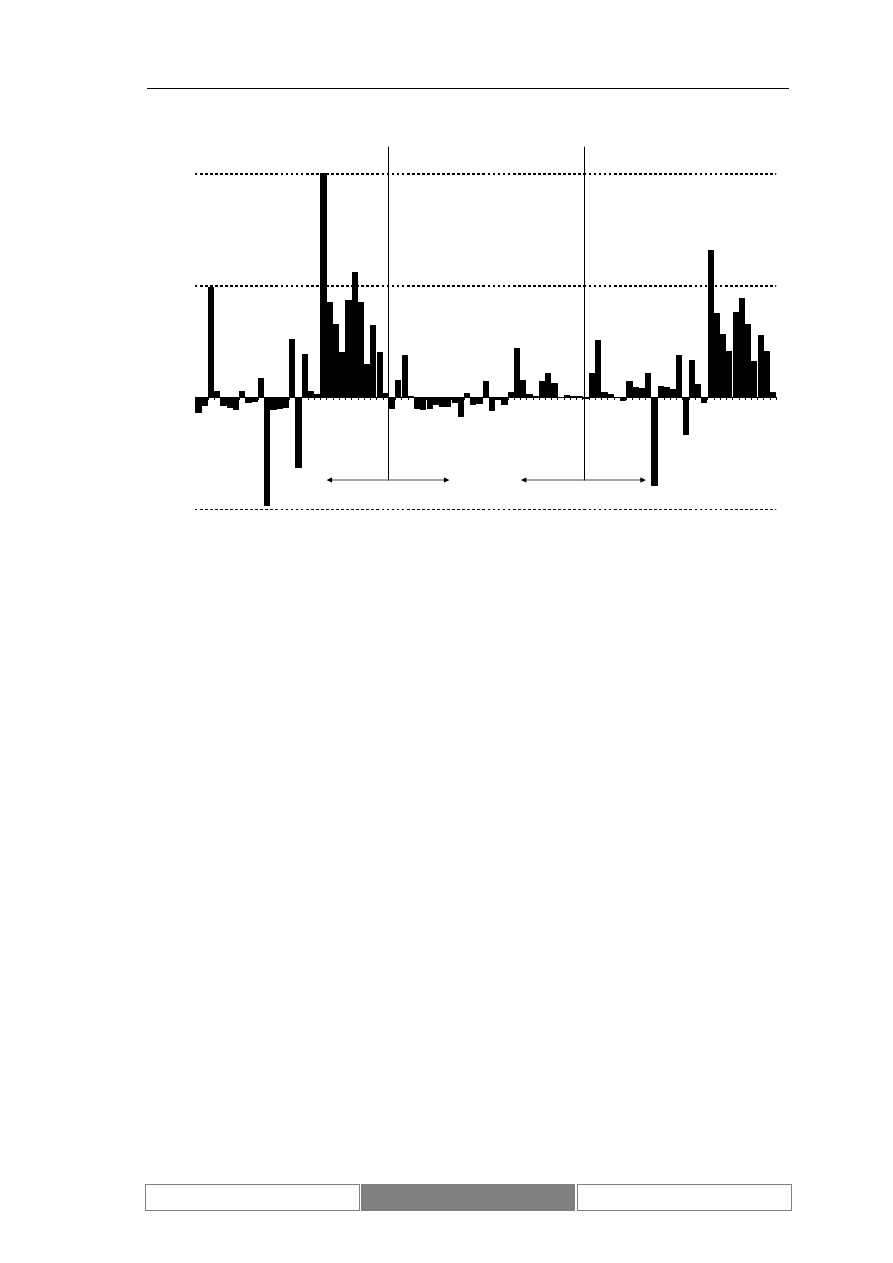
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
57
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 22.
Korelacja między zmiennymi (współczynnik Pearson’a)
Wraz ze zmieniającą się sytuacją na giełdzie zmianie ulegają również zależności
pomiędzy zmiennymi opisującymi jej stan. Diagram 23 przedstawia korelacje liczone
w kolejnych, rozłącznych okresach pięciodniowych. Wybrany został tak krótki okres
czasu, w którym liczony jest współczynnik korelacji, aby pokazać zmieniające się
zależności. Z powodu małej liczności danych nie jest to dowód zmienności zależności.
Stanowi natomiast przesłankę do założenia istnienia takiej zmienności. Prawdziwość
tej hipotezy zostanie wykazana eksperymentalnie w Rozdziale 10.5.
Wykres przedstawia korelację prognozowanej zmiany ceny i wartości oscylatora
MACD. Widoczne są intensywne zmiany nie tylko wartości współczynnika korelacji
ale również jego znaku. Często osiągane są maksymalne wartości korelacji. Zmienność
zależności determinuje konieczność dostosowywania się systemu do nowych
warunków. Sposób realizacji tego dostosowania w proponowanym systemie został
przedstawiony w dalszej części rozprawy.
NIKKEI Sygnał
kupuj/sprzedaj
NIKKEI Zmiana
Zamkni
ę
cia
DJIA Zmiana
Zamkni
ę
cia
DJIA WILLIAMS
DAX Sygnał
kupuj/sprzedaj
DAX WILLIAMS
DAX Zmiana
Zamkni
ę
cia
DAX RSI 5
-0,5
0
0,5
1
GSE
(DAX)
TSE
(NIKKEI
)
NYSE
(DJIA)
TSE
(NIKKEI
)

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
58
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 23.
Zmienność w czasie korelacji między zmianą ceny indeksu a oscylatorem
MACD (okno 5 dni)
6.3.
Wybór zmiennych do nauki i prognozy
W wyniku przedstawionych w poprzednich rozdziałach przekształceń do
dyspozycji systemu prognozującego jest 370 zmiennych. Opisują one prognozowaną
giełdę wraz z pięciodniową historią, dwie inne duże giełdy oraz dwa kursy walut. W
początkowym okresie badań konstruowana była jedna sieć neuronowa o złożonej,
modułowej architekturze, której celem była prognoza wartości indeksu giełdowego dla
całego przedziału testowego (Jaruszewicz, Mańdziuk 2004). Jednak z uwagi na wzrost
liczby zdefiniowanych przekształceń i co za tym idzie liczby danych wejściowych oraz
zaobserwowaną zmienność zależności założono, że system powinien dynamicznie
modyfikować architekturę sieci neuronowej wykorzystywanej do prognozy. Pozwala
to na dynamiczne dostosowywanie się algorytmu do zmieniającej się użyteczności
poszczególnych danych. W tym celu co 5 dni wybierany jest zestaw zmiennych
wejściowych dla sieci neuronowej. Jednocześnie liczba zmiennych determinuje
architekturę sieci.
-1
-0.5
0
0.5
1
1
6
11
16
21
26
31
36
41
46
51
56
61
66
71
76
81
86
91

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
59
Teoria i zastosowania
Implementacja
Wyniki badań
Do
efektywnego
przeszukiwania
przestrzeni
potencjalnych
zestawów
zmiennych wykorzystany został algorytm genetyczny. Ogólna idea algorytmów
genetycznych została przedstawiona w Rozdziale 4.2. W populacji chromosomów
każdy z nich opisuje zestaw zmiennych do wykorzystania w nauce sieci neuronowej.
Rozwój populacji w kolejnych generacjach pozwala na znalezienie rozwiązania
bliskiego optymalnemu. Wybrany zestaw danych stanowi podstawę do ostatecznej
nauki sieci neuronowej oraz wykonania testów prognozy.
W opisywanych eksperymentach algorytm genetyczny przy elastycznej
możliwości wyboru liczby zmiennych proponował zbiory o rozmiarze około 10
zmiennych. Ze względu na wydajność pracy algorytmu genetycznego zmienne nie
były wybierane bezpośrednio z całej dostępnej puli. Wstępny wybór został
ograniczony do wszystkich zmiennych opisujących giełdę prognozowaną w bieżącym
dniu (30 zmiennych opisujących indeks DAX), zmiennych bezpośrednio opisujących
wartość indeksu (wartość zamknięcia, średnie kroczące i procentowe zmiany) dla
pięciu wcześniejszych dni (40 zmiennych opisujących indeks DAX) oraz wartości
zmian indeksów na pozostałych giełdach i zmian wartości stosunków kursów walut
(4 zmienne opisujące indeksy NIKKEI i DJIA oraz kursy EUR/USD i USD/JPY).
Kolejne dwa rozdziały opisują szczegóły działania algorytmu genetycznego oraz
sieci neuronowej. Przedstawiona została analiza stanów pośrednich w czasie działania
algorytmów oraz generowanych wyników.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
60
Teoria i zastosowania
Implementacja
Wyniki badań
7.
Implementacja systemu
7.1.
Implementacja algorytmu genetycznego
Chromosom
Podstawową informacją jaką niesie chromosom jest lista zmiennych wejściowych
dla sieci neuronowej. Zestaw genów w chromosomie jest listą liczb naturalnych, które
stanowią
indeksy
poszczególnych
zmiennych
dostępnych
dla
algorytmu
genetycznego. Zarówno krzyżowanie jak i mutacja operują na listach indeksów
zmiennych. Liczba kodowanych zmiennych określa rozmiar chromosomu.
Jednocześnie jest to rozmiar warstwy wejściowej sieci neuronowej, która będzie uczona
na podstawie kodowanych przez chromosom zmiennych. Sieci wykorzystywane w
opisywanych badaniach posiadają jedną warstwę ukrytą, która ma rozmiar połowy
rozmiaru warstwy wejściowej. Warstwa wyjściowa składa się z pojedynczego neuronu
prognozującego oczekiwaną zmianę. W ten sposób rozmiar chromosomu jednocześnie
determinuje architekturę sieci neuronowej. Algorytm genetyczny buduje chromosomy
z puli dostępnych zmiennych, zdefiniowanych w poprzednim rozdziale. Swoboda
wyboru zmiennych z dostępnej puli może być ograniczona poprzez tzw. zmienne
wymuszone. Zmienne wymuszone nie podlegają mutacji i przy każdej operacji
genetycznej pozostają w chromosomie. W finalnym eksperymencie stosowana była
jedna zmienna wymuszona – zmiana wartości zamknięcia indeksu DAX w ciągu
ostatniego dnia. W efekcie, w czasie pracy algorytmu genetycznego każdy chromosom
obligatoryjnie kodował zmianę wartości zamknięcia indeksu na prognozowanej
giełdzie. Zmienna ta mogła być zamieniona na inną w późniejszym procesie
dodatkowej poprawy rozwiązania proponowanego przez algorytm genetyczny.
Istotną cechą chromosomu, charakterystyczną dla niniejszych badań jest
możliwość nauki prognozy dokonywanej przez opisywane przez niego sieci
neuronowe. Badania wykazały, że istnieją układy zmiennych wejściowych, dla których
sieć neuronowa nie jest w stanie skutecznie się nauczyć. Chromosom, dla którego
wszystkie lub dowolna sieć neuronowa (zależnie od wyboru sposobu wyliczenia

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
61
Teoria i zastosowania
Implementacja
Wyniki badań
przystosowania) nie były w stanie dokonywać postępów w nauce został nazwany
martwym. Pozostałe chromosomy są określane jako żywe. Szczegółowa analiza
powstawania martwych chromosomów została przedstawiona w Rozdziale 9.3.
Przystosowanie chromosomu jest wyznaczane na podstawie błędu prognozy
sieci neuronowych o architekturze kodowanej przez chromosom. Dla każdego
chromosomu wykorzystywane są trzy sieci neuronowe o różnych zestawach losowo
wybranych wag oraz tej samej architekturze. Badania porównawcze wykazały, że
najbardziej skuteczna jest ocena chromosomu na podstawie wartości średniej błędu
wszystkich sieci neuronowych [33]. Alternatywnie przystosowanie może być określone
na podstawie wartości błędu najlepszej sieci neuronowej [34].
)
,
,
(
2
1
k
i
i
i
e
e
avg
p
K
−
=
,
[33]
)
,
,
min(
2
1
k
i
i
i
e
e
p
K
−
=
,
[34]
gdzie
i
p
jest przystosowaniem i-tego chromosomu,
j
i
e
jest błędem j-tej sieci
neuronowej przypisanej do i-tego chromosomu. Wartość błędu sieci zdefiniowana jako
moduł różnicy między wartością uzyskaną a oczekiwaną zawiera się w przedziale
[0,2]. W efekcie przystosowanie chromosomu przyjmuje wartości z tego samego
przedziału. Większe wartości przystosowania oznaczają lepsze przystosowanie danego
osobnika. W eksperymentach przedstawionych w dalszej części rozprawy przyjęto k=3
(trzy sieci neuronowe przypisane do chromosomu).
Operator krzyżowania
Ogólna idea krzyżowania oraz przykład krzyżowania punktowego zostały
opisane w Rozdziale 4.2 (Diagram 10). Chromosom, tak jak zostało to opisane w
poprzednim punkcie koduje listę zmiennych wejściowych dla sieci neuronowej.
Operator krzyżowania działa wyłącznie na liście kodowanych zmiennych. Tylko w
tym zakresie materiał genetyczny podlega wymianie przy tworzeniu nowych
osobników. W przypadku krzyżowania punktowego występuje bezpośrednia
wymiana fragmentów genomu. Zaproponowany został alternatywny sposób
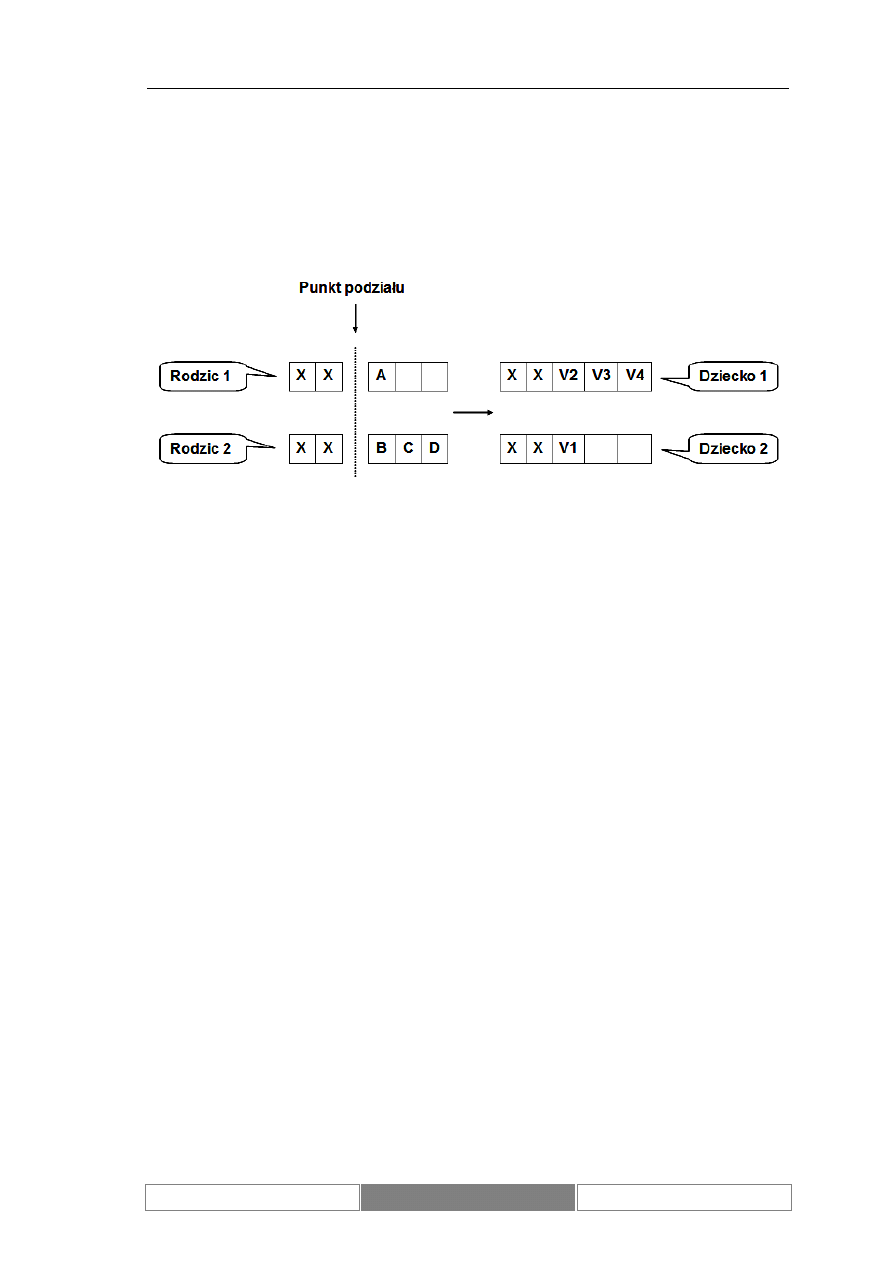
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
62
Teoria i zastosowania
Implementacja
Wyniki badań
krzyżowania – krzyżowanie iloczynowe (Diagram 24). Uwzględnia ono część wspólną
list kodowanych zmiennych (oznaczonych jako X), która przenoszona jest do
chromosomów potomnych. Pozostałe zmienne są dobierane losowo (zmienne V1-V4),
dopełniając do docelowych rozmiarów odpowiadających rozmiarom rodziców.
Diagram 24.
Schemat krzyżowania iloczynowego
Krzyżowanie jest obligatoryjne, tzn. odbywa się z prawdopodobieństwem
równym 1. Natomiast wymiana osobników w populacji w wyniku krzyżowania jest
uzależniona od przystosowania powstałych chromosomów. Sposób wyboru rodziców
oraz zastępowanie ich przez osobniki potomne zostały opisane w dalszym punkcie
pracy przedstawiającym krok iteracji algorytmu.
W przypadku kiedy zachodzi konieczność dobrania nowych zmiennych istnieje
możliwość uwzględnienia wcześniejszych wyborów w toku pracy algorytmu. Na
potrzeby takiego wyboru dla każdej zmiennej prowadzona jest statystyka. Wyróżniono
trzy typy zmiennych:
1.
Zmienne z najlepszych chromosomów – jest to zbiór wszystkich zmiennych
występujących w najlepszych chromosomach znalezionych w danym
kroku działania algorytmu genetycznego;
2.
Zmienne często wybierane – jest to zbiór wszystkich zmiennych, dla
których ich występowanie w bieżącej generacji jest większe niż
przeciętne;

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
63
Teoria i zastosowania
Implementacja
Wyniki badań
3.
Pozostałe zmienne – jest to zbiór wszystkich zmiennych, które nie spełniają
warunków dla typów 1,2.
W przypadku konieczności uzupełnienia listy kodowanych przez chromosom
zmiennych wybór nowej zmiennej odbywa się zgodnie ze zdefiniowanymi
prawdopodobieństwami równymi 1, 0.75, 0.5 odpowiednio dla zmiennych typu 1, 2, 3.
Statystyki, o których mowa powyżej, liczone są od ustalonej iteracji. Podczas
wcześniejszych iteracji lub przy wyłączonej funkcjonalności preferencji, zmienne są
wybierane
z
puli
wszystkich
dostępnych
zmiennych
z
równym
prawdopodobieństwem.
Celem powyższego działania jest pogłębianie poszukiwań w najbardziej
obiecujących kierunkach.
Operator mutacji
Mutacja chromosomu polega na wymianie określonej liczby losowo wybranych
zmiennych kodowanych przez genom. Domyślnie w czasie jednej mutacji zmianie
podlega jedna zmienna. Istnieje możliwość wyłączenia mutacji dla najlepszego
chromosomu w populacji w celu jego ochrony. Jednak w finalnych eksperymentach nie
było takiego ograniczenia. Na potrzeby zachowania różnorodności populacji
zaproponowana została również mutacja zmieniająca liczbę kodowanych zmiennych.
W zależności od typu, dodaje ona lub usuwa losowo wybraną zmienną. Nowe
zmienne są wybierane z puli dostępnych, zgodnie z preferencjami opisanymi w
punkcie dotyczącym krzyżowania. Mutacja ta pozwala na wprowadzenie do populacji
osobników o nowych rozmiarach. Sterowanie działaniem mutacji rozmiaru odbywa się
poprzez
zmiany
prawdopodobieństwa,
z
którym
do
niej
dochodzi.
Prawdopodobieństwo to jest ustalane na podstawie bieżącego stanu populacji.
Pozostałe operatory – krzyżowania oraz standardowa mutacja nie pozwalają na
wprowadzenie do populacji chromosomów o rozmiarach innych niż rozmiar
rodziców.
W każdej iteracji wszystkie chromosomy są przeznaczone do mutacji, jednakże
dochodzi do niej zgodnie ze zdefiniowanym prawdopodobieństwem. Poniżej

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
64
Teoria i zastosowania
Implementacja
Wyniki badań
przedstawione zostały kolejne kroki działania algorytmu genetycznego w postaci
zastosowanej w niniejszych badaniach.
Inicjalizacja zmiennych oraz startowej populacji
W pierwszym kroku algorytmu genetycznego ma miejsce inicjalizacja wszystkich
zmiennych sterujących pracą algorytmu. Wartości kluczowych parametrów zostały
zaprezentowane w Rozdziale 8.3. Formularz służący do wybierania przez
użytkownika wartości parametrów przedstawia Diagram 52 (Załącznik C).
Przed właściwą pracą algorytmu genetycznego odbywa się również etap
budowania struktur danych, w szczególności tablic chromosomów stanowiących
populacje rodziców oraz dzieci. Liczność populacji definiowana przez użytkownika
jest stała w czasie pracy algorytmu. Tworzona jest startowa populacja zbudowana z
losowych chromosomów. Zmienne są losowane spośród wszystkich dostępnych z
jednakowym prawdopodobieństwem. Rozmiary chromosomów są dobrane tak, żeby
równomiernie pokryć ustalony zakres wielkości.
W kolejnym kroku wyznaczane są przystosowania chromosomów startowej
populacji. Obliczanie przystosowania chromosomów opiera się na procesie nauki i
testowaniu sieci neuronowej. Wiąże się to z dużą pracochłonnością. Z tego powodu
obliczenia są wykonywane w sposób równoległy przez pulę wątków o liczbie
zdefiniowanej przez użytkownika. Pozwala to na osiągnięcie istotnego przyspieszenia
obliczeń na wieloprocesorowych komputerach. Elastyczność przyjętego mechanizmu
pozwala optymalnie wykorzystać zarówno domowy komputer jak i wysokowydajne
serwery.
Iteracja algorytmu
W każdej iteracji algorytmu genetycznego powstają nowe chromosomy tworząc
kolejne generacje osobników. Podstawowym obciążeniem obliczeniowym algorytmu
jest wyznaczenie przystosowania wszystkich nowych chromosomów zarówno w
populacji rodziców (efekt działania mutacji) jak i dzieci (wynik krzyżowania). Po
ustaleniu ocen wszystkich chromosomów wyliczane i zapamiętywane są parametry

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
65
Teoria i zastosowania
Implementacja
Wyniki badań
populacji. Są to między innymi średnie, minimalne i maksymalne przystosowania,
liczba zmian w populacji w wyniku krzyżowania i mutacji oraz liczba żywych
chromosomów. Wyznaczony zostaje chromosom o najlepszym przystosowaniu. Jeśli
istnieje więcej niż jeden taki chromosom jako najlepszy przyjmuje się pierwszy ze
znalezionych.
Przygotowanie do zastosowania krzyżowania wymaga wybrania z populacji
losowych par chromosomów (selekcja turniejowa). W każdej takiej parze następuje
porównanie wartości przystosowań chromosomów. Chromosom zwycięzca będzie
jednym z rodziców dziecka, jakie powstanie w wyniku krzyżowania. Chromosomowi
przegranemu będzie grozić zastąpienie przez chromosom potomny swojego
konkurenta. Chromosom potomny powstaje w wyniku krzyżowania rodziców
zwycięzców z sąsiednich par. Populacja rodziców uzupełniana jest osobnikami z
populacji dzieci, jeżeli nowy chromosom ma większe lub równe przystosowanie niż
zastępowany. Schemat zastępowania chromosomów w procesie krzyżowania
przedstawia Diagram 25. Wymiana ma jednak miejsce po kolejnej iteracji, w której
dokonane zostaną obliczenia przystosowań wszystkich nowych i zmienionych
chromosomów.
Na koniec każdej iteracji, zgodnie z bieżącymi parametrami następuje losowa
mutacja chromosomów w populacji rodziców. W przypadku zbliżania się średniego
rozmiaru chromosomów w populacji do rozmiarów minimalnych lub maksymalnych
ustalana jest dodatnia wartość prawdopodobieństwa mutacji liczby kodowanych
zmiennych. Powoduje to zmiany rozmiarów losowo wybranych chromosomów tak,
żeby umożliwić populacji przekroczenie osiągniętego progu oraz zapewnić
zwiększenie różnorodności rozmiarów.
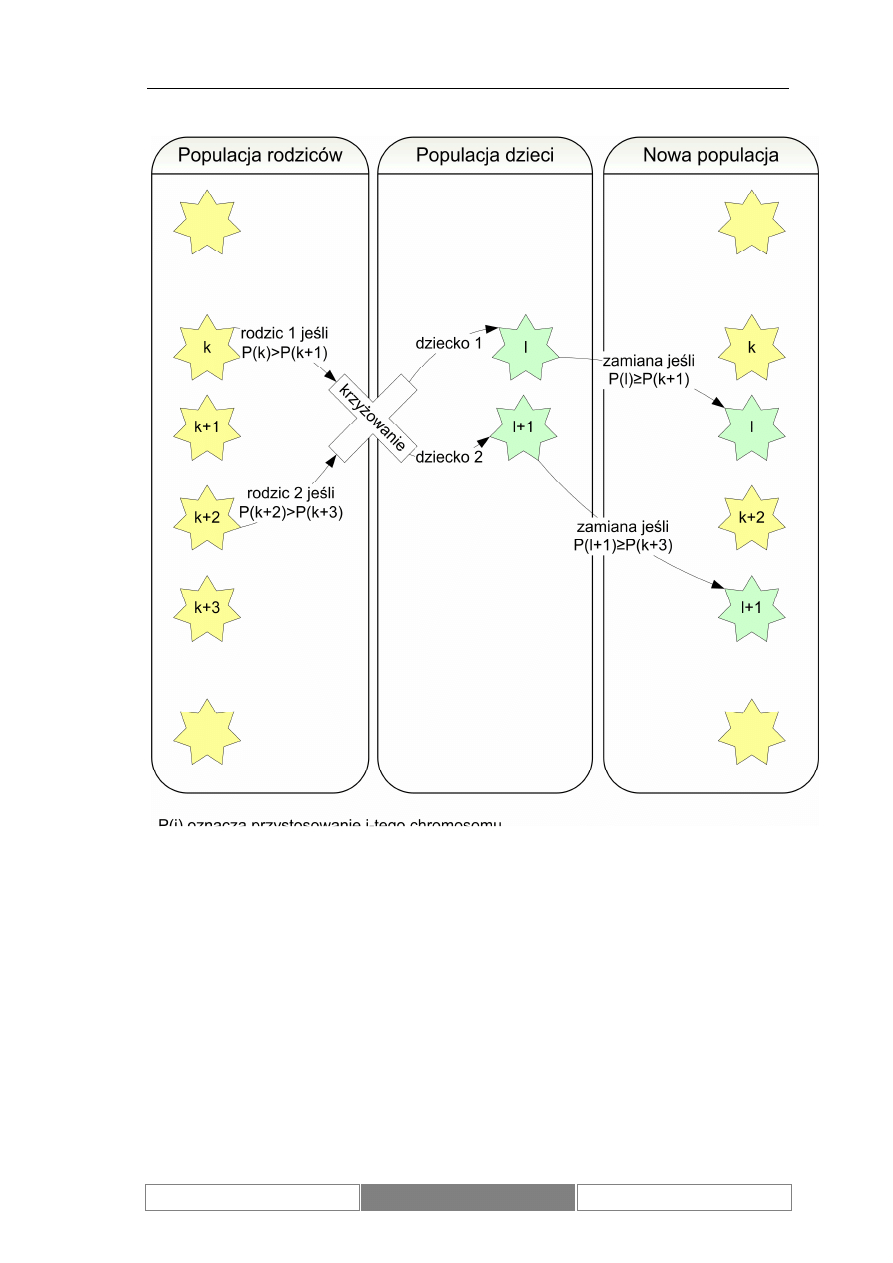
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
66
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 25.
Schemat wymiany chromosomów w procesie krzyżowania
Na koniec każdej iteracji uzupełniana jest statystyka wybieranych przez
populację zmiennych. Ma to miejsce po przekroczeniu określonego progu liczby
iteracji. Statystyka ma zastosowanie przy preferencji wyboru zmiennych w czasie
operacji krzyżowania i mutacji.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
67
Teoria i zastosowania
Implementacja
Wyniki badań
Parametry sterujące pracą algorytmu genetycznego
W każdej iteracji kontroli i ewentualnym zmianom podlega wielkość
prawdopodobieństwa mutacji. Zdefiniowane są dwie wartości bazowe. Pierwsza ma
zastosowanie przed przekroczeniem ustalonego progu liczby generacji, druga po
przekroczeniu tego progu. Jeśli nie są spełnione dodatkowe warunki modyfikacji
prawdopodobieństwa mutacji, to ma ono wartość bazową.
Prawdopodobieństwo mutacji może ulec zmianie w sytuacji osiągnięcia przez
populację średniego przystosowania bliskiego przystosowaniu maksymalnemu
(najlepszego osobnika). Spełnienie tego warunku oznacza zbyt duże skupienie się na
potencjalnie lokalnych rozwiązaniach. W takim przypadku prawdopodobieństwo
mutacji
jest
zwiększane
do
ustalonej
wartości.
Celem
zwiększenia
prawdopodobieństwa mutacji jest w tym przypadku zwiększenie różnorodności
populacji
w
sytuacji
zbyt
silnej
dominacji
najlepszego
chromosomu.
Prawdopodobieństwo mutacji wraca do wartości bazowej w momencie, kiedy
warunek przestanie być spełniany.
Dodatkowy warunek określający możliwość mutacji jest związany z
występowaniem w populacji chromosomów żywych. Mutacja chromosomów żywych,
niezależnie od innych parametrów sterujących rozwojem populacji, jest dozwolona
jedynie po przekroczeniu zdefiniowanego progu ich liczby. Stosowny próg jest
również określony dla ponownego wstrzymania mutacji żywych chromosomów, jeśli
ich liczba w populacji spadnie. Zapobiega to możliwości modyfikowania
chromosomów, których sieci neuronowe były w stanie nauczyć się prognozy w
sytuacji, kiedy takich osobników jest w populacji relatywnie niedużo.
Warunki zatrzymania algorytmu genetycznego
Zatrzymanie pracy algorytmu genetycznego ma miejsce po osiągnięciu jednego z
trzech warunków.
1.
Przez określoną liczbę ostatnich iteracji nie został znaleziony nowy
najlepszy chromosom. Oznacza to długotrwały brak postępów w
poszukiwaniu coraz lepszych rozwiązań. Warunek jest sprawdzany po

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
68
Teoria i zastosowania
Implementacja
Wyniki badań
osiągnięciu zdefiniowanego progu liczby iteracji, zapobiegając zbyt
wczesnemu zatrzymaniu algorytmu.
2.
Określony procent osobników w populacji charakteryzuje się
przystosowaniem bliskim średniemu przystosowaniu populacji (zgodnie
ze zdefiniowanym progiem). Warunek ten pozwala na zakończenie pracy
algorytmu w przypadku przekroczenia progu zbyt małej różnorodności
populacji, która uniemożliwiałaby dalszy rozwój.
3.
Osiągnięta została zdefiniowana wcześniej maksymalna liczba iteracji.
Z powodu zaimplementowanego w systemie mechanizmu zwiększania
prawdopodobieństwa mutacji w sytuacji zdefiniowanej w warunku 2, spełnienie
tego warunku nie zostało odnotowane w dotychczasowych badaniach.
Najczęściej algorytm genetyczny zostaje zatrzymany w wyniku nie znalezienia
kolejnego najlepszego chromosomu przez określoną liczbę iteracji.
Dodatkowe przeszukanie przestrzeni rozwiązań
Zaproponowany został algorytm dodatkowego przeszukania przestrzeni
rozwiązań, który jest wykorzystywany po zakończeniu działania algorytmu
genetycznego. Opiera się on na sprawdzeniu nowych zestawów zmiennych,
zbudowanych na podstawie najlepszego chromosomu znalezionego przez algorytm
genetyczny. Nowe zestawy zmiennych powstają poprzez wymianę kolejnych
zmiennych zestawu zaproponowanego przez algorytm genetyczny na pozostałe
dostępne zmienne. Poniżej przedstawiona została definicja algorytmu tworzenia
nowych zestawów zmiennych:
1.
Dany jest zestaw zmiennych zaproponowanych przez algorytm
genetyczny:
{
}
r
c
c
c
Z
,
,
,
2
1
K
=
,
W
c
i
i
∈
∀
, gdzie r jest rozmiarem
chromosomu, W oznacza zbiór wszystkich dostępnych zmiennych.
2.
r
W
k
r
j
−
=
∀
∧
=
∀
K
K
1
1
zbuduj zestaw zmiennych
{
}
r
j
k
j
j
k
j
c
c
z
c
c
c
Z
,
,
,
,
,
,
,
1
1
2
1
K
K
+
−
=
taki, że
Z
W
z
k
j
k
j
\
∈
∀
∀
.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
69
Teoria i zastosowania
Implementacja
Wyniki badań
Dla każdego zestawu
k
j
Z
wyliczany jest błąd nauki sieci neuronowej,
analogicznie do wyznaczania przystosowania chromosomu. Algorytm ten jest
powtarzany iteracyjnie. W każdej kolejnej iteracji zbiór
k
j
Z
, dla którego błąd prognozy
był najmniejszy i jednocześnie mniejszy od błędu dla zestawu Z staje się zbiorem
wyjściowym Z. Przeszukiwanie powtarzane jest aż do spełnienia jednego z poniższych
warunków zatrzymania.
Warunki zatrzymania dodatkowego przeszukania
Liczba iteracji algorytmu przeszukiwania może być stała, wybrana przez
użytkownika lub ustalona na maksymalną. W proponowanym rozwiązaniu
maksymalna liczba iteracji jest równa rozmiarowi najlepszego chromosomu. Warunki
zatrzymania dodatkowego przeszukiwania są następujące:
1.
Osiągnięta została określona liczba iteracji.
2.
W bieżącej iteracji nie został znaleziony nowy najlepszy chromosom
k
j
Z
.
7.2.
Implementacja sieci neuronowej
Ogólna architektura sieci neuronowych oraz metoda nauki zostały opisane w
Rozdziale 4.3. Wprowadzony został podział dostępnych do treningu i testów
rekordów na rekordy uczące, walidacyjne i testowe. Poniżej przedstawione zostały
dwa aspekty implementacji algorytmu nauki sieci neuronowej.
Wydzielenie rekordów walidacyjnych służy ustaleniu właściwego momentu
zatrzymania nauki sieci neuronowej oraz oceny sieci w czasie pracy algorytmu
genetycznego. Nauka powinna być przerwana w momencie kiedy błąd prognozy na
rekordach walidacyjnych, które nie były wykorzystane w czasie nauki, zacznie
wzrastać. Zapewnia to właściwą generalizację działania sieci neuronowej, od której
oczekuje się poprawnej prognozy dla przyszłych, nieznanych obserwacji. Poniższe
wzory [35][36] definiują warunki zatrzymania nauki w związku ze wzrostem błędu
sieci na próbce rekordów walidacyjnych. Wystąpienie dowolnego z nich powoduje
zatrzymanie procesu nauki sieci.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
70
Teoria i zastosowania
Implementacja
Wyniki badań
Warunek 1:
>
−
−
−
−
+
−
>
−
−
−
−
−
>
−
−
−
1
1
1
)
,
(
)
1
(
)
2
,
1
(
)
1
(
)
1
,
(
)
(
ε
κ
κ
λ
κ
ε
λ
ε
λ
i
i
AVG
i
V
i
i
AVG
i
V
i
i
AVG
i
V
L
[35]
Warunek 2:
)
0
(
)
1
(
)
(
2
V
i
V
ε
+
>
[36]
gdzie V(i) oznacza błąd prognozy dla i-tego rekordu walidacyjnego, AVG(k,l) jest
średnią wartością błędu w przedziale rekordów [k,l]. Parametry
1
ε
i
2
ε
określają
wartości progowe dla odpowiednich warunków. Im mniejsze wartości progów, tym
warunki są bardziej czułe na zmiany wartości błędów. Wzór [35] definiuje warunek
zatrzymujący naukę po kolejnych
κ
wzrostach błędu (tzw. współczynnik sekwencji
kolejnych zmian) w stosunku do średniej wartości z ostatnich
λ
rekordów (tzw.
współczynnik wygładzenia). Dodatkowy warunek [36] sprawdza czy aktualny błąd
V(i) nie jest większy o zdefiniowaną wartość procentową
2
ε
niż błąd V(0) przed
rozpoczęciem procesu nauki. Niezależnie od opisanych powyżej warunków, liczba
iteracji nauki jest ograniczona przez zdefiniowany próg.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
71
Teoria i zastosowania
Implementacja
Wyniki badań
Dział C.
Wyniki badań
Poniższy
dział
zawiera
analizę
działania
zaproponowanego systemu neuro-genetycznego
oraz
definicję
finalnego
eksperymentu
prezentującego
jego
skuteczność.
Szeroko
opisane zostały wyniki uzyskane przez system
oraz alternatywne metody heurystyczne.
8.
Definicja eksperymentu
8.1.
Mierniki jakości prognozy
Skuteczność prognozy sieci neuronowej została zaprezentowana na trzy
sposoby. Teoretyczna jakość prognozy jest opisywana za pomocą błędu
średniokwadratowego [37] oraz średniego błędu bezwzględnego [38].
∑
−
=
=
′
−
=
1
0
2
)
(
1
n
i
i
i
i
c
c
n
mse
[37]
∑
−
=
=
′
−
=
1
0
1
n
i
i
i
i
c
c
n
e
,
[38]
gdzie
i
c
oznacza rzeczywistą procentową zmianę wartości zamknięcia indeksu
w dniu i,
i
c
′
oznacza prognozowaną zmianę tej wartości. Ponieważ prognozowana
zmiana jest zmianą procentową, składnik (
i
i
c
c
′
−
) jest równoważny procentowemu
błędowi prognozy wartości w dniu i.
Charakter bardziej praktyczny ma ocena skuteczności prognozy jako wynik
hipotetycznego inwestowania na giełdzie [39]:

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
72
Teoria i zastosowania
Implementacja
Wyniki badań
)
,
,
(
l
k
A
M
p
=
,
[39]
gdzie M oznacza zdefiniowany model inwestycyjny w rozumieniu reguł i
warunków, A jest algorytmem inwestowania w danym modelu, k, l wyznaczają okres
czasu, w którym odbywają się inwestycje. W takim przypadku sukces mierzy się
finansowym zyskiem p.
Model inwestycyjny definiuje możliwe do wykonania transakcje. Każdego dnia
wybierana jest jedna z trzech operacji: kupuj indeksy, sprzedaj indeksy lub czekaj.
Wykonanie operacji „kupuj” zależy od aktualnie posiadanej kwoty pieniędzy. W
jednym ruchu możliwy jest zakup jedynie maksymalnej liczby indeksów, których
bieżąca wartość jest z dokładnością do jednego indeksu równa posiadanej kwocie
pieniędzy. W przypadku operacji „sprzedaj” wszystkie posiadane indeksy są
zamieniane na kwotę pieniędzy, z uwzględnieniem bieżącej wartości indeksu. Na
zakończenie okresu inwestowania wszystkie posiadane indeksy są sprzedawane.
Sygnały kupna i sprzedaży są podawane na koniec każdego dnia, kiedy znane są
bieżące wartości zmiennych. W efekcie realizacja transakcji na podstawie
prognozowanego sygnału może mieć miejsce najwcześniej w momencie otwarcia
giełdy następnego dnia. W proponowanym modelu transakcje są realizowane po cenie
otwarcia dnia następnego. Zdefiniowanie problemu badawczego jako prognozy
jednodniowej wyklucza możliwość podejmowania realnych inwestycji z powodu
istotnego wpływu kosztów transakcji przy dużej ich liczbie. Z tego powodu
zaproponowany model nie przewiduje kosztów wykonania operacji. Jednak w celach
poznawczych przeprowadzona została analiza wpływu kosztów na wynik końcowy.
W Rozdziale 8.2 opisane zostały założenia eksperymentu prezentującego
możliwości proponowanego systemu. Algorytm oparty na prognozie systemu neuro-
genetycznego wraz z alternatywnymi algorytmami testowymi został opisany w
Rozdziale 8.4.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
73
Teoria i zastosowania
Implementacja
Wyniki badań
8.2.
Scenariusz eksperymentu
Podstawą eksperymentu są kolejne prognozy zmiany wartości indeksu na koniec
następnego dnia, wykonywane przez sieć neuronową zdefiniowaną na podstawie
zestawu zmiennych wskazanych przez algorytm genetyczny. Co pięć dni wyznaczana
jest kolejna, przeznaczona dla nowej sytuacji na rynku, sieć neuronowa.
Na całość eksperymentu składają się prognozy dla kolejnych 100 dni pracy giełd,
które zostały uwzględnione w systemie. Dni te obejmują okres od 2004/04/07 do
2004/08/26. Pojedyncza sieć neuronowa jest wykorzystywana w pięciodniowym oknie
czasowym. W efekcie eksperyment dzieli się na 20 kroków, w których każdorazowo
konstruowana jest nowa sieć neuronowa dopasowana do zmieniających się zależności
na giełdzie. Algorytm genetyczny na potrzeby wyliczania przystosowania
chromosomów wykorzystuje zestaw 295 rekordów (dni) poprzedzających dane
testowe. Na podstawie pierwszych 290 dni wykonywane są modyfikacje wag zgodnie
z algorytmem propagacji wstecznej błędu (Rozdział 4.3). Kolejnych 5 rekordów
traktowanych jest jako walidacyjne. Na ich podstawie system sprawdza spełnienie
warunków zatrzymania algorytmu nauki oraz ocenia przystosowanie chromosomów.
Po zakończeniu pracy algorytmu genetycznego i wybraniu najlepszej sieci neuronowej,
kolejne pięć rekordów stanowi okno, w którym prognozowane są zmiany wartości
indeksu jako wynik eksperymentu w danym kroku. W każdym z pięciu dni okna
wykonywana jest prognoza z wykorzystaniem tej samej sieci (bez douczania), na
podstawie nowych danych, dostępnych w bieżącym dniu. Sposób podziału próbki
rekordów na opisane powyżej zbiory przedstawia Diagram 26. W efekcie prognoza
wykonywana jest każdego dnia ciągłego zbioru 100 dni. W każdym z kroków testy
wykonywane są na rekordach niewykorzystanych w żaden sposób w procesie doboru
zestawu zmiennych oraz nauki sieci neuronowej.
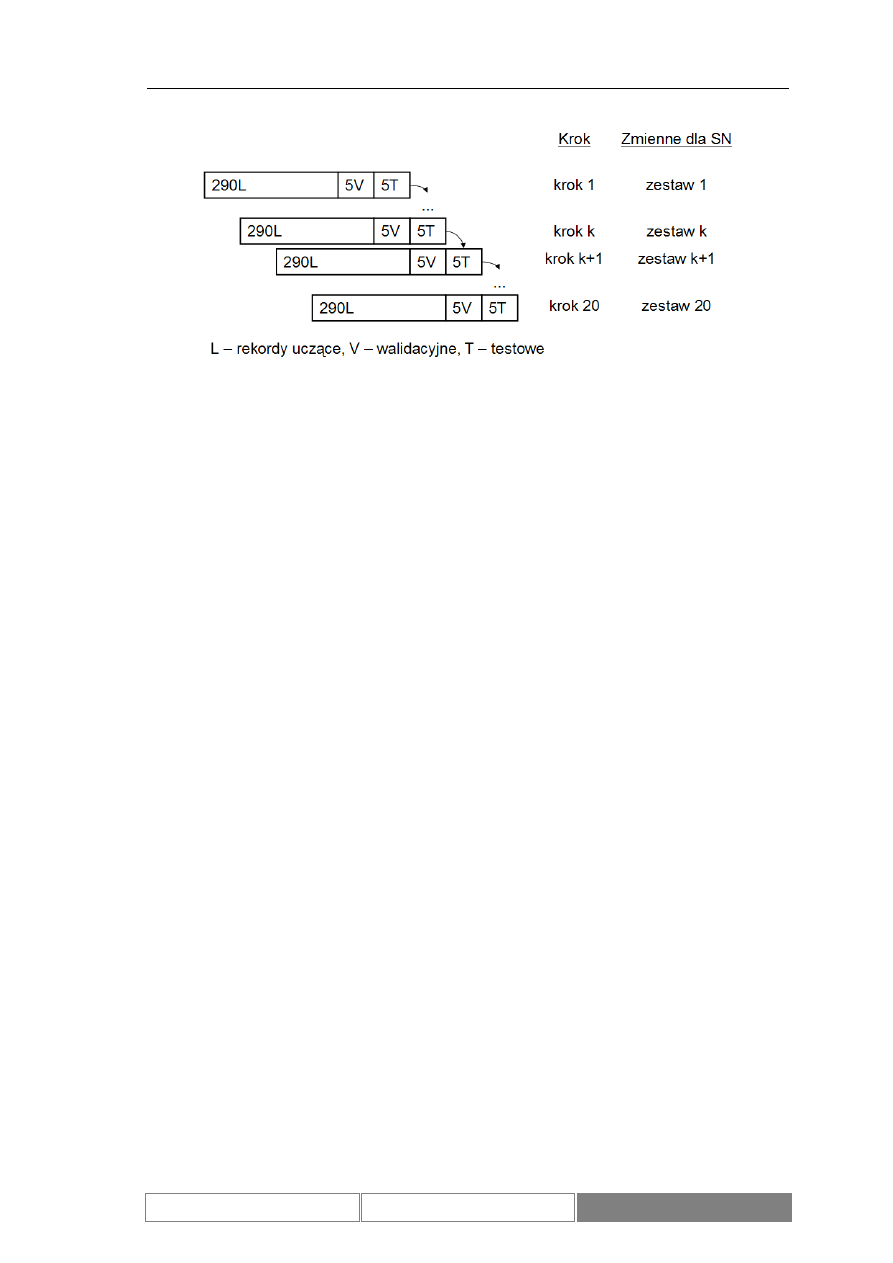
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
74
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 26.
Podział rekordów w kolejnych krokach eksperymentu
8.3.
Ustawienia parametrów systemu
W poniższej tabeli przedstawione zostały wartości kluczowych parametrów
pracy algorytmów zastosowanych w systemie. Ich znaczenie zostało podane w
rozdziałach opisujących implementację algorytmów.
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
75
Teoria i zastosowania
Implementacja
Wyniki badań
Atrybuty algorytmu genetycznego
Wartość
Liczba chromosomów
48
Maksymalna liczba iteracji
500
Zakres rozmiarów chromosomów w startowej populacji
od 3 do 10
Liczba zmiennych wymuszonych
1
Liczba możliwych warstw ukrytych sieci neuronowych
1
Liczba sieci neuronowych przypisanych do pojedynczego chromosomu
3
Najlepszy chromosom tylko wtedy gdy wszystkie sieci neuronowe są żywe
tak
Liczba dodatkowych iteracji przeszukujących przestrzeń rozwiązań
1
Liczba iteracji nauki sieci neuronowej w czasie wyznaczania przystosowania
200
Prawdopodobieństwo mutacji dla martwego chromosomu
1
Prawdopodobieństwo mutacji dla żywego chromosomu, jeżeli średnie
przystosowanie populacji jest bliskie najlepszemu
0.2
Próg zmiany prawdopodobieństwa mutacji
20%
Prawdopodobieństwo mutacji dla żywego chromosomu przed zmianą
parametrów w wyniku przekroczenia progu iteracji
0.2
Prawdopodobieństwo mutacji dla żywego chromosomu po zmianie
parametrów w wyniku przekroczenia progu iteracji
0.05
Liczba możliwych zmian w chromosomie w czasie jednej mutacji
1
Pozwól na mutacje żywych chromosomów, jeżeli ich liczba jest większa niż
90%
Zabroń mutacji żywych chromosomów, jeżeli ich liczba jest mniejsza niż
50%
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
76
Teoria i zastosowania
Implementacja
Wyniki badań
Atrybuty nauki sieci neuronowej
Algorytm
genetyczny
Końcowa nauka
Liczba rekordów uczących
290
Liczba rekordów walidacyjnych
5
Liczba rekordów testowych
0
5
Początkowy współczynnik uczenia (
0
α
)
0.8
Końcowy współczynnik uczenia (
k
α
)
0.1
Współczynnik momentu (
γ
)
0.2
Po każdej iteracji wartość współczynnika uczenia
wraca do stanu początkowego
tak
Maksymalna liczba iteracji nauki
200
2000
Próg dla zmiany błędu (
1
ε
)
10
-7
Próg dla wartości błędu (
2
ε
)
0.1
Współczynnik sekwencji kolejnych zmian dla
zatrzymania (
κ
)
3
Współczynnik wygładzenia (
λ
)
100
10
Tabela III.
Wspólne parametry algorytmu genetycznego i nauki sieci neuronowej
8.4.
Algorytmy testowe
Dla porównania wyników uzyskanych przez system neuro-genetyczny zostało
zaproponowanych pięć dodatkowych algorytmów inwestycyjnych. Algorytm oparty
na działaniu proponowanego systemu (algorytm SNG) został skonfrontowany z
metodami heurystycznymi. Poniżej przedstawione zostały definicje wykorzystanych
algorytmów.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
77
Teoria i zastosowania
Implementacja
Wyniki badań
Algorytm SNG – „system neuro-genetyczny”
Inwestowanie na podstawie algorytmu SNG (wzór [40]) opiera się na prognozie
zmiany wartości indeksu wykonanej przez system neuro-genetyczny. Skuteczność
związana jest wprost ze skutecznością prognozy sieci neuronowej.
[40]
Algorytm LS – „losowe sygnały”
Algorytm ten losuje z równym prawdopodobieństwem sygnały kupna i
sprzedaży. Ponieważ w praktyce system neuro-genetyczny nie daje prognozy równej 0
(sygnał „czekaj”), to analogicznie możliwość ta została wykluczona w algorytmie
losowym. Jednocześnie przeprowadzony eksperyment pokazał brak istotnego wpływu
takiego założenia na wynik działania algorytmu losowego.
Algorytm KT – „kupuj i trzymaj”
Jest to popularna strategia typu „kupuj i trzymaj”. W pierwszym kroku za całą
dostępną kwotę kupowane są indeksy. Na zakończenie wszystkie posiadane indeksy
są sprzedawane. W międzyczasie nie są wykonywane żadne transakcje. Strategia ta
sprawdza się najlepiej w sytuacji dużego wzrostu wartości indeksu w badanym okresie
czasu.
[41]
jeśli (iteracja = pierwsza) sygnał := kupuj
jeśli (iteracja = ostatnia) sygnał := sprzedaj
w pozostałych przypadkach sygnał := czekaj
jeśli (prognozowana zmiana jest dodatnia) sygnał := kupuj
jeśli (prognozowana zmiana jest ujemna) sygnał := sprzedaj
jeśli (prognozowana zmiana jest równa 0) sygnał := czekaj

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
78
Teoria i zastosowania
Implementacja
Wyniki badań
Algorytm OZ – „utrzymanie ostatniej zmiany”
Algorytm opisany wzorem [42] opiera się na założeniu, że kierunek zmian na
giełdzie jest częściej zachowany niż się zmienia. Strategia sprawdza się w przypadku
stabilnej sytuacji na giełdzie przy stałych długotrwałych trendach.
[42]
Algorytm MACD – „prognoza oscylatora MACD”
Algorytm [43] jest analogiczny do Algorytmu SNG. Jako narzędzie do prognozy
wykorzystane są sygnały generowane przez oscylator MACD. Skuteczność zależy od
sprawdzalności prognoz tego oscylatora.
[43]
Algorytm PRF – „profetyczny”
Ostatni z zaproponowanych algorytmów zakłada wiedzę o faktycznej zmianie
wartości indeksu w ciągu kolejnego, prognozowanego dnia. Pozwala to na konstrukcję
optymalnego sposobu inwestowania przy zadanych warunkach eksperymentu.
Praktycznie nie jest możliwe osiągnięcie skuteczności tego algorytmu za pomocą
systemu bez wiedzy o przyszłości. Z tego powodu wynik algorytmu PRF stanowi
górne ograniczenie dla pozostałych przedstawionych algorytmów.
[44]
jeśli (rzeczywista zmiana jest dodatnia) sygnał := kupuj
jeśli (rzeczywista zmiana jest ujemna) sygnał := sprzedaj
jeśli (rzeczywista zmiana jest równa 0) sygnał := czekaj
sygnał := sygnał MACD zgodnie z [12]
jeśli (ostatnia zmiana jest dodatnia) sygnał := kupuj
jeśli (ostatnia zmiana jest ujemna) sygnał := sprzedaj
jeśli (brak zmiany) sygnał := czekaj

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
79
Teoria i zastosowania
Implementacja
Wyniki badań
9.
Charakterystyka działania systemu
9.1.
Rozwój populacji
Poniżej przedstawiona została charakterystyka oraz analiza zmian kluczowych
parametrów opisujących populację w kolejnych iteracjach. W wyniku działania
operatorów genetycznych mutacji i krzyżowania, osobniki populacji podlegają ciągłym
przemianom. Modyfikacje w kodowanych danych widoczne są w populacji jako
zmieniające się przystosowania oraz rozmiary chromosomów. Dodatkowe cechy
opisujące populację, to zmieniająca się liczba żywych chromosomów oraz momenty, w
których znajdowany był najlepszy osobnik.
Rozmiar chromosomów
Populacja startowa składa się z chromosomów o różnej liczbie kodowanych
zmiennych. W drodze krzyżowania i związanej z tym wymiany chromosomów
zmieniają się rozmiary chromosomów. Przedstawia to Diagram 27 dla populacji o
wyjściowych rozmiarach chromosomów z przedziału [4,11], na którym widoczne są
poszukiwania przez algorytm optymalnego rozwiązania w chromosomach o różnych
rozmiarach. Początkowo dominowała tendencja wzrostu liczby zmiennych w
zestawach. W czasie iteracji nr 22 średni rozmiar chromosomu zbliżył się do
największego. Algorytm przewiduje w tej sytuacji aktywację mutacji rozmiaru, która
pozwala na zwiększanie liczby zmiennych w losowo wybranych chromosomach.
Diagram 28 przedstawia liczbę mutacji rozmiaru w kolejnych iteracjach algorytmu
genetycznego. Widoczna jest intensywność tego procesu w iteracjach z przedziału
[22,120]. W tym czasie w populacji znalazły się chromosomy o rozmiarze 13
kodowanych zmiennych. Średni rozmiar chromosomów waha się w przedziale [10,11],
gdzie skupiona jest uwaga algorytmu genetycznego. W tym czasie znalezione zostało
pierwsze istotnie dobre rozwiązanie (w iteracji 38, por. Diagram 32). Od iteracji 120
algorytm genetyczny zaczął preferować chromosomy o mniejszych rozmiarach. W
czasie iteracji z przedziału [163,379] średni rozmiar mieścił się w przedziale [8,9]
kodowanych zmiennych. Zmiana obszaru poszukiwań okazała się trafna. Najlepszy
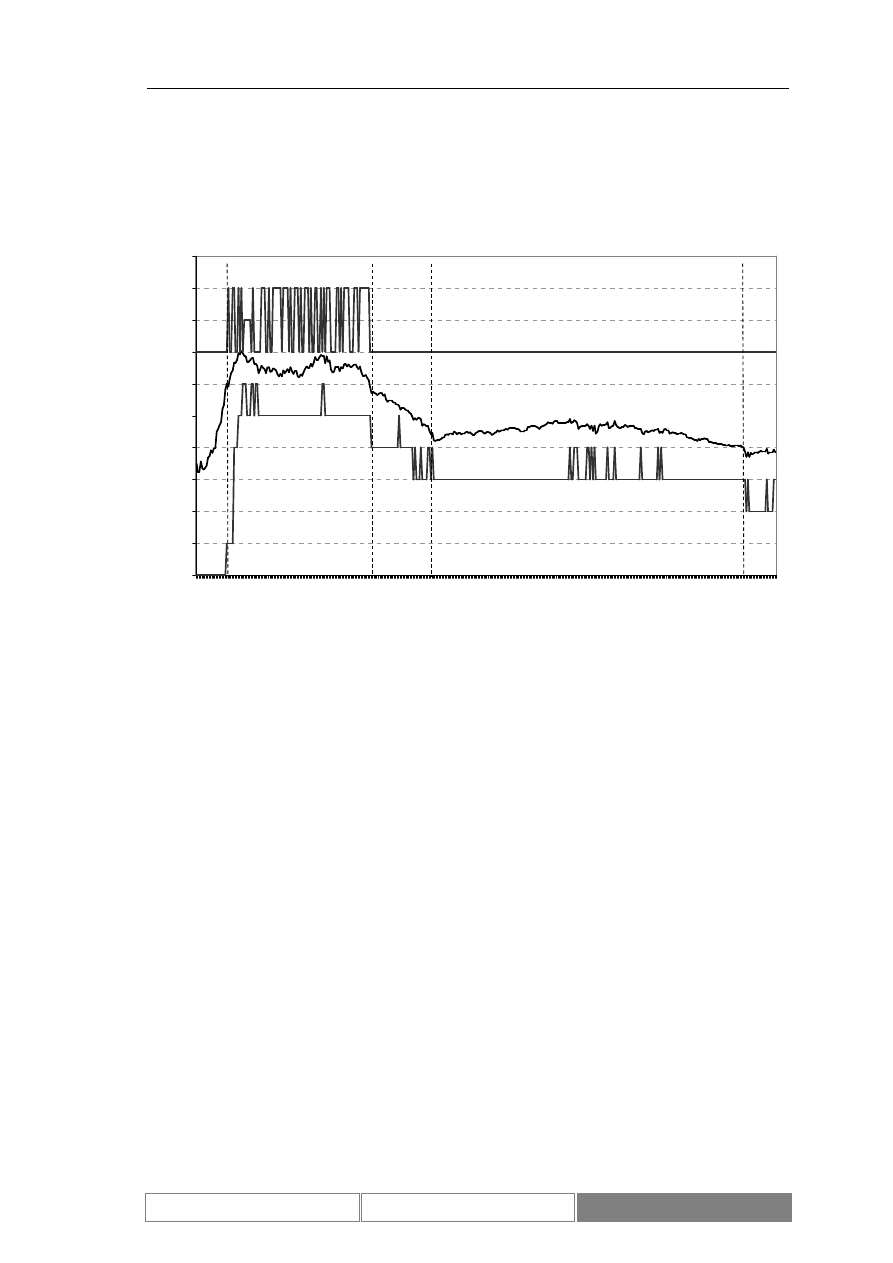
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
80
Teoria i zastosowania
Implementacja
Wyniki badań
chromosom ze wszystkich znalezionych przez algorytm genetyczny powstał w
iteracji 267. Rozmiary chromosomów nie ulegały istotnym zmianom w dalszych
iteracjach algorytmu genetycznego.
Diagram 27.
Rozmiary chromosomów w populacji przez kolejne iteracje – największy,
średni, najmniejszy
4
5
6
7
8
9
10
11
12
13
14
0
13
26
39
52
65
78
91 10
4
11
7
13
0
14
3
15
6
16
9
18
2
19
5
20
8
22
1
23
4
24
7
26
0
27
3
28
6
29
9
31
2
32
5
33
8
35
1
36
4
37
7
39
0
Iteracje algorytmu genetycznego
L
ic
z
b
a
k
o
d
o
w
a
n
y
c
h
z
m
ie
n
n
y
c
h
22
120
379
163
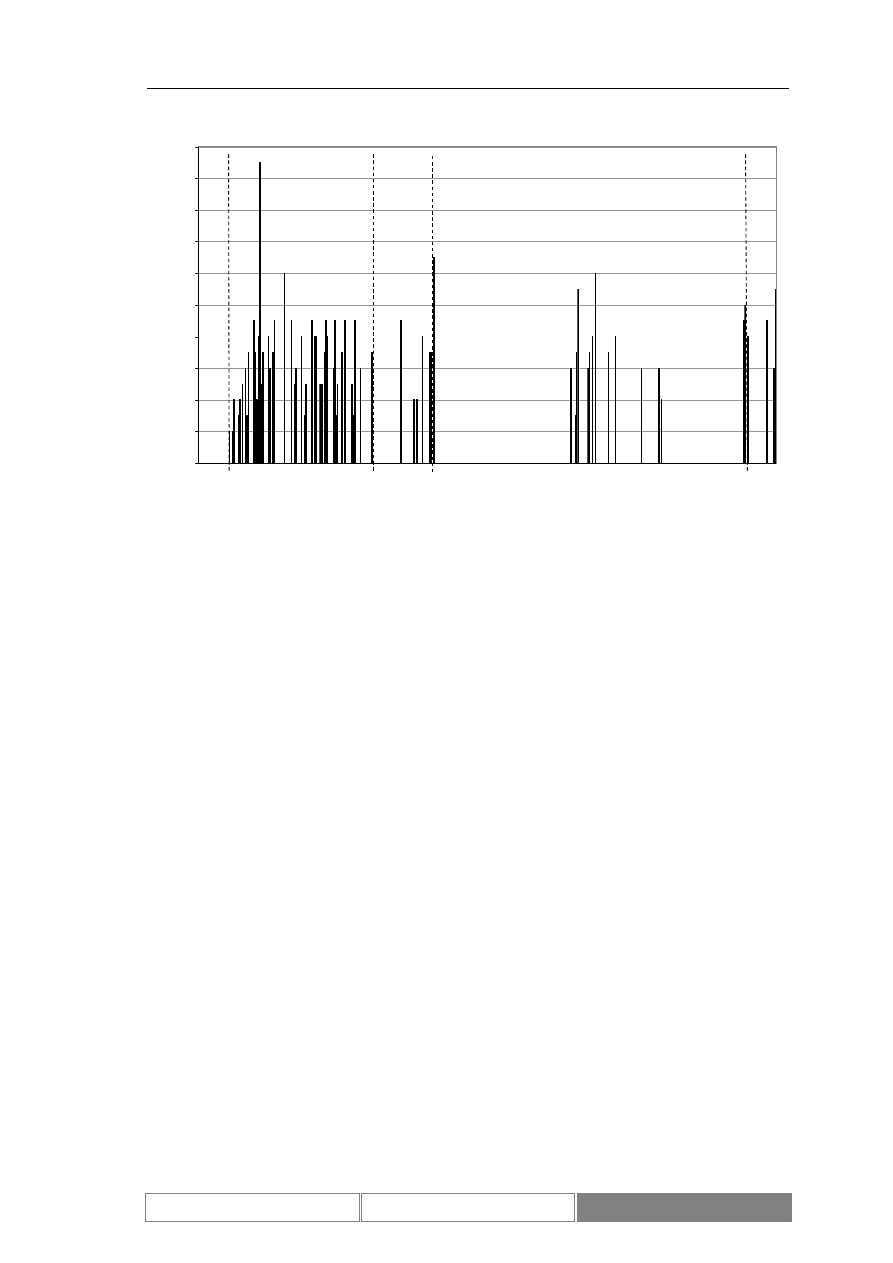
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
81
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 28.
Liczba mutacji rozmiaru w kolejnych iteracjach
Diagram 29 prezentuje różnorodność rozmiarów najlepszych chromosomów
wskazywanych na zakończenie pracy algorytmu genetycznego w kolejnych krokach
eksperymentu. Wyraźna jest różnorodność w wybieranych rozmiarach chromosomów
- wybierane były zestawy od 4 do 11 zmiennych. Przy zapewnieniu swobody wyboru
algorytmu genetycznego znaczenie ma możliwość zmiany w czasie mutacji rozmiaru
chromosomu poza zdefiniowany wcześniej przedział. Dzięki implementacji mutacji
rozmiaru mogły być znalezione trzy chromosomy (w krokach 5, 7, 11) o 11
kodowanych zmiennych, pomimo początkowego ograniczenia w populacji rozmiaru
chromosomów do przedziału [3,10].
0
2
4
6
8
10
12
14
16
18
20
0
13
26
39
52
65
78
91 10
4
11
7
13
0
14
3
15
6
16
9
18
2
19
5
20
8
22
1
23
4
24
7
26
0
27
3
28
6
29
9
31
2
32
5
33
8
35
1
36
4
37
7
39
0
Iteracje algorytmu genetycznego
L
ic
z
b
a
m
u
ta
c
ji
r
o
z
m
ia
ru
22
120
379
163
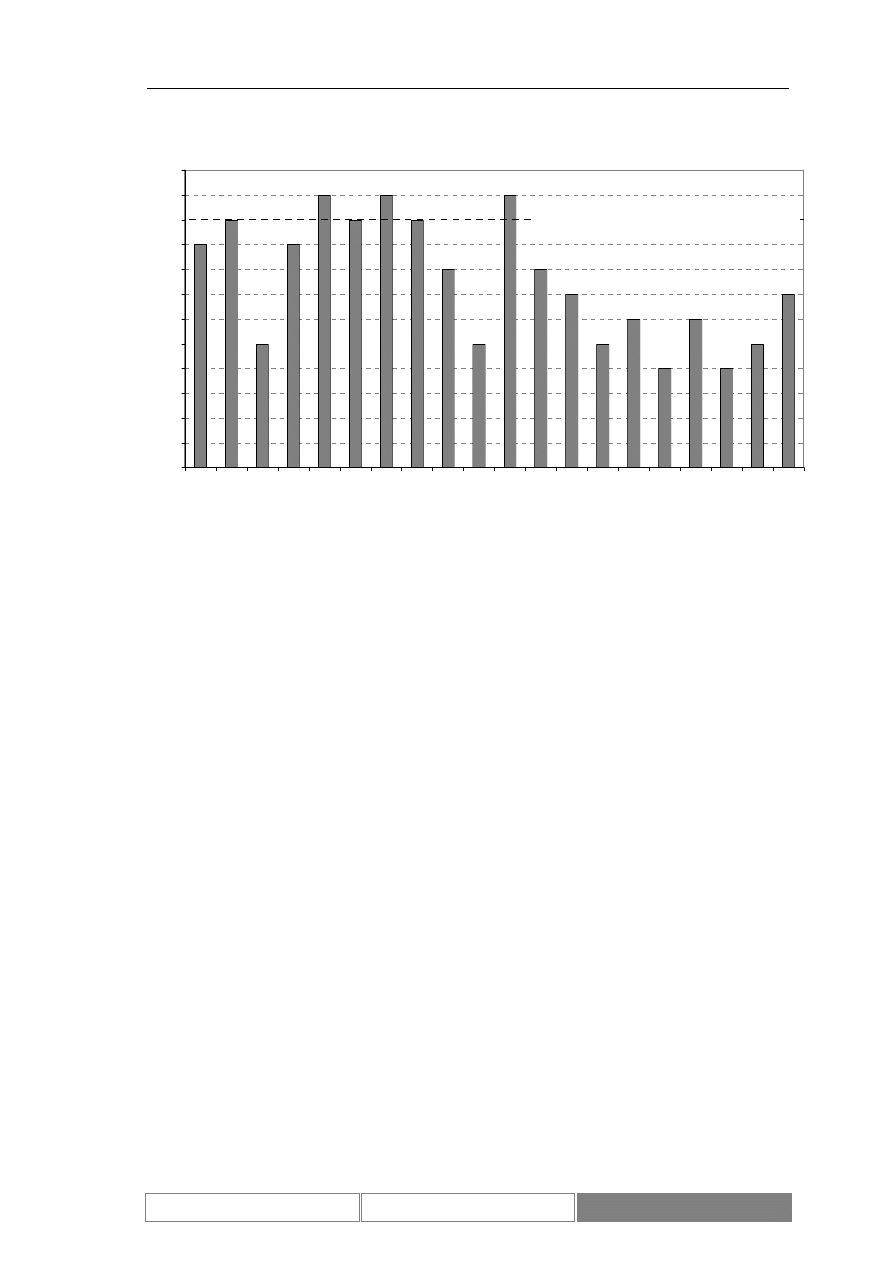
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
82
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 29.
Rozmiary najlepszych chromosomów wybieranych w 20 niezależnych krokach
eksperymentu
Mutacja zmiennych i krzyżowanie
Operator mutacji działa zgodnie ze zdefiniowanym prawdopodobieństwem,
które determinuje poziom średniej liczby zmian w populacji. Wykres liczby zmian
powstałych w wyniku mutacji przedstawia Diagram 30. Po osiągnięciu określonej
liczby iteracji (tutaj 100) prawdopodobieństwo mutacji zostaje zmniejszone, dzięki
czemu zmienność populacji maleje, pozwalając na bardziej dokładne przeszukanie
przestrzeni dotychczasowych rozwiązań.
0
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Kolejne kroki eksperymentu
L
ic
z
b
a
k
o
d
o
w
a
n
y
c
h
z
m
ie
n
n
y
c
h
górna granica rozmiaru chromosomów w pocz
ą
tkowej populacji
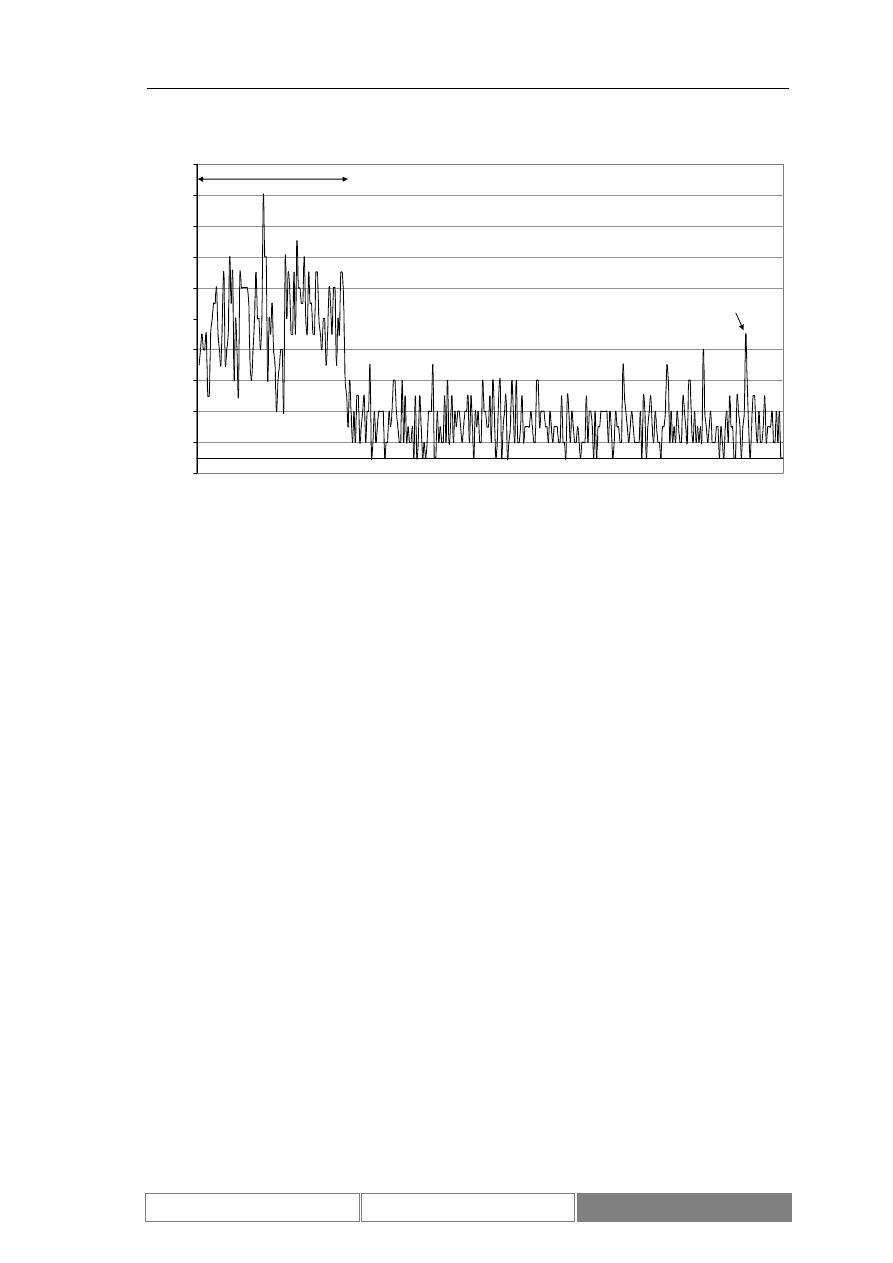
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
83
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 30.
Liczba mutacji zmiennych w kolejnych iteracjach
Liczba nowych osobników w populacji, dodanych w procesie krzyżowania nie
jest związana z prawdopodobieństwem jak to ma miejsce w przypadku mutacji. Nowe
osobniki zastępują rodziców, jeżeli mają od nich większe lub równe przystosowanie.
Diagram 31 przedstawia przebieg procesu krzyżowania jako łączną liczbę osobników
wymienionych w populacji (zarówno żywych jak i martwych) w kolejnych iteracjach.
Widoczne są duże wahania wpływu krzyżowania na populację. W początkowym
okresie czasu (iteracje 1-124) chromosomy podlegają licznym przemianom z łatwością
zwiększając swoje przystosowanie (Diagram 31, por. Diagram 32). W tym czasie
osobniki powstałe w wyniku krzyżowania często zastępują swoich rodziców.
Tendencja ta słabnie wraz ze wzrostem średniego przystosowania całej populacji.
Jednak nawet w tej fazie zauważalne są istotne wzrosty liczby nowych osobników
powstałych w wyniku krzyżowania (np. w iteracji 383).
375
-1
1
3
5
7
9
11
13
15
17
19
0
13
26
39
52
65
78
91 10
4
11
7
13
0
14
3
15
6
16
9
18
2
19
5
20
8
22
1
23
4
24
7
26
0
27
3
28
6
29
9
31
2
32
5
33
8
35
1
36
4
37
7
39
0
Iteracje algorytmu genetycznego
L
ic
z
b
a
m
u
ta
c
ji
1-100
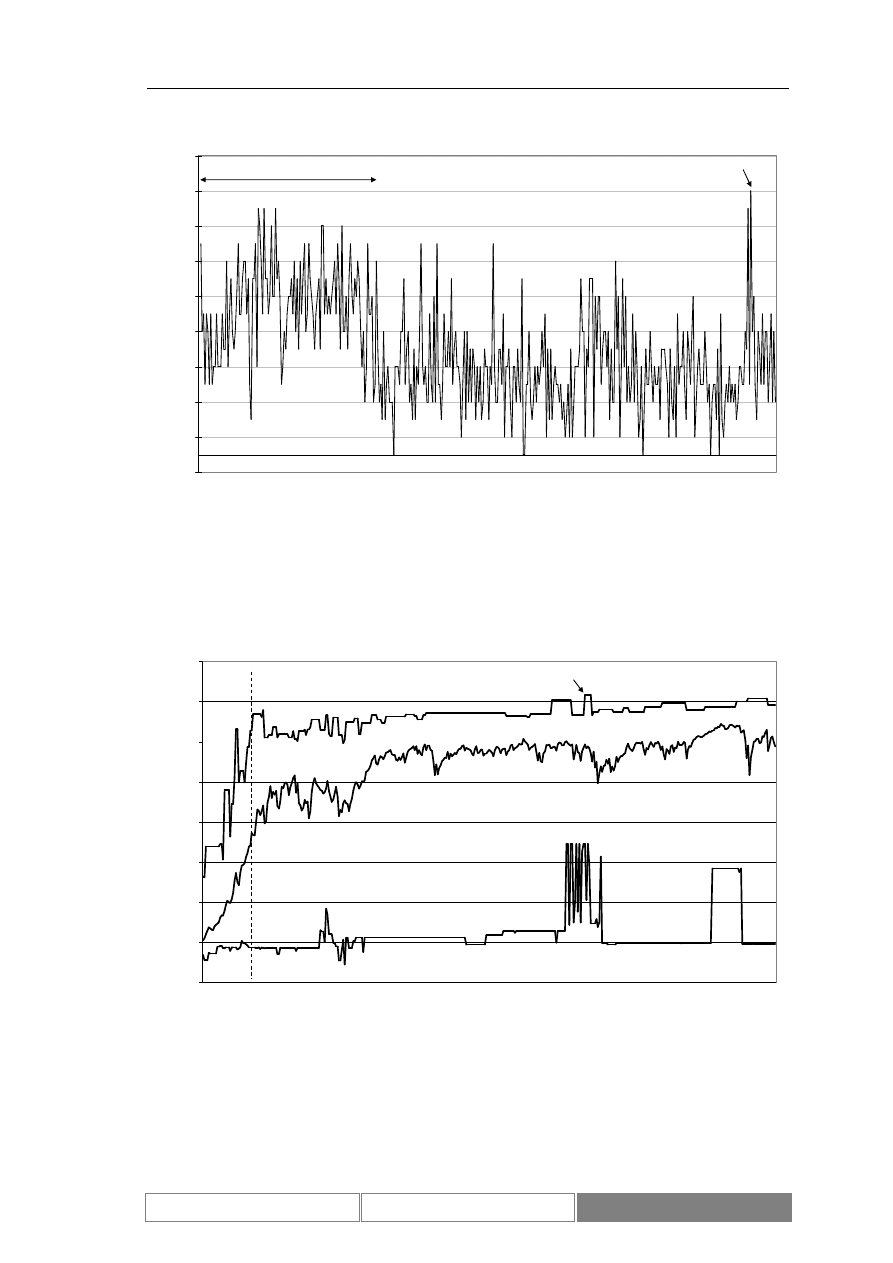
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
84
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 31.
Liczba osobników wymienionych w populacji w kolejnych iteracjach w
wyniku krzyżowania
Diagram 32.
Przystosowanie chromosomów w populacji przez kolejne iteracje – najgorsze
(najwyższa linia), średnie, najlepsze (najniższa linia).
383
-1
1
3
5
7
9
11
13
15
17
0
13
26
39
52
65
78
91 10
4
11
7
13
0
14
3
15
6
16
9
18
2
19
5
20
8
22
1
23
4
24
7
26
0
27
3
28
6
29
9
31
2
32
5
33
8
35
1
36
4
37
7
39
0
Iteracje algorytmu genetycznego
L
ic
z
b
a
o
s
o
b
n
ik
ó
w
w
y
m
ie
n
io
n
y
c
h
w
w
y
n
ik
u
k
rz
y
ż
o
w
a
n
ia
1-124
1,82
1,83
1,84
1,85
1,86
1,87
1,88
1,89
1,9
0
13
26
39
52
65
78
91 10
4
11
7
13
0
14
3
15
6
16
9
18
2
19
5
20
8
22
1
23
4
24
7
26
0
27
3
28
6
29
9
31
2
32
5
33
8
35
1
36
4
37
7
39
0
Iteracje algorytmu genetycznego
W
a
rt
o
ś
ć
p
rz
y
s
to
s
o
w
a
n
ia
najlepszy chromosom (iteracja 267)
38
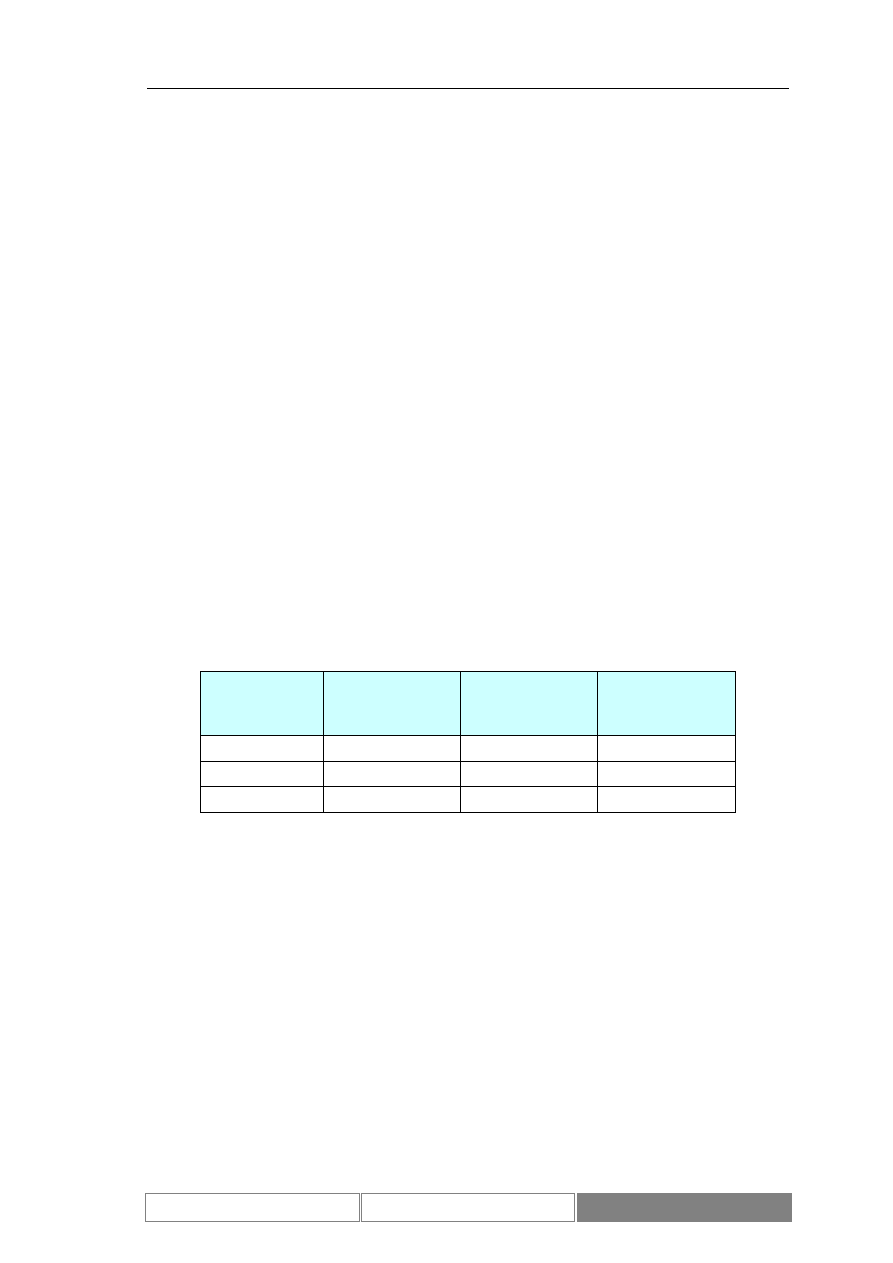
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
85
Teoria i zastosowania
Implementacja
Wyniki badań
Podsumowanie zmian w populacji w funkcji kolejnych iteracji zawiera Tabela IV.
Wyraźnie widoczna jest różnica w szybkości zmian w populacji w różnych fazach
działania algorytmu. W czasie pierwszych 100 iteracji średnia liczba zmienionych w
pojedynczej iteracji chromosomów wynosi 17.5. W ostatnich 300 iteracjach liczba ta jest
równa 7.2. Oznacza to ponad dwukrotnie większą dynamikę zmian w populacji w
ciągu pierwszych 100 iteracji. Zmianie ulega w każdej iteracji tej fazy prawie 40%
chromosomów. W dużej mierze spowodowane jest to zwiększonym w tych iteracjach
prawdopodobieństwem mutacji. W efekcie liczba zmian z tego powodu jest
czterokrotnie większa niż w ciągu ostatnich 300 iteracji. Jednak również proces
krzyżowania wnosi do populacji średnio w pojedynczej iteracji prawie dwukrotnie
więcej nowych osobników w pierwszych 100 iteracjach niż w kolejnych. Opisana
dynamika zmian w populacji jest pożądana dla skutecznej pracy algorytmu
genetycznego. W początkowej fazie intensywnie poszukiwane są potencjalnie
najbardziej korzystne rozwiązania. Jednocześnie konieczne jest eliminowanie z
populacji rozwiązań nietrafionych.
Operator
Średnia z iteracji
[1-100]
Średnia z iteracji
[101-400]
Średnia z iteracji
[1-400]
Mutacje
8.9(19%)
2.2(5%)
3.9(8%)
Krzyżowania
8.6(18%)
5(10%)
5.9(12%)
Łącznie
17.5(37%)
7.2(15%)
9.8(20%)
Tabela IV.
Średnie liczby zmian w populacji (o liczności 48 chromosomów) w wyniku działania
operatorów genetycznych
Przystosowanie chromosomów
Podstawową cechą populacji określającą skuteczność proponowanych przez nią
rozwiązań jest wartość przystosowania osobników. Algorytm dąży do optymalizacji
rozwiązania poprzez zapewnienie przetrwania w kolejnych populacjach najlepszych
chromosomów. Jednocześnie musi być zachowana różnorodność populacji tak, żeby
możliwe było odnajdowanie nowych rozwiązań często odległych od znalezionych do

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
86
Teoria i zastosowania
Implementacja
Wyniki badań
danej chwili. Diagram 32 prezentuje przystosowanie najniższe, średnie oraz najwyższe
w ramach kolejnych iteracji algorytmu. Obecna jest tendencja wzrostu średniego
przystosowania. Znajdowane są kolejne najlepsze chromosomy widoczne jako zmiany
wartości najlepszego przystosowania. W iteracji 38 znaleziony został pierwszy osobnik
o istotnie korzystnym przystosowaniu. Późniejsze zmiany miały charakter kolejnych
poprawek znalezionego rozwiązania. Ostatecznie najlepsze rozwiązanie zostało
znalezione w iteracji 267. Przykłady najlepszych chromosomów znajdowanych przez
algorytm genetyczny zostały przedstawione w następnym rozdziale.
W sytuacji, kiedy średni rozmiar chromosomów w populacji jest bliski
najmniejszemu lub największemu, możliwe są mutacje rozmiaru chromosomów.
Analiza zmian średniego przystosowania w trakcie mutacji rozmiaru chromosomów
pokazuje pogorszenie średniej jakości populacji wraz ze wzrostem liczby mutacji
(iteracje: 41, 60, 275, 381; Diagram 33). Wynika to z losowego wyboru nowych
zmiennych lub ich losowego usuwania w zmutowanych chromosomach. Może to
spowodować spadek wyników osiąganych przez sieć neuronową opisywaną przez ten
chromosom. Jednak kiedy mutacja rozmiaru przestaje być konieczna (przestaje być
prawdziwy warunek umożliwiający mutację) i zostaje wyłączona jakość populacji
wraca do pierwotnego poziomu.
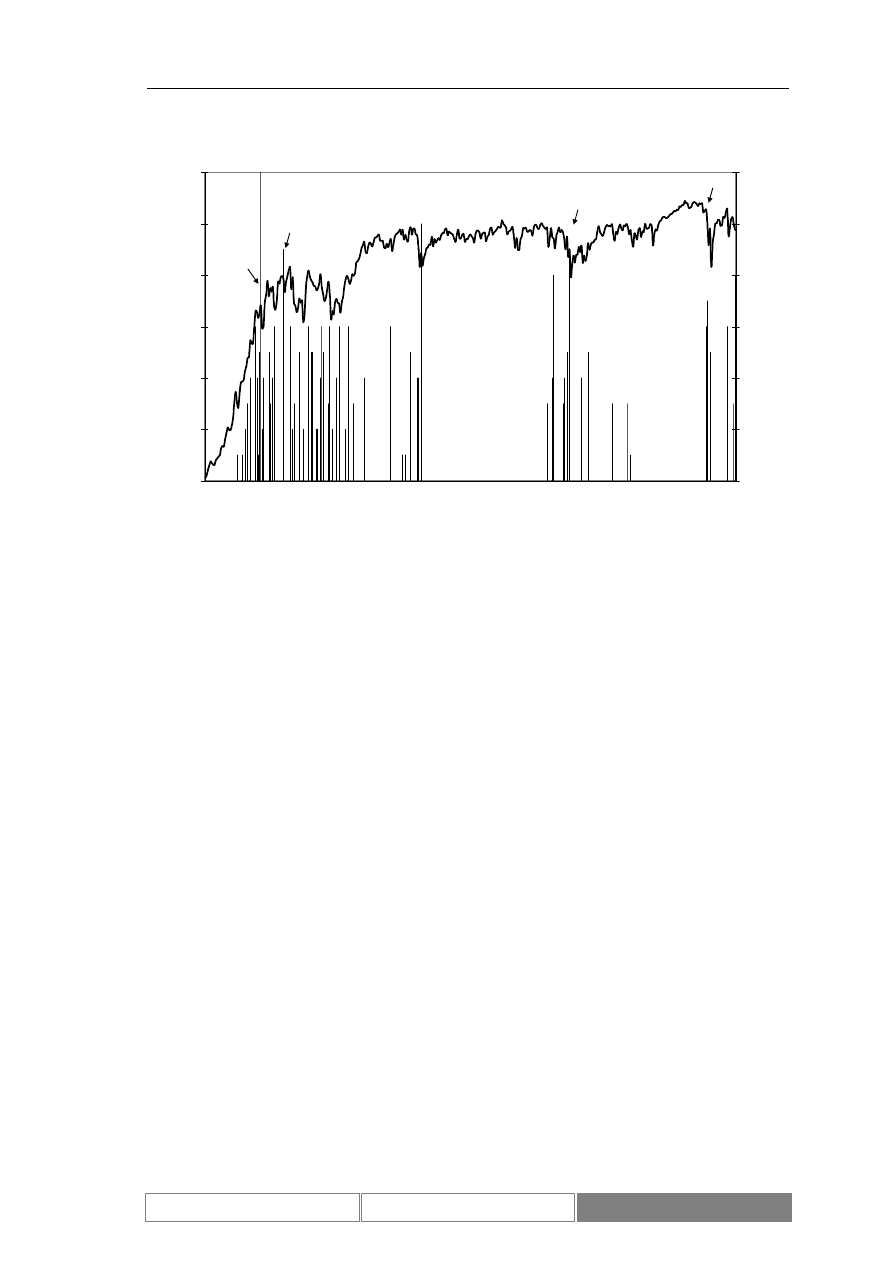
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
87
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 33.
Średnie przystosowanie populacji (linia ciągła) na tle liczby mutacji rozmiaru
(pionowe słupki)
Charakterystyczna jest również różnorodność wartości przystosowania
chromosomów w populacji. Diagram 34 przedstawia wartości błędów każdej z trzech
sieci neuronowych kodowanych przez najlepsze chromosomy wybierane przez
algorytm genetyczny w 20 niezależnych krokach eksperymentu. Diagram 35
prezentuje wartości błędów dla sieci kodowanych przez wszystkie chromosomy
populacji w ostatniej iteracji algorytmu genetycznego w pierwszym kroku
eksperymentu. Wśród najlepszych chromosomów stosunkowo rzadko występują
różnice w wartości błędów pomiędzy sieciami opisanymi przez ten sam chromosom,
ale o różnych, losowych wagach. Wyraźne różnice są widoczne w najlepszych
chromosomach o numerach: 13, 15, 17 i 18 (Diagram 34). Zdecydowanie większe
różnice występują w ramach pozostałych chromosomów w populacji. Dla tych
chromosomów rozbieżności w wynikach sieci są zdecydowanie częstsze i bardziej
wyraźne. Obserwowane są sytuacje, w których dwie sieci były w stanie się nauczyć,
natomiast zestaw wag trzeciej z nich uniemożliwił naukę (chromosomy 1 i 16, Diagram
35). Wskazać można cztery chromosomy (numer 5, 27, 33 i 45; Diagram 35), dla których
1,83
1,84
1,85
1,86
1,87
1,88
1,89
0
1
3
2
6
3
9
5
2
6
5
7
8
9
1
1
0
4
1
1
7
1
3
0
1
4
3
1
5
6
1
6
9
1
8
2
1
9
5
2
0
8
2
2
1
2
3
4
2
4
7
2
6
0
2
7
3
2
8
6
2
9
9
3
1
2
3
2
5
3
3
8
3
5
1
3
6
4
3
7
7
3
9
0
Iteracje algorytmu genetycznego
W
a
rt
o
ś
ć
p
rz
y
s
to
s
o
w
a
n
ia
3
5
7
9
11
13
15
L
ic
z
b
a
m
u
ta
c
ji
r
o
z
m
ia
ru
41
60
275
381
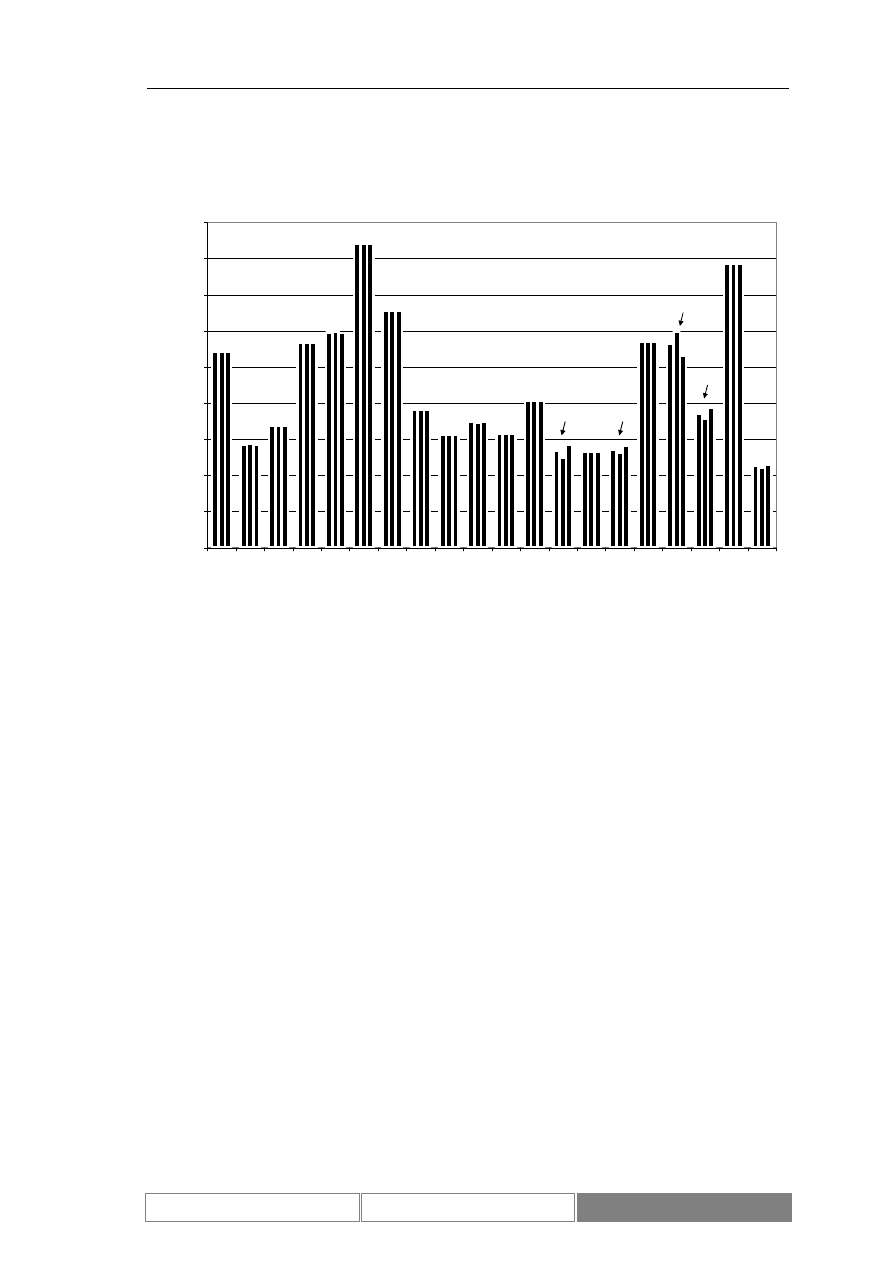
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
88
Teoria i zastosowania
Implementacja
Wyniki badań
żadna sieć neuronowa nie była w stanie nauczyć się prognozy i te chromosomy w
populacji są oznaczone jako martwe.
Diagram 34.
Wartości błędów prognozy dla trzech sieci neuronowych kodowanych przez
najlepsze chromosomy wybrane przez algorytm genetyczny w kolejnych 20 krokach
eksperymentu
0
0,02
0,04
0,06
0,08
0,1
0,12
0,14
0,16
0,18
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Numer kroku eksperymentu
B
ł
ą
d
p
ro
g
n
o
z
y
13
15
17
18

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
89
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 35.
Wartości błędów prognozy dla trzech sieci neuronowych wszystkich
chromosomów z populacji w ostatniej iteracji pierwszego kroku eksperymentu
Chromosomy żywe i martwe
Ciekawą obserwacją jest występowanie w populacji martwych osobników.
Startowa populacja powstaje w sposób losowy. Istnieje więc prawdopodobieństwo
występowania w niej chromosomów, dla których sieć neuronowa nie może się nauczyć
prognozy. Diagram 36 przedstawia dwie typowe sytuacje. Pokazane zostały dwie
populacje z różnych kroków tego samego eksperymentu. Każdy krok obejmuje inny od
pozostałych zakres dni testowych. Parametry systemu pozostają bez zmian. Populacja
A w początkowych iteracjach zawiera niewiele martwych chromosomów. Stan ten nie
zmienia się zasadniczo w ciągu kolejnych iteracji. Inaczej wygląda sytuacja w drugiej z
zaprezentowanych populacji (Populacja B). Tutaj zdecydowana większość
chromosomów w pierwszej iteracji jest martwa. Jednak szybko rośnie liczba żywych
chromosomów. Po 30 iteracjach następuje względna stabilizacja liczby żywych
chromosomów. Od 110 iteracji liczba żywych chromosomów w populacji utrzymuje się
na poziomie około 95% wszystkich osobników.
0
0,02
0,04
0,06
0,08
0,1
0,12
0,14
0,16
0,18
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
Numer chromosomu w populacji
B
ł
ą
d
p
ro
g
n
o
z
y
M
a
rt
w
y
c
h
ro
m
o
s
o
m
M
a
rt
w
y
c
h
ro
m
o
s
o
m
M
a
rt
w
y
c
h
ro
m
o
s
o
m
M
a
rt
w
y
c
h
ro
m
o
s
o
m
1
5
16
27
33
45
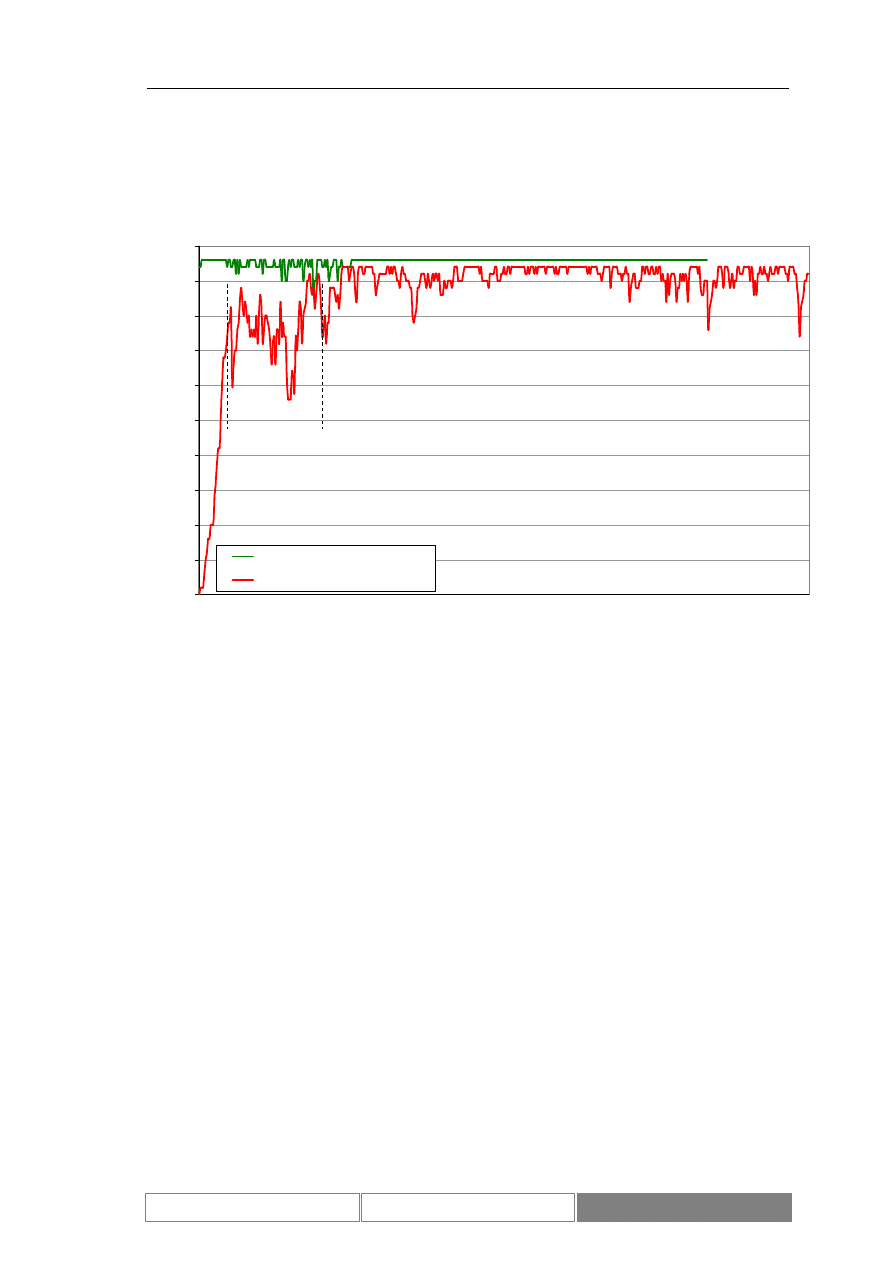
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
90
Teoria i zastosowania
Implementacja
Wyniki badań
Szczegółowe przyczyny powstawania martwych chromosomów z perspektywy
działania sieci neuronowych zostały opisane w Rozdziale 9.3.
Diagram 36.
Liczba żywych chromosomów w poszczególnych iteracjach dla dwóch
niezależnych populacji
Populacje w ostatnich iteracjach
Algorytm genetyczny ma możliwość zakończenia swojej pracy przed
osiągnięciem zakładanej liczby iteracji. Najlepsze chromosomy były znajdowane w
przybliżeniu w połowie z planowanych 500 iteracji. W jednym przypadku od 22
iteracji nie został znaleziony kolejny najlepszy osobnik. Najczęstszą przyczyną
zakończenia pracy algorytmu było spełnienie warunku nie znalezienia najlepszego
chromosomu w ciągu ostatnich iteracji. Warunek ten zaczyna działać po przekroczeniu
ustalonego progu liczby iteracji, równego 400 (80% maksymalnej liczby iteracji).
Zaledwie w 3 przypadkach na 20, liczba iteracji osiągnęła zdefiniowane maksimum
500 iteracji. Nie jest widoczna korelacja pomiędzy zakończeniem pracy algorytmu w
0
5
10
15
20
25
30
35
40
45
50
1
19
37
55 73
91 109 127 145 163 181 199 217 235 253 271 289 307 325 343 361 379 397 415 433 451 469
Iteracje algorytmu genetycznego
L
ic
z
b
a
ż
y
w
y
c
h
c
h
ro
m
o
s
o
m
ó
w
Liczba
ż
ywych (populacja A)
Liczba
ż
ywych (populacja B)
30
110

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
91
Teoria i zastosowania
Implementacja
Wyniki badań
mniejszej liczbie iteracji lub wczesną generacją najlepszego chromosomu a wartością
jego funkcji oceny.
Po zakończeniu działania algorytmu genetycznego, zaproponowany zestaw
zmiennych może być zmodyfikowany w ramach procedury przeszukującej przestrzeń
rozwiązań (patrz Rozdział 7.1). W 12 z 20 kroków wybrane przez algorytm genetyczny
najlepsze rozwiązanie zostało poprawione w wyniku działania tej procedury.
Pozostałe najlepsze chromosomy powstały w ramach podstawowego algorytmu
genetycznego i nie zostały poprawione w ramach dodatkowej optymalizacji
rozwiązania.
9.2.
Charakterystyka preferowanych zmiennych
Preferencje wyboru zmiennych
Diagram 37 przedstawia liczbę wystąpień wybranych zmiennych w zakresach
iteracji: [0-100], [101-200], [201-300], [301-400]. Zaprezentowane wartości to średnie
liczby wystąpień zmiennych prognozowanej giełdy GSE na przestrzeni kolejnych 100
iteracji algorytmu genetycznego.
Algorytm genetyczny wyraźnie preferuje niektóre zmienne. W podanym
przykładzie są to oscylatory Impet (dla k=10, 20), Stochastyczny (SO) oraz numer dnia
w tygodniu. Preferencje te zmieniają się w czasie, co widać po różnicach wartości dla
kolejnych przedziałów iteracji. Zmienna „numer dnia” przez zdecydowaną większość
iteracji nie była wybierana znacząco częściej niż inne zmienne. Natomiast w przedziale
iteracji [301-400] częstość wyboru tej zmiennej była porównywalna z najczęściej
występującymi w populacji. Odmienny typ zachowania to zmniejszanie znaczenia
zmiennej po początkowej preferencji. Przykładem takich zmiennych są oscylatory
MACD, Williams, Stochastyczny (FSO), ROC (dla k=5).
Charakterystyczna jest znaczna częstość występowania zmiennych najbardziej
preferowanych. W dużej mierze wynika to z wpływu większego prawdopodobieństwa
wyboru tych zmiennych wraz ze wzrostem liczby wystąpień oraz z faktu znajdowania
się w najlepszych chromosomach (preferowane kategorie zmiennej).
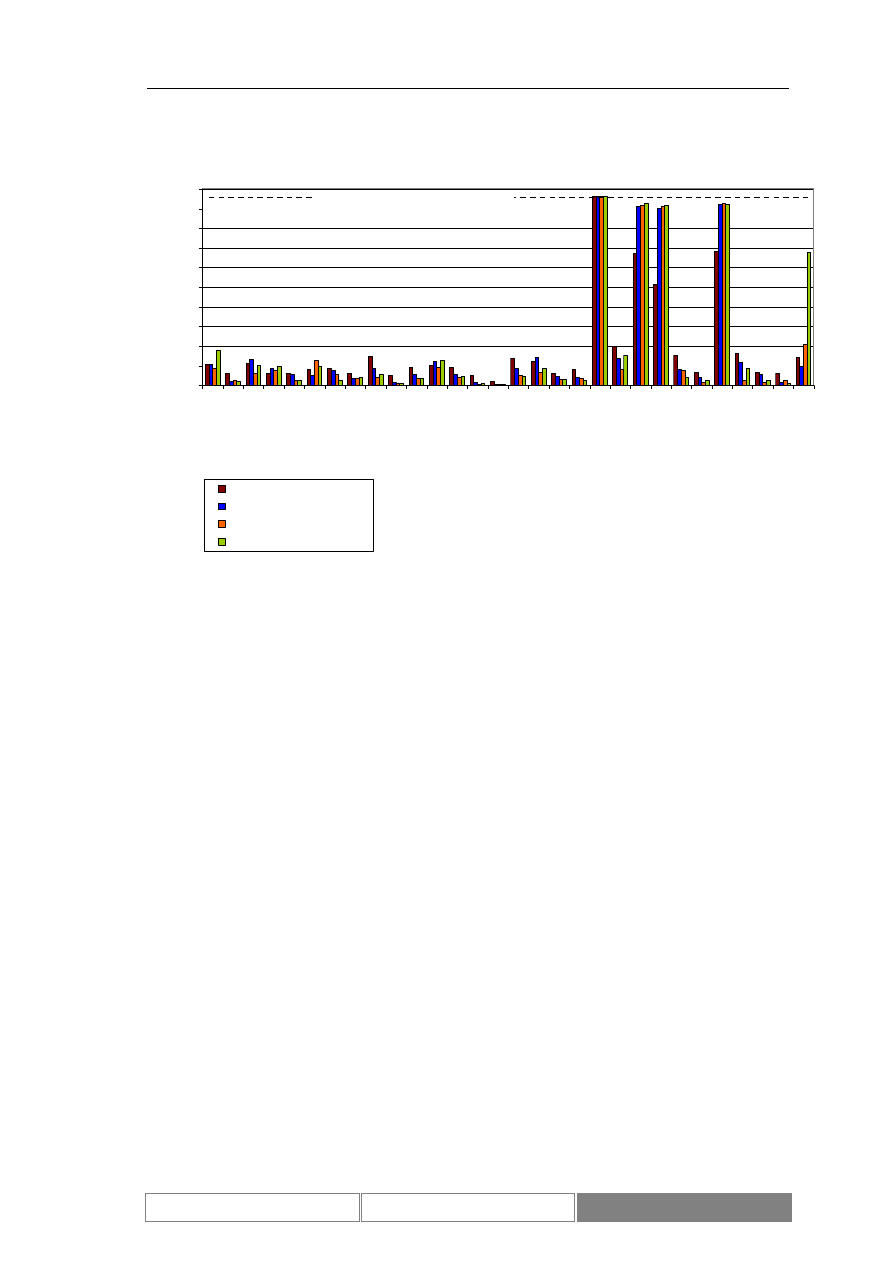
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
92
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 37.
Średnie liczby wystąpień zmiennych prognozowanej giełdy we wszystkich
chromosomach w iteracjach: [0-100], [101-200], [201-300], [301-400]
Najlepsze chromosomy
Poniższa analiza obejmuje pojedynczy krok algorytmu genetycznego, w czasie
którego w ciągu kolejnych iteracji znajdowane są aktualnie najlepsze chromosomy. Na
podstawie
wybranego,
pojedynczego
przebiegu
algorytmu
genetycznego
przedstawiony został sposób dochodzenia do optymalnego rozwiązania. Z powodu
dużej liczby analizowanych zmiennych nie jest możliwe umieszczenie w niniejszym
dokumencie, w sposób czytelny schematu wszystkich omawianych chromosomów.
We wszystkich chromosomach obecna jest zmienna „zmiana wartości
zamknięcia indeksu”. Jest to zmienna wymuszona, co oznacza, że nie mogła ulec
zmianie w kolejnych iteracjach algorytmu. Jedynie dodatkowe iteracje przeszukujące
przestrzeń rozwiązań po zakończeniu działania algorytmu genetycznego mogły ją
zamienić na inną. Poza zmienną wymuszoną, we wszystkich kolejnych najlepszych
chromosomach występują trzy zmienne, które nie były ani razu wymienione na inne.
0
5
10
15
20
25
30
35
40
45
50
W
a
rt
o
ś
ć
O
Z
m
ia
n
a
O
(%
)
M
O
V
A
V
G
5
M
O
V
A
V
G
1
0
M
O
V
A
V
G
2
0
W
a
rt
o
ś
ć
C
W
a
rt
o
ś
ć
H
W
a
rt
o
ś
ć
L
M
A
C
D
W
IL
L
IA
M
S
5
d
n
i
Z
m
ia
n
a
(
%
)
1
0
d
n
i
Z
m
ia
n
a
(
%
)
2
0
d
n
i
Z
m
ia
n
a
(
%
)
M
A
C
D
s
y
g
n
a
ł
k
u
p
u
j/
s
p
rz
e
d
a
j
W
IL
L
IA
M
S
s
y
g
n
a
ł
k
u
p
u
j/
s
p
rz
e
d
a
j
2
A
V
G
's
s
y
g
n
a
ł
k
u
p
u
j/
s
p
rz
e
d
a
j
M
A
C
D
l
in
ia
s
y
g
n
a
łu
T
y
p
f
o
rm
a
c
ji
F
o
rm
a
c
ja
Z
m
ia
n
a
C
(%
)
IM
P
E
T
5
IM
P
E
T
1
0
IM
P
E
T
2
0
R
O
C
5
R
S
I
5
S
O
F
S
O
R
O
C
1
0
R
O
C
2
0
N
u
m
e
r
d
n
ia
Ś
re
d
n
ia
l
ic
z
b
a
w
y
s
t
ą
p
ie
ń
w
c
h
ro
m
o
s
o
m
a
c
h
Ś
rednia z iteracji [0-100]
Ś
rednia z iteracji [101-200]
Ś
rednia z iteracji [201-300]
Ś
rednia z iteracji [301-400]
poziom równy liczbie chromosomów w populacji

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
93
Teoria i zastosowania
Implementacja
Wyniki badań
Są to zmienne najczęściej występujące w populacji (por. Diagram 37): wartość
Oscylatora Stochastycznego (SO) oraz Impetu (dla k=10, 20) – obie zmienne dotyczą
prognozowanej giełdy GSE. Kolejną grupą zmiennych powtarzającą się regularnie w
większości najlepszych chromosomów i występującą w trzech ostatnich z nich są:
numer dnia w tygodniu, 20- i 10-dniowa procentowa zmiana indeksu dla różnych dni
historii oraz Oscylator Impet (dla k=5).
Trzecią grupą są zmienne, które okresowo pojawiały się w najlepszych
chromosomach. Stanowią one obraz poszukiwań algorytmu genetycznego, który na
zasadzie prób i błędów wybierał najlepszy zestaw. Ze zmiennych tych algorytm
wycofywał się po pewnym okresie preferencji.
Reasumując, zidentyfikowane zostały trzy grupy zmiennych: 1) występujące we
wszystkich najlepszych chromosomach, 2) występujące w większość najlepszych
chromosomów, 3) wymieniane w procesie optymalizacji rozwiązania. Analiza
pokazuje konsekwencję wyborów dokonywanych przez algorytm genetyczny oraz
specyfikę jego działania. Zmienne, które pomimo wcześniejszego powodzenia w
dłuższym horyzoncie czasu nie sprawdzały się, były usuwane. Układ najbardziej
korzystnych zmiennych był zachowywany jako trzon zestawu proponowanego do
dalszej nauki.
Wykorzystanie oscylatorów
We wcześniejszym punkcie przedstawione zostały preferencje wybieranych
przez algorytm genetyczny zmiennych. Istotne znaczenie w wyborach algorytmu
miały między innymi oscylatory Impet (dla k=10, 20), Stochastyczny (SO). Poniższa
Tabela V przedstawia występowanie oscylatorów wśród wybieranych zmiennych w
kolejnych 20 niezależnych krokach eksperymentu. Na 20 kroków jedynie w 3 nie został
wskazany żaden z dostępnych oscylatorów. W pozostałych krokach wybierane były
oscylatory, najczęściej Impet (8 razy), MACD oraz Stochastyczny (po 5 razy). Jako
uzupełnienie analizy preferencji zmiennych w czasie pracy algorytmu genetycznego,
pokazuje to znaczenie tego typu zmiennych dla prognozy zmiany wartości indeksu.
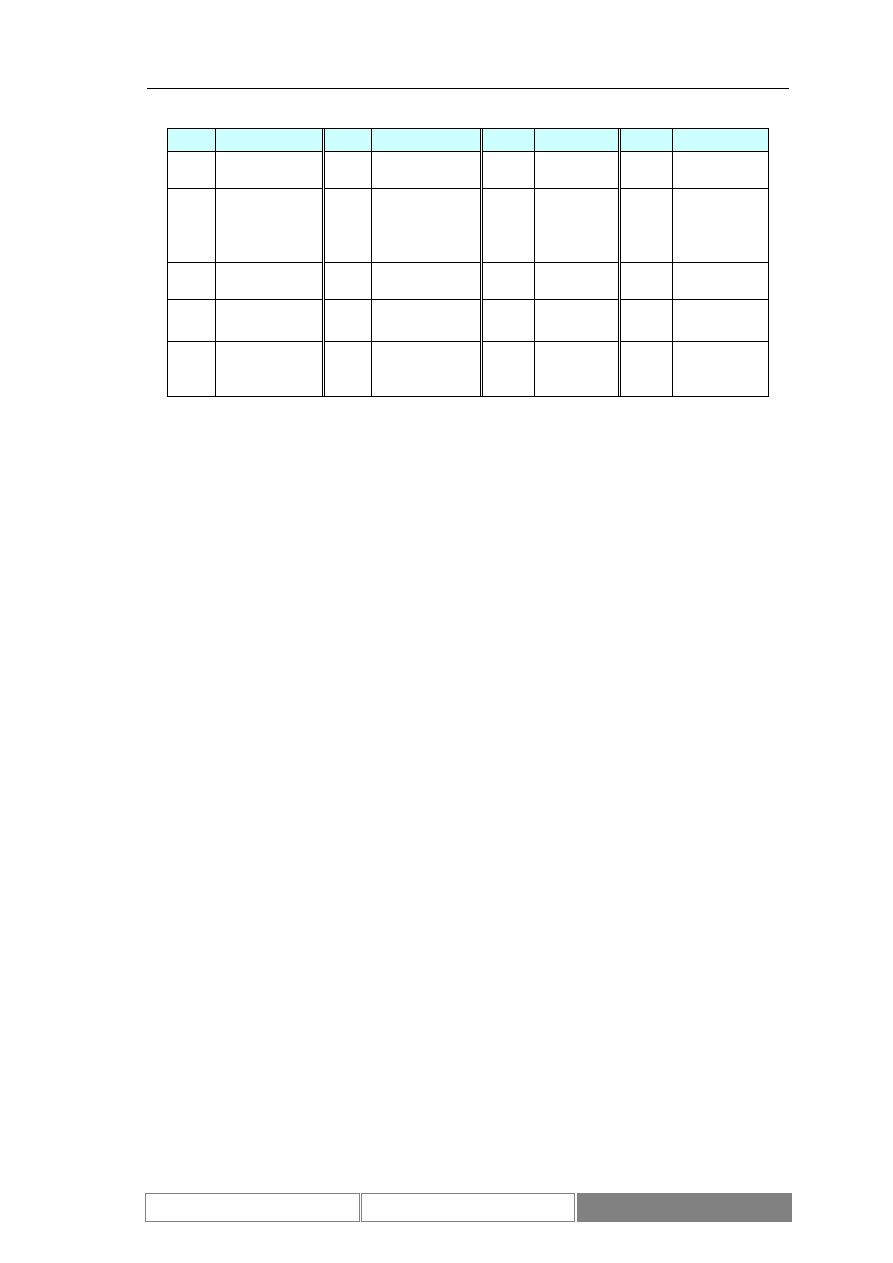
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
94
Teoria i zastosowania
Implementacja
Wyniki badań
Krok Oscylator
Krok Oscylator
Krok
Oscylator
Krok
Oscylator
1
Stochastyczny
Impet
6
Stochastyczny
ROC
11
ROC
16
Dwie średnie
2
-
7
Stochastyczny
Impet
Williams
MACD
12
Williams
17
Impet
3
Stochastyczny
8
Impet
Dwie średnie
13
Impet
18
-
4
Stochastyczny
Impet
9
MACD
14
MACD
19
Dwie średnie
MACD
5
RSI
ROC
MACD
10
-
15
Impet
Williams
20
Impet
Tabela V.
Występowanie oscylatorów w kolejnych krokach eksperymentu
Wykorzystanie zmiennych z innych giełd i wskaźników kursowych
Poniżej przedstawione zostało porównanie procentowej obecności zmiennych
pochodzących z różnych giełd oraz wskaźników kursowych wśród zbiorów
proponowanych przez algorytm genetyczny i ich udziału w zbiorze dostępnych
zmiennych. Pod uwagę były brane zmienne wchodzące w skład zestawów
wykorzystywanych do prognozy w kolejnych 20 krokach eksperymentu. Preferencje
wyboru zmiennych z giełd innych niż prognozowana są wyraźnie wyższe od ich
statystycznej dostępności. Algorytm genetyczny konsekwentnie uwzględnia je w
proponowanych zestawach zmiennych. Potwierdza to zasadność uwzględnienia tych
zmiennych w danych, na których opiera się prognoza. Jednocześnie kolejność
względem stopnia wykorzystania jest zgodna z wartościami współczynnika korelacji z
prognozowaną zmienną.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
95
Teoria i zastosowania
Implementacja
Wyniki badań
Zakres danych
Występowanie w zmiennych
wybieranych przez AG
Występowanie w zbiorze
zmiennych dostępnych dla AG
GSE
84.11%
94.59%
NYSE
6.62%
1.35%
TSE
3.97%
1.35%
USD/JPY
3.31%
1.35%
EUR/USD
1.99%
1.35%
Tabela VI.
Wykorzystanie zmiennych z giełd oraz wskaźników kursowych
9.3.
Możliwość nauki sieci neuronowej
W Rozdziale 9.1 (Diagram 36) przedstawiona została zmienność liczby martwych
chromosomów w populacji w kolejnych iteracjach. Ponieważ chromosomy w startowej
populacji są generowane w sposób losowy, liczba martwych chromosomów
początkowo może być duża. Niezależnie od sytuacji wyjściowej populacja dąży do
eliminacji martwych chromosomów. W efekcie ich liczba spada wraz z kolejnymi
iteracjami.
Chromosom jest określany jako martwy w przypadku, gdy żadna z trzech sieci
neuronowych przez niego zdefiniowanych nie może się nauczyć. Skuteczność nauki
jest oceniania w kategoriach błędu prognozy na podstawie rekordów walidacyjnych,
które nie były wykorzystane w czasie doboru wag. Diagram 38 przedstawia cztery
podstawowe typy charakterystyk zmienności błędu sieci neuronowej w czasie nauki.
Możliwość nauki zależy od zbioru zmiennych wejściowych kodowanych przez
chromosom. Sieć neuronowa typu A nie była w stanie poprawić swojego błędu
prognozy dla danego zestawu zmiennych. Wraz z kolejnymi iteracjami jej skuteczność
dla rekordów walidacyjnych konsekwentnie spadała. Na podstawie zdefiniowanych
warunków zatrzymania nauka została szybko przerwana jako nie rokująca nadziei na
poprawę. Kolejne sieci neuronowe były w stanie osiągnąć zadowalające postępy w
nauce. Wprawdzie typy B i C również charakteryzują się wzrostem błędu ponad jego
wyjściową wartość, ale istnieje układ wag, dla których błąd ten jest akceptowalny,
osiągając wartość minimalną. W tych przypadkach stan wag sieci neuronowej po
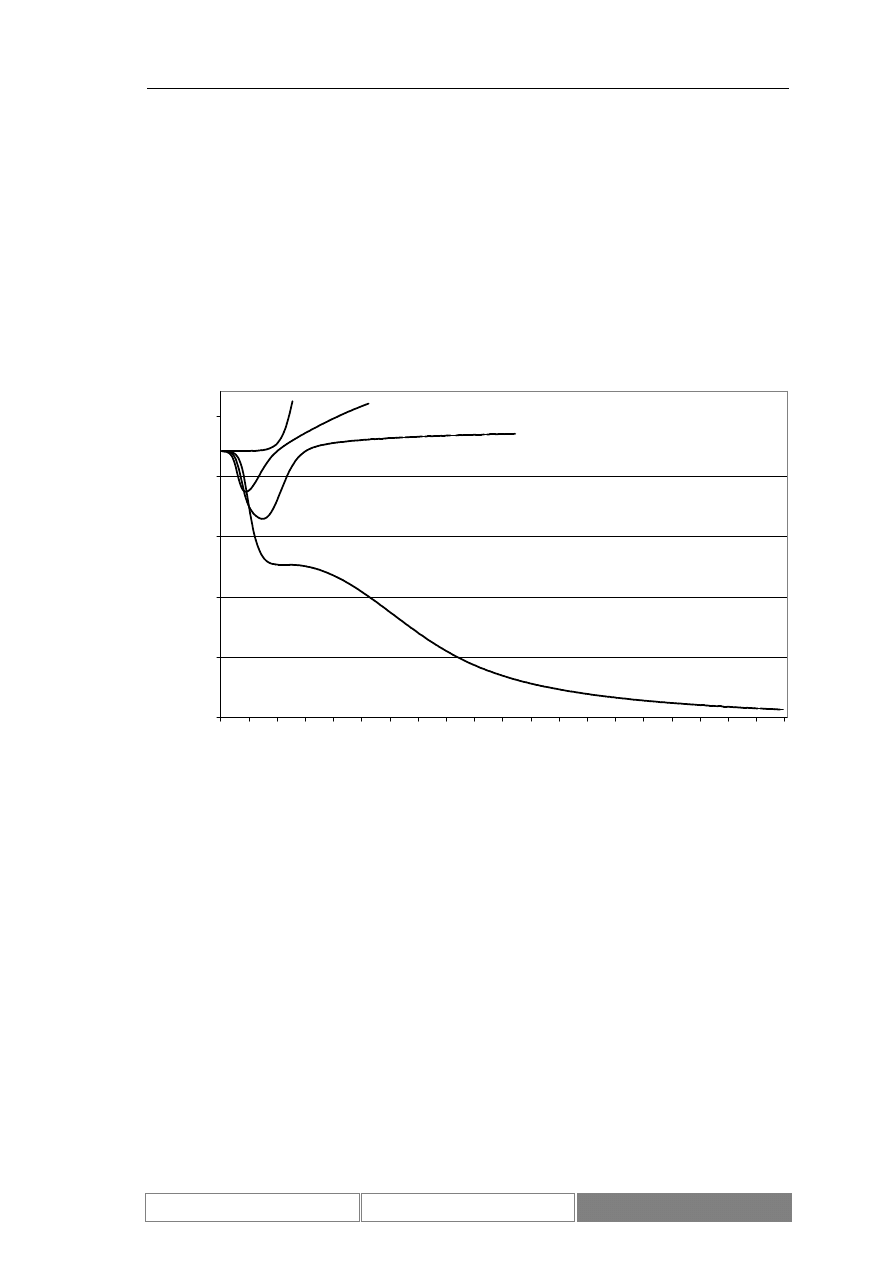
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
96
Teoria i zastosowania
Implementacja
Wyniki badań
spełnieniu warunku zatrzymania jest odtwarzany z punktu, w którym błąd osiągnął
minimalną wartość. Ostatnim typem jest sieć neuronowa, która nie osiągnęła
minimalnego błędu na próbce walidacyjnej w ciągu zadanej maksymalnej możliwej
liczby iteracji. Jest to przypadek skutecznej nauki, która mogła być kontynuowana. Jej
przerwanie warunkiem maksymalnej liczby iteracji ma miejsce jedynie w czasie
obliczeń algorytmu genetycznego. W finalnej nauce wybranej sieci neuronowej
maksymalna liczba iteracji jest ustalona na odpowiednio wysokim poziomie.
Diagram 38.
Błędy sieci neuronowych dla rekordów walidacyjnych
0,017
0,022
0,027
0,032
0,037
0,042
1
11
21
31
41
51
61
71
81
91 101 111 121 131 141 151 161 171 181 191 201
Iteracje nauki
B
ł
ą
d
p
ro
g
n
o
z
y
A
B
C
D

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
97
Teoria i zastosowania
Implementacja
Wyniki badań
10.
Wyniki eksperymentów
10.1.
Wyniki jakościowe
W niniejszym rozdziale zaprezentowane zostały numeryczne własności
prognozy systemu neuro-genetycznego. Diagram 39 przedstawia rozkład błędów
prognozy w kolejnych 100 dniach testowych zgodnie ze wzorami [37][38]
odpowiednio kwadratowy (dolna część wykresu) i bezwzględny (górna część
wykresu). Istotne wartości numeryczne błędów zawiera Tabela VII. Poszczególne
wartości umieszczone w tabeli odpowiadają kolejnym elementom
i
i
c
c
′
−
zgodnie z
powyższymi wzorami.
Diagram 39.
Rozkład błędów - kwadratowy (linia) i bezwzględny (słupki)
22
86
20
-2,0E-04
-1,5E-04
-1,0E-04
-5,0E-05
0,0E+00
5,0E-05
1,0E-04
1,5E-04
2,0E-04
2,5E-04
3,0E-04
1
5
9 13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81 85 89 93 97
0,0E+00
2,0E-06
4,0E-06
6,0E-06
8,0E-06
1,0E-05
1,2E-05
1,4E-05
1,6E-05
1,8E-05
2,0E-05
2,2E-05
2,4E-05

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
98
Teoria i zastosowania
Implementacja
Wyniki badań
Wartość średnia
Wartość maksymalna z
i
i
c
c
′
−
Wartość minimalna z
i
i
c
c
′
−
Błąd bezwzględny (e) –
wartości bezwzględne
8.53924966E
−
03
2.78283722E
−
04 1.05632097E
−
06
Błąd kwadratowy (mse)
1.10453991E
−
04
7.74418301E
−
06 1.11581400E
−
10
Tabela VII.
Wartości błędów prognozy
Rozkład błędów numerycznych charakteryzuje się dużą zmiennością. W
przypadku błędu bezwzględnego waha się on w przedziale o rozmiarze 3 rzędów
wielkości (w przypadku modułów błędów). Dla błędu średniokwadratowego wahania
występują w zakresie 5 rzędów wielkości. Największe błędy występują w dniach 20, 22
i 86. W tych przypadkach system prognozował zbyt duży wzrost lub zbyt mały spadek
wartości indeksu. W przeciwieństwie do dni 20 i 22 pomyłka w dniu 86 miała wyraźny
wpływ na wynik (Rozdział 10.2).
10.2.
Wyniki finansowe – podstawowy eksperyment
Tabela VIII prezentuje wyniki finansowe po 100 dniach inwestowania dla
każdego z algorytmów. Przedstawiona została procentowa wartość zmiany
początkowego budżetu, który we wszystkich przypadkach wynosił 100 000 jednostek.
Algorytm wykorzystujący rzeczywiste przyszłe wartości indeksów (algorytm
profetyczny) uzyskał zdecydowanie najlepszy wynik, jednak ze względu na brak
praktycznego zastosowania nie będzie on dalej rozważany (służy on jedynie jako górne
teoretyczne ograniczenie skuteczności metod predykcyjnych). Z pozostałych metod
najlepszy wynik został uzyskany przez algorytm oparty na prognozie systemu neuro-
genetycznego. Jest on o 13% lepszy niż następny w kolejności oparty na prognozie
oscylatora MACD.
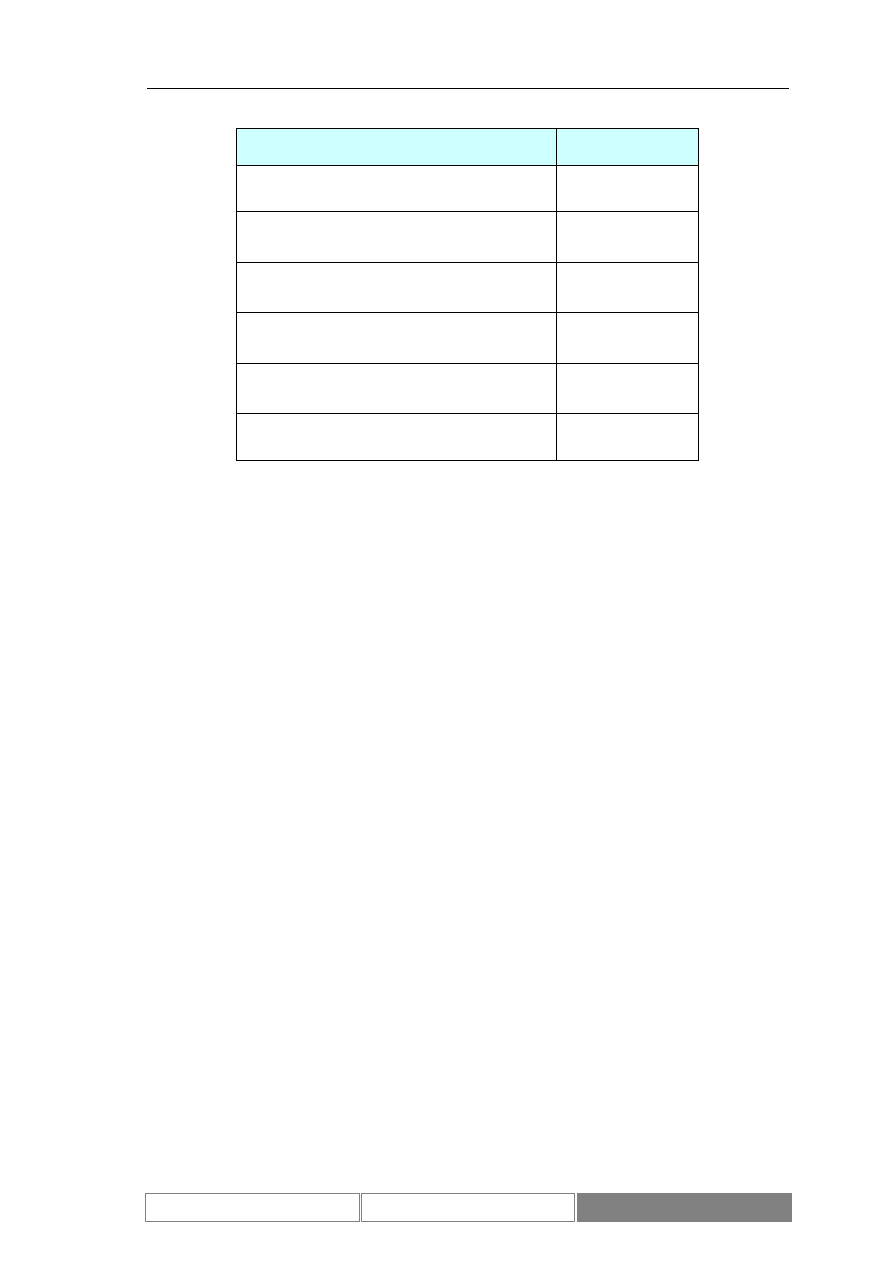
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
99
Teoria i zastosowania
Implementacja
Wyniki badań
Algorytm
Wynik [%]
Algorytm SNG (system neuro-genetyczny)
9.32
Algorytm LS (losowe sygnały)
−
2.73
Algorytm KT (kupuj i trzymaj)
−
5.45
Algorytm OZ (utrzymanie ostatniej zmiany)
−
8.00
Algorytm MACD (prognoza oscylatora MACD)
−
3.58
Algorytm PRF (profetyczny)
39.56
Tabela VIII.
Wyniki dla algorytmów SNG, LS, KT, OZ, MACD, PRF
Diagram 40 przedstawia wyniki inwestowania uzyskane przez algorytmy w
okresie 100 dni testowych. W przypadku algorytmu opartego na losowaniu sygnałów,
wybrany został przebieg odpowiadający przeciętnemu wynikowi uzyskanemu dla
10 000 prób. Od dnia 19 algorytm SNG sukcesywnie zdobywa przewagę nad
pozostałymi metodami. Szczególnie jest to widoczne od dnia 48. Najbardziej
kosztowne błędy zostały popełnione przez algorytm SNG w dniach o numerach 14
oraz 86. Pozostałe algorytmy nie popełniły znacząco więcej błędów powodujących
spadek wartości, jednak nie były one w stanie wykorzystać zmian wartości indeksu dla
zwiększania kapitału. Z tego powodu ostateczny wynik algorytmów LS, KT, OZ i
MACD jest gorszy od algorytmu SNG. Diagram 41 przedstawia sukcesywne
zdobywanie przewagi przez zaproponowaną metodę nad pozostałymi algorytmami (z
wyjątkiem algorytmu profetycznego). Diagram ten prezentuje różnice bieżącej
wartości kapitału pomiędzy algorytmem SNG a algorytmami konkurencyjnymi.
Wartości dodatnie świadczą o przewadze algorytmu opartego na prognozie sieci
neuronowej. Ważną obserwacją jest występowanie okresów, w których algorytm SNG
dorównuje skutecznością algorytmowi wykorzystującemu wiedzę o przyszłych
wartościach indeksu (algorytm PRF). Wyróżnić można sześć takich okresów: [1,14],
[18,27], [37,44], [48,52], [68,74], [97,100].
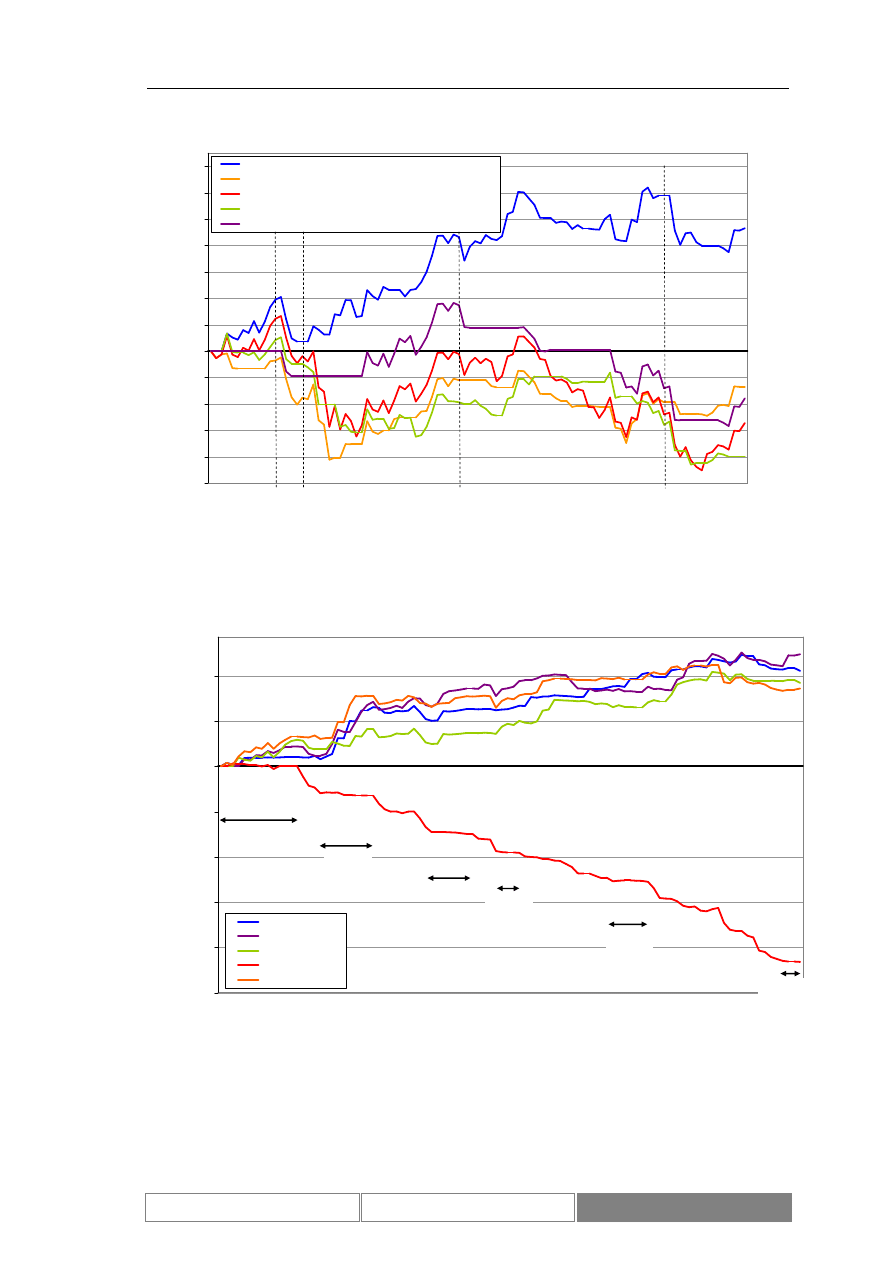
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
100
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 40.
Wyniki uzyskane przez algorytmy SNG, LS, MACD, KT, OZ
Diagram 41.
Różnice wyników pomiędzy algorytmem SNG a pozostałymi algorytmami LS,
KT, OZ, MACD, PRF
14
19
48
86
-10000
-8000
-6000
-4000
-2000
0
2000
4000
6000
8000
10000
12000
14000
1
6
11
16
21
26
31
36
41
46
51
56
61
66
71
76
81
86
91
96
Kolejne dni testu
W
y
n
ik
g
ry
-
z
m
ia
n
a
p
o
c
z
ą
tk
o
w
e
g
o
b
u
d
ż
e
tu
Algorytm SNG (system neuro-genetyczny)
Algorytm LS (losowe sygnały)
Algorytm KT (kupuj i trzymaj)
Algorytm OZ (utrzymanie ostatniej zmiany)
Algorytm MACD (prognoza oscylatora MACD)
KT
OZ
SNG
LS
MACD
-35000
-28000
-21000
-14000
-7000
0
7000
14000
1
5
9
13
17
21
25
29
33
37
41
45
49
53
57
61
65
69
73
77
81
85
89
93
97
Kolejne dni testu
R
ó
ż
n
ic
a
w
y
n
ik
u
a
lg
o
ry
tm
ó
w
SNG, KT
SNG, OZ
SNG, MACD
SNG, PRF
SNG, LS
[1,14]
[18,27]
[37,44]
[48,52]
[68,74]
[97,100]
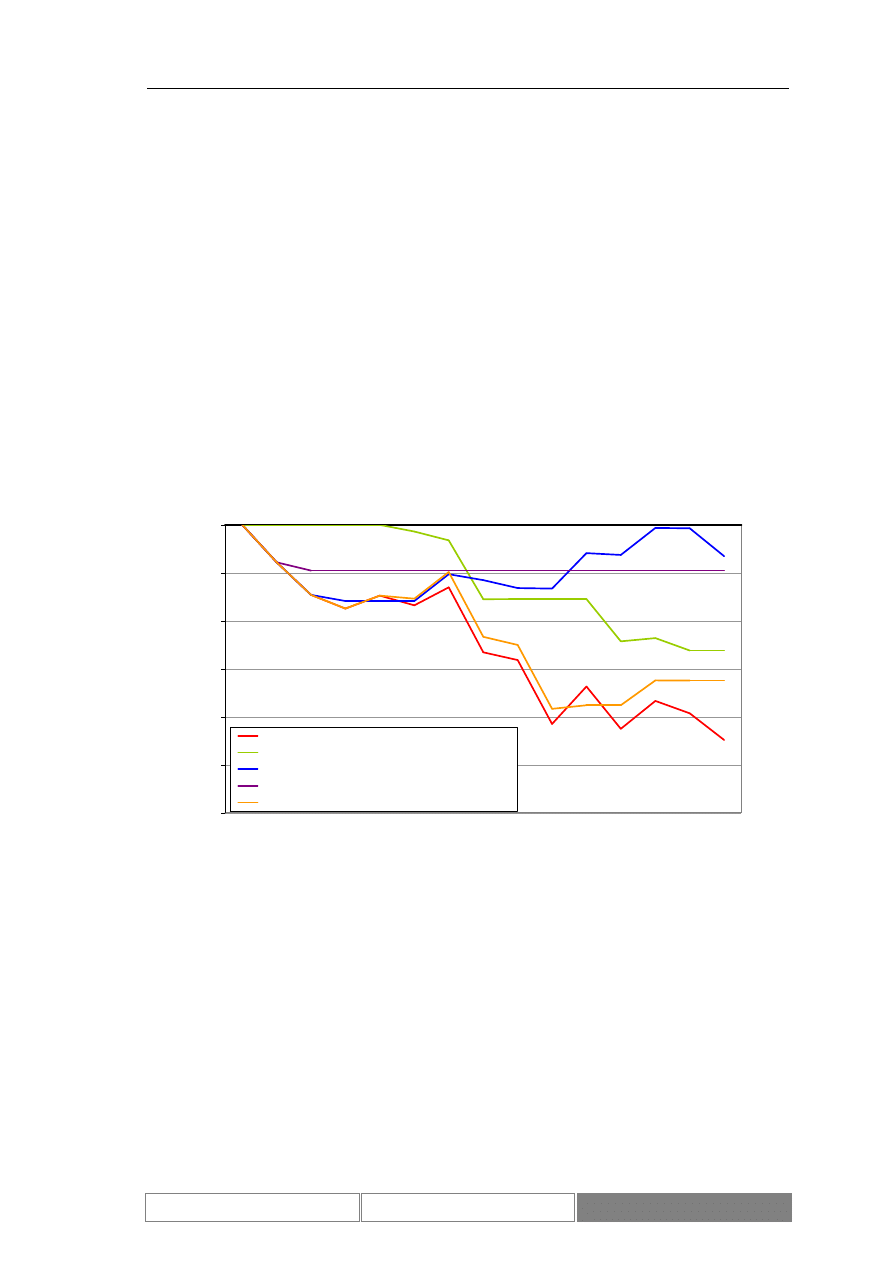
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
101
Teoria i zastosowania
Implementacja
Wyniki badań
Kolejne dwa diagramy przedstawiają wyniki przeprowadzonych testów w
podzbiorach dni testowych charakteryzujących się znacząco większą liczbą spadków
(dni [14,28], Diagram 42) oraz wzrostów (dni [28,59], Diagram 43) wartości indeksu. Do
testów wykorzystane zostały prognozy uzyskane w eksperymencie trwającym przez
pełne 100 dni. W obu przypadkach algorytm oparty na prognozie systemu neuro-
genetycznego okazał się najbardziej skuteczny, jednak różnica w stosunku do
kolejnego algorytmu nie jest już tak duża jak w przypadku pełnego okresu 100 dni.
Przy tendencji spadkowej najbliższy skutecznością okazał się algorytm MACD. Dla
tendencji wzrostowej zbliżony wynik uzyskał algorytm KT, który wprost zależy od
końcowej zmiany wartości indeksu.
Diagram 42.
Wyniki algorytmów SNG, LS, KT, OZ, MACD przy trendzie malejącym
-12000
-10000
-8000
-6000
-4000
-2000
0
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Kolejne dni testu
W
y
n
ik
g
ry
-
z
m
ia
n
a
p
o
c
z
ą
tk
o
w
e
g
o
b
u
d
ż
e
tu
Algorytm KT (kupuj i trzymaj)
Algorytm OZ (utrzymanie ostatniej zmiany)
Algorytm SNG (system neuro-genetyczny)
Algorytm MACD (prognoza oscylatora MACD)
Algorytm LS (losowe sygnały)
SNG
MACD
KT
OZ
LS
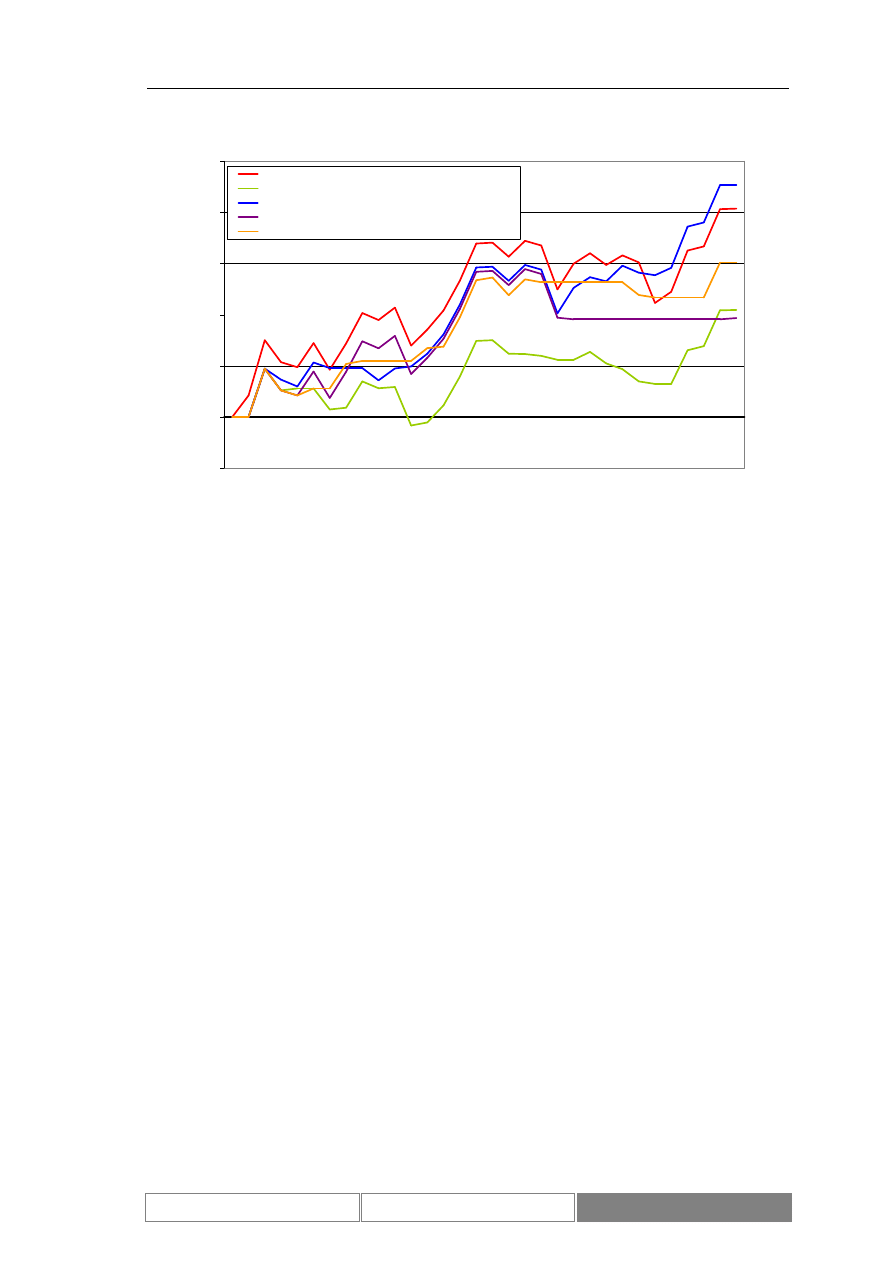
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
102
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 43.
Wyniki algorytmów SNG, LS, KT, OZ, MACD przy trendzie rosnącym
10.3.
Analiza liczby realizowanych transakcji
Przedstawiane algorytmy inwestowania proponują sygnały kupna i sprzedaży
zależnie od spodziewanej przyszłej wartości indeksu. Nie biorą one jednak pod uwagę
bieżącego stanu budżetu. Z tego powodu możliwe jest występowanie sytuacji, w której
transakcja proponowana przez algorytm nie może być zrealizowana. Przede
wszystkim ma to miejsce w przypadku algorytmu MACD. Prawie połowa transakcji
nie jest faktycznie realizowana. Dla pozostałych algorytmów jedynie pojedyncze
sygnały nie powodują realizacji transakcji. Podsumowanie liczby transakcji
przedstawia Tabela IX. Przyjęto, że występowanie dwóch lub więcej takich samych
sygnałów w kolejnych dniach oznacza pojedynczy sygnał.
-2000
0
2000
4000
6000
8000
10000
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
Kolejne dni testu
W
y
n
ik
g
ry
-
z
m
ia
n
a
p
o
c
z
ą
tk
o
w
e
g
o
b
u
d
ż
e
tu
Algorytm KT (kupuj i trzymaj)
Algorytm OZ (utrzymanie ostatniej zmiany)
Algorytm SNG (system neuro-genetyczny)
Algorytm MACD (prognoza oscylatora MACD)
Algorytm LS (losowe sygnały)
SNG
MACD
KT
OZ
LS

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
103
Teoria i zastosowania
Implementacja
Wyniki badań
Algorytm
Liczba
planowanych
transakcji
Liczba
zrealizowanych
transakcji
Algorytm SNG (system neuro-genetyczny)
51
50
Algorytm LS (losowe sygnały)
46
46
Algorytm KT (kupuj i trzymaj)
2
2
Algorytm OZ (utrzymanie ostatniej zmiany)
56
54
Algorytm MACD (prognoza oscylatora MACD)
21
12
Algorytm PRF (profetyczny)
57
56
Tabela IX.
Liczby transakcji planowanych i zrealizowanych przez algorytmy SNG, LS, KT, OZ,
MACD, PRF
10.4.
Analiza statystyczna działania algorytmu opartego o losowe sygnały
Algorytm oparty na decyzjach inwestycyjnych podejmowanych w sposób
losowy jest jednym z typowych punktów odniesienia dla weryfikowanych metod
predykcji. Wyniki inwestowania osiągane przez algorytm oparty na losowych
sygnałach charakteryzują się znaczną rozpiętością. W celu określenia parametrów
charakteryzujących działanie algorytmu przeprowadzona została podstawowa analiza
statystyczna oparta na 10 000 przebiegów eksperymentu. Podstawowe własności
statystyczne zawiera Tabela X. Wyniki mieszczą się w przedziale (
−
22%,18%) w
stosunku do początkowego budżetu, przy wartości średniej równej
−
2.7%. Rozkład
charakteryzuje się znacznym odchyleniem standardowym.
Przeprowadzony został test statystyczny Kołmogorowa-Smirnowa przy
hipotezie, że rozkład wyników algorytmu LS jest rozkładem normalnym. Histogram
wyników przedstawia Diagram 44. Zgodnie z testem, badany rozkład jest rozkładem
normalnym (poziom istotności równy 0.0004). Jest to zgodne z oczekiwaniami i
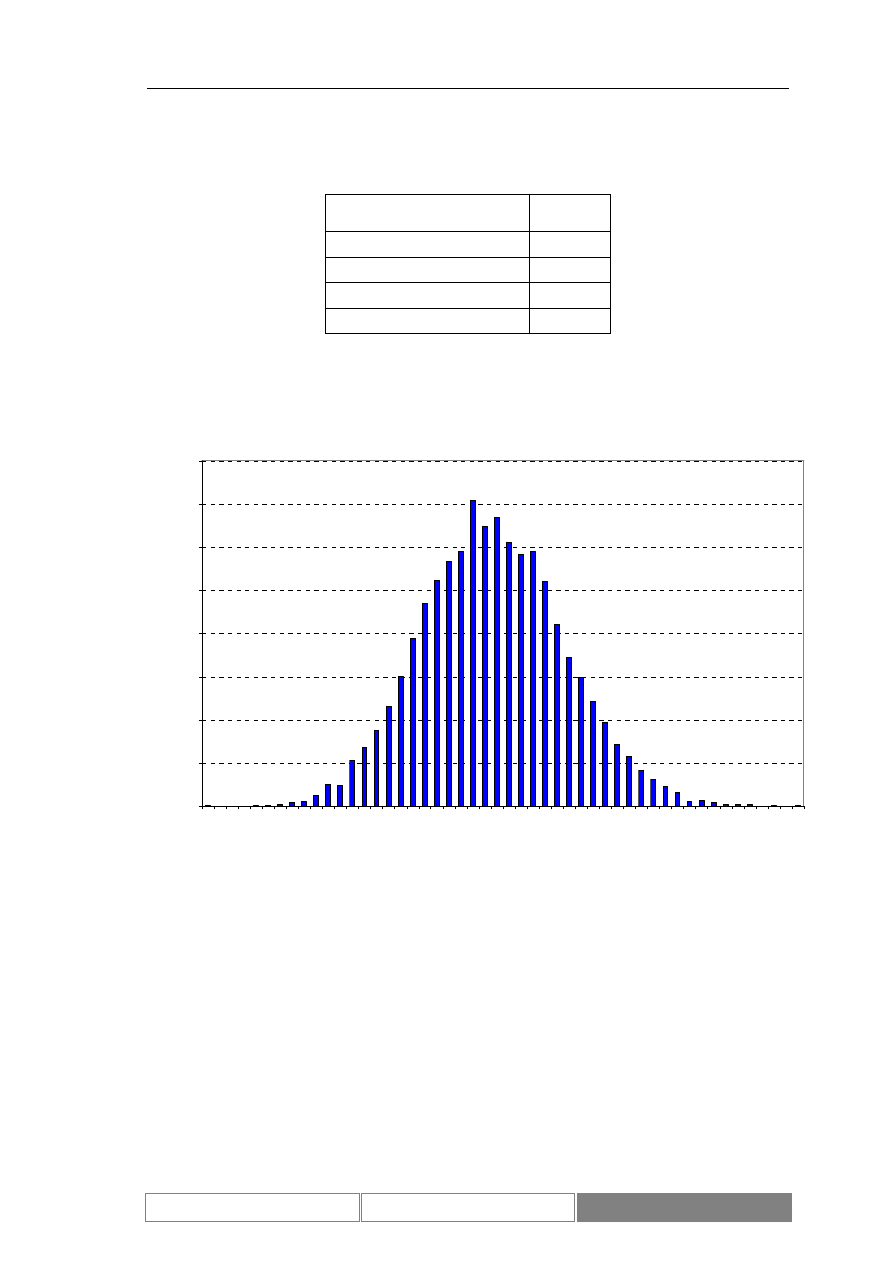
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
104
Teoria i zastosowania
Implementacja
Wyniki badań
pozwala na porównanie wyników systemu SNG z przeciętną (w rozumieniu
uzyskanego wyniku) grą losową.
Liczba obserwacji
10 000
Odchylenie standardowe
4 790
Średni wynik
−
2 726
Wynik minimalny
−
21 965
Wynik maksymalny
17 865
Tabela X.
Własności statystyczne próbki 10 000 wyników uzyskanych przez algorytm LS
Diagram 44.
Histogram wyników uzyskanych przez algorytm LS dla 10 000 prób
10.5.
Weryfikacja wpływu zmienności zależności
Zaproponowany został eksperyment weryfikujący wpływ na wynik
inwestowania postulowanej zmienności zależności na giełdzie. Eksperyment został
zaprojektowany na bazie podstawowego eksperymentu prezentowanego we
wcześniejszych rozdziałach. W eksperymencie podstawowym, w każdym kroku
wyznaczany jest zestaw zmiennych wykorzystywanych w prognozie dla kolejnych 5
0
100
200
300
400
500
600
700
800
-2
1
5
6
7
-2
0
7
7
0
-1
9
9
7
4
-1
9
1
7
7
-1
8
3
8
0
-1
7
5
8
4
-1
6
7
8
7
-1
5
9
9
1
-1
5
1
9
4
-1
4
3
9
7
-1
3
6
0
1
-1
2
8
0
4
-1
2
0
0
8
-1
1
2
1
1
-1
0
4
1
4
-9
6
1
8
-8
8
2
1
-8
0
2
5
-7
2
2
8
-6
4
3
1
-5
6
3
5
-4
8
3
8
-4
0
4
1
-3
2
4
5
-2
4
4
8
-1
6
5
2
-8
5
5
-5
8
7
3
8
1
5
3
5
2
3
3
1
3
1
2
8
3
9
2
5
4
7
2
1
5
5
1
8
6
3
1
4
7
1
1
1
7
9
0
8
8
7
0
4
9
5
0
1
1
0
2
9
7
1
1
0
9
4
1
1
8
9
1
1
2
6
8
7
1
3
4
8
4
1
4
2
8
1
1
5
0
7
7
1
5
8
7
4
1
6
6
7
0
1
7
4
6
7
L
ic
z
b
a
w
y
s
t
ą
p
ie
ń
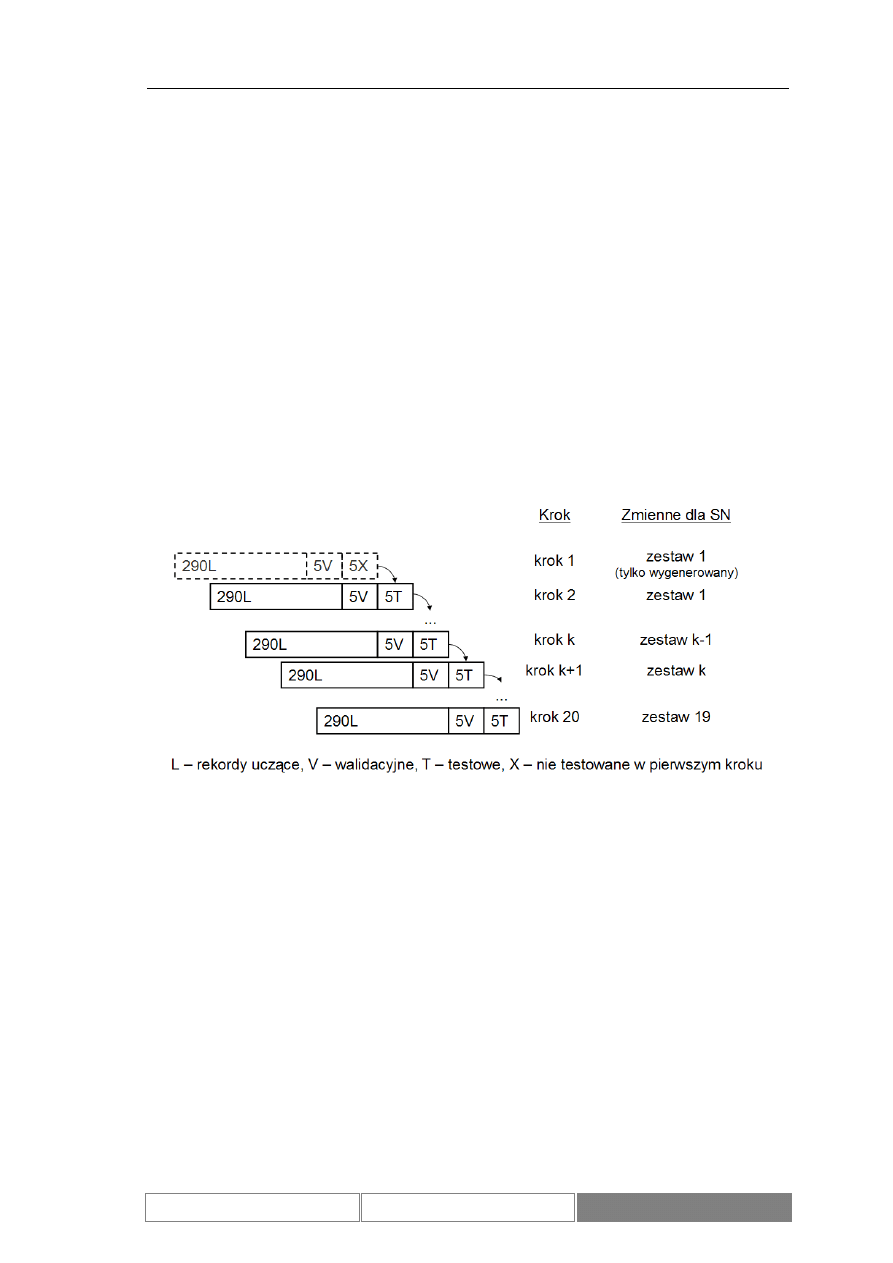
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
105
Teoria i zastosowania
Implementacja
Wyniki badań
dni danego kroku. Sieć neuronowa jest uczona na podstawie wybranych zmiennych,
wykorzystując dane dostępne w dniach poprzedzających pierwszy dzień bieżącego
kroku. Modyfikacja eksperymentu polega na wykorzystaniu do prognoz w bieżącym
kroku sieci neuronowej ustalonej w kroku poprzednim. Sieć ta jest douczana,
uwzględniając nowe dane, wynikające z przesunięcia. Jedyna różnica w stosunku do
podstawowego eksperymentu polega więc na wykorzystaniu przez sieci różnych
zestawów zmiennych – warunki i zakres wykorzystywanych danych pozostają bez
zmian. Zakres testów został ograniczony do 95 dni, ponieważ prognoza nie była
wykonana w pierwszym kroku eksperymentu, kiedy jedynie został wybrany zestaw
zmiennych. Schemat podziału rekordów wraz z zaznaczonym pominiętym oknem
czasowym przedstawia Diagram 45.
Diagram 45.
Podział rekordów dla kolejnych kroków eksperymentu z przesuniętym oknem
czasowym.
Porównane zostały wyniki inwestowania za pomocą algorytmu SNG
działającego w sposób opisany w podstawowym eksperymencie z wynikiem
algorytmu zmodyfikowanego o uwzględnienie zbioru zmiennych z wcześniejszego
kroku (algorytm z-SNG). Zysk z inwestycji uzyskanych przez algorytm SNG wyniósł
w testowym przedziale czasu 8.32% (o 1% mniej niż dla 100 dni podstawowego
eksperymentu). Zastosowanie algorytmu z-SNG spowodowało zakończenie
eksperymentu stratą 2.27%. Jest to jednak wynik lepszy niż spadek wartości indeksu,
który wyniósł 4.99%. Przebieg zmian zysku w czasie trwania eksperymentu (Diagram
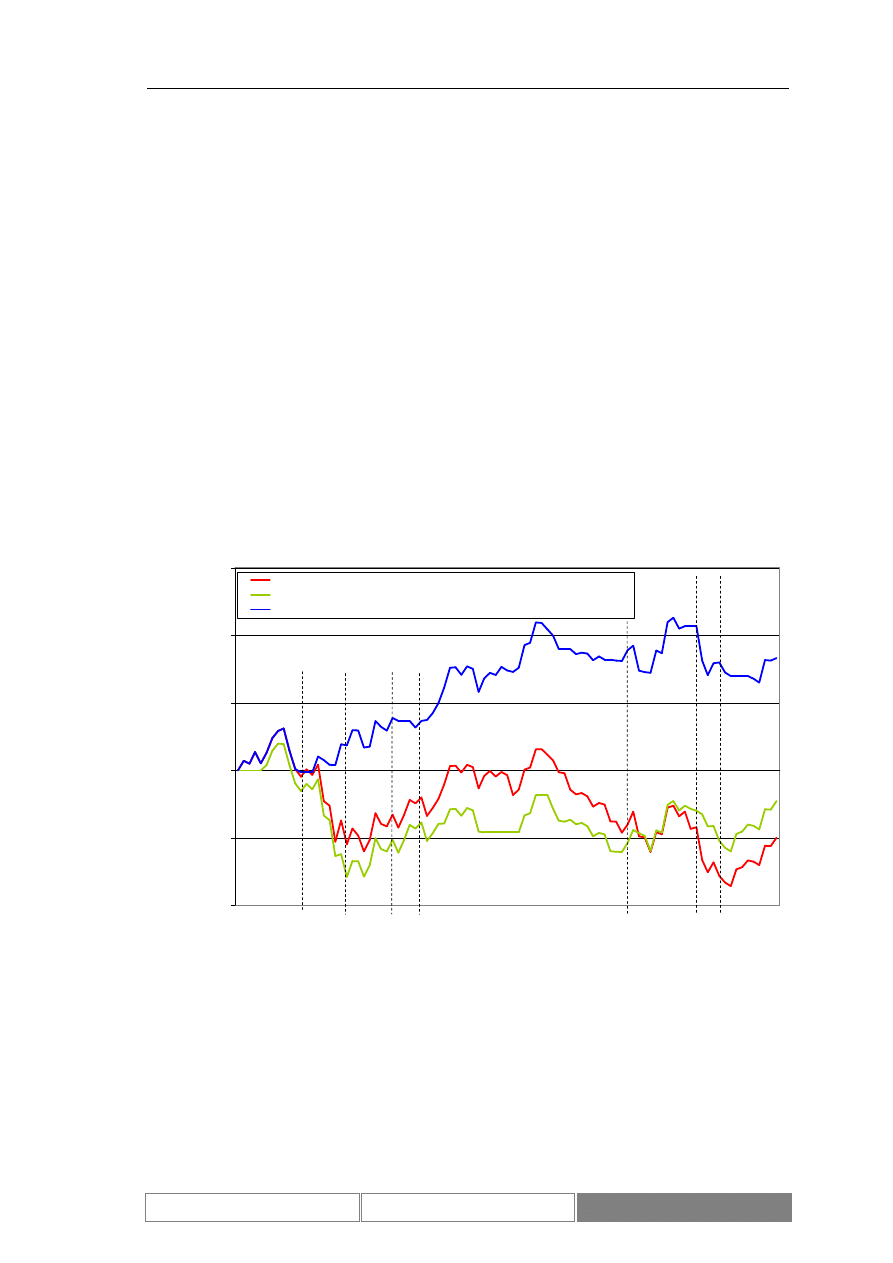
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
106
Teoria i zastosowania
Implementacja
Wyniki badań
46) dla metody z-SNG jest zbliżony do wyników metody „kupuj i trzymaj”. Przewaga
tej pierwszej wynika z dobrego inwestowania w końcowej fazie eksperymentu.
Analiza różnic pomiędzy wynikami uzyskanymi przez porównywane algorytmy
(Diagram 47) ujawnia okresy, w których algorytm z-SNG zmniejsza swoją stratę w
stosunku do algorytmu SNG. Są to dni [29,33], 69, 81 oraz [85,95]. Różnica w tych
dniach wyraźnie maleje, jednak nie na tyle, żeby wyrównać wyniki obu algorytmów.
Przewaga pierwotnego algorytmu SNG opiera się na właściwych decyzjach w krótkim
okresie – dni [13,20] oraz dłuższym czasie dobrych inwestycji z dni [33,69]. Powyższa
analiza uzasadnia stosowanie algorytmu, który przystosowuje się do zmieniającej się
sytuacji na giełdzie. Jednocześnie sieć neuronowa zmuszona do prognozy w kolejnym
kroku nadal zachowuje sensowność działania, aczkolwiek możliwości prognozy są w
tym przypadku znacząco ograniczone.
Diagram 46.
Wyniki inwestowania dla algorytmów KT, SNG, z-SNG (wykorzystanie
zestawu zmiennych z wcześniejszego kroku)
81
20
29
33
69
85
13
-10000
-5000
0
5000
10000
15000
1
5
9
13 17 21 25 29 33 37 41 45 49 53 57 61 65 69 73 77 81 85 89 93
Kolejne dni testu
W
y
n
ik
g
ry
-
z
m
ia
n
a
p
o
c
z
ą
tk
o
w
e
g
o
b
u
d
ż
e
tu
Algorytm KT (kupuj i trzymaj)
Algorytm z-SNG (zmodyfikowany system neuro-genetyczny)
Algorytm SNG (system neuro-genetyczny)
SNG
z-SNG
KT
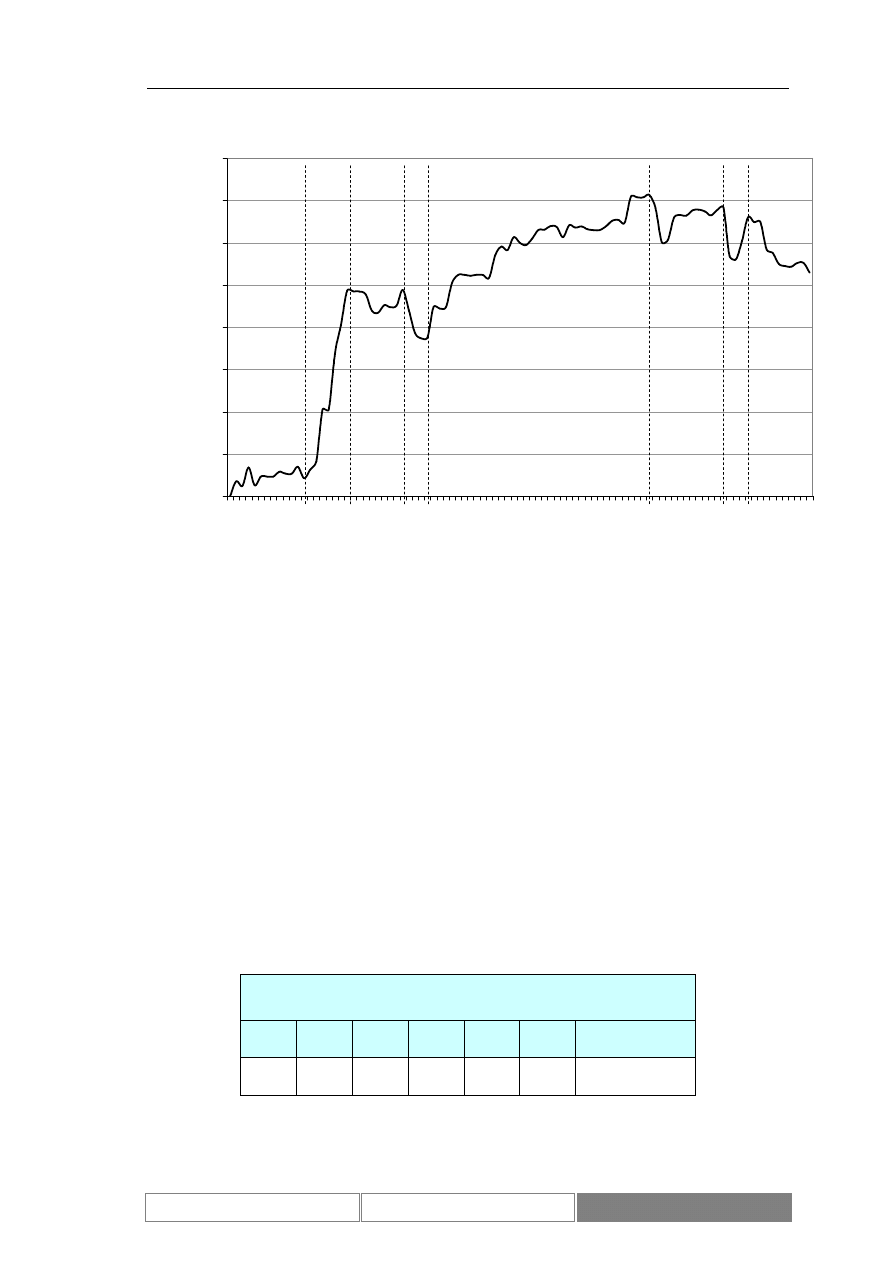
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
107
Teoria i zastosowania
Implementacja
Wyniki badań
Diagram 47.
Różnice wyników algorytmów SNG, z-SNG
10.6.
Weryfikacja powtarzalności wyników
Powtórzenie eksperymentu
W celu weryfikacji stopnia powtarzalności wyników podstawowy eksperyment
(Rozdział 10.2) został powtórzony z niezmienionymi ustawieniami parametrów oraz w
tym samym przedziale dni testu. Tabela XI zawiera wyniki sześciu niezależnych
przebiegów. Osiągnięte rezultaty zawierają się w przedziale [3.41%,9.32%] przy
wartości średniej 5.44%. Rozpiętość wyników wynosi 6%. Wszystkie przebiegi
charakteryzują się wynikami lepszymi od pozostałych rozważanych algorytmów, za
wyjątkiem algorytmu profetycznego.
Wynik [%] w poszczególnych przebiegach algorytmu SNG
1
2
3
4
5
6
wartość średnia
9.32
4.68 3.51 3.41 5.96 7.67
5.44
Tabela XI.
Wyniki powtórzonych przebiegów algorytmu SNG
85
81
69
33
29
20
13
0
2000
4000
6000
8000
10000
12000
14000
16000
1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85 88 91 94
Kolejne dni testu
R
ó
ż
n
ic
a
w
y
n
ik
ó
w

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
108
Teoria i zastosowania
Implementacja
Wyniki badań
Istotną cechą charakterystyczną eksperymentu powtórzonego w kolejnych
przebiegach są podobieństwa zestawów zmiennych wybieranych przez algorytm
genetyczny. Przeprowadzona została szczegółowa analiza wybieranych zmiennych w
pierwszych trzech przebiegach algorytmu (Załącznik B zawiera pełną listę zmiennych).
Porównywane były zmienne wybierane w poszczególnych 20 krokach eksperymentu.
W każdym kroku, dla każdego z odpowiadających sobie zestawów wyznaczona
została liczba zmiennych identycznych w każdym z trzech zestawów lub identycznych
w dwóch zestawach. W stosunku do całkowitej liczby zmiennych wybranych we
wszystkich zestawach, dla wszystkich kroków eksperymentu 43% zmiennych
wybieranych było w każdym z trzech przebiegów. Zaobserwowano 26% zmiennych
występujących wyłącznie w dwóch przebiegach algorytmu SNG. Pozostałe 31%
zmiennych było wybieranych wyłącznie w pojedynczych przebiegach. Porównanie to
pokazuje powtarzalność preferencji wyborów algorytmu genetycznego w niezależnych
przebiegach eksperymentu. Zaobserwowane zostały zbiory zmiennych stanowiące
„trzon” zestawów proponowanych przez różne przebiegi algorytmu w tych samych
krokach eksperymentu.
Alternatywny okres testów
Eksperyment został również powtórzony w innym okresie czasu. Tabela XII
przedstawia wyniki uzyskane przez testowane algorytmy w czasie 100 kolejnych dni
roboczych okresu 2002/08/01 – 2002/12/18. Różnica w wyniku algorytmu SNG w
stosunku do algorytmu KT pozostała na poziomie 15%, analogicznie do pierwszego
przebiegu podstawowego eksperymentu. Różnica w stosunku do algorytmów LS i
MACD wyniosła 7%. Bardzo dobry rezultat osiągnięty przez algorytm profetyczny
wynika z dużych wahań wartości indeksu w badanym okresie czasu.
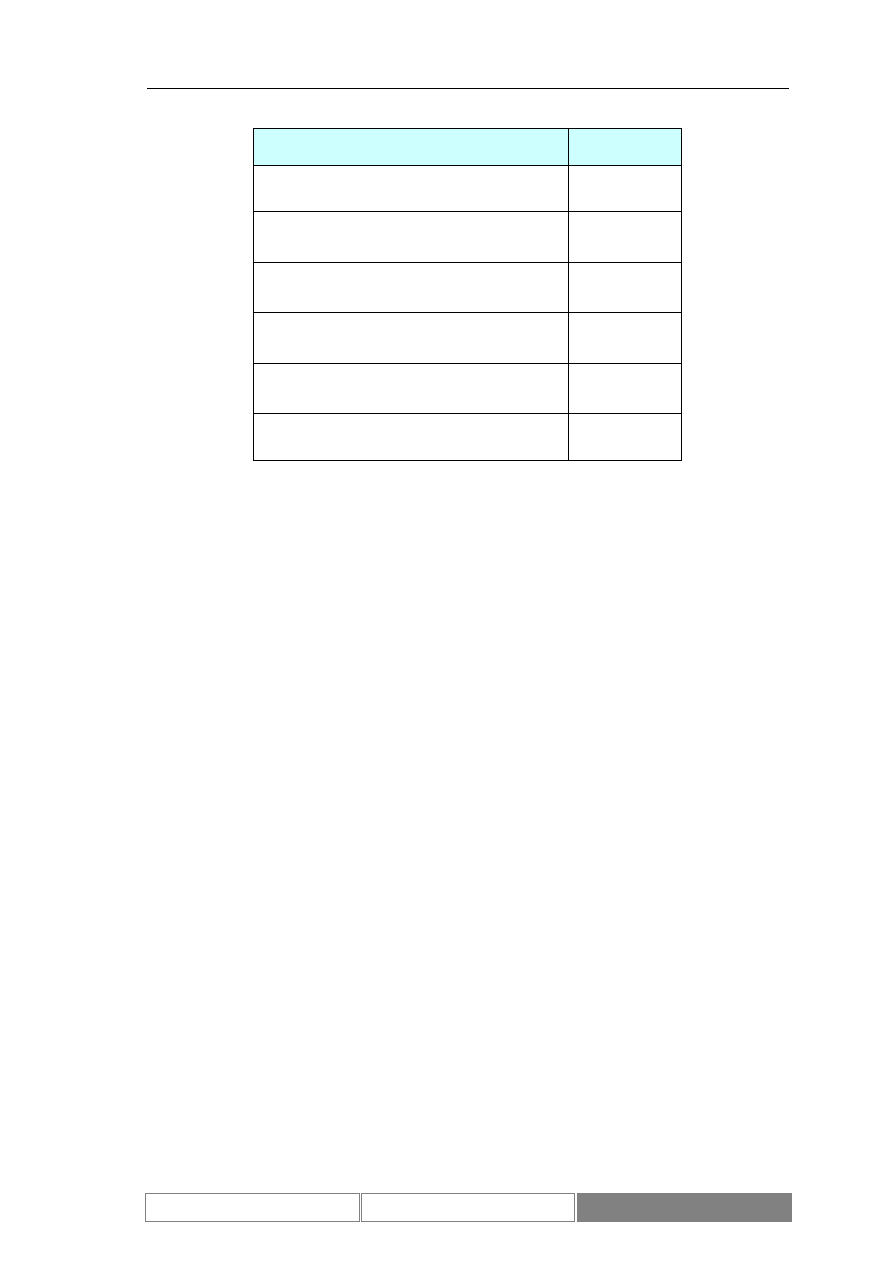
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
109
Teoria i zastosowania
Implementacja
Wyniki badań
Algorytm
Wynik [%]
Algorytm SNG (system neuro-genetyczny)
0.19
Algorytm LS (losowe sygnały)
−
7.14
Algorytm KT (kupuj i trzymaj)
−
15.21
Algorytm OZ (utrzymanie ostatniej zmiany)
−
26.45
Algorytm MACD (prognoza oscylatora MACD)
−
7.39
Algorytm PRF (profetyczny)
222.03
Tabela XII.
Wyniki dla algorytmów SNG, LS, KT, OZ, MACD, PRF w okresie 2002/08/01 – 2002/12/18
10.7.
Weryfikacja stabilności wyników
W
celu
oceny
stabilności
działania
systemu
neuro-genetycznego
przeprowadzone zostały dodatkowe badania. Przy zastosowaniu algorytmu SNG
inwestycje zostały przeprowadzone w okresach 100 dni przesuniętych w stosunku do
okresu testów z pierwotnego eksperymentu o 5, 10, 15 i 20 dni. Dzięki zachowaniu
stałej liczby dni inwestowania, wyniki poszczególnych eksperymentów mogą być ze
sobą bezpośrednio porównane. Policzone zostały procentowe różnice pomiędzy
wynikami osiągniętymi przy kolejnych przesunięciach w stosunku do wyniku dla
poprzedniego przesunięcia. Tabela XIII prezentuje zestawienie uzyskanych rezultatów.
Przy analizowanych 5-dniowych przesunięciach uzyskiwane wyniki różnią się
maksymalnie o 2.08% dla pojedynczego przesunięcia. Zmiana wyniku dla przesunięcia
łącznie o 20 dni w stosunku do pierwotnego eksperymentu wynosi
−
0.02%. Pokazuje
to stabilność wyników uzyskiwanych przez system neuro-genetyczny w kolejnych
krokach eksperymentu.
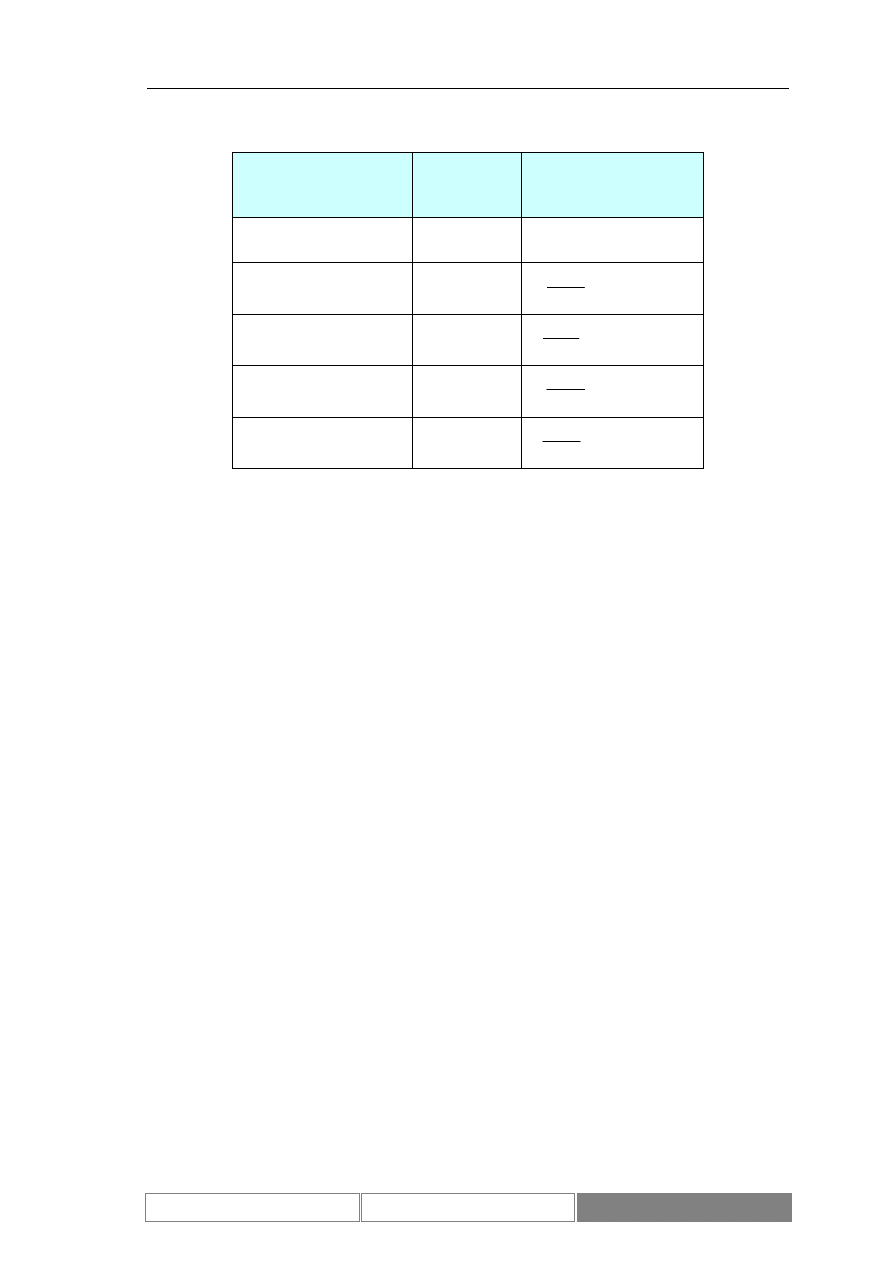
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
110
Teoria i zastosowania
Implementacja
Wyniki badań
Przesunięcie okresu
testów algorytmu SNG
Wynik
Różnica w stosunku do
poprzedniego wyniku
Brak przesunięcia –
pierwotny eksperyment
a=109 315,36
n.d.
Przesunięcie o 5 dni
b=110 076,75
%
100
a
b
a
−
= 0.70%
Przesunięcie o 10 dni
c=108 214,21
%
100
b
c
b
−
=
−
1.69%
Przesunięcie o 15 dni
d=110 467,53
%
100
c
d
c
−
= 2.08%
Przesunięcie o 20 dni
e=109 297,39
%
100
d
e
d
−
=
−
1.06%
Tabela XIII.
Zestawienie wyników algorytmu SNG dla okresu testu przesuniętego o 5, 10, 15 i 20 dni
w stosunku do pierwotnego eksperymentu
10.8.
Analiza uwzględnienia kosztów transakcji
Podstawowe założenia opisywanych badań nie pozwalają na bezpośrednie
zastosowanie ich wyników do rzeczywistego inwestowania na giełdzie. Między
innymi z powodu kosztów transakcji większe znaczenie ma prognoza
długoterminowa, która pozwala na inwestycje w dłuższym horyzoncie czasu.
Przeprowadzona została jednak analiza wpływu kosztów transakcji na wynik systemu
neuro-genetycznego w zdefiniowanym wcześniej modelu inwestycyjnym. Tabela XIV
zawiera zestawienie wyników uwzględniających wysokość kosztu transakcji. Koszt
obejmuje zarówno transakcje kupna jak i sprzedaży, zmniejszając dostępny budżet o
ustalony procent kwoty transakcji. Porównanie obejmuje koszty transakcji w
przedziale [0%,0.4%]. Do porównania wybrany został pierwszy przebieg algorytmu
SNG oraz pozostałe algorytmy wykorzystywane we wcześniejszych analizach. Dla
wszystkich analizowanych kosztów transakcji, algorytm SNG zachowuje istotną
przewagę nad algorytmami LS i OZ. Progiem kosztów transakcji, do którego algorytm
SNG zachował istotną przewagę nad pozostałymi algorytmami (poza PRF) jest 0.3%.
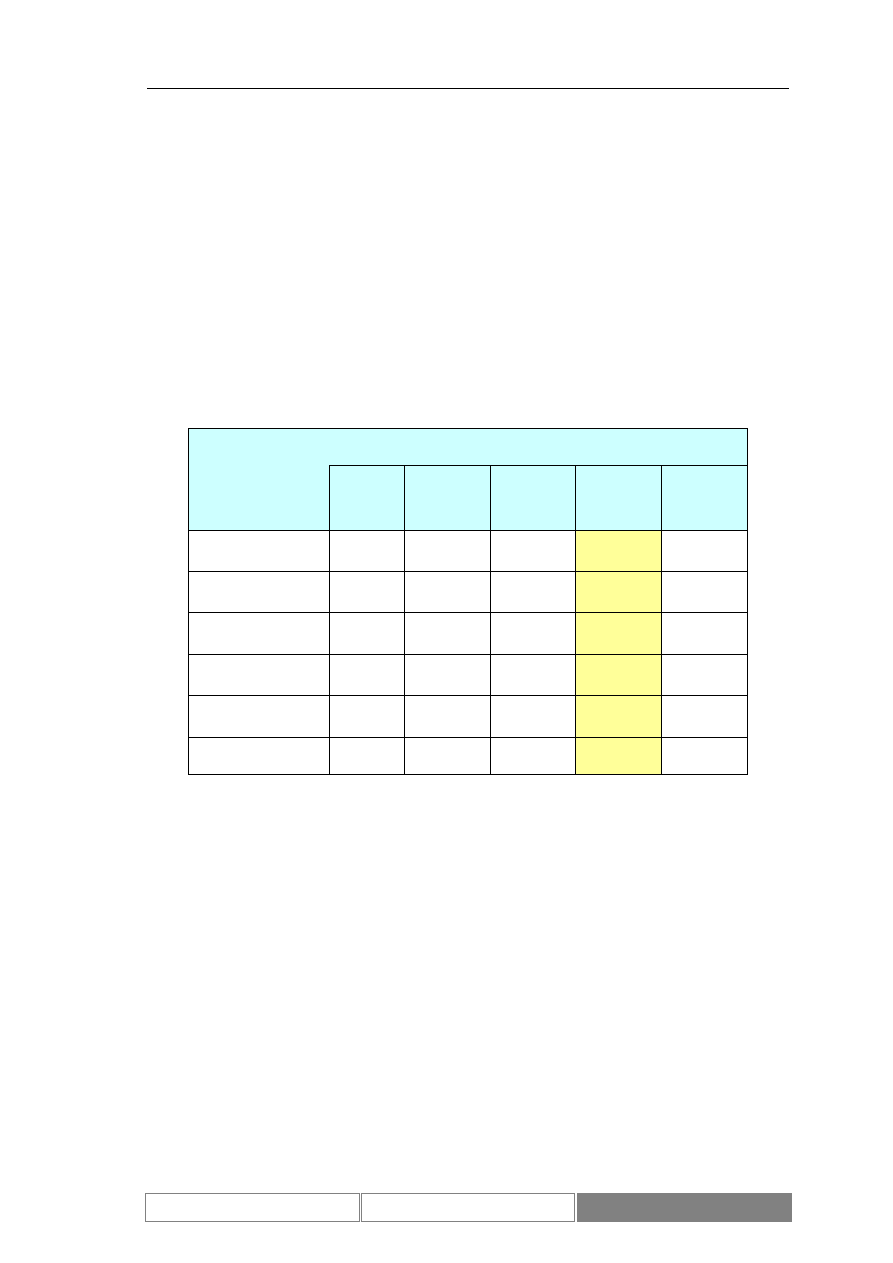
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
111
Teoria i zastosowania
Implementacja
Wyniki badań
Od wartości kosztu 0.3% algorytm SNG daje słabszy wynik niż algorytmy KT, MACD.
Należy pamiętać, że w modelu uwzględniającym koszty transakcji algorytm KT jest
uprzywilejowany, z racji uwzględnienia jedynie dwóch transakcji w całym procesie
inwestowania. Przewaga algorytmu MACD przy większych wartościach kosztu
transakcji wynika z czterokrotnie mniejszej liczby zrealizowanych transakcji (por.
Tabela IX, Rozdział 10.3). Różnica w wyniku działania algorytmu SNG i algorytmu
PRF maleje wraz z coraz większym kosztem transakcji. Tempo zmiany wynosi średnio
2% na każde 0.1% kosztu transakcji. Wynika to z większej liczby transakcji
zrealizowanych w czasie działania algorytmu PRF niż SNG.
Wynik [%]
koszt transakcji
algorytm
0%
0.1%
0.2%
0.3%
0.4%
Algorytm SNG
9.32
3.96
−
0.83
−
5.63
−
10.00
Algorytm LS
−
2.73
−
7.36
−
11.73
−
15.89
−
19.88
Algorytm KT
−
5.45
−
5.64
−
5.83
−
6.01
−
6.20
Algorytm OZ
−
8.00
−
12.48
−
16.98
−
21.25
−
25.17
Algorytm MACD
−
3.58
−
4.67
−
5.87
−
6.89
−
8.03
Algorytm PRF
39.56
32.12
24.98
18.21
12.03
Tabela XIV.
Wyniki z uwzględnieniem kosztów transakcji dla algorytmów SNG, LS, KT, OZ, MACD,
PRF

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
112
Teoria i zastosowania
Implementacja
Wyniki badań
11.
Podsumowanie i wnioski
W rozprawie zaproponowany został system neuro-genetyczny, którego celem
jest prognoza zmiany w ciągu jednego dnia wartości indeksu giełdowego DAX na
niemieckiej giełdzie GSE. System opiera się na zastosowaniu sieci neuronowych oraz
algorytmu genetycznego. Za pomocą przekształceń zdefiniowanych w analizie
technicznej wygenerowane zostały zmienne opisujące stan giełdy. Uwzględniona
została informacja nie tylko z prognozowanej giełdy, ale również z innych dużych
giełd światowych: japońskiej TSE (indeks NIKKEI) oraz amerykańskiej NYSE (indeks
DJIA). Z powodu dużej liczby możliwych do wykorzystania zmiennych oraz
nieznanych wprost zależności przyszłej wartości indeksu DAX od wartości
historycznych, zastosowany został algorytm genetyczny, którego zadaniem był wybór
podzbioru zmiennych dla jak najbardziej skutecznej prognozy. Zaproponowane
podejście neuro-genetyczne do prognozy przyniosło dobre wyniki, zweryfikowane
eksperymentalnie za pomocą hipotetycznego inwestowania na giełdzie. Uzyskany
został wynik o 13% lepszy od kolejnego najlepszego spośród testowanych algorytmów,
opartego na sygnałach generowanych przez oscylator MACD. Różnica w stosunku do
techniki inwestowania „kupuj i trzymaj” wyniosła 15%. Jednocześnie potwierdzona
została skuteczność proponowanej metody zarówno podczas trendu wzrostowego jak i
spadkowego. Analogiczne wyniki zostały uzyskane przy kilkukrotnym powtórzeniu
eksperymentu, w tym również dla innego, rozłącznego okresu czasu.
Wybór zmiennych do ostatecznej nauki i finalnej prognozy był wykonywany
przez algorytm genetyczny w sposób logiczny i skuteczny. Wyraźnie widoczne są stałe
preferencje zestawów zmiennych, które nie są wymieniane w kolejnych iteracjach.
Zostały one uznane przez algorytm genetyczny za ważne dla prawidłowej prognozy.
Natomiast zmienne, których wpływ na prognozę jest ograniczony w czasie są
zamieniane na inne, z dostępnej puli. Potwierdzona została użyteczność zmiennych
opisanych przez analizę techniczną, przede wszystkim oscylatorów. W zdecydowanej
większości kroków oscylatory wchodziły w skład zbioru wykorzystywanego w nauce
prognozy. Widoczne są również istotne statystycznie preferencje zmiennych z giełd
innych niż prognozowana. Postulowany w hipotezach badawczych (hipoteza 2) wpływ

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
113
Teoria i zastosowania
Implementacja
Wyniki badań
dużych giełd światowych oraz ogólnych wskaźników kursów walut znalazł
potwierdzenie w wyborach dokonywanych przez algorytm genetyczny.
Zauważone i przeanalizowane zostały również specyficzne dla danego
zastosowania cechy działania algorytmu genetycznego. Specyficzne zbiory zmiennych
zakodowanych w chromosomach oraz w konsekwencji ich ocena poprzez naukę i test
sieci skutkuje występowaniem tzw. martwych chromosomów. Są to osobniki, dla
których pomimo tego, że kodują syntaktycznie poprawne rozwiązanie, sieć neuronowa
nie jest w stanie nauczyć się prognozy. Oznacza to, że proponowany przez martwy
chromosom zestaw zmiennych jest bezużyteczny dla prognozy opartej o stosowane
algorytmy. Analiza częstości występowania w populacji martwych chromosomów
wykazuje, że są one skutecznie eliminowane w czasie pracy algorytmu genetycznego,
niezależnie od ich początkowej liczności.
Zmienność zależności w czasie między parametrami opisującymi giełdę a
prognozowaną wartością stanowiła wyjściowy postulat (hipoteza 1) oparty na
doświadczeniu
eksperckim,
wstępnie
potwierdzony
za
pomocą
analizy
współczynników korelacji. Na powyższym założeniu opiera się podstawowa idea
wykorzystania algorytmu genetycznego do dynamicznego doboru danych
wejściowych dla sieci neuronowej. Skuteczność tego podejścia została wykazana
poprzez analizę wyników osiągniętych przez algorytm wykorzystujący zestaw
zmiennych wskazany we wcześniejszym kroku. Różnica zysku z inwestycji w tym
porównaniu wynosi 6% na korzyść podstawowego systemu neuro-genetycznego.
Jednocześnie system wykorzystujący wcześniejszy zestaw zmiennych nadal wykazuje
pewną skuteczność w generowaniu sygnałów inwestycyjnych.
Zaproponowany system neuro-genetyczny stanowi zamknięcie spójnego etapu
badań objętych rozprawą doktorską. Koncepcja realizacji badań rozwijała się od
zastosowania prostych sieci neuronowych, poprzez sieci modularne uwzględniające
dużą liczbę zmiennych, do zastosowania algorytmu genetycznego w wyborze
zmiennych ze zbioru zbyt licznego do bezpośredniego zastosowania w sieci
neuronowej. W ostatnim etapie badań uwzględnione zostały zmieniające się zależności
pomiędzy zmiennymi opisującymi giełdę. W efekcie zaprojektowany został system

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
114
Teoria i zastosowania
Implementacja
Wyniki badań
dynamicznie dostosowujący się do charakteru bieżących danych. System działa w
sposób autonomiczny, nie wymagając manualnej modyfikacji parametrów jego pracy.
Rozwój techniczny systemu szedł w parze z poszerzaniem zakresu
wykorzystywanych danych. Zbiór dostępnych zmiennych zmieniał się od kilku
zmiennych opisujących prognozowaną giełdę, do szerokiego spektrum wskaźników
uwzględniających trzy międzynarodowe giełdy oraz kursy walut. Zaprojektowany
został algorytm wyznaczania formacji, które mają charakter subiektywnej analizy
kształtu wykresu wartości indeksu. Zwiększanie zbioru dostępnych zmiennych oraz
rozbudowa systemu podlegały wzajemnemu sprzężeniu zwrotnemu. Coraz większe
możliwości systemu pozwalały na uwzględnienie większej liczby zmiennych.
Zwiększający się zakres danych wymuszał nowe mechanizmy działania systemu w
celu ich skutecznego wykorzystania.
Kierunki dalszych badań obejmują dwa podstawowe elementy systemu.
Elastyczność działania algorytmu genetycznego pozwala na uwzględnienie zmiennych
wykraczających poza analizę techniczną. Szczególnie wartościowe może się okazać
dołączenie zmiennych o charakterze numerycznym z zakresu analizy fundamentalnej.
Pozwoli to na szersze spojrzenie na prognozowany rynek. Drugi kierunek rozwoju
może polegać na zastąpieniu wykorzystywanej sieci neuronowej alternatywnym
narzędziem do prognozy. Obiecującą propozycją jest tutaj metoda wektorów
wspomagających (SVM).
Oparcie zaproponowanego w pracy systemu neuro-genetycznego na trzech
głównych filarach: analizie danych, algorytmie genetycznym oraz uniwersalnym
narzędziu do prognozy umożliwia w przyszłości wielokierunkowy rozwój niniejszych
badań.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
115
Referencje
1.
Y. Baram, Partial Classification: The Benefit of Deferred Decision, IEEE
Transactions on Pattern Analysis and Machine Intelligence 20 1998, s. 769-776.
2.
N. Bauerle, U. Riedel, Technical Notes and Correspondence, IEEE Transactions
on Automatic Control 49 2004, s. 442-447.
3.
Y. Bengio, P. Frasconi, Input-Output HMM's for Sequence Processing, IEEE
Transactions on Neural Networks 7 1996, s. 1231-1249.
4.
Y. Bengio, V.-P. Lauzon, R. Ducharme, Experiments on the Aapplication of
IOHMMs to Model Financial Rreturns Series, IEEE Transactions on Neural
Networks 12 2001, s. 113-123.
5.
P. Bernstein, Intelektualna Historia Wall Street, WIG PRESS 1998.
6.
F. Black and M. Scholes, The Pricing of Options and Corporate Liabilities, J.
Political Economy 81 1973, s. 637-654.
7.
L. J. Cao, K. S. Chua, W. K. Chong, H. P. Lee, Q. M. Gu, A Comparison of PCA,
KPCA and ICA for Dimensionality Reduction in Suport Vector Machine,
Neurocomputing 55 2003, s. 321-336.
8.
L. Cao, F. Tay, Support Vector Machine with Adaptive Parameters in Financial
Time Series
Forecasting, IEEE Transactions on Neural Networks 14 2003, s.
1506-1518.
9.
E. Capobianco, Independent Component Analysis and Resolution Pursuit with
Wavelet and Bosine Packets, Neurocomputing 48 2002, s. 779-806.
10.
T. Chenoweth, Z. Obradovic, A Multi-component Nonlinear Prediction System
for the SP500 Index, Neurocomputing 10 1996, s. 275-290.
11.
Y. Cheung, L. Xu, Independent Component Ordering in ICA Time Series
Analysis, Neurocomputing 41 2001, s. 145-152.
12.
F.-L. Chung, T.-C. Fu, V. Ng, R. Luk, An Evolutionary Approach to Pattern-
Based Time Series Segmentation, IEEE Transactions on Evolutionary
Computation 8 2004, s. 471-489.
13.
H. Chung, J.-B. Kim, A Structured Financial Statement Analysis and the Direct
Prediction of Stock Prices in Korea, Asia-Pacific Financial Markets 8 2001, s. 87-
117.
14.
M. Costantino, R. Colligham, R. Morgan, R. Garigliano, Natural Language
Processing and Information Extraction: Qualitative Analysis of Financial News
Articles, Proceedings of the Conference on Computational Intelligence for
Financial Engineering 1997.
15.
M. Costantino, R. Colligham, R. Morgan, Qualitative Information in Finance:
Natural Language Processing and Information Extraction, NeuroVest Journal 4
1996.
16.
P. Coveney, R. Highfield, Frontiers of Complexity, The Search for Order in a
Chaotic World, Ballantine Book 1996.
17.
T. Cover, An Algorithm for Maximizing Expected Log Investment Return, IEEE
Transactions on Information Theory 30 1994, s. 369-373.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
116
18.
G. Deco, R. Neuneier, B. Schurmann, Non-parametric Data Selection for
Neural Learning in Non-stationary Time Series, Neural Networks 10 1997, s.
401-407.
19.
M. Dempster, T. Payne, Y. Romahi, G. Thompson, Computational Learning
Techniques for Intraday FX Trading Using Popular Technical Indicators, IEEE
Transactions on Neural Networks 12 2001, s. 744-754.
20.
W. Dębski, Rynek Finansowy i Jego Mechanizmy, PWN Warszawa 2005.
21.
A. Dorosz, M. Puławski, Giełdy pieniężne, w: Giełdy w gospodarce światowej,
W. Januszkiewicz (red.), PWE, Warszawa 1991.
22.
E. Erkip, T. Cover, The Efficiency of Investment Information, IEEE Transactions
on Information Theory 44 1998, s. 1026-1040.
23.
J. Fieldsend, S. Singh, Pareto Evolutionary Neural Networks, IEEE
Transactions on Neural Networks 16 2005, s. 338-354.
24.
E. Gately, Neural Networks for Financial Forecasting, John Wiley & Sons 1996.
25.
V. Gavrishchaka, S. Ganguli, Volatility Forecasting from Multiscale and High-
dimensional Market Data, Neurocomputing 55 2003, s. 285-305.
26.
R. Gencay, M. Qi, Pricing and Hedging Derivative Securities with Neural
Networks: Bayesian Regularization, Early Stopping, and Bagging, IEEE
Transactions on Neural Networks 12 2001, s. 726-734.
27.
T. Gestel, J. Suykens, D.-E. Baestaens, A. Lambrechts, G. Lanckriet, B.
Vandaele, B. De Moor, J. Vandewalle, Financial Time Series Prediction Using
Least Squares Support Vector Machnies Within the Evidence Framework, IEEE
Transactions on Neural Networks 12 2001, s. 809-820.
28.
M. Grzenda, B. Macukow, Evolutionary neural networks based optimization
for short-term load forecasting, Control and Cybernetics 31 no.2 2002, str. 371-
382.
29.
T. H. Hann, E. Steurer, Much Ado About Nothing? Exchange Rate Forecasting:
Neural Networks vs. Linear Models Using Monthly and Weekly Data,
Neurocomputing 10 1996, s. 323-339.
30.
J. V. Hansen, R. D. Nelson, Data Mining of Time Series Using Stacked
Generalizers, Neurocomputing 43 2002, s. 173-184.
31.
S. Hayward, The Role of Heterogeneous Agents Past and Forward Time
Horizons in Formulating Computational Models, Computational Economics 25
2002, s. 25-40.
32.
M. Heller, Początek Jest Wszędzie, Nowa Hipoteza Pochodzenia
Wszechświata, Prószyński i Spółka 2002.
33.
M. Jaruszewicz, J. Mańdziuk, Short Term Weather Forecasting with Neural
Networks, ICNNSC proceedings 2002a, s. 843-848.
34.
M. Jaruszewicz, J. Mańdziuk, Application of PCA Method to Weather
Prediction Task, ICONIP proceedings 2002b, s. 2359-2366.
35.
M. Jaruszewicz, J. Mańdziuk, One Day Prediction of NIKKEI Index
Considering Information From Other Stock Markets, ICAISC 2004, Lect. Notes
in Art. Int., s. 1130-1135.
36.
M. Jaruszewicz, J. Mańdziuk, Neuro-Genetic System for DAX Index Prediction,
EXIT 2006, s. 42-49.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
117
37.
G. John, P. Miller, R. Kerber, Stock Selection Using Rule Induction, IEEE
Expert 1996, s. 52-58.
38.
M. Kaboudan, Genetic Programming Prediction of Stock Prices, Computational
Economics 16 2000, s. 207-236.
39.
S. Kamitsuji, R. Shibata, Effectiveness of Stochastic Neural Network for
Prediction of Fall or Rise of TOPIX, Asia-Pacific Financial Markets 10 2003, s.
187-204.
40.
A. Kim, Ch. Shelton, T. Poggio, Modeling Stock Order Flows and Learning
Market-making from Data, MIT 2002.
41.
K. Kim, W. Lee, Stock Market Prediction Using Artificial Neural Networks with
Optimal Feature Transformation, Neural Computing & Applications 13 2004, s.
255-260.
42.
S. Kim, Time-delay Recurrent Neural Network for Temporal Correlations and
Prediction, Neurocomputing 20 1998, s. 253-263.
43.
V. Kodogiannis, A. Lolis, Forecasting Financial Time Series Using Neural
Network and Fuzzy System-based Techniques, Neural Computing &
Applications 11 2002, s. 90-102.
44.
K. Kohara, Y. Fukuhara, Y. Nakamura, Selective Presentation Learning for
Neural Network Forecasting of Stock Market, Neural Computing &
Applications 4 1996, s. 143-148.
45.
N. Kohzadi, M. S. Boyd, B. Kermanshahi, I. Kaastra, A Comparison of
Artificial Neural Network and Time Series Models for Forecasting Commodity
Prices, Neurocomputing 10 1996, s. 169-181.
46.
R. Kosiński, Sztuczne Sieci Neuronowe – Dynamika Nieliniowa i Chaos, WNT
2002.
47.
T. L. Lai, S. P.-S. Wong, Valuation of American Options via Basis Functions,
IEEE Transactions on Automatic Control 49 2004, s. 374-385.
48.
M. Last, Y. Klein, A. Kandel, Knowledge Discovery in Time Series Databases,
IEEE Transactions on Systems 31 2001, s. 160-169.
49.
LeBaron, Empirical Regularities From Interacting Long- and Short-Memory
Investors in an Agent-Based Stock Market, IEEE Transactions on Evolutionary
Computation 5 2001, s. 442-455.
50.
R. Lee, iJADE Stock Advisor: An Intelligent Agent Based Stock Prediction
System Using Hybrid RBF Recurrent Network, IEEE Transactions on Systems
34 2004, s. 421-428.
51.
A. Łachwa, Rozmyty Świat Zbiorów, Liczb, Relacji, Faktów, Reguł i Decyzji,
EXIT 2001.
52.
B. Malkiel, Błądząc po Wall Street, WIG PRESS 2003.
53.
M. Malliaris, L. Salchenberger, Using Neural Networks to Forecast the S\&P
100 Implied Volatility, Neurocomputing 10 1996, s. 183-195.
54.
R. Mantegna, E. Stanley, An Introduction to Econophysics. Correlations and
Complexity in Finance., Cambridge University Press 2000.
55.
J. Mańdziuk, Sieci Neuronowe Typu Hopfielda, Teoria i przykłady
zastosowań, EXIT 2000.
56.
J. Moody, M. Saffell, Learning to Trade via Direct Reinforcement, IEEE
Transactions on Neural Networks 12 2001, s. 875-889.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
118
57.
J. Murphy, Analiza Techniczna Rynków Finansowych, WIG Press, Warszawa
1999.
58.
M. Nałęcz, W. Duch, J. Korbicz, L. Rutkowski, R. Tadeusiewicz (red.),
Biocybernetyka i Inżynieria Biomedyczna 2000, tom 6, Sieci Neuronowe, EXIT
2000.
59.
W. O'Neil, Profit Maximizing and Price Distortion Minimizing Codes for a
Channel Model of an Asset Market, IEEE Transactions on Information Theory
41 1995, s. 2009-2014.
60.
D. Ormoneit, A Regularization Approach to Continuous Learning with an
Application to Financial Derivatives Pricing, Neural Networks 12 1999, s. 1405-
1412.
61.
S. Osowski, Sieci Neuronowe do przetwarzania informacji, OW PW 2000.
62.
T. Poddig, H. Rehkegler, A 'world' Model of Integrated Financial Markets
Using Artificial Neural Networks, Neurocomputing 10 1996, s. 251-273.
63.
M. Pring, Psychologia Inwestowania, Oficyna Ekonomiczna 2001.
64.
D. Rutkowska, M. Piliński, L. Rutkowski, Sieci neuronowe, algorytmy
genetyczne i systemy rozmyte, PWN 1997.
65.
D.Rutkowska, Inteligentne systemy obliczeniowe. Algorytmy i sieci
neuronowe w systemach rozmytych, Akademicka Oficyna Wydawnicza PLJ,
Warszawa 1997.
66.
E. Saad, D. Prokhorov, D. Wunsch, Comparative Study of Stock Trend
Prediction Using Time Delay, Recurrent and Probabilistic Neural Networks,
IEEE Transactions on Neural Networks 9 1998, s. 1456-1470.
67.
L. Shepp, A Model for Stock Price Fluctuations Based on Information, IEEE
Transactions on Information Theory 48 2002, s. 1372-1378.
68.
A. Shmilovici, Y. Alon-Brimer, S. Hauser, Using a Stochastic Complexity
Measure to Check the Efficient Market Hypothesis, Computational Economics
22 2003, s. 273-284.
69.
A. Sopoćko, Rynkowe Instrumenty Finansowe, PWN Warszawa 2005.
70.
F. Tay, L. Cao, Modyfied Support Vector Machines in Financial Time Series
Forecasting, Neurocomputing 48 2002, s. 847-861.
71.
S. Thawornwong, D. Enke, The Adaptive Selection of Financial and Economic
Variables for Use with Artificial Neural Networks, Neurocomputing 56 2004, s.
205-232.
72.
P. Tino, Ch. Schittenkopf, G. Dorffner, Financial Volatility Trading Using
Recurrent Neural Networks, IEEE Transactions on Neural Networks 12 2001, s.
865-874.
73.
N. Vandewalle, M. Ausloos, Ph. Boveroux, A. Minguet, How the Financial
Crash of October 1997 could have been predicted, The European Physical
Journal B 4 1998, s. 139-141.
74.
V. Vapnik, The Nature of Statistical Learning Theory, Springer 1995.
75.
V. Vapnik, Statistical Learning Theory, Wiley 1998.
76.
H. Walk, S. Yakowitz, Iterative Nonparametric Estimation of a Log-Optimal
Portfolio Selection Function, IEEE Transactions on Information Theory 48 2002,
s. 324-333.

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
119
77.
L. Xu, RBF Nets, Mixture Experts, and Bayesian Ying-Yang Learning,
Neurocomputing 19 1998, s. 223-257.
78.
J. Yao, C. Tan, A Case Study on Using Neural Networks to Perform Technical
Forecasting of Forex, Neurocomputing 34 2000, s. 79-98.
Źródła danych
1.
www.parkiet.com.pl - dane wykorzystane w przedstawionych eksperymentach
2.
www.bossa.pl - alternatywne źródło danych
3.
finance.yahoo.com - alternatywne źródło danych
4.
www.money.pl - alternatywne źródło danych
5.
www.economagic.com - płatne zbiory danych
6.
www.globalfinancialdata.com/index.php3 - płatne zbiory danych
7.
www.nber.org - dane makroekonomiczne
8.
neatideas.com/data/index.htm - dane makroekonomiczne
9.
www.nber.org/~freeman/wrps.html - dane socjologiczne
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
120
Załącznik A.
Lista i opis zmiennych
Nazwa zmiennej
Opis zmiennej
Skalowanie
value O
wartość otwarcia indeksu
tak
value C
wartość zamknięcia indeksu
tak
value L
wartość najmniejsza indeksu
tak
value H
wartość największa indeksu
tak
change O(%)
ostatnia procentowa zmiana wartości otwarcia
tak
close change (%)
ostatnia procentowa zmiana wartości zamknięcia
tak
10 days change (%)
procentowa zmiana wartości otwarcia w ciągu 10 dni
tak
20 days change (%)
procentowa zmiana wartości otwarcia w ciągu 20 dni
tak
5 days change (%)
procentowa zmiana wartości otwarcia w ciągu 5 dni
tak
pattern shifted
formacja
tak
type of pattern shifted
rodzaj formacji
tak
2 AVG's buy/sell signal
sygnał wygenerowany przez oscylator Dwie Średnie
nie
MACD buy/sell signal
sygnał wygenerowany przez oscylator MACD
nie
WILLIAMS buy/sell signal
sygnał wygenerowany przez oscylator Williams
nie
mov avg 10
średnia krocząca dla 10 dni
tak
mov avg 20
średnia krocząca dla 20 dni
tak
mov avg 5
średnia krocząca dla 5 dni
tak
impet 10
wartość oscylatora Impet z parametrem 10
tak
impet 20
wartość oscylatora Impet z parametrem 20
tak
impet 5
wartość oscylatora Impet z parametrem 5
tak
MACD
wartość oscylatora MACD
tak
MACD signal line
wartość linii sygnału MACD
tak
ROC 10
wartość oscylatora ROC z parametrem 10
tak
ROC 20
wartość oscylatora ROC z parametrem 20
tak
ROC 5
wartość oscylatora ROC z parametrem 5
tak
RSI 5
wartość oscylatora RSI z parametrem 5
tak
SO
wartość oscylatora Stochastycznego (SO)
tak
FSO
wartość oscylatora Szybkiego Stochastycznego (FSO)
tak
WILLIAMS
wartość oscylatora Williams
tak
DAY NO
numer dnia w tygodniu (pn.-nd.)
tak
Tabela XV.
Lista zmiennych wykorzystywanych w nauce prognozy

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
121
Załącznik B.
Zmienne wybierane w niezależnych przebiegach algorytmu genetycznego

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
122
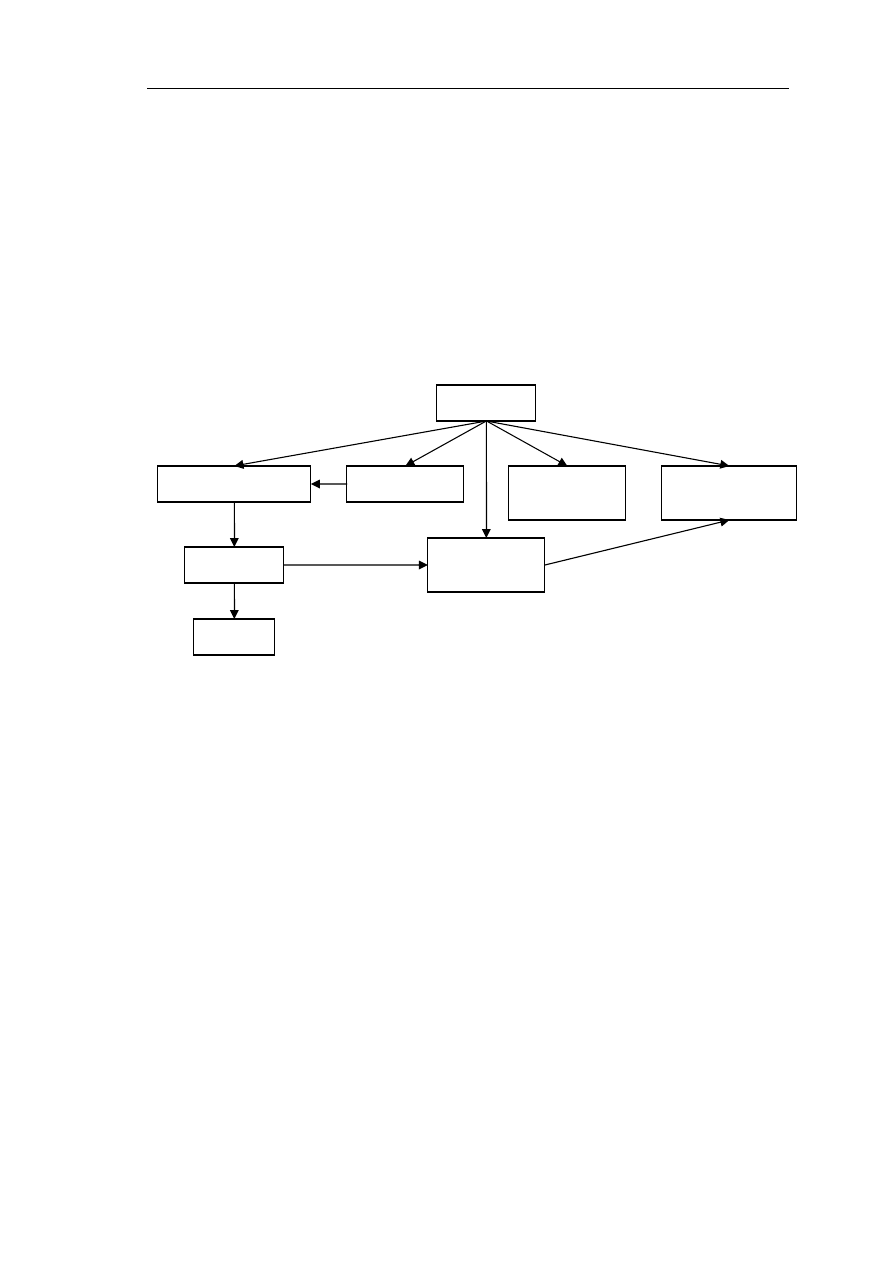
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
123
Załącznik C.
Aplikacja
System został zaimplementowany w języku c# pakietu MS Visual Studio 2000.
Obiektowość języka została wykorzystana do budowy klas odpowiadających
poszczególnym modułom systemu. Diagram 48 prezentuje model klas. Zaznaczone są
wywołania metod z innych klas (pokazany jest kierunek od klasy wywołującej do
wywoływanej metody).
Diagram 48.
Uproszczony model klas
Najbardziej czasochłonne obliczenia wykonywane w trakcie pracy algorytmu
genetycznego są realizowane w podziale na wątki. Liczba wątków jest ustalana przez
operatora.
Dzięki
temu
system
może
wykorzystać
moc
obliczeniową
wieloprocesorowych maszyn. Oprócz własnego obszaru pamięci wątki wykorzystują
obszar wspólny. Ogranicza to możliwość wykorzystania mocy farmy serwerów. Testy
przeprowadzane były na komputerze wyposażonym w procesor 3 GHz w technologii
HyperThreading, która daje dostęp do dwóch wirtualnych procesorów. W
przedstawionej konfiguracji pojedynczy krok eksperymentu (przygotowanie danych,
iteracje algorytmu genetycznego, nauka sieci neuronowej i test prognozy) trwa średnio
8 godzin. Czas pracy w dużej mierze zależy do liczby faktycznie wykonanych iteracji
algorytmu genetycznego.
Sieć neuronowa
Warstwa
Neuron
System
Chromosom
Operacje na
macierzach
Operacje na
plikach
Przekształcenia
danych
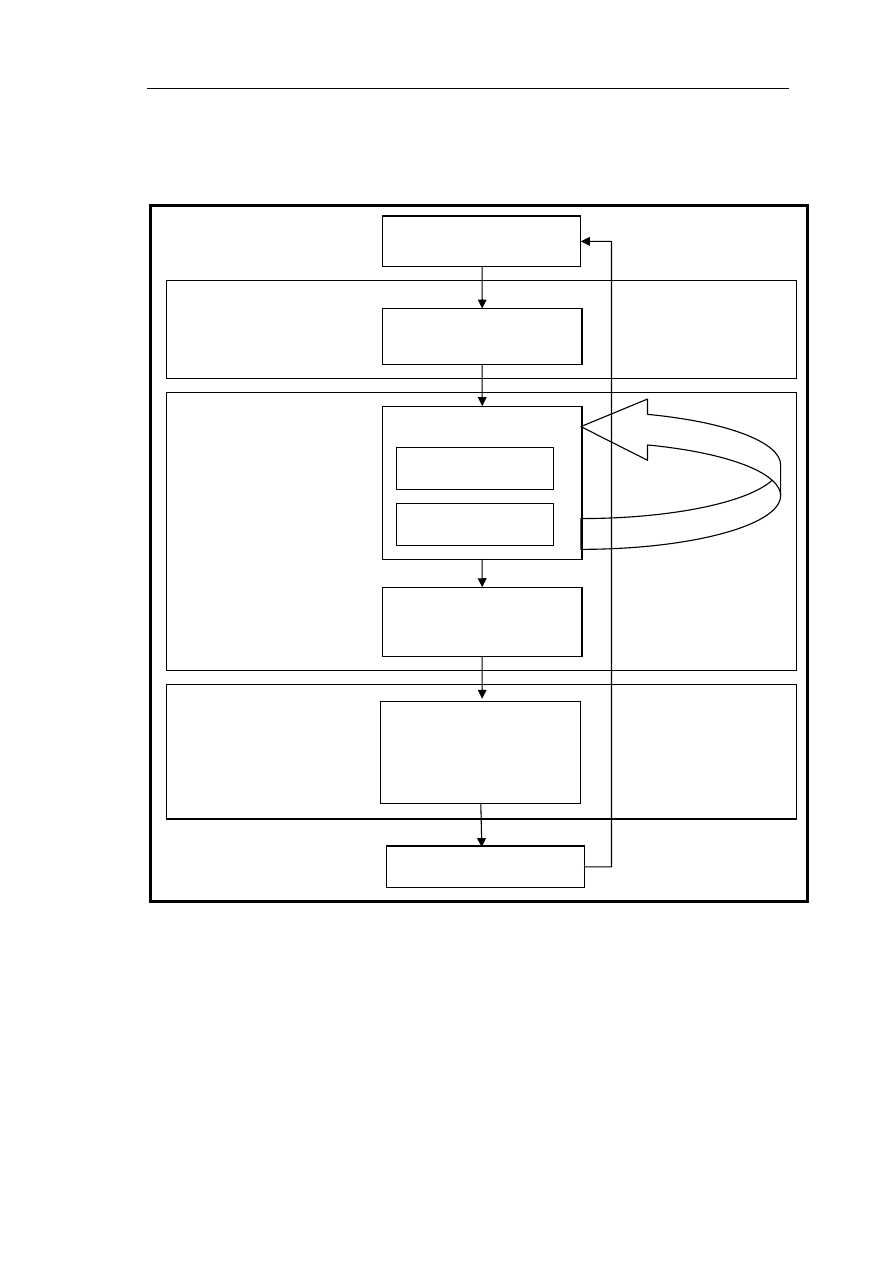
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
124
Poniżej znajduje się ogólny schemat blokowy systemu neuro-genetycznego.
Każdy z elementów został przedstawiony w Rozdziałach 4, 7.
Diagram 49.
Ogólny schemat działania systemu
Diagram 50 przedstawia model wywołań poszczególnych modułów i elementów
systemu wraz z informacją o przesyłanych zwrotnie danych. Model został ograniczony
do najważniejszych wywołań i danych w scenariuszu: przygotowanie danych,
uruchomienie algorytmu genetycznego, nauka sieci neuronowej, test sieci.
Sie
ć
Neuronowa:
Nauka
Test
Algorytm Genetyczny:
Znalezienie Najlepszego Osobnika
Wybór danych:
Wybór zmiennych dla AG
3. Modyfikacje populacji
Pokolenie P
Pokolenie P-1
1. Ustalenie
ś
rodowiska: okno
czasowe T
4. Wybór najlepszego osobnika
5. Ko
ń
cowa nauka wybranego
osobnika
6. Prognozy dla kolejnych 5 dni
okna
6. Nowe okno czasowe T = T+5
2. Wst
ę
pny dobór danych
wej
ś
ciowych
Przekształcenia
algorytmu
genetycznego
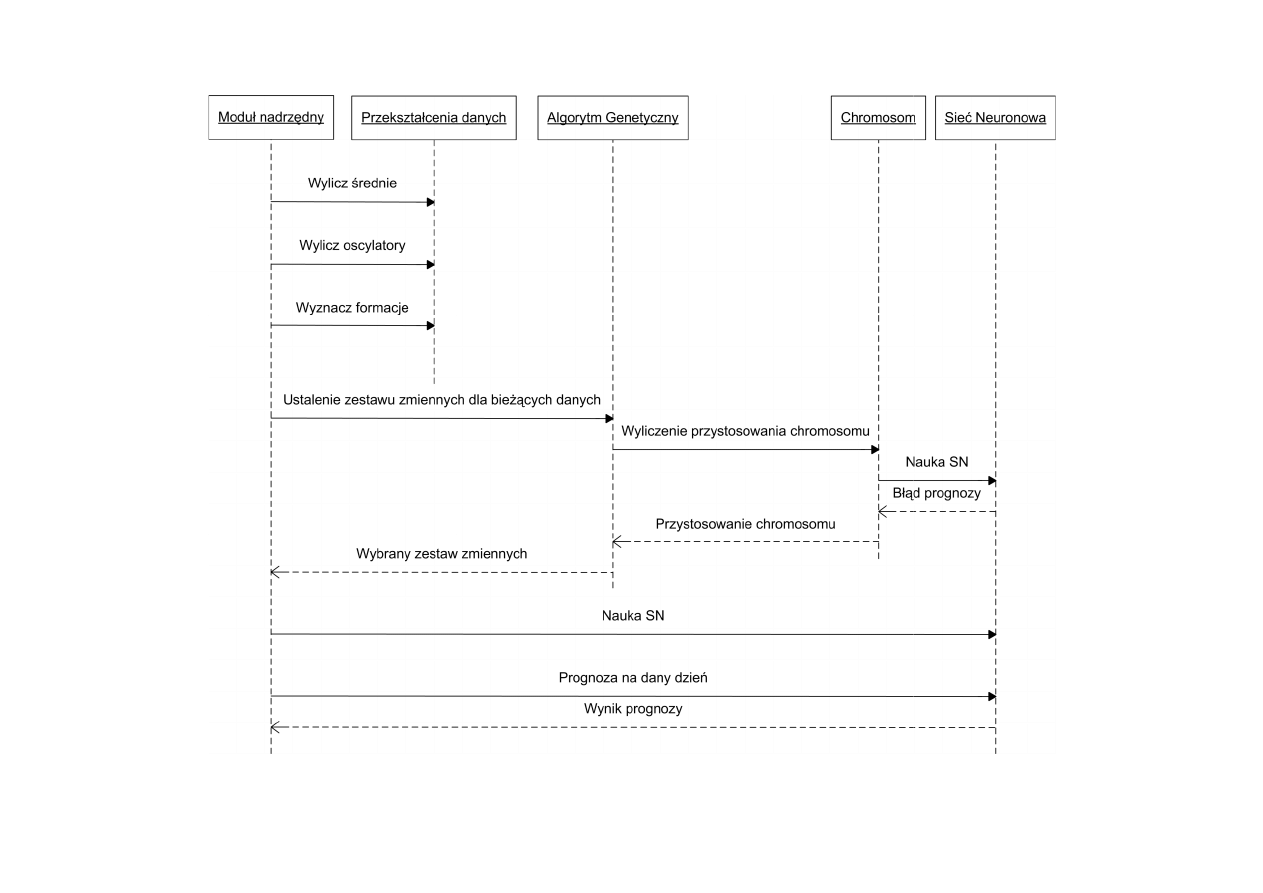

Diagram 50.
Uproszczony schemat przepływu danych
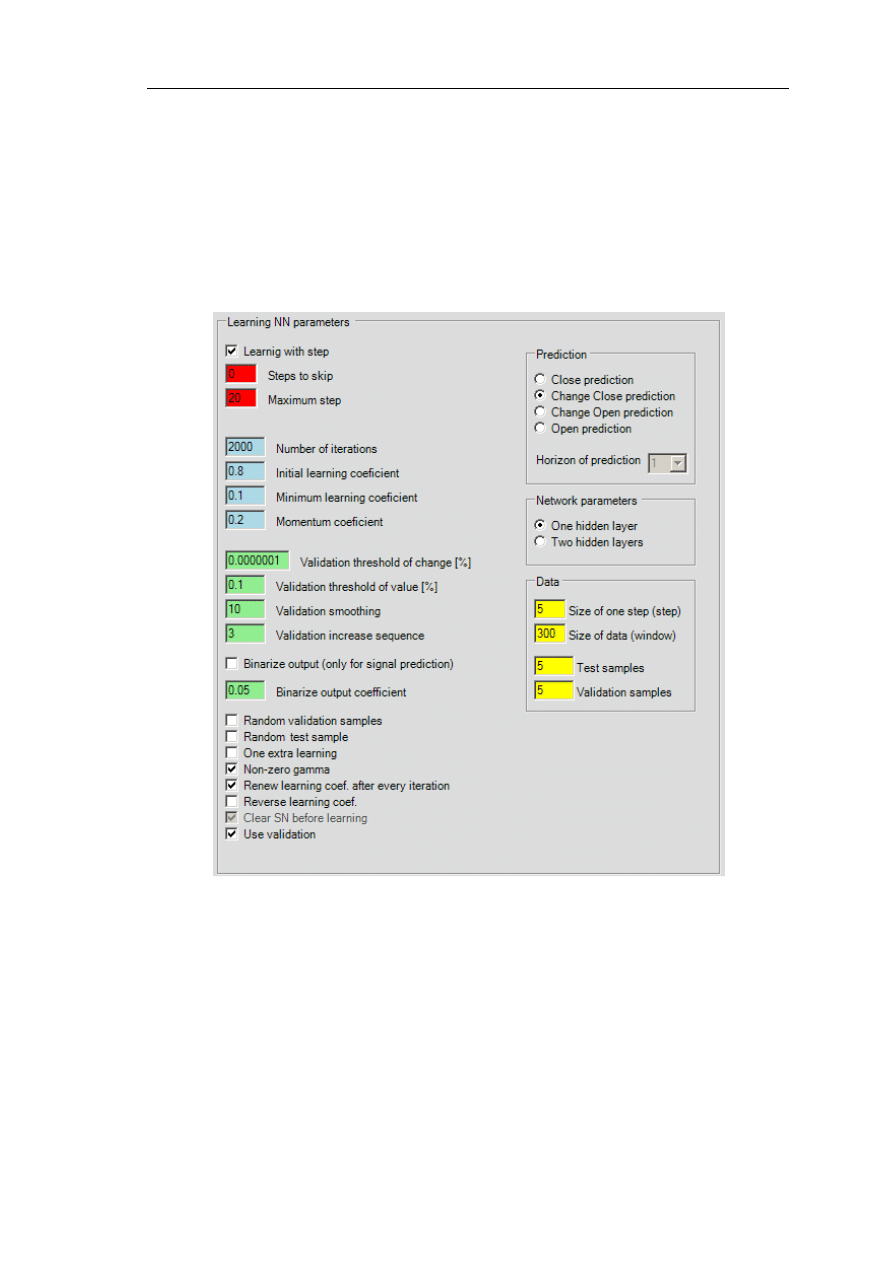
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
127
Kolejne dwa diagramy prezentują ekrany aplikacji do ustawiania parametrów
pracy sieci neuronowych oraz algorytmu genetycznego. Istotne z parametrów zostały
opisane w Rozdziale 8.3. Wszystkie parametry posiadają wartości domyślne.
Jednocześnie system udostępnia szereg predefiniowanych zestawów parametrów
odpowiadających przeprowadzanym eksperymentom.
Diagram 51.
Formularz wyboru parametrów nauki sieci neuronowej
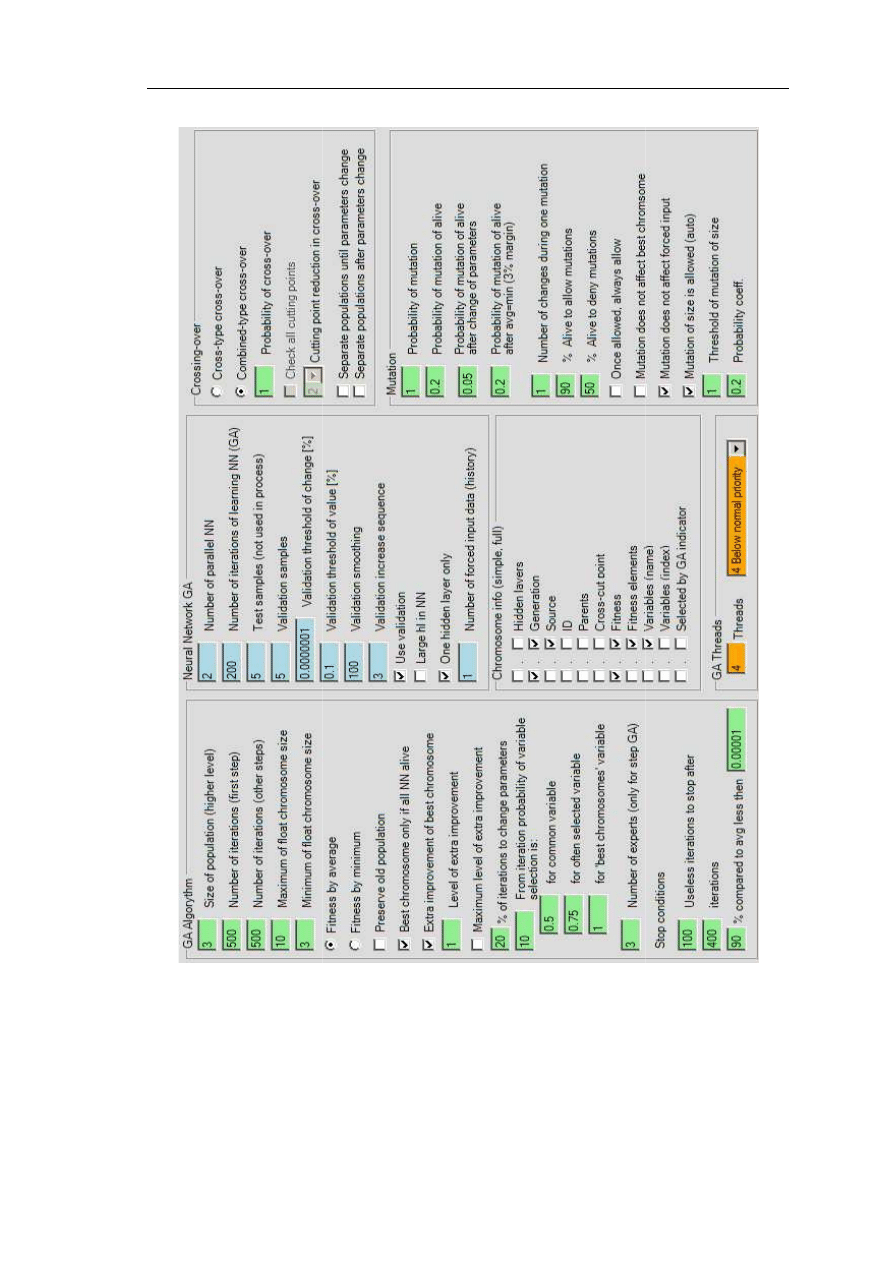
Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
Diagram 52.
Formularz wyboru parametrów działania algorytmu genetycznego
genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
Formularz wyboru parametrów działania algorytmu genetycznego
128
Formularz wyboru parametrów działania algorytmu genetycznego

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
129
Załącznik D.
Lista diagramów i tabel
Diagram 1.
Schemat działania systemu neuro-genetycznego ............................................................................................... 4
Diagram 2.
Świece japońskie – znaczenie poszczególnych elementów ............................................................................. 14
Diagram 3.
Wykresy liniowe – linie trendu (A, B), linie wsparcia (1) i oporu (2) ............................................................ 15
Diagram 4.
Formacje: głowa i ramiona, trójkąt ..................................................................................................................... 16
Diagram 5.
Formacje świecowe: zasłona ciemnej chmury (a), gwiazda wieczorna (b) ................................................... 17
Diagram 6.
Formacje świecowe: trójka hossy (a), trójka bessy (b) ...................................................................................... 17
Diagram 7.
Wartości indeksu DAX w okresie od 1995/01/30 do 2004/09/01 ..................................................................... 30
Diagram 8.
Wartości indeksu w okresie testowym od 2004/04/07 do 2004/08/26 ............................................................. 30
Diagram 9.
Dzienne zmiany wartości zamknięcia indeksu w okresie testowym od 2004/04/07 do 2004/08/26 ........... 31
Diagram 10.
Schemat krzyżowania jednopunktowego ......................................................................................................... 34
Diagram 11.
Model sieci neuronowej ....................................................................................................................................... 36
Diagram 12.
Model neuronu ..................................................................................................................................................... 37
Diagram 13.
Sigmoidalna funkcja aktywacja dla współczynnika β=10 i β=1 ...................................................................... 37
Diagram 14.
Model odwróconej sieci neuronowej w nauce metodą propagacji wstecznej............................................... 39
Diagram 15.
Kodowanie sygnałów kupna (wartości dodatnie) i sprzedaży (wartości ujemne) ...................................... 46
Diagram 16.
Działanie algorytmu wyznaczania formacji (S-szczyt, D-dno) ....................................................................... 48
Diagram 17.
Wartości indeksu oraz średnie 5-, 10-, 20-dniowe ............................................................................................ 53
Diagram 18.
Wartości oscylatorów MACD i Williams .......................................................................................................... 53
Diagram 19.
Wartości oscylatora Impet dla k=5, 10, 20 ......................................................................................................... 54
Diagram 20.
Wartości oscylatorów RSI, Stochastycznego (SO), Szybkiego Stochastycznego (FSO)................................ 54
Diagram 21.
Wartości oscylatora ROC dla k=5, 10, 20 (horyzont 50 dni) ............................................................................ 55
Diagram 22.
Korelacja między zmiennymi (współczynnik Pearson’a) ............................................................................... 57
Diagram 23.
Zmienność w czasie korelacji między zmianą ceny indeksu a oscylatorem MACD (okno 5 dni) ............. 58
Diagram 24.
Schemat krzyżowania iloczynowego ................................................................................................................. 62
Diagram 25.
Schemat wymiany chromosomów w procesie krzyżowania .......................................................................... 66
Diagram 26.
Podział rekordów w kolejnych krokach eksperymentu .................................................................................. 74
Diagram 27.
Rozmiary chromosomów w populacji przez kolejne iteracje – największy, średni, najmniejszy............... 80
Diagram 28.
Liczba mutacji rozmiaru w kolejnych iteracjach .............................................................................................. 81
Diagram 29.
Rozmiary najlepszych chromosomów wybieranych w 20 niezależnych krokach eksperymentu ............. 82
Diagram 30.
Liczba mutacji zmiennych w kolejnych iteracjach ........................................................................................... 83
Diagram 31.
Liczba osobników wymienionych w populacji w kolejnych iteracjach w wyniku krzyżowania ............... 84
Diagram 32.
Przystosowanie chromosomów w populacji przez kolejne iteracje – najgorsze (najwyższa linia),
średnie, najlepsze (najniższa linia). .................................................................................................................... 84
Diagram 33.
Średnie przystosowanie populacji (linia ciągła) na tle liczby mutacji rozmiaru (pionowe słupki) ............ 87
Diagram 34.
Wartości błędów prognozy dla trzech sieci neuronowych kodowanych przez najlepsze
chromosomy wybrane przez algorytm genetyczny w kolejnych 20 krokach eksperymentu ..................... 88
Diagram 35.
Wartości błędów prognozy dla trzech sieci neuronowych wszystkich chromosomów z populacji
w ostatniej iteracji pierwszego kroku eksperymentu ...................................................................................... 89
Diagram 36.
Liczba żywych chromosomów w poszczególnych iteracjach dla dwóch niezależnych populacji ............. 90
Diagram 37.
Średnie liczby wystąpień zmiennych prognozowanej giełdy we wszystkich chromosomach w
iteracjach: [0-100], [101-200], [201-300], [301-400] ............................................................................................. 92
Diagram 38.
Błędy sieci neuronowych dla rekordów walidacyjnych .................................................................................. 96
Diagram 39.
Rozkład błędów - kwadratowy (linia) i bezwzględny (słupki) ...................................................................... 97
Diagram 40.
Wyniki uzyskane przez algorytmy SNG, LS, MACD, KT, OZ ..................................................................... 100
Diagram 41.
Różnice wyników pomiędzy algorytmem SNG a pozostałymi algorytmami LS, KT, OZ, MACD,
PRF ....................................................................................................................................................................... 100
Diagram 42.
Wyniki algorytmów SNG, LS, KT, OZ, MACD przy trendzie malejącym .................................................. 101
Diagram 43.
Wyniki algorytmów SNG, LS, KT, OZ, MACD przy trendzie rosnącym.................................................... 102
Diagram 44.
Histogram wyników uzyskanych przez algorytm LS dla 10 000 prób ........................................................ 104
Diagram 45.
Podział rekordów dla kolejnych kroków eksperymentu z przesuniętym oknem czasowym. ................. 105
Diagram 46.
Wyniki inwestowania dla algorytmów KT, SNG, z-SNG (wykorzystanie zestawu zmiennych z
wcześniejszego kroku) ....................................................................................................................................... 106
Diagram 47.
Różnice wyników algorytmów SNG, z-SNG .................................................................................................. 107
Diagram 48.
Uproszczony model klas ................................................................................................................................... 123
Diagram 49.
Ogólny schemat działania systemu ................................................................................................................. 124
Diagram 50.
Uproszczony schemat przepływu danych ...................................................................................................... 126
Diagram 51.
Formularz wyboru parametrów nauki sieci neuronowej .............................................................................. 127
Diagram 52.
Formularz wyboru parametrów działania algorytmu genetycznego .......................................................... 128

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
130

Neuro-genetyczny system komputerowy do prognozowania zmiany indeksu giełdowego
131
Tabela I.
Charakterystyka zbioru wartości indeksu DAX ............................................................................................... 31
Tabela II.
Formacje zidentyfikowane w danych w okresie od 1995/01/30 do 2004/09/01 ............................................. 50
Tabela III.
Wspólne parametry algorytmu genetycznego i nauki sieci neuronowej ...................................................... 76
Tabela IV.
Średnie liczby zmian w populacji (o liczności 48 chromosomów) w wyniku działania
operatorów genetycznych ................................................................................................................................... 85
Tabela V.
Występowanie oscylatorów w kolejnych krokach eksperymentu ................................................................. 94
Tabela VI.
Wykorzystanie zmiennych z giełd oraz wskaźników kursowych ................................................................. 95
Tabela VII.
Wartości błędów prognozy ................................................................................................................................. 98
Tabela VIII.
Wyniki dla algorytmów SNG, LS, KT, OZ, MACD, PRF ................................................................................ 99
Tabela IX.
Liczby transakcji planowanych i zrealizowanych przez algorytmy SNG, LS, KT, OZ, MACD,
PRF ....................................................................................................................................................................... 103
Tabela X.
Własności statystyczne próbki 10 000 wyników uzyskanych przez algorytm LS ...................................... 104
Tabela XI.
Wyniki powtórzonych przebiegów algorytmu SNG ..................................................................................... 107
Tabela XII.
Wyniki dla algorytmów SNG, LS, KT, OZ, MACD, PRF w okresie 2002/08/01 – 2002/12/18 ................... 109
Tabela XIII.
Zestawienie wyników algorytmu SNG dla okresu testu przesuniętego o 5, 10, 15 i 20 dni w
stosunku do pierwotnego eksperymentu ........................................................................................................ 110
Tabela XIV.
Wyniki z uwzględnieniem kosztów transakcji dla algorytmów SNG, LS, KT, OZ, MACD, PRF ............ 111
Tabela XV.
Lista zmiennych wykorzystywanych w nauce prognozy ............................................................................. 120
Wyszukiwarka
Podobne podstrony:
Windows Vista brak dostępu do Indeksu wydajności systemu, KOMPUTER - SERWIS - EDUKACJA, 02 Windows V
Niektóre prawne aspekty włamań do systemu komputerowego
Windows 98 i Windows XP na jednym komputerze, Do Systemu, Instrukcje instalacji
Laboratorium z Architektury systemów komputerowych, Urządzenia do ręcznego wprowadzania danych klawi
Projekt realizacji prac prowadzących do naprawy systemu komputerowego mającego na?lu
Niektóre prawne aspekty włamań do systemu komputerowego
System operacyjny do nowego komputera napisać miała mała firma Microsoft z Seattle
Omów konfigurowanie komputera do pracy w sieci lokalnej lub globalnej w systemie Windows Vista
Projekt realizacji prac prowadzących do lokalizacji i usunięcia usterki systemu komputerowego zgłosz
1 Wprowadzenie do systemow komputerowych i Internetu
10 Reprezentacja liczb w systemie komputerowymid 11082 ppt
wyklad 2012 10 25 (Struktury systemów komputerowych)
Abstrakcyjne wyobrażenie elementów systemu komputerowego
Podstawy Informatyki Wykład V Struktury systemów komputerowych
Przytulia wonna, Botanika - Systematyka roślin do druku
Sit sztywny, Botanika - Systematyka roślin do druku
Opis oprogramowania wspomagające analizę komponentów systemu komputerowego, Prace kontrolne
więcej podobnych podstron